Adaptive Changes in Neuronal Synchronization in Macaque V4

Abstract

A fundamental property of cortical neurons is the capacity to exhibit adaptive changes or plasticity. Whether adaptive changes in cortical responses are accompanied by changes in synchrony between individual neurons and local population activity in sensory cortex is unclear. This issue is important as synchronized neural activity is hypothesized to play an important role in propagating information in neuronal circuits. Here, we show that rapid adaptation (300 ms) to a stimulus of fixed orientation modulates the strength of oscillatory neuronal synchronization in macaque visual cortex (area V4) and influences the ability of neurons to distinguish small changes in stimulus orientation. Specifically, rapid adaptation increases the synchronization of individual neuronal responses with local population activity in the gamma frequency band (30–80 Hz). In contrast to previous reports that gamma synchronization is associated with an increase in firing rates in V4, we found that the postadaptation increase in gamma synchronization is associated with a decrease in neuronal responses. The increase in gamma-band synchronization after adaptation is functionally significant as it is correlated with an improvement in neuronal orientation discrimination performance. Thus, adaptive synchronization between the spiking activity of individual neurons and their local population can enhance temporally insensitive, rate-based-coding schemes for sensory discrimination.

Introduction

Neuronal ensembles in many brain regions, including visual (Gray et al., 1989; Engel et al., 1991; Fries et al., 2001), auditory (Brosch et al., 2002), somatosensory (Cardin et el., 2009), motor (Murthy and Fetz, 1992), parietal cortex (Pesaran et al., 2002), prefrontal cortex (Buschman and Miller, 2007), and the hippocampus (Bragin et al., 1995), across a variety of species, including insects, mammals, and humans (Gray et al., 1989; Engel et al., 1991; Stopfer et al., 1997; Fries et al., 2001; Cardin et al., 2009; Pesaran et al., 2009), exhibit oscillations in the gamma frequency band (30–80 Hz). Synchronized neural activity in the gamma band has been hypothesized to play an important role in propagating information in neuronal networks by amplifying the responses of postsynaptic targets (Salinas and Sejnowski, 2000; Fries, 2005; Womelsdorf et al., 2006). Thus, gamma synchronization has been found to be critically involved in sensory processing (Gray et al., 1989; Engel et al., 1991; Fries, 2005; Cardin et al., 2009), grouping (Gray et al., 1989; Engel et al., 1991), attention (Fries et al., 2001; Taylor et al., 2005; Womelsdorf et al., 2006; Gregoriou et al., 2009; Chalk et al., 2010), working memory (Pesaran et al., 2009), and behavioral reaction times (Womelsdorf et al., 2006). However, whether a fundamental feature of individual neurons, such as their capacity to exhibit adaptive changes or plasticity, is influenced by gamma synchronization is unclear. Although EEG studies in humans have shown that certain forms of associative learning may be accompanied by gamma synchronization (Miltner et al., 1999; van Wingerden et al., 2010), whether and how synchrony between individual neurons and local population activity in sensory cortex is altered when neurons undergo adaptation or plasticity remains unclear. Recently, several studies have addressed the relationship between neuronal synchronization and adaptive cortical changes during learning and memory (Masquelier et al., 2009; Rutishauser et al., 2010; van Wingerden et al., 2010). However, these studies have focused on long-term forms of plasticity while ignoring plastic changes occurring at more rapid timescales.

We examined the impact of neuronal synchronization on feature coding in the context of rapid, adaptation-induced plasticity in macaque visual cortex (area V4). It has been shown that visual cortical neurons can exhibit plasticity of feature coding even after brief exposure (at the timescale of visual fixation) to a stimulus of fixed structure (Müller et al., 1999; Yao and Dan, 2001; Dragoi et al., 2002; Felsen et al., 2002; Gutnisky and Dragoi, 2008). Here, we demonstrate that, although rapid adaptation reduces the response magnitude of individual V4 neurons, it causes an orientation-specific increase in the synchronization between individual neuron responses and local population activity in the gamma frequency band. Moreover, this increase is correlated with an improvement in stimulus discrimination. Thus, contrary to expectation that gamma synchronization amplifies neuronal firing rates, we find that increased synchrony between neuronal and population activity is associated with a reduction in neuronal responses and an improvement in neuronal discrimination.

Materials and Methods

Behavioral paradigms.

Two male rhesus monkeys (Macaca mulatta) were trained to fixate a small spot (0.1°) presented on a video monitor placed at a distance of 57 cm from the monkey's eye. Monkeys were required to hold fixation within a 1° window throughout stimulus presentation to earn a juice reward; the trial was automatically aborted if fixation instability exceeded 0.25° at any time during stimulus presentation. Stimuli were presented on a CRT color monitor (Dell; 60 Hz refresh rate, running MATLAB and using Psychophysics Toolbox), positioned 57 cm in the front of the animal. All stimuli were static and consisted of 5 × 5° sine-wave gratings of 1.4 cycles/deg spatial frequency and 50% contrast level presented binocularly. Monkeys triggered the trial by holding a bar. After 300 ms of fixation, an adapting stimulus was flashed for 300 ms in the center of the receptive fields of the neurons. After a 100 ms blank, a 300 ms test stimulus of random orientation (eight equally spaced orientations spanning 0–180°; random spatial phase for each test orientation) was flashed at the same visual location. The adapting stimulus was either a 5 × 5° random dot patch consisting of dark dots on a gray background (control condition) or a sine-wave grating of identical spatial characteristics as the test stimulus, but fixed orientation (adaptation condition). Both the adaptor and test stimuli had the same mean luminance. Each test orientation was randomly presented 20 times in each of the control and adaptation orientation conditions (trials were randomly interleaved). Stimulus presentation and eye position monitoring was recorded and synchronized with neuronal data using the ECM (experiment control module) programmable device (FHC). Eye position was continuously monitored using an eye tracker system (EyeLink II; SR Research) that offers a binocular 1 kHz sampling rate. Eye position was calibrated before each experiment using a five-point calibration procedure in which the animal was required to fixate on each one of five points (one in the center, two in the vertical, and two in the horizontal axes or the diagonals) in steps of 4, 8, and 12° from the central fixation spot. The eye tracker gains were adjusted to be linear for the horizontal and vertical eye deflections. The fixation pattern was carefully analyzed to rule out any systematic bias and inconsistency during fixation when identical stimuli were presented under different conditions (control and adaptation). Microsaccades were analyzed every 10 ms by using a vector velocity threshold of 10°/s (this corresponds to a 0.1° eye movement between consecutive 10 ms intervals). To rule out any systematic bias and inconsistency during the control and adaptation conditions, we analyzed the eye position on the x- and y-axes, as well as the number and speed of microsaccades (these measures did not depend significantly on stimulus condition).

Single-unit recordings using multiple electrodes.

We used a standard Crist grid to advance microelectrodes (tungsten/glass, 1–2 MΩ at 1 kHz) transdurally through stainless-steel guide tubes into area V4 (identified using structural MRI). On each session, we advanced transdurally between four and eight microelectrodes into the surface of V4 (electrode penetrations were made between the lunate and superior temporal sulci; the minimal spacing between electrodes was 1 mm). The real-time neuronal signals from multiple channels (up to 32; simultaneous 40 kHz A/D conversion on each channel) were recorded using the Multichannel Acquisition Processor system (MAP; Plexon). Single-unit recordings were amplified, filtered, and viewed on an oscilloscope, and heard through a speaker. The spike waveforms were sorted when data acquisition was terminated using the off-line sorter program of Plexon. When a unit is isolated, its receptive field was mapped with a bar moved by hand or using reverse correlation while the animal maintained fixation. Receptive fields were recorded at parafoveal locations between 2 and 8 mm eccentricity. Recording sites were selected on the basis of the quality of the signal (signal-to-noise ratio) and their receptive field position. Since our experiments involved oriented stimuli, we rejected from the analysis those single units with an orientation selectivity index (Wörgötter et al., 1991; Dragoi et al., 2002) <0.1, in agreement with our previous experiments in V1 (Dragoi et al., 2002). As a measure of neuronal discrimination performance, we calculated the capacity of the neurons (d′) to discriminate between orientations within 22.5° of the preferred of the cell as the difference between the mean spike rates at the two nearby orientations divided by the root-mean-square SD (Green and Swets, 1966). These measures, mean firing rate and response SD, were calculated from the trial-by-trial mean responses during the entire 300 ms presentation of the test stimulus in each condition (control and adaptation). Mean d′ was calculated by averaging the d′ values obtained for each test orientation pair around the peak orientation, θ (i.e., θ − 22.5° and θ + 22.5°).

Local field potentials.

Real-time neuronal signals were recorded from multiple channels (up to 16 channels; 40 kHz A/D conversion on each channel) using the Multichannel Acquisition Processor system (MAP; Plexon). Low-frequency signals were prefiltered between 0.7 to 170 Hz, further amplified, and digitized at 1 kHz as local field potential (LFP) signals. To correct for the time delays induced in the LFP signals by the filters in headstages and preamplification boards, we used the software correction FPAlign provided by Plexon (http://www.plexon.com/downloads.html). LFPs were further filtered between 0.5 and 100 Hz using a fourth-order Butterworth filter. To remove line artifacts, we applied a digital notch at 60 Hz (fourth-order elliptic filter; 0.1 db peak-to-peak ripples; 40 db stopband attenuation). All filtering was applied by using forward and backwards filtering to obtain zero phase shifts. We discarded all LFPs that had more than three points outside the mean ± 4 SDs to avoid influence of irregular artifact noise from muscle activity or other sources. The amplitude of LFPs was measured in each trial by SD, peak–valley amplitude, or average voltage for specific periods of interest. We assessed whether LFPs are selective for orientation and whether adaptation affects LFP amplitude tuning by performing a trial-by-trial ANOVA test. We estimated the LFP power density during the presentation of the test stimuli and during the intertrial interval using sliding windows of ±150 ms length in steps of 10 ms. To obtain optimal spectral concentration (Mitra and Pesaran, 1999; Jarvis and Mitra, 2001; Pesaran et al., 2002; Womelsdorf et al., 2006), we used the multitaper method by multiplying each data epoch with the taper and then Fourier transformed. The power spectral density was normalized by dividing the average power spectrum during the 300 ms fixation period before the presentation of the adapting stimulus (averaged across all trials in a session). This helped balance the power spectrum between low and high frequency within same amplitude range (raw LFP power is domain at low frequency) and also made it possible to compare stimulus and adaptation driving component among recordings at different electrodes and brain activity status. We defined the average power of alpha, beta, and gamma bands as the mean power at frequencies between 8 and 13 Hz, 15 and 30 Hz, and 35 and 80 Hz.

To examine whether adaptation increases the coupling between the spike trains and LFPs, we calculated the spike-triggered average (STA) and spike-field coherence (SFC). The coherence between two signals is a complex quantity whose magnitude is a measure of the phase synchrony for a given frequency. We computed STA by averaging the LFP signal within a window centered ±150 ms on each elicited spike. To quantify STA, we calculate its power spectrum (i.e., the magnitude of all frequency components of the STA as a function of frequency). SFC was computed by dividing the power spectrum of the STA by the average of all power spectra of the LFP segments that were used to obtain the STA (Womelsdorf et al., 2006). Thus, SFC is independent of the firing rate of the single units and the power spectrum of the LFPs. SFC ranges from 0, lack of synchronization, to 1, perfect phase synchronization. We also assessed the temporal SFC spectrum by using windows of ±150 ms that were moved over the data in 10 ms steps from 100 ms before the onset of the adapting stimulus to 100 ms after the disappearance of the test stimulus. To eliminate bias caused by the finiteness of the data set, we computed the z-scored SFC values. Indeed, since coherence estimates have a positive bias that decreases with an increase in the amount of data, we applied a nonlinear, z transformation, to the coherence spectra using the following equation: z = β(q − β), where $\sqrt{-\left(V-2\right)*\log \left(1-|C{|}^2\right)}$, β = 1.15, C is the spike-field coherence, and V is number of degrees of freedom (cf. Jarvis and Mitra, 2001). Under null hypothesis, the z-transformed SFC value is distributed as a normal variate with variance equal to 1. The z-scored SFC indicates how many SDs the observed SFC differs from zero.

To test the statistical significance of SFC values, we used the bootstrap method. To this end, we counted the total number of spikes recorded under a specific condition (control or adaptation), and then randomly sampled the same number of LFP segments to calculate pseudo-SFC values. Pseudo-SFC was calculated 2000 times using random LFP sampling. The p value was the number of pseudo-SFC values greater than the experimentally derived SFC value (divided by 2000). An SFC value was considered significant if the bootstrap p value was <0.05. To eliminate the spike rate bias in the SFC calculation after adaptation, we computed the “balanced” SFC of paired conditions (for both control and adaptation). In the low firing rate condition (typically the adaptation condition), the balanced SFC value is the experimentally derived SFC value; in the high firing rate condition (typically the control condition), we randomly selected the same number of spikes as in the low firing rate condition to compute the balanced SFC value. To reduce sampling variability, we computed balanced SFC using 20 different random samplings, and then averaged the obtained SFC values.

Computational model.

The simulated neuronal network consisted of leaky integrate-and-fire (LIF) cells, with random, recurrent connections. Each cell received modulated background input in the gamma band at 60 Hz and background noise (Masuda and Doiron, 2007; Masuda, 2009). Membrane voltages therefore oscillated with increased power in the gamma band (Fries et al., 2001; Masuda, 2009; Schroeder and Lakatos, 2009). In the absence of a driving signal (stimulus), cells fired during each cycle with a small probability. Although individual cells fired irregularly, the 60 Hz background input was apparent in the spiking activity of the population (Brunel and Hakim, 1999). Each cell in the network received external input from a presynaptic pool of LIF neurons. Rapid adaptation was modeled by depressing the strength of both recurrent and external synaptic connections, and impacted the neuronal response, spike–LFP synchrony, and signal discrimination.

Each LIF neuron in the network received modulated, direct current input, and uncorrelated background noise (Burkitt, 2006). The membrane voltage of the ith neuron in the network was therefore described by the following:

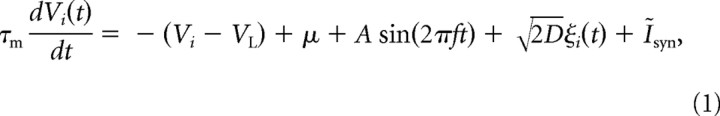with membrane time constant τ_m = 10 ms, and leak reversal potential V_L = −65 mV. Here, μ modeled the DC component of the background input, 1 ≤ i ≤ 50 represents the neuron number, and Ĩ_syn = R_mI_syn, the synaptic current multiplied by the total membrane resistance (Masuda, 2009). The stochastic component of the input, ξ_i(t), was assumed to be white and uncorrelated between cells, so that <ξ_i(t)ξ_j(t − τ)〉 = δ_ijδ(τ) (de la Rocha et al., 2007). When the membrane potential reached threshold V_T = −55 mV, an action potential was fired, the potential reset to V_T = −70 mV, and the cell entered a refractory period for τ_T = 2 ms.

The term Asin(2πft) modeled a background subthreshold voltage modulation due to rhythmic background activity reflected as increased power in the gamma band of the LFP. When μ = 3.975 mV and A = 2.435, in the absence of white noise, the voltage oscillated between −60.4 and −61.65 mV. The difference between the peak of the membrane voltage and the firing threshold was ΔV ≈ 5.4 mV. Background oscillations were therefore relatively weak, yet impacted the ability of cells to code information (Schroeder and Lakatos, 2009). In the presence of only white noise input (Ĩ_syn = 0), when D = 32.5 cells fired at frequencies between 0.2 and 0.6 Hz.

All cells received statistically identical excitatory external input. Within the postsynaptic network, the probability that one cell connected to another was p = 0.25. The total input to each cell is given by Ĩ_syn = Ĩ_net + Ĩ_ext, where Ĩ_net = α_netΣ_n1 Σ_m1 g_E^net S(t − t_n1,m1^net)(V − V_E) and Ĩ_ext = αΣ_n2 Σ_m2 g_E^net S(t − t_n2,m2^ext)(V − V_E) are inputs from recurrent connections and an external population, respectively. Here, V_E = 0 mV is the excitatory reversal potential, g_E^net and g_E^ext are synaptic strengths, t_n,m^net is the mth firing time of cell n in the population, and similarly with t_n,m^ext for external inputs. The synaptic interactions were modeled using α functions, so that S(t) = (t/τ)exp(1 − t/τ) when t > 0. The presynaptic population was modeled similarly using Equation 1, although the synaptic input, Ĩ_syn, was not modeled explicitly. Instead, we varied the presynaptic firing rate by changing μ.

In the above equation, the critical parameters are α_net and α. These parameters scale the strength of the input from the presynaptic pool (α) and the strength of the recurrent connections (α_net). These two parameters were changed to model short-term synaptic depression. In the absence of depression, α = α_net = 1, so that all inputs are at full strength. Therefore, 1 − α was used as a measure of depression strength. For simplicity, the depression of the recurrent connection between the postsynaptic cells was assumed to be proportional to the depression of inputs from the presynaptic pool [i.e., 1 − α_net = β(1 − α)]. In the control situation, the parameter α was in the range [0.85, 1]. After the presentation of an adapting stimulus, synapses were assumed to be transiently depressed, which we model by setting 0.6 ≤ α < 0.85 and 0.2 ≤ β ≤ 0.5.

The presynaptic population consisted of 200 cells. To bring the SFC values of the presynaptic pool within an acceptable range, some spikes in the presynaptic pool were jittered. This was done uniformly across trials so that the SFC of the upstream population was fixed around 0.36. The output of these cells was used to drive the postsynaptic population of 50 recurrently connected cells. After a brief transient (33 ms), the mean and variance of the firing rate of the postsynaptic cells were computed over a 300 ms time window (same window length used in the analysis of experimental data). Other parameters used in our simulation were g_E^ext = 0.00375, g_E^net = 0.068, τ = 1 ms, and β = 0.25. We used α = 0.85 and α = 0.65 in the control and adaptation conditions, respectively. The firing rates of the neurons in the presynaptic pool were chosen so that the firing rates of neurons in the postsynaptic pool were controlled over the range [10, 42] Hz.

Results

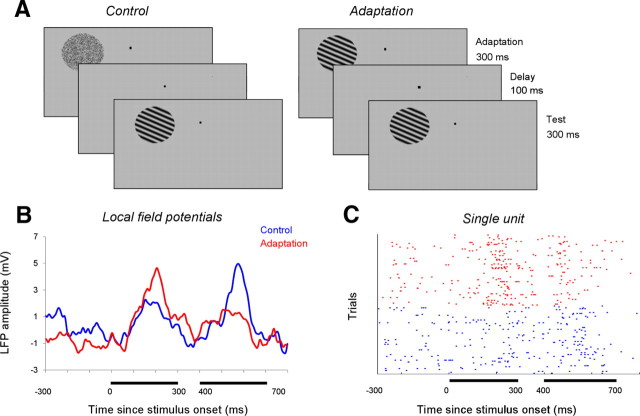
We simultaneously recorded spikes from single units and LFP signals from multiple V4 sites while monkeys fixated a small red spot (Fig. 1A). While animals fixated, an adapting stimulus was flashed in the center of the receptive field of the neurons for 300 ms. After a 100 ms blank, a test stimulus of random orientation (eight equally spaced orientations spanning 0–180°) was presented for 300 ms. The adapting stimulus was either a random dot patch (control condition) or a sine-wave grating with spatial characteristics identical with those of the test stimulus, but fixed orientation within 45° of the peak orientation of each cell (adaptation condition). The orientation range of the adapting stimulus was chosen based on our previous orientation adaptation experiments in V1 (Dragoi et al., 2002; Gutnisky and Dragoi, 2008), reporting strong effects on neuronal signaling when the adaptor is relatively close to the preferred orientation of the cell. Each test orientation was randomly presented 20 times in the control and adaptation conditions (control and adaptation trials were randomly interleaved). Figure 1, B and C, shows the responses at a typical pair of recording sites (spikes and LFP) during control and adaptation. The traces in Figure 1B show the time-locked mean LFP waveforms produced by the stimuli evoking an increase in the response to the adaptor (a 90° oriented grating in this example), as well as the test. In the control condition, the LFP signal is strongly modulated by stimulus orientation (the mean response to the oriented test stimulus is larger than the response to the random-dot adaptor). The example in Figure 1, B and C, shows a suppression of the mean response to the test stimulus following adaptation.

Figure 1.

Rapid adaptation in V4 neurons. A, Schematic description of the orientation adaptation protocol. After 300 ms of fixation, an adapting stimulus was presented for 300 ms as a random dot patch (control condition) or a sine-wave grating of fixed orientation (adaptation condition). After a 100 ms blank, the adapting stimulus was followed by a 300 ms test stimulus of random orientation. B, Example of LFP responses at one recording site in control (blue) and adaptation (red). The raw signal is low-pass filtered at 300 Hz, and the DC component is removed. Each set of lines represents the average response across all trials and test orientations in each condition (the adapting orientation is 45°). The horizontal lines mark the 300 ms time windows during which the adapting and test stimuli were presented. C, The raster plot represents the spike times of one V4 neuron responding to the adapting and test stimuli in the control (blue) and adaptation (red) conditions. For display purposes, the control and adaptation trials were grouped.

Overall, for the population of cells and LFP responses (n = 124), we found that adaptation significantly reduces peak firing rates and mean LFP power (p < 0.05, Wilcoxon's signed rank test) (Fig. 2). Indeed, we found that adaptation reduced the peak firing rates of the cells (Fig. 2A; measured at the peak orientation by averaging trial-by-trial responses throughout the presentation of the test stimulus). For small orientation difference ranges between the adapting stimulus and the peak orientation of the cell, neurons reduced their firing rate by ∼30% (measured at optimal orientation in the control condition). However, as the orientation difference increases the decrease in firing rate becomes smaller (20% or less).

Figure 2.

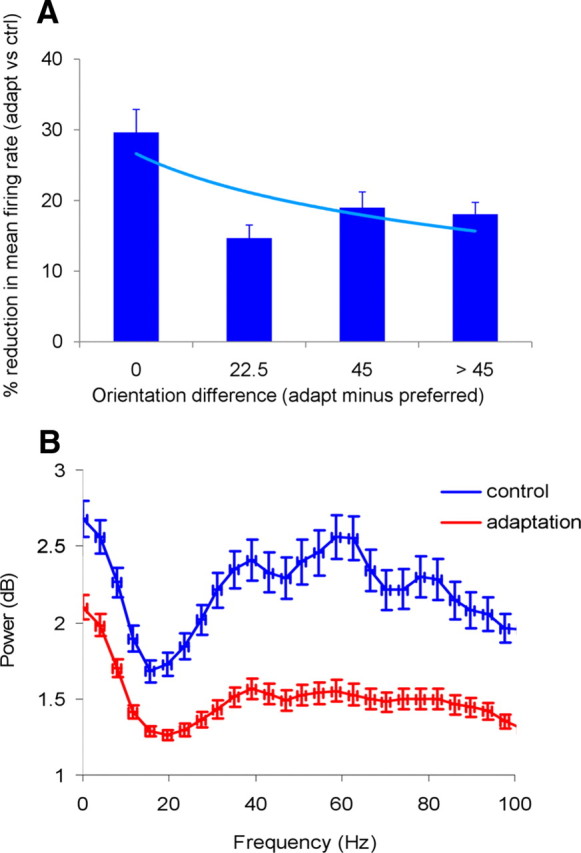
A, Adaptation-induced reduction in the response magnitude of V4 neurons as a function of the orientation difference between the adaptor and the preferred orientation of the cells. We analyzed the population of 124 cells adapted to a broad range of orientations. Cells were grouped in 22.5° bins based on the absolute difference between their preferred orientation and that of the adaptor (the numbers on the x-axis represent the lower bound of each bin; the last bin groups all the cells that prefer orientations at least 45° away from the adaptor). Adaptation reduces the peak firing rates of the cells measured at the peak orientation by averaging trial-by-trial responses throughout the presentation of the test stimulus. The firing rate reduction after adaptation is strongest when the adaptor is within 22.5° of the preferred orientation of the cells. The light blue line represents the exponential fit. B, Mean power spectral density during control and adaptation for the population of LFP responses. The power spectral density was normalized by dividing the log power in each trial by the average power spectrum during the 300 ms fixation period before the presentation of the adapting stimulus (averaged across all trials in a session). Adaptation decreases mean LFP power significantly in all frequency bands. Error bars represent SEM.

We next examined whether adaptation influences LFPs in specific frequency bands (Fig. 2B) by calculating the time–frequency power spectrum of the LFP responses (n = 124). The power was computed by considering the entire range of test orientations. The power spectral density was normalized by dividing the log power in each trial to the average power spectrum during the 300 ms fixation period before the presentation of the adapting stimulus (averaged across all trials in a session). This normalization is necessary to eliminate the contribution to the total power of slow fluctuations in ongoing activity. Overall, we found that adaptation decreases LFP power significantly in all frequency bands [p < 0.01 for each frequency band (i.e., alpha, beta, and gamma), Wilcoxon's signed-rank test].

Adaptation increases spike–LFP gamma synchronization

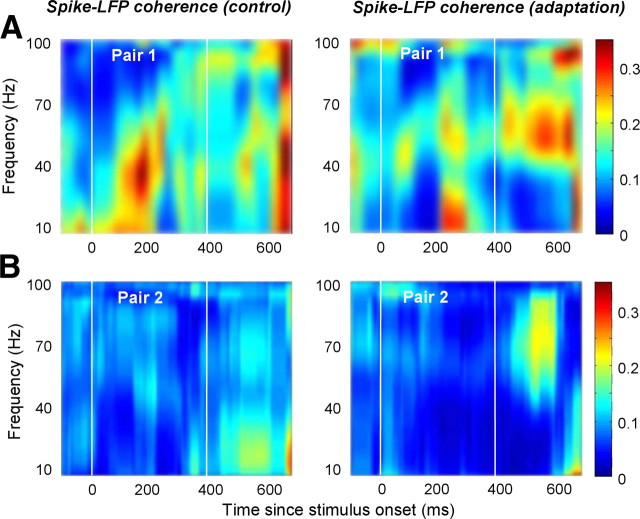
To examine the effect of adaptation on neuronal synchronization, we computed the SFC, which measures phase synchronization between spikes and LFPs at different frequencies (Fries et al., 1997, 2001); SFC varies between 0 and 1, and is insensitive to the reduction in overall LFP power and spike rate after adaptation. To compute SFC, we first obtained the STAs of the LFP responses (Murthy and Fetz, 1992) during the presentation of the test stimuli for 227 pairs of recording sites (only the signal pairs on different electrodes were analyzed) that exhibited significant response modulation by stimulus orientation (STA reflects the mean LFP signal associated with the spike of a neuron). Figure 3 shows representative examples of spike-field coherence from two pairs of recording sites during control and adaptation. Spike-field coherence was computed as a function of frequency and time and was averaged across trials in control and adaptation conditions (in each example, the adapting stimulus was within 45° of the peak orientation of each recording site, and test orientations were presented within 22.5° of the adapting orientation). In these examples, rapid adaptation caused an increase in gamma-band spike-field coherence in the interval in which the test stimulus was presented (i.e., ∼400 ms following the adaptor onset; because of the ±150 ms width of the analysis window, the time of the increase in gamma SFC cannot be precisely assessed). In contrast, spike-field coherence at lower frequencies was either unchanged or slightly decreased. These results were confirmed by analysis of data from all pairs of recording sites within 2 mm of each other (Fig. 4) to show that adaptation causes enhanced local gamma-band synchrony.

Figure 3.

Examples of spike–LFP coherence as a function of time. A, B, Spike-field coherence from two pairs of recording sites during control (left) and adaptation (right). The x-axis represents time relative to the onset of the test stimulus. The two vertical lines mark the times when the adapting and test stimuli are presented.

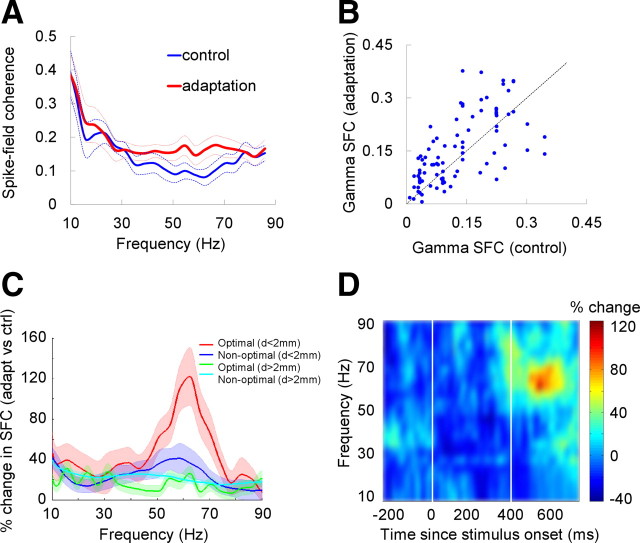
Figure 4.

Adaptation increases spike–LFP gamma synchronization. A, Mean control and adaptation spike–LFP coherence as a function of frequency for the entire population of pairs (located within 2 mm of each other). B, Scatter plot showing the mean spike–LFP gamma coherence (30–80 Hz) in control and adaptation for the same population of pairs shown in A. C, Adaptation increases gamma-band synchrony but does not significantly alter low-frequency synchronization. A significant increase in spike-field gamma coherence was observed only when both recording sites were located within 2 mm of each other and were stimulated within 22.5° of their optimal orientation. At lower frequencies, there is an apparent discrepancy between the mean SFC values shown in A and the percentage SFC change after adaptation. This discrepancy is explained by the large variance of SFC changes after adaptation at low frequencies (e.g., the same absolute change in small SFC control values will cause larger relative SFC changes than for larger control SFC values). The light ribbons represent the SEMs. D, Mean changes in spike–LFP coherence after adaptation for the population of nearby recording sites that were stimulated close to their preferred orientation (see C, red line). Adaptation causes a distinct peak in the gamma frequency range specifically during the presentation of the test stimulus. The x-axis represents time relative to the onset of the adapting stimulus. The two vertical lines mark the times when the adapting and test stimuli are presented.

We reasoned that, since LFPs are composed of extracellular voltage fluctuations including local excitatory and inhibitory intracortical inputs (Logothetis, 2003) originating from recording sites within 2 mm or less (Katzner et al., 2009), the effect of adaptation on SFC would be more pronounced when the recording sites are closer to each other. We thus divided our population of spike–LFP pairs based on whether the distance between the two recording sites is smaller or greater than 2 mm. We found (Fig. 4A,B) that, for nearby recording sites (<2 mm; n = 91; we have not included spike–LFP pairs recorded on the same electrode; including these pairs does not significantly change the magnitude of the postadaptation increase in gamma synchronization), adaptation increases the synchronization of V4 neurons in the gamma band (mean increase in SFC after adaptation is 48%; p < 0.01, Wilcoxon's signed-rank test). Importantly, for nearby recording sites (<2 mm), adaptation increased the number of spike–LFP pairs that exhibited significant gamma-band synchronization (α = 0.05; control, 62.5% pairs; adaptation, 73.2% pairs; bootstrap method). Adaptation caused statistically nonsignificant changes in low-frequency synchronization (in the theta, alpha, and beta frequency bands; p > 0.2 for all comparisons, Wilcoxon's signed-rank test). Importantly, for nearby recording sites (<2 mm), adaptation increased the number of spike–LFP pairs that exhibited significant gamma-band synchronization (α = 0.05; control, 62.5% pairs; adaptation, 73.2% pairs).

Although SFC should be insensitive to the mean firing rate of the cell (according to its definition), it is possible that extremely low spiking cells may lead to SFC values that are biased toward high synchronization levels. To control for this possibility, we calculated the z-scores of SFC values in control and adaptation (Jarvis and Mitra, 2001) by calculating the expected SD of the coherence distribution given the number of degrees of freedom (i.e., the number of spikes * number of tapers), and then transforming the measured coherence to the rate to this SD. We found that, even when we compared the z-scored coherence values, gamma SFC was significantly elevated after adaptation (p < 0.01, Wilcoxon's sign-ranked test). Furthermore, to eliminate the spike rate bias in the postadaptation SFC calculation, we computed the “balanced” SFC (see Materials and Methods) for both the control and adaptation conditions. Consistent with our main result, we found that adaptation increases the balanced median gamma SFC by 50.78% (p < 0.04, Wilcoxon's sign-ranked test).

The postadaptation increase in spike-field gamma coherence was observed only when both recording sites were stimulated with test stimuli near the preferred orientation [within 22.5° of the peak orientations (Fig. 4C); the mean percentage change in SFC has been calculated by computing the percentage SFC change in adaptation vs control for each spike–LFP pair, and then averaging the calculated percentages to obtain the mean coherence values]. Nonoptimal test orientations (at least 45° difference between the stimulus orientation and the peak orientation at each recording site) drastically reduced the spike rate, LFP amplitude, and SFC in the control condition, without an accompanying increase in spike-field gamma coherence after adaptation (p > 0.1, Wilcoxon's signed-rank test). Importantly, for pairs of electrodes located at distances >2 mm, the postadaptation changes in spike-field coherence were statistically nonsignificant regardless of stimulus orientation (p > 0.1, Wilcoxon's signed-rank test). We have also performed a temporal analysis of the mean changes in spike–LFP coherence after adaptation for the population of nearby recording sites that were stimulated close to their preferred orientation (that contributed to Fig. 4C, red line). As shown in Figure 4D, adaptation causes a distinct peak in the gamma frequency range specifically during the presentation of the test stimulus (p < 0.01, Wilcoxon's signed-rank test). Together, these results are consistent with the idea that low-frequency extracellular voltage fluctuations measured by LFPs reflect changes in local population activity and that most neuronal connections are local (Logothetis, 2003; Katzner et al., 2009).

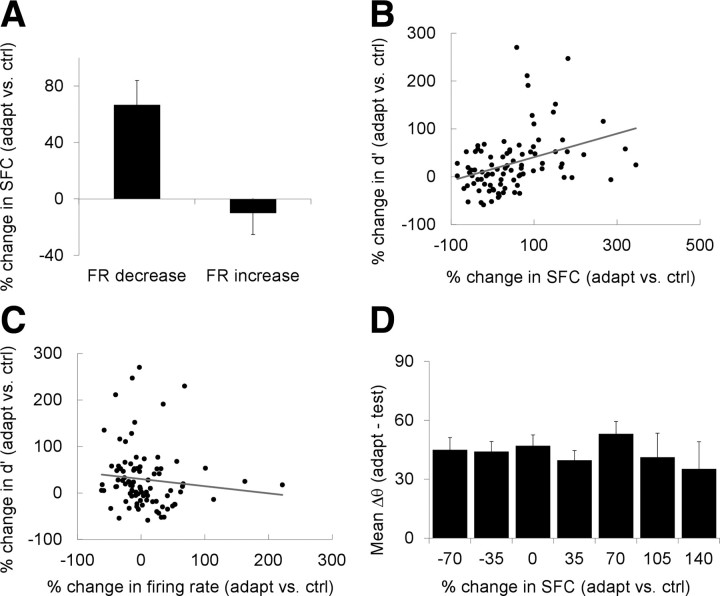
Contrary to the idea that gamma synchronization is accompanied by an increase in neuronal firing rates, we found that, after adaptation, the increase in spike-field gamma coherence is associated with a statistically significant decrease in neuronal responses (Fig. 5A). Thus, for each neuron, we averaged the changes in spike–LFP coherence after adaptation by pooling all of the recording sites stimulated with optimal orientations and located within 2 mm of each other (Fig. 4C, red line). By examining the relationship between the changes in spike–LFP coherence after adaptation and the changes in mean firing rates at the same orientations for which we calculated gamma coherence, we found that those neurons exhibiting a statistically significant decrease in firing rate also showed an increase in gamma synchronization (Fig. 5A) (p < 0.0001), whereas the cells exhibiting an increase in firing rate showed no change in gamma synchronization (p > 0.3; between the two groups of cells, the postadaptation change in mean spike-field coherence was highly significant, p < 0.00005). In light of previous reports that gamma synchronization in V4 is accompanied by an increase in firing rates (Fries et al., 1997, 2001; Fries, 2005), this result is interesting.

Figure 5.

Relationship between gamma synchronization after adaptation and neuronal discrimination performance. A, The increase in spike-field gamma coherence is associated with a statistically significant decrease in neuronal responses after adaptation. B, The postadaptation change in gamma synchronization impacts the ability of the neurons to discriminate stimulus orientation. There is a positive correlation between the change in spike-field gamma coherence after adaptation and the change in neuronal discriminability (d′). The gray line represents the linear regression fit. C, Relationship between the change of neurons in firing rate after adaptation and the changes in discrimination performance (d′). D, Relationship between the change in spike-field coherence after adaptation (ΔSFC) and the orientation difference between the test orientations used in d′ calculation and the adapting stimulus (Δθ). We calculated the mean difference between the two test orientations and the adapting stimulus (Δθ) across the cells in each ΔSFC bin. In all panels, the numbers on the x-axis represent the upper bound of the interval used in binning the data. Error bars represent SEM.

The fact that the increase in SFC peaks around the refresh rate of the monitor (60 Hz) might constitute a potential problem. To rule out this confound, we used a 60 Hz notch filter (see Materials and Methods) designed to eliminate the 60 Hz noise from our LFP signal. Nonetheless, if spike–LFP coherence was contaminated by 60 Hz oscillations due to the monitor refresh rate, we would have seen a distinct, significant, 60 Hz peak in spike-field coherence in all the conditions that were tested. However, we failed to observe a gamma-band increase in spike-field coherence at 60 Hz when test stimuli were nonoptimal or when the distance between electrodes was >2 mm (compare Fig. 4C). To ensure that 60 Hz noise is not an issue in our experiments, we computed the mean normalized autocorrelation function for the entire population of cells that clearly shows the absence of a 60 Hz peak. In addition, the mean power spectrum for our population of spike trains also reveals the absence of a 60 Hz component that is significantly different from the power at other frequencies (power has been computed during the presentation of the 300 ms test stimulus; error bars represent SD; p > 0.1). The cross-correlation between the monitor 60 Hz refresh pulses and spikes and LFPs for our entire population also does not show a signature of locking.

Another possible confound in our study is attention, which may potentially have contributed to an increase in gamma synchronization after adaptation. Indeed, attention has been previously found to increase neuronal responses and gamma synchrony in V4 (Fries et al., 1997, 2001). However, the fact that (1) all stimuli were presented during passive fixation, (2) the presentation of adapting and test orientations was randomized, and (3) the increase in gamma synchrony is orientation dependent rules out attention as a significant factor. Indeed, if monkeys allocated more attention in trials in which the adapting stimulus was an oriented grating, we would have expected an increase in gamma synchrony (with respect to the control condition) after stimulation to all test orientations, not only to specific orientations (Fig. 3C). However, the increase in gamma coherence after adaptation was observed only when the test orientations were presented near the peak orientation of the cells (Fig. 4C). We also failed to find a statistically significant relationship between the horizontal/vertical saccade amplitude and frequency and stimulus condition (control vs adaptation; p > 0.2, Wilcoxon's signed-rank test for all comparisons). In addition, we failed to find a significant relationship between horizontal and vertical microsaccade amplitude and frequency and the postadaptation increase in spike-field gamma coherence (p > 0.2, Wilcoxon's signed-rank test for all comparisons). Together, these arguments indicate that the postadaptation increase in gamma coherence is unlikely to have been contaminated by attention and/or fixational eye movements.

Relationship between gamma synchronization and neuronal discriminability

We further examined whether the increase in gamma spike–LFP synchronization after adaptation impacts the coding of sensory information by V4 neurons. Gamma synchronization has often been hypothesized to modulate firing rates via precise spike synchronization among local excitatory neurons, and to subsequently influence visual behavior, such as perceptual binding or behavioral responses. However, apart from increased firing rates, there has been little experimental evidence for the impact of spike–LFP gamma synchronization on the capacity of a neuron to encode information. We thus investigated whether the ability to discriminate stimulus orientation, a ubiquitous property of visual cortical neurons, is influenced by the postadaptation change in the degree of synchrony between individual neurons and their local population. Although adaptation has been shown to increase neuronal discriminability (Müller et al., 1999; Dragoi et al., 2002; Felsen et al., 2002), whether this phenomenon may be related to gamma synchronization has not been examined. We reasoned that an increase in spike-field gamma coherence after adaptation (ΔSFC > 0) would allow an efficient summation of action potentials, which, in conjunction with the adaptation-induced suppression in response variance, would increase the ability of the neurons to discriminate orientation.

This issue was addressed by examining the relationship between ΔSFC and the changes in the capacity of a neuron (d′) (Green and Swets, 1966) to discriminate nearby orientations (22.5° apart). Therefore, we calculated the mean spike–LFP coherence (before and after adaptation) for the pairs of recording sites located within 2 mm of each other that were stimulated within 22.5° of their preferred orientations (these pairs contributed to the overall increase in gamma synchrony after adaptation shown in Fig. 4C, red line). Orientation discriminability was calculated as the mean d′ for pairs of stimuli within 22.5° of the peak orientation of the cell, which were presented near the adapting orientation (within 45°). The choice of test orientations used in the calculation of d′ was motivated by the fact that stimuli at nonpreferred orientations did not cause a significant change in SFC after adaptation (compare Fig. 4C) and elicited only weak neuronal responses. After adaptation, we found a significant increase in d′ for our population of cells (mean increase, 29.4%; p < 0.03, Wilcoxon's signed-rank test; the mean d′ in control was 0.8421, and the mean d′ after adaptation was 0.9615). Figure 5B reveals a significant positive correlation (r = 0.41, p < 0.02, Pearson's correlation) between the adaptation-induced changes in neuronal discrimination performance (Δd′) and ΔSFC. Since discriminability, d′, is proportional to the ratio between the response difference at two nearby orientations (which we refer to as response slope) and response variability, we examined how these two measures relate to spike-field coherence. We found a significant positive correlation between ΔSFC and the postadaptation change in response slope (r = 0.25, p < 0.02, Pearson's correlation) and a significant negative correlation between ΔSFC and the postadaptation change in response variance (r = −0.21, p < 0.05, Pearson's correlation). Therefore, adaptation may increase spike–LFP coherence to improve the difference in neuronal responses to nearby orientations (response slope) and decrease response variability to enhance neuronal discrimination performance.

Since adaptation also changes neuronal firing rates, we examined the relationship between the decrease in neuronal responses and changes in discriminability. Although we did not find a significant correlation between changes in firing rates and changes in d′ after adaptation (Fig. 5C) (r = −0.09; p > 0.4), there was a tendency for those neurons exhibiting a decrease in firing rate to also display an improvement in discrimination performance (p < 0.05). Given that changes in orientation discrimination after adaptation are known to be orientation dependent (Dragoi et al., 2002; Felsen et al., 2002), one possible interpretation of the result shown in Figure 5B is that the cells for which the postadaptation change in spike-field coherence was high may have been stimulated with test orientations close to the adaptor. To rule out this confound, for each neuron we calculated the mean orientation difference (Δθ) between the test orientations for which we assessed neuronal discrimination performance and the adapting orientation as a function of ΔSFC. However, as shown in Figure 5D, we failed to find a significant correlation between Δθ and ΔSFC (p > 0.2, Pearson's correlation). This indicates that the changes in neuronal discriminability after adaptation are significantly related to the changes in spike-field coherence and are not an artifact of stimulus orientation. Overall, these results indicate that increased spike–LFP gamma synchronization after adaptation might have influenced the ability of the neurons to carry information about incoming stimuli.

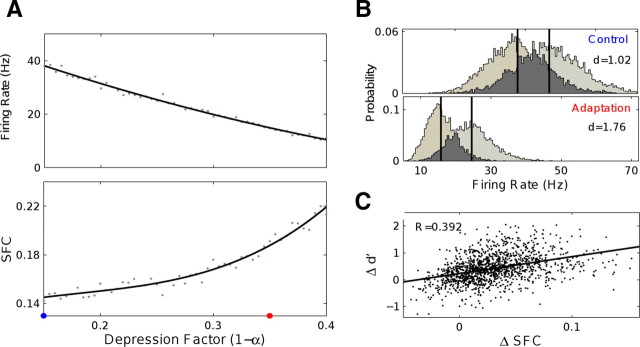
We further used a computational model to test whether the increase in neuronal synchronization after adaptation is consistent with an improvement in the discrimination ability of neurons. We modeled a randomly coupled network of 50 integrate-and-fire neurons (connection probability, p = 0.25), receiving noisy background input with a spectral peak in the gamma range (60 Hz) from an excitatory presynaptic population of 200 cells. The simulated neurons were thus assumed to be part of a larger group of V4 cells exhibiting oscillations in the gamma range. Adaptation was assumed to induce synaptic depression (Dragoi et al., 2000), which was modeled by multiplying the synaptic strengths by a factor 0 < α < 1 (see Materials and Methods). Individual spike trains in the presynaptic pool were irregular and displayed an SFC consistent with experimental data. As expected, adaptation resulted in decreased firing rates and response variability. Moreover, synaptic depression by itself resulted in increased SFC in the postsynaptic pool (Fig. 6A). Examining the effect of different adaptation strengths shows that, as in the experimental data, changes in SFC are strongly correlated with changes in firing rates. This is explained by the fact that depression in input strength decreases postsynaptic activity but also increases the likelihood that spikes occur nearer the maxima of the oscillatory part of the input. A concurrent reduction in reverberatory activity in the recurrent postsynaptic network amplifies this effect.

Figure 6.

Short-term plasticity explains increased SFC and neuronal discriminability after adaptation. A network of 50 integrate-and-fire (IF) neurons with a 25% recurrent connection probability received input from a presynaptic population of 200 IF cells. All cells in the simulation received noisy background input with a strong spectral component at 60 Hz. Adaptation was assumed to scale the synaptic weights by a depression factor α. A, Consistent with experimental data, the model network displayed decreasing response rate (top) and increasing SFC (bottom) with an increase in depression strength. B, The responses to two different orientations is modeled by presenting two levels of input to the presynaptic population. Shown are the control (α= 0.85; blue dot) and adapted (α= 0.65; red dot) response distributions of responses from 50 cells to 90 presentations of the stimulus (4500 values in each distribution). Adaptation increased discriminability in the postsynaptic pool as measured by d′. The difference between the mean responses (vertical lines) remained high after adaptation, while the population response variance was decreased. C, Change in discrimination performance (Δd′) is positively correlated with the change in spike field coherence (ΔSFC) (compare with Fig. 5B). Shown are results obtained from network responses from 1000 trials with varying depression strength (0.65 < α < 1). The line represents a regression fit. To emphasize the effect of recurrent connections, SFC was held constant in the presynaptic population in these simulations.

To examine the impact of adaptation on discriminability, we simulated the network response to two different stimuli presented to the presynaptic population. Despite the decrease in response magnitude after adaptation in the postsynaptic network, the network gain remained high due to an increased efficiency of input integration at higher SFC. As shown in Figure 6B, this effect together with decreased response variability led to increased stimulus discriminability, as measured by d′. The strong dependence between SFC and d′ can also be observed when examining the response of individual cells in the network (Fig. 6C).

Discussion

The central result of our study is that brief adaptation increases the degree of synchrony between individual spike trains and local population activity in the gamma frequency band, and that these changes are associated with an improvement in feature coding by V4 neurons. Our experimental results and computational model demonstrate that adaptive synchronization between the spiking activity of individual neurons and their local population can be used to enhance temporally insensitive, rate-based, coding schemes for sensory discrimination. In area V4, the capacity of neurons to synchronize their responses with the local population activity in the gamma band has been mainly studied in relation to spatial attention. The major finding of previous investigations was that increased neuronal firing rates during visual attention cause precise spike synchronization among local excitatory neurons (Fries et al., 2001; Womelsdorf et al., 2006). Subsequently, it was hypothesized that synchronized networks have a high impact on the ability of postsynaptic targets to perform computations (Fries, 2005). In contrast to these findings, we show here that an increase in spike–LFP gamma synchronization can occur even when neuronal firing is decreased. This is a potential homeostatic mechanism: A reduction of firing rates after adaptation could balance the increase in drive to postsynaptic targets due to strengthened gamma synchrony to maintain network stability.

Importantly, our study demonstrates a significant correlation between the spike-field gamma coherence after adaptation and the capacity of neurons to discriminate between nearby stimuli. This result reveals a novel effect of gamma synchronization—despite a decrease in neuronal response after adaptation, the increase in spike-field synchrony may be used to enhance the ability of neurons to carry information about incoming stimuli. The relationship between gamma synchrony and feature coding has been indirectly suggested by attention studies in V4. An increase in gamma-range synchronization and neuronal discrimination performance has been reported when oriented stimuli are attended (McAdams and Maunsell, 1999). However, evidence linking these two effects of attention, the increase in gamma synchronization and the increase in stimulus discrimination, has been missing. More recently, theoretical studies have suggested that gamma oscillations of spiking neuronal populations can enhance signal discrimination by decreasing the variance of the responses (Masuda and Doiron, 2007), and that synchrony could enhance the response gain of neurons (Salinas and Sejnowski, 2000), and facilitate learning and decoding (Börgers et al., 2008; Masquelier et al., 2009). Our simple model shows that adaptation-induced changes in synaptic strength can explain experimentally observed changes in network dynamics, and the accompanying increase in stimulus discriminability. In conjunction with other adaptive changes in population responses to oriented stimuli (Felsen et al., 2002; Gutnisky and Dragoi, 2008), this mechanism may play an important part in the processing of visual information.

The relationship between gamma synchronization and the changes in neuronal responses reported here differ from the previous studies in V4 focused on spatial attention. Whereas attention has been found to increase gamma frequency in both LFP power and spike-field coherence and reduce low-frequency synchronization (Fries et al., 2001), adaptation strongly enhances gamma spike-field coherence but suppresses gamma LFP power, while not affecting low-frequency oscillations. These differences are important. The direct measure of the strength of synchronized activity of a neuronal population in the gamma frequency band is given by the magnitude of LFP gamma power (i.e., an increase in the power spectrum in the gamma band). Spike-field coherence measures the relative timing of the spiking of a neuron to the population response and does not necessarily imply the presence of a population rhythm (Wang, 2010). The fact that adaptation, unlike attention, causes a decreased spectral power in the gamma frequency band of LFP signals, but an increase in spike–LFP synchronization, could indicate that the firing of the neurons could be locked to different phases of different frequencies within the gamma range. In addition, different mechanisms could be involved in the changes in neuronal synchronization during attention and adaptation. Indeed, attention has been reported to increase neuronal firing rates while adaptation mainly reduces neuronal responses near the adapting orientation (Dragoi et al., 2000, 2002; Gutnisky and Dragoi, 2008). Whereas the increase in responses during attention could be due to top-down excitatory mechanisms that selectively increase response gain (McAdams and Maunsell, 1999), adaptation mainly reflects suppressive mechanisms involving feedforward input and local interactions (Chelaru and Dragoi, 2008). An increase in local inhibition due to adaptation could further increase gamma synchronization to improve neuronal discrimination performance. This is consistent with recent experimental evidence in mouse barrel cortex (Cardin et al., 2009) indicating that selectively activating fast-spiking interneurons enhances the gamma rhythm and controls sensory responses (Sohal et al., 2009).

Our results represent the first experimental evidence that extrastriate neurons change their synchronization with local population activity in a dynamic manner after brief exposure to image features. Although adaptation has been thoroughly investigated in early visual cortex (Movshon and Lennie, 1979; Saul and Cynader, 1989; Müller et al., 1999; Dragoi et al., 2000, 2002), whether and how neurons in higher visual areas undergo rapid adaptation has been poorly understood. Examining this issue is not only important for understanding how the neural code changes in real time but could also provide clues for understanding cortical processing during natural viewing conditions. Indeed, it has been hypothesized that cortical adaptation occurs spontaneously during natural viewing when, during periods of visual fixation (between saccades), the portions of a scene that fall within the receptive field of a visual cortical neuron are well correlated in local features, such as orientation (Dragoi and Sur, 2006).

We suggest a novel mechanism that could potentially explain why adaptation increases neuronal discrimination performance in visual cortex. Short-term synaptic depression has been hypothesized to be involved in the improvement of feature coding after rapid adaptation (Dragoi et al., 2000; Chelaru and Dragoi, 2008), yet the neuronal mechanism by which neurons improve their postadaptation discrimination performance remains unclear. Our results suggest a possible link between the adaptive changes in gamma oscillations and the coding performance of neuronal populations. The change in neuronal synchronization after adaptation could constitute a network strategy that complements the effect of changes in network performance via changes in neuronal correlations (Abbott and Dayan, 1999; Pouget et al., 2000; Reich et al., 2001). Thus, we have previously shown that, after adaptation, neuronal populations in primary visual cortex are able to encode information more accurately by exhibiting a reduction in correlated variability (noise correlations). However, our analysis indicates that the reduction in noise correlations after adaptation is unlikely to occur in area V4. Indeed, we found that, whereas the mean spike count correlation before adaptation was 0.1025, adaptation caused only a slight decrease in correlations (mean correlation, 0.0971; p > 0.1). Future work will determine whether and how these two network strategies (i.e., the increase in gamma synchronization and the reduction in noise correlations after adaptation) may operate synergistically in different cortical areas to improve neural coding in neuronal populations.

Notes

Supplemental material for this article is available at http://nba.uth.tmc.edu/Assets/pdf/other/suppl_information.pdf. This section illustrates the spike density and LFP power for our examplar spike–LFP pairs, shows the adaptation-induced changes in gamma power as a function of orientation, shows examples of spike-triggered averages, presents the changes in gamma synchronization as a function of electrode distance, and presents evidence that our single-unit recordings are uncontaminated by 60 Hz noise. This material has not been peer reviewed.