Chloride Ions in the Pore of Glycine and GABA Channels Shape the Time Course and Voltage Dependence of Agonist Currents

Abstract

In the vertebrate CNS, fast synaptic inhibition is mediated by GABA and glycine receptors. We recently reported that the time course of these synaptic currents is slower when intracellular chloride is high. Here we extend these findings to measure the effects of both extracellular and intracellular chloride on the deactivation of glycine and GABA currents at both negative and positive holding potentials. Currents were elicited by fast agonist application to outside-out patches from HEK-293 cells expressing rat glycine or GABA receptors. The slowing effect of high extracellular chloride on current decay was detectable only in low intracellular chloride (4 mm). Our main finding is that glycine and GABA receptors “sense” chloride concentrations because of interactions between the M2 pore-lining domain and the permeating ions. This hypothesis is supported by the observation that the sensitivity of channel gating to intracellular chloride is abolished if the channel is engineered to become cation selective or if positive charges in the external pore vestibule are eliminated by mutagenesis. The appropriate interaction between permeating ions and channel pore is also necessary to maintain the channel voltage sensitivity of gating, which prolongs current decay at depolarized potentials. Voltage dependence is abolished by the same mutations that suppress the effect of intracellular chloride and also by replacing chloride with another permeant ion, thiocyanate. These observations suggest that permeant chloride affects gating by a foot-in-the-door effect, binding to a channel site with asymmetrical access from the intracellular and extracellular sides of the membrane.

Introduction

At fast synapses, the time course of the postsynaptic current is determined mainly by the properties of the ligand-gated ion channel involved. Transmitter levels in the synaptic cleft rise rapidly during release, reaching millimolar concentrations that persist only for less than a millisecond (Clements, 1996). Thus, synaptic current decay does not reflect the time course of the transmitter concentration but mirrors the activity of postsynaptic receptors, namely for how long the channel opens, after binding the transmitter. The decline in synaptic current and in receptor open probability, commonly referred to as deactivation, depends on how stable the channel is in the bound open state and on how quickly it can lose the bound transmitter, once it has closed, rather than reopening (Edmonds et al., 1995). The single-molecule equivalent of the time course of deactivation is the duration of the burst of openings observed when the receptor is bound to the transmitter (Wyllie et al., 1998). Hence, the most physiologically important property of a synaptic, ligand-gated ion channel is its deactivation kinetics and how this can be modulated by the synapse environment.

Cys-loop superfamily receptors mediate much of fast synaptic transmission in both the periphery, as ACh nicotinic channels at the neuromuscular junction, and the CNS, in which GABA and glycine channels mediate practically all fast synaptic inhibition. It has been known for a long time that deactivation in this superfamily is affected by the membrane potential. This effect is relatively modest (e-fold for 110 or 95 mV for muscle nicotinic and glycine channels, respectively; Magleby and Stevens, 1972; Legendre, 1999), and its direction in first approximation seems to depend on whether the channel is permeable to cations or anions. Thus, cation-permeable nicotinic receptors remain active for a longer time at negative potentials, whereas anionic, inhibitory glycine channels are open for longer at depolarized potentials (but see Adams et al., 1982).

Deactivation is also affected by the nature of the permeant ion, as shown for nicotinic channels in amphibian skeletal muscle and molluscan neurons (Van Helden et al., 1977; Ascher et al., 1978; Marchais and Marty, 1979). In these preparations, replacing the main extracellular permeant cation sodium with cesium or lithium changed deactivation, monitored as the time course of synaptic current decay or as the channel lifetime estimated from noise analysis or voltage-induced relaxations. Similar effects of permeant anions were described for crayfish muscle and Aplysia buccal ganglion inhibitory synapses (Onodera and Takeuchi, 1979; Adams et al., 1982).

In addition to that, we recently reported that the intracellular concentration of the permeant ion also affects deactivation kinetics in glycine and GABA_A channels (Pitt et al., 2008; Houston et al., 2009). The effect is particularly conspicuous for glycine channels, in which the (common) choice to record with high chloride concentrations in the patch pipette slows current decay by approximately threefold versus more physiological conditions, in which intracellular chloride is in the low millimolar range.

The present work is a first characterization of the structural basis of this effect in glycine and GABA channels.

Materials and Methods

Heterologous expression of glycine and GABA receptors.

Human embryonic kidney 293 cells (American Type Culture Collection-CRL-1573; LGC Promochem) were maintained at 37°C in a 95% air/5% CO₂ incubator in DMEM supplemented with 0.11 g/L sodium pyruvate, 10% v/v heat-inactivated fetal bovine serum, 100 U/ml penicillin G, 100 μg/ml streptomycin sulfate, and 2 mm l-glutamine (all from Invitrogen). Cells (passaged every 2–3 d, up to 30 times) were plated 12 h before transfection by calcium phosphate-DNA coprecipitation (details as in the study by Groot-Kormelink et al., 2002). The total amount of DNA was kept constant at 3 μg/dish. Rat α1 and β GlyR subunits (GenBank accession numbers AJ310834 and AJ310839) were transfected at a ratio of 1:40 to minimize contamination by homomeric α1 receptors (Burzomato et al., 2003). Rat α1, β2, and γ2_L GABA receptors subunits (GenBank accession numbers AY574250, AY574251, and AY574252) were transfected at a ratio of 1:1:1. All recordings were performed 16–48 h after transfection. All cDNA receptor subunits were subcloned into the pCI vector (Promega).

Site-directed mutagenesis was performed using the QuikChange mutagenesis kit (Stratagene). The construct for the Gly α1^ΔGLIC chimera was obtained in two steps. First, residues from position 310 to 420 (mature polypeptide numbering) were removed from the M3–M4 intracellular loop of the α1 GlyR subunit. The deleted segment was replaced by the M3–M4 intracellular loop of the proton-gated cation channel from Gloeobacter violaceus, a short, 7 aa peptide (SQPARAA) that was inserted at position 311. The resulting M3–M4 sequence (from position 307 in the chimera) was FVSR-SQPARAA-KIDK. All constructs were verified by sequencing the whole open-reading frame.

Electrophysiological recording.

Unless otherwise stated, cells were bathed in a high chloride (131 mm) extracellular solution containing the following (in mm): 102.7 NaCl, 20 Na gluconate, 2 KCl, 2 CaCl₂, 1.2 MgCl₂, 10 HEPES, 14 glucose, 15 sucrose, and 20 tetraethylammonium (TEA)-Cl, pH adjusted to 7.4 with NaOH (osmolarity ∼320 mOsm). The composition of all other solutions used is detailed in Table 1.

Table 1.

Extracellular and intracellular solutions used for the electrophysiological recordings

	Composition (mm) of extracellular solutions, pH adjusted to 7.4 with NaOH
	NaCl	NaGluc	NaSCN	KCl	KGluc	CaCl2	MgCl2	HEPES	TEA-Cl	Sucrose	Glucose
ExtCl-131	102.7	20		2		2	1.2	10	20	15	14
ExtCl-10		139.1			2	2	1.2	10	3.6	15	14
ExtSCN		9	132.5		2	2	1.2	10		15	14

	Composition (mm) of intracellular solutions, pH adjusted to 7.2 with KOH
	KSCN	KCl	KGluc	EGTA	CaCl2	MgCl2	HEPES	TEA-Cl	MgATP	Sucrose	Vj (mV)
IntCl-131		107.1		11	1	1	10	20	2	14	−2.2
IntCl-10			121.1	11	1	1	10	6	2	14	−11.4
IntCl-15			111.1	11	1	1	10	11	2	35	−12.8
IntCl-4			121.1	11	1	1	10		2	52	−14.6
IntSCN	132.5			11	1	1	10		2	14

The junction potential (V_j) was calculated for the different intracellular solutions with reference to Ext_Cl-131 using Clampex 8.1 and a temperature of 21°C. Gluc, Gluconate; Ext, extracellular; Int, intracellular.

Patch pipettes were pulled from thick-walled borosilicate glass (GC150F; Harvard Apparatus) and fire polished to a resistance of 8–12 MΩ. Agonist-evoked currents were recorded with an Axopatch 200B amplifier (Molecular Devices) from outside-out patches held at −100 mV, unless otherwise specified. Patches were stepped to this holding voltage 0.2 s before the agonist was applied (voltage step duration, 2 s) and otherwise held at −40 mV. No correction for junction potential was applied (the maximum calculated voltage error was −14.6 mV; for 4 mm internal chloride, see Table 1). In experiments investigating the voltage dependence of deactivation, patches were held at 0 mV and stepped to five different potentials (from −100 to +60 mV in 40 mV steps) in a similar manner. Five agonist responses were obtained at each holding potential.

Agonist application.

All concentration jumps were performed using a piezo stepper (Burleigh Instruments) with an application tool made from theta tube glass (2 mm outer diameter, 1.7 mm inner diameter, septum 0.117; catalog #14-072-01, Hilgenberg; final tip diameter, 150 μm). Voltage commands for the piezo stepper were square pulses conditioned by low-pass eight-pole Bessel filtering (−3 dB frequency 5 kHz) to smooth oscillations. Pulse duration was 1 ms for all combinations, except for the Gly channel mutated to be cationic (α1^A−1E), which required 2.5–3 ms steps.

The exchange time was estimated by recording the open-tip response to the application of diluted extracellular solution (70% water) after rupture of the patch. Only patches in which the 20–80% exchange time was faster than 150 μs were included in the analysis. Only patches with open-tip responses with a half-width value between 1 and 2 ms (for 1 ms command pulses) were accepted for analysis.

Agonist solutions were freshly prepared every day by diluting in the appropriate external solution aliquots from frozen stock solutions (1 m, in water). Agonists were applied at a concentration known to elicit maximum response. For both GABA and Gly, this was found to be 3 mm for wild-type receptors and 20–50 mm for mutant receptors.

Traces shown are averages of 5 or 10 individual agonist currents (for the voltage experiments and the experiments on the effects of chloride, respectively). For both Gly and GABA receptors, agonist pulses were separated by at least 5 s. Responses were averaged and included in the analysis only if the rundown in peak amplitude did not exceed 5%. The time course of deactivation (between 98 and 5% of the peak current level) was fitted with one-, two-, or three-exponential components (program Clampfit 9.0). The traces were fitted with the lowest number of components that gave a good fit (two in most cases), the fit was accepted if the correlation coefficient was higher than 0.9. For ease of comparison, data are reported as weighted time constants.

Computer simulations of hindered diffusion of chloride: overview.

We produced a mathematical model of a multitaper conical pipette joined to a patch with a simplified geometry to simulate our agonist currents recorded from outside-out patches under voltage clamp. This was done to assess whether our observations can be accounted for purely by an artifact of recording, namely the hindered diffusion of chloride ions at the tip of the pipette, rather than by an effect of chloride ions on the channels. Hindered diffusion could result in transient depletion or accumulation of chloride when the channels in the patch are activated, and this in turn would result in instantaneous changes in the driving force that could alter the time course of the agonist-induced current.

We used a simplified Markov model with only an open and a shut state to simulate the conductance changes. The two rates were chosen to give rise times and deactivation times similar to the experimental values (1 and 20 ms, respectively), and the pipette bulk chloride concentration was set at either 130 or 10 mm. The results of the simulations incorporating hindered chloride diffusion were compared with the ideal current time course obtained when chloride is “clamped” at its initial pipette concentration.

Mathematical model of ion diffusion in the pipette and patch.

Figure 3a shows the model we used in the numerical simulation of chloride concentration changes at the intracellular end of the channels in the patch. Because of the radial symmetry, the change in the concentration of chloride C(t, z) in time along the axis of the pipette can be described by a one-dimensional diffusion equation through an arbitrary passage section (Crank, 1975; Oliva et al., 1988; see also Cannell and Nichols, 1991):

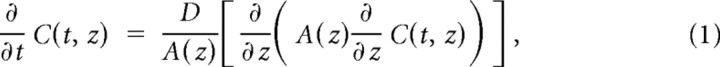where A(z) is the area of the passage section and D is the chloride ions diffusion coefficient in aqueous solutions (set to 2 μm²/ms; Lobo et al., 1998; Adam et al., 2007). By definition, Equation 1 already incorporates Neumann-type boundary conditions (e.g., imposes that ion fluxes through the pipette walls should be null).

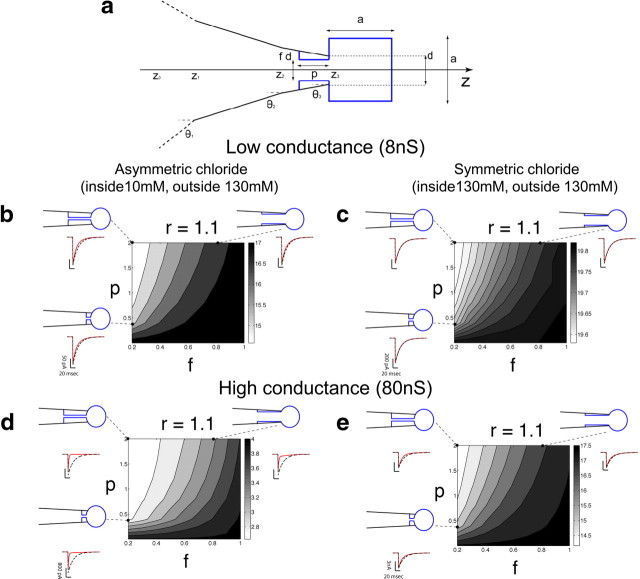
Figure 3.

Hindered diffusion of chloride in an outside-out patch has a limited effect on the time course of agonist-induced current relaxations. The patch is modeled as a r = 1.1 μm diameter equivalent sphere (a), and chloride diffusion is calculated for a range of geometries, varying both the width of the unclogged tip lumen (f = 20–100% of the maximum possible, 1 μm) and the length of the restricted passage between the patch and the pipette shank (p = 0–2 μm). The contour plots in b–e show the effect of different pipette geometries on the time constant of decay, for agonist currents elicited by a short (1ms) pulse of saturating agonist in the presence of hindered chloride diffusion. This was calculated assuming an underlying agonist-gated conductance of 8 or 80 nS, i.e., two to three times greater than that required to produce the biggest currents observed in our experiments with asymmetric and symmetric chloride, respectively. For low conductances, the deactivation time constant became up to 25% faster in asymmetrical chloride (grayscale in b), whereas it was barely affected in symmetric chloride (c). Traces for representative geometries are shown around each panel (dashed black traces for clamped chloride, red for hindered diffusion; the conditions that give rise to these traces are shown by the dashed lines and dots connecting the traces to the graphs). For high conductances, the deactivation was profoundly distorted in the case of asymmetrical chloride (d), and the decay time constant was reduced from 20 ms (clamped chloride) to up to 2 ms (an unrealistic scenario given that this conductance is at least 20–30 times larger than in our experiments). On the contrary, hindered diffusion had a limited impact when chloride was symmetric, speeding up the decay time by 25% at most (e).

The geometry of the tip of the patch pipette, drawn in black in Figure 3a, is completely specified by the tip outer diameter d, set to 1 μm, and by the semi-angle θ of the cone, set to 8°. θ was tapered to 5.5° and 3°, in the last 4.5 and 5 μm of the pipette length, respectively, on the basis of actual observations of our patch pipettes (which are pulled in a multistep process). A total length of L = 65 μm was chosen for the tapered portion of the pipette to numerically simulate the evolution of the chloride concentration inside the pipette tip, imposing the following Dirichlet-type boundary condition to mimic the constant bulk concentration for coordinates z₀, farther away from the tip:

The numerical value of L was set such that z₀ is sufficiently far from the region where the instantaneous changes in concentration occurred (i.e., near the pipette tip opening), correctly approximating the role of a bulk concentration inside the pipette tip.

At any point inside the pipette tip, the section area A(z) is given by the area of a circle, πR(z)², where the radius R(z) depends on the location z and on the taper of the pipette (Fig. 3a), according to the following formulae:

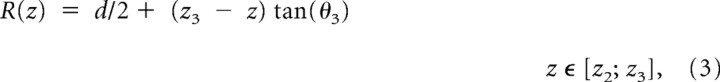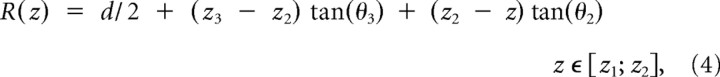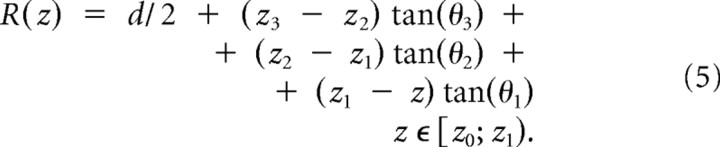Equations 3–5 take into account the piecewise values of θ at any given z, as well as the effect of multitapering.

The outside-out patch membrane was approximated as a cube (sketched in blue in Fig. 3a) as in previous studies (Oliva et al., 1988; Cannell and Nichols, 1991). This effective geometry approximates a spherical membrane patch, without requiring the implementation of a two-dimensional diffusion equation. In our model, the patch extends inside the pipette tip, sealing to the inner glass wall, as does a real Ω-shaped membrane patch protruding outside the pipette tip. This feature was fully specified by two parameters, the length p and the fraction f of the tip lumen left unclogged by the membrane. Varying these parameters allows us to explore the effects of reducing free access between the pipette bulk solution and the membrane patch. Then, when p > 0, the section area A(z) is given by the circle of radius chosen as the minimum between R(z) and fd/2, within the range [z₃ − p; z₃]. For values of the z larger than z₃, the section area A(z) = a² is simply given by the area of the cube of edge a. The exploration of the model geometry was performed referring indirectly to the parameter a, by specifying the radius r of an equivalent sphere of the same volume, r = a(4π/3)^−1/3.

Finally, the presence of the membrane patch, separating the extracellular medium from the pipette solution and allowing chloride ions movement through the channels, was made explicit.

Consistently with the assumptions of Equation 1, the flux Φ(t) of chloride ions across the membrane was considered only at the rightmost vertical wall of the patch-box in Figure 3a, thus appearing for z = z₃ + a in the right hand side of equation 1. By definition, Φ(t) is related to the ion current i(t) and to a set of biophysical variables defining ligand-gated conductance changes:

where z_Cl is the valence of chloride, F is the Faraday constant, and dv = A(z)dz is the infinitesimal volume the flux is referred to. The ionic current i(t) depends on the number of ligand-gated channels N, their single-channel conductance g, the fraction x(t) of channels open at a given time t, the Nernst equilibrium potential E_Cl, and the transmembrane electric potential V_cmd imposed by the voltage-clamp amplifier, with an ohmic relationship:

E_Cl depends on the actual concentration next to the inner side of the membrane patch and is given by

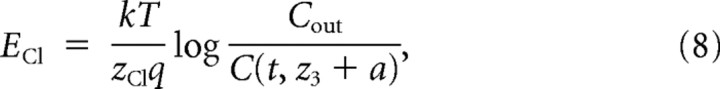where k is Boltzmann's constant, T is the absolute temperature (300K), and q is the elementary charge.

Finally, the definition of the model includes the description of the kinetics of the fraction x(t), described as a Markov chain model with two states, in which only the opening transition probability α depends on the instantaneous concentration of the agonist, G(t) outside the membrane patch (Destexhe et al., 1994):

The external diffusion of agonist G(t) is assumed to occur instantaneously and to reach all the points of the membrane patch at exactly the same time. It is assumed that G(t) changes as a square pulse, with amplitude G_max and duration Δ. α and β are the transition rate constants between one state and the other.

From this kinetic scheme, a first-order linear differential equation can be derived as

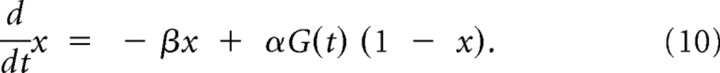Because G(t) is piecewise constant, Equation 10 was iteratively computed (step size, 10 μs and 2 nm) by using its analytical solution, for computational efficiency.

The model was computer simulated by an implicit scheme for unconditional numerical stability (Press et al., 1992), implemented in MATLAB (MathWorks) and available on ModelDB (accession number 127190, http://senselab.med.yale.edu/modeldb; Hines et al., 2004).

Homology modeling of the transmembrane region of the α1 GlyR.

Three sets of homology models of the transmembrane region were generated using the open GLIC structure [Protein Data Bank (PDB) identification number 3EHZ; Hilf and Dutzler, 2009], the closed ELIC structure (PDB identification number 2VL0; Hilf and Dutzler, 2008), and the closed Torpedo nicotinic acetylcholine receptor structure (PDB identification number 2BG9; Unwin, 2005) as templates. The homology models were generated for a chimera of the glycine receptor α1 subunit, in which the long intracellular M3–M4 loop was replaced with a shortened sequence from GLIC (see above and Fig. 4). Sequences were aligned with Muscle (Edgar, 2004), and 100 homology models each were generated using Modeller 9v8 (Sali and Blundell, 1993). Models were ranked by the objective function of Modeller, and the stereochemical properties of the best model in each instance was assessed with PROCHECK (Laskowski et al., 1993). The three selected models were subjected to 1000 steps of energy minimization in vacuo using the GROMOS 43b1 force field (Van Gunsteren et al., 1996) in GROMACS 3.3.3 (Lindahl et al., 2001). Using a chloride ion as the probe, energetically favorable binding sites were computed using Grid (Goodford, 1985). Electrostatic surface of the protein was generated using APBS (Adaptive Poisson-Boltzmann Solver) (Baker et al., 2001). Images were generated using PyMOL 1.3 (The PyMOL Molecular Graphics System; Schrödinger; http://www.pymol.org).

Figure 4.

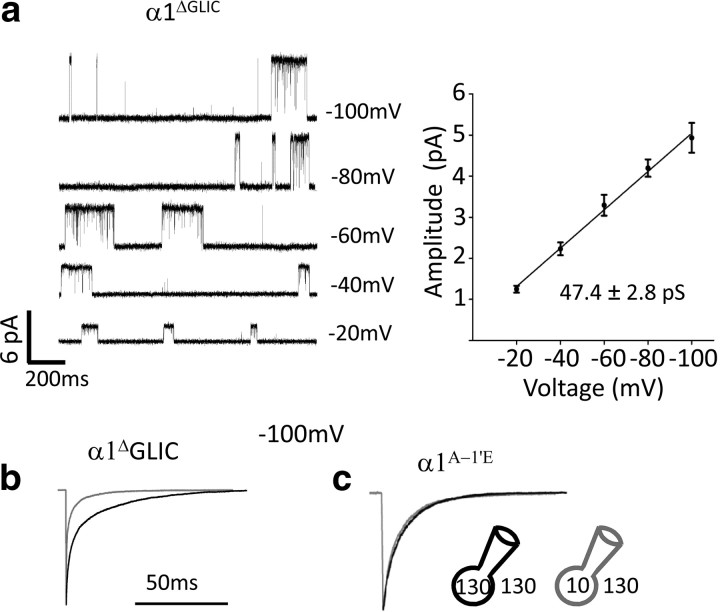
The effect of intracellular chloride on the time course of inward currents requires the channel to be anion selective but is independent of the cytoplasmic domain of the receptor. a, Replacing the long M3–M4 cytoplasmic loop of α1 GlyRs with the ortholog's 7 aa loop from the prokaryotic GLIC channel (α1^ΔGLIC) did not affect the single-channel conductance of wild-type α1 GlyRs. Traces are cell-attached recordings obtained in the presence of 10 μm Gly in the pipette. b, The deactivation of currents evoked from the α1^ΔGLIC chimera by glycine concentration jumps (1 ms, 3 mm) retained the same sensitivity of wild-type channels to the intracellular chloride concentration. c, The effect of chloride was abolished when the α1 GlyR was made cation permeable by mutating Ala −1′ in M2 to Glu (α1^A−1E).

Results

Both intracellular and extracellular chloride ions shape the decay of synaptic-like glycine and GABA currents

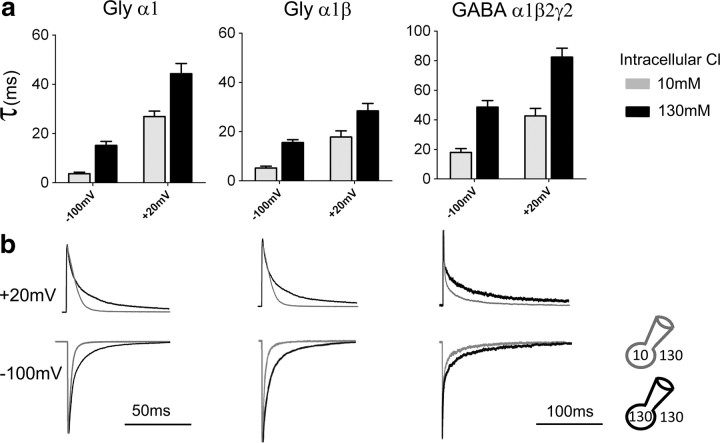
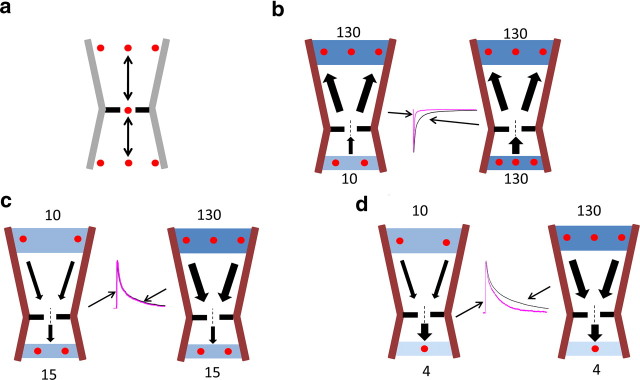
The results in Figure 1 extend our previous findings (Pitt et al., 2008; Houston et al., 2009) and compare the effect of changes in intracellular chloride on the kinetics of the main anion-permeable ion channels in the Cys-loop superfamily (homomeric and heteromeric GlyR and GABAR) at both negative and positive holding potentials. The traces (Fig. 1b) are average responses to the rapid, brief application of saturating Gly or GABA concentrations to outside-out patches (1 ms, 3 mm). Current decay for this relaxation to zero agonist concentration reflects receptor deactivation and is expected to have the same time constants as the single-channel burst distribution in the presence of very low steady-state agonist concentration (Wyllie et al., 1998). The traces in Figure 1b and the values of the weighted decay time constants (τ) in Figure 1a show that this decay was consistently slower in symmetrical high chloride solution (131 mm on both sides of the membrane, black traces and bars) than in the presence of low intracellular chloride (10 mm [Cl⁻]_in, 131 mm [Cl⁻]_o, gray traces and bars, current peaks scaled to the corresponding responses in symmetrical chloride).

Figure 1.

The deactivation time course for Gly and GABA receptors is shaped by the intracellular chloride concentration, regardless of the direction of current flow. Outside-out current responses elicited by 1 ms, 3 mm Gly or GABA decay more quickly if intracellular chloride is low (i.e., 10 mm, gray traces in b, pipette solution internal_Cl-10; Table 1) than in the presence of high intracellular chloride (131 mm, black traces, pipette solution internal_Cl-131; Table 1; in all recordings in b, extracellular chloride was 131 mm, solution external_Cl-131). The current is inward (chloride goes out) when the patch is held at −100 mV and outward at +20 mV. a, Summary of the weighted τ of the current relaxations. b, Representative outward and inward currents in the presence of 10 mm (gray trace) or 131 mm intracellular Cl (black trace). Traces are averages of 5–10 individual responses, normalized to the peak to allow comparison of their decay phase. Time constant values are reported in Table 2.

Low intracellular chloride speeded up current decay to an extent approximately similar across receptors (Table 2, top section), making the decay of inward currents approximately threefold faster for heteromeric GABA or Gly channels and fourfold faster for homomeric GlyRs. This effect was present regardless of the direction of ion flow, i.e., both at a negative holding potential (−100 mV), when chloride ions go out of the patch and at +20 mV holding potential. This positive holding potential is such that, for both ionic conditions used in the recordings, agonist current is outward (i.e., chloride ions go in). The effect of changing intracellular chloride was maintained when the chloride driving force was kept constant (e.g., by appropriately adjusting the holding voltage corrected for junction potential; α1 homomeric GlyR, data not shown). Glycine and GABA currents deactivate more slowly when the membrane is depolarized (Bormann et al., 1987; Fig. 1b, top row). At +20 mV holding potential, reducing intracellular chloride from 131 to 10 mm made current deactivation faster, but the effect was somewhat smaller than that observed at negative potential, with a 37–45% reduction in the weighted τ (Table 2).

Table 2.

Effect of intracellular and extracellular chloride on the deactivation time constants of agonist currents

Voltage	Modulation by intracellular chloride, extracellular chloride fixed at 130 mm
	α1 GlyR Intracellular Cl		p	α1β GlyR Intracellular Cl		p	α1β2γ2L GABA Intracellular Cl		p
	10 mm	130 mm		10 mm	130 mm		10 mm	130 mm
−100 mV	3.7 ± 0.6 (13)	15.2 ± 1.6 (10)	<0.0001	5.2 ± 0.7 (6)	15.6 ± 1.2 (10)	<0.0001	18.0 ± 2.6 (7)	48.7 ± 4.4 (7)	<0.001
+20 mV	26.9 ± 2.2 (14)	42.8 ± 4.2 (10)	<0.0001	17.8 ± 2.5 (6)	28.4 ± 3.0 (10)	0.0262	42.7 ± 5.0 (6)	82.5 ± 6.0 (6)	<0.001

Voltage	Modulation by extracellular chloride, intracellular chloride fixed at 15 mm
	α1 GlyR Extracellular Cl		p	α1β GlyR Extracellular Cl		p	α1β2γ2L GABA Extracellular Cl		p
	10 mm	130 mm		10 mm	130 mm		10 mm	130 mm
−100 mV	5.3 ± 0.4 (8)	6.4 ± 0.4 (9)	0.19	7.6 ± 2.0 (5)	8.4 ± 1.1 (5)	0.73	28.1 ± 5.5 (6)	30.6 ± 3.1 (6)	0.71
+40 mV	26.1 ± 2.0 (6)	25.0 ± 4.4 (11)	0.70	24.1 ± 1.2 (6)	22.1 ± 2.3 (13)	0.53	37.4 ± 3.5(8)	38.8 ± 3.1 (6)	0.77

Voltage	Modulation by extracellular chloride, intracellular chloride fixed at 4 mm
	α1 GlyR Extracellular Cl		p	α1β GlyR Extracellular Cl		p	α1β2γ2L GABA Extracellular Cl		p
	10 mm	130 mm		10 mm	130 mm		10 mm	130 mm
+40 mV	12.2 ± 0.7 (8)	29.5 ± 3.4 (11)	0.0005	18.9 ± 1.3 (7)	27.5 ± 4.5 (8)	0.045	14.1 ± 1.3 (5)	22.4 ± 1.4 (6)	0.0021

The columns give the weighted time constants of decay for currents elicited in outside-out patches by the application of 1 ms pulses of saturating concentrations of glycine or GABA (3 mm; see Materials and Methods). Values are averages ± SEM, expressed in milliseconds. Number of patches in parentheses. p values from unpaired, two-tailed t tests. The top shows the effect of intracellular chloride, measured using pipette solutions containing either 10 or 130 mm chloride, on different patches, in the presence of 130 mm extracellular chloride, for both inward (−100 mV) and outward (+20 mV) currents. The middle shows the lack of effect of changes in extracellular chloride concentration when the pipette chloride concentration was held at 15 mm. High extracellular chloride slows outward currents only if intracellular chloride is low (bottom, 4 mm). In these recording conditions, inward currents were too small for reliable measurement because of the decrease in driving force and single-channel conductance.

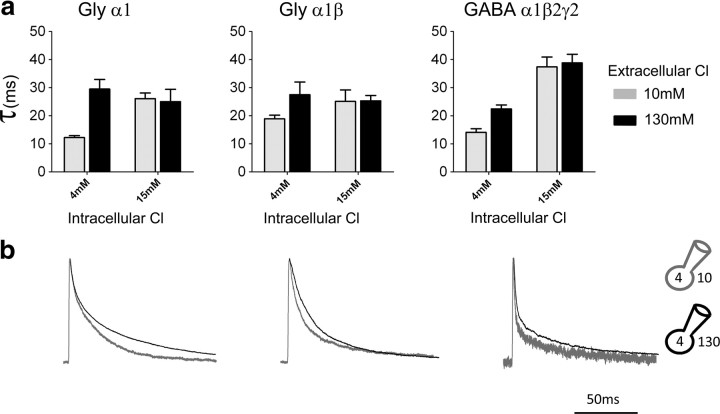
We next investigated whether changes in extracellular chloride could affect current kinetics. When intracellular chloride was held at 15 mm or higher, reducing extracellular chloride (from 131 to 10 mm) had no effect (Table 2, middle section). It was only when intracellular chloride was further reduced, to 4 mm, that lowering extracellular chloride (from 131 to 10 mm) did make current deactivation faster for all the receptors examined, as shown by the outward current traces in Figure 2b (holding potential was set at +40 mV to increase the signal, particularly in low extracellular chloride). The decrease in weighted τ was between 30 and 60% (Fig. 2a).

Figure 2.

The extracellular chloride concentration affects the decay of outward currents only if intracellular chloride is very low. a, Summary of the weighted decay τ of current relaxations at two different concentrations of extracellular chloride, 10 mm (external_Cl-10, gray bars), or 131 mm (external_Cl-131, black bars), in the presence of either 4 mm intracellular chloride (left pair of columns in each bar graph, internal_Cl-4) or 15 mm intracellular chloride (right pair of columns of each bar graph, internal_Cl-15). b, Outward currents recorded with 4 mm chloride in the pipette decay more quickly when extracellular chloride is low (10 mm, gray traces) than when it is high (131 mm, black). Traces are normalized to their peak to allow easier comparison of their decay time course.

The effect of chloride on the kinetics of agonist current decay is not an artifact of hindered diffusion in the pipette tip

Before exploring the structural basis of the chloride effect, we asked ourselves whether it was attributable to a real difference in channel kinetics. The currents we measure are carried by chloride, and because of that, the chloride concentration can change rapidly near the channel. If this concentration does not equilibrate quickly enough with the bulk of the pipette solution because of slow diffusion, the current itself could produce a local “chloride shift,” running down its own instantaneous driving force and making the current decay faster than the decay of the underlying conductance. In an outside-out patch, this could occur on the intracellular face because of restricted diffusion between the small volume delimited by the patch membrane and the bulk solution in the pipette itself. It is plausible also that this chloride shift could have a greater impact when intracellular chloride is low, and this could give rise to the appearance that intracellular chloride concentration directly shapes current decay.

In first approximation, such chloride shifts cannot account for all the features of our data. First of all, larger currents should produce a greater artifact, but in our observations the peak current amplitude in a patch and the decay time constant were not correlated (correlation coefficient r = 0.2, 12 patches, α1 GlyR, 10 mm intracellular chloride). In addition to that, we already know that intracellular chloride affects channel kinetics in single-channel experiments (in which the patch current is small and the chloride shift artifact must be unimportant), to an extent that is sufficient to explain the change in macroscopic current decay (Pitt et al., 2008).

Rather than relying solely on these arguments, we modeled chloride diffusion in the intracellular compartment of an outside-out patch, to calculate its impact in realistic conditions. The model (Fig. 3a; see Materials and Methods) assumed channel conductance to decay with a 20 ms time constant in response to 1 ms agonist pulses, regardless of chloride concentrations (this kinetics matches that predicted in high symmetrical chloride by our outside-out single-channel analysis; Pitt et al., 2008).

We first examined the effect of hindered chloride diffusion on long currents, produced by 200 ms agonist pulses at saturating concentration, with realistic, midrange parameters for the patch and pipette geometry (patch radius, r = 1.1, p = 0.4, f = 0.5, as defined in Materials and Methods) and with a range of values for the agonist-evoked conductance. In the ideal situation, with chloride clamped to its bulk concentration, increasing conductance scales currents linearly and does not change their kinetics. On the contrary, in the case of hindered chloride diffusion in a geometrically realistic pipette, agonist currents were distorted in both amplitude and time course, decaying purely because of chloride depletion/accumulation, especially for large conductances and asymmetrical chloride (data not shown). This confirmed the importance of testing whether similar distortions could be expected for the time course of currents evoked by the short (i.e., 1 ms) agonist applications we used in our experiments.

In these calculations, we used two values for the agonist-gated conductance: in the patch (8 and 80 nS) as a worst-case scenario: these would give rise to currents twofold to threefold bigger than the maximum currents ever recorded in our experiments with low (10 mm) or high (130 mm) pipette chloride concentrations, respectively. We then proceeded to examine the effects of changing the model geometry, restricting diffusion between the proximity of the patch and the bulk solution. Pipette geometry was described by three parameters: the patch radius (r = 1.1 μm), the part of the membrane trapped into the pipette lumen (p = 0–2 μm), and the size of the lumen (f = 20–100% of the pipette tip diameter). The contour plots in Figure 3b–e show, as a grayscale, the absolute values of the decay time constant expected with hindered diffusion for each pair of parameters on the axes (f, p). Three representative cases of patch/pipette geometries are sketched at the side of each graph, and the corresponding current traces are shown in red and compared with the predictions from the ideal clamped chloride case (black, dashed traces).

Predictably, hindered chloride diffusion has the worst impact when the narrow portion of the pipette lumen is longer and smaller in diameter, in asymmetrical chloride and at high agonist-evoked conductance, with the most extreme cases shown in Figure 3d. Here changes in chloride driving force were very large and distorted both the shape and the amplitude of the current. However, this case is very far from being realistic, because the agonist-evoked conductance value set here would give rise to currents 20–30 times larger than the largest we recorded in these conditions. When the conductance is set to a reasonable value (8 nS, still exceeding by twofold to threefold the likely maximum value in the patch), the distortion was limited (Fig. 3b), and the decay time constant became 12–27% faster than its “ideal” 20 ms value (e.g., 17.5–14.5 ms). The greatest distortion took place with the most extreme patch geometry (e.g., with an 80% restriction of a 2-μm-long lumen; Fig. 3b, top left corner). Similar changes are expected for a realistic modeling of the currents in symmetrical chloride (high conductance; Fig. 3e).

These calculations show that, in our experimental conditions (high conductance in symmetrical chloride and low conductance in asymmetric chloride), the impact of chloride diffusion on the decay of agonist evoked currents is likely to be limited. Hence, most of the changes that we observed in our experiments must be attributable to the direct effect of chloride on the channel rather than to an artifact of diffusion.

Deleting the GlyR cytoplasmic M3–M4 loop does not change the effect of intracellular chloride

So far we have established that chloride has a robust effect on the time course of agonist current relaxations, but we do not know where the ions act on the receptor. We tested all our mutations with the protocol that gave us the largest effects of chloride, i.e., recording inward currents produced by chloride exit at negative holding potentials. Given the striking effects of intracellular chloride, we examined first the receptor domains accessible to intracellular chloride.

We first considered the cytoplasmic domain, which comprises a short M1–M2 loop and the much longer M3–M4 loop. Charged residues in M3–M4 affect eukaryotic Cys-loop channel conductance (Kelley et al., 2003) by lining the portals that funnel ions from the cytoplasm to the pore (Unwin, 2005; Peters et al., 2010). Nevertheless, they are not essential, and function is preserved when the long eukaryotic M3–M4 sequence is replaced (in GABA_C channels) with the 7 aa polypeptide found here in the prokaryotic channel GLIC (Bocquet et al., 2007; Jansen et al., 2008).

We constructed a similar GlyR α1^ΔGLIC chimera, which expressed well and had macroscopic properties similar to those of the wild-type homomeric α1 GlyR (EC₅₀ = 42.4 ± 3.7 μm and nH = 2.6 ± 0.1, n = 4; compared with EC₅₀ = 78.8 ± 7.2 μm and nH = 3.3 ± 0.2 for wild-type GlyR (Beato et al., 2002). Fig. 4a shows that the single-channel conductance of the chimera was very similar to that of wild type homomeric α1 GlyRs (slope conductance, 47.4 ± 2.8 pS, n = 5 vs 47.3 ± 2.1 pS for the wild-type channel; Moroni et al., 2011), confirming that the positively charged residues in the membrane-associated helix eliminated in the chimera have only a weak effect on channel conductance in α1 GlyRs (Carland et al., 2009).

Figure 4b shows that the chimera retained robust sensitivity to the effects of intracellular chloride, despite the absence of most of the M3–M4 loop. Thus, currents produced by brief saturating pulses of Gly (1 ms, 3 mm) decayed approximately three times faster in low intracellular chloride, just as in wild-type GlyRs (Table 3), unequivocally showing that the M3–M4 loop is not involved in the effect of chloride on channel kinetics.

Table 3.

Modulation by intracellular chloride of inward currents in mutant α1, α1β GlyR, and α1β2γ2 GABA receptors

Receptor type	α1, GlyR Intracellular Cl			Gly α1β, α1 mutants Intracellular Cl			Gly α1β, β mutants Intracellular Cl			α1β2γ2, α1 mutants Intracellular Cl			α1β2γ2, β2 mutants Intracellular Cl			α1β2γ2, γ2 mutants Intracellular Cl
	10 mm	130 mm	p	10 mm	130 mm	p	10 mm	130 mm	p	10mm	130 mm	p	10 mm	130 mm	p	10 mm	130 mm	p
19′	0.42 ± 0.05 (11)	0.48 ± 0.05 (7)	0.43	0.97 ± 0.09 (7)	0.96 ± 0.13 (8)	0.95	N/A	N/A	N/A	4.6 ± 0.6 (9)	5.2 ± 0.4 (9)	0.44	7.8 ± 0.9 (5)	20.1 ± 2.7 (6)	<0.0001	7.9 ± 1.1 (7)	18.8 ± 2.5 (10)	0.0039
24′	1.08 ± 0.12 (5)	1.54 ± 0.17 (12)	0.12	0.61 ± 0.07 (7)	1.05 ± 0.17 (5)	0.023	4.3 ± 0.5 (8)	12.8 ± 1.3 (6)	0.0002	6.8 ± 0.5 (10)	11.3 ± 1.8 (9)	0.02	6.1 ± 0.9 (8)	14.2 ± 1.4 (13)	0.0005	14.7 ± 2.4 (7)	35.8 ± 5.2 (6)	<0.001
29′	15.5 ± 0.9 (12)	16.8 ± 1.3 (11)	0.43	55.4 ± 4.3 (6)	67.6 ± 4.0 (8)	0.063	6.4 ± 0.7 (5)	10.9 ± 1.2 (7)	0.0171	9.7 ± 0.8 (10)	17.8 ± 1.2 (11)	<0.0001	N/A	N/A	N/A	26.9 ± 3.8 (7)	51.2 ± 2.4 (7)	<0.0002
α1Δ GLIC	13.2 ± 1.2 (12)	44.7 ± 4.4 (13)	<0.0001
A−1′E	44.0 ± 1.7 (8)	46.4 ± 2.3 (10)	0.45

The columns give the weighted time constants of decay for currents elicited in outside-out patches by the application of 1 ms pulses of saturating concentrations of glycine or GABA (3 mm; see Materials and Methods). Values are averages ± SEM, expressed in milliseconds. Number of patches in parentheses. p values from unpaired, two-tailed t test. The effect of intracellular chloride concentrations on the time course of the current relaxation was tested by using pipette solutions containing either 10 or 130 mm chloride on different patches. The current relaxation was measured for inward current only (−100 mV). Residues at positions 19′, 24′, and 29′ were neutralized to Ala or Cys depending on the expression level attainable. Mutants highlighted in bold abolish or decrease drastically the effect of the chloride modulation on the time course of the current relaxation.

Modulation by intracellular chloride disappears if Gly channels are mutated to be cationic

Another possibility is that intracellular chloride affects channel gating as it permeates and therefore acts via the M2 pore-lining region. Anion permeation of homomeric α1 GlyR can be greatly reduced by introducing a negative charge in position −1′ of M2 (α1^A−1E, using the “prime” numbering for M2, in which α1R²⁵² is designated 0′; Fig. 5a), and this makes the channel cation selective (e.g., P_Cl/P_Na = 0.34; Keramidas et al., 2000, 2002). This mutation (Fig. 4c, Table 3) completely abolished the effect of intracellular chloride, making the decay of currents evoked by rapid Gly applications identical in the presence of high or low intracellular chloride. It is worth noting that this cationic GlyR retains an intact intracellular M1–M2 loop, so this experiment suggests also that this other intracellular domain does not play a major role in the effect of intracellular chloride.

Figure 5.

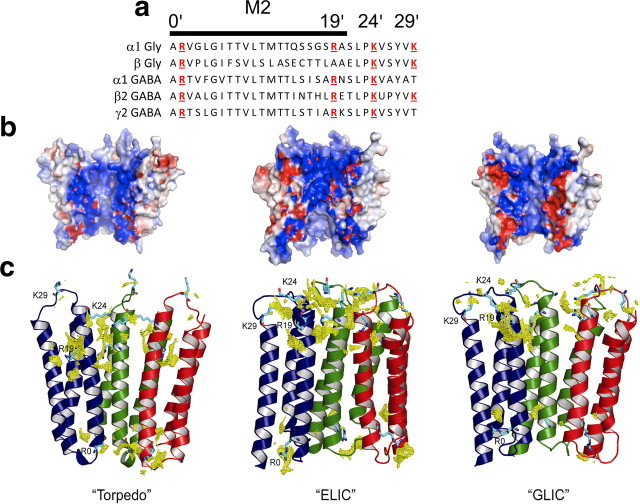
The channel pore: electrostatic surface potential and chloride density of the interior of the pore in homology models of the α1 GlyR. a, Alignment of residues in M2, the main pore-lining region of glycine and GABA channels. Positively charged residues are highlighted in red. b, Homology models of the α1 Gly homomeric receptor from different templates: the Torpedo receptor (PDB identification number 2BG9; Unwin, 2005), ELIC (PDB identification number 2VL0; Hilf and Dutzler, 2008), and GLIC (PDB identification number 3EHZ; Hilf and Dutzler, 2009). For clarity, the front two subunits of each pentamer have been removed. The electrostatic potential (calculated with PyMOL ABPS) is displayed in a range of −5kT (red) to +5kT (blue). c, Chloride densities for the same homology models (calculated with the program GRID; Goodford, 1985) are shown as yellow meshes. For clarity, only the M1, M2, and M3 helices of three subunits (colored blue, green, and red) are shown. The side chains of positively charged residues (R0′, R19′, K24′, and K29′) are shown in cyan.

Charged residues in the M2 domain of α subunits are essential to the effect of chloride on GlyR and GABA receptors

We next asked which of the M2 residues (see the alignment in Fig. 5a) interact with permeant anions to change deactivation kinetics. We constructed several homology models based on known pentameric ligand-gated ion channel structures (from Torpedo, ELIC, and GLIC; Unwin, 2005; Hilf and Dutzler, 2008, 2009; Fig. 5b,c) to identify residues in the pore that are accessible to anions. We also performed electrostatics calculations and GRID (Goodford, 1985; Fig. 5b,c) to identify regions of the structure that are energetically favorable for chloride binding.

We proceeded to mutate systematically the M2 residues, extracellular to A−1′, that are likely to be exposed to the ions permeating the open channel, choosing the hydrophilic residues most conserved in the Gly/GABA M2 and the positions that are thought to be exposed to the pore environment on the basis of accessibility data for GABA and ACh channels (Xu and Akabas, 1993, 1996; Cymes et al., 2005).

The first obvious candidate is R0′. The role of this residue could not be examined, because GlyR α1 subunits mutated here fail to express currents both alone and in combination with the β subunit, regardless of whether the mutation is conservative (to K) or not (to A; data not shown). The lethal effect of mutating R0′ to N, E, A, or H is thought to be caused by failure of trafficking or assembly (Langosch et al., 1993; Lynch et al., 1997; Rea et al., 2002).

The mostly hydrophobic residues in the next section of M2 (6′-13′) may form the gate of the closed channel. The effect on chloride modulation of mutating L9′, T6′, or T13′ to alanine was hard to assess, because it produced spontaneously active α1 or α1β Gly receptors, making HEK-293 cells unhealthy (even if cultured in the presence of glycine antagonists) and agonist currents hard to measure against the high spontaneous background. In addition to that, the decay time of currents elicited by short Gly pulses was very slow in these mutants. The heteromeric α1^T13′Aβ GlyR was the only combination that did not open spontaneously. Its current relaxations retained chloride modulation, becoming almost three times faster in 10 mm intracellular chloride (53.0 ± 8.0, n = 8 vs 118.9 ± 9.5, n = 10; p = 0.031).

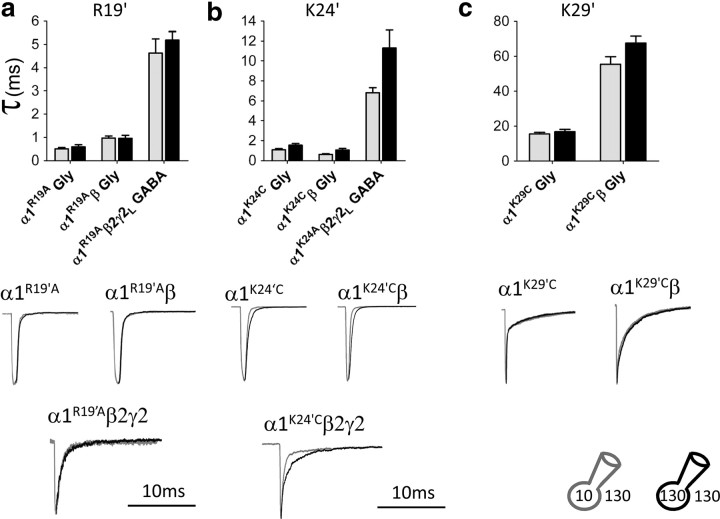
Above T13′, most GlyR and GABAR subunits contain three positively charged amino acids in M2 and in the M2–M3 loop, forming rings of charges in this part of the pore. We mutated, one at a time, these residues (R19′, K24′, and K29′) in α1 homomeric GlyRs to A or C and measured the effect of changing intracellular chloride. As shown in Figure 6, a and c, mutating the positive charge in 19′ or 29′ abolished the effect of chloride on agonist current decay. The R19′A mutation had also a major effect per se on channel deactivation, making it ∼30-fold faster than in wild type and almost insensitive to intracellular chloride (Fig. 6a, Table 3; decay τ, 0.48 ± 0.05 ms, n = 7 in 131 mm Cl⁻ vs 0.42 ± 0.05 ms, n = 11 in 10 mm Cl⁻, i.e., a 14% decrease in low chloride). Mutating this residue to L or Q causes startle disease, a loss-of-function GlyR channelopathy in man (Shiang et al., 1993; Langosch et al., 1994), so it is not surprising that the currents we record, in response to a synaptic-like application of Gly, also have a much faster decay. It is conceivable that this residue is not involved in mediating chloride modulation but that mutating it changes channel deactivation so much that the effect of chloride becomes undetectable or is somehow occluded downstream of the chloride binding site(s). However, another mutation in this area, K29′C, also abolishes the effect of intracellular chloride but without affecting the time course of deactivation (Fig. 6c, Table 3). In this mutant, the agonist current decay time constant was very similar to that of wild-type channels (weighted τ, 16.8 ± 1.3 ms, n = 11 in 131 mm Cl⁻ vs 15.5 ± 1.0 ms, n = 12 in 10 mm Cl⁻, i.e., an 8% decrease). Mutating the middle residue (K24′C), another position associated with startle disease in man (Lewis et al., 1998), had an intermediate effect, shortening deactivation by ∼10-fold and halving the effect of chloride (Fig. 6b, Table 3; average weighted τ, 1.54 ± 0.17 ms, n = 12 in 131 mm Cl⁻ vs 1.08 ± 0.12 ms, n = 5 in 10 mm Cl⁻, i.e., a 30% decrease in low chloride).

Figure 6.

Mutating the positively charged residues in the extracellular part of the M2 domain abolishes the effect of intracellular chloride concentrations on the rate of current relaxation. a, Neutralizing the positive charge in position 19′ of the α subunit of the α1, α1β Gly, and α1β2γ2 GABA receptor by mutating Arg to Ala abolishes the effect of intracellular chloride on the relaxation of inward current responses. The weighted decay time constants are the same in low intracellular chloride (10 mm; gray columns and traces) and in high intracellular chloride (131 mm; black columns and traces). This mutation also speeds up the current decay. b, The chloride effect is reduced but not abolished if a more extracellular residue is neutralized (mutation K24′C). c, Neutralizing the most extracellular of the three charged residues (present only in GlyR subunits, mutation K29′C) abolishes the effect of intracellular chloride but leaves the decay time of the current response unchanged. Mutations of the positively charged residues on non-α subunits did not affect the sensitivity to chloride modulation (see Table 3).

A similar pattern was observed when the three mutations were expressed in the α subunit of heteromeric α1β GlyRs or in the α subunit of the α1β2γ2_L GABA receptor (Fig. 6, Table 3). Thus, intracellular chloride modulation was abolished in both α1^R19′Aβ and α1^K29′Cβ, although the two mutations had opposite effects on the deactivation time course, with a 15-fold speeding up and a fourfold slowing, respectively. Mutating the middle residue, α1^K24′Aβ, again speeded up deactivation and reduced, but did not eliminate, the effect of intracellular chloride. In the GABA receptor, only two positive charges are present in α1 (position 29′ is a T), but the effect of chloride was abolished or much reduced by mutations R19′A and K24′A, respectively.

When we extended our mutational scan to the equivalent positions of the non-α subunits, we found that the mutations that abolished intracellular chloride modulation in the α subunits were ineffective when inserted in the non-α subunits of the same receptors (i.e., GlyR β and GABAR β2 and γ2_L; Table 3). Mutation of these residues in the non-α subunits had variable effects on the channel kinetics per se. In particular, neutralizing K24′ and K29′ in the GlyR β subunit left channel deactivation practically unchanged, whereas similar mutations in positions 19′ and 24′ of the GABAR β2 and γ2_L subunits accelerated deactivation by up to approximately twofold.

Permeant ions and voltage dependence of anionic receptors

We proceeded to test whether other permeant anions reproduced the effect of chloride, by replacing almost all of the internal and external chloride with an equimolar amount of thiocyanate (SCN⁻; residual chloride, 6.4 mm). Thiocyanate was chosen because it is the most permeant ion in anionic Cys-loop channels.

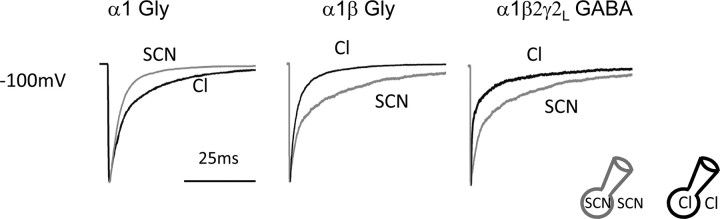
As shown by the traces in Figure 7, the time course of decay of synaptic-like GlyR or GABAR currents is strongly influenced by the nature of the permeating ion. Deactivation in SCN⁻ was slower than in chloride for the heteromeric receptors α1β GlyR and α1β2γ2_L GABAR (Table 4, Figs. 7, 8). These channels are known also to have a lower unitary conductance in thiocyanate, in line with the idea that thiocyanate ions binds more tightly than chloride in their pore (Bormann et al., 1987). However, this was not the case in homomeric α1 GlyR, in which deactivation was faster in thiocyanate than in chloride.

Figure 7.

The time course and voltage sensitivity of current relaxations are shaped by the nature of the main permeating ion and its interaction with the channel. Replacing intracellular and extracellular chloride (black traces) with SCN (gray traces) drastically alters the time course of the current relaxation for Gly and GABA receptors in a manner that differs for the different channel types.

Table 4.

Effect of holding potential on the time course of agonist-induced chloride and thiocyanate currents for wild-type and mutant Gly and GABA receptors

Receptor type	τ60mV/τ−100mV
	Cl	SCN
Gly α1	4.0 ± 0.4 (10)	2.2 ± 0.2 (10)
Gly α1R19′A	1.2 ± 0.1 (10)
Gly α1A−1′E (cationic)	1.6 ± 0.1 (10)
Gly α1β	3.0 ± 0.4 (9)	1.4 ± 0.3 (8)
Gly α1R19′Aβ	1.5 ± 0.1 (7)
GABA α1β2γ2	1.7 ± 0.2 (6)	1.0 ± 0.1 (6)
GABA α1R19′Aβ2γ2	1.7 ± 0.3 (7)

Outside-out agonist relaxations were obtained as in the previous experiments. The columns show the magnitude of the effect of holding potential as the ratios between the weighted time constants of decay at + 60 mV and that at −100 mV holding potential, with SEM and (in parentheses) the number of patches. This effect is strongly decreased or abolished when chloride is replaced with SCN. Neutralization of the charged residues in the 19′ position of the α1 M2 domain reduces drastically the voltage dependence of the current relaxation of α1 and α1β Gly receptors.

Figure 8.

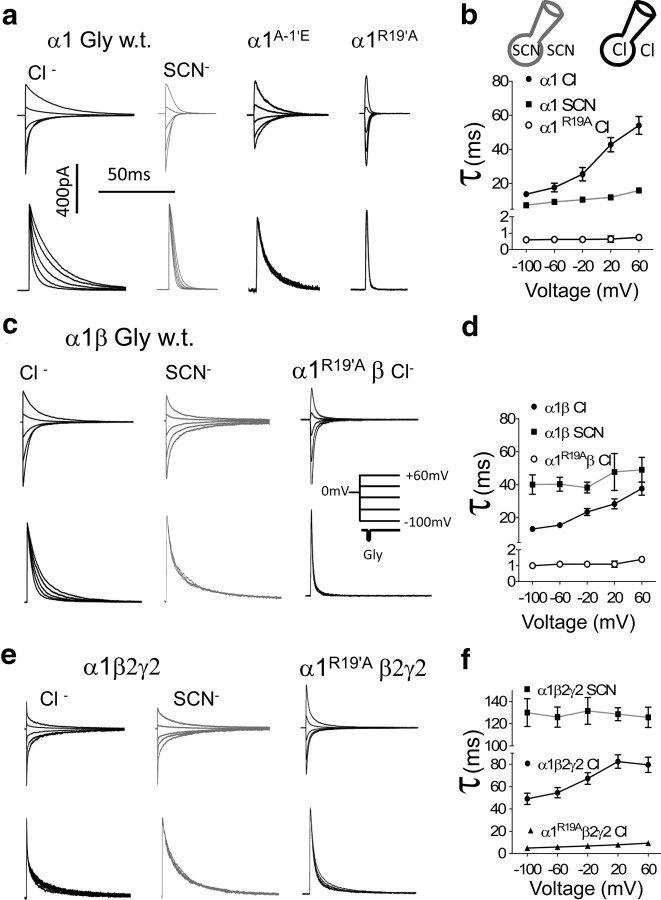
The nature of the permeating ion affects the time course of the current relaxation and its voltage dependence for α1 and α1β Gly receptors and for α1β2γ2 GABA receptors. Replacing symmetrical high chloride (black) with SCN (gray) changes the time course of the current relaxation Gly and GABA receptors over a range of voltages (from −100 to +60 mV) as shown in a (Gly homomeric), c (Gly heteromeric), and e (GABA). The bottom part of these panels shows the same traces normalized to their peaks and inverted as necessary to facilitate comparison of the decay phase at each voltage. b, d, and f show the values of the weighted τ of wild-type and mutant GlyR and GABAR plotted against the holding potential. Note how the decay of wild-type currents carried by chloride slows with depolarization, whereas currents carried by thiocyanate are almost insensitive to voltage. The effect of voltage is also abolished in chloride-insensitive mutants, such as the GlyR mutated to be cationic (α1^A−1′E, third family of traces in a), the α1^R19′A mutants in both homomeric and heteromeric Gly receptors (last families of traces in a and c), and the α1^R19′Aβ2γ2 GABA receptors (last family of traces in e) (see also Tables 3, 4).

The traces in Figure 8, a, c, and e, are families of agonist responses obtained at a range of holding potentials and show another important effect of the choice of permeant ion. Currents carried by thiocyanate are much less sensitive than chloride currents to the effect of depolarization on their time course. When chloride carries the current, the decay of homomeric GlyR currents slows by approximately fourfold as the holding potential is changed from −100 to +60 mV (τ₊₆₀/τ₋₁₀₀, 4.0 ± 0.3, n = 10; Fig. 8b, filled circles), but this effect of voltage is halved for thiocyanate currents (to 2.2 ± 0.2, n = 10; Fig. 8a, second family of traces; Fig. 8b, filled squares). Similar effects were observed for heteromeric α1β GlyR and α1β2γ2_L GABAR (Fig. 8, Table 4). This finding raises the possibility that voltage sensing in Cys-loop channels requires an interaction between the channel and the ions permeating the pore (Ascher et al., 1978; Marchais and Marty, 1979). If that is true, the same interventions that abolished chloride modulation should also reduce the voltage dependence of currents carried by chloride. This prediction was confirmed by the experiments in Figure 8a, in which engineering the homomeric Gly channel to be cationic made it much less voltage dependent (τ₊₆₀/τ₋₁₀₀, 1.6; Table 4). In agreement with this, the most effective mutation on chloride modulation, R19′A, also made the decay of chloride currents completely insensitive to the holding potential. This was true for homomeric α1 GlyR (Fig. 8a, and open circles in b) and for heteromeric α1β GlyR and α1β2γ2_L GABAR (mutations in the α subunits; Fig. 8, Table 4).

Discussion

Our data show that the deactivation time course of the main anion-selective channels in the Cys-loop superfamily is profoundly affected by the concentration and nature of the permeant ions in both the intracellular and extracellular compartments. This effect was easy to detect when we changed intracellular chloride concentrations and measured chloride efflux. On the contrary, the effect of extracellular chloride concentrations on the time course of chloride influx became apparent only when intracellular chloride was drastically reduced.

Figure 9a shows the simplest possible way in which a permeant ion can affect channel open time: the permeant ion prolongs deactivation while it is going through the pore, interacting at a single site (red dot in the middle), by either directly preventing the gate from closing or somehow stabilizing the open state of the protein. This single site is equally accessible to intracellular and extracellular ions concentrated in the inner and outer vestibules (red dots). This explanation is much too simple to account for all our observations, in particular for the differences in the effects of intracellular and extracellular chloride on outward and inward currents. This is not surprising, given that these channels contain at least two binding sites for anions (Bormann et al., 1987). The diagrams in Figure 9, b and c, show a scheme for the effect of the permeant ion that allows us to explain all the results of experiments with different chloride concentrations and holding potentials, while keeping assumptions simple and plausible in the light of what we know of the channel structure. The pore of Cys-loop channels is thought to consist of a wide extracellular vestibule, which narrows and widens again (but to a lesser extent) toward the intracellular compartment (Unwin, 2005; Paas et al., 2005; Hilf and Dutzler, 2009; Bocquet et al., 2009; Pittel et al., 2010, Hibbs and Gouaux, 2011). We know that both the extracellular and intracellular vestibules of anion-selective channels contain positively charged residues, whose side chains are exposed to the pore environment, concentrate the permeant ions, and influence single-channel conductance (O'Mara et al., 2005; Ivanov et al., 2007, see also Hansen et al., 2008; Song and Corry, 2010). In our diagrams, the permeant ion is depicted to affect channel kinetics at a site in the narrowest point (“active site,” dashed line) by the simplest, foot-in-the door effect (it is unknown whether that is the case). At negative holding potentials with high extracellular chloride, chloride goes out, and this site is vacated relatively quickly, as the ions exit through the wide outer vestibule (thick arrows in both diagrams in Fig. 9b). If intracellular chloride is high (Fig. 9b, right diagram), the occupancy of the active site is kept high, because it is constantly replenished by the ions concentrated in the inner vestibule. It must be the rate of chloride reaching this active site from the inside that limits its occupancy and its effect, because reducing intracellular chloride strongly speeds up deactivation (Fig. 9b, left diagram, see representative experimental traces).

Figure 9.

A hypothetical structural basis for the effects of chloride on channel deactivation. a, In the simplest mechanism, intracellular and extracellular chloride ions (red dots) equilibrate with a single site, in the middle of the pore, which mediates a foot-in-the-door effect. This site is equally accessible to intracellular and extracellular chloride, concentrated in the vestibules. This scheme cannot explain why changes in extracellular chloride can change currents carried by chloride inflow only when intracellular chloride is very low. b, A hypothetical mechanism for the effect of intracellular chloride on chloride outflow. The channel pore here is more realistic in that it is asymmetrical and its extracellular vestibule is wider than the intracellular one. The concentrations of chloride in the bulk extracellular and intracellular solutions are depicted as blue bands with red dots representing some of the chloride ions. These ions can move (arrows), as the current flows, to occupy a more central position (active site) in the channel gate (gap in the black line). Occupancy at this site affects current kinetics (see representative experimental traces for each condition). Occupancy here is controlled by the intracellular chloride concentration, because exit from this site through the wide extracellular vestibule is fast and non-rate limiting (thick arrows), regardless of extracellular chloride concentration. c, When chloride flows into the cell, occupancy of the central “active” site is controlled by chloride exit through the narrow inner vestibule. This remains the rate-limiting step (thin arrow) even with intracellular chloride as low as 15 mm and changes in extracellular chloride have no effect. d, For currents carried by chloride inflow, exit from the active site through the narrow intracellular vestibule becomes fast (thick arrow) and ceases to be rate limiting when intracellular chloride is very low (4 mm). Now occupancy of the active site is controlled by the extracellular chloride concentration and increasing it slows the channel closing.

The bottom four diagrams show what happens when chloride goes in (positive holding potentials). The active site now can lose chloride only to the narrow inner vestibule and the intracellular compartment, and it is this exit that is rate limiting. Even if intracellular chloride is lowered from 130 to 15 mm (Fig. 9c), exit rate stays slow, keeping the active site occupancy long and therefore the channel stays open a long time. Because the inner vestibule is narrow and controls chloride exit, deactivation does not depend on replenishing the active site from the outside. Thus, reducing extracellular chloride concentration has no effect on deactivation unless we drastically reduce intracellular chloride to 4 mm (Fig. 9d), when presumably the exit toward the intracellular compartments becomes fast and non-rate limiting.

The recently published structure of the Caenorhabditis elegans glutamate-gated chloride channel (Hibbs and Gouaux, 2011) shows that anions can interact with the pore at two different types of sites. One is the narrowest part of the actual permeation path, in which anions shed part of their solvation shell (anion-selective channels have a slightly smaller diameter than cation-selective ones; Keramidas et al., 2002). The other sites are positively charged “pockets” on the intracellular side of the likely channel gate. It is tempting to speculate that these sites are the structural basis for the stronger effects of intracellular versus extracellular chloride. In addition to that, these pockets may be different in heteromeric channels, given they are delimited by the −2′ residue, which is a Pro in the α subunits but an Ala in the β subunits of GlyR or GABA_A.

Modulation by anions was seen to a greater or smaller extent in all the three channels we tested (homomeric and heteromeric glycine channels and heteromeric GABA_A channels) and was suppressed if the channel anion selectivity was engineered away by mutating the pore-lining M2 domain. This suggests that the interaction of the appropriate ion with the appropriate M2 residues is key to this effect. Not all of the M2 residues can be examined by mutations, because all mutants of R0′ are lethal to channel expression and/or function (Langosch et al., 1993; Lynch et al., 1997; Rea et al., 2002). Nevertheless, several positions in the external vestibule of this domain were found to be important for the permeant ion effect, in particular, the positive charge of residues 19′ and 29′ of the principal (α) subunit. Notably, eliminating one or the other of these positive charges suppresses the permeant ion effect, regardless of the direction of ion flow. Interestingly, the mutations that remove the effect of chloride on deactivation (R19′A or A−1′E, which makes the channel permeable to cations) abolished also the voltage dependence of all the anion-selective channels we tested. Thus, the correct interaction of the permeant anion with the pore is needed also to make the currents slower at positive holding potentials (as proposed for cationic channels; Ascher et al., 1978; Marchais and Marty, 1979). Indeed, the voltage dependence of the kinetics of these channels was suppressed also if we changed the main permeant ion (to thiocyanate).

The limitations of the structural information available for these channels (see homology models in Fig. 5; note that only one of the three charged residues, 29′, is conserved in the C. elegans GluCl channel; Hibbs and Gouaux, 2011) make it difficult to produce a robust, immediately testable hypothesis of how the mutations affect the anion modulation. In principle, eliminating the charge in the side chain of these positions could produce one of several distinct effects (or a combination of them). The simplest explanation would be that the mutation disrupts the anion binding site itself (regardless of whether the ion acts via a foot-in-the-door effect or in a more indirect way). This seems somewhat unlikely, given that there are several mutations that abolish anion modulation and that none of them is likely to be in the narrowest point of the channel. The position of these residues in the outer vestibule would at most suggest that their role is to increase the local concentration of the anions that are going to bind to the real “active” site. However, in this case, it is hard to see how deactivation kinetics when chloride goes out can be affected by mutating these outer residues but not by decreasing external chloride (see above). It would seem therefore that the effect of the mutations has to be more complex than this. Therefore, this uncoupling of the effect of permeant ions from deactivation could also involve interference of these residues with the transduction chain that leads from the binding site to the gate. The fact that the abolition of the effect of chloride is seen both with mutations that speed up deactivation (R19′A) and with mutations that leave it unchanged (K29′C) implies that the mutations do not completely disrupt gating, but a thorough kinetic analysis will be required to fully understand the effect.