Metal-Sulfur Valence Orbital Interaction Energies in Metal–Dithiolene Complexes: Determination of Charge and Overlap Interaction Energies by Comparison of Core and Valence Ionization Energy Shifts

Abstract

The electronic interactions between metals and dithiolenes are important in the biological processes of many metalloenzymes as well as in diverse chemical and material applications. Of special note is the ability of the dithiolene ligand to support metal centers in multiple coordination environments and oxidation states. To better understand the nature of metal-dithiolene electronic interactions, new capabilities in gas-phase core photoelectron spectroscopy for molecules with high sublimation temperatures have been developed and applied to a series of molecules of the type Cp₂M(bdt) (Cp = η⁵-cyclopentadienyl, M = Ti, V, Mo, and bdt = benzenedithiolato). Comparison of the gas-phase core and valence ionization energy shifts provides a unique quantitative energy measure of valence orbital overlap interactions between the metal and sulfur orbitals that is separated from the effects of charge redistribution. The results explain the large amount of sulfur character in the redox-active orbitals and the ‘leveling’ of oxidation state energies in metal-dithiolene systems. The experimentally-determined orbital interaction energies reveal a previously unidentified overlap interaction of the predominantly sulfur HOMO of the bdt ligand with filled π orbitals of the Cp ligands, suggesting that direct dithiolene interactions with other ligands bound to the metal could be significant for other metal-dithiolene systems in chemistry and biology.

INTRODUCTION

Though metal-dithiolene complexes have been known for nearly fifty years,^1,2 the discovery of their presence in Mo/W enzymes has stimulated additional interest in the versatility and applications of the metal-dithiolene unit.^3,4 The proposed catalytic cycles of these enzymes often involve multiple oxidation states as catalysis proceeds.^4–8 Molybdopterin (MPT), a cofactor unique to all mononuclear Mo/W enzymes,⁴ possesses an enedithiolate unit that binds the metal.⁸ While the exact function of the enedithiolate in MPT is still debated,⁹ it is likely needed to stabilize higher metal oxidation states during catalysis, thus leveling the energy required for electron transfer. This metal-dithiolene electronic interaction can also be utilized in applications ranging from sensors¹⁰ to photochemical¹¹ and electronic devices^12,13 to catalysts¹⁴ where the dithiolene ligands are used to stabilize metal centers in multiple oxidation states during electron transfer processes. To further the understanding of the role of metal-dithiolenes in biological systems as well as in chemical and material applications, it is helpful to have quantitative information and understanding of the energies associated with the metal-dithiolene interaction.

Fundamental studies of the electronic interactions in metal-dithiolenes began with the classic molecular orbital description of bent-metallocene-dithiolene complexes posited by Lauher and Hoffmann in 1976.¹⁵ From their interpretation, the non-innocent character of dithiolene ligands arises from the ability of the HOMO of the dithiolene fragment to donate electron density to the metal center through the formation of a covalent bonding interaction, provided the metal has an empty d orbital of the requisite energy and symmetry.

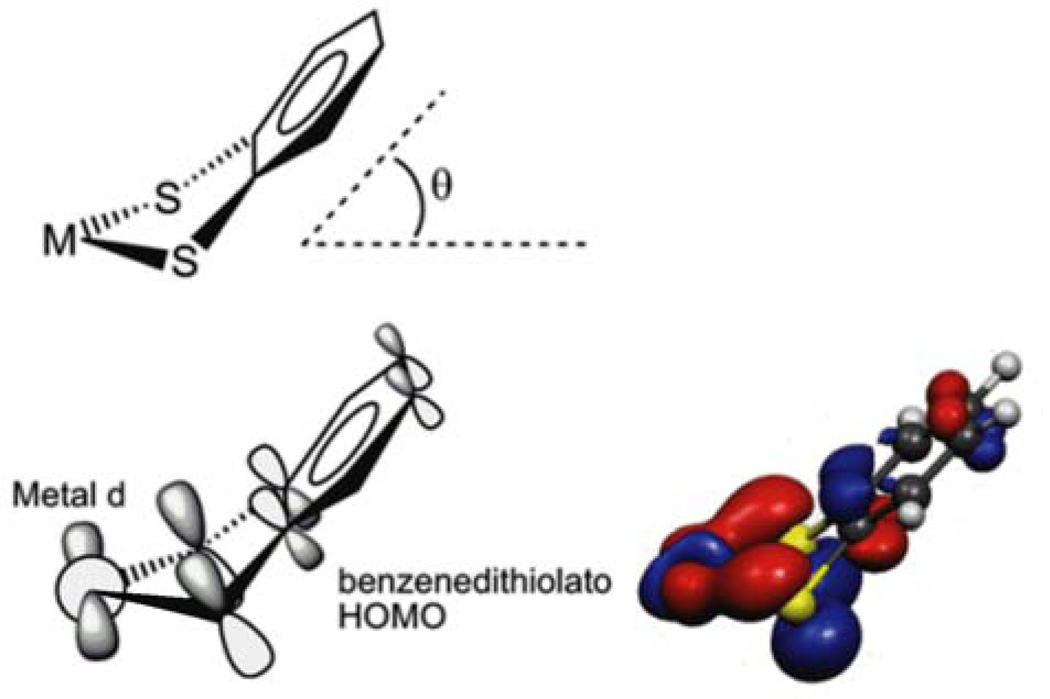
Figure 1 shows a schematic of the overlap interaction of the HOMO of a dithiolene, in this case the benzenedithiolato (bdt) ligand, with the pertinent metal d orbital, and depicts how the overlap interaction is modulated by the fold angle of the dithiolene. The HOMO of the planar dithiolene fragment is predominantly the symmetric combination of the out-of-plane S pπ orbitals (hereafter labeled S_π+) with a smaller but important contribution from the ene π bond that is antibonding with respect to the S pπ orbitals and hence destabilizes the S_π+ orbital. In the bonding of the dithiolene to the metal, the fold angle (θ) is defined as the angle between the metal-disulfur plane and the disulfur-ene plane. At a fold angle near zero degrees the dithiolene S_π+ orbital and metal d orbital are nearly orthogonal, and as the fold angle increases the overlap between these orbitals increases. The redox properties of metal-dithiolenes are the result of sulfur-based orbitals that are at energies similar to those of the metal d orbitals and capable of donating electron density to the metal as the occupation of the metal d orbital decreases from d² to d¹ to d⁰ and the fold angle increases.

Figure 1.

A depiction of the metal-dithiolene interaction showing the orbital overlap of the HOMO from a benzenedithiolato ligand with a metal d orbital and the definition of the metal-dithiolene fold angle θ.

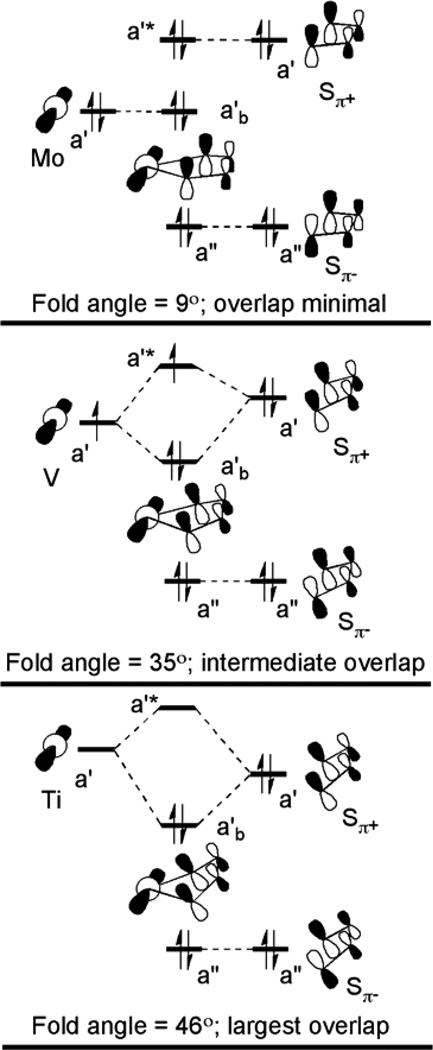
A strong correlation has been found between the formal metal electron count and the degree of folding.^16–18 This is illustrated in Figure 2 for a series of bent-metallocene-benzenedithiolato (bdt) molecules of the form Cp₂M(bdt) (M = Mo, V, Ti) where the metals are in the same formal oxidation state but have different formal metal d electron counts (d², d¹, and d⁰). When the metal d orbital is doubly occupied, as in the case of the Mo complex at the top of Figure 2, the interaction with the S_π+ orbital is a net antibonding filled-filled interaction, and the structure shows a fold angle near zero degrees to minimize the overlap interaction.¹⁶ When the metal d orbital is unoccupied the S_π+ orbital can donate electrons to the metal in a bonding interaction, and the fold angle increases for optimum interaction, as for the Ti complex at the bottom of Figure 2.¹⁷ When the metal d orbital is singly occupied intermediate fold angles are observed as for the V complex in the middle of Figure 2.¹⁸ It is noteworthy that the known enzyme crystal structures also show a variation in the fold angle between the dithiolene and the Mo center.^19–23

Figure 2.

Molecular orbital depiction of the interaction of the metal and S_π+ and S_π− orbitals in the model compound series, Cp₂M(bdt) (M = Mo, V, Ti), and the corresponding change in the fold angle determined from crystal structures of the molecules.

Not shown in the qualitative orbital interaction diagram of Figure 2 are the other occupied orbitals of the Cp₂M(bdt) complexes. The next set of occupied orbitals below the frontier orbitals depicted in Figure 2 derives predominantly from the occupied Cp π orbitals (e₁" orbitals of the Cp⁻ fragment in D_5h symmetry) that donate to the metal center. As will be seen, these orbitals of the cyclopentadienyl ligands are relevant to the discussion. Deeper still are the direct metal-sulfur σ bonds that account for the chelate bonding. In the molecular orbital description of the full complexes the direct metal-sulfur σ bonds are orthogonal to the frontier orbitals. This orthogonality is depicted qualitatively in Figures 1 and 2 where the direct metal-sulfur σ bonds shown as lines between the metal and sulfur atoms are near the nodes of the idealized metal-based orbital, which is necessary for this molecular orbital to be the most stable of the metal-based orbitals. Thus the metal-sulfur σ bonds are expected to have less interaction with the lowest metal-based orbital due to both avoided overlap and larger energy separation from the orbitals in Figure 2.

Metal-dithiolene compounds and molybdoenzymes have been the focus of many spectroscopic studies of the electronic structures.^8,23–27 X-ray absorption spectroscopy has been used to help identify the covalency of the metal-dithiolene interaction as well as determine the oxidation states for the ligand and metal.^28–31 Gas-phase ultraviolet photoelectron spectroscopy (UPS) studies have shown the leveling effect that dithiolenes have on the valence ionizations.^23,32 Previous valence photoelectron studies of the molecules in Figure 2 have shown that the metal-dithiolene interaction effectively maintains the highest occupied molecular orbital ionization in a narrow energy range, which helps to level the redox potentials between d², d¹, and d⁰ states during a catalytic cycle.^32,33 While these studies have helped reveal the nature of the metal-dithiolene interaction, they only qualitatively give a sense of the stabilizing energy generated from the folding interaction because of the inability to separate the shifts in energy due to the changes in orbital overlap interaction from those due to changes in the charge distribution.

APPROACH

The purpose of the present study is to separate and determine, quantitatively, the energy effects of the charge potential and orbital overlap in the metal-dithiolene interaction. Figure 2 shows a qualitative molecular orbital diagram of the relative energies and interactions between the benzenedithiolate orbitals and the metal d orbital. The task is to experimentally determine the energies of all levels in Figure 2. The key valence orbitals of the metal-dithiolene interaction identified in the study by Lauher and Hoffmann are the bonding and antibonding combinations of the metal d and dithiolene S_π+ orbitals, labeled a'_b and a'* respectively, in Figure 2. The third orbital shown in Figure 2, labeled a", is predominantly the antisymmetric combination of the two S pπ orbitals (hereafter labeled S_π−). This orbital has both planar and perpendicular nodes in the bdt fragment and thus little overlap with the metal d orbitals in this energy region. As will be seen, the bdt S_π− orbital is useful in revealing the charge potential experienced by the dithiolene in the molecule.^23,32

The energies of ionization from the bonding a'_b and antibonding a'* molecular orbitals and the nonbonding a" molecular orbital are measured by gas-phase valence photoelectron spectroscopy. The ionization energies are directly related to the negative of the orbital energies in a Hartree-Fock calculation by Koopmans’ approximation, neglecting electron correlation and electron relaxation in a ‘frozen’ molecular ion.³⁴ Similar relationships to the experimental ionization energies have been discussed for Kohn-Sham orbital energies obtained from density functional theory calculations.³⁵ Of course, molecular orbitals are theoretical and conceptual approximations to the total electron wavefunction and their energies are approximate contributions to the total energy. However, the actual molecular ionization energies are fundamentally important without these theoretical constructs because the energies contribute directly to thermodynamic cycles of molecular behavior, and therefore are the more experimentally relevant quantities. For instance, the gas-phase ionization energy of a molecule is the major determining factor of the solution oxidation potential.^36,37 This study focuses on experimental energy measurements that are true differences in total energy between molecular electronic states, using the language of molecular orbitals.

The challenge for determining the experimental interaction energies depicted in Figure 2 is to determine the energy of the bent-metallocene fragment metal d orbital on the left of the interaction diagrams and the bdt fragment orbitals on the right of the diagrams. The energies of the fragment orbitals within the full molecule (hereafter referred to as fragment orbitals energies, FOEs) are shifted from the energies of the orbitals in the isolated fragments primarily due to the charge redistribution within the molecule when the ligand is bound. The charge redistribution can have a large effect on the charge potential contribution to the ionization energies of the orbitals, with smaller and generally proportional contributions from the change in electron relaxation and correlation with ionization. The shifts in core ionization energies are primarily a measure of the change in charge potential because the core orbitals have little overlap interaction energies with other orbitals. The valence FOEs are also similarly affected by the change in charge potential. Knowing the relationship between the fragment core and valence charge distribution shifts allows for the determination of the FOEs, and a complete experimental orbital interaction energy diagram based on ionization energies can be obtained that is conceptually similar to a theoretical molecular orbital energy diagram.

CORRELATION OF CORE AND VALENCE IONIZATION ENERGY SHIFTS

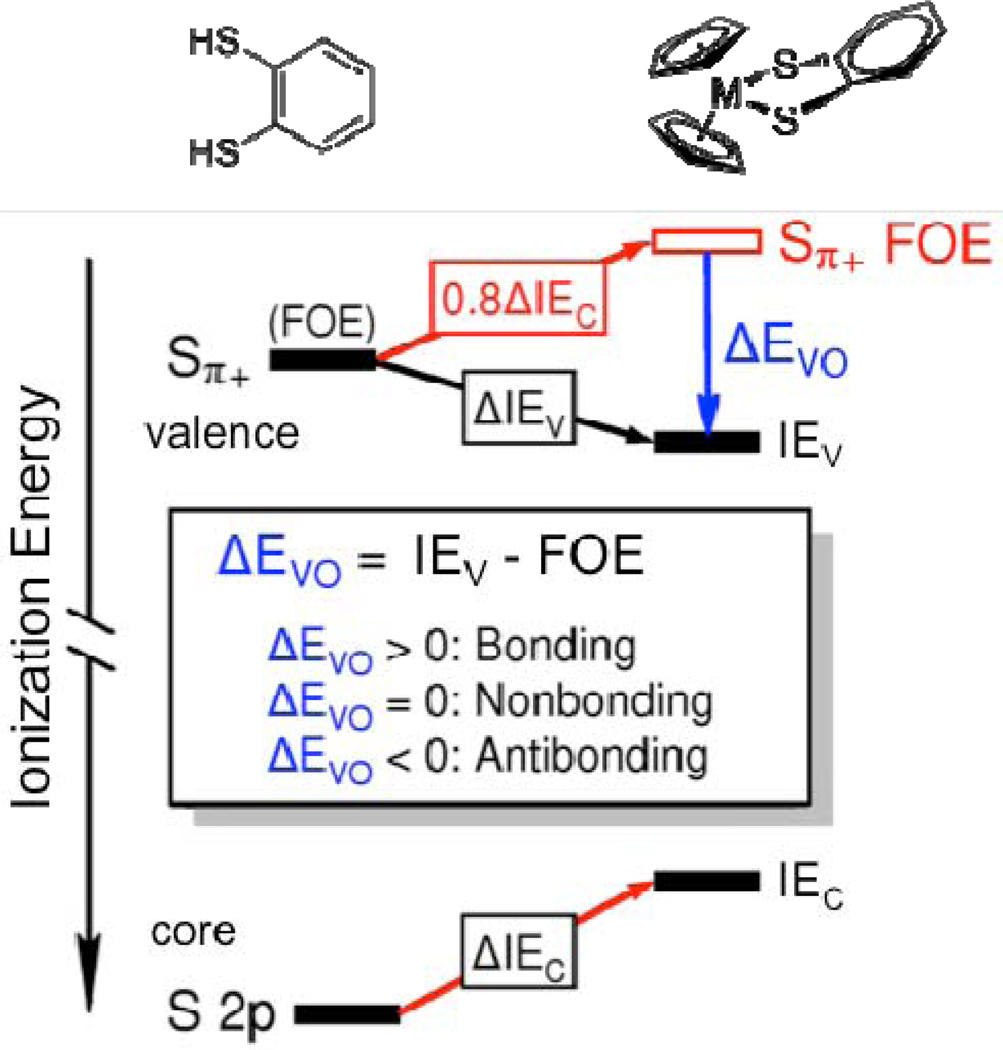
The principles of this analysis were originally formulated by William L. Jolly^38–40 and are illustrated schematically for the bdt S_π+ FOE in Figure 3. Jolly found empirically that the ionization energy shift of a valence orbital localized on an atom, ΔIE_V, was 0.80 ±0.07 of the ionization energy shift of the core orbital on that atom, ΔIE_C.^38–40 Deviations of ΔIE_V from 0.80ΔIE_C were accounted for by the overlap of valence orbitals in bonding and anti-bonding interactions. Here we extend the concept of a localized orbital ionization potential (termed LOIP in Jolly’s analysis), in which the orbital is localized on a single atom, to the concept of a fragment orbital energy (FOE), in which the orbital may be delocalized within a fragment of a complex. Deviation of the actual molecular ionization energy from the corresponding FOE is a result of the overlap interaction energy of the fragment orbital with the rest of the molecule. The difference between the experimentally observed valence orbital ionization, IE_V, and the predicted fragment orbital energy, FOE, is termed the valence overlap interaction energy ΔE_VO. In this formalism, a negative ΔE_VO corresponds to an anti-bonding interaction where the measured molecular ionization energy is lower than predicted by the change in charge potential alone. A positive difference in ΔE_VO corresponds to a bonding interaction where the measured molecular ionization energy is more stable than the corresponding FOE. A value of zero, where the predicted FOE and the measured molecular ionization energy are identical, indicates a net non-bonding or zero-overlap interaction.

Figure 3.

A schematic depiction of the S_π+ orbital interaction energies. The black bars are the experimentally measured ionization energies of the valence (IE_V) and core (IE_C) orbitals with the observed valence and core ionization shifts between the two molecules given by ΔIE_V and ΔIE_C, respectively. For H₂bdt (shown on the left) the valence ionization energy is the same as the S_π+ fragment orbital energy (FOE) because there is no overlap of this orbital with the H atom orbitals. For Cp₂M(bdt) (shown on the right) the fragment orbital energies are shifted due to the change in charge potential (depicted by the red arrows). The valence ionization shift due to the change in charge potential is approximately 0.8 times core ionization energy shift ΔIE_C between the two molecules. Deviation of the observed valence ionization energy from the projected S_π+ fragment orbital energy is the shift in energy due to valence orbital overlap, ΔE_VO. This figure depicts a bonding interaction in which the valence ionization energy IE_V is stabilized by orbital overlap interaction compared to the projected S_π+ FOE, which yields a ΔE_VO > 0.

Jolly and others have demonstrated the efficacy of this method on a diverse array of small molecules^{38,39,41–43} and some low sublimation temperature organometallic systems.^44–48 However, the main hurdle in allowing this technique to be more applicable to a wide array of inorganic and organometallic systems was the difficulty of measuring gas-phase XPS ionization energies for high sublimation temperature molecules. Our recent development of a gas-phase X-ray photoelectron spectrometer for controlled high temperature (currently up to 220°C) sublimations of solid samples at low pressures (< 10⁻⁵ Torr) has made the study of these systems possible.⁴⁹

MATERIALS, INSTRUMENTS AND METHODS

Synthesis

The compounds, Cp₂M(bdt) (M = Ti, V, Mo) and Cp₂MoH₂ were synthesized according to previous literature methods^{16, 50} or modifications as described below. All solvents and the starting materials, Cp₂MoCl₂ and Cp₂TiCl₂ (Alfa Aeser), Cp₂V (Strem) and 1,2-benznedithiol (Aldrich), were purchased and used without further purification. Identification of the compounds was aided by electronic absorption spectroscopy (solutions in dichloromethane using a modified Cary 14 with OLIS software, 200–900 nm) and mass spectrometry (direct ionization using a JEOL HX110).

Cp₂V(CH₃)₂

Dimethylvanadocene was prepared following a modified version of the method by Foust and Rausch.⁵¹ Dichlorovanadocene (1.07 g, 4.25 mmol) was weighed under an inert atmosphere into a 250 mL Schlenk flask equipped with a stirbar. To this was added 80 mL of dry and degassed toluene. Methyllithium (4.25 mL of 1–2 M in ether) was added to a 10 mL Schlenk flask under an inert atmosphere. Both flasks were cooled to 0 °C under Ar, and the methyllithium solution was then carefully cannula transferred over the course of two hours to the stirring dichlorovanadocene suspension, during which time the solution had become dark in color. The reaction mixture was stirred for an additional hour at room temperature and then filtered over an M frit (under Ar) into a 250 mL round bottom flask. The collected solid on the frit was not washed. The filtrate solvent was completely removed (without heating) in vacuo to yield a black solid. The 250 mL flask with the black solid was equipped with a cold finger, and the pressure reduced to 0.01 torr. The flask was then heated to 45 °C and left under active vacuum for 15 hours. The desired product was obtained as a black solid on the cold finger and was collected under an inert atmosphere (224 mg, 25%). X-band CW EPR (toluene, rt): g_iso = 2.00, a_V = 64 G, a_H = 4.7 G.

Photoelectron spectroscopy

The gas-phase UPS spectra were collected according to published methods.⁵² The instrument is interfaced via a National Instruments PCIe-6259 multi-function data acquisition card with customized software. Resolution measured during data collection (taken as the FWHM of the Ar ²P_3/2) was 0.025–0.030 eV. The sublimation temperature of the Cp₂Mo(bdt) and Cp₂Ti(bdt) samples (measured at 10⁻⁵ Torr and using a “K” type thermocouple attached to an aluminum sample cell) was 180–200°C. The sublimation temperature for Cp₂V(CH₃)₂ was 30–40°C. H₂bdt vaporized at room temperature and was introduced to the instrument via a Young’s tube connected to the gas inlet system. The samples showed no signs of decomposition during collection. The UPS spectrum of Cp₂V(bdt) was collected previously.³² Peak positions for ionization bands were determined by analytical representations of the bands with asymmetric Gaussians as described previously.⁵³ The standard deviation in the determination of peak positions is less than ±0.02 eV.

The gas-phase XPS spectra were collected on a custom built gas-phase photoelectron spectrometer built around a 360 mm mean radius, 80 mm gap hemispherical analyzer⁵⁴ (McPherson). The ionization source was Mg Kα, referenced at 1253.46 eV from a Spec XR 50 dual anode X-ray gun controlled by a Spec XRC 1000 controller. The measured emission current of the source was 20.1 mA. Two sheets of 0.002 mm thick aluminum, one located on the X-ray gun cap and the other on the sample cell⁵⁵ were used to limit Bremsstrahlung scattering reaching the sample. The aluminum window on the cell also served to effectively isolate the sample vapor from the X-ray source. The sample cell was a custom-made aluminum cell that could be heated via a resistive heater bar. Temperatures were monitored with a K-type thermocouple. The exit slit from the sample cell measured 0.76 mm × 6.35 mm. The entrance slit into the analyzer chamber measured 3 mm × 7 mm. The kinetic energies of the electrons were analyzed with a constant retarding potential (0.0 V) while sweeping the deflecting potential of the two spheres (positive inner sphere and negative outer sphere). Due to the ratio of the radius of the inner sphere to the outer sphere, a constant potential ratio between the two spheres of 0.80 V was used to focus electrons near the center of the hemisphere. The ratio of the kinetic energy of the electron to the deflecting potential of the outer sphere (KE/PE) was measured as 4.0569 by referencing the Xe 3d_5/2 (676.4 eV) to the Ar 2p_3/2 (248.6). The detector is an electron multiplier, run with an operating bias of 2000 V. The instrument and custom software for data collection and analysis are interfaced using a National Instruments PCIe-6259 multifunctional data acquisition card. The details of this interface have been described elsewhere.⁵² During data collection, spectra were calibrated to the Ar 2p_3/2 ionization at 248.6 eV. Resolution and sensitivity are proportional to the electron kinetic energy being measured. The FWHM of the Ar 2p_3/2 ionization (≈1000 eV kinetic energy) was around 2.5–3 eV for the experiments. Calibration to the Ar 2p_3/2 was made between individual scans of regions of interest during the experiment to keep instrumental drift to a minimum. In the gas-phase XPS experiments, the sublimation temperatures at operating pressures of 7.0×10⁻⁶–1.0×10⁻⁵ torr for the metal-dithiolene compounds were 180–200°C while Cp₂MoH₂ and Cp₂V(CH₃)₂ sublimed at 30–40°C. H₂bdt vaporized at room temperature and was introduced via an attached Young’s tube. There was no sign of decomposition of any of the compounds during the collection.

For the XPS experiments individual scans of the data regions of interest were saved and fit individually after correcting for background. The best fit was determined in a similar fashion to that described above for the UPS data. For the ionizations of the S 2p, a single Gaussian was used to fit the unresolved S 2p_3/2 and 2p_1/2 peaks (spin-orbit coupling of S 2p < 2 eV). Core ionization energies reported in the tables are the averages of seven to fourteen individual data collections and fits for the peaks of interest, and the standard deviations of the peak positions are reported with the averages. The individual data are presented in the SI.

Even without a high-intensity tunable photon source such as a synchrotron, sensitivities of this instrument are sufficient to analyze the core ionizations of sulfur, which has a relatively low photoionization cross section using a Mg Kα source (0.039 Mbarn at 1253.6 eV).⁵⁶ Thus, a readily accessible means to analyze the core ionization energies for a much broader range of organometallic systems, including the metal-dithiolene systems described in this study, is now available.

Computations

Electronic structure calculations were performed using the Amsterdam Density Functional theory suite (ADF 2008.01b, with default program parameters unless otherwise noted).^57–61 The geometries of the molecules were optimized using Becke’s exchange functional⁶² and Perdew’s correlation functional^63,64 (BP86) and a triple-zeta basis set with Slater-type orbitals and a single polarization (TZP) on all elements. Relativistic effects were accounted for using the Zero Order Regular Approximation (relativistic scalar ZORA).^65,66 Analytical frequency calculations were performed on all optimized structures and showed no imaginary frequencies. Vertical ionization energies were approximated as the ΔSCF between the geometry optimized ground state of the molecule and the cationic molecule of the same geometry. The wavefunction was transformed to a basis of the neutral bdt (S₂C₆H₄) and bent-metallocene (Cp₂M) fragment orbitals to evaluate the character of the molecular orbitals in terms of the fragment orbitals.

RESULTS AND DISCUSSION

The core and valence ionization energies along with the analysis of the fragment orbital energies (FOEs) and overlap interaction energies of the benzenedithiolate (bdt) ligand with the bent-metallocene fragments of the Mo, V and Ti complexes are collected in Tables 1–4. The valence ionization energies of the bent-metallocene-dithiolenes have been reported previously.^23,32 The gas-phase XPS core ionization spectra are shown in the Supporting Information, along with the statistical determination of the core ionization energies used in this analysis. The standard deviations in the determination of the core ionization energies are typically ±0.1–0.2 eV with the present instrumentation, and as much as ±0.3 eV for the V 2p_3/2 core ionizations where the cross-section for ionization is low and the spectra had poor signal-to-noise. This uncertainty in the absolute peak positions limits the precision of the orbital interaction energy analysis. However, the important quantities are the shifts of the ionizations, and the collective combination of the core and valence ionization energy shifts leads to a consistent picture of metal-dithiolene orbital interactions.

Table 1.

S 2p core and valence ionization energies (eV) and subsequent orbital interaction energy analysis for the bdt S_π− fragment orbital.

Compound	S 2p3/2 IE	ΔIECa	0.8ΔIEC	FOEb	IEVc	ΔEVOd
H2bdt	169.3±0.1	0.0	0.0	8.97±0.02	8.97±0.02	0.0	nonbonding
Cp2Mo(bdt)	167.2±0.2	−2.1±0.2	−1.7±0.2	7.3±0.2	7.24±0.02	−0.1±0.2	≈nonbonding
Cp2V(bdt)	167.2±0.2	−2.1±0.2	−1.7±0.2	7.3±0.2	7.21±0.0232	−0.1±0.2	≈nonbonding
Cp2Ti(bdt)	167.4±0.2	−1.9±0.2	−1.5±0.2	7.5±0.2	7.38±0.02	−0.1±0.2	≈nonbonding

^aCore ionization energy shift = S 2p IE(Cp₂M(bdt)) − 169.3.

^bS_π− fragment orbital energy observed for H₂bdt and indicated for the metal complexes = 8.97 + 0.8ΔIE_C.

^cObserved molecular ionization energies predominantly associated with S_π−.

^dOverlap interaction energy corrected for charge potential = IE_V − FOE.

Table 4.

V 2p core and valence ionization energies (eV) and orbital interaction energy analysis for the predominantly V 3d valence orbital of the bent-metallocene fragment.

Compound	V 2p3/2 IE	ΔIECa	0.8ΔIEC	FOEb	IEVc	ΔEVOd
Cp2V(CH3)2	518.7±0.3	0.0	0.0	6.42±0.02	6.42±0.02	0.0	nonbonding
Cp2V(bdt)	519.4±0.2	0.7±0.3	0.5±0.3	6.9±0.3	6.78±0.02(a'b)	−0.1±0.3	nonbonding

^aCore ionization energy shift = V 2p IE(Cp₂V(bdt)) −518.7.

^bPredominantly V 3d fragment orbital energy observed for Cp₂V(CH₃)₂ and indicated for Cp₂V(bdt) = 6.42 + 0.8ΔIE_C.

^cObserved molecular ionization energies predominantly associated with the V 3d orbital.

^dOverlap interaction energy shift corrected for charge potential = IE_V − FOE.

Benzenedithiolato fragment S_π− orbital ionization

Consider first the information for the bdt fragment S_π− orbital interaction with the bent-metallocenes shown in Table 1. This is the bdt fragment orbital that is not expected to have substantial overlap interaction with the bent-metallocene fragment and thus provides an initial test of the core-valence ionization correlation model in the absence of overlap interactions in the bent-metallocenes. In order to determine the bdt S_π− FOE, the core and valence ionization energies of the H₂bdt molecule are used as reference. In H₂bdt the hydrogen atoms bonded to the S atoms have no p orbitals with which to overlap with the out-of-plane S pπ orbitals, and thus the H₂bdt molecular ionization energy corresponding to removal of electrons from the S_π− orbital is also the S_π− FOE. When the dithiolate fragment bonds to the metal, the core and valence ionizations of the dithiolate fragment are shifted due to the increase in negative charge on the dithiolato fragment that destabilizes the orbitals to lower ionization energies.

Table 1 shows that the S 2p core ionization energies of the bdt ligands in the Mo, V, and Ti complexes are found to shift in each case by about 2.0 eV to lower ionization energy compared to the S 2p core ionization energy of H₂bdt. The shift to lower energy of the sulfur core ionizations in the complexes compared to the sulfur core ionization in H₂bdt is consistent with the formal 2– charge of the dithiolene coordinated to the metal. The more negative charge potential on the ligand destabilizes the core orbital and lowers the ionization energy. The shift is large in comparison to typical valence ionization shifts due to valence orbital overlap effects, and underscores the importance of taking into account the effects of charge redistribution. The similarity of the shift for each of the metal complexes is reasonable because each metal center formally has a 4+ charge, and the metal–sulfur distance, as measured in crystal structures, is around 2.4 Å for each complex, so the two-center charge potential effect is similar. The 0.2 eV smaller shift in the case of the Ti complex would indicate that bdt is a better donor in this case, which is expected because the Ti is formally d⁰ and has an empty d orbital to which the bdt can donate, but this cannot be concluded with confidence from the core ionizations alone due to the standard deviation of these experiments. However, the valence ionizations support this conclusion as discussed below.

In the core-valence ionization correlation model, about 80% of the change in the core ionization energy is also experienced by the valence ionization energies localized on that atom.³⁸ This shift is used to predict the fragment orbital energies (FOE) in the potential field of the molecule listed in Table 1. The experimentally observed molecular valence ionization energies associated with the S_π− fragment orbital are listed in this table as IE_V. The predicted S_π− FOE is the same as the measured IE_V for all three bent-metallocene-dithiolene complexes within the current standard deviation of our measurements (Table 1), indicating an essentially nonbonding interaction of the bdt fragment S_π− orbital with the bent-metallocene fragment orbitals within the approximations of this analysis. This result of an essentially nonbonding interaction of the S_π− fragment orbital with the metal is consistent with expectations based on the nodal properties of the orbitals, and contributes to validation of this analysis based on correlation of the core and valence ionizations. The ≈1.6 eV shift in the IE_V from H₂bdt to the metal-dithiolene complexes is fully accounted for by the S 2p core ionization energy shifts, and the size of this shift underscores the importance of adjusting the FOEs for the change in charge potential.

Cp₂Mo(bdt)

The focus turns now to the interaction energy of the bent-metallocene fragment metal d-based orbital with the bdt fragment S_π+ orbital as depicted in Figures 1 and 2. The Cp₂Mo(bdt) molecule formally has a d² electron configuration and the metal d-based orbital of the bent-metallocene fragment and the S_π+ orbital of the bdt fragment are each doubly occupied. The fold angle is small and therefore the overlap interaction between these two orbitals is expected to be small.

Cp₂Mo fragment metal d-based orbital ionization

The core and valence ionizations of the isoelectronic dihydride molecule Cp₂MoH₂ are used as references to determine the metal d–based Cp₂Mo fragment orbital energy in the Cp₂Mo(bdt) molecule. Again, the H atoms of Cp₂MoH₂ do not have occupied p orbitals for overlap interactions with the metal, so the metal-based HOMO ionization energy of Cp₂MoH₂ is the same as the FOE in this case. The shifts of the core and valence ionizations from the reference molecule Cp₂MoH₂ to Cp₂Mo(bdt) can be used to estimate the metal-based FOE in the latter molecule. The analysis is shown in Table 2. The Mo core 3d ionizations show an increase in ionization energy going from the dihydride to the dithiolato ligand of 0.7 eV. This yields a 0.6 eV shift of the predominantly 4d Cp₂Mo valence fragment orbital energy from the dihydride to the dithiolene complex, and predicts a FOE of 7.0±0.1 eV. As will be seen in the following section, this is about 0.3 eV more stable than the bdt S_π+ FOE. The energy match between these fragment orbitals would lead to significant filled-filled energy interaction if there is substantial overlap between the fragment orbitals. The observed a'_b ionization energy of the Cp₂Mo(bdt) molecule is 7.04±0.02 eV, essentially the same as the fragment orbital energy. Thus, the valence overlap interaction energy ΔE_VO for this metal d-based orbital with the dithiolene fragment is zero within the standard deviations of our measurements. This indicates an essentially non-bonding, zero-overlap interaction from the perspective of the metal-based orbital. As shown in Figure 2, this is consistent with the near zero fold angle of the bdt ligand with the metal, such that the bdt S_π+ fragment orbital is nearly orthogonal with the doubly–occupied metal d orbital. The agreement of the observed valence ionization energy with the energy predicted by the core–valence ionization energy correlation gives further support to the principles of this analysis.

Table 2.

Mo 3d core and valence ionization energies (eV) and subsequent orbital interaction energy analysis for the predominantly Mo 4d valence orbital of the bent-metallocene fragment.

Compound	Mo 3d5/2 IE	ΔIECa	0.8ΔIEC	FOEb	IEVc	ΔEVOd
Cp2MoH2	233.9±0.1	0.0	0.0	6.43±0.02	6.43±0.02	0.0	nonbonding
Cp2Mo(bdt)	234.6±0.1	0.7±0.1	0.6±0.1	7.0±0.1	7.04±0.02(a'b)	0.0±0.1	nonbonding

^aCore ionization energy shift = Mo 3d IE(Cp₂Mo(bdt)) − 233.9.

^bPredominantly Mo 4d fragment orbital energy observed for Cp₂MoH₂ and indicated for Cp₂Mo(bdt) = 6.43 + 0.8ΔIE_C.

^cObserved molecular ionization energies predominantly associated with the Mo 4d orbital.

^dOverlap interaction energy corrected for charge potential = IE_V − FOE.

Benzenedithiolato fragment S_π+ orbital interaction

The valence ionization that correlates primarily to the S_π+ fragment orbital can be evaluated similarly for overlap interaction with the bent-metallocene fragment. Just as for the analysis of the S_π− fragment orbital presented previously, the H₂bdt molecule is used as reference for determining the S_π+ FOE as shown in Table 3. The S_π+ FOE of H₂bdt is shifted 1.7 eV to lower ionization energy in Cp₂Mo(bdt) based on the shift of the core ionization energies. This shift is the major reason that the S_π+ FOE is ≈0.3 eV less stable than the Mo d-based FOE, and that the redox-active HOMO of the molecule has substantial sulfur character.

Table 3.

S 2p core and valence ionization energies (eV) and orbital interaction energy analysis for the bdt S_π+ fragment orbital.

Compound	S 2p3/2 IE	ΔIECa	0.8ΔIEC	FOEb	IEVc	ΔEVOd
H2bdt	169.3±0.1	0.0	0.0	8.39±0.02	––	0.0	nonbonding
Cp2Mo(bdt)	167.2±0.2	−2.1±0.2	−1.7±0.2	6.7±0.2	6.30±0.02(a'*)	−0.4±0.2	antibonding
Cp2V(bdt)	167.2±0.2	−2.1±0.2	−1.7±0.2	6.7±0.2	6.17±0.0232(a'*)	−0.5±0.2	antibonding
Cp2Ti(bdt)	167.4±0.2	−1.9±0.2	−1.5±0.2	6.9±0.2	7.18±0.02(a'b)	0.3±0.2	bonding

^aCore ionization energy shift = 169.3 − S 2p IE(Cp₂M(bdt)).

^bS_π+ fragment orbital energy observed for H₂bdt and indicated for the metal complexes = 8.39 + 0.8ΔIE_C.

^cObserved molecular ionization energies.

^dOverlap interaction energy corrected for charge potential = IE_V − FOE.

For the d² Mo complex the molecular a'* ionization occurs at 0.4±0.2 eV lower ionization energy than the S_π+ FOE in this molecule. This indicates that the S_π+ fragment orbital has significant filled-filled overlap interaction with the bent-metallocene fragment and that the molecular a'* orbital is anti-bonding with respect to the bdt fragment S_π+ orbital. This result was not expected based on the small fold angle of the bdt fragment and the small overlap of the S_π+ orbital with the metal d-based orbital, as supported by the observation that the corresponding bonding combination, the molecular a'_b orbital, does not shift from the metal d-based FOE as expected.

This unexpected shift of the a'* ionization from the S_π+ fragment orbital energy indicates that either there is an additional filled-filled overlap interaction of the S_π+ fragment orbital with the bent-metallocene fragment that is not shown in Figure 2 or that an assumption in the core-valence ionization correlation model is not correct. The purpose of this study is to explore the experimental information from the ionizations, but computations can assist in testing the validity of certain inherent assumptions in the correlation model. One of the assumptions is that the near-zero fold angle observed for the molecule in the crystal is also present for the molecule in the gas phase, where the ionizations are measured. Computation of the optimized geometry in the gas phase supports the small angle (2° optimized in the gas phase, 9° observed in the crystal structure). Another assumption is that distortions within the bdt fragment from H₂bdt to Cp₂Mo(bdt) are minor and do not significantly influence the bdt orbital energies. The distance between the two S atoms as measured in crystal structures increases from 3.06 Å in H₂bdt⁶⁷ to 3.58 in Cp₂Ti(bdt) to 3.72 in Cp₂V(bdt) to 3.94 in Cp₂Mo(bdt). DFT calculations also show the increasing distance between the S atoms, and in addition the spatial distribution of the S_π+ orbital is observed to twist slightly (≈10°) out of the π–system upon interaction with the metal center. However, in computations where the H₂bdt molecule was forced into a geometry with the S atoms ≈3.9 Å apart and the S–H bonds rotated 10° out of plane, the first ionization of the molecule was lowered by only 0.05 eV, which is small in comparison to the ≈0.4 eV lowering that is observed. Furthermore, the observation that the S_π− orbital consistently shows a near nonbonding interaction indicates that the structural distortions are minor effects on the energy. Thus, the computations support the assumptions in the model.

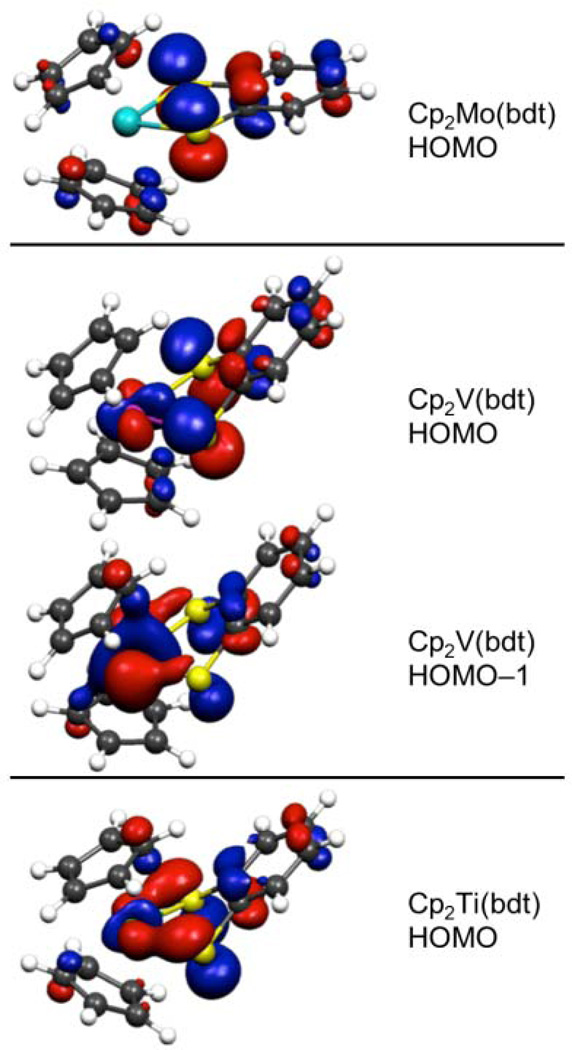
However, the computations also reveal the cause of the lowering of the molecular a'* ionization energy with respect to the S_π+ fragment orbital energy and all other occupied fragment orbital energies in the molecule. The calculations show a significant amount of carbon π character (≈15%) from the Cp rings interacting with the S_π+ in an antibonding fashion (Figure 4). The corresponding bonding combination of this interaction is shown in the Supporting Information. Population analysis in a basis of the fragment orbitals confirmed that there was significant Cp character in the HOMO of the Mo complex (18%). While the interaction of the Cp π orbitals with the S_π+ was not anticipated before these experiments, Cp ring character has been observed to mix similarly with I π orbitals in a Re system.⁶⁸ If it is assumed that the S_π+ fragment orbital is truly nonbonding with respect to the metal center in the Mo compound as the FOE analysis of the metal suggests, then all of the 0.4±0.2 eV destabilization energy is due to the antibonding interaction of the S_π+ fragment orbital with the Cp rings.

Figure 4.

The orbital surface plots of the Cp₂M(bdt) molecules that show appreciable character from the S_π+ orbital. Each orbital also exhibits a significant amount of Cp character in an antibonding interaction with the dithiolene system that was not previously described.

Cp₂V(bdt)

This molecule formally has a d¹ electron configuration. However, as will be shown, a description in which the metal d-based orbital is singly occupied and the S_π+ orbital of the bdt fragment is doubly occupied is not a reasonable representation of the electronic structure of this molecule, even qualitatively. Previous He I/He II photoelectron experiments and DFT calculations³² have indicated that there is a large amount of mixing of metal and sulfur character in the doubly-occupied a'_b and the singly-occupied a'* ionizations. This mixing might be expected if the metal d-based fragment orbital energy and the S_π+ fragment orbital energy are in close proximity, given that the fold angle (35° from the crystal structure, 34° calculated from the gas-phase computations) will produce overlap interaction between the fragment orbitals (Figure 1). The S_π+ FOE of ≈6.7 eV is given in Table 3. The Cp₂V metal d–based fragment orbital energy may be estimated by comparing the core and valence ionizations of Cp₂V(bdt) with those of Cp₂V(CH₃)₂ (Table 4). The e symmetry orbitals of the C–H bonds of the methyl groups have linear combinations with symmetry simlar to the S_π+ and S_π− orbitals of the dithiolenes, but without a fold angle they are largely orthogonal to the metal d-based fragment orbital and furthermore are several eV deeper in energy, so there is little interaction energy between these orbitals and the HOMO ionization of Cp₂V(CH₃)₂ will reflect the metal-based Cp₂V fragment orbital energy. The V 2p_3/2 core ionization energy of Cp₂V(bdt) is observed at approximately 0.7 eV greater ionization energy than that of the reference molecule Cp₂V(CH₃)₂, similar to the 0.7 eV shift between Cp₂Mo(bdt) and Cp₂MoH₂ discussed in the previous section. The corresponding valence shift from the HOMO ionization of Cp₂V(CH₃)₂ places the Cp₂V metal d–based FOE in Cp₂V(bdt) at about 6.9 eV, which is just 0.2 eV more stable than the S_π+ fragment orbital energy. If this separation is correct, the resulting molecular a'_b orbital that ionizes at 6.78 eV should have just slightly greater metal fragment character than S_π+ fragment character, and the singly-occupied molecular a'* orbital that ionizes at 6.17 eV should have slightly greater S_π+ fragment character than metal fragment character. Regardless of the actual percent distribution between these orbitals or the method of evaluation, the electronic structure of this molecule does not correspond to the traditional description of a singly-occupied metal d orbital on a V atom in a formal 4+ oxidation state. Given that the S_π+ fragment orbital energy is slightly less stable than the metal d-based fragment orbital energy, an equal or better first approximation to the description is that the singly-occupied orbital is the S_π+ fragment orbital rather than metal d orbital.

Because of the extensive mixing of metal and sulfur character in the molecular a'_b and a'* orbitals and ionizations, it is not possible to identify these ionizations as predominantly associated with either the bent-metallocene fragment or the bdt fragment. The a'_b ionization occurs at about 0.1 eV lower ionization energy than the metal-based FOE, and the a'* ionization occurs at about 0.5 eV lower ionization energy than the S_π+ FOE. Part of the shift of both of these ionizations to lower energy is a consequence of the Cp interaction with the S_π+ character in each of these orbitals as discussed in the preceding section. In this case the overlap interaction energy between the metal-based fragment orbital and the S_π+ fragment orbital can be estimated as follows. Given that the difference between these fragment orbital energies is about 0.2 eV and the a'_b and a'* orbitals are extensively mixed, the rest of the 0.6 eV splitting between the a'_b and a'* ionizations is due to the overlap interaction energy. Approximately half of this 0.4 eV energy difference, 0.2 eV, is the stabilization of the a'_b ionization by the overlap interaction between the metal-based and S_π+ fragment orbitals.

Cp₂Ti(bdt)

This molecule formally has a d⁰ electron configuration and the a'* orbital is unoccupied, so it is not possible to measure its ionization energy. Likewise, reference molecules such as Cp₂TiH₂ and Cp₂Ti(CH₃)₂ do not have a metal-based valence ionization with which to obtain the Cp₂Ti metal-based FOE in the absence of overlap interactions. Based on the trend of the Mo complex where the metal-based FOE is about 7.0 eV and the V complex where the metal-based FOE is about 6.9 eV, the metal-based FOE in Cp₂Ti(bdt) is expected to be less than 6.9 eV. Table 3 shows that the bdt S_π+ FOE is about 6.9 eV, so the metal d-based fragment orbital and the bdt S_π+ fragment orbital have now switched their relative energy compared to the Mo and V complexes. Cp₂Ti(bdt) has the largest fold angle (46° from the crystal structure, 44° calculated for the gas phase) and the S_π+ orbital is expected to have a substantial mixing and interaction energy with the formally vacant metal-based orbital. The bonding a'_b orbital ionization at 7.18 eV is about 0.3 eV greater than the bdt S_π+ fragment orbital energy. This orbital also experiences the destabilizing interaction with the Cp rings, so 0.3 eV is a lower bound to the overlap interaction energy in the Ti complex. Thus, this complex shows the largest overlap interaction energy between the bent-metallocene and bdt fragments.

SUMMARY AND CONCLUSIONS

Valence ionization energies are reflections of the electronic structure and bonding in a molecule, but when evaluating the ionization energy shifts in terms of orbital overlap and bonding interactions, it is important first to know the magnitude of the shifts due to changes in the charge potential distribution. The shifts in the core ionization energies provide a probe of the changes in charge potential that can be translated to the valence ionization energies through the approach of core-valence ionization correlations. These experiments show that the charge potential energy shifts can be quite large in comparison to the orbital overlap interaction energies, as illustrated dramatically in Figure 5. In this case the S_π+ and S_π− orbitals of the bdt fragment experience a much greater negative charge potential when the bdt ligand is coordinated to the metals in the Cp₂M(bdt) complexes than when the bdt fragment is protonated in the H₂bdt dithiol reference molecule. The sulfur core ionizations are shifted ≈2 eV to lower ionization energy from H₂bdt to Cp₂M(bdt). The direction of the shift is consistent with the formal 2– charge of the dithiolene ligands in the complexes. The sulfur core ionization energies do not vary significantly among the bent-metallocene compounds, but there is a slight indication, supported by the valence ionization energies, of greater donation of charge from the dithiolene fragment to the metal in the case of the Ti complex, consistent with the greater fold angle and the formally unoccupied metal d orbital in this molecule. Likewise, the metal core ionization energies are stabilized ≈0.7 eV in going from the Cp₂MoH₂ and Cp₂V(CH₃)₂ reference molecules to the Cp₂M(bdt) molecules by the increase in positive charge potential in the bent-metallocene fragments.

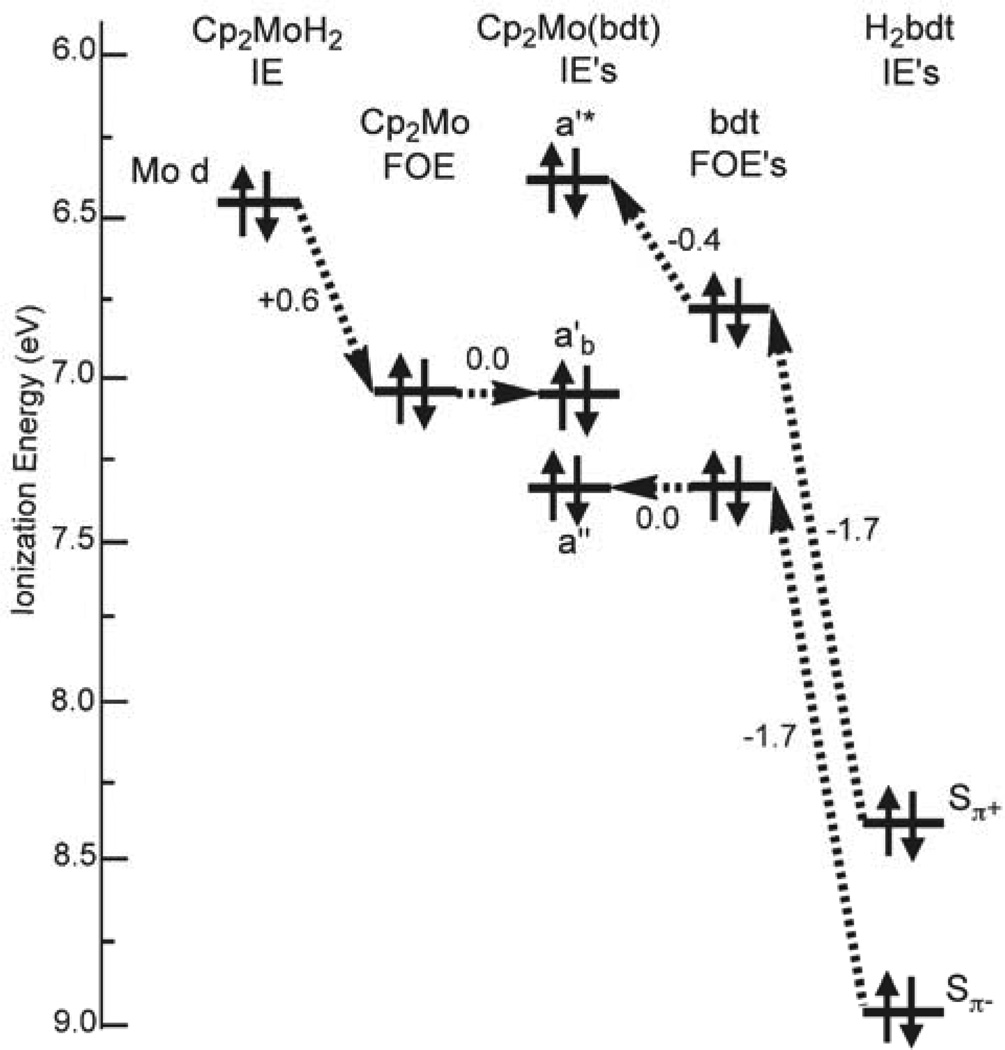
Figure 5.

Ionization energy correlation diagram for Cp₂Mo(bdt). The energy shifts from the valence ionizations of Cp₂MoH₂ and H₂bdt to the Cp₂Mo and bdt fragment orbital energies (FOEs) in the Cp₂Mo(bdt) molecule are determined by the core-valence ionization energy correlation.

The shifts in core ionization energies allow an estimate of the shifts in valence fragment orbital energies due to the change in charge potential according to the core-valence correlation model. Taken together with the molecular ionization energies measured by gas-phase photoelectron spectroscopy, this ionization information allows construction of quantitative energy level diagrams of the interactions between the bent-metallocene and dithiolene valence fragment orbitals. The results for the valence orbital ionization energies of all three molecules are compared in Figure 6. For all three molecules, after the ≈1.5–1.7 eV shift of the bdt S_π− fragment orbital energy due largely to the increase in negative charge potential at the ligand, the molecular a" ionization energy is obtained without further shift within the certainty of these experiments. The lack of significant overlap interaction of the S_π− orbital with the orbitals of the bent-metallocene fragment indicated by this result is consistent with the nodal properties of these orbitals. For the Mo complex, after the ≈0.6 eV shift of the Mo d-based fragment orbital energy due to the increase in positive charge potential at the metal from the reference molecule, the molecular a'_b ionization is obtained without further shift. Little overlap interaction energy of this d-based orbital with the bdt fragment S_π+ is expected because of the small fold angle in this molecule. These measurements support Jolly’s empirically derived factor of 0.80 for the ratio of core to valence energy changes with the changes in charge potential.³⁸

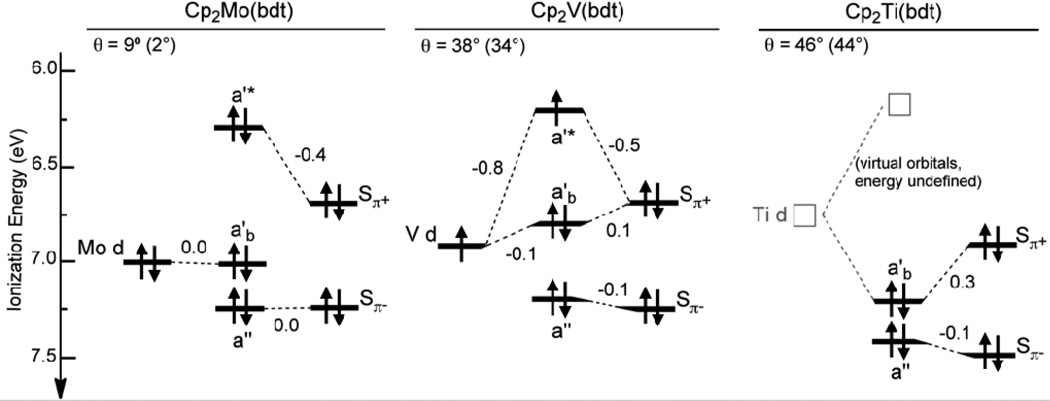
Figure 6.

Summary of the molecular ionization energies measured by gas-phase photoelectron spectroscopy (indicated by the orbital symmetry labels) and the bent-metallocene and bdt fragment orbital energies obtained by the core/valence ionization correlation model (indicated by the metal d and S_π± labels). The angles θ are the fold angles as measured from crystal structures (values optimized from gas-phase calculations in parentheses).

The diagram in Figure 6 also visually displays the destabilization of the a'* ionizations compared to the estimated fragment orbital energies. A substantial portion of this destabilization is due to interaction of the bdt S_π+ fragment orbital with the filled cyclopentadienyl π orbitals. This Cp_π/S_π+ orbital interaction partially obscures the overlap interaction energy of the S_π+ orbital with the bent-metallocene metal d-based orbital for the V and Ti complexes, where the fold angle is appreciable and there is substantial bdt sulfur character in both the a'_b and a'* molecular orbitals depicted in the diagram. The ionizations of the Mo complex show that the destabilization of the a'* ionization from the S_π+ fragment orbital energy caused by interaction with the cyclopentadienyls is about 0.4 eV. Removing the cyclopentadienyl interaction energy from the a'_b ionizations of the V and Ti complexes yields a metal–d/S_π+ overlap interaction energy of about 0.2–0.3 eV in the case of the V complex and substantially greater than 0.3 eV in the case of the Ti complex. Although the precise values of these overlap interaction energies are not determined by this analysis, the trend of increasing metal-d/S_π+ interaction energy with increasing fold angle is observed.

In summary, the ionizations have provided experimental measures of four factors that determine the energy and high sulfur character of the redox-active HOMO of these bent-metallocene-dithiolene complexes:

1. The symmetric combination of the two out-of-plane S pπ orbitals is destabilized by interaction with the C=C π bond of the dithiolene, such that the resulting S_π+ orbital becomes the HOMO of the dithiolene fragment. For the bdt fragment the ionizations show that the S_π+ is 0.6 eV less stable than the S_π−, which is important for the symmetry-allowed ability of the S_π+ to donate electron density to the metal.

2. The S_π+ of the bdt fragment in the complexes is destabilized ≈1.7 eV from the S_π+ of H₂bdt, while the metal-based d orbitals are stabilized ≈0.6 eV from the corresponding dihydride or dialkyl complexes, due to the charge redistribution in the molecules. This destabilization of the S_π+ FOE relative to the metal FOE is a major factor in determining the substantial sulfur character in the HOMO of the metal complexes.

3. The ability of the S_π+ to mix with the metal d-based orbital and level the energy of oxidation as the fold angle increases is favored by the close energy match between these fragment orbitals. The FOE analysis indicates that the energy separation between the metal d-based and S_π+ fragment orbitals is less than ≈0.3 eV.

4. The additional mixing of the S_π+ with the filled Cp π further destabilizes the HOMO of the bent-metallocene-dithiolene complexes by as much as ≈0.4 eV, which substantially reduces the energy for oxidation. The significance of overlap contributions from other ligands often presumed to be innocent, in this case the Cp ligands, has not been appreciated previously.

With the ability to measure gas-phase core ionization energies for a wide range of molecules, including those that require high temperatures for vaporization, it is now possible to extend the utility of Jolly’s model of localized orbital ionization potentials (LOIPs) put forth more than two decades ago^45,69 to a broader model of fragment orbital energies (FOEs) in organometallic compounds illustrated in this work. Further improvements in the sensitivity and resolution of gas-phase XPS for the study of large molecules will allow more detailed analysis and understanding of the valence electronic interaction energies of organometallic and inorganic systems.