Abstract
Elementary mode analysis is a useful metabolic pathway analysis tool in understanding and analyzing cellular metabolism, since elementary modes can represent metabolic pathways with unique and minimal sets of enzyme-catalyzed reactions of a metabolic network under steady state conditions. However, computation of the elementary modes of a genome- scale metabolic network with 100–1000 reactions is very expensive and sometimes not feasible with the commonly used serial Nullspace Algorithm. In this work, we develop a distributed memory parallelization of the Nullspace Algorithm to handle efficiently the computation of the elementary modes of a large metabolic network. We give an implementation in C++ language with the support of MPI library functions for the parallel communication. Our proposed algorithm is accompanied with an analysis of the complexity and identification of major bottlenecks during computation of all possible pathways of a large metabolic network. The algorithm includes methods to achieve load balancing among the compute-nodes and specific communication patterns to reduce the communication overhead and improve efficiency.
Keywords: Biochemical network, Metabolic pathway, Nullspace Algorithm, Elementary flux mode
1. Introduction
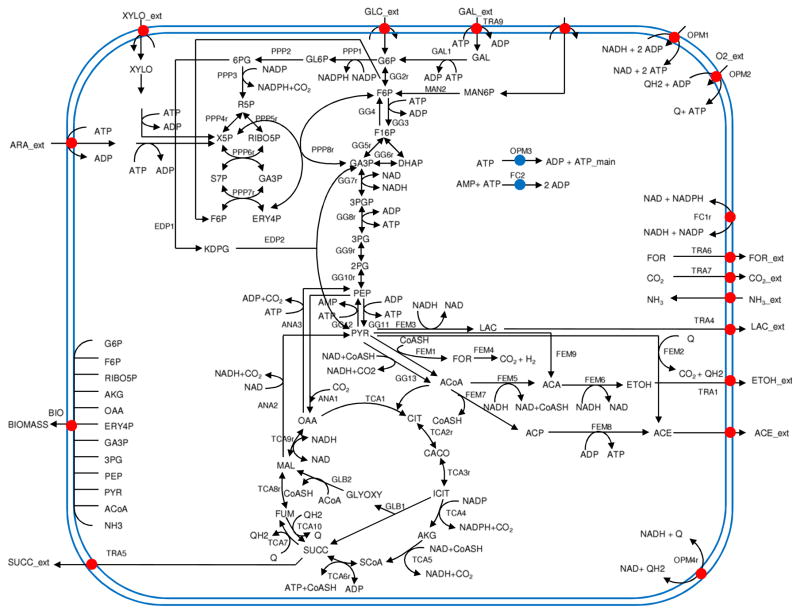
Analysis of the metabolic networks is a common practice in biotechnology and metabolic engineering [1–4]. Reconstruction of complete metabolic networks of various organisms has allowed researchers to further concentrate on the discovery and analysis of the feasible metabolic pathways. The reconstructed metabolic networks of Escherichia coli [5], Saccharomyces cerevisiae [6,7], Streptomyces coelicolor [8], Helicobacter pylori [9], Haemophilus influenzae [10] and human mitochondria [11,12] require efficient and accurate computational methods for their analysis. By definition, a metabolic network is comprised of metabolites together with a collection of chemical reactions which consume or produce the respective metabolites. An example of the metabolic network for the central metabolism of E. coli microorganism strain is given in Fig. 1. In this figure, metabolites outside the boundary are classified as external, while those inside the boundary are internal and subject to mass balance constraints [13–16]. External metabolites can be further classified as substrates (inputs such as glucose, galactose, mannose, etc.) and/or products (outputs such as ethanol, lactic acid, or succinic acid) depending on the direction of the corresponding reaction. Reactions which exchange between internal and external metabolites, such as the glucose-uptake reaction GG1, are called exchange reactions or external reactions. Reactions just between internal metabolites, such as the reaction GG2r converting glucose-6-phosphate (G6P) into fructose-6-phosphate (F6P), are internal to the network.
Fig. 1.
Metabolic network of E. Coli [17].
A metabolic pathway contains a subset of reactions of a metabolic network which have non-zero reaction rates (or fluxes) at a given moment, and thus constitutes a possible state of the cellular metabolism. Feasible metabolic pathways, such as elementary flux modes [13], have been used to describe the cell functions and capabilities such as growth and regulation [18,19], estimation of product yields [14], evaluation of metabolic network robustness [19] and rational design of efficient and robust whole-cell biocatalysts [20,17]. An elementary flux mode is an admissible metabolic pathway which cannot be feasible if any one of its reactions is removed or its flux is set to zero.
The remainder of this paper is organized as follows. In Section 2 we give an overview of the background and related work. We state the definition of the stoichiometry model and its mathematical representation, define elementary flux modes and extreme pathways and the conditions for their admissibility, and give a description of the Nullspace Algorithm, the basis for our parallel implementation. Section 3 gives a pseudocode of the serial Nullspace Algorithm and points out its major bottlenecks. The section also presents the computational complexity analysis of the algorithm implementation. The parallel Nullspace Algorithm is given in Section 4. Section 5 shows the results of implementing the algorithm on specific parallel architectures using the metabolic network models for E. coli and S. cerevisiae. Finally, in Section 6 we sketch some future developments and applications of the algorithm.
2. Background and related work
Since the introduction of elementary flux modes into the problem of modeling and analyzing biochemical reaction networks, two algorithms have been proposed. First, the Canonical Basis Algorithm [15] was developed, followed by the more efficient Nullspace Algorithm [21–27]. Both algorithms are based on convex analysis and the Double Description Method [28] used in the mathematical problem of enumerating the extreme rays in a convex polyhedral cone.
Here, we briefly give the outline of the theory used in the modeling of the metabolic networks and computing the elementary flux modes.
2.1. Stoichiometry model
The stoichiometry model which describes a given metabolic network can be represented mathematically by a stoichiometry matrix, Nm×q, with each row corresponding to one of the m metabolites and each column corresponding to one of the q reactions. Element Ni,j of the stoichiometry matrix, if non-zero, denotes the stoichiometric coefficient for the ith metabolite in the equation of the jth reaction. A positive [negative] stoichiometric coefficient Ni,j denotes the molar concentration of the ith metabolite produced [consumed] with a unit flux for the jth reaction. Additionally, reactions are denoted as reversible or irreversible to reflect their thermodynamic constraints. This property of directionality implies that the reaction may or may not flow in both directions. Beside the metabolite connectivity imposed by the reaction definitions, an additional requirement is given in the form of mass balance of the internal metabolites in the metabolic network [13–16]. The flux or reaction rate is the numerical value which expresses the speed of the individual reaction. Fluxes for irreversible reactions are constrained to be non-negative. The set of active reactions is represented by a vector x of length q in which each entry is the flux for the corresponding reaction. By assuming the internal metabolite concentrations remain constant at the steady state, the mass-balance equations for all internal metabolites can be written as follows [13–16]:
| (1) |
The elements in the flux vector x whose indices correspond to active reactions have non-zero values. In addition, if a reaction is irreversible the corresponding entry in the vector x has a non-negative value. Since the number of metabolites is usually much smaller than that of reactions in a metabolic network, the system of linear equations (1) is underdetermined.
2.2. Elementary flux modes and extreme pathways
If a flux vector x satisfies Eq. (1) plus the applicable non-negativity constraints, we also call it an admissible [flux] mode. Of all the admissible modes, the ones of particular interest are the elementary [flux] modes, described below.
Definition 1 (Elementary mode and extreme pathway). Let the Nm×q stoichiometry matrix be representing m internal metabolites and q reactions connecting these metabolites. A flux vector is a q-vector x of reaction rates. The vector x is said to be admissible if it satisfies the following two conditions:
pseudo steady-state: Nx = 0. Metabolite concentrations remain constant within the metabolic network;
-
thermodynamics: xi≥0 if the ith reaction is irreversible.
An admissible vector is said to be an elementary mode, elementary flux mode, or elementary pathway if it satisfies the above two conditions plus [13,29,15,30]:
-
elementarity: there is no other vector v (v ≠ x and v ≠ 0) fulfilling conditions 1 and 2, such that the set of indices of the non-zero elements in v is a strictly proper subset of set of indices of the non-zero elements in x.
A vector x is an extreme pathway if it is an elementary pathway and also satisfies the following:
independence: x is said to be extreme if it cannot be written as a convex combination of any other admissible pathways.
In [16], an extreme pathway is defined as a member of a set of elementary modes which are obtained when the internal reversible reactions of the metabolic network are split into pairs of irreversible reactions. However, if sufficiently many internal reversible reactions are split, then the metabolic network will not admit a completely reversible pathway. In this case the set of extreme pathways would coincide with the “minimal generating set” for all admissible pathways [16,31]. Geometrically, the set of admissible extreme pathways would form a pointed polyhedral cone [31].
2.3. Compression of metabolic networks
Metabolic networks may be reduced in size with respect to the total number of participating metabolites and reactions to remove redundancies and impossible combinations [25,32]. Among the heuristics applied in order to compress the stoichiometric model are: detection of conservation relations, strictly detailed balanced reactions, enzyme subsets and uniquely consumed (or produced) metabolites [29]. Some of the reduction heuristics match the methods for removal of redundant constraints in a linear programming problem [33]. All the methods in this paper assume that the network has been already compressed, eliminating all redundant constraints. The resulting stoichiometry matrix has full row rank.
To illustrate the compression on the genome-scale metabolic networks, in Table 1 we give the original and compressed size of representative metabolic networks for several organisms. The data was taken from the BiGG database [34].
Table 1.
Compression of genome-scale metabolic networks.
| Organism | Original size (m × q(qrev)) | Compressed size (m × q(qrev)) |
|---|---|---|
| E. coli iJR904 | 904 × 1361(674) | 284 × 740(389) |
| E. coli iAF1260 | 1972 × 2980(1450) | 579 × 1567(769) |
| S. cerevisiae iND750 | 1177 × 1498(778) | 269 × 597(345) |
| M. barkeri iAF692 | 698 × 830(406) | 140 × 300(181) |
| H. pylori iIT341 | 562 × 702(388) | 100 × 236(164) |
| S. aureus iSB619 | 741 × 911(473) | 162 × 368(215) |
2.4. Nullspace Algorithm
The two algorithms typically used for the computation of elementary modes are the Canonical Basis Algorithm [15] and the subsequent Nullspace Algorithm [21–27]. Both algorithms are based on convex analysis and computation of the extreme rays of a convex polyhedral cone. The Nullspace Algorithm is more efficient for metabolic networks and is the subject of this paper.
The Nullspace Algorithm begins by computing an initial basis for the right nullspace of the m × q stoichiometry matrix such that the sign constraints are automatically satisfied for the first q − m reactions. It then proceeds to form convex combination of these vectors to impose the sign and elementarity constraints on the remaining reactions one-by-one, until a complete set of elementary flux vectors are computed. In the following, we state some of the basic properties of the Nullspace Algorithm.
Proposition 1
If Nm×q is a stoichiometry matrix with full row rank m, then the columns may be permuted such that a basis for the right nullspace of N has the form
| (2) |
Proof
Apply elementary row operations (represented by the nonsingular matrix X) to the matrix N to obtain the reduced row echelon form
| (3) |
The new matrix has the same nullspace, which has the form (2) by inspection.
For the application of Proposition 1 it is sufficient to use compression techniques from Section 2.3 which will reduce the original stoichiometry matrix to the one of full row rank, even though it may be further reduced. In addition, we will take further advantage of the reduced row echelon form already computed to obtain the initial basis for the nullspace. Therefore, we shall henceforth assume that the stoichiometry matrix N has been compressed, reduced to row echelon form, and that the columns (i.e. reactions) have been permuted so that the row echelon form has the form (3). This is equivalent to finding q − m columns which form a (q − m) × (q − m) non-singular matrix and putting them first. We further assume that the corresponding q − m reactions are all irreversible, otherwise we must split sufficiently many reversible reactions into pairs of irreversible reactions to make this possible. Many networks do not require such splitting of reversible reactions.
If Z̄ denotes the set of indices corresponding to the nonzero entries of a given vector, then N *, Z̄ will denote the submatrix of N formed by extracting the columns corresponding to those non-zero entries. It has been shown in [23,31] that nullity(N *, Z̄) = 1 if and only if x is elementary mode. Here nullity(A) denotes the dimension of the right nullspace of a matrix A. During the course of the Nullspace Algorithm, we enforce the following property on each prospective elementary vector x at each stage k so that at the end, this property implies that x is elementary according to Definition 1.
Proposition 2
Let the Nullspace Algorithm be in its kth iteration of execution where k = q − m + 1, …, q. A vector x is an elementary flux mode with respect to reactions 1, …, k corresponding to first k columns of matrix N iff
| (4) |
where Z̄k is the union of the set of indices of non-zero values among first k entries of vector x together with all indices (k + 1), …, q.
The property in Eq. (4) enforces the elementarity over the first k reactions. It will be observed that each column of the initial basis K from Eq. (2) satisfies the partial elementary property above for k = q − m. As a simple consequence of the above property, a vector satisfying this condition cannot have more non-zero entries than one plus the number of rows in N, leading to the following.
Proposition 3
Let x be a column-vector which is an elementary flux mode to the stoichiometry matrix Nm×q i.e. Nx = 0. An upper bound on the number of non-zero elements in the vector x is given by
| (5) |
where |Z̄| denotes the cardinality of Z̄.
The upper bound stated in Proposition 3 is given for the full elementary property of Definition 1. At the kth iteration, since the entries of a prospective vector x corresponding to indices (k + 1), …, q are all considered implicitly nonzero, the number of nonzeros among the first k entries is reduced from 1 + m to 1 + m − (q − k). The result leads to the following necessary condition for elementarity that can be applied very fast.
Proposition 4
Let x be a column-vector in the right nullspace matrix K of the stoichiometry matrix Nm×q i.e. Nx = 0. Let the first k elements of the vector x have non-negative values in the positions corresponding to irreversible reactions, and condition (4) is satisfied. Denote by Z̄1, …, k the set of indices of nonzero elements in the subvector x1, …, k. If the matrices are in reduced row echelon form as in Proposition 1, then
| (6) |
Proof
Follows from Proposition 3.
In brief, the Nullspace Algorithm is an iterative procedure which starts with a nullspace basis as in Proposition 1. At each iteration it forms new prospective elementary modes by pair-wise convex combinations of the partial elementary modes it has accumulated so far. Each prospective elementary mode is tested to be elementary, first by testing the condition of Proposition 4 and then by that of Proposition 2. The steps to execute the Nullspace Algorithm are sketched in Algorithm 1, and the way the computation is split into its essential parts is shown in Algorithm 2.
Algorithm 1.
Nullspace Algorithm (sketch) [31].
Assume we have a stoichiometry matrix Nm×q that has full row rank m and in the form as given in Proposition 1, compressed if needed using the methods of Section 2.3. Further, let qirrev and q − qirrev be the number of irreversible and reversible reactions, respectively. The Nullspace Algorithm may be briefly sketched as follows:
|
Algorithm 2.
[K] = SERIAL_NSP(N, K)
| Input: | |
| reduced stoichiometry matrix (Nm×q); | |
| initial nullspace of the form | |
| Output: | |
| bit-valued matrix of elementary modes Kq×nems | |
| 1: | for k = q − m + 1 to q do |
| 2: | {find pairs of columns which when combined form candidate columns. Algorithm 3} |
| 3: | combinations ⇐ GENERATE_CANDIDATES (K) |
| 4: | {remove duplicate columns by means of sorting. Algorithm 7} |
| 5: | combinations ⇐ RADIXSORT(R(1), combinations) |
| 6: | combinations ⇐ REMOVE_DUPLICATES(R(1), combinations) |
| 7: | {accept those candidate columns which satisfy Proposition 5. Algorithm 8} |
| 8: | combinations ⇐ RANKTESTS(N, K, combinations) |
| 9: | {expand K matrix, i.e. its R(1) and R(2) submatrices. Algorithm 9} |
| 10: | K ⇐ EXPAND(K, combinations) |
| 11: | end for |
The sketch of the Nullspace Algorithm presented omitted several improvements to the efficiency for clarity. First, during every iteration, each new column is normalized with respect to the 1-norm. Second, we are able to keep the matrix R(1) as a bit-valued matrix and compress it into a matrix scaled down by a factor equal to the length of the machine word (32 or 64 bit). Accordingly, the compressed matrix R(1) as stored in memory has the dimension of (q/width) × nems, where width = 32 or 64.
We take advantage of the special row-echelon form of N to obtain a reduced-cost rank test, more properly called a nullity test.
Proposition 5 (Proof in Appendix)
Let the Nullspace Algorithm be in its kth iteration of execution as k ranges over q − m + 1, …, q. Let Z̄1, …, q−m be the set of indices corresponding to non-zero entries in x1, …, q−m, and let Zq−m+1, …, k be the set of indices corresponding to zero entries in xq−m+1, …, k. A vector x is an elementary flux mode with respect to reactions 1, …, k corresponding to the first k columns of matrix N iff
| (8) |
Proposition 5 gives a nullity test over a smaller submatrix and thus reduces the cost of its computation. This reduced nullity test decreases the size of both dimensions of the submatrix by the same value, equal to the number of non-zero entries in the sub-vector xq−m+1,…, k.
2.5. Complexity of the Nullspace Algorithm
Enumeration of the elementary flux modes is equivalent to the problem of enumeration of vertices in a bounded polyhedron (polytope) [35]. The complexity of this problem is still an open question in computational geometry. In order to illustrate and give the intuition to the possible hardness of the elementary mode computation it may be worth referring to the two earlier results [35,36]. First, it is not possible to generate in polynomial total time all elementary flux modes that have non-zero flux for the specific reaction unless P = NP. Second, deciding if there exists an elementary flux mode that has nonzero flux for k specified reactions can be solved in polynomial time via a linear program if k ≤ 1, but is NP-complete for k ≥ 2. The two results are obtained as a corollary to the problem of enumeration of negative cycles in a weighted directed graph [37]. In these enumeration problems, it is common to analyze the complexity as a function of the combined size of the input and the output. In summary, it is unknown if the complexity of the problem of the enumeration of elementary flux modes is polynomial as a function of the combined size of the metabolic network and the final number of elementary flux modes. We do observe in practice that the number of final elementary modes can be orders of magnitude larger than the dimensions of the initial system, and the number of partial modes present during intermediate stages of the algorithm can sometimes be significantly larger than the number of final modes.
3. Serial Nullspace Algorithm
The serial Nullspace Algorithm given in Algorithm 2 takes as input the compressed stoichiometry matrix in the reduced row echelon form (Proposition 1), initial nullspace, and the information on reaction reversibility/irreversibility. The algorithm is executed in m iterations, each of them corresponding to one of the m reactions.
Algorithm 2 is comprised of the generation of the candidate columns (Algorithm 3), sorting (Algorithm 7) and removal of the duplicate candidate columns, numerical rank testing (Algorithm 8) and update of the current nullspace matrix K (R(1) and R(2)) (Algorithm 9). In an effort to eliminate the duplicate bit-valued candidate columns we first sort them according to their binary values and then use one scan to eliminate the duplicates. This operation requires an efficient sorting method to reduce the cost of removing duplicate columns. Candidate columns are sorted using a variation of radixsort algorithm [38] in order to attain linear complexity. We give the outline of the radixsort over an array of bit-valued columns in Algorithm 7 in Appendix B.
Algorithm 3.
[combinations]=GENERATE_CANDIDATES(K)
| Input: | |
| current nullspace matrix | |
| Output: | |
| pairs of indices of columns forming candidates (combinations) | |
| 1: | irrev + ⇐ (i: and (∃j: jth reaction is irreversible, )} |
| 2: | irrev − ⇐ (i: and (∃j: jth reaction is irreversible, )} |
| 3: | rev ⇐ (i: and (∀j: jth reaction is reversible or )} |
| 4: | {combine columns that can annihilate the element in the current row} |
| 5: | S ⇐ {(ii, jj): (ii, jj) ∈ (irrev+ × irrev−) ∪ ((irrev+ ∪ irrev− ∪ rev) × rev)} |
| 6: | for each (ii, jj) ∈ S do |
| 7: | form candidate column from the pair of columns indexed by (ii, jj) |
| 8: | if candidate satisfies Proposition 4, add (ii, jj) to combinations |
| 9: | end for |
Algorithm 8.
[combinations] = RANKTESTS(N, K, combinations)
| Input: | |
| reduced stoichiometry matrix Nm×q; current nullspace matrix ; | |
| array of pairs of column-generating indices (combinations) | |
| Output: | |
| array column-generating pairs valid elementary modes (combinations) | |
| 1: | k ⇐ size(R(1), 1) |
| 2: | for each (ii, jj) ∈ combinations do |
| 3: | x1×k ⇐ or |
| 4: | aa ⇐ indices of non-zero entries in x1…q−m |
| 5: | bb ⇐ indices of zero entries in xq−m+1….k |
| 6: | {if Proposition 5 is not satisfied reject candidate} |
| 7: | if NULLITY(Nbb, aa) ≠ 1 then |
| 8: | combinations ⇐ combinations\(ii, jj) |
| 9: | end if |
| 10: | end for |
Algorithm 9.
[K] = EXPAND(K, combinations)
| Input: | |
| current nullspace matrix array of column-generating pairs of indices (combinations) | |
| Output: | |
| updated matrix K | |
| 1: | k ⇐ size(R(1), 1) |
| 2: | eps ⇐ 10−10 |
| 3: | for each (ii, jj) ∈ combinations do |
| 4: | xk ×1 ⇐ or |
| 5: | y(q −r) ×1 ⇐ linear combination of and so that y1 = 0 |
| 6: | {for simplicity we omit the check if improperly adopted tolerance assigns zero value erroneously} |
| 7: | y (fabs(y) < eps) ⇐ 0 |
| 8: | y ⇐ y/||y||1 |
| 9: | R(1) ⇐ [R(1) x] |
| 10: | R(2) ⇐ [R(2) y] |
| 11: | end for |
| 12: | if kth reaction is irreversible then |
| 13: | delete from K columns with negative elements in current row |
| 14: | end if |
The idea in Algorithm 7 is to sort bit-columns by first cutting all columns horizontally into chunks of width equal to 2d (where d = 3,4,5, …,) and in q/2d iterations sort the columns using the idea from the radix-sort. In every iteration, columns would be sorted according to the value in the respective chunk. Complexity of this operation is , where nems is the number of candidate columns at the given iteration. With the proper selection for width d, we may assume that the constant factor before nems is small enough to assume linear complexity. In B we also give the pseudocode of the subroutines for rank tests and expansion of nullspace matrix in every iteration.
3.1. Computational Complexity Analysis
Due to the unpredictable expansion of the size of elementary mode matrix during each iteration of the computation of elementary modes, it is difficult to directly estimate the computational cost within the bottlenecks of the algorithm. We observe from the algorithmic structure and implementation that the three major bottlenecks are (ordered by decreasing overall observed costs) (i) the generation of new candidate elementary mode columns, (ii) the evaluation of the numerical rank tests, and (iii) sorting to eliminate duplicate candidate elementary mode columns. Thus, we may decompose the total computational cost per iteration as T(nems) as:
| (9) |
where Tgencands, Trank_tests, Tsorting are the computational costs for generation of candidate columns, evaluation of numerical rank test, and sorting of bit-valued candidates, respectively. The complexity for the generation of candidate columns Tgencands has an upper bound of . Sorting can be accomplished with almost linear complexity using the variation of the radixsort algorithm as earlier described. Elimination of the duplicate candidate columns after sorting has linear complexity and is of negligible cost. For the rank test we used LU decomposition with full pivoting [39]. The complexity of the single LU-based rank test is cubic in terms of the dimensions of submatrix over which the rank is evaluated. It has linear complexity in terms of the total number of candidate elementary mode columns. We use the reduced rank test derived in Proposition 5 to decrease the cost of individual rank computation. It remains to study how the numerical precision of the rank computation would behave as the size of the initial stoichiometry problem grows, and if the more robust singular value decomposition would be necessary.
4. Parallel Nullspace Algorithm
For the metabolic networks which after compression have the number of both metabolites and reactions on the order of 102–103, the existing software is unable to complete the computation of the elementary flux modes. Thus, we resort to the idea of parallelizing the Nullspace Algorithm.
We assume that the algorithm is designed for a parallel environment of P compute-nodes, where each compute-node has its own memory and executes an instance of the parallel program. The compute-nodes exchange messages over an unspecified network architecture. This parallel environment corresponds to a distributed memory system, though our proposed algorithm may be easily expanded into hybrid parallel implementation with the shared-memory paradigm. For convenience, in the sequel we will refer to compute-nodes as simply nodes.
In Algorithm 4 we give the parallel Nullspace Algorithm with an introduction of communication in line 7. We parallelize the tasks of generating candidate columns as in Algorithm 5 and by proper load balancing attain that each participating compute- node generates approximately the same number of candidate columns.
Algorithm 4.
[K]=PARALLEL_NSP(N, K)
| Input: | |
| reduced stoichiometry matrix (Nm×q); initial nullspace matrix | |
| Output: | |
| bit-valued matrix of elementary modes Kq×nems | |
| 1: | for k = q − m + 1 to q do |
| 2: | combinations ⇐ GENERATE_CANDIDATES_PARALLEL (K) |
| 3: | combinations ⇐ RADIXSORT(R(1), combinations, width) |
| 4: | combinations ⇐ REMOVE_DUPLICATES(R(1), combinations) |
| 5: | combinations ⇐ RANKTESTS (N, R(1), combinations) |
| 6: | {communicate columns and merge} |
| 7: | combinations ⇐ COMMUNICATE_TREE(R(1), combinations) |
| 8: | K ⇐ EXPAND(K, combinations) |
| 9: | end for |
Algorithm 5.
[combinations] = GENERATE_CANDIDATES_PARALLEL (K)
| Input: | |
| current nullspace matrix | |
| Output: | |
| pairs of indices of columns forming candidates (combinations) | |
| 1: | irrev + ⇐ {i: and (∃j: jth reaction is irreversible, )} |
| 2: | irrev − ⇐ {i: and (∃j: jth reaction is irreversible, )} |
| 3: | rev ⇐ {i: and (∀j: jth reaction is reversible or )} |
| 4: | irrev_p− ⇐ {i: i ∈ irrev− and i = proc_id(mod P)} |
| 5: | rev_p ⇐ {i: i ∈ rev and i = proc_id(mod P)} |
| 6: | S ⇐ {(ii, jj): (ii, jj) ∈ (irrev + × irrev_p−) ∪ ( (irrev+ ∪ irrev_p− ∪ rev_p) × rev)} |
| 7: | for each (ii, jj) ∈ S do |
| 8: | form candidate column from the pair of columns indexed by (ii, jj) |
| 9: | if candidate satisfies Proposition 4 add to combinations |
| 10: | end for |
Load balancing is needed to assure that there is no serious time discrepancy among the compute-nodes when they perform the sorting and the evaluation of numerical rank tests. Each compute-node generates its share of candidate elementary mode columns, and filters those which are valid elementary modes at the given iteration according to the same criteria as in serial Nullspace Algorithm. However, different compute-nodes may generate identical candidate elementary mode columns, and compute-nodes will have to communicate to remove these duplicated bit-columns. The result of communication among compute-nodes is the complete set of elementary modes after processing the kth reaction. In a carefully designed communication pattern, compute-nodes would exchange their generated elementary modes, and each compute-node would merge the arrays of bit-columns obtained from other compute-nodes with its local set of elementary mode columns. The disadvantage of this approach, which we have also implemented, is in the ALL-TO-ALL merge and communication pattern. The cost of communication among compute-nodes is negligible compared to the total cost of the merge and elimination of duplicated elementary modes which is performed on the compute-nodes locally. In Section 4.2 we analyze the complexity and give an improved communication algorithm for exchange of candidate elementary modes among compute-nodes and efficient merge. Subroutines for sorting, elimination of duplicated candidates, and rank tests remain unmodified from the serial Nullspace Algorithm.
4.1. Load Balancing
As shown in lines 4–5 of Algorithm 5 we partition the arrays of indices of columns of matrix irrev− and rev among the compute-nodes evenly. However, since the R(1) bit-matrix remains in sorted order at the beginning of each iteration, the generated candidate elementary mode bit-columns at every compute-node may have non-uniform overall density of non-zero entries. This imbalance would occur if we assigned to each compute-node the contiguous range of indices from arrays irrev− and rev. If this was the case, compute-nodes would generate the set of candidate columns of non-uniform “sparsity” and thus produce an unequal number of candidate columns which satisfy Proposition 4. This would result in the poor load balancing in the sections of the algorithm corresponding to the “sort & removal of duplicated columns” and “rank tests of candidate columns”. As a solution to this problem, we assigned to each compute-node the set of indices from both irrev− and rev which have values congruent to the compute-node identifier modulo total number of compute-nodes P, as illustrated in Algorithm 5.
The comparison between “sequential” and “interleaved” generation of candidate columns is given in Table 2. The imbalance rate in the two sections of algorithm across P compute-nodes is used as a measure, as given in Eq. (10)
Table 2.
Imbalance rate of interleaved and sequential generation of candidates.
| Number of compute-nodes
|
||||||
|---|---|---|---|---|---|---|
| 2 | 4 | 8 | 16 | 32 | ||
| Sequential | Sort and removal of duplicated columns | 1.91 | 2.55 | 4.75 | 6.49 | 14.57 |
| Rank tests of candidate columns | 2.04 | 2.97 | 5.35 | 10.13 | 34.34 | |
| Interleaved | Sort and removal of duplicated columns | 1.00 | 1.03 | 1.03 | 1.08 | 1.10 |
| Rank tests of candidate columns | 1.02 | 1.02 | 1.04 | 1.07 | 1.12 | |
| (10) |
where task corresponds to the “sort and removal of duplicated columns” or “rank tests of candidate columns”, while is the time ith compute-node spent performing the task.
4.2. Computational Complexity Analysis
In order to estimate the complexity of the parallel Nullspace Algorithm, we have to include the computational complexity term corresponding to the communication among compute-nodes. We try to attain the load balanced situation where every compute-node approximately generates the same number of elementary flux modes as described in Section 4.1. Initially, we implemented the ALL-TO-ALL broadcast communication pattern in the environment of P compute-nodes. The network parameters given are the latency ts and the per-word transfer time tw [40]. The per-word transfer time is inversely proportional to the available bandwidth between the compute-nodes. Every compute-node generates candidate elementary modes, validates that they represent admissible elementary modes by means of the numerical rank test, and communicates them to the other compute-nodes to eliminate the duplicate columns and merge. The elementary mode columns sent between compute- nodes are in sorted order, and only a proper merge subroutine is needed to eliminate duplicates. In the ALL-TO-ALL communication, every compute-node broadcasts its local set of elementary mode columns it generated to all other compute-nodes, and each compute-node does the same task of merging the received sorted columns and eliminates the duplicates from it. Note that the elementary mode columns are communicated as pairs of indices of current nullspace matrix and not as full bit-columns, for the reason of more compactness. At the end of this communication, every compute-node will have the same result, i.e. the complete nullspace matrix of the elementary flux modes at the end of current iteration of the Nullspace Algorithm. For network architectures of ring, 2D-mesh, and hypercube the cost of ALL-TO-ALL communication, if we assume that each compute-node has to send the message of approximately the same size M, can be estimated [40]. In the case when very large messages are sent over the network, what is the case in our algorithm, the cost may be approximated as
| (11) |
where M is the message length measured in units of pairs of indices being sent over the network, and P is the number of participating compute-nodes. This approximation remains the same, irrespective of the network architecture [40].
In order to sort the received messages, each compute-node has to merge P − 1 received messages. In each merge, duplicates are being eliminated. Let tc be the per unit of operation cost in the merge procedure. The computational cost of a single merge of two sorted arrays of length len1 and len2, is equal to tc(len1 + len2). We can only give an upper bound on the complexity of this merge task at a single compute-node, as follows:
| (12) |
We notice in the case of good load balancing, the product PM remains the same for the given kth iteration as the number of compute-nodes P grows. Accordingly, we note that while the cost of communication will remain the same, the cost of merging the received messages will grow with P. Therefore, this would require the re-design of the communication and merge pattern.
We may reduce the cost of merging the received messages with an alternative communication and merge pattern which corresponds to the hypercube communication. It may be illustrated with a TREE-LIKE communication and merge, as a complete binary tree of height log P and P leaf nodes, where P corresponds to the total number of compute-nodes. The complete binary tree nodes at each level of the tree correspond to those compute-nodes which are being used in the current iteration. We may equally use the term hypercube or tree since the tree may be embedded in a log P-dimensional hypercube almost symmetrically [40]. For convenience we will refer to the TREE-LIKE communication and merge in the rest of this paper. In the first phase, there will be log P iterations of unidirectional point-to-point communication among pairs of compute-nodes on the same level of the tree. At the kth iteration (k ∈ {1, …, log P}), each compute-node i such that i = 0 (mod2k) will receive the message from compute-node j = i + 2k−1. Approximately, the size of the message sent will be of length 2k−1M. The cost of each iteration has an upper bound equal to the value of merging two messages of length 2k−1M, i.e. tc2kM. At the end of the first phase, the resulting nullspace matrix will be contained in compute-node 0. We assume that the number of compute-nodes P is a power of two, in order to maintain a complete binary tree. Accordingly, we assume that due to proper load balancing, prior to communication each compute-node has precomputed approximately M elementary mode columns and needs to distribute them to other compute-nodes for merge and elimination of duplicates. The cost of this merge operation may be expressed as:
| (13) |
Hence, when compared to the result in Eq. (12), the cost of merging given in Eq. (13) is reduced by the factor of P. Since the product PM is constant as P scales, the cost of merge will remain constant as well for the particular iteration of the algorithm.
Apart from estimating the cost of merge, we estimate the cost of TREE-LIKE communication across the network. In every kth iteration the cost of exchanging a message of size 2k−1M between two compute-nodes is equal to ts + tw2k−1M [40]. The cost of ONE-TO-ALL broadcast from the compute-node 0 after all data is merged is equal to (ts + twPM) log P, and thus the total communication cost may be estimated as:
| (14) |
The last approximation follows from the assumption that start up time is much smaller than the per-word transfer time [40]. Accordingly, we conclude that the communication cost will grow with a factor of log P, unlike in (11) where it remains unchanged.
However, the cost estimates just given are upper bounds. The final set of merged columns which are broadcasted from compute-node 0 may be significantly smaller, because a large share of duplicated elementary mode columns are eliminated before the broadcast. In the experimental results on the computing platforms which were used to test the software, the communication time was negligible compared to the total time required to merge and eliminate duplicates at each computenode, as will be shown later.
5. Experimental evaluation
5.1. Experimental setup
We present the computational times obtained with both the serial and parallel Nullspace Algorithm. We plot the runtime over five similar, but distinct models of the metabolic networks of the central metabolism of E. coli using our serial implementation (available at http://elmocomp.sourceforge.net) METATOOL v5.1 [29,21] and EFMTools [27]. Further, we time the results for the same set of models for our parallel implementation and observe the scalability as the number of compute-nodes grows. For both serial and parallel implementation we use the Template Numerical Toolkit [41] from the National Institute of Technology and the C++ library of linear algebra functions adapted from the Java Matrix Library [42] developed by Mathworks and NIST.
We time the results of our parallel program on two distinct computing platforms: “Calhoun” of the Minnesota Supercomputing Institute and Blue Gene/P of IBM. In the following discussion, we use the terms compute node, processor and core, to describe the hardware of the computing platforms. Note that compute-node as used in the Section 4 refers to the abstract node which executes one instance of the parallel program in the message-passing distributed memory communication environment.
The parallel program was compiled with Intel C++ compiler and OpenMPI on “Calhoun” platform. “Calhoun” has 512 Intel Xeon 5355 (Clovertown) class multi-chip modules (MCMs). Each MCM is composed of two dies. These dies are two separate pieces of silicon connected to each other and arranged on a single module. Each die has two processor cores that share a 4 MB L2 cache. Each MCM communicates with the main memory in the system via a 1,333 MHz front-side bus (FSB). “Calhoun” is configured to have 256 compute nodes, 2 interactive nodes, 5 server nodes, total of 2048 cores, 4 TB total main memory. Each node within the system has two quad-core 2.66 GHz Intel Xeon (Clovertown) – class processors and 16 GB memory running at 1,333 MHz. All of the systems within Calhoun are interconnected with a 20-gigabit non-blocking InfiniBand fabric used for interprocess communication (IPC). The InfiniBand fabric is a high-bandwidth, low-latency network, the intent of which is to accommodate high-speed communication for large MPI jobs. The nodes are also interconnected with two 1-gigabit ethernet networks for administration and file access, respectively.
The architecture of Blue Gene/P has been described elsewhere [43], but it is important to provide a brief overview of the components of Blue Gene/P to understand the results presented here. The smallest component in the system is the chip. Single chip has a PowerPC 450 quad-core processor. Each processor core runs at a frequency of 850 MHz, and each processor core can perform four floating-point operations per cycle, giving a theoretical peak performance of 13.6 gigaFLOPS/chip. The chip is soldered to a small processor card, one per card, together with 2 GB DRAM memory to create the compute card.
The I/O card is the next building block. This card is physically very similar to the compute card. However, the I/O card has the integrated Ethernet enabled for communication with the outside world. The I/O cards and the compute cards form a socalled node card. The node card has 2 rows of 16 compute cards and 0–2 I/O nodes depending on the I/O configuration. Further, a midplane has 16 node cards. A rack holds 2 midplanes, for a total of 32 node cards or 1024 compute cards. A full petaflop system contains 72 racks. Finally, the compute-nodes may be configured at boot time to operate in one of three modes: (a) symmetric multi-processing mode, (b) virtual node mode and (c) dual mode. Symmetric-multiprocessing mode runs the main process on one processor and can spawn up to 3 threads on remaining processors. In dual mode CPUs with rank 0 and 2 run a main program process, and each can spawn an additional thread. Virtual node mode runs the program on all four processors, without additional threading.
5.2. Serial program
Results of the execution of the three distinct implementations over different metabolic networks are shown in Table 3. As pointed out earlier [25] and in Section 2.3, the compression of the stoichiometric matrix is very important in reducing the computational cost. We present the results over five models of central metabolism of E. coli for METATOOL, our implementation, and EFMTools. EFMTools and our implementation perform the identical iterative compression procedure of the given metabolic network, while METATOOL does not. A major bottleneck is in the generation of candidate elementary modes described in Algorithms 3 and 5, followed to smaller extent by the evaluation of numerical rank tests and sorting, respectively. The serial program was timed on Intel Pentium D CPU 3 GHz, dual-core, 2 GB main memory.
Table 3.
Results for serial Nullspace Algorithm.
| Original networka | Compressed networkb | Time (s)
|
#EFM | ||
|---|---|---|---|---|---|
| METATOOL 5.1 | NSP impl. | EFMTools | |||
| E. coli 47 × 59(21) | 26 × 38(13) | 13 | 3.16 | 3.91 | 44,354 |
| E. coli 41 × 61(19) | 26 × 40(12) | 16 | 2.65 | 4.89 | 38,002 |
| E. coli 49 × 64(19) | 26 × 41(12) | 73 | 11.64 | 14.36 | 92,594 |
| E. coli 50 × 66(19) | 27 × 43(13) | 195 | 39.51 | 49.04 | 188,729 |
| E. coli 50 × 66(28) | 29 × 45(19) | NCc | 1372.77 | 929.94 | 1,224,785 |
Dimensions of stoichiometry matrix; number of reversible reactions given in parentheses.
Dimensions of the compressed metabolic network.
NC (computation did not complete).
5.3. Parallel program
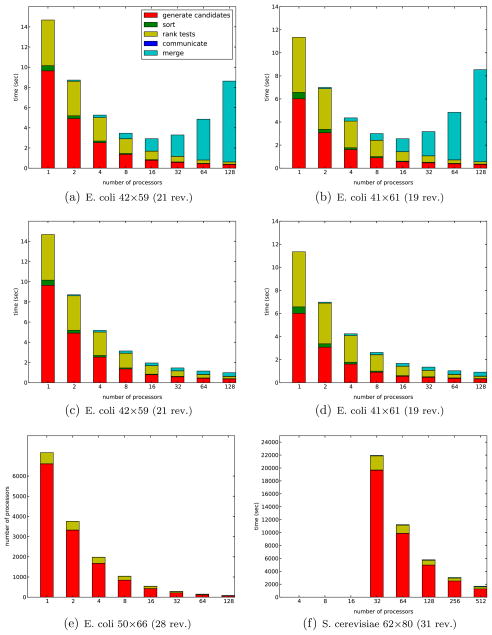
We give the results for the parallel implementation over the same set of the metabolic network models as for the serial implementation. We also include the timing results for the S. cerevisiae metabolic network, due to its higher computational cost. With the ALL-TO-ALL communication and merge implemented we have seen the increase in the cost of merge proportional to the increase of the number of participating processors P, as is demonstrated in Fig. C.2(a) and (b) for the two metabolic network models of E. coli having 59 and 61 reactions, respectively. When we replace the ALL-TO-ALL communication and merge pattern with the TREE-LIKE communication and merge, we observe the reduced cost of merging local and remote columns in Fig. C.2(c) and (d).
Fig. C.2.
Parallel Nullspace Algorithm (a), (b) ALL-TO-ALL and (c)–(f) TREE-LIKE communication and merge pattern. Subfigures (a)–(f) are results of computation on Blue Gene/P parallel platform.
This is consistent with our theoretical prediction that the TREE-LIKE communication and merge pattern reduces the overhead. For the three remaining variations of the metabolic networks of the central metabolism of E. coli, differing by the number of reactions, metabolites and reversible reactions, we present the timing results obtained on afore mentioned Intel Xeon (Clovertown) and Blue Gene/P computing platforms in the Tables D.5 and D.6. Both tables contain the results for the more efficient TREE-LIKE communication and merge pattern. Within the tables, the metabolic networks are annotated with the size of their original and compressed stoichiometry network accompanied with the number of reversible reactions (in the parentheses), since the core Nullspace Algorithm accepts the compressed stoichiometric network as input. In addition to the E. coli models, we present in the Table 4 the results of the metabolic network obtained for the S. cerevisiae strain, which contains 62 metabolites and 80 reactions, of which 31 reactions are reversible. Fig. C.2(e) gives the diagram for the parallel program over the E. coli 50 × 66(28) network, while Fig. C.2(f) gives the similar diagram for the computation given in Table 4 corresponding to S. cerevisiae 62 × 80(31) metabolic network, computed using the Blue Gene/P parallel platform.
Table D.5.
Results for parallel Nullspace Algorithm on Intel Xeon (Clovertown) machine for E. coli metabolic networks.
| Time (s)
|
#EM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1p | 2p | 4p | 8p | 16p | 32p | 64p | 128p | ||||
| E. coli | Original | Gen. cand. | 13.45 | 7.12 | 3.73 | 1.92 | 1.28 | 1.21 | 1.17 | 0.81 | 92,594 |
| 49 × 64(19)a | sorting | 0.84 | 0.42 | 0.33 | 0.10 | 0.05 | 0.05 | 0.02 | 0.01 | ||
| Compressed | rank tests | 2.55 | 1.98 | 1.35 | 0.89 | 0.55 | 0.39 | 0.30 | 0.10 | ||
| 26 × 41(12)b | comm. | 0.00 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.04 | 0.08 | ||
| merge | 0.00 | 0.02 | 0.05 | 0.05 | 0.05 | 0.06 | 0.06 | 0.07 | |||
| Total | 17.10 | 9.72 | 5.65 | 3.09 | 2.16 | 2.01 | 1.92 | 1.39 | |||
| E. coli | Original | Gen. cand. | 46.99 | 23.86 | 11.95 | 6.39 | 3.73 | 2.37 | 1.32 | 0.73 | 188,729 |
| 50 × 66(19) | sorting | 2.94 | 1.48 | 0.82 | 0.55 | 0.27 | 0.11 | 0.06 | 0.03 | ||
| Compressed | rank tests | 8.15 | 6.27 | 4.27 | 2.74 | 1.54 | 0.90 | 0.69 | 0.47 | ||
| 27 × 43(13) | comm. | 0.00 | 0.01 | 0.02 | 0.05 | 0.05 | 0.06 | 0.06 | 0.08 | ||
| merge | 0.00 | 0.05 | 0.08 | 0.09 | 0.10 | 0.11 | 0.11 | 0.12 | |||
| Total | 58.90 | 32.35 | 17.71 | 10.31 | 6.57 | 3.91 | 2.31 | 1.63 | |||
| E. coli | Original | Gen. cand. | 2189.32 | 1077.90 | 538.30 | 268.93 | 135.53 | 67.48 | 37.35 | 21.25 | 1,224,785 |
| 50 × 66(28) | sorting | 84.58 | 26.60 | 14.07 | 10.84 | 5.55 | 1.99 | 1.35 | 1.32 | ||
| Compressed | rank tests | 91.60 | 70.40 | 48.58 | 30.57 | 17.89 | 10.06 | 5.27 | 2.85 | ||
| 29 × 45(19) | comm. | 0 | 0.06 | 0.14 | 0.3 | 0.27 | 0.28 | 0.31 | 0.4 | ||
| merge | 0 | 0.80 | 1.26 | 1.42 | 1.47 | 1.56 | 1.67 | 1.79 | |||
| Total | 2381.49 | 1185.06 | 609.42 | 318.80 | 166.29 | 86.30 | 50.97 | 36.16 | |||
Dimensions of stoichiometry matrix of the metabolic network; number of reversible reactions given in parentheses.
Dimensions of stoichiometry matrix of the reduced metabolic network.
Table D.6.
Results for parallel Nullspace Algorithm on Blue Gene/P for E. coli metabolic networks.
| Time (s)
|
#EM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1p | 2p | 4p | 8p | 16p | 32p | 64p | 128p | ||||
| E. coli | Original | Gen. cand. | 33.89 | 17.03 | 8.60 | 4.39 | 2.31 | 1.34 | 0.81 | 0.55 | 92,594 |
| 49 × 64(19) | sorting | 2.04 | 1.06 | 0.56 | 0.30 | 0.17 | 0.10 | 0.07 | 0.04 | ||
| Compressed | rank tests | 16.39 | 12.65 | 8.65 | 5.56 | 3.24 | 1.91 | 1.05 | 0.50 | ||
| 26 × 41(12) | comm. | 0.00 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.04 | 0.05 | ||
| merge | 0.00 | 0.19 | 0.31 | 0.39 | 0.44 | 0.48 | 0.50 | 0.52 | |||
| Total | 53.77 | 31.92 | 18.87 | 11.37 | 6.93 | 4.53 | 3.21 | 2.50 | |||
| E. coli | Original | Gen. cand. | 117.46 | 58.85 | 29.52 | 14.86 | 7.55 | 3.97 | 2.14 | 1.24 | 188,729 |
| 50 × 66(19) | sorting | 7.24 | 3.67 | 1.89 | 0.97 | 0.50 | 0.27 | 0.15 | 0.9 | ||
| Compressed | rank tests | 51.81 | 39.50 | 27.13 | 17.01 | 9.81 | 5.60 | 2.93 | 1.41 | ||
| 27 × 43(13) | comm. | 0.00 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 | 0.04 | 0.04 | ||
| merge | 0.00 | 0.37 | 0.57 | 0.71 | 0.79 | 0.85 | 0.87 | 0.92 | |||
| Total | 180.92 | 105.95 | 62.17 | 35.98 | 20.96 | 12.51 | 7.91 | 5.59 | |||
| E. coli | Original | Gen. cand. | 6599.20 | 3319.78 | 1672.14 | 840.44 | 424.64 | 215.29 | 109.75 | 56.47 | 1,224,785 |
| 50 × 66(28) | sorting | 10.38 | 8.61 | 5.90 | 3.78 | 2.25 | 1.29 | 0.73 | 0.40 | ||
| Compressed | rank tests | 552.02 | 425.86 | 296.53 | 189.23 | 108.91 | 61.12 | 31.30 | 16.89 | ||
| 29 × 45(19) | comm. | 0.0 | 0.10 | 0.20 | 0.43 | 1.03 | 1.14 | 0.93 | 0.95 | ||
| merge | 0.0 | 3.81 | 5.89 | 6.95 | 7.25 | 7.87 | 8.40 | 9.05 | |||
| Total | 7174.93 | 3776.32 | 1999.33 | 1062.70 | 567.08 | 307.20 | 173.04 | 103.76 | |||
Table 4.
Parallel Nullspace Algorithm on Blue Gene/P machine for S. cerevisiae metabolic network.
| Time (s)
|
#EM | |||||||
|---|---|---|---|---|---|---|---|---|
| 32p | 64p | 128p | 256p | 512p | ||||
| S. cerevisiae | Original | Gen. cand. | 19,644.09 | 9,870.03 | 4,958.74 | 2,500.09 | 1281.13 | 13,322,495 |
| 62 × 80(31) | sorting | 45.09 | 24.97 | 15.17 | 9.96 | 6.53 | ||
| Compressed | rank tests | 2,169.65 | 1,244.22 | 726.45 | 435.44 | 299.25 | ||
| 38 × 58(20) | comm. | 1.22 | 1.22 | 1.24 | 1.26 | 1.28 | ||
| merge | 80.03 | 86.09 | 90.05 | 95.88 | 100.59 | |||
| Total | 22,153.23 | 11,414.66 | 5,952.08 | 3,203.84 | 1847.72 | |||
| Relative CPU Power ratioa | 1.0 | 1.030 | 1.075 | 1.157 | 1.335 | |||
Relative CPU power ratio = (number_of_processors × total_time)/(32 × total_time_on_32_proc).
From the experiments using the proposed parallel Nullspace Algorithm we see that the rank tests may not scale as well as the remaining portions. The reason is that all compute-nodes at the given iteration evaluate the rank tests on approximately similar number of candidate columns. However, some compute-nodes may be evaluating the rank tests on submatrices of different sizes which depends on the number and position of non-zero elements in the candidate column.
5.4. Other parallelizations of elementary mode computation
In [44,45] parallelizations of the older Canonical Basis Algorithm was proposed for computation of extreme pathways. The parallel approach in [44] is not specific with respect to the attained load balancing and relies on a custom based API for socket communication rather than standard message-passing interface (MPI). In addition to using the older Canonical Basis Algorithm, both approaches relied on a combinatorial search of the candidate matrix rather than the algebraic rank test as in our approach, which has proved to be more efficient [25].
In [39], an alternative way of parallelizing the Nullspace Algorithm is proposed in the form of using the divide-and-conquer approach to split the set of all elementary flux modes into disjoint subsets across a subset of reactions. The “divide” part of divide-and-conquer was still carried out manually but the method shows enough promise that we foresee its future use and incorporation within our algorithm and software. There are two issues to be addressed in the divide-and-conquer approach. First, it is unclear how to select the optimal subset of reactions that would lead to the good load balancing during parallel computation. Second, it is not known how to ensure that the total number of intermediate candidate elementary modes decreases as the problem is divided up, something of critical importance since this is the major time and memory bottleneck of the Nullspace Algorithm.
Recently, the EFMTools software for the computation of elementary flux modes came out with a shared-memory parallelization. The shared-memory parallelization was proposed in [27], where multiple threads may search the same data structure to generate candidate elementary flux modes. However, the use of this approach has its limits imposed by the available number of processor cores (threads) and the contention during shared memory access. The distributed-memory approach we propose here is complementary to the shared-memory parallelization implemented in EFMTools.
An out-of-core computation model is proposed in [44,27], and in future we will incorporate it in our software. The out-of-core feature may reduce the memory requirements during the computation of elementary flux modes, but at additional time expense.
6. Discussion and conclusions
The core of this work has been to develop an efficient and scalable distributed memory parallel Nullspace Algorithm for the computation of minimal metabolic pathways in metabolic networks, the so-called elementary flux modes, and expose and remove the major bottlenecks.
We implemented the serial and parallel version of the Nullspace Algorithm based on the algebraic rank test. The parallel algorithm and its implementation are based on the heuristic which attains good load balancing and good scalability, across the metabolic network of different dimensions. Algorithm implementation was tested on the Blue Gene/P and Intel Xeon (Clovertown) parallel platforms, attaining the computation of more than 13 million elementary flux modes. For the future work and research, we intend to address several issues. First, we will improve the data structure and algorithm for the generation of candidate elementary modes for the purpose of improving the cache performance and memory locality. Second, we intend to address the issue of numerical error present in the evaluation of algebraic rank test by means of matrix decompositions. The error occurs due to the nature of floating point operations in larger problems, and we may address this issue using exact modular arithmetic as it was already proposed in [27]. Third, we will incorporate the shared-memory parallel paradigm to work with the current distributed-memory parallelization which was implemented by means of MPI. Fourth, we intend to work out the alternative divide-and-conquer approach towards solving the problem of computing elementary flux modes. Finally, we would incorporate the optional out-of-core computation into the current implementation to reduce the memory requirements inherent when the software is used over large metabolic networks.
Algorithm 6.
[combinations] = COMMUNICATE_TREE (K, combinations)
| Input: | |
| current nullspace matrix ; | |
| local set of pairs of column indices which generate new candidates (combinations) | |
| Output: | |
| merged set of column-generating pairs of indices (combinations) | |
| 1: | proc_id ⇐ identifier of the local compute-node |
| 2: | for i = 1 to log P do |
| 3: | if proc_id = 0 (mod2i) then |
| 4: | receive columns from compute-node proc_id + 2i−1 |
| 5: | merge the local set of columns with the received columns |
| 6: | else |
| 7: | send columns to compute-node proc_id − 2i−1 |
| 8: | end if |
| 9: | end for |
| 10: | if proc_id = 0 then |
| 11: | broadcast the columns to all other compute-nodes |
| 12: | end if |
Acknowledgments
This work was partially supported by NIH Grant GM077529, NSF Grants 0534286 and 0916750 and by the Biomedical Informatics and Computational Biology Program of the University of Minnesota, Rochester. We are grateful for resources and technical support from the University of Minnesota Supercomputing Institute, and would like to thank Can Ergenikan, David Poter and Shuxia Zhang for their help. We also thank the IBM Rochester Blue Gene Center, Cindy Mestad and Steven Westerbeck for their support. Finally, we thank Palsson’s Lab for the access to BiGG database of genome-scale metabolic networks.
Appendix A. Proofs
Proof of Algorithm 5
The reduced rank test is derived from the reduced row echelon form of the compressed stoichiometry matrix as is obtained in Proposition 1, which has the form ÑT = (N1 I). We assume without loss of generality that N = ÑT is m × q (by removing redundant rows in advance if necessary) matrix. At the stage k of the Nullspace Algorithm, matrix N can be further decomposed to:
| (A.1) |
As stated in Proposition 2 we must select all the columns of the stoichiometric matrix whose indices correspond to nonzero elements among x1, …, xk at stage k and the first k − (q − m) rows. According to Proposition 2 we would have that:
| (A.2) |
To compute the rank of the submatrix obtained in this way we have:
| (A.3) |
and from (A.2) and (A.3) we have that
| (A.4) |
or expressed in terms of nullity of the matrix
| (A.5) |
Appendix B. Algorithms
Algorithm 7.
[combinations] = RADIXSORT(R(1), combinations, width)
| Input: | |
| R(1) – bit pattern matrix used to generate new candidates | |
| combinations – pairs of column indices which generate new candidates | |
| width – width of the sequence of bits over which elementary radix sort is performed | |
| Output: | |
| combinations – reordered pairs of indices so that corresponding columns are sorted | |
| 1: | r ⇐ size(R(1), 1) |
| 2: | col_length ⇐ number of machine words in r bits |
| 3: | for i = 1 to col_length do |
| 4: | factor ⇐ {number of sequences of length width in current word} |
| 5: | for j = 1 to factor do |
| 6: | counting ⇐ zeros (1, 2width) |
| 7: | for k = 1 to length(combinations) do |
| 8: | (ii, jj) ⇐ combinationsk |
| 9: | aa ⇐ or |
| 10: | aa ⇐ (aa shl j · width) and (2width − 1) |
| 11: | countingaa ⇐ countingaa + 1 |
| 12: | end for |
| 13: | for k = 1 to 2width do |
| 14: | countingk ⇐ countingk + countingk−1 |
| 15: | end for |
| 16: | for k = length(combinations) downto 1 do |
| 17: | (ii, jj) ⇐ combinations(k) |
| 18: | aa ⇐ or |
| 19: | aa ⇐ (aa shl j · width) and 2width − 1 |
| 20: | combinations_sorted[countingaa − 1] ⇐ combinationsk |
| 21: | countingaa ⇐ countingaa − 1 |
| 22: | end for |
| 23: | combinations ⇐ combinations_sorted |
| 24: | end for |
| 25: | end for |
Appendix C. Figure
See Fig. C.2.
Appendix D. Tables
See Tables D.5 and D.6.
Contributor Information
Cong T. Trinh, Email: ctrinh@utk.edu.
Friedrich Srienc, Email: srienc@umn.edu.
Carlos P. Sosa, Email: cpsosa@msi.umn.edu.
Daniel Boley, Email: boley@cs.umn.edu.
References
- 1.Torres N, Voit E. Pathway Analysis and Optimization in Metabolic Engineering. Cambridge University Press; 2002. [Google Scholar]
- 2.Carlson PR. PhD Thesis. University of Minnesota; 2003. Metabolic pathway analysis and engineering of prokaryotic and eukaryotic organisms. [Google Scholar]
- 3.Vijayasankaran N, Carlson R, Srienc F. Metabolic pathway structures for recombinant protein synthesis in Escherichia coli. Applied Microbiology and Biotechnology. 2005;68(6):737–746. doi: 10.1007/s00253-005-1920-7. [DOI] [PubMed] [Google Scholar]
- 4.Trinh C. PhD Thesis. University of Minnesota; 2008. Inverse metabolic engineering: a rational approach for efficient and robust microorganism development. [Google Scholar]
- 5.Reed J, Vo T, Schilling C, Palsson B. An expanded genome-scale model of Escherichia coli K-12 (iJR904 GSM/GPR) Genome Biology. 2003;4(9):435–443. doi: 10.1186/gb-2003-4-9-r54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Duarte N, Herrgard M, Palsson B. Reconstruction and validation of Saccharomyces cerevisiae iND750, a fully compartmentalized genomescale metabolic model. Genome Research. 2004;14(7):1298–1309. doi: 10.1101/gr.2250904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Forster J, Famili I, Fu P, Palsson B. Genome-scale reconstruction of the Saccharomyces cerevisiae metabolic network. Genome Research. 2003;13:644–653. doi: 10.1101/gr.234503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Borodina I, Krabben P, Nielsen J. Genome-scale analysis of Streptomyces coelicolor A3(2) metabolism. Genome Research. 2005;15(1):820–829. doi: 10.1101/gr.3364705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schilling C, Covert M, Famili I, Church G, Edwards J, Palsson B. Genome-scale metabolic model of Helicobacter pylori 26695. Journal of Bacteriology. 2002;184(16):4582–4593. doi: 10.1128/JB.184.16.4582-4593.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schilling CH, Palsson B. Assessment of the metabolic capabilities of Haemophilus influenzae rd through a genome-scale pathway analysis. Journal of Theoretical Biology. 2000;203(3):249–283. doi: 10.1006/jtbi.2000.1088. [DOI] [PubMed] [Google Scholar]
- 11.Ma H, Sorokin A, Mazein A, Selkov A, Selkov E, Demin O, Goryanin I. The Edinburgh human metabolic network reconstruction and its functional analysis. Molecular Systems Biology. 2007;3 doi: 10.1038/msb4100177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Duarte NC, Becker SA, Jamshidi N, Thiele I, Mo ML, Vo TD, Srivas R, Palsson B. Global reconstruction of the human metabolic network based on genomic and bibliomic data. Proceedings of the National Academy of Sciences of the USA. 2007;104(6):1777–1782. doi: 10.1073/pnas.0610772104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schuster S, Hilgetag C. On elementary flux modes in biochemical reaction systems at steady state. Journal of Biological Systems. 1994;2(2):165–182. [Google Scholar]
- 14.Schuster S, Fell D, Dandekar T. A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nature Biotechnology. 2000;18(3):326–332. doi: 10.1038/73786. [DOI] [PubMed] [Google Scholar]
- 15.Schuster S, Hilgetag C, Woods J, Fell D. Reaction routes in biochemical reaction systems: algebraic properties, validated calculation procedure and example from nucleotide metabolism. Mathematical Biology. 2002;45(2):153–181. doi: 10.1007/s002850200143. [DOI] [PubMed] [Google Scholar]
- 16.Schilling CH, Letscher D, Palsson B. Theory for the systemic definition of metabolic pathways and their use in interpreting metabolic function from a pathway-oriented perspective. Journal of Theoretical Biology. 2000;203(3):229–248. doi: 10.1006/jtbi.2000.1073. [DOI] [PubMed] [Google Scholar]
- 17.Trinh C, Unrean P, Srienc F. A minimal Escherichia coli cell for most efficient ethanol production from hexoses and pentoses. Applied and Environmental Microbiology. 2008;74(12):3634–3643. doi: 10.1128/AEM.02708-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Carlson R. Metabolic systems cost-benefit analysis for interpreting network structure and regulation. Nucleic Acids Research. 2007;23(16):1258–1264. doi: 10.1093/bioinformatics/btm082. [DOI] [PubMed] [Google Scholar]
- 19.Stelling J, Klamt S, Bettenbrock K, Schuster S, Gilles ED. Metabolic network structure determines key aspects of functionality and regulation. Nature. 2002;420(6912):190–193. doi: 10.1038/nature01166. [DOI] [PubMed] [Google Scholar]
- 20.Trinh C, Carlson R, Wlaschin A, Srienc F. Design, construction and performance of the most efficient biomass producing E. coli bacterium. Metabolic Engineering. 2006;8(6):628–638. doi: 10.1016/j.ymben.2006.07.006. [DOI] [PubMed] [Google Scholar]
- 21.von Kamp A, Schuster S. Metatool 5.0: fast and flexible elementary modes analysis. Bioinformatics. 2006;22(15):1930–1931. doi: 10.1093/bioinformatics/btl267. [DOI] [PubMed] [Google Scholar]
- 22.Wagner C. Nullspace approach to determine the elementary modes of chemical reaction systems. J Phys Chem. 2004;108(7):2425–2431. [Google Scholar]
- 23.Urbanczik R, Wagner C. An improved algorithm for stoichiometric network analysis: theory and applications. Bioinformatics. 2005;21(7):1203–1210. doi: 10.1093/bioinformatics/bti127. [DOI] [PubMed] [Google Scholar]
- 24.Klamt S, Stelling J, Ginkel M, Gilles E. FluxAnalyzer: exploring structure, pathways, and flux distributions in metabolic networks on interactive flux maps. Bioinformatics. 2003;19(2):261–269. doi: 10.1093/bioinformatics/19.2.261. [DOI] [PubMed] [Google Scholar]
- 25.Gagneur J, Klamt S. Computation of elementary modes: a unifying framework and the new binary approach. BMC Bioinformatics. 2004;5 doi: 10.1186/1471-2105-5-175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Klamt S, Saez-Rodriguez J, Gilles ED. Structural and functional analysis of cellular networks with CellNetAnalyzer. BMC Systems Biology. 2007;1 doi: 10.1186/1752-0509-1-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Terzer M, Stelling J. Large scale computation of elementary flux modes with bit pattern trees. Bioinformatics. 2008;24(19):2229–2235. doi: 10.1093/bioinformatics/btn401. [DOI] [PubMed] [Google Scholar]
- 28.Fukuda K, Prodon A. Double description method revisited. In: Deza M, Euler R, Manoussakis I, editors. Combinatorics and Computer Science. Springer; 1996. pp. 91–111. also Tech. Report, Mathematics, ETH, 1995. < ftp://ftp.ifor.math.ethz.ch/pub/fukuda/reports/ddrev960315.ps.gz>. [Google Scholar]
- 29.Pfeiffer T, Sanchez-Valdenebro I, Nuno J, Montero F, Schuster S. METATOOL: for studying metabolic networks. Bioinformatics. 1999;15(3):251–257. doi: 10.1093/bioinformatics/15.3.251. [DOI] [PubMed] [Google Scholar]
- 30.Klamt S, Stelling J. Two approaches for metabolic pathway analysis? Trends in Biotechnology. 2003;21(2):64–69. doi: 10.1016/s0167-7799(02)00034-3. [DOI] [PubMed] [Google Scholar]
- 31.Jevremovic D, Trinh C, Srienc F, Boley D. On algebraic properties of extreme pathways in metabolic networks. Journal of Computational Biology. 2010;17(2):107–119. doi: 10.1089/cmb.2009.0020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Urbanczik R, Wagner C. Functional stoichiometric analysis of metabolic networks. Bioinformatics. 2005;21(22):4176–4180. doi: 10.1093/bioinformatics/bti674. [DOI] [PubMed] [Google Scholar]
- 33.Luenberger DG. Linear and Nonlinear Programming. 2. Springer; 2003. [Google Scholar]
- 34.Schellenberger J, Park J, Conrad T, Palsson B. BiGG: a biochemical genetic and genomic knowledgebase of large scale metabolic reconstructions. BMC Bioinformatics. 2010;11 doi: 10.1186/1471-2105-11-213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Acuña V, Marchetti-Spaccamela A, Sagot M, Stougie L. A note on the complexity of finding and enumerating elementary modes. Biosystems. 2010;99(3):210–214. doi: 10.1016/j.biosystems.2009.11.004. [DOI] [PubMed] [Google Scholar]
- 36.Acuña V, Chierichetti F, Lacroix V, Marchetti-Spaccamela A, Sagot M, Stougie L. Modes and cuts in metabolic networks: complexity and algorithms. BioSystems. 2009;95(1):51–60. doi: 10.1016/j.biosystems.2008.06.015. [DOI] [PubMed] [Google Scholar]
- 37.Khachiyan L, Boros E, Borys K, Elbassioni K, Gurvich V. Generating all vertices of a polyhedron is hard. Proceedings of the seventeenth annual ACMSIAM symposium on discrete algorithms. 2006:758–765. [Google Scholar]
- 38.Cormen TH, Leiserson C, Rivest R, Stein C. Introduction to Algorithms. 2. The MIT Press; 2001. [Google Scholar]
- 39.Klamt S, Gagneur J, von Kamp A. Algorithmic approaches for computing elementary modes in large biochemical reaction networks. Systems Biology, IEE Proceedings. 2005;152(4):249–255. doi: 10.1049/ip-syb:20050035. [DOI] [PubMed] [Google Scholar]
- 40.Grama A, Karypis G, Kumar V, Gupta A. Introduction to Parallel Computing. 2. Addison-Wesley; 2003. [Google Scholar]
- 41.Template Numerical Toolkit. < http://math.nist.gov/tnt/>.
- 42.Java Matrix Library. < http://math.nist.gov/javanumerics/jama>.
- 43.Sosa C, Knudsen B. IBM System Blue Gene Solution: Blue Gene/P Application Development. 2008 < http://www.redbooks.ibm.com/abstracts/sg247287.html>.
- 44.Samatova N, Geist A, Ostrouchov G, Melechko A. Parallel out-of-core algorithm for genome-scale enumeration of metabolic systemic pathways. Proceedings of the International Parallel and Distributed Symposium, IPDPS. 2002:185–192. [Google Scholar]
- 45.Lee L, Varner J, Ko K. Parallel extreme pathway computation for metabolic networks. In: Mycroft A, editor. SAS’95, Static Analysis Symposium, Proceedings of the 2004 IEEE Computational Systems Bioinformatics Conference (CSB 2004); Springer; 2004. pp. 33–50. [Google Scholar]