Nonparametric Multiple Imputation for ROC Analysis When Some Biomarker Values Are Missing at Random

SUMMARY

The receiver operating characteristics (ROC) curve is a widely used tool for evaluating discriminative and diagnostic power of a biomarker. When the biomarker value is missing for some observations, the ROC analysis based solely on the complete cases loses efficiency due to the reduced sample size, and more importantly, it is subject to potential bias. In this paper, we investigate nonparametric multiple imputation methods for ROC analysis when some biomarker values are missing at random (MAR) and there are auxiliary variables that are fully observed and predictive of biomarker values and/or missingness of biomarker values. While a direct application of standard nonparametric imputation is robust to model misspecification, its finite sample performance suffers from curse of dimensionality as the number of auxiliary variables increases. To address this problem, we propose new nonparametric imputation methods, which achieve dimension reduction through the use of one or two working models, namely, models for prediction and propensity scores. The proposed imputation methods provide a platform for a full range of ROC analysis, and hence are more flexible than existing methods that primarily focus on estimating the area under the ROC curve (AUC). We conduct simulation studies to evaluate the finite sample performance of the proposed methods, and find that the proposed methods are robust to various types of model misidentification and outperform the standard nonparametric approach even when the number of auxiliary variables is moderate. We further illustrate the proposed methods using an observational study of maternal depression during pregnancy.

1. Introduction

First proposed in the 1950s, the receiver operating characteristic (ROC) analysis is one of the most commonly used statistical tools for evaluating biomarkers for diagnostic tests [1]. In a typical diagnostic test setting, a biomarker is measured from both the diseased and nondiseased subjects. Without loss of generality, we assume throughout that a large biomarker value is indicative of disease. Typically, a well-suited test is more likely to produce large biomarker values in the diseased population than in the nondiseased population. In an ideal setting, the diseased and nondiseased subjects are perfectly separated with regard to their biomarker values. However, more often than not, the distribution of biomarker values in the diseased overlaps with the distribution in the nondiseased. In these cases, it is meaningful to summarize the discrimination power of the biomarker using the ROC analysis, which characterizes the two most important properties of a test, sensitivity (the proportion of diseased subjects who are correctly identified as such) and 1-specificity (the proportion of nondiseased subjects who are incorrectly identified), by varying a threshold over the range of the biomarker values. When the biomarker values are missing for some subjects (e.g., due to inadequate biomarker samples, or invalid/unreturned questionnaires), a naive ROC analysis that only uses subjects with observed biomarker values is subject to potential bias when missingness depends on the observed data, i.e., missing at random (MAR) [2]. In addition, the naive estimate is subject to loss of efficiency even when missingness is independent of all data, i.e., missing completely at random (MCAR) [2]. Nevertheless, in many biomedical studies, additional information (i.e., auxiliary variables) are available to researchers, such as baseline variables or measurements from other tests, which may be predictive of biomarker values or missingness of biomarker values. Hence, those auxiliary variables can be utilized to improve the ROC analysis. In this paper, we investigate appropriate ROC analysis in the presence of missing biomarker values that utilizes the auxiliary variables, under the assumption of MAR.

Many methods have been proposed for the general missing data problem under the assumption of MAR and we refer to the text by Little and Rubin [2] for a complete review. In this paper, we focus on multiple imputation (MI) methods, which generate multiple imputed complete datasets to account for uncertainty of imputation. Model-based approaches have been proposed to impute missing values and have been shown to perform well in many settings [2]. However, it is well known that model-based imputation approaches are subject to misspecification of the parametric models. To overcome this difficulty, nonparametric imputation approaches can be used, which avoid using parametric models for imputation and hence are more robust to model misspecification. For example, one can define a similarity measure between observations based on auxiliary variables and adopt a K – nearest neighbor (K-NN) approach to identify candidates for imputation; intuitively, the observations that are most similar to the one with a missing value are considered suitable candidates for imputation.

As the number of auxiliary variables can be large in practice, observed data often turn out to be sparse in the high dimensional space of all possible values of auxiliary variables. Therefore, a common challenge in nonparametric imputation is to identify observations that are reasonably “similar” to the ones with missing biomarker values when the number of auxiliary variables considered in the similarity measure is large. This is also known as the curse of dimensionality in nonparametric regression literature. To alleviate this problem, we propose to reduce the dimension of auxiliary variables through the use of prediction scores for biomarker values, which is similar to prognostic scores defined by Hansen [3]. In addition, we propose to use a propensity score model for missingness of biomarkers in combination with the prediction score model to improve the robustness of the nonparametric MI method. The resulting method based on both working models is expected to be doubly robust, i.e., it is consistent if either or both working models are correctly specified. Furthermore, we add a bootstrap step into the proposed nonparametric MI methods to account for uncertainty in estimating parameters in the working model(s) so that the standard MI variance formula can be used [4]. Our approach of using prediction and propensity scores to construct doubly robust estimators is similar to the approach first proposed for survival data by Zeng [5] and subsequently extended to missing data problem in regression settings by Zeng and Chen [6]; the key difference is that our research focuses on multiple imputation methods, which are more flexible and better suited for ROC analysis.

A nice feature of the proposed MI approaches is that they allow for a full range of ROC analysis, e.g., any summary statistic of a ROC curve can be computed. Among the limited research on the ROC analysis in the presence of missing biomarker values, Long et al. [7] discuss a doubly robust semiparametric approach specifically for estimating the area under the ROC curve (AUC), and the extension of their method, say, to plot the ROC curve, is not straightforward. In this work, we discuss the estimation of the AUC as well as plotting the ROC curve. Other analyses based on a ROC curve can be performed along similar lines. We also emphasize that we focus on the case of missing biomarker values and assume that the disease status is confirmed for all subjects. There is a related but different missing data problem in ROC analysis, often known as the verification bias in the literature, where the disease status is only verified in a subset of the observations and unknown in the rest; this problem has been investigated by Zhou [8, 9, 10], and more recently by Rotnitzky et al. [11] and Fluss et al. [12]. Since the selection for testing may depend on the disease status and/or other variables, the naive ROC analysis based on disease-verified subjects may be subject to bias.

The remainder of this article is organized as follows. In Section 2, we first describe a standard nonparametric MI method via K-NN, and then propose a nonparametric MI method based on estimated prediction scores and a nonparametric MI method based on both estimated prediction and propensity scores; we also introduce a bootstrap step in estimation of the working model parameters. In Section 3, we evaluate the finite sample performance of the proposed methods through simulations. In Section 4, we illustrate our methods using data from an observational study of postpartum depression among pregnant women. Finally, we provide some discussion remarks in Section 5.

2. Methodology

Suppose we are interested in using a biomarker to detect the disease status, and let D denote the true disease status (D = 0 for nondiseased and 1 for diseased) and X denote the biomarker value, which is unavailable for some subjects. We write X_D to represent the biomarker value for a subject with disease status D, i.e., X₀ and X₁ represent biomarker values for the nondiseased and diseased, respectively. Let δ denote the missing indicator of X, i.e., δ = 1 if X is observed, and δ = 0 otherwise. For each disease group (D = 0 or 1), we denote the set of all subjects with observed X by 𝒪_D = {i : δ_i = 1 and D_i = D} and the set of subjects with missing X by ℳ_D = {i : δ_i = 0 and D_i = D}. Lastly, we introduce the auxiliary variables that are predictive of X or δ by Z = (Z⁽¹⁾, …, Z^(P)), which are fully observed. Following convention, we use bold font to denote vectors. We emphasize that, throughout, we assume MAR, i.e., δ ⫫ X | Z.

In the rest of this section, we first describe the standard and the proposed nonparametric MI methods for the estimation of AUC, i.e., θ = Pr(X₁ > X₀), and then discuss, as an example, the estimation of the ROC curve itself based on the imputed datasets. We note that when all biomarker values are available (observed or through imputation), the estimate of θ and its variance follow readily from Equations (5.5) and (5.10) in [1]. In particular, the estimate of θ is as follows,

$$\widehat{\theta }=n_0^{-1}{n}_1^{-1}{\displaystyle \sum _{i=1}^{n_1}}{\displaystyle \sum _{j=1}^{n_0}}\{\mathrm{I}(X_{1i}>X_{0j})+0.5\mathrm{I}(X_{1i}=X_{0j})\},$$ (1)

where n₀ and n₁ denote the number of subjects in the nondiseased and diseased group, respectively.

2.1. Standard Nonparametric MI

We now describe a standard nonparametric MI approach via K-NN. In order to identity observations that are suitable candidates of imputation, we first need to define a distance (or similarity) measure between observations; we here adopt a weighted Euclidian distance, i.e., $d(i,j)=\sqrt{{\displaystyle {\sum }_{p=1}^P}{w}_p{(Z_i^{(p)}-Z_j^{(p)})}^2}$, where w_p is a positive weight and may represent importance of each auxiliary variable and ∑_p w_p = 1. For each given observation i ∈ ℳ_D, one can order the distance d(i, j) for all observation j’s with the same disease status (i.e., j ∈ 𝒪_D). The K observations with the shortest distances are then identified as the nearest neighbors of observation i, denoted by 𝒦_i. One then randomly chooses an observation out of 𝒦_i for imputation. After the biomarker values for all observations in ℳ₀ and ℳ₁ are imputed, an imputed complete dataset is obtained. This imputation procedure is repeated multiple times (L). We denote the estimate of θ following Equation (1) based on the l^th (1 ≤ l ≤ L) imputed complete dataset by θ̂^(l), and denote the estimate of its variance by ${\widehat{\sigma }}_{(l)}^2$. The resulting nonparametric MI estimate of θ is then defined as ${\widehat{\theta }}_{\mathit{\text{MI}}}=L^{-1}{\displaystyle {\sum }_{l=1}^L}{\widehat{\theta }}_{(l)}$, and its variance is computed as ${\widehat{\sigma }}_{\mathit{\text{MI}}}^2={\overline{\sigma }}_{\mathit{\text{MI}}}^2+(1+L^{-1})B_{\mathit{\text{MI}}}$, following Rubin and Schenker [4], where ${\overline{\sigma }}_{\mathit{\text{MI}}}^2=L^{-1}{\displaystyle {\sum }_{l=1}^L}{\widehat{\sigma }}_{(l)}^2$ and B_MI is the sample variance of L estimates, namely, {θ̂_(l), l = 1, …, L}.

2.2. Nonparametric MI Based on Prediction Scores

When the number of auxiliary variables is more than a few, the standard method discussed in Section 2.1 often encounters difficulties in identifying “similar” observations for imputation in a finite sample. To address this issue, we first consider a nonparametric MI method based on prediction scores of biomarker values. We denote the subset of the auxiliary variables that are predictive of X by Z₁ (Z₁ ⊆ Z). The proposed MI procedure consists of four steps detailed below:

1. We first fit a working model for the biomarker values via linear regression, i.e., E(X) = α^TW₁, using observations in 𝒪₀∪𝒪₁, where W₁ may include Z₁, D, and their interaction terms. We denote the estimate of α by α̂.

2. We then compute a prediction score for each subject, namely, s₁ = α̂^TW₁ for all observations, i.e., 𝒪₀ ∪ 𝒪₁ ∪ ℳ₀ ∪ ℳ₁.

3. The next step is to select appropriate observed biomarker values for imputation based on estimated prediction scores. For each observation i ∈ ℳ_D, we identify K observations with the smallest absolute difference (|s_1i − s_1j|, where j ∈ 𝒪_D), denoted by 𝒦_i. We then impute the missing biomarker value of observation i with X_j (j ∈ 𝒦_i), where j is randomly selected out of 𝒦_i. Once all observations in ℳ₀ and ℳ₁ are imputed with suitable biomarker values, we obtain an imputed complete dataset. This is repeated multiple times (L). We denote the estimate of θ and its estimated variance from the l^th (1 ≤ l ≤ L) imputed dataset by θ̂_(l) and ${\widehat{\sigma }}_{(l)}^2$.

4. We then summarize across all L imputed datasets and compute the MI estimate of θ and its variance following Section 2.1, denoted by θ̂_{MI − 1} and ${\widehat{\sigma }}_{\mathit{\text{MI}}-1}^2$, respectively.

2.3. Nonparametric MI Based on Prediction and Propensity Scores

As will be shown in Section 2.6, one disadvantage of the MI method discussed in Section 2.2 is its dependency on a correctly specified working model to ensure the consistency of θ̂_{MI − 1}. In practice, the functional form of the working model may not reflect the true relationship between D, Z and X, or, influential auxiliary variables may be left out of the working model. Under those circumstances, θ̂_{MI − 1} may not be consistent. To address this issue, we introduce a second working model of propensity scores [13] which includes a set of auxiliary variables Z₂ (Z₂ ⊆ Z) as the covariates that are predictive of δ and could be different from Z₁. The nearest neighbors for imputation are then identified on a two-dimensional space, namely, one for prediction scores and the other for propensity scores, in contrast to the one-dimensional space of prediction scores in Section 2.2. Specifically, we propose the following four-step procedure:

1. We first fit the working model for X using observations in 𝒪₀ ∪ 𝒪₁ and the working model for δ using all observations (𝒪₀ ∪ 𝒪₁ ∪ ℳ₀ ∪ ℳ₁). The prediction score model, namely, E(X) = α^TW₁, is fitted as discussed in Section 2.2. We employ a logistic regression model for δ, i.e., logit(Pr(δ = 1)) = β^TW₂, where W₂ may include Z₂, D, and their interaction terms. We denote the estimate of β by β̂.

2. We then compute two scores for all observations based on the working models in Step 1 by plugging in the respective estimates, i.e., s₁ = α̂^TW₁ and s₂ = α̂^TW₂. Considering that the two scores may be on different scales, we standardize their values to mean 0 and standard deviation 1, and denote the standardized values by (s̃₁, s̃₂).

3. To impute missing X for each observation i ∈ ℳ_D, we define its nearest neighbors among observations with the same disease status (i.e., 𝒪_D) based on the standardized scores, (s̃₁, s̃₂). We calculate a weighted Euclidian distance as a similarity measure, i.e., d(i, j) = {w₁(s̃_1i − s̃_1j)² + w₂(s̃_2i − s̃_2j)²}^0.5 for all j ∈ 𝒪_D, where w₁ and w₂ are positive weights and w₁ + w₂ = 1. Similar to Section 2.2, we identify K observations in 𝒪_D that have the shortest distance to observation i ∈ ℳ_D, denoted by 𝒦_i; and then randomly draw one observation out of 𝒦_i for imputation. Similar to Step 3 in Section 2.2, the estimate of θ and its estimated variance can be obtained for each imputed complete dataset.

4. The MI estimates of θ and σ² are then summarized across all L imputed datasets in the same way as in Sections 2.1 and 2.2, and are denoted by θ̂_{MI − 2} and ${\widehat{\sigma }}_{\mathit{\text{MI}}-2}^2$.

2.4. Bootstrap MI

In Sections 2.2 and 2.3, the estimates of the regression coefficients in the working models, namely, α̂ and β̂, are directly plugged into the calculation of the predictive/propensity scores and are fixed throughout multiple imputation; in other words, these MI procedures fail to account for uncertainty in estimating α and β. As a result, these MI procedures are improper (Little and Rubin [2]; Chapter 10); while the resulting estimators for θ, namely, θ̂_{MI − 1} and θ̂_{MI − 2}, are still consistent, the standard MI variances (i.e., ${\widehat{\sigma }}_{\mathit{\text{MI}}-1}^2\text{ and }{\widehat{\sigma }}_{\mathit{\text{MI}}-2}^2$) tend to underestimate their true variabilities. To address this issue, we now introduce a bootstrap step and describe this updated approach for the nonparametric MI method discussed in Section 2.3 as follows:

1. We draw the l^th (1 ≤ l ≤ L) bootstrap sample with replacement from the original observed dataset and fit working models as described in Step 1 in Section 2.3 using the bootstrap sample to obtain estimated regression coefficients, α̂^(l) and β̂^(l).

2. Following Steps 2 through 3 detailed in Section 2.3, we compute the standardized scores ${\tilde{s}}_1^{(l)}\text{ and }{\tilde{s}}_2^{(l)}$ using α̂^(l) and β̂^(l) and impute the missing X in the original data set. Subsequently, the estimate of θ and its estimated variance can be obtained for the l^th imputed complete dataset, which are denoted by ${\widehat{\theta }}_{\mathit{\text{MIB}}-2}^{(l)}\text{ and }{({\widehat{\sigma }}_{\mathit{\text{MIB}}-2}^{(l)})}^2$, respectively.

3. We calculate the bootstrap MI estimate of θ as the average across all L samples, i.e., ${\widehat{\theta }}_{\mathit{\text{MIB}}-2}=L^{-1}{\displaystyle {\sum }_{l=1}^L}{\widehat{\theta }}_{\mathit{\text{MIB}}-2}^{(l)}$. The according variance adjusting for both within and across sample variation is ${\widehat{\sigma }}_{\mathit{\text{MIB}}-2}^2={\overline{\sigma }}_{\mathit{\text{MIB}}-2}^2+(1+L^{-1})B_{\mathit{\text{MIB}}-2}$, where ${\overline{\sigma }}_{\mathit{\text{MIB}}-2}^2=L^{-1}{\displaystyle {\sum }_{l=1}^L}{({\widehat{\sigma }}_{\mathit{\text{MIB}}-2}^{(l)})}^2$ and B_{MIB − 2} is the sample variance of L point estimates, $\{{\widehat{\theta }}_{\mathit{\text{MIB}}-2}^{(l)},l=1,\cdots ,L\}$.

Similarly, a bootstrap step can be incorporated into the nonparametric MI method discussed in Section 2.2, which is based solely on prediction scores, and we denote this new estimator by θ̂_{MIB − 1} with variance ${\widehat{\sigma }}_{\mathit{\text{MIB}}-1}^2$. The addition of a bootstrap step in MI has been used in other settings [14, 15]; it introduces uncertainty of estimating parameters in working models and makes the resulting MI procedures proper [2]. Consequently, the standard MI variance formula by Rubin and Schenker [4] can be directly used to estimate the variances of these MI estimators, namely, θ̂_{MIB − 1} and θ̂_{MIB − 2}.

We further note that it is straightforward to show that all nonparametric MI estimators discussed in Sections 2.1 through 2.4 are equivalent when there is only one auxiliary variable available (P = 1).

2.5. ROC Curve Based on Multiple Imputation

As noted in Section 1 that one advantage of the proposed MI approaches is that they provide a platform to derive any summary statistics in the ROC analysis. As an example, we now discuss how to plot the ROC curve based on the imputed datasets. This is applicable to all MI approaches discussed previously (Sections 2.1 through 2.4).

The ROC curve plots the true positive rate, TP(c) = Pr(X_D > c | D = 1)+0.5 Pr(X_D = c | D = 1), against the false positive rate, FP(c) = Pr(X_D > c | D = 0) + 0.5 Pr(X_D = c | D = 0), for a threshold value, c, in the range of the biomarker values. We calculate the above pair for each imputed dataset, $({\widehat{\text{FP}}}_{(l)}(c),{\widehat{\text{TP}}}_{(l)}(c))$ for 1 ≤ l ≤ L, and compute the respective average value on each axis, i.e. $(\overline{\text{FP}}(c),\overline{\text{TP}}(c))$, where $\overline{\text{FP}}(c)=L^{-1}{\displaystyle {\sum }_{l=1}^L}{\widehat{\text{FP}}}_{(l)}(c)\text{ and }\overline{\text{TP}}(c)=L^{-1}{\displaystyle {\sum }_{l=1}^L}{\widehat{\text{TP}}}_{(l)}(c)$. By varying the value of the threshold, we can plot the entire ROC curve for multiply imputed datasets for any of the proposed methods.

2.6. Properties of Proposed MI Methods

We now discuss the properties of the proposed MI methods.

Proposition 1. If the working model for prediction scores (s₁) is correctly specified, X and δ are independent given s₁.

Along the lines of Hansen [3], it is straightforward to prove Proposition 1. It follows immediately from Proposition 1 that it is valid to impute missing values conditional on prediction scores, if its working model is correctly specified; hence, θ̂_{MI − 1} and θ̂_{MIB − 1} are consistent, if the working model for prediction scores is correctly specified and the usual regularity conditions underlying K-NN methods [16, 17] are satisfied. However, if the working model for prediction scores is misspecified, then θ̂_{MI − 1} and θ̂_{MIB − 1} are subject to potential bias.

Proposition 2. If at least one of the two working models for prediction scores (s₁) and for propensity scores (s₂) is correctly specified, X and δ are independent given s₁ and s₂.

Along the lines of Zeng [5], it is straightforward to prove Proposition 2. It follows immediately from Proposition 2 that it is valid to impute missing values conditional on prediction and propensity scores, when one of the working models is correctly specified; hence, θ̂_{MI − 2} and θ̂_{MIB − 2} are consistent, if either or both of the two working models are correctly specified and the usual regularity conditions underlying K-NN methods are satisfied. If both weights are positive, then both prediction and propensity scores are used to define distance and the resulting estimators are doubly robust. If one weight is set to zero, then either prediction or propensity scores are used to define distance and the resulting estimators are no longer doubly robust; they are consistent only if the corresponding working model is correctly specified. Thus, the addition of propensity scores makes the resulting MI methods doubly robust.

3. Simulation

In this section, we evaluate the finite sample performance of the proposed MI methods under various true models for the biomarker value (X) as well as its missing mechanism (δ). Throughout, we let a_P denote a P-vector of a and I_P denote the identity matrix of P dimension. In all simulations, the auxiliary variables are generated from a P-dimensional multivariate Gaussian distribution, i.e., Z⁰ ~ MVN(μ_Z, Σ) with (μ_Z) = 0_P and Σ = I_P (P = 5). Assuming that ${\mathbf{Z}}_1^0({\mathbf{Z}}_1^0\subseteq {\mathbf{Z}}^0)$ is predictive of X, the biomarker value (X) is generated under two schemes. In the first scheme (to be discussed in Section 3.1), X is generated from X = μ_X + ε, where ${\mu }_X={\alpha }_0+{\alpha }_{1}D+{\mathit{\alpha }}_2^{\mathrm{T}}{\mathbf{Z}}_1^0+{\mathit{\alpha }}_3^{\mathrm{T}}D{\mathbf{Z}}_1^0$ is the mean of X given ${\mathbf{Z}}_1^0$ and ε is a random error; we set α₀ = 0.5, α₁ = 2.5, α₂ = 0.5_P and α₃ = 1_P. Under the second scheme (to be discussed in Section 3.2), X is generated from log(X) = μ_log(X) + ε, where ${\mu }_{\text{log}(X)}={\alpha }_0+{\alpha }_{1}D+{\mathit{\alpha }}_2^{\mathrm{T}}{\mathbf{Z}}_1^0+{\mathit{\alpha }}_3^{\mathrm{T}}D{\mathbf{Z}}_1^0$ is the mean of log(X) given ${\mathbf{Z}}_1^0$, ε is a random error, and the base of the logarithm function is 1.1 throughout; we set α₀ = 0.5, α₁ = 2, α₂ = 0.5_P and α₃ = 2_P. We write the according true regression coefficients under either scheme as $\mathit{\alpha }={({\alpha }_0,{\alpha }_1,{\mathit{\alpha }}_2^{\mathrm{T}},{\mathit{\alpha }}_3^{\mathrm{T}})}^{\mathrm{T}}$. In addition, we consider either Gaussian random errors, i.e., ε ~ N(0, 1), or skewed non-Gaussian errors, i.e., ε = 5{ν − E(ν)} with ν ~ Beta(5, 1). Assuming that ${\mathbf{Z}}_2^0({\mathbf{Z}}_2^0\subseteq {\mathbf{Z}}^0)$ is predictive of δ, we generate δ from a logit model, i.e., $\text{logit}(\text{Pr}(\delta =1))={\beta }_0+{\beta }_{1}D+{\mathit{\beta }}_2^{\mathrm{T}}{\mathbf{Z}}_2^0+{\mathit{\beta }}_3^{\mathrm{T}}D{\mathbf{Z}}_2^0$ and write $\mathit{\beta }={({\beta }_0,{\beta }_1,{\mathit{\beta }}_2^{\mathrm{T}},{\mathit{\beta }}_3^{\mathrm{T}})}^{\mathrm{T}}$; we set β₀ = 0.1, β₁ = 0.2, β₂ = 0.1_P, β₃ = 0.2_P. The resulting probabilities of missing X range from 56.9% to 96.8%.

For each Monte Carlo data set, we follow the MI methods presented in Sections 2.1 through 2.4 to compute the standard nonparametric MI estimator (θ̂_MI) and the proposed nonparametric MI estimators (θ̂_{MI − 1}, θ̂_{MI − 2}, θ̂_{MIB − 1}, and θ̂_{MIB − 2}); for θ̂_{MI − 2} and θ̂_{MIB − 2}, both weights are set to 0.5 when defining d(i, j). Throughout our simulations, we use a linear regression model with covariates Z₁, D, and their interaction terms to estimate prediction scores and a logistic model with covariates Z₂, D, and their interaction terms to estimate propensity scores, respectively. For the sake of simplicity, we will only refer to the set of auxiliary variables used in the working models hereafter, knowing that the disease status (D) as well as their interaction terms will always be included. For each true model for X, we evaluate the performance of the proposed estimators under the following five scenarios: (a) both working models use the correct set of covariates, i.e., ${\mathbf{Z}}_1={\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2={\mathbf{Z}}_2^0$; (b) the working model for propensity scores is misspecified and only uses the first two covariates, i.e., ${\mathbf{Z}}_1={\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2\subset {\mathbf{Z}}_2^0$ (i.e., Z₂ is a proper subset of ${\mathbf{Z}}_2^0$); (c) the working model for prediction scores is misspecified and only uses the first two covariates, i.e., ${\mathbf{Z}}_1\subset {\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2={\mathbf{Z}}_2^0$; (d) both working models are misspecified and only use the first two covariates, i.e., ${\mathbf{Z}}_1\subset {\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2\subset {\mathbf{Z}}_2^0$; and (e) the working model for prediction scores includes the correct set of covariates and P noise variables, and the propensity score working model is misspecified and only uses the first two covariates, i.e., ${\mathbf{Z}}_1\supset {\mathbf{Z}}_1^0$ (i.e., Z₁ is a proper superset of ${\mathbf{Z}}_1^0$) and ${\mathbf{Z}}_2\supset {\mathbf{Z}}_2^0$.

In addition to the MI estimators discussed in Section 2, we compute an estimator of θ, denoted by θ̂_GS, assuming all biomarker values are observed, as a gold standard to benchmark bias in finite samples as well as loss of efficiency due to missing data; we note that θ̂_GS is not applicable in real-life studies. For comparison, we also compute a so-called naive estimator (denoted by θ̂_o), which uses only observations in 𝒪₀ ∪ 𝒪₁. Of note, in one extreme case of ${\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2^0$ being mutually exclusive, it can be readily shown that θ̂_o is unbiased. Hence, we focus on the other extreme case where ${\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2^0$ are identical (${\mathbf{Z}}_1^0={\mathbf{Z}}_2^0={\mathbf{Z}}^0$) in the simulations. To assess potential loss of efficiency due to nonparametric nature of the proposed MI methods, we compute an estimator (denoted by θ̂_MIP) based on a parametric imputation procedure [18], which is implemented in the R package, mice [19]; basically, we impute missing X using mice and then compute θ̂_MIP using the standard MI rule.

For each setting, we generate 1000 simulated datasets with a sample size of n₁ = n₀ = 100, and we summarize the simulation results using the following quantities: relative bias (RB) measured as the percentage of true θ, mean standard error (SE), Monte Carlo standard deviation (SD), root mean squared error (rMSE), and coverage rate (CR) of the 95% Wald’s confidence intervals (CI). We use K = 3 nearest neighbors and L = 10 imputed datasets in Sections 3.1 and 3.2 and evaluate other choices in Section 3.3.

3.1. Mean of X is Linear in ${\mathbf{Z}}_1^0$

In the setting of ${\mu }_X={\alpha }_0+{\alpha }_{1}D+{\mathit{\alpha }}_2^{\mathrm{T}}{\mathbf{Z}}_1^0+{\mathit{\alpha }}_3^{\mathrm{T}}D{\mathbf{Z}}_1^0$, we first consider the case of Gaussian errors (Table I). The naive estimator (θ̂_o) underestimates the true value substantially. In all scenarios, the proposed MI estimators with a bootstrap step have SEs that are closer to SDs and coverage rates that are closer to the nominal level compared to the MI methods without a bootstrap step, and the improvement can be small in some cases such as Scenario (a) and considerable in some cases such as Scenario (b); in addition, the SD of the proposed doubly robust MI estimator (θ̂_{MI − 2}) is comparable to that of the parametric MI estimator (θ̂_MIP), indicating that there is minimal loss of efficiency in estimating AUC as a result of using nonparametric imputation methods, likely due to that the AUC is estimated using only ranks of biomarker values; it is also noteworthy that the SDs of both θ̂_MI−2 and θ̂_{MI − P} are not much larger than that of θ̂_GS. In Scenario (a), the working models for both prediction and propensity scores are correctly specified. The standard nonparametric estimator (θ̂_MI) exhibits moderate bias and unsatisfactory coverage rate, likely due to curse of dimensionality. Our proposed nonparametric MI estimators as well as the parametric MI estimator exhibit negligible bias and improved coverage rates, and their SDs are comparable. In Scenario (b), the working model for propensity scores is misspecified; since θ̂_MI, θ̂_{MI − 1}, and θ̂_{MIB − 1} depend on only the working model for prediction scores, these estimators remain the same in Scenario (b) as those in Scenario (a) and are not duplicated in Table I. Despite the misspecification of the working model for propensity scores in Scenario (b), θ̂_{MI − 2} and θ̂_{MIB − 2} still exhibit negligible bias, due to its double robustness. In Scenario (c), the working model for prediction scores is misspecified. θ̂_MI, θ̂_{MI − 1} and θ̂_{MIB − 1} exhibit substantial bias and inadequate coverage rates, since they rely entirely on the misspecified working model for prediction scores. In comparison, θ̂_{MI − 2} and θ̂_{MIB − 2} have substantially smaller bias as a result of their double robustness, since the working model for propensity scores is still correctly specified. In Scenario (d), both working models are misspecified; as previously noted, estimation of θ̂_MI, θ̂_{MI − 1}, and θ̂_{MIB − 1} does not involve propensity scores, and therefore they remain identical as those in Scenario (c). The performance of θ̂_{MI − 2} and θ̂_{MIB − 2} is similar to that of θ̂_{MI − 1} and θ̂_{MIB − 1}; and all four proposed methods still perform slightly better than θ̂_MI and θ̂_MIP. In Scenario (e), θ̂_MI has a considerably larger bias compared to the proposed methods, suggesting that the performance of θ̂_MI deteriorates very quickly as the dimension of the auxiliary variables increases due to curse of dimensionality. On the other hand, the performance of all proposed methods remains comparable to their respective performance in Scenarios (a) and (b), as a result of effective dimension reduction.

Table I.

Comparison of θ̂_GS, θ̂_o, θ̂_MI, θ̂_{MI − 1}, θ̂_{MI − 2}, θ̂_{MIB − 1}, and θ̂_{MIB − 2}, when E(X) is linear in ${\mathbf{Z}}_1^0$. RB, relative bias of AUC estimate; SE, mean of the standard error estimates; SD, Monte Carlo standard deviation of parameter estimates; rMSE, root mean squared errors; CR, coverage rate of 95% Wald’s confidence interval. In this setting, the working models are correctly specified for θ̂_{MI − 1}, θ̂_{MI − 2}, θ̂_{MIB − 1}, and θ̂_{MIB − 2}, when the correct subset of covariates is included.

	Gaussian Errors					Non-Gaussian Errors
	RB (%)	SE	SD	rMSE	CR	RB (%)	SE	SD	rMSE	CR
θ̂GS	−0.3	0.037	0.039	0.039	0.930	−0.4	0.037	0.039	0.039	0.932
θ̂o	−12.5	0.062	0.063	0.112	0.600	−12.3	0.062	0.065	0.113	0.632
	(a) ${\mathbf{Z}}_1={\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2={\mathbf{Z}}_2^0$
θ̂MIP	−0.5	0.040	0.041	0.041	0.924	−0.6	0.039	0.040	0.040	0.942
θ̂MI	−2.5	0.041	0.054	0.057	0.850	−2.0	0.041	0.052	0.054	0.866
θ̂MI − 1	−0.3	0.038	0.044	0.044	0.916	0.0	0.038	0.041	0.041	0.930
θ̂MI − 2	0.1	0.038	0.045	0.045	0.912	0.4	0.038	0.043	0.043	0.924
θ̂MIB − 1	−0.3	0.039	0.044	0.044	0.926	0.0	0.038	0.041	0.041	0.932
θ̂MIB − 2	0.0	0.040	0.045	0.045	0.924	0.4	0.039	0.043	0.043	0.934
	(b) ${\mathbf{Z}}_1={\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2\subset {\mathbf{Z}}_2^0$
θ̂MI − 2	−0.3	0.039	0.045	0.045	0.914	0.2	0.038	0.044	0.044	0.916
θ̂MIB − 2	−0.3	0.040	0.045	0.045	0.928	0.2	0.039	0.044	0.044	0.930
	(c) ${\mathbf{Z}}_1\subset {\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2={\mathbf{Z}}_2^0$
θ̂MIP	−7.2	0.051	0.051	0.074	0.846	−7.0	0.050	0.052	0.074	0.840
θ̂MI	−8.1	0.045	0.061	0.086	0.656	−7.8	0.045	0.062	0.085	0.656
θ̂MI − 1	−7.7	0.044	0.061	0.084	0.676	−7.3	0.045	0.059	0.081	0.686
θ̂MI − 2	−0.9	0.040	0.048	0.048	0.908	−0.5	0.040	0.046	0.046	0.900
θ̂MIB − 1	−8.0	0.048	0.059	0.084	0.694	−7.5	0.047	0.059	0.082	0.720
θ̂MIB − 2	−2.6	0.047	0.049	0.052	0.920	−1.9	0.046	0.048	0.050	0.928
	(d) ${\mathbf{Z}}_1\subset {\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2\subset {\mathbf{Z}}_2^0$
θ̂MI − 2	−7.8	0.045	0.062	0.084	0.650	−7.2	0.044	0.060	0.081	0.686
θ̂MIB − 2	−7.8	0.047	0.060	0.083	0.690	−7.3	0.046	0.059	0.081	0.710
	(e) ${\mathbf{Z}}_1\supset {\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2\subset {\mathbf{Z}}_2^0$
θ̂MIP	−1.1	0.041	0.041	0.042	0.940	−0.8	0.039	0.040	0.040	0.948
θ̂MI	−4.7	0.043	0.057	0.066	0.776	−4.4	0.043	0.057	0.066	0.786
θ̂MI − 1	−0.1	0.038	0.043	0.043	0.914	−0.2	0.038	0.042	0.042	0.932
θ̂MI − 2	0.0	0.038	0.045	0.045	0.906	0.0	0.038	0.043	0.043	0.926
θ̂MIB − 1	−0.3	0.040	0.043	0.043	0.934	−0.3	0.039	0.041	0.041	0.942
θ̂MIB − 2	−0.2	0.040	0.044	0.044	0.926	−0.1	0.039	0.043	0.043	0.936

We then consider the case of non-Gaussian errors (Table I). The same conclusions can be drawn on comparisons across different methods within the five scenarios investigated. Note that a linear regression working model for prediction scores is still valid for the case of non-Gaussian errors, although it is efficient for the case of Gaussian errors.

3.2. Mean of log(X) is Linear in ${\mathbf{Z}}_1^0$

We now investigate robustness of the proposed approaches when the mean of log(X), not X, is linear, i.e., ${\mu }_{\text{log}(X)}={\alpha }_0+{\alpha }_{1}D+{\mathit{\alpha }}_2^{\mathrm{T}}{\mathbf{Z}}_1^0+{\mathit{\alpha }}_3^{\mathrm{T}}D{\mathbf{Z}}_1^0$ (II). In this case, the working model for prediction scores is always misspecified regardless of whether the correct set of covariates is used; as a result, θ̂_MIP exhibits larger bias in Scenario (a) of II compared to Scenario (a) of Table I. We, again, first consider the case of Gaussian errors (Table II). Most of the comparisons reported in Section 3.1 still hold. Interestingly, θ̂_{MI − 1} in Scenario (a) and θ̂_{MI − 2} in Scenario (b) still exhibit negligible bias when the correct set of covariates is included in the working model for prediction scores but the mean structure is misspecified. In addition, the magnitude of improvement associated with the use of a bootstrap step is greater in this setting compared to that in Section 3.1. For instance, under Scenario (a), the CR improves 4.2%, from θ̂_{MI − 1} (92.4%) to θ̂_{MIB − 1} (96.6%), and 3.8%, from θ̂_{MI − 2} (91.6%) to θ̂_{MIB − 2} (95.4%). This is in comparison to an improvement of 1.0% and 1.2% in Table I Scenario (a). Similarly, in Scenario (b) when ${\mathbf{Z}}_2\subset {\mathbf{Z}}_2^0$, the CR improves 4.4%, from 91.8% (θ̂_{MI − 2}) to 96.2% (θ̂_{MIB − 2}). Although to a lesser degree, the same is also true for Scenarios (c), (d), and (e). In the case of non-Gaussian errors (Table II), the main conclusions remain unchanged and the performance of the proposed θ̂_{MI − 2} and θ̂_{MIB − 2} is still doubly robust.

Table II.

Comparison of θ̂_GS, θ̂_o, θ̂_MI, θ̂_{MI − 1}, θ̂_{MI − 2}, θ̂_{MIB − 1}, and θ̂_{MIB − 2}, when E(log(X)) is linear in ${\mathbf{Z}}_1^0$. RB, relative bias of AUC estimate; SE, mean of the standard error estimates; SD, Monte Carlo standard deviation of parameter estimates; rMSE, root mean squared errors; CR, coverage rate of 95% Wald’s confidence interval. In this setting, as the working model for X assumes that E(X) is linear in Z₁, it is misspecified for θ̂_{MI − 1}, θ̂_{MI − 2}, θ̂_{MIB − 1}, and θ̂_{MIB − 2} under all scenarios, even if the correct subset of ${\mathbf{Z}}_1^0$ is used.

	Gaussian Errors					Non-Gaussian Errors
	RB (%)	SE	SD	rMSE	CR	RB (%)	SE	SD	rMSE	CR
θ̂GS	−0.4	0.041	0.040	0.040	0.956	−0.1	0.041	0.039	0.039	0.954
θ̂o	−8.9	0.065	0.052	0.074	0.926	−6.0	0.064	0.050	0.060	0.960
	(a) ${\mathbf{Z}}_1={\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2={\mathbf{Z}}_2^0$
θ̂MIP	−3.0	0.054	0.049	0.052	0.948	3.2	0.055	0.046	0.049	0.956
θ̂MI	−3.9	0.049	0.053	0.057	0.936	−2.2	0.050	0.052	0.054	0.958
θ̂MI − 1	−1.0	0.046	0.055	0.055	0.924	0.2	0.047	0.055	0.055	0.930
θ̂MI − 2	−0.6	0.046	0.054	0.054	0.916	0.6	0.047	0.055	0.055	0.928
θ̂MIB − 1	−1.7	0.052	0.051	0.051	0.966	−0.6	0.053	0.050	0.050	0.972
θ̂MIB − 2	−1.3	0.05	0.052	0.053	0.954	−0.1	0.051	0.052	0.052	0.950
	(b) ${\mathbf{Z}}_1={\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2\subset {\mathbf{Z}}_2^0$
θ̂MI − 2	−1.4	0.046	0.054	0.055	0.918	−0.1	0.047	0.055	0.055	0.932
θ̂MIB − 2	−2.0	0.051	0.052	0.053	0.962	−0.7	0.051	0.051	0.051	0.958
	(c) ${\mathbf{Z}}_1\subset {\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2={\mathbf{Z}}_2^0$
θ̂MIP	−1.9	0.056	0.040	0.041	0.998	−1.4	0.057	0.040	0.041	0.994
θ̂MI	−6.3	0.051	0.050	0.062	0.914	−3.9	0.051	0.048	0.053	0.956
θ̂MI − 1	−6.1	0.051	0.050	0.061	0.922	−4.0	0.051	0.050	0.055	0.944
θ̂MI − 2	−2.1	0.047	0.054	0.055	0.930	−0.4	0.048	0.054	0.054	0.932
θ̂MIB − 1	−6.6	0.055	0.047	0.061	0.942	−4.1	0.055	0.046	0.052	0.966
θ̂MIB − 2	−3.4	0.053	0.051	0.054	0.974	−1.3	0.053	0.051	0.051	0.968
	(d) ${\mathbf{Z}}_1\subset {\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2\subset {\mathbf{Z}}_2^0$
θ̂MI − 2	−6.3	0.051	0.050	0.062	0.908	−3.9	0.051	0.050	0.055	0.948
θ̂MIB − 2	−6.4	0.053	0.048	0.061	0.934	−3.9	0.053	0.047	0.052	0.968
	(e) ${\mathbf{Z}}_1\supset {\mathbf{Z}}_1^0\text{ and }{\mathbf{Z}}_2\subset {\mathbf{Z}}_2^0$
θ̂MIP	1.7	0.054	0.047	0.047	0.954	2.2	0.055	0.045	0.046	0.966
θ̂MI	−4.7	0.050	0.051	0.058	0.932	−3.3	0.051	0.048	0.052	0.952
θ̂MI − 1	−0.4	0.046	0.055	0.055	0.912	0.0	0.047	0.052	0.052	0.932
θ̂MI − 2	−1.0	0.046	0.053	0.053	0.934	−0.4	0.047	0.053	0.053	0.928
θ̂MIB − 1	−2.2	0.054	0.048	0.049	0.972	−1.6	0.054	0.045	0.046	0.988
θ̂MIB − 2	−2.4	0.052	0.048	0.050	0.974	−1.5	0.053	0.046	0.047	0.978

3.3. Impact of K and L

We also investigate other choices of K and L in the MI procedures for both linear and nonlinear true models (results not shown). We find that a larger number of imputed datasets (e.g., L = 100) leads to no more than a marginal improvement (e.g., an increase of less than 1% in CR). When a larger number of nearest neighbors (e.g., K = 10) is used in the MI procedures, all methods perform slightly worse, likely because the candidates identified for imputation are less similar to the observation with missing biomarker values as K increases. However, this impact on the proposed methods is smaller compared to the standard MI method, likely due to the dimension reduction feature of the proposed methods.

3.4. Summary

In summary, the proposed nonparametric MI methods outperform the standard nonparametric MI method even for a moderate number of auxiliary variables, and their efficiency is comparable to that of a parametric MI method. As shown in Scenario (e) in Tables I and II, the inclusion of noise covariates in a working model has a minimal impact on the proposed estimators, whereas its impact on the standard nonparametric MI method is considerable. Therefore, one could include all auxiliary variables that are potentially predictive of biomarker values or its missingness in the working models, when using the proposed methods. We also observe that θ̂_{MI − 2} and θ̂_{MIB − 2} exhibit the expected double robustness against misspecification of either working model, whereas θ̂_MIP is subject to substantial bias when the working model for X is misspecified. Since the proposed nonparametric MI methods do not directly use auxiliary variables to impute X and instead use them to define distance between observations, they also exhibit a robustness to misspecification of the mean structure as long as the correct set of covariates is included. In addition, the bootstrap estimators generally further improve the performance of the 95% Wald CI by accounting for uncertainty in estimating α̂ and β̂. Our results also show that a relatively small number of imputation data sets suffices, e.g., L = 10, which is consistent with the literature [2], and a small number of nearest neighbors is preferred, e.g., K = 3, in finite samples.

4. Data Analysis

We now illustrate the proposed methods using an observational study of maternal depression during pregnancy. In this study, the disease of interest is the presence of depression during pregnancy and the true disease status (D) is established through a clinical assessment of the Mood Module of the Structured Clinical Interview for DSM-IV Axis I Disorder (SCID) [20]. However, this evaluation is not only lengthy but also requires administration by a well trained professional. In practice, a brief self-administered questionnaire, Edinburgh Postnatal Depression Scale (EPDS) [21], is often used instead, which consists of ten questions and usually takes only a few minutes to complete. Therefore, it is meaningful to investigate the ability of the EPDS score to predict the depression status; in other words, the EPDS score is considered the biomarker of interest (X). Since the completion of the EPDS questionnaire is voluntary in this study, the EPDS score is unavailable for a considerable portion of the participants. In the same study, researchers also assessed the Structured Interview Guide for the Hamilton Rating Scale for Depression to obtain 17-item (HRSD17), which is known to be highly correlated with EPDS. In our analysis, six other baseline variables are also considered, namely, maternal age, race, martial status, education level, gravidity and parity. Both HRSD17 and the above baseline covariates are fully observed and regarded as the auxiliary variables (Z) in this analysis.

We first compute the naive estimator, θ̂_o = 0.861 (SE = 0.038). Subsequently, we conduct a sensitivity analysis to evaluate the impact of the number of auxiliary variables included in the working models; specifically, we compute all nonparametric MI estimators when working models include one auxiliary variable (HRSD17), two auxiliary variables (HRSD17 and age), and all seven auxiliary variables. When only one covariate is included in the working models, all nonparametric imputation methods are equivalent and give the same estimate of θ, 0.870, and the same SE, 0.019. The results using two covariates (Setting (a)) and seven covariates (Setting (b)) are summarized in Table III. In Setting (a), we observe that the standard nonparametric MI estimate (θ̂_MI = 0.864), as well as the proposed MI estimators, all of which are in the range of [0.860,0.867], are similar to the naive estimate (θ̂_o = 0.861), suggesting that the missing mechanism may be completely at random (MCAR). The SEs of both the standard nonparametric MI and the proposed MI estimators are in the range of [0.018,0.019], which are almost half of the SE of the naive estimator (0.038), suggesting considerably efficiency gain through the use of auxiliary information. In Setting (b), the proposed AUC estimators range between 0.869 and 0.880 and are slightly higher than the corresponding estimates in Setting (a), and in particular, θ̂_{MIB − 1} and θ̂_{MIB − 2} are very close to their respective estimate in Setting (a); θ̂_MI, however, is 0.892, which is substantially higher than its estimate in Setting (a), likely due to the increased dimension of auxiliary variables (from two to seven). This reaffirms that the proposed methods are less sensitive to inclusion of a large number of auxiliary variables as a result of dimension reduction achieved before imputation.

Table III.

Comparison of θ̂_MI, θ̂_{MI − 1}, θ̂_{MI − 2}, θ̂_{MIB − 1}, and θ̂_{MIB − 2}, when (a) only two auxiliary variable are used in the working models, and (b) all seven auxiliary variables are used in the working models. SE, standard error.

	(a)		(b)
	Estimate	SE	Estimate	SE
θ̂MI	0.864	0.019	0.892	0.017
θ̂MI − 1	0.866	0.019	0.880	0.017
θ̂MI − 2	0.860	0.019	0.872	0.019
θ̂MIB − 1	0.867	0.018	0.869	0.025
θ̂MIB − 2	0.867	0.018	0.872	0.020

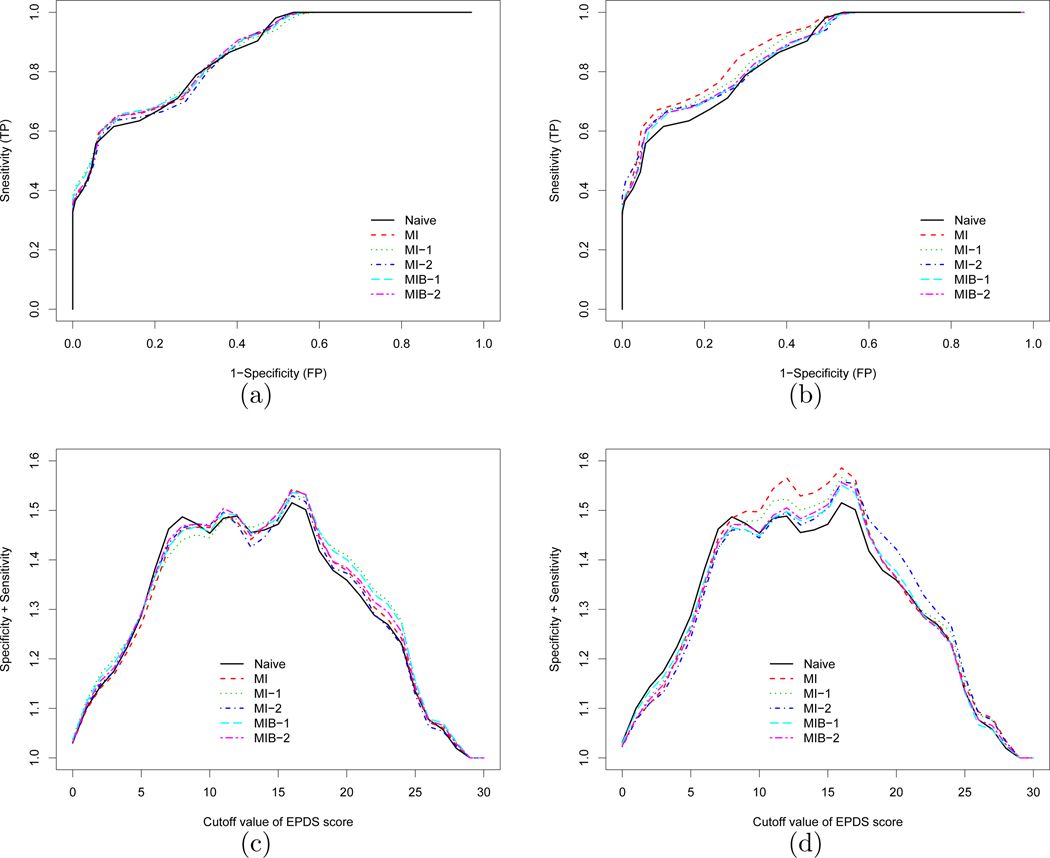
We also plot the ROC curve for each method in Figure 1. When only two auxiliary variables are included in the working models (Panel (a)), the ROC curve based on the standard approach is similar to the ones using the proposed approaches. This is consistent with the similarity in the point estimate of AUC in Table III Setting (a). However, when all seven auxiliary variables are included in the working models, the curves diverge (Panel (b)). While the ROC curve based on the proposed methods remain similar, they are generally lower than the ROC curve based on the standard approach (red dashed line). We note that the naive ROC curves (solid black lines) are identical on both panels; thus, they can serve as a benchmark for comparisons across Panels (a) and (b). As the ROC curve can be used to identify an optimal threshold (or cutoff) biomarker value, say, maximizing the sum of sensitivity and specificity, we plot in Figure 1 this sum over the range of the EPDS score (X) for each method when only two (Panel (c)) and all seven (Panel (d)) auxiliary variables are included in the working models. We find that an EPDS score of 16 is the unanimous optimum threshold that attains the maximum sum among all methods. Similarly, the solid black lines from the naive approach can serve as a benchmark when comparing Panels (c) and (d); our data analysis again shows that the number of auxiliary variable has a smaller impact on the proposed MI estimators than the standard approach.

Figure 1.

Comparison of the naive, standard nonparametric, and proposed MI approaches; the ROC curves when (a) only two auxiliary variables or (b) all seven auxiliary variables are included in the working models; the sum of sensitivity and specificity for all cutoff values of EPDS score when (c) only two auxiliary variables or (d) all seven auxiliary variables are included in the working models.

5. Discussion

In this paper, we investigate nonparametric MI methods based on prediction scores alone or in combination with propensity scores and show that our proposed methods have several attractive features. First, they alleviate the issue of curse of dimensionality, a well-known issue for nonparametric methods in the presence of a large number of auxiliary variables. While we focus on the K-NN nonparametric imputation, other nonparametric methods can be readily adopted for imputation, say, kernel methods [22]. Furthermore, our methods can take advantage of modern regression models for high-dimensional data, say, lasso models [23], when building working models for prediction and propensity scores. Second, our proposed methods using both prediction and propensity scores are doubly robust, which are consistent when at least one working model is correctly specified. In addition, our numerical results show that the proposed MI estimators perform well as long as the correct set of covariates is included, even when the mean structure of a working model is misspecified. By correctly accounting for uncertainty in estimating parameters in the working models (i.e., α̂ and β̂), our estimators are further improved through a bootstrap step (i.e., θ̂_{MIB − 1} and θ̂_{MIB − 2}). As a result, it is recommended that θ̂_{MIB − 2} be used in practice.

The proposed methods are also very flexible. First, they provide a platform for estimating any measure of interest in a ROC analysis, e.g., the ROC curve itself, which, in turn, can be used to identify an optimal threshold (or cutoff) value, say, maximizing the sum of specificity and sensitivity, as illustrated in Section 4. Second, the proposed methods can be extended to the case where multiple biomarkers are compared and they all have missing values. When multivariate biomarker values of a subject is either completely observed or completely missing (e.g., either the questionnaire is completed and returned by a subject or not returned at all), imputation will be similar to what is proposed in Section 2. When multivariate biomarker values are partially observed and follow certain missing patterns, the observed (partial) biomarker values may be utilized in step-wise imputation procedures.

When using the MI method based on both predication and propensity scores, weights play an important role for defining distance between observations. As long as the weights are positive, the main results in Proposition 2 hold; thus, in our numerical studies, we fix the weights to 0.5. However, the use of weights allows investigators to incorporate their prior beliefs on validity of two working models, e.g., one could use a larger weight or even put the entire weight on the working model that is more likely to hold; we are currently investigating the impact of varying weights and the strategies of choosing weights in finite samples. Future research will also include extensions to more complicated missing patterns including missing disease status or missing auxiliary variables and sensitivity analysis in the case of missing not at random (MNAR) [2].