Genome-scale phylogenetic function annotation of large and diverse protein families

Abstract

The Statistical Inference of Function Through Evolutionary Relationships (SIFTER) framework uses a statistical graphical model that applies phylogenetic principles to automate precise protein function prediction. Here we present a revised approach (SIFTER version 2.0) that enables annotations on a genomic scale. SIFTER 2.0 produces equivalently precise predictions compared to the earlier version on a carefully studied family and on a collection of 100 protein families. We have added an approximation method to SIFTER 2.0 and show a 500-fold improvement in speed with minimal impact on prediction results in the functionally diverse sulfotransferase protein family. On the Nudix protein family, previously inaccessible to the SIFTER framework because of the 66 possible molecular functions, SIFTER achieved 47.4% accuracy on experimental data (where BLAST achieved 34.0%). Finally, we used SIFTER to annotate all of the Schizosaccharomyces pombe proteins with experimental functional characterizations, based on annotations from proteins in 46 fungal genomes. SIFTER precisely predicted molecular function for 45.5% of the characterized proteins in this genome, as compared with four current function prediction methods that precisely predicted function for 62.6%, 30.6%, 6.0%, and 5.7% of these proteins. We use both precision-recall curves and ROC analyses to compare these genome-scale predictions across the different methods and to assess performance on different types of applications. SIFTER 2.0 is capable of predicting protein molecular function for large and functionally diverse protein families using an approximate statistical model, enabling phylogenetics-based protein function prediction for genome-wide analyses. The code for SIFTER and protein family data are available at http://sifter.berkeley.edu.

Automated protein function prediction is an important challenge for computational biology because protein function is difficult to describe and represent, protein databases are littered with annotation errors, and our understanding of how molecular functions arise and mutate over evolutionary time is far from complete. Because biologists depend on protein function annotations for insight and analysis, automated methods have been used extensively to compensate for the relative dearth of experimental characterizations. Although there are 10⁷ protein sequences in the comprehensive UniProt database (The UniProt Consortium 2010), <5% have annotations from the Gene Ontology Annotation (GOA) database (Barrell et al. 2009). Far fewer (0.2%) have been manually annotated, and only 0.25% of those manual annotations are from the molecular function ontology in Gene Ontology (GO) (The Gene Ontology Consortium 2010) and are based on experimental evidence. Because of the need for so many annotations, function prediction methods are often assessed based on annotation quantity rather than quality, increasing the number of false positive function annotations and polluting databases (Galperin and Koonin 1998; Brenner 1999; Schnoes et al. 2009). These errors propagate in databases: A query protein may have the same function as that of the matched database protein in vivo, but the protein in the database is incorrectly described. This problem could be managed in part by having every protein annotation supported by traceable evidence, such as in the GOA database. Moreover, function prediction methods that incorporate evidence codes and provide reliability measures would seem less prone to error propagation.

Phylogenetics has been proposed as a powerful approach to meet the challenges of protein function prediction, in an approach sometimes termed “phylogenomics” (Eisen 1998). Phylogenetics-based protein function prediction uses a reconciled phylogeny for a protein family to make predictions, rather than transferring annotations based on pairwise sequence comparisons. Phylogeny-based methods rely on two assumptions: that function evolves parsimoniously within a phylogeny, so the branching structure of a phylogeny is more indicative of functional similarity than path length within the phylogeny; and that functional divergence tends to follow a gene duplication event, because protein redundancy may allow mutation events that otherwise would be selected against. We have found that the former assumption improves functional prediction by enabling a systematic methodology by which different annotations for proteins in a tree can be integrated to make predictions. However, the assumption that gene duplication events promote functional mutations is less helpful for prediction, in particular because the process of reconciling gene and species trees produces many spurious duplication events, often obscuring the signal. The role of gene duplication in phylogeny-based function prediction may be overemphasized relative to the evolutionary history of actual function mutations, particularly as early studies focused on families with an atypically low degree of gene duplication (Eisen and Hanawalt 1999).

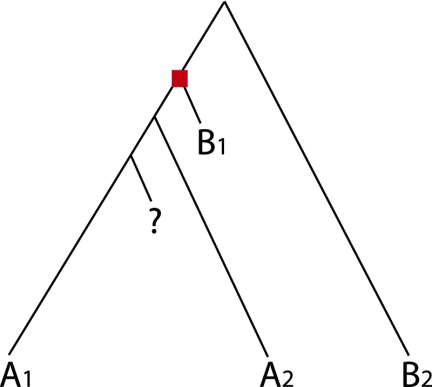
The phylogenetics-based approach to protein function prediction has many advantages. Lineage-specific rate variation is a complex phenomenon prevalent across a wide range of families (e.g., Thomas et al. 2006) that can create a situation in which the most similar sequences according to BLAST (i.e., those with the shortest path length in the tree) may not be the sequences most recently diverged from the query sequence. In one example of lineage-specific rate variation (Fig. 1), the path length between the query protein (labeled “?”) ranks the remaining proteins differently than the branching order would rank the proteins in terms of assumed functional similarity. Additional proteins that are siblings of the (functionally different) protein with the shortest branch length (B₁ in the figure) with similarly short branch lengths will provide increasingly strong support for the incorrect function. Thus, the approach of using the most significant hits according to BLAST is systematically flawed and may yield erroneous results even as the number of known protein sequences increases. Use of a phylogeny specifically incorporates the evolutionary history, minimizing problems due to rate variation, and suggests an evolutionarily principled means of merging functional evidence from homologous proteins. In particular, phylogenetic distance can be thought of as a measure of the accuracy of annotating a query protein with a neighboring protein's known function. Instead of pairwise comparisons, a tree is the natural structure to specify and explore how molecular function evolved within protein families.

Figure 1.

Sequence similarity does not directly reflect phylogeny. The proteins in this tree have either molecular function A or B. There is a duplication event indicated by a red square and the query protein is denoted by “?”. The most significant BLAST hit for the query protein will be B₁ because the path length in the phylogeny from the query protein to B₁ is the shortest. Thus, BLAST-based prediction methods will transfer B to the query protein. However, it is more likely that the tree has only one functional mutation, in which ancestral function B mutated to function A on the left-hand side of the bifurcation after the duplication event. So A is a better annotation for the query protein. A phylogenetics-based approach reaches this conclusion naturally. Example adapted from Eisen (1998).

While originally applied manually, phylogenetics-based protein function prediction has been deployed in automated methods. One such method, Orthostrapper (Storm and Sonnhammer 2002), uses bootstrapping to identify orthologous clusters of proteins and transfers function annotations within each of these clusters. Because these clusters have variable sizes, Orthostrapper tends to transfer either multiple or zero annotations to unannotated proteins. Our framework, SIFTER (Statistical Inference of Function Through Evolutionary Relationships) (Engelhardt et al. 2005, 2006), uses a statistical model of function evolution to incorporate annotations throughout an evolutionary tree, making predictions supported by posterior probabilities for every protein. We fix the tree structure to the phylogeny reconstructed from sequence data and use a conditional probability model that describes how molecular function evolves within the tree. This statistical model enables access to a broad set of statistical tools for parameter estimation and computation of posterior probabilities of the molecular functions. We chose this statistical approach because it yields predictions that are relatively robust to noise by merging evidence across a tree. Robustness is essential in this problem, given that each protein family contains few functional annotations, and there is noise in both the annotations and the reconstructed phylogeny.

The major drawback to phylogenetics-based methods is speed. The SIFTER model nominally has exponential computational complexity in the number of candidate functions within a protein family. In Pfam release 24.0, there were 753 families with nine or more molecular functions with experimental evidence from the GOA database within the family's proteins, and these families were 7.5 times larger on average than families with fewer than six candidate functions. Based on Pfam-A, it is possible that >33.5% of proteins from a single species could be contained within these large families, which are currently inaccessible to SIFTER and related methods. Motivated by these families, in this new version of SIFTER we have implemented a straightforward and effective approximation that enables tractable computation of function predictions in large, functionally diverse families, and opens the door to whole-genome annotation. Exact computation of posterior probabilities is exponential in the number of candidate functions to account for the possibility, however small, that a protein has the ability to perform any combination of the M candidate functions for that family, where there are 2^M possible combinations. Our approximation truncates the number of molecular function combinations that are considered; for example, when we truncate at level 2, we only allow for the possibility that each protein has 0, 1, or 2 of the M candidate functions, but no more. This approach is effective because the probability of a protein having more than a few functions is small, both in our model and in vivo.

In this new version of SIFTER, we also wanted the model of molecular function evolution to be flexible enough to enable the encoding of prior biological knowledge and to allow us to construct the transition rate matrix in a semantically meaningful way from a smaller set of parameters that in principle can be estimated from the data. The fundamental change to SIFTER that meets these requirements is a general model of evolution based on a continuous-time Markov chain. This also simplifies the machinery required to compute posterior probabilities and to estimate the model parameters.

When exact computation is feasible, we show that SIFTER 2.0 produces almost identical results to SIFTER 1.1. We demonstrate that the posteriors computed using truncation provide a good approximation to the exact posteriors at all levels of truncation. We apply SIFTER with approximate computation to the Nudix family, which is computationally infeasible for SIFTER 1.1 due to the number of candidate functions. We illustrate that SIFTER is now suitable for genome-wide analysis by applying it to a genome-scale prediction task for Schizosaccharomyces pombe proteins, and compare its performance with four other methods.

Results

Throughout this section, we ran BLAST, PFP (Hawkins et al. 2006), ConFunc (Wass and Sternberg 2008), and FFPred (Lobley et al. 2008) for function prediction to compare against SIFTER results, whenever it was viable to run those methods. We ran BLAST in two different ways (see Methods) in order to include both a method that uses textual annotations (BLAST) and GOA database annotations (BLAST-GO). We define “accuracy” as the percentage of proteins for which the functional term with the highest rank is an exact match to one of the experimental annotations for that protein, with rank ties broken in favor of the correct prediction. Our ROC-like analysis shows the relative increase of the true positive rate (exact matches of predicted to characterized functions) versus the false positive rate as the cutoff threshold is made more permissive (see Methods).

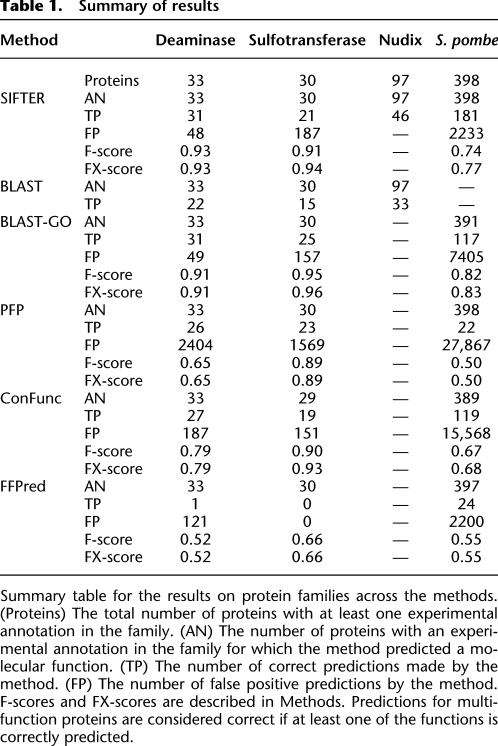
The accuracy measure provides a single overall assessment, but the accuracy measure and our ROC-like analysis ignore the GO hierarchy, so predictions that are less precise than (but consistent with) the true term are considered incorrect. Therefore, we also computed the F-score and an extended F-score (FX-score) of the prediction results. These scores compare the sets of annotated and predicted terms by including in each set all terms that are ancestral to each specific term in the GO hierarchy (see Methods). The FX-score assumes that predictions that are more specific than the annotated terms are correct so that methods are not penalized because of overly general annotations from the GOA database. Prediction results are summarized in Table 1. Our precision-recall curves show the relative precision and recall when ancestral terms are included in the set of predictions and in the annotations, as for the F-scores (see Methods). All methods were run, and their predictions extracted, as described in Methods.

Table 1.

Summary of results

SIFTER 2.0 produces equivalent results to SIFTER 1.1

SIFTER 2.0 is based on approximate posterior probabilities obtained from a truncation as well as a new evolutionary model based on a continuous Markov chain model of functional evolution. We first assess the impact of these changes on prediction in the small families previously used to benchmark SIFTER 1.1. We compare the results from SIFTER 2.0 to those from SIFTER 1.1 on a gold-standard protein family considered in previous work (Engelhardt et al. 2006). On the AMP/adenosine deaminase Pfam family, we found that SIFTER 1.1 produced identical predictions and near-identical ROC-like curves to the results using exact computation from SIFTER 2.0. SIFTER (both 1.1 and 2.0) and BLAST-GO both achieved 93.9% accuracy, missing predictions for two of the 33 characterized proteins, whereas ConFunc achieved 81.8% accuracy, PFP achieved 78.8% accuracy, BLAST achieved 66.7% accuracy, and FFPred achieved 3% accuracy. (Complete results are in the Supplemental Material.)

To compare SIFTER 2.0 with SIFTER 1.1 more thoroughly, we selected 100 protein families from Pfam with GOA database annotations and ran leave-one-out cross-validation for both versions of SIFTER on these families. Both versions made predictions for the 1632 proteins with experimental annotations across the 100 families, and SIFTER 2.0 achieved 72.5% accuracy, whereas SIFTER 1.1 achieved 70.0% accuracy. The two versions agreed on 95.3% of the predictions. We found that SIFTER 2.0 using exact computation took approximately twice as long as SIFTER 1.1, where the bulk of the difference was spent on the most functionally diverse families; if we limit the families to have six or fewer candidate functions rather than 11, SIFTER 2.0 takes only 2% longer than SIFTER 1.1. (Complete experiment details are in the Supplemental Material.) These results illustrate that the new model for SIFTER produces equivalent predictions based on exact computation as compared to the specialized model in SIFTER 1.1. However, these analyses ignore a large percentage of proteins, as large and functionally diverse families were excluded from these 100 families because SIFTER 1.1 could not be applied to them.

Sulfotransferase family

We applied SIFTER 2.0 to the sulfotransferase family (PF00685) from Pfam 20.0. We reconstructed a phylogeny with 539 proteins, 48 of which have experimental annotations in the GOA database. There are nine SIFTER candidate functions, eight of which are sulfotransferases acting on a specific compound, and one of which is “nucleotide binding.” These enzymes are responsible for the transfer of sulfate groups to specific compounds. Researchers have shown their critical role in mediation of intercellular communication (Bowman and Bertozzi 1999). Human sulfotransferases are extensively studied because of their role in metabolizing steroids, hormones, and environmental toxins (Allai-Hassani et al. 2007), and because they are biologically linked to neuronal development and maintenance (Gibbs et al. 2006). Plasmodium falciparum, the causative agent of malaria, makes use of its own sulfotransferase proteins as cell-surface receptors to enter into the host and thus these proteins are a target for malaria prevention drugs (Chai et al. 2002).

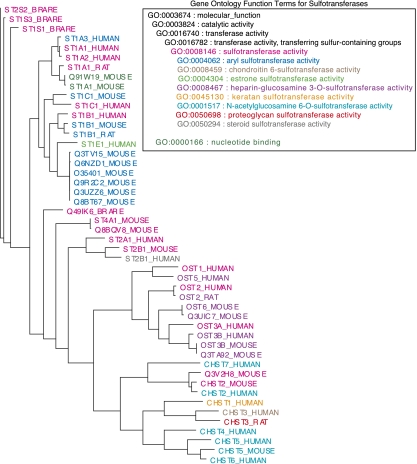
The phylogeny for this family including 48 proteins with experimental functional annotations from the GOA database (Fig. 2) shows that 18 of these 48 proteins have only “sulfotransferase” annotations. We excluded these from the accuracy measures and ROC-like analyses because they are not sufficiently precise descriptions of molecular function; we left them in to compute the precision-recall curves and F-scores because they are consistent with the true function. Thirty proteins remained in the experimentally annotated data set, 28 of which have one of eight specific sulfotransferase annotations. Five of these sulfotransferase functions appear only once in the tree. The five proteins with singleton annotations will necessarily have incorrect predictions in SIFTER's leave-one-out cross-validation, as no correct annotation is available within the tree, and the model parameters do not facilitate mutations to unobserved molecular functions. We used a more recent version of the GOA database for BLAST-GO than for SIFTER and other methods, which positively affects its performance (e.g., “estrone sulfotransferase activity” is an experimental annotation for one protein for SIFTER, thus impossible to predict, but is an experimental annotation for six proteins for BLAST-GO). The PFP database contained 27 of the 30 experimental annotations (all but the annotations for rat sequences), and we could not exclude self-annotations.

Figure 2.

Phylogeny of experimentally characterized proteins in the sulfotransferase family (PF00685). The colors indicate the experimentally characterized protein functions, as specified in the key.

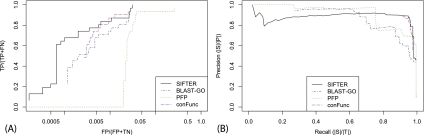
Evaluating SIFTER using leave-one-out cross-validation with exact computation yields 70.0% accuracy. For comparison, BLAST-GO achieves 83.3% accuracy, PFP achieves 76.7%, FFPred achieves 0% accuracy, ConFunc achieves 63.3% accuracy, and BLAST achieves 50% accuracy. The ROC-like analysis (Fig. 3A) shows that SIFTER performs better than all methods across all false positive rates, except for a small region where PFP performs slightly better. SIFTER has 187 false positive annotations at the most permissive cutoff, whereas PFP has 1569.

Figure 3.

Sulfotransferase family prediction comparison. (A) The ROC-like analysis of SIFTER with BLAST, BLAST-GO, PFP, and ConFunc for the sulfotransferase family of proteins. We did not include FFPred because there were not sufficient numbers of true positive predictions to show up on this plot. Note that the x-axis is on a log scale. (B) The precision-recall analysis of SIFTER with BLAST, BLAST-GO, PFP, ConFunc, and FFPred.

The precision-recall analysis (Fig. 3B) shows SIFTER performing better than the other methods at high levels of recall, offering the option of particularly high precision, with ConFunc performing almost as well. PFP performs well at the lowest and highest levels of recall, but we cannot assume that this performance generalizes to unannotated proteins (we did not remove self-annotations in PFP). BLAST-GO shows good performance below 0.6 recall, where precision goes down fairly dramatically. Although PFP has more accurate predictions than SIFTER, the F-score is lower, indicating that there were more false positive predictions with PFP. ConFunc used both experimental and non-experimental GOA annotations and does well at high levels of recall. The difference between the F-score and the FX-score for ConFunc was relatively large, indicating that the predictions for some of the proteins with a general sulfotransferase annotation were more specific (as with SIFTER). FFPred did poorly because it had trained parameters for only one of the candidate functions for this family; this is also reflected in its low F-score. BLAST made correct predictions for six proteins that were missed by SIFTER, including four with unique function annotations. This illustrates a possible benefit of using multiple sources of protein annotations within SIFTER rather than relying strictly on annotations from the GOA database.

Results from each of the methods discussed here, including SIFTER, necessarily depend on which version of each database was used (e.g., UniProt, Pfam, and GOA). PFP, FFPred, and ConFunc all use as input manually built databases that are drawn from various versions of publicly available databases, and so the input data are effectively untouchable. For SIFTER, we can compare different versions of databases for the same family, but it is difficult to generalize conclusions because the changes appear to be version- and family-specific (for further discussion, see the Supplemental Material). Our results here reflect practical application of these methods but yield only limited insight into the impact of database version on results.

To assess the accuracy of the truncation approximation, we compared the performance of exact leave-one-out cross-validation with each of the eight possible truncations in the sulfotransferases. The ROC-like analysis (Supplemental Fig. 6) shows that the impact of the truncation is small at all levels. Truncation levels 8 through 3 achieved the same level of accuracy as the exact algorithm (70.0%), missing the same proteins, and levels 2 and 1 achieved 66.7% accuracy. At level 1, SIFTER made an incorrect prediction for the protein OST5_HUMAN; at level 2, SIFTER made incorrect predictions for ST1B1_MOUSE and ST1C1_MOUSE. The approximation improved the run time by a significant margin—500-fold in the case of T = 2—with minimal reduction in the quality of the results (Supplemental Fig. 7).

Nudix family

The Nudix hydrolase family (PF00293) includes 3703 proteins in Pfam release 20.0. Nudix proteins are characterized by the highly conserved 23-amino-acid motif GX₅EX₇REUXEEGU (where U is a hydrophobic residue and X is any amino acid). Initially, they were discovered to have activity on nucleoside diphosphates, but a number of non-nucleoside substrates have since been identified (Koonin 1993; Bessman et al. 1996). The functions suggest roles in nucleotide pool sanitation, the removal of toxic metabolic intermediates, mRNA stability, and signaling (McLennan 2006). While the Nudix motif forms a loop–α-helix–loop structure, providing a scaffold for coordinating cation binding and catalysis, residues that govern substrate specificity lie outside of the motif (Koonin 1993; Mildvan et al. 2005).

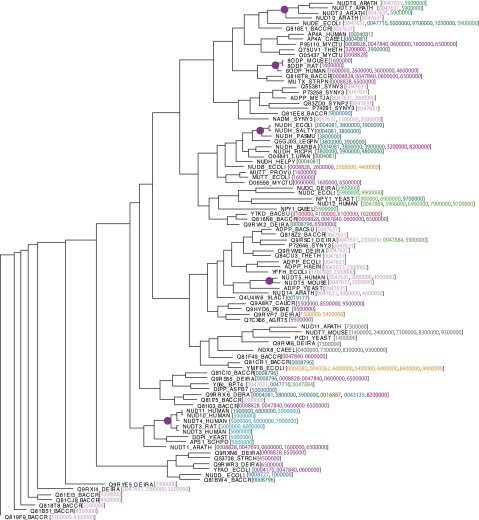
Function prediction in the Nudix family is difficult because sequence diversity reduces the alignment quality of these proteins, which, in turn, reduces the quality of the phylogeny. A bootstrap analysis of the alignment for the experimentally characterized proteins had an average node bootstrap support of 38%, and there are only five small clades with >95% bootstrap support (Fig. 4). Attempts have been made to use structural alignments as a scaffold, but these too suffer from the family's diversity (Ranatunga et al. 2004). The impact on SIFTER is noise in the tree reconstruction, but SIFTER's statistical model was chosen for robustness to this noise. Furthermore, the tree shows numerous examples of possible parallel functional evolution, and many of these proteins have multiple functions.

Figure 4.

A reconciled phylogeny of the experimentally characterized hydrolase proteins found in the Nudix family. The colored numbers in brackets after the protein name represent a clustering of the proteins into their biological functions, determined from our own literature search and described in more detail in future work. The purple dots represent clades that have >95% bootstrap support.

Our own manual literature search revealed 97 proteins with experimentally characterized functions. Comparing the 37 Nudix proteins with experimental annotation in the GOA database against our literature search identified mistakes in the GOA database, so we used only the annotations from our literature search. We also found the set of GO terms for this family incomplete and inconsistent, so we augmented the ontology with 98 additional molecular function terms and rearranged the hierarchy for biochemical accuracy. (See the Supplemental Material; complete details will be published elsewhere.) The Nudix family then had 66 candidate functions, which is a prohibitively large number of candidate functions for SIFTER with no truncation. Even truncating at two, the 4356 × 4356 parameter matrix made computation intractable. Thus, we computed posterior probabilities at truncation level 1.

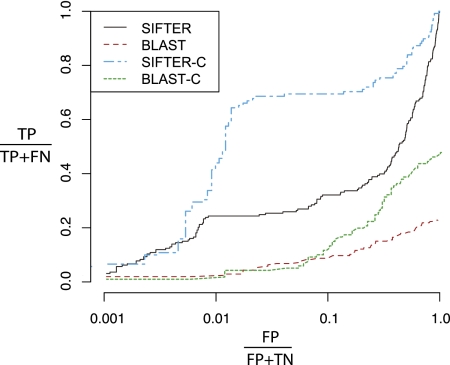
On the Nudix family, SIFTER achieved 47.4% accuracy, whereas BLAST achieved 34.0% accuracy. In the ROC-like analysis (Fig. 5), we see that SIFTER outperforms BLAST at all levels of false positives. Approximately 2.4% of annotations are correct in BLAST at 99% specificity, whereas for SIFTER, 24.4% of the annotations are correct at 99% specificity. The SIFTER curve shows that, although functional diversity limits prediction quality within this family, SIFTER still performs comparatively well, especially at low levels of false positives. While overall accuracy is relatively high for BLAST, the ROC-like analysis shows a general weakness of the BLAST results. Including all predicted terms at any E-value ≤0.01, only 23.3% of the correct Nudix annotations show up at all. This percentage is lower than the total number of correctly annotated proteins because 48 of the proteins have multiple functions. This study focuses on SIFTER's ability to handle extremely large numbers of candidate functions and on the limitations of the Gene Ontology. As such, we do not have a precision-recall analysis because we rebuilt the Gene Ontology for this family and because the BLAST keyword script did not include all ancestral terms of the candidate functions, which is prohibitively time-consuming to build.

Figure 5.

A comparison of BLAST and SIFTER for the Nudix family of proteins. SIFTER consistently dominates BLAST annotations under this criterion. The SIFTER-C and the BLAST-C lines are the evaluation of SIFTER and BLAST using the generalized Nudix hydrolase terms as experimental annotations. It is interesting that, at >99% specificity, both BLAST and SIFTER performed as well or better on the original data sets than the generalized data sets. Note that the x-axis is on a log scale.

We used this family's functional diversity to examine the trade-off between sensitivity and functional term precision. We manually substituted general ancestral terms for candidate functions and saw the accuracy of both methods improve considerably: SIFTER achieved 78.4% accuracy, and BLAST achieved 42.0% accuracy. The ROC-like analysis also shows improvements (Fig. 5): SIFTER predicts 43.6% of the annotations correctly at 99% specificity, and BLAST predicts 1.7% of the annotations correctly at 99% specificity. The reason that generalized BLAST performs poorly relative to the non-generalized BLAST at high specificity is that a large number of general but incorrect hydrolase predictions are made with low corresponding E-values; although these terms were ignored when the candidate functions were specific, they were considered incorrect when the candidate functions were generalized. These experiments (see the Supplemental Material) tell us that biologists needing general function predictions for a set of proteins may sacrifice term precision in return for more accurate predictions. However, based on our GO analysis, it remains to be seen whether the GO hierarchy can be reliably used to generalize protein function.

Proteins from S. pombe

We tested whether SIFTER 2.0 could be applied to whole-genome functional annotation. Using the complete genome sequences of 46 fungal species (Supplemental Fig. 10), we built 241 Pfam protein families that contained experimental annotations from S. pombe and at least one other fungal organism, with a total of 398 S. pombe proteins (see Methods). There are 15 families with nine or more candidate functions; analysis with SIFTER 1.1 is not possible on these families. Results are summarized in Table 2.

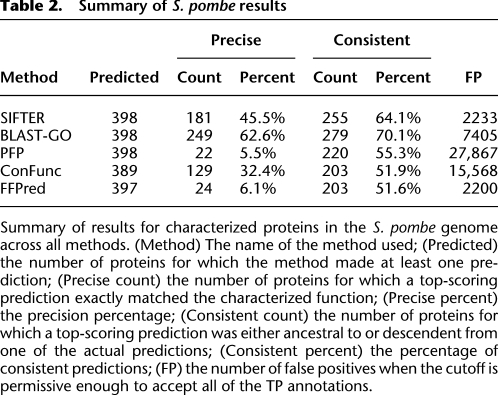
Table 2.

Summary of S. pombe results

SIFTER achieved 45.5% accuracy (181 of the 398 S. pombe proteins). We define a prediction as “consistent” when the predicted term is a descendant of the protein's functional annotation in the GO hierarchy. Consistent predictions are not necessarily incorrect, but simply more specific in the GO hierarchy than the annotated term. SIFTER achieved 64.1% consistency (255 consistent predictions for 398 proteins). For comparison, BLAST-GO achieved 62.6% accuracy and 70.1% consistency. PFP achieved 5.7% accuracy and 5.7% consistency. FFPred achieved 6.1% accuracy (24 of 393 proteins for which it made predictions) and 6.1% consistency. ConFunc achieved 30.6% accuracy (119 of 389 proteins for which it made predictions) and 51.9% consistency. The PFP database did not contain annotations from S. pombe, so the results do not include self-annotations. For BLAST-GO, 93 of the 249 correct predictions required breaking ties in favor of the correct annotation. For ConFunc, 69 correct predictions and 110 consistent predictions required breaking ties in favor of the correct or consistent annotation. The FX-score considers a predicted term that is more specific than the annotation term to be correct, so we see that SIFTER has a large improvement between F-score and FX-score based on this characteristic. For these metrics, BLAST-GO performs better than SIFTER on these data, and both perform better than the other methods. As with the sulfotransferase family, one reason BLAST-GO may be performing better with these metrics is because a different version of the GOA database is used.

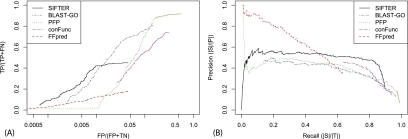
A ROC-like analysis (Fig. 6A) illustrates the benefit of SIFTER at low levels of false positives. There were 27,867 false positives in the PFP predictions (Table 2), as compared with SIFTER's 2233 false positives. The ROC-like analysis shows that, across low levels of false positives, SIFTER provides a large number of precise and correct predictions for the S. pombe proteins relative to the other four methods. BLAST-GO, PFP, and ConFunc value quantity of annotations over quality. The true positive rate for SIFTER does not reach 100% for two reasons. First, SIFTER only makes predictions at the most specific level of annotation, so more general experimental annotations for a protein, which make up approximately half of all annotations, are counted as a false negative regardless of whether the annotation is consistent with the prediction. Second, the held-out S. pombe experimental annotations were not always contained within the candidate functions. The average number of SIFTER candidate functions including the S. pombe protein annotations is 4.2; holding out the S. pombe annotations, there are an average of 3.6 candidate functions. Thus, the experimental annotations for the S. pombe proteins account for ∼15% of the functional diversity in these families, and the absences of these predictions are counted as false negatives.

Figure 6.

S. pombe function prediction comparison. (A) The ROC-like analysis of SIFTER with BLAST-GO, PFP, ConFunc, and FFPred. Note that the x-axis is on a log scale. (B) The precision-recall analysis of SIFTER with BLAST-GO, PFP, ConFunc, and FFPred.

In the precision-recall curve (Fig. 6B), FFPred shows high precision at low levels of recall relative to the other methods; this is because the support vector machine used in FFPred was only trained on a few general molecular function terms, and those terms are often correctly predicted. However, the set of predicted terms and their ancestors only includes ∼60% of the set of true terms, so recall suffers. Between 0.5 and 0.9 recall, SIFTER precision dominates the other methods for most of the plot, with PFP performing better above 0.9 recall. This illustrates that PFP predicts almost the complete set of annotations; however, the correct predictions are only a small proportion of the total predictions.

The performance of these methods can be understood by examining their predictions. PFP tends to annotate proteins with general predictions, so many predictions are consistent with the experimental annotations, but few are as precise. For example, the protein HMCS_SCHPO, annotated in the GOA database with “hydroxymethylglutaryl-CoA synthase activity,” was predicted to have the general “transferase activity” by PFP. The precise term “hydroxymethylglutaryl-CoA synthase activity” appeared in the list of predictions with a much lower score. BLAST-GO annotates HMCS_SCHPO with the precise term by transferring this experimental annotation from the very similar HMCS_YEAST sequence. FFPred uses a support vector machine that is built to make predictions for only a subset of the GO function terms. Thus, FFPred predictions tend to be more general than the experimental annotation. For example, the same HMCS_SCHPO protein had a single prediction for the general term “transferase activity.” ConFunc tends to predict more general terms, but it had better accuracy because often both general and specific terms had the same maximal score. For example, the same HMCS_SCHPO protein had two annotations with the same high score: the precise term and a more general term. This explains why more than half of the precise predictions were tie-breakers with an average of 10 highest-scoring terms.

Despite the harsh restriction of experimental evidence that we required for the S. pombe proteins included in this experiment, which limited the number of proteins, we are optimistic regarding SIFTER's potential for whole-genome annotation. In our fungal data set, S. pombe had 5004 proteins, so we produce predictions for ∼8% of the proteins in the genome. Seeding SIFTER with proteins from species outside of fungi may improve accuracy by increasing the number of available experimental annotations. As of Pfam 24.0, 88.5% of S. pombe proteins have at least one Pfam domain assignment, which comes with a precomputed phylogeny, eliminating the bulk of the computational effort of phylogeny-based function prediction. Extrapolating from our experiments, we expect SIFTER 2.0 runs to take on the order of 12 h for the full set of families with S. pombe proteins.

Discussion

This study addressed molecular function prediction in large and functionally diverse protein families. Taking as our point of departure the statistical approach to phylogenetics-based functional prediction embodied in SIFTER, we developed a novel transition model based on a continuous-time Markov chain to improve the extensibility of the method, making the evolutionary model completely general and enabling straightforward extensions to SIFTER to include additional types of biological data. Furthermore, we reduced the exponential time complexity of SIFTER via a simple but effective approximation that truncates possible function combinations within each protein. We found that the accuracy of SIFTER 2.0 is comparable to SIFTER 1.1. We showed in the sulfotransferases that the truncation approximation has excellent performance at all levels of truncation. We saw that SIFTER with approximate computation performed far better than BLAST on the Nudix family, which was beyond the scope of SIFTER 1.1. We showed that SIFTER can be applied in an automated way to annotate whole genomes using a gold-standard S. pombe data set containing proteins from fungal genomes. SIFTER excels in producing precise predictions in this domain relative to other popular methods for full-genome annotation.

There are several directions to pursue in envisaging further improvements to SIFTER and to protein function prediction generally. Many of these directions exploit the flexibility of SIFTER and are readily accessible in its current version; in particular, SIFTER does not use any precompiled databases or parameters estimated from training data, but takes as input a phylogeny of protein sequences and annotations for those protein sequences (and how those annotations are related to each other). As such, one can imagine using many different resources for the annotations (e.g., EC numbers, GO biological process and cellular component ontologies, or text annotations from the nr database) or protein families (e.g., significant hits in BLAST for seed proteins, phylogenies from the PANDIT database) (Whelan et al. 2006). While some of these alternative data types require further research, such as whether cellular components conform to the assumptions of a phylogenetic analysis, most are immediately implementable.

Another extension to SIFTER would be to use the GO hierarchy to produce more general predictions with higher confidence. In particular, one may propagate the posterior probabilities of the candidate terms to the root of the GO hierarchy to find posterior probabilities for the more general terms in the GO DAG. This process would use the same model of the GO DAG for incorporating evidence from the GOA database to the set of candidate terms. This would improve coverage but reduce precision of the predictions, particularly in the S. pombe data set. This extension would allow SIFTER to produce general functional terms as the highest-ranked predictions, analogous to some of the methods compared here.

SIFTER currently does not make use of additional information to help with prediction, such as sequence motifs, binding sites, expression data, or protein structure. One benefit of phylogenetic trees and graphical models generally is that they combine different sources of information in an evolutionarily principled way, so SIFTER may be extended to act as a meta-predictor that integrates other protein data. This could be implemented by augmenting the probabilistic model underlying SIFTER, letting the parameters depend on auxiliary information such as motifs or structure. The new SIFTER model was designed to enable extensions to different data types for application to many problems in protein science. While we have shown that SIFTER makes high-quality functional predictions and addresses some open issues in the field of protein function prediction, it also serves as a general platform for future enhancements.

Methods

SIFTER 2.0

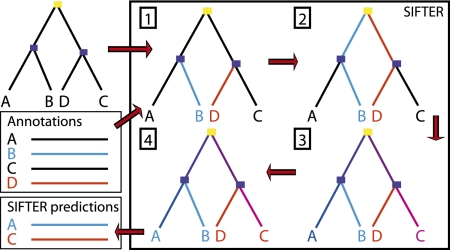
We briefly describe SIFTER's data integration, then focus on the Markov chain model and the approximate computation of posterior probabilities (Fig. 7; for further details, see the Supplemental Material).

Figure 7.

Overview of SIFTER method. (1) A reconciled protein phylogeny and a file containing some of the family's proteins with annotations (blue and red functions) are input into SIFTER. SIFTER incorporates the observations from the annotation file into the phylogeny. (2) Message passing propagates the observations from the leaf nodes to the root of the tree. (3) Message passing then propagates information from the complete set of observations back down to the leaves of the tree, enabling extraction of posterior probabilities at every node in the tree. Intuitively, posterior probabilities at a node take into account every observation scaled by the tree distance. (4) Predictions can be extracted from the tree using, in our case, the function with the maximum posterior probability for each protein.

From database data to a model

We extracted the protein families studied here from the Pfam database (Finn et al. 2010), and we used the manually curated alignments found in Pfam for phylogeny reconstruction. All trees were reconciled using the Forester v.1.92 program (Zmasek and Eddy 2001); the reference species tree is from the Pfam database. When we used GOA annotations (Barrell et al. 2009), we used the annotations with experimental evidence codes IDA, IMP, and TAS. Where we independently found experimental characterizations in the literature, we labeled that annotation as TAS.

In the SIFTER model, each protein i is associated with a random vector X_i, where each Boolean component represents one candidate function that takes value 1 when protein i has that function and 0 if the function is not associated with protein i. We choose the “candidate functions” for a particular family by using the GO directed acyclic graph (DAG) structure to find the most specific annotation terms associated with member proteins that are neither ancestors nor descendants of each other. For any protein, we can compute the probability of all of the candidate terms by putting a generic probabilistic model on the GO DAG (see the Supplemental Material). After selecting the set of candidate terms, we compute the probability of the candidate terms for each protein (whether or not it has experimental evidence).

Markov chain model

The structure of the evolutionary model underlying SIFTER is given by the phylogeny; we must specify the conditional probabilities at each node in the tree. SIFTER 2.0 uses a first-order Markov chain, which makes the Markovian assumption that future states are independent of past states given complete information about the present state. Similar assumptions have long been used to model the evolution of molecular sequences (Dayhoff et al. 1978; Henikoff and Henikoff 1992).

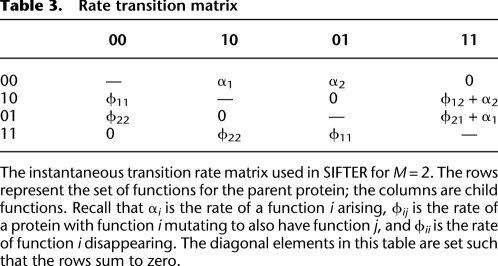
Let M be the number of candidate functions in the model, and let N be the number of leaf proteins. Our Markov chain has three sets of parameters. The parameters σ_spe and σ_dup describe the scaling of time after speciation and duplication events, respectively. The vector parameter α = {α₁, …, α_M} describes the rate of function i spontaneously arising when none of the candidate functions are observed in the ancestor protein. The matrix parameter Φ = {φ₁₁, φ₁₂, …, φ_MM} represents rates of mutation and loss: The off-diagonal elements φ_ij, i ≠ j, describe the rate for a protein with function i mutating to perform function j (while retaining function i), and the diagonal elements φ_ii describe the rate at which function i is lost.

Using parameters Φ and α, we can build the transition rate matrix Q for a Markov chain that describes the instantaneous rate of change in functional activity from an ancestor to its descendant. For example, the matrix Q for two candidate functions has on its rows (parent states) and columns (child states) all possible combinations of two functions for the parent and child proteins, namely, {00, 01, 10, 11}. In this terminology, “01” (for example) means that the first candidate function is not present (0) and the second candidate function is present (1) in a protein's state. A transition rate matrix Q, defined by variables Φ and α, is shown in Table 3 for M = 2, and is constructed analogously for M > 2 candidate functions.

Table 3.

Rate transition matrix

We constrain the rows of the matrix Φ to positive values that sum to at most M. Similarly, we constrain the α parameters to the M simplex. Furthermore, we constrain these parameters away from zero so as to avoid creating sink states or unreachable states in the Markov chain when estimating parameters (specifically, all parameters are constrained to be >0.01). Because Φ and α are used to construct the transition rate matrix Q, each non-zero, off-diagonal entry in matrix Q implicitly has a finite upper bound and positive lower bound. For additional intuition, see the Supplemental Material.

The conditional probability of a child configuration given a parent configuration is as follows, from the definition of a continuous-time Markov chain:

In this equation, X_i is the random vector associated with protein i, 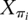is the random vector associated with protein i's immediate ancestor, t_i is the length of the branch between X_i and 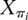, j and k index the power set S, s_j and s_k ∈ S, and exp is the matrix exponential function, such that

Element (k, j) of the transition probability matrix exp(t_iσQ) is the probability that an ancestor protein in state k mutates to state j in the descendant protein during time t_i (here, the phylogenetic branch length, which must be non-negative). The joint probability of the tree is:

The parameters of this model can be estimated using generalized expectation maximization (GEM) (Gelman et al. 2003), which is not currently applied to any data set other than the AMP/adenosine deaminase family because of the large number of parameters relative to the number of available annotations. For a complete description, see the Supplemental Material.

SIFTER's approximate computation

The time complexity to compute posterior probabilities for the SIFTER model is linear in the number of proteins, but exponential in the number of candidate functions due to the 2^M possible combinations of candidate functions for each protein in the transition rate matrix, which has (2^M)² entries. Computing matrix exponentials explicitly for each branch in the tree has a computational complexity of O(N((2^M)^2·3)). When M is large, the time to compute posterior probabilities is dominated by the exponential complexity in the number of candidate functions. Our approximation allows at most T candidate functions with value 1 in the transition rate matrix power set. This shrinks the number of elements under consideration to

In the Nudix family, setting T = 1, the set of candidates has 67 elements (each candidate term and the empty set), which means that there are 4489 elements in the transition rate matrix Q. Without truncation, the power set has ∼7.38 × 10¹⁹ elements, and the Q matrix has ∼5.44 × 10³⁹ elements. Computation time is reduced from infeasibly long to seconds.

Application of SIFTER

We ran SIFTER 2.0 as follows. We set default parameter values to φ_ii = 0.5, φ_ij = 1.0 for i ≠ j, σ_spe = 0.03, σ_dup = 0.05, and α_i = 1.0. We estimated parameters only for the AMP/adenosine deaminase family (see the Supplemental Material); for the remaining families, the number of parameters is larger than the number of available observations, making estimation unproductive. We ran leave-one-out cross-validation on the protein families by removing evidence associated with a single protein and computing the posterior probabilities. All experiments where timing results were reported were run on Dell Precision 390 Workstation computers with Intel Core2Duo 2.6 GHz processors and 2 Gb RAM.

Methods for comparison

The BLAST assessment was performed on the non-redundant (nr) set of proteins downloaded from the NCBI website on December 11, 2006. We ran BLASTP (version 2.2.4) (Altschul et al. 1990) with an E-value cutoff of 0.01. For each query protein we removed any exact matches from the same species to ensure that the query protein did not receive its own database annotation (emulating a leave-one-out experiment). We transferred the functional term(s) associated with the most significant BLAST hit that had an annotation with keywords within the candidate functions for that protein family; for more details, see the Supplemental Material. If multiple proteins shared an E-value, we transferred all of the annotations and broke ties in favor of the correct prediction. Historically, when researchers use BLAST for large-scale molecular function annotation, the function of either the most significant non-identity hit or the most significant non-identity annotated hit is transferred to the query protein, often leading to no prediction or an incorrect (or overly general) prediction. We found that restricting BLAST annotations to the candidate functions increases the overall accuracy of the BLAST predictions. We did not compute F-scores, FX-scores, or precision-recall curves for this comparison method because the keyword script did not include all ancestral nodes in the GO hierarchy. The metrics for the results were computed by determining true positive and false positive annotations for E-value cutoffs between 0 and 0.01.

The BLAST-GO assessment was performed on the SWISS-PROT/TrEMBL proteins downloaded from the UniProt website on June 21, 2010, so its annotations were more recent than those used by other methods. We ran BLASTP (version 2.2.23) (Altschul et al. 1990) with an E-value cutoff of 0.01. For each query protein, we first removed any exact matches (by name) to ensure that the query protein did not receive its own annotation. Given a ranked list of proteins by E-value, we found the highest ranking protein with at least one experimentally validated molecular function term from the GOA UniProt 80.0 database that was also in the set of candidate functions for that protein family and transferred those functional terms. (For the S. pombe experiment, we did not limit the transferred terms to candidate functional terms because the correct term was not necessarily in the set of candidate functions for the protein family.) If multiple proteins shared an E-value, we transferred all available annotations and broke ties in favor of the correct prediction. The metrics for the results were computed by determining true positive and false positive annotations for E-value cutoffs between 0 and 0.01.

We ran Protein Function Prediction (PFP) downloaded in August 2009 (Hawkins et al. 2006) from the executable provided by the authors, with the default settings. We computed the metrics for the results based on the PFP scores. We could not remove annotations from the PFP database that were for the proteins that we were querying, so cross-validation was not possible.

We ran FFPred (Lobley et al. 2008) from the executable provided by the authors, with the default settings. FFPred uses a large amount of third-party software, all of which was downloaded in August 2009. We computed all of the metrics for the results using the scores. We did not find any of the annotations in our test sets also present in the FFPred training data.

The authors of ConFunc (Wass and Sternberg 2008) applied their method (August 2009) to our sequence data in the cross-validation setting, guaranteeing that none of the sequences were self-annotated from their database. The UniProt and associated GOA database were both downloaded in January 2009. Per the authors' suggestions, we used the ratio of the GO term's associated protein's PSI-BLAST E-value, or C-value, compared to the lowest GO term C-value for that sequence to compute metrics for the results. We empirically confirmed this to be the most accurate scoring mechanism.

Metrics for evaluation

To compute accuracy for a given data set, we counted the number of proteins for which the top-ranked prediction exactly matched the experimental annotation, and divided by the total number of proteins. In the case of multiple experimental annotations or top-ranked predictions, we counted the protein as having an accurate prediction when the intersection of the two sets was not empty. For the deaminase, sulfotransferase, and Nudix families, we filtered the experimental annotations and the prediction terms to include only SIFTER's candidate functions for the family.

To compute the F-score and extended F-scores, we included each annotation and predicted term (i.e., the terms with the maximum score for SIFTER, PFP, and FFPred, or minimum score for BLAST-GO and ConFunc), and all ancestral terms of these terms including the root of the GO hierarchy in the set of predicted terms P and the set of experimental annotations T (each term in each set was present only once). The intersection of these two sets is the number of correct predictions C. Using | · | for the cardinality of a set, we can define precision as |C|/|P| and recall as |C|/|T|. Then the F-score is the harmonic mean of precision and recall, or F = 2|C|/(|P| + |T|). The FX-score considers predicted terms that are more specific than the most specific annotation to be correct (i.e., in the set T). To compute the FX-score, when the predicted term was more specific than the most specific annotation (and this annotation was ancestral to the predicted term), we added the count of more specific predicted terms to both the set of correct terms C and the set of true terms T, and then we computed the F-score of these modified sets.

Our ROC-like analysis evaluates the fraction of true positives as compared with the fraction of false positives across all cutoff values, where a positive prediction is one that has a posterior probability above the cutoff. This is not a standard ROC analysis: Instead of one correct and one incorrect classification, there are (e.g., in the case of the sulfotransferase family) one correct and eight incorrect classifications for every protein. We only consider exact term matches, so predictions that are consistent with, but not equal to, the correct annotation are treated as false positives. Some of the methods will not have ROC-like curves that start or end at the standard position; at the left end of the y-axis this is because identical scores on both false positive and true positive annotations force the curves to start higher on the x- and y-axes, and near the right end of the y-axis this is because there are not always scores for the total number of incorrect annotations for each protein. In the case of SIFTER, we built the ROC-like curve based on the leave-one-out runs, where, for each protein, using a cutoff from 1.0 to 0.0, we compute the number of false positives (FPs) divided by the total number of FPs plus true negatives (TNs), and plot this against the number of true positives (TPs) divided by the total number of TPs plus false negatives (FNs). Because the number of false positives varied so widely between methods, we divided the x-axis fraction by the maximum of FP + TN over all of the methods (and we include the number of false positives for each method in Tables 1 and 2).

We also present precision-recall curves for results from the different methods as a metric that does not penalize predictions that are consistent with, but more general than, the annotation. In particular, we compute the set of true function terms T as for the F-scores, and compute the set of predicted terms P including only the predicted terms (and their ancestral terms) with a score above a cutoff (or below for BLAST-GO and ConFunc); the set of correct terms C is then the intersection of these two sets. Then, as for the ROC-like analysis, we compute T, P, and C for all possible values of the cutoff (although the set T does not vary across cutoffs). We can plot recall, |S|/|T|, versus precision, |S|/|P|, across all values of the cutoff. These curves are not monotone because the precision may not increase in a monotone way as the sets C and P increase in size at different relative rates, so their ratio does not always increase.

Here we have adapted two standard evaluation metrics (ROC-like and precision-recall) to compare GO functional predictions, each with different measures of correctness. The ROC-like metric applied here highlights the quality of the precise predictions from each method, whereas the precision-recall metric applied here highlights prediction consistency and completeness. Both metrics have shortcomings: ROC-like analysis considers predictions that are more general than the true, precise molecular function to be incorrect, whereas the precision-recall metric assumes that the structure of GO is correct and rewards imprecise predictions. SIFTER was designed to make accurate and precise functional predictions, which are critical for important biological applications including experimental characterization of protein activity. The ROC-like analysis and associated accuracy measure used here are helpful to evaluate predictions based on these design criteria. Other applications, including some types of whole-genome annotation, may benefit from more general function annotations while minimizing the number of predictions inconsistent with the true molecular function; the F-scores and the precision-recall metric may be more appropriate to assess the different methods in this regime.

Data set preparation

Sulfotransferase family

The GOA UniProt 37.0 contained experimental GO molecular function annotations for 48 proteins. These 18 proteins were included to compute the F-scores and FX-scores for every method. The alignment for the full phylogeny was from Pfam 20.0. The subset of sequences with experimental annotations was aligned using hmmalign (Eddy 1998) with the sulfotransferase HMM profile from Pfam release 20.0. The phylogenies were reconstructed using PAUP* version 4.0b10 maximum parsimony with the BLOSUM50 matrix.

Nudix family

The Nudix family alignment was taken from Pfam 20.0, and we reconstructed the phylogeny from the neighbor-joining algorithm in PAUP* version 4.0b10 (Swofford 2001) because of the large size of the family. The subset of sequences with experimental annotations was aligned using hmmalign (Eddy 1998) with the Nudix HMM profile from Pfam release 20.0. This smaller phylogeny was built using PAUP* version 4.0b10 maximum parsimony with the BLOSUM50 matrix. The bootstrap analysis of the smaller tree using neighbor joining was performed using PHYLIP (Felsenstein 1989) downloaded October 2006 with 100 replicates. Function annotations were assigned to proteins from the literature by contrasting different levels of experimental evidence for a given hydrolase to prune the less specific substrates from a larger list of assayed compounds. We set the truncation level to T = 1 for all of the SIFTER Nudix experiments. We ran BLAST on this family because we could manually build the text parser to include all of the candidate functions from our modified ontology. We did not run BLAST-GO, PFP, FFPred, or ConFunc here because the reorganized GO hierarchy would not enable a comparison between SIFTER or BLAST results and results from these GO-based methods.

Fungal genomes data

The genomes from 46 different fungal species had been sequenced as of June 2006. Gene finding was performed in each genome using several different methods; for details, see Stajich (2006). We searched each resulting protein for Pfam domains using hmmsearch (Eddy 1998) for the Pfam-A domains available in Pfam version 20.0. We aligned each set of homologous fungal proteins to each other using hmmalign based on the Pfam-A HMM profile for that family domain (Eddy 1998). We reconstructed phylogenies for each domain with PAUP* version 4.0b10, using maximum parsimony with a BLOSUM50 matrix when the size of the alignment file was <10,000 kB, and neighbor joining with default parameters when the size of the file exceeded that. We reconciled the trees against a species tree (Supplemental Fig. 10) using Forester version 1.92 (Zmasek and Eddy 2001). Pfam domains with fewer than four protein sequences from the 46 fungal genomes were eliminated.

We gathered molecular function annotations for each fungal protein in a Pfam-A domain from the GOA database by running BLAST version 2.2.4 (Altschul et al. 1990) for each protein against the UNI-PROT fasta database, downloaded September 23, 2006 (The UniProt Consortium 2010), with an E-value cutoff of 1 × 10⁻¹⁰⁰. We found exact hits with identical species to map the UNI-PROT identifiers to the proteins in the fungal genomes. We extracted molecular function annotations from the GOA UniProt database 42.0.

For each family with experimental annotations from multiple species including S. pombe, we removed the experimental annotations for S. pombe proteins in order to predict those annotations using the available experimental annotations. We computed posterior probabilities once for each family, using SIFTER default parameters. SIFTER runs were performed exactly for families with fewer than nine candidate functions; otherwise, we truncated at two for nine to 19 candidate functions and at one for 20 or more candidate functions. As elsewhere, if there were multiple predictions for a single protein (because it was in multiple Pfam-A families), we used the correct one to compute accuracy. We did not run BLAST because it is prohibitively time-consuming to build a keyword parser for all of these molecular functions.