Abstract

Empirical relationships between phytoplankton biomass and nutrient concentrations established across a wide range of different ecosystems constitute fundamental quantitative tools for predicting effects of nutrient management plans. Nutrient management plans based on such relationships, mostly established over trends of increasing rather than decreasing nutrient concentrations, assume full reversibility of coastal eutrophication. Monitoring data from 28 ecosystems located in four well-studied regions were analyzed to study the generality of chlorophyll a versus nutrient relationships and their applicability for ecosystem management. We demonstrate significant differences across regions as well as between specific coastal ecosystems within regions in the response of chlorophyll a to changing nitrogen concentrations. We also show that the chlorophyll a versus nitrogen relationships over time constitute convoluted trajectories rather than simple unique relationships. The ratio of chlorophyll a to total nitrogen almost doubled over the last 30–40 years across all regions. The uniformity of these trends, or shifting baselines, suggest they may result from large-scale changes, possibly associated with global climate change and increasing human stress on coastal ecosystems. Ecosystem management must, therefore, develop adaptation strategies to face shifting baselines and maintain ecosystem services at a sustainable level rather than striving to restore an ecosystem state of the past.
Introduction
Increased nutrient inputs to coastal ecosystems, derived from the rapid rise in fertilizer use in agriculture, production of manure from farm animals, domestic sewage, and atmospheric deposition associated with fossil fuel combustion,1−4 have led to the global spread of coastal eutrophication since the late 1970s. Realization of the negative effects of eutrophication, involving the loss of value of coastal ecosystem services,1,5,6 prompted efforts, initiated in the late 1980s, to reduce nutrient inputs. The result was expected to be a phase of oligotrophication with decreasing primary production(7) which would reverse the effects of eutrophication and return coastal ecosystems to an earlier state.4,8,9 However, recent analyses have provided evidence that reduced nutrient inputs often fail to fully reverse the trajectories of ecosystems during eutrophication and have challenged the assumption that oligotrophication drives coastal ecosystems back to their original condition.(10)
The expectation that reduced nutrient inputs would reverse eutrophication effects originated from predictions derived from broad-scale relationships between chlorophyll a concentration (Chla), as an indicator of algal biomass, and nutrient concentrations across coastal ecosystems.11−13 These relationships were comparable to those developed in the 1970s for lake ecosystems14−16 and confirmed experimentally (e.g., (17−19)). Yet, the empirical basis supporting use of the general relationship to predict oligotrophication responses was lacking, as all case studies and experimental tests to the 1990s reflected ecosystem responses to addition of nutrients, rather than to their removal. Hence, the use of relationships between Chla and nutrient concentrations to predict the response of coastal ecosystems to oligotrophication rests on the assumption that eutrophication is a fully reversible process involving a single path identical for eutrophication and oligotrophication trajectories. This fundamental tenet underlying coastal ecosystem management has not been sufficiently tested to date, but the current availability of dozens of cases of individual ecosystems undergoing eutrophication and subsequent oligotrophication now allows such tests to be conducted.
Empirical relationships between Chla and nutrient concentrations, presented as general static relationships, have been based on data from many different ecosystems encompassing wide ranges of Chla and nutrient concentrations.12,13,20 However, the broad, order-of-magnitude variability characteristic of these relationships may not represent only random variability, but may partially derive from diverse and idiosyncratic responses within individual ecosystems and/or changes in the nature of these relationships over time. Indeed, our conceptual understanding of ecosystem functioning has evolved from the initial expectation of a uniform response to accommodate a diversity of responses to nutrient inputs.(8)
Increased availability of long-term time series describing the responses of coastal ecosystems to changes in nutrient concentrations now makes it possible to connect the dots in Chla–nutrient relationships to examine the trajectories of individual ecosystems over time(10) as well as to examine variability in trajectories among ecosystems. Such analyses may provide an improved basis to derive expectations on the possible response of individual coastal ecosystems to increases as well as to decreases in nutrient inputs.
Here we use long-term monitoring data to explore the existence of general patterns in the relationship between Chla and nutrient concentrations in 28 coastal ecosystems from four different regions where eutrophication has led to the implementation of management plans to reduce nutrient inputs. We aim to examine whether the relationship between Chla and nutrient concentration follows similar pathways through periods of eutrophication and oligotrophication. We do so by deconstructing general Chla–nutrient relationship to examine the variability among regions and individual ecosystems, as well as the variability in these relationships over time.
Data Sources and Processing
Water quality data were obtained from four public monitoring databases in Europe and North America (Table 1), constituting some of the most comprehensive and long-term data sets in the world. Although some of the databases had observations prior to 1977, the analysis was restricted to 1977–2006 for consistency across regions. The compiled database included over 45 000 observations of nutrient as well as chlorophyll a concentrations from the surface layer. Nutrient and Chla concentrations, the most widely used indicators of nutrient-driven eutrophication in the literature, were used as proxies of organic enrichment in coastal ecosystems.(1) Sampling stations with salinity <6 were discarded from the analysis to focus on mesohaline and polyhaline coastal ecosystems.
Table 1. Surface Samples of Water Quality Data Used in the Analysisa.
| no. of observations |
no. of annual means |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| region | no. of coastal ecosystems | years | TN | TP | Chla | TN | TP | Chla | source |
| Chesapeake Bay | 7 | 1984–2006 | 17133 | 17465 | 21427 | 149 | 149 | 159 | www.chesapeakebay.net |
| Denmark coast | 10 | 1977–2006 | 12409 | 12354 | 12211 | 256 | 257 | 257 | www.dmu.dk |
| Tampa Bay | 4 | 1977–2006b | 12825 | 17889 | 17885 | 104 | 120 | 120 | www.tbeptech.org |
| Wadden Sea (Dutch part) | 7 | 1977–2006c | 3828 | 3878 | 3323 | 203 | 200 | 204 | www.waterbase.nl |
Data were downloaded from public monitoring databases with long time series (>20 years) of coastal ecosystems from four regions.
No TN data before 1981.
TN and TP calculated as sum of measured particulate and filtered fractions between 1991 and 1996.
For each coastal ecosystem (n = 28) within the four regions, annual means of total nitrogen (TN), total phosphorus (TP), and Chla were computed from a general linear model(9) after employing a log-transformation to normalize the concentrations.
Stationi described spatial differences between monitoring stations within the ecosystem, yearj described the interannual variation, and monthk described the seasonal pattern. Annual means were chosen, as opposed to seasonal means, to achieve comparable values across all regions, i.e., unbiased by seasonal differences between regions. Observations of Chla with zero concentration (n = 47) were replaced by 0.1 μg L–1, an adequately small concentration allowing for log-transformation. The model 1 accounted for the heterogeneity in time and space of the monitoring data by separating variations into spatial (stationi) and temporal (yearj and monthk) components. Comparable yearly estimates were computed for each ecosystem by back-transforming (i.e., using the exponential function) the marginal means of the factor yearj in model 1 to represent the geometric mean of all stations in each coastal ecosystem over all months (January–December). This resulted in 712, 726, and 740 annual mean values for TN, TP, and Chla, respectively, almost evenly distributed across ecosystems (Table 1). Weights to be used in the subsequent analyses of mean values were computed as the inverse variance of the mean estimates.
Analysis of Chla–Nutrient Relationships
General linear models of weighted annual means of Chla vs TN and TP were computed for all yearly means combined (“global model”), for each of the four regions specifically (“regional models”) and for individual ecosystems within each of the regions. The number of observations used in the regressions was equal to or less than the total number of means (Table 1), because there were years without matching Chla and TN or TP concentrations. The established relationships were compared to those reported from other studies in the literature.12,13,20 We present the general global and regional models as functions of TN as well as TP to illustrate the relationship to both major nutrients. The models for individual ecosystems were presented for TN only, as nitrogen is reported to be the main nutrient limiting primary production in the four studied regions, although phosphorus limitation may occur in spring and in oligohaline waters (Chesapeake Bay: (21,22); Denmark coast:23,24; Tampa Bay: (25); Dutch Wadden Sea: (26,27)). However, the results may, to some extent, apply to TP as well since TN and TP are commonly correlated in coastal ecosystems. The generality of the regional relationships across time and space was examined by analyzing the residuals for differences among ecosystems within regions and time (interannual variation), because if the regional relationships were indeed generic to all coastal ecosystems within regions and constant over time there would be no systematic variations in the residuals. The residuals were analyzed for differences among ecosystems within regions by means of analysis of variance (ANOVA), and changes in the residuals over time were investigated using linear regression and Generalized Additive Model (GAM) for a linear and smoothed trend, respectively. The Chla–TN relationship was further spatially broken down by estimating the relationships for each individual ecosystem in the four regions (28 regression equations).
Finally, we explored if time trajectories of individual ecosystems conformed to the general power relationship (linear relationship on the log–log scale). This was done by connecting the dots representing the annual mean concentrations of Chla and TN in individual ecosystems to form trajectories describing the temporal dynamics during periods of eutrophication and oligotrophication. A semiparametric GAM was employed to investigate the time trajectory of the Chla–TN relationship, using a quadratic LOESS smoother to describe and test the significance (likelihood ratio test) of departures in time from a linear parametric Chla–TN relationship, i.e., analyzing if years were randomly distributed around the linear Chla–TN relationship or systematically deviating over time. Weights for the Chla means could not be employed by the GAM method (in SAS version 9.2). For plotting the time trajectory, a smooth trend for TN was modeled using time as a nonparametric effect in GAM, and Chla predictions were obtained by scoring the semiparametric GAM with the smooth TN trend.
Results
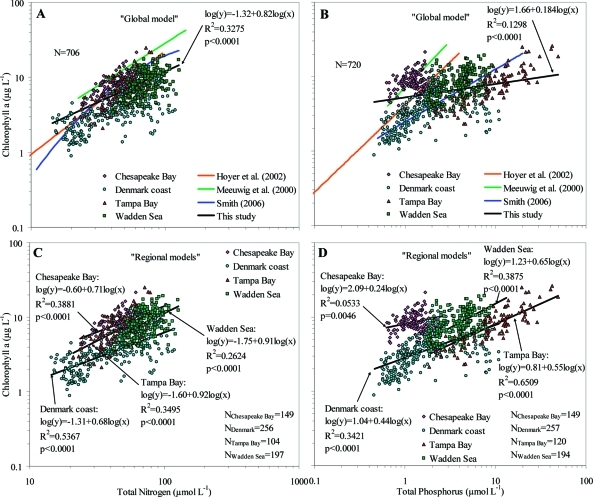
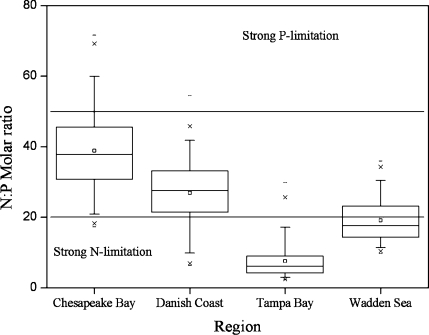
Chla and nutrient concentrations varied broadly across systems (Figure 1) and over time. The average TN:TP molar ratio varied among regions with levels indicating combined N and P limitation to strong N limitation from 7.6 in Tampa Bay, 19.1 in the Wadden Sea, 26.9 in Danish coastal waters, to 38.8 in Chesapeake Bay (Figure 2). Log-transformed TN and TP were significantly correlated for all data combined (r = 0.58, p < 0.0001, n = 707) and for all regions separately (Chesapeake Bay: r = 0.40, p < 0.0001, n = 149; Denmark coast: r = 0.80, p < 0.0001, n = 256; Tampa Bay: r = 0.52, p < 0.0001, n = 104; Wadden Sea: r = 0.72, p < 0.0001, n = 198). Despite indications of a stronger N than P limitation (Figure 2) and the significant correlations between TN and TP, ”global” and “regional” models are presented both for TN and TP.
Figure 1.
Relationships between annual mean Chla and annual mean TN (left panel, A and C) and TP (right panel, B and D) concentrations for all data combined (“Global model”, A and B) and for the four regions separately (“Regional models”, C and D). Solid black lines show the fitted log–log regression equations from this study, with associated statistics listed in the plots, and the “Global model” is compared to relationships (A and B) developed elsewhere (Florida coast,(12) Finnish estuaries,(20) global(13)).
Figure 2.
Box and whiskers plot of the TN:TP molar ratio for the four regions compared to thresholds for N deficient (TN:TP < 20) and P deficient (TN:TP > 50) phytoplankton growth reported by Guildford and Hecky.(11) Boxes show lower and upper quartiles with median (line) and mean (square) inside the box. Whiskers mark the 95% confidence intervals, crosses are the 1st and 99th percentiles, and dash symbols show minimum and maximum values.
Chla concentration was scaled as the 0.82 power of TN across ecosystems (Figure 1A). The power exponent was somewhat lower than that of previously reported relationships (Chla ∼ TN1.38 in (12); Chla ∼ TN1.13 in (20)), although the Chla values predicted for individual TN concentrations were comparable to those delivered by these relationships. A weaker relationship was obtained for Chla in relation to TP (lower R2) scaling as the 0.184 power of TP (Figure 1B), well below those found in previous studies (Chla ∼ TP1.17 in (12); Chla ∼ TP0.71 in (13); Chla ∼ TP1.26 in (20)), consistent with indications that N is the primary limiting nutrient in the ecosystems investigated here. However, Chla concentrations ranged about 1 order of magnitude for any given TN or TP concentration (Figure 1), also comparable to previous analyses.(13) Similar to this study, Hoyer et al.(12) used annual means, whereas Meeuwig et al.(20) used means over the productive season and Smith(13) used a combined data set of both annual and seasonal means.
Spatial Partitioning of the Chla–Nutrient Relationship
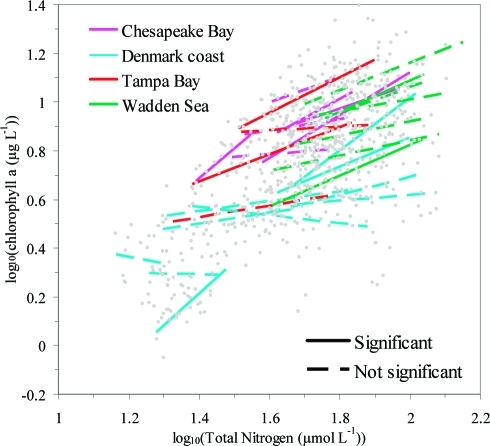
The relationship between Chla and TN differed significantly among regions (F6,698 = 93.45, p < 0.0001), with power exponents ranging from 0.68 to 0.92 (Figure 1C). Significant differences among regions were also found for the Chla–TP relationship (F6,680 = 178.98, p < 0.0001), although the power exponents were consistently lower than for the Chla–TN relationships ranging from 0.24 to 0.65 (Figure 1D). TN was better at describing variations in Chla for Chesapeake Bay and Denmark coast, whereas TP gave a higher R2 value for the Wadden Sea and Tampa Bay. Chla–TN relationships were also variable within regions, as significant variation among individual coastal ecosystems within regions was observed for the residuals (Table 2, Figure S1) derived from regional Chla–TN relationships (Figure 1C). Further analysis of linear relationships between Chla and TN for individual coastal ecosystems showed a broad range of relationships, spanning from lack of significant relationships at some sites with very low scaling exponent (e.g., −0.28 for Århus Bay, Denmark, p = 0.5766) to very high scaling exponent (e.g., 1.30 for Køge Bay, Denmark, p = 0.0197) within any one region (Table 3, Figure 3). Indeed, over half of the Chla–TN relationships describing interannual changes at individual coastal areas were not statistically significant, even though some of these coastal areas experienced large changes in TN concentrations (Table 3, Figure 3). Whereas only 11 out of 28 ecosystems displayed a significant linear relationship between Chla and TN (Table 3), this number is still significantly higher than the 1 or 2 significant relationships that would be expected by chance alone in the absence of an overall relationship between Chla and TN.
Table 2. Analysis of Variance for Differences between Ecosystems within Each Region Taking Differences in TN Levels into Accounta.
| region | dfecosystem | dferror | F | p |
|---|---|---|---|---|
| Chesapeake Bay | 7 | 142 | 4.89 | <0.0001 |
| Denmark coast | 10 | 246 | 23.73 | <0.0001 |
| Tampa Bay | 4 | 100 | 14.00 | <0.0001 |
| Wadden Sea | 7 | 155 | 29.46 | <0.0001 |
Table 3. Regressions between log(Chla) and log(TN) for Different Coastal Areas and Trajectory Analyses for Temporal Departures from Linear Relationshipa.
| linear regression log(Chla)–log(TN) |
trajectory analysis |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| region | area | short name | no. of years | relationship | RMSE | p | RMSE | χ2 | p |
| Chesapeake Bay | Choptank | CHO | 23 | –1.44 + 0.87x | 0.24 | 0.0034 | 0.17 | 19.31 | <0.0001 |
| Chesapeake Bay | James River | JMS | 23 | 1.37 + 0.12x | 0.22 | 0.6646 | 0.18 | 7.61 | 0.0236 |
| Chesapeake Bay | Mainstem mesohaline | MH | 18 | –0.93 + 0.79x | 0.14 | 0.0303 | 0.13 | 6.46 | 0.0412 |
| Chesapeake Bay | Mainstem polyhaline | PH | 18 | –2.36 + 1.22x | 0.22 | 0.0409 | 0.19 | 8.87 | 0.0124 |
| Chesapeake Bay | Patuxent | PAX | 21 | 0.30 + 0.54x | 0.25 | 0.2233 | 0.21 | 7.50 | 0.0237 |
| Chesapeake Bay | Potomac | POT | 23 | 0.16 + 0.50x | 0.19 | 0.0484 | 0.17 | 8.21 | 0.0175 |
| Chesapeake Bay | Rappahannock | RPP | 23 | 1.19 + 0.23x | 0.26 | 0.5519 | 0.17 | 15.54 | 0.0005 |
| Denmark coast | Flensborg Fjord | FLF | 21 | 0.46 + 0.22x | 0.17 | 0.2019 | 0.14 | 11.98 | 0.0025 |
| Denmark coast | Horsens Fjord | HOF | 26 | 1.85 + –0.17x | 0.24 | 0.4580 | 0.31 | 3.24 | 0.1920 |
| Denmark coast | Køge Bay | KØB | 21 | –3.71 + 1.30x | 0.15 | 0.0002 | 0.13 | 7.88 | 0.0197 |
| Denmark coast | Limfjorden | LIM | 25 | –0.84 + 0.61x | 0.28 | 0.0374 | 0.24 | 9.93 | 0.0067 |
| Denmark coast | Nissum Bredning | NIB | 25 | 0.62 + 0.20x | 0.24 | 0.2645 | 0.26 | 5.00 | 0.0802 |
| Denmark coast | Odense Fjord | ODF | 30 | 0.85 + 0.12x | 0.20 | 0.4680 | 0.26 | 21.57 | <0.0001 |
| Denmark coast | Roskilde Fjord | ROF | 29 | –0.11 + 0.37x | 0.17 | 0.0679 | 0.23 | 1.01 | 0.5893 |
| Denmark coast | Skive Fjord | SKF | 25 | –2.67 + 1.09x | 0.20 | <0.0001 | 0.20 | 17.21 | 0.0002 |
| Denmark coast | Sydfynske Øhav | SFØ | 29 | 0.78 + –0.03x | 0.21 | 0.9148 | 0.16 | 22.36 | <0.0001 |
| Denmark coast | Århus Bay | ÅRB | 25 | 1.61 + –0.28x | 0.23 | 0.5766 | 0.22 | 5.76 | 0.0554 |
| Tampa Bay | Hillsborough Bay | HB | 26 | –0.50 + 0.73x | 0.25 | 0.0046 | 0.19 | 21.81 | <0.0001 |
| Tampa Bay | Lower Tampa Bay | LTB | 26 | 0.43 + 0.24x | 0.23 | 0.1956 | 0.20 | 11.30 | 0.0038 |
| Tampa Bay | Middle Tampa Bay | MTB | 26 | –0.25 + 0.56x | 0.28 | 0.0387 | 0.19 | 35.61 | <0.0001 |
| Tampa Bay | Old Tampa Bay | OTB | 26 | 1.74 + 0.08x | 0.20 | 0.6882 | 0.15 | 23.56 | <0.0001 |
| Wadden Sea | Dantziggat | DG | 26 | 0.10 + 0.56x | 0.27 | 0.0880 | 0.24 | 13.43 | 0.0012 |
| Wadden Sea | Doove Balg | DB | 25 | 1.19 + 0.25x | 0.29 | 0.4630 | 0.30 | 3.16 | 0.2063 |
| Wadden Sea | Huibertgat | HG | 29 | –1.05 + 0.64x | 0.18 | <0.0000 | 0.19 | 1.93 | 0.3872 |
| Wadden Sea | Lauwers | LW | 29 | 0.03 + 0.52x | 0.23 | 0.0875 | 0.24 | 0.71 | 0.7062 |
| Wadden Sea | Marsdiep | MD | 30 | 0.52 + 0.31x | 0.18 | 0.0583 | 0.17 | 2.90 | 0.2276 |
| Wadden Sea | Vliestroom | VS | 29 | 0.78 + 0.29x | 0.20 | 0.1102 | 0.19 | 3.84 | 0.1499 |
| Wadden Sea | Zoutkamperlaag | ZK | 29 | –0.44 + 0.64x | 0.26 | 0.0486 | 0.22 | 5.98 | 0.0515 |
Linear relationship, residual mean square error (RMSE, weighted) and significance level (p) refer to the linear regression of log(Chla) vs. log(TN). Temporal departures from the linear relationship were investigated by means of GAM; RMSE was calculated as the deviance per observation (unweighted), χ2 and p derive from likelihood ratio test statistics. Number of observations is equal to the number of years. Significant relationships (p < 0.05) are highlighted in bold.
Figure 3.
Linear regressions between log(Chla) and log(TN) for individual ecosystems (n = 28) in four regions. Annual means of Chla and TN used for the regressions are shown by gray dots.
Temporal Chla–TN Trajectories
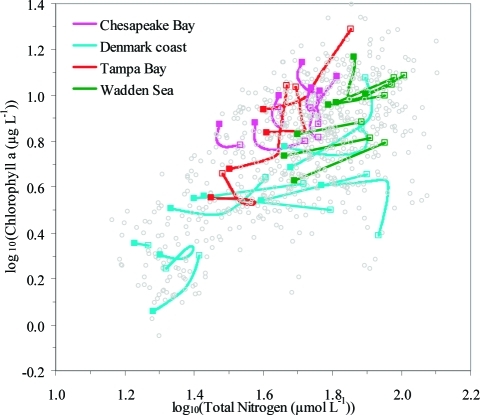
The large fraction of coastal ecosystems experiencing no significant relationship between Chla and TN despite large changes in TN suggests that the Chla–TN trajectories of individual sites are complex and more convoluted than expected from the assumption of a simple power scaling of Chla to TN. Indeed this was confirmed by visual inspection of the trajectories of individual ecosystems (Figure 4) and, more formally, by statistical tests (using GAM) of the departures from a power relationship. Actually, 18 out of 28 of the coastal areas investigated (64%) had significant time departures from a simple power scaling of Chla to TN (Table 3).
Figure 4.
Smoothed time trajectories, obtained by means of GAM, of the log(Chla) vs log(TN) relationships for the 28 ecosystems representing the four regions. Open and filled symbols mark the start and end of the trajectories, and the annual means used for computing the trajectories are shown by gray dots. Linear relationships are shown for ecosystems (n = 10), where time departures from a stationary power relationship between Chla and TN was not significant (Table 3). A close-up of the trajectories for the different regions can be found in Figure S2.
Most (17 out of 28) of the trajectories for coastal ecosystems deviated from a simple and monotonic increase or decrease in Chla with increasing or decreasing TN predicted from power relationships (Figure 4, Figure S2). The smoothed trajectories of the individual coastal ecosystems generally showed an initial decline in Chla with decreasing TN followed by stabilization or even an increase with further reductions in TN (Figure 4). In fact, 43% (12 out of 28) of the trajectories ended with a higher Chla concentration and more than half of these were from Chesapeake Bay, where decreases in TN were generally smaller (Figure 4, Figure S2). This finding is in sharp contrast with the expected simple response (according to the global and regional models) in Chla concentration with decreasing TN concentration, which was observed only for 29% of the coastal areas investigated (8 of 28 areas, Table 3, decreasing linear slopes in Figure 4).
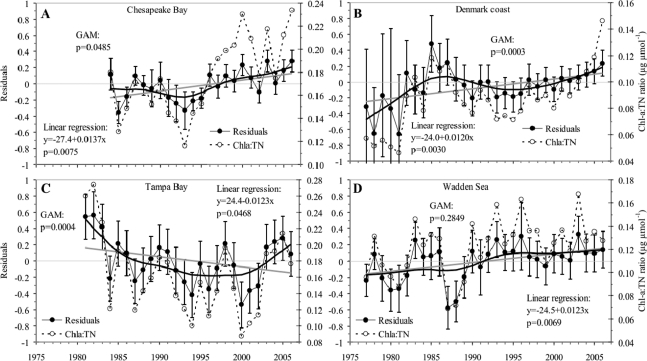
The examination of these trajectories (Figure 4) suggests that the yield of Chla for any given TN concentration has increased in coastal ecosystems since the onset of nutrient abatement in the late 1980s in the majority of the watersheds.9,10,22,25 A shift in the yield of Chla for any given TN should be reflected in an increase in the residuals of power Chla to TN relationships. Indeed, an analysis of residuals from the regional Chla vs TN power relationships showed that the residuals were not randomly distributed over time but rather shifted significantly from the mid 1970s to present (Figure 5). In particular, there was a significant linear trend toward increasing residuals for the Chesapeake Bay, Danish coastal areas, and the Dutch Wadden Sea, whereas Tampa Bay showed an overall decreasing trend driven by large positive residuals in the first 3 years with data (Figure 5C). Closer inspection, using a nonparametric regression model (GAM), revealed that (1) residuals increased from 1977 to the mid 1980s in Danish coastal areas and the Wadden Sea, (2) residuals declined between the mid 1980s and the early 1990s in all regions investigated, and (3) residuals increased during the past decade in all four regions (GAM models in Figure 5). The remarkable and, to some extent, consistent trends toward shifting Chla residuals across regions corresponds to an increase in the intercept of the power relationship between Chla and TN over time, implying that these relationships may systematically underestimate Chla expected for a specific reduction in TN into the future.
Figure 5.
Trends in residuals (annual means with 95% confidence interval of the mean value) from region-specific regressions (Figure 1C) between log(Chla) and log(TN) investigated by linear regression and a nonparametric GAM with statistics listed. For comparison the ratio between annual mean Chla and TN is also shown.
An analysis of the Chla:TN ratio across systems showed similar trends, as the mean ratio has increased consistently since the mid 1970s to present for three of the four regions (Figure 5). The data series revealed a 2-fold range in the Chla:TN ratios and suggests nearly a doubling of the average Chla per unit of TN over this 30-year period.
All four regions have experienced decreasing concentrations of total phosphorus (TP) during the study period due to point source abatement. The trends in the residuals of the Chla–TN relationship over time were correlated to the decreasing trends in TP taking spatial variations between areas into account (Table 4), albeit negatively for all regions except Tampa Bay. However, Tampa Bay, where the watershed is highly urbanized and contains large deposits of phosphate rock,(25) had the highest TP concentrations and the lowest TN:TP ratios of all four regions (Figure 2). Thus, the increasing trend in the residuals could not be causally linked to patterns of potential phosphorus limitation.
Table 4. Analysis of Variance from Analyzing Residuals from Region-Specific Relationships (log(Chla)–log(TN) Relationship in Figure 11C) vs. log(TP) with an Intercept Specific to the Coastal Ecosystem, i.e., Residual = αecosystem + β × log(TP)a.
| TP-dependent slope |
ecosystem-specific intercept |
||||||
|---|---|---|---|---|---|---|---|
| region | dferror | β | F | p | dfecosystem | F | p |
| Chesapeake Bay | 141 | –0.30 | 4.13 | 0.0440 | 7 | 5.36 | <0.0001 |
| Denmark coast | 245 | –0.07 | 2.32 | 0.1289 | 10 | 24.07 | <0.0001 |
| Tampa Bay | 99 | 0.24 | 13.46 | 0.0004 | 4 | 17.42 | <0.0001 |
| Wadden Sea | 184 | –0.21 | 10.45 | 0.0015 | 7 | 31.14 | <0.0001 |
Residuals were weighted by the inverse variance of the annual Chla means.
Discussion
Widespread evidence of coastal eutrophication starting in the 1970s led scientists to develop predictive frameworks to guide nutrient abatement plans, building on early experiences from freshwater management.14,15 Our mechanistic understanding of eutrophication processes has evolved in parallel from simple nutrient-driven relationship to complex models involving various trophic levels and ecosystem-specific features.(8) Yet, the belief that phytoplankton biomass should decline with decreasing nutrient inputs, and thus concentrations, in a manner similar to the way it increased remains a pervasive principle in the management of coastal ecosystem (e.g., (12)). The results presented challenge this belief, with important implications for nutrient management and the evaluation of its effectiveness.
Nutrient inputs from land and atmosphere can be controlled by appropriate management measures, but nutrient inputs from sediments(28) and exchanges over the open boundary(29) can also be considerable. Except for systems with strong light limitation increasing inputs of nutrients enhances phytoplankton growth and consequently biomass,8,30 but total inputs from all nutrient sources are difficult to estimate, resulting in poor relationships between nutrient loading from land and phytoplankton production.(31) Total nutrient concentrations, representing a balance between inputs and losses, constitute good general predictors for phytoplankton biomass(31) and can be linked to nutrient input from land through system-specific relations (e.g., (32)). Therefore, a general relationship describing the effect of nutrient enrichment on phytoplankton biomass would be expected for total nutrient concentrations.
Should we Expect a Simple, General Chla–Nutrient Relationship?
Recognition of the prevalent role of nutrients, particularly nitrogen, in limiting phytoplankton abundance in marine ecosystems33−35 drove efforts to derive a general relationship allowing the prediction of chlorophyll a from nitrogen concentrations. Power functions of various kinds were used to describe the relationship between Chla and nutrients as such models are quite flexible and easy to estimate by linear regression on a log–log scale. Chla–nutrient relationships are expected to eventually flatten out because of density-dependent processes, such as self-shading and allelopathy.(36) This implies a slope <1 on the log–log scale as found in the global and regional models presented here (Figure 1), as well as in models presented by Nixon et al.,(37) who reported a scaling exponent of 0.72. However, some studies reported slopes >1,12,13,20 suggesting that other mechanisms enhancing Chla covaried positively with nutrient levels in the ecosystems studied. Carstensen and Henriksen(32) found that the slope decreased from 0.92 to 0.53 when a system-specific intercept was included in the relationship, also indicating a positive covariation between TN levels and other mechanisms favoring high Chla concentrations. Our results, combined with those from Carstensen and Henriksen(32) and Nixon et al.,(37) suggest that Chla should scale to TN with a scaling exponent between 0.5 and 1.
Nitrogen is generally believed to be the main limiting nutrient in coastal ecosystems although some systems may also display phosphorus limitation(34) and the debate of nitrogen versus phosphorus limitation is still ongoing.(35) In our study Chla correlated with both TN and TP, which were intercorrelated, but TN was a better predictor of Chla for Chesapeake Bay and Denmark coast, while TP was a better predictor for Tampa Bay and Wadden Sea (Figure 1C and D), although both of these regions have TN:TP ratios consistent with nitrogen limitation (Figure 2). TP levels in Meeuwig et al.(20) and Hoyer et al.(12) were generally low compared to TP values in our study, despite similar ranges for Chla, suggesting that phosphorus limitation could be more pronounced in the systems they studied. Our study confirms the reported predominant nitrogen limitation of the regions examined here, consistent with previous reports for these regions.22,23,25,27
Although general relationships between Chla and nutrients were indeed derived, e.g., by Smith(13) and here (Figure 1), these were all based on data pooled from many different ecosystems covering several orders of magnitude for both Chla and nutrients. Thus, in principle, these relationships could be driven by differences among ecosystems rather than by a common response pattern. There is overwhelming evidence that system-specific attributes modulate the response of phytoplankton to nutrient enrichment.(8) Monbet(38) documented significant differences in Chla responses (almost by a factor of 10) to nitrogen levels between micro- and macrotidal estuaries, because increased tidal mixing enhances light limitation by increased vertical mixing and resuspension of sediments. Moreover, increased vertical mixing also enhances grazing pressure on phytoplankton by benthic grazers. Petersen et al.(39) reported a 5–6 fold decrease in Chla, whereas nutrient levels changed much less, following a regime shift from a bottom-up to a top-down controlled coastal ecosystem. Very shallow coastal ecosystems dominated by macrophytes also respond to changes in nutrient inputs differently from phytoplankton-dominated ones.(37) Differences in the labile fraction of N and P would similarly lead to deviations from a general relationship based on total nutrients(32) as would differences in the degree of N versus P limitation. Moreover, latitudinal and temperature differences affect the turnover of nutrients and the annual mean Chla for a given nutrient concentration. Evidently, many factors besides nutrient enrichment could lead to changes in Chla and thus account for the order-of-magnitude variability around the general relationship between Chla and nutrients. Hence, nutrient concentrations set an order-of-magnitude range for the annual average Chla concentration for coastal ecosystems, but do not allow prediction of Chla trajectories in response to changes in nutrient concentrations within these boundaries.
Are Spatial Differences Important?
The results presented here clearly demonstrate that the general relationship between Chla and TN conceals important diversity in the nature of the relationship and the underlying response of Chla to changing nitrogen concentrations in individual coastal areas. Chesapeake Bay had the highest Chla relative to TN, followed by Tampa Bay, Wadden Sea, and the Denmark coast. Several ecosystem features could potentially account for these regional differences in the Chla–TN relationships. All the studied regions are classified as microtidal but the tidal range in the Wadden Sea (∼ 1.5–2 m) is higher than for the other regions (<1 m).(38) Tampa Bay is a relatively shallow (∼ 4 m) and wind-exposed ecosystem where average Secchi depths range from 1 m in Hillsborough Bay to 2.5–3 m in Lower Tampa Bay,(25) suggesting potential light limitation. High abundances of filter feeders characterize the Danish coastal sites that are mostly well-mixed to the bottom,(23) and a relatively large fraction of TN is refractory due to mixing with Baltic Sea water.(32) Additional features could be added as candidates to account for the reported regional differences in Chla–TN relationships.
Whereas the general relationships help delineate the Chla concentration expected for a particular TN concentration, this only applies to the mean Chla to be expected for a universe of coastal ecosystems with similar TN concentrations, but not to any one individual ecosystem in particular. The key consideration in using this general relationship is that the error in the prediction of Chla can only be assumed to be randomly distributed within the broad order-of-magnitude error bounds about the predicted Chla for such hypothetical population of coastal ecosystems with similar TN. Yet, this does not hold for any one individual coastal ecosystem. Hence, the general relationship is not only invalid to predict the particular value of Chla to be expected for a particular change, increase or decrease, in TN for a particular coastal ecosystem, but is also invalid to predict even the ensuing direction of change (increasing, decreasing, or no change). Indeed, individual systems showed the full range of TN–Chla relationships, including positive, negative ones, and no relationship, stressing the need to develop system-specific predictions.
Do Chla–TN Relationships Change over Time?
The order of magnitude error characteristic of the general Chla–TN relationship includes differences in the Chla level at a particular TN concentration among individual ecosystems, but also includes dynamic changes in the yield of Chla for a particular TN concentration over time. More than half of the 28 ecosystems had significant time departures from a static power relationship between Chla and TN (Table 3), implying that the residuals of the relationship were not randomly distributed over time. Indeed, the stabilization or increase of Chla over time despite decreasing TN concentrations observed in most ecosystems (Figure 4) is likely to be the main reason for the low number of significant linear relationships between Chla and TN across the ecosystems studied (39% in Table 3). The complex trajectories of Chla concentration with changes in TN concentration resemble those reported by Duarte et al.,(10) but these complex trajectories do not only result from idiosyncratic responses to nutrient reduction but from shifts over time in the yield of Chla for any one TN concentration.
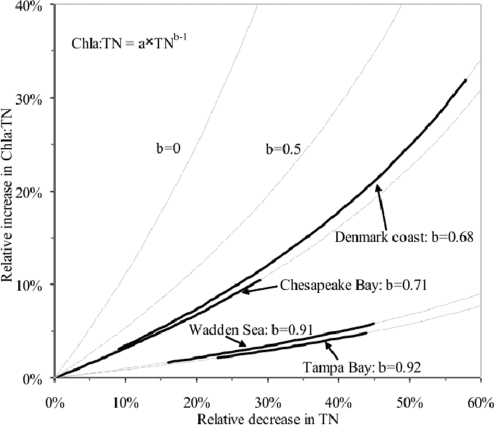
The shift in Chla for any given TN concentration over time (assessed by the time trend in the residuals from the Chla–TN relationship as well as the Chla:TN ratio, Figure 5) could not be explained from corresponding changes in TP with time. If the functional relationship between Chla and TN flattens out with a diminishing Chla yield per unit nitrogen as TN increases, as implied by a power relationship Chla = a × TNb where b < 1, then an increase in the Chla:TN ratio (Chla:TN = a × TNb-1 and b < 1) is expected with decreasing TN concentrations over time (Figure 6). However, the estimated power relationships for the 4 regions (Figure 1C) could only account for increases in the Chla:TN ratio of <11% for Chesapeake Bay, < 32% for Denmark coast, < 5% for Tampa Bay, and <6% for Wadden Sea (Figure 6), much lower than the observed increases in the Chla:TN (Figure 5). Even power relationships with a lower exponent (e.g., b = 0.5) or no relationship at all (b = 0) could not fully account for the almost doubling of the Chla:TN ratio over time observed here (Figure 6).
Figure 6.
Predicted increases in the Chla:TN ratio for declining TN levels (equation inserted) computed from the estimated power relationships for the 4 regions as well as for a square root relationship (b = 0.5) and no relationship (b = 0). Thick lines show estimated reduction ranges in TN during the study period for the different ecosystems (Chesapeake Bay: −17% to 29%, Denmark coast: 9–57%, Tampa Bay: 23–44%, Wadden Sea: 16–45%).
Thus, the trends in Chla:TN cannot be explained as an artifact from overestimating the exponent in the Chla–TN relationship, and reflect, therefore, a functional change in the ecosystem, consistent within but also among regions. The increase in the yield of Chla for any given TN concentration over time cannot be accounted for by system-specific attributes that did not change over time, such as the tidal mixing regime.(38) Hence, the actual yield for any TN concentration depends on other factors, including the taxonomic composition of the community, the turnover of nitrogen in water and sediments, the partitioning of nitrogen in pools of different availability to phytoplankton, and the role of other limiting factors, including other nutrients and light availability, loss factors, including grazers and diseases, and stresses (e.g., high temperature or high UV radiation).
Does the Increase in Chla Yield Per Unit Nitrogen Signal a Global Change?
A higher-order process, acting across large scales, is required to account for the almost consistent shift in the yield of Chla per unit TN across regions. Indeed, the baselines determining the structure and function of coastal ecosystems are shifting rapidly, and this may affect the response of phytoplankton to nutrient concentrations in multiple ways.(10) Some possible explanations for this shift are described in the following. Increasing CO2 concentrations and water temperature, and decreasing pH may alter phytoplankton communities directly at many levels, from physiological processes to nutrient requirements and community structure. For instance, experimental and comparative analyses (e.g., (40−42)) show that warmer temperatures lead to reduced mean cell size and a shift from diatoms to cyanobacteria,(43) which could reduce the removal of microalgal biomass by grazers under a warmer climate (e.g., (42)). Increasing genus richness stimulates the resource use efficiency of the phytoplankton community.(44) Large-scale changes in the food web structure and function of coastal ecosystems derived from overfishing and excess harvest of filter feeders, both global phenomena, erode ecosystem buffers and triggers increased phytoplankton biomass enhancing the vulnerability of coastal ecosystems to eutrophication (e.g., (45−47)). For example, Casini et al.(48) showed that cod overfishing in the Baltic Sea led to decreases in zooplankton through trophic cascades, alleviating the grazing pressure on phytoplankton. Eutrophication and overfishing may lead to proliferation of jellyfish altering the food-web through increasing predation on protists and thus reducing the pelagic grazing pressure on phytoplankton.(49)
The parallel trend toward increase in Chla yield per unit nitrogen over the past decade in all regions examined here could be the result of the major shift in the baselines for the functioning of coastal ecosystems resulting from the combined effects of climate change, overfishing, and, possibly, other components of global change. Whereas the trajectories of individual ecosystems in Chla–TN plots appear idiosyncratic, the coherent trend in the residuals and the general increase in the yield of Chla per unit nitrogen over time indicate that there is a common, underlying shift in ecosystem baselines affecting the behavior of individual ecosystems, rendering the relationship between Chla and TN dynamic over time.
Ecosystem Management with Shifting Baselines
The departure of individual ecosystems from the general relationship between Chla and TN derived from global comparative analyses calls for a reconsideration of the predictive tools underpinning management actions. Trends in the yield of Chla per unit nitrogen over time results in a bias in the prediction of Chla concentration as the intercept of the relationship between Chla and TN concentration shifts over time. Hence, regression equations produced during the eutrophication phase in the late 1980s generally underestimated the Chla concentration corresponding to more recent and lower TN concentrations obtained during the oligotrophication phase. Moreover, the apparent idiosyncrasy of Chla vs TN relationships among systems, reflected in a range of slopes and intercepts of Chla vs TN regressions among coastal areas (Table 3, Figure 4), could partially result from shifting Chla to TN ratios over time. The shift in the functional relationship between Chla and TN over time demonstrated here helps explain the reported failure to revert eutrophied coastal ecosystems to their previous state following reduction of nutrient inputs.(10) This calls for a reconsideration of our conceptual model of eutrophication to face the complexity of the operating factors, differences between coastal ecosystems,(8) regime shifts, and shifting baselines.(10)
Persistent eutrophication may sustain elevated Chla through feedback mechanisms significantly altering ecosystem functions, potentially leading to hysteresis in the pressure–response relationship.50,51 Feedbacks associated with eutrophication-enhanced hypoxia could lead to hysteresis through disrupting benthic food webs, alleviating benthic grazing pressure on phytoplankton, and stimulating nitrogen-fixing cyanobacteria blooms through the release of sediment phosphate.52−54 In fact, Chesapeake Bay and the Danish coastal sites have experienced seasonal hypoxia of increasing extent throughout the study period22,23 that could explain changes in the Chla:TN ratios for these two regions. Feedback mechanisms enhanced through persistent eutrophication may be potentially reversible over time and must be considered together with shifting baselines in predicting Chla responses to reduced nutrient inputs.
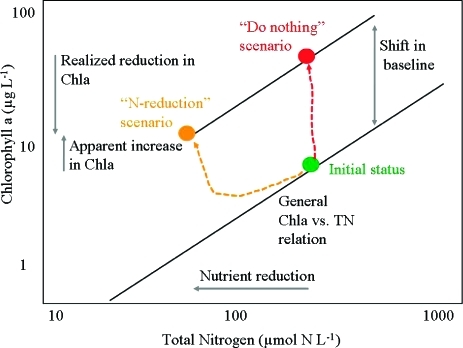
Whereas the lack of reduction in Chla concentrations following nutrient reductions demonstrated here may be disturbing to managers, our analysis contains important lessons that can help improve the design and assessment of managerial actions. The effectiveness of responses in Chla concentration following nutrient reduction plans should not be assessed relative to the Chla concentration at the time nutrient reduction was initiated but relative to the Chla concentration the ecosystem would support if nutrients had not been controlled. This rationale is illustrated in Figure 7, which considers what would be the trajectory of a hypothetical coastal area under two scenarios: (1) a “do nothing” scenario, where nutrient concentrations do not change over time and where the ecosystem will exhibit a trajectory that departs from the general regression line to occupy a position of increased Chla due to the increase in the yield of chlorophyll per unit nitrogen over time, and (2) a “nutrient reduction” scenario, where the ecosystem will follow a trajectory that leads to an increase in Chla relative to the initial state, due to the increase in the yield of chlorophyll per unit nitrogen, but that in fact represents a reduction in the realized Chla concentration relative to the “do nothing” scenario (Figure 7). The key message underlying this conceptual model is that shifting baselines imply that the present state of the system is not an adequate reference to evaluate the effectiveness of nutrient reduction plans, as the future status of the ecosystem would differ from that at present under a “do nothing” scenario. Moreover, the confidence of Chla predictions for nutrient reduction scenarios will weaken, as the uncertainty of predicting the shifting baselines has to be included as well. Trajectories of recovery are even more complex in the potential presence of hysteresis responses,10,55 and declining Chla could result from small changes in nutrient inputs if a proper functioning of the coastal ecosystem is reestablished. Thus, despite observed increases in Chla concentrations it is still important to stress that nutrient reductions do release pressure on the ecosystem and improve conditions relative to what these would have been under a “do nothing” scenario.
Figure 7.
Conceptual model demonstrating the implications of shifts in the yield of Chlorophyll a per unit total nitrogen in coastal ecosystems for the evaluation of the outcome of managerial actions to reduce nitrogen concentrations. The possible outcomes of two alternative strategies, “do nothing” and “nutrient reduction”, are shown.
Provided the importance of changing baselines for the setting and evaluation of actions to reverse eutrophication, it is fundamental that our understanding of the causes of such shift in baselines improves to allow forecasting the trajectories of individual coastal ecosystems. A better understanding of the dynamics of coastal ecosystems forced by both changes in nutrient inputs, derived from factors operating at the basin scale, and shifting baselines derived from forces operating at various scales is fundamental to achieve this goal. This requires a research agenda that faces the complex interactions, operating at multiple levels, controlling the variability in the yield of chlorophyll per unit nitrogen over time. The mechanisms leading to shifts in the yield of chlorophyll per unit nitrogen must be investigated under a range of scales, from physiological experiments, to investigate the responses to increasing CO2 and temperature, to mesocosm scales where effects from changes in food webs can be investigated. These experiments should be supplemented by modeling efforts, specifically addressing shifting baselines and regime shifts (e.g., (56)), to synthesize experimental results at the ecosystem scale and improve predictions of nutrient management. This research agenda must also include research on trajectories at the ecosystem level involving the investigation of replicated experimental coastal ecosystems, subject to deliberate manipulation of nutrients, over decadal time scales such as those included in this study. This approach is comparable to long-term whole-ecosystem experiments conducted at the Experimental Lakes Area in Canada(57) or the Hubbard Brook watersheds,(58) but should involve longer time scales and improved replication. Only these large-scale experiments, conducted at the ecosystem level and sustained over long time scales, hold the power, when supported by mechanistic understanding, to resolve the forces driving complex trajectories of coastal ecosystems through time necessary to gain the capacity to forecast them with sufficient accuracy, a precondition for effective management.
The results presented here confirm that the expectation that the response of coastal ecosystems to increasing or decreasing nutrient concentrations can be predicted from a single general relationship is unsupported. In particular, the results presented provide evidence for idiosyncratic Chla–TN relationships for individual ecosystems and suggest that much of the variability in the trajectories and Chla–TN relationships among individual systems derives from consistent shifts in the yield of chlorophyll per unit nitrogen. These shifts, derived from large-scale forcing likely associated with global change, imply that future Chla concentration in coastal areas cannot be predicted from current Chla–nutrient relationships. These results indicate that ecological sciences must progress to face uncertainty and shifting baselines and be able to operate with relative, rather than absolute, predictions and targets. The challenge of our times governed by global change rests in that, as the French poet Paul Valery put it, “the future is no longer what it used to be”.
Acknowledgments
This research is a contribution to the Thresholds Integrated Project (contract FP6-003933-2) and WISER (contract FP7-226273), funded by the European Commission. D.K.-J. was also funded by the Danish Agency for Science, Technology and Innovation. We thank Jens Würgler Hansen, Timo Tamminen, Holly Greening, Jim Cloern, and Scott Nixon for comments on earlier versions of the paper as well as Emilio Agustí for encouragement, challenging insights, and discussion.
Supporting Information Available
Figures S1 and S2. This material is available free of charge via the Internet at http://pubs.acs.org.
Supplementary Material
References
- Nixon S. W. Coastal marine eutrophication - A definition, social causes, and future concerns. Ophelia 1995, 41, 199–219. [Google Scholar]
- Vitousek P. M.; Mooney H. A.; Lubchenco J.; Melillo J. M. Human domination of Earth’s ecosystems. Science 1997, 277, 494–499. [Google Scholar]
- Vidal M.; Duarte C. M.; Sanchez M. C. Coastal eutrophication research in Europe: Progress and imbalances. Mar. Pollut. Bull. 1999, 38, 851–854. [Google Scholar]
- Boesch D. F. Challenges and opportunities for science in reducing nutrient over-enrichment of coastal ecosystems. Estuaries 2002, 25, 886–900. [Google Scholar]
- Duarte C. M. Submerged aquatic vegetation in relation to different nutrient regimes. Ophelia 1995, 41, 87–112. [Google Scholar]
- Costanza R.; d’Arge R.; de Groot R.; Farber S.; Grasso M.; Hannon B.; Limburg K.; Naeem S.; O’Neill R. V.; Paruelo J.; Raskin R. G.; Sutton P.; van den Belt M. The value of the world’s ecosystem services and natural capital. Nature 1997, 387, 253–260. [Google Scholar]
- Nixon S. W. Eutrophication and the macroscope. Hydrobiologia 2009, 629, 5–19. [Google Scholar]
- Cloern J. E. Our evolving conceptual model of the coastal eutrophication problem. Mar. Ecol.: Prog. Ser. 2001, 210, 223–253. [Google Scholar]
- Carstensen J.; Conley D. J.; Andersen J. H.; Aertebjerg G. Coastal eutrophication and trend reversal: A Danish case study. Limnol. Oceanogr. 2006, 51, 398–408. [Google Scholar]
- Duarte C. M.; Conley D. J.; Carstensen J.; Sánchez-Camacho M. Return to Neverland: Shifting baselines affect eutrophication restoration targets. Estuaries Coasts 2009, 32, 29–36. [Google Scholar]
- Guildford S. J.; Hecky R. E. Total nitrogen, total phosphorus, and nutrient limitation in lakes and oceans: Is there a common relationship?. Limnol. Oceanogr. 2000, 45, 1213–1223. [Google Scholar]
- Hoyer M. V.; Frazer T. K.; Notestein S. K.; Canfield D. E. Jr. Nutrient, chlorophyll, and water clarity relationships in Florida’s nearshore coastal waters with comparisons to freshwater lakes. Can. J. Fish. Aquat. Sci. 2002, 59, 1024–1031. [Google Scholar]
- Smith V. Responses of estuarine and coastal marine phytoplankton to nitrogen and phosphorus enrichment. Limnol. Oceanogr. 2006, 51, 377–384. [Google Scholar]
- Sakamoto M. Primary production by phytoplankton community in some Japanese lakes and its dependence on lake depth. Arch. Hydrobiol. 1966, 62, 1–28. [Google Scholar]
- Vollenweider R. A.Scientific Fundamentals of the Eutrophication of Lakes and Flowing Waters with Particular Reference to Nitrogen and Phosphorus As Factors of Eutrophication; Organisation for Economic Cooperation and Development Technical Report DA S/SCI/68.27.250; OECD: Paris, 1968. [Google Scholar]
- Dillon P. J.; Rigler F. H. The phosphorus–chlorophyll relationship in lakes. Limnol. Oceanogr. 1974, 19, 767–773. [Google Scholar]
- Nixon S. W.; Pilson M. E. Q.; Oviatt C. A.; Donoghay P.; Sullivan B.; Seitzinger S.; Rudnick D.; Frithsen J.. Eutrophication of a coastal marine ecosystem - An experimental study using MERL microsoms. In Flows of Energy and Materials in Marine Ecosystems; Fasham M. J. R., Ed.; Theory and Practice; Plenum Press: New York, 1984; pp 105–135. [Google Scholar]
- Nixon S. W.; Oviatt C. A.; Frithsen J.; Sullivan B. Nutrients and the productivity of estuarine and coastal marine ecosystems. J. Limnol. Soc. South Africa. 1986, 12, 43–71. [Google Scholar]
- Olsen Y.; Agustí S.; Andersen T.; Duarte C. M.; Gasol J. M.; Gismervik I.; Heiskanen A.-S.; Hoell E.; Kuuppo R.; Lignell R.; Reinertsen H.; Sommer U.; Stibor H.; Tamminen T.; Vadstein O.; Vaqué D.; Vidal M. A comparative study of responses in plankton food web structure and function in contrasting European coastal waters exposed to experimental nutrient addition. Limnol. Oceanogr. 2006, 51, 488–503. [Google Scholar]
- Meeuwig J. J.; Kauppila P.; Pitkänen H. Predicting coastal eutrophication in the Baltic: A limnological approach. Can. J. Fish. Aquat. Sci. 2000, 57, 844–855. [Google Scholar]
- Fisher T. R.; Gustafsson G. A.; Sellner K.; Lacouture R.; Haas L. W.; Wetzel R. L.; Magnien R.; Everitt D.; Michaels B.; Karrh R. Spatial and temporal variation of resource limitation in Chesapeake Bay. Mar. Biol. 1999, 133, 763–778. [Google Scholar]
- Kemp W. M.; Boynton W. R.; Adolf J. E.; Boesch D. F.; Boicourt W. C.; Brush G.; Cornwell J. C.; Fisher T. R.; Glibert P. M.; Hagy J. D.; Harding L. W.; Houde E. D.; Kimmel D. G.; Miller W. D.; Newell R. I. E.; Roman M. R.; Smith E. M.; Stevenson J. C. Eutrophication of Chesapeake Bay: Historical trends and ecological interactions. Mar. Ecol.: Prog. Ser. 2005, 303, 1–29. [Google Scholar]
- Conley D. J.; Kaas H.; Møhlenberg F.; Rasmussen B.; Windolf J. Characteristics of Danish estuaries. Estuaries 2000, 23, 820–837. [Google Scholar]
- Carstensen J.; Henriksen P.; Heiskanen A.-S. Summer algal blooms in shallow estuaries: Definition, mechanisms, and link to eutrophication. Limnol. Oceanogr. 2007, 52, 370–384. [Google Scholar]
- Greening H.; Janicki A. Toward reversal of eutrophic conditions in a subtropical estuary: water quality and seagrass response to nitrogen loading reductions in Tampa Bay, USA. Environ. Manage. 2006, 38, 163–178. [DOI] [PubMed] [Google Scholar]
- Philippart C. J. M.; Cadée G. C.; van Raaphorst W.; Riegman R. Long-term phytoplankton–nutrient interactions in a shallow coastal sea: Algal community structure, nutrient budgets, and denitrification potential. Limnol. Oceanogr. 2000, 45, 131–144. [Google Scholar]
- Colijn F.; Cadée G. C. Is phytoplankton growth in the Wadden Sea light or nitrogen limited?. J. Sea Res. 2003, 49, 83–93. [Google Scholar]
- Jørgensen B. B.Material flux in the sediment. In Eutrophication in Coastal Marine Ecosystems; Jørgensen B. B., Richardson K., Eds.; American Geophysical Union: Washington, DC, 1996; pp 115–135. [Google Scholar]
- Mackas D. L.; Harrison P. J. Nitrogenous nutrient sources and sinks in the Juan de Fuca Strait/Strait of Georgia/Puget Sound estuarine system: Assessing the potential for eutrophication. Estuar. Coast Shelf. Sci. 1997, 44, 1–21. [Google Scholar]
- Carstensen J.; Conley D. J.; Müller-Karulis B. Spatial and temporal resolution of carbon fluxes in a shallow coastal ecosystem. Mar. Ecol.: Prog. Ser. 2003, 252, 35–50. [Google Scholar]
- Borum J.Shallow waters and land/sea boundaries. In Eutrophication in Coastal Marine Ecosystems; Jørgensen B. B., Richardson K., Eds.; American Geophysical Union: Washington, DC, 1996; pp 179–203. [Google Scholar]
- Carstensen J.; Henriksen P. Phytoplankton biomass response to nitrogen inputs: a method for WFD boundary setting applied to Danish coastal waters. Hydrobiologia 2009, 633, 137–149. [Google Scholar]
- Downing J. A. Marine nitrogen:phosphorus stoichiometry and the global N:P cycle. Biogeochemistry 1997, 37, 237–252. [Google Scholar]
- Howarth R. W.; Marino R. Nitrogen as the limiting nutrient for eutrophication in coastal marine ecosystems: Evolving views over 3 decades. Limnol. Oceanogr. 2006, 51, 364–376. [Google Scholar]
- Conley D. J.; Paerl H. W.; Howarth R. W.; Boesch D. F.; Seitzinger S. P.; Havens K. E.; Lancelot C.; Likens G. E. Controlling Eutrophication: Nitrogen and Phosphorus. Science 2009, 323, 1014–1015. [DOI] [PubMed] [Google Scholar]
- Prairie Y.-T.; Duarte C. M.; Kalff J. Unifying nutrient-chlorophyll relationships in lakes. Can. J. Fish. Aquat. Sci. 1989, 46, 1176–1182. [Google Scholar]
- Nixon S. W.; Buckley B.; Granger S.; Bintz J. Responses of very shallow marine ecosystems to nutrient enrichment. Hum. Ecol. Risk. Assess. 2001, 7, 1457–1481. [Google Scholar]
- Monbet Y. Control of phytoplankton biomass in estuaries: A comparative analysis of microtidal and macrotidal estuaries. Estuaries 1992, 15, 563–571. [Google Scholar]
- Petersen J. K.; Hansen J. W.; Laursen M. B.; Clausen P.; Carstensen J.; Conley D. J. Regime shift in a coastal marine ecosystem. Ecol. Appl. 2008, 18, 497–510. [DOI] [PubMed] [Google Scholar]
- Agawin N. S. R.; Duarte C. M.; Agustí S. Growth and abundance of Synechococcus sp. in a Mediterranean Bay: Seasonality and relationship with temperature. Mar. Ecol.: Prog. Ser. 1998, 170, 45–53. [Google Scholar]
- Agawin N. S. R.; Duarte C. M.; Agustí S. Nutrient and temperature control of the contribution of picoplankton to phytoplankton biomass and production. Limnol. Oceanogr. 2000, 45, 591–600. [Google Scholar]
- Sommer U.; Lengfellner K. Climate change and the timing, magnitude, and composition of the phytoplankton spring bloom. Global Change Biol. 2008, 14, 1199–1208. [Google Scholar]
- Paerl H. W.; Huisman J. Blooms like it hot. Science 2008, 320, 57–58. [DOI] [PubMed] [Google Scholar]
- Ptacnik R.; Solimini A. G.; Andersen T.; Tamminen T.; Brettum P.; Lepistö L.; Willén E.; Rekolainen S. Diversity predicts stability and resource use efficiency in natural phytoplankton communities. Proc. Natl. Acad. Sci., U.S.A. 2008, 105, 5134–5138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Officer C.; Smayda T.; Mann R. Benthic filter feeding: A natural eutrophication control. Mar. Ecol.: Prog. Ser. 1982, 9, 203–210. [Google Scholar]
- Daskalov G. M.; Grishin A. N.; Rodionov S.; Mihneva V. Trophic cascades triggered by overfishing reveal possible mechanisms of ecosystem regime shifts. Proc. Natl. Acad. Sci., U.S.A. 2007, 104, 10518–10523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heck K. L.; Valentine J. F. The primacy of top-down effects in shallow benthic ecosystems. Estuaries Coasts 2007, 30, 371–381. [Google Scholar]
- Casini M.; Lövgren J.; Hjelm J.; Cardinale M.; Molinero J.-C.; Kornilovs G. Multi-level trophic cascades in a heavily exploited open marine ecosystem. Proc. R. Soc. B 2008, 275, 1793–1801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson A. J.; Bakun A.; Hays G. C.; Gibbons M. J. The jellyfish joyride: Causes, consequences and management responses to a more gelatinous future. Trends Ecol. Evol. 2009, 24, 312–322. [DOI] [PubMed] [Google Scholar]
- Scheffer M.; Carpenter S.; Foley J. A.; Folke C.; Walker B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [DOI] [PubMed] [Google Scholar]
- Scheffer M.; Carpenter S. Catastrophic regime shifts in ecosystems: Linking theory to observation. Trends Ecol. Evol. 2003, 18, 648–656. [Google Scholar]
- Vahtera E.; Conley D. J.; Gustafsson B. G.; Kuosa H.; Pitkänen H.; Savchuk O. P.; Tamminen T.; Viitasalo M.; Voss M.; Wasmund N.; Wulff F. Internal ecosystem feedbacks enhance nitrogen-fixing cyanobacteria blooms and complicate management in the Baltic Sea. Ambio 2007, 36, 186–193. [DOI] [PubMed] [Google Scholar]
- Diaz R. J.; Rosenberg R. Spreading dead zones and consequences for marine ecosystems. Science 2008, 321, 926–929. [DOI] [PubMed] [Google Scholar]
- Conley D. J.; Björck S.; Bonsdorff E.; Carstensen J.; Destouni G.; Gustafsson B. G.; Hietanen S.; Kortekaas M.; Kuosa H.; Meier H. E. M.; Müller-Karulis B.; Nordberg K.; Norkko A.; Nürnberg G.; Pitkänen H.; Rabalais N. N.; Rosenberg R.; Savchuk O. P.; Slomp C. P.; Voss M.; Wulff F.; Zillén L. Hypoxia-related processes in the Baltic Sea. Environ. Sci. Technol. 2009, 43, 3412–3420. [DOI] [PubMed] [Google Scholar]
- Kemp W. M.; Testa J. M.; Conley D. J.; Gilbert D.; Hagy J. D. Temporal responses of coastal hypoxia to nutrient loading and physical controls. Biogeosciences 2009, 6, 2985–3008. [Google Scholar]
- Liu Y.; Evans M A.; Scavia D. Gulf of Mexico hypoxia: Exploring increasing sensitivity to nitrogen loads. Environ. Sci. Technol. 2010, 44, 5836–5841. [DOI] [PubMed] [Google Scholar]
- Schindler D. W. Eutrophication and recovery in experimental lakes: Implications for lake management. Science 1974, 184, 897–899. [DOI] [PubMed] [Google Scholar]
- Likens G. E.; Bormann F. H.; Johnson N. M.; Fisher D. W.; Pierce R. S. Effects of forest cutting and herbicide treatment on nutrient budgets in the Hubbard Brook watershed ecosystem. Ecol. Monogr. 1970, 40, 23–47. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.