Design and Control of a 1-DOF MRI Compatible Pneumatically Actuated Robot with Long Transmission Lines

Abstract

This paper presents the design and control of an MRI-compatible 1-DOF needle driver robot and its precise position control using pneumatic actuation with long transmission lines. MRI provides superior image quality compared to other imaging modalities such as CT or ultrasound, but imposes severe limitations on the material and actuator choice (to prevent image distortion) due to its strong magnetic field. We are primarily interested in developing a pneumatically actuated breast biopsy robot with a large force bandwidth and precise targeting capability during radio-frequency ablation (RFA) of breast tumor, and exploring the possibility of using long pneumatic transmission lines from outside the MRI room to the device in the magnet to prevent any image distortion whatsoever. This paper presents a model of the entire pneumatic system. The pneumatic lines are approximated by a first order system with time delay, because its dynamics are governed by the telegraph equation with varying coefficients and boundary conditions, which cannot be solved precisely. The slow response of long pneumatic lines and valve subsystems make position control challenging. This is further compounded by the presence of non-uniform friction in the device. Sliding mode control (SMC) was adopted, where friction was treated as an uncertainty term to drive the system onto the sliding surface. Three different controllers were designed, developed, and evaluated to achieve precise position control of the RFA probe. Experimental results revealed that all SMCs gave satisfactory performance with long transmission lines. We also performed several experiments with a 3-DOF fiber-optic force sensor attached to the needle driver to evaluate the performance of the device in the MRI under continuous imaging.

I. Introduction

Magnetic Resonance Imaging (MRI) technique has been gaining popularity in recent years, especially in clinical diagnosis, due to its superior imaging capabilities compared to CT or ultrasound. A recent study reported in [1] stated that MRI helps to detect cancer in the contralateral breast that was otherwise missed by mammography and clinical examination (negative predictive value of the cancer using MRI was 99%). A more recent study concluded that MRI can improve the ability to diagnose Ductal Carcinoma in-situ (DCIS) with high nuclear grade [2]. Furthermore, another recent study demonstrated that the higher field strength of 3.0 Tesla provided an overall better image quality and differential diagnosis of enhancing lesions was possible with higher diagnostic confidence at the higher field strength of 3.0 Tesla [3]. This strongly suggests the need for using MRI as a detection tool for breast cancer. Furthermore, coupling diagnosis with MRI based biopsy will lead to better delineation of the tumor margin.

With its superior imaging capability, MRI is also gaining popularity as an interventional tool to guide the interventional device precisely to the appropriate target. Several researchers have developed different MRI-compatible surgical robotic systems, and some of them have been used in clinical trials [4]–[7]. Stoianovici et al. [6] developed a pneumatically actuated robot for prostate interventions based on a newly invented pneumatic motor; Fischer et al. [8] designed a pneumatically operated MRI-compatible needle placement robot for prostate interventions; Zemiti et al. [9] developed a CT and MR-compatible robot for abdominal and thoracic punctures with specially designed pneumatic motor, and Kokes et al. [7] developed a 1-DOF MRI-compatible robot for RFA of breast tumor using hydraulic actuation.

The working principle of MRI requires strong magnetic field ranging from 1.5T up to 7T; therefore, ferromagnetic materials are strictly prohibited inside the MRI. Apart from ferromagnetic materials, several other metals are also not used in the MRI, since they can produce significant artifacts in the image. The strong magnetic field also limits the actuation techniques that can be used in MRI. Traditional electrical motors are no longer usable, since they are based on electromagnetic effect. The magnetic field generated by the motors interferes with the homogeneous magnetic field in the MRI bore, and hence, degrades the image quality; needless to say that these motors are attracted by the strong magnetic field, and become harmful projectile for the MRI machine as well as the personnel in the room. Several actuation techniques suitable for MRI environment are summarized in a survey paper by Elhawary et al. [10]. The majority of MRI-compatible actuation techniques fall into four categories: remote manual actuation, ultrasonic/Piezo motors, hydraulic transmission, and pneumatic transmission.

Among all four methods, remote manual actuation renders slower procedure and lower resolution [10]. For ultrasonic/Piezo motors, the image quality can not be guaranteed, since the piezoceramic elements are often embedded inside ferrous materials [10]. Also, ultrasonic/Piezo motors cause moderate signal noise ratio (SNR) loss when in motion, since they are operated with high-frequency electrical signals [6], [11], and should not be operated while imaging [12]. Hydraulic and pneumatic actuation techniques on the other hand offer the advantage of maintaining a high SNR [13]. Pneumatic actuation is back drivable and natural impedance due to the compressibility of air makes it more favourable for fast or force-control applications. Furthermore, pneumatic system is easier to maintain compared to hydraulic system, since hydraulic systems can suffer from cavitation and fluid leakage. Therefore, we chose to adopt pneumatic actuation in our experimental prototype.

In the 1990’s, Ben-Dov et al. [14] presented a force-controlled pneumatic actuator in a teleoperation application. Richer et al. [15] developed a detailed mathematical model of pneumatics, based on which, a high performance pneumatic force-controller using sliding mode control was developed [16]. Zhu et al. [17] has implemented impedance control for a linear pneumatic actuator for contact tasks. Several approaches have also been explored to reduce the cost of the pneumatic system. Wu et al. [18] studied the observability of the pneumatic system with the hope of replacing expensive pressure sensors. This work was followed by a nonlinear observer design that estimated the pressure information in the pneumatic system and worked with a robust observer-based controller to obtain a low-cost precision pneumatic servo system, presented by Gulati et al. [19]. Barth et al. [20] implemented a sliding mode controller in a pneumatic system, with on-off solenoid valves using PWM-control techniques.

In traditional pneumatic systems, valves were placed close to the cylinders to avoid the influence of transmission line dynamics and the pneumatic control problem focused on the nonlinearity of traditional proportional mass flow rate valves and the pressure dynamics in the cylinder chambers. Most controllers aimed at force control, and neglected the friction effect on piston motion. To make the pneumatic system MRI-compatible, the parts that will be within the MRI have to be built with MRI-compatible materials, and the non compatible materials have to be placed away from the MRI, preferably inside the control room. Since the commercially available pressure sensors and proportional valves are not MRI compatible, they have to be placed away from the magnet in our application. Hence, long pneumatic transmission lines up to 9 meters are unavoidable. Such long transmission lines can significantly slow down the pressure response from the valve input to the cylinder chamber pressure, because it takes time not only for the pressure wave to travel from one end of the transmission line to the other but also takes time for the pressure to build up, since the volume of the transmission lines is non-negligible and the system mass flow rate delivery capability is not unlimited. Also, the material limitation requires the structure of the pneumatic device be built with high strength polymer material. However, due to the inherent material characteristic of polymers, non-uniform (position dependent) friction with static friction significantly higher than dynamic friction, is present in our device. This makes precise position control extremely challenging.

In this paper, an MRI-compatible 1-DOF prototype device is developed, using pneumatic actuation with long transmission lines. In addition to modeling the system, we have designed, implemented, and evaluated three controllers using sliding mode control, for precise position control of the needle in the MRI. The paper is organized as follows. In Section II, the 1-DOF prototype device is described, including the pneumatic system and the control hardware. Model for this system is presented in Section III and controller design is described in Section IV. Section V gives experimental results of all the controllers implemented and Section VI gives MRI-compatibility results. Finally, concluding remarks are made in Section VII.

II. MRI-Compatible Pneumatic System

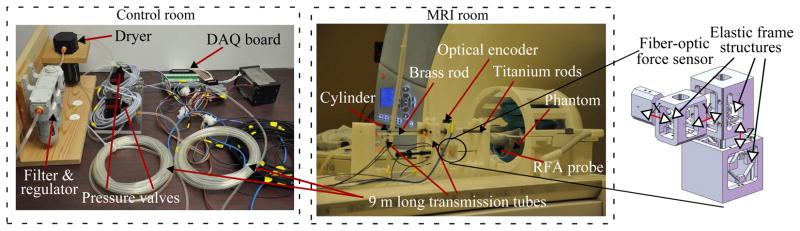
To evaluate pneumatic controllers in the MRI, we have built an MRI-compatible 1-DOF prototype pneumatic system, as is shown in Figure 1.

Fig. 1.

MRI-compatible 1-DOF prototype pneumatic system. The center image shows the experimental setup inside the MRI; all equipment that is not MRI-compatible has been place inside the control room; the right image shows the 3-D fiber-optic force sensor.

A. 1-DOF Prototype Pneumatic System

The structure of the 1-DOF device was built using polymer materials (mainly Derlin^®) to ensure MRI-compatibility. The guiding rods are made of titanium, a known MRI-compatible metal. The iglide^® M250 linear bearing was used with the slider, to which the cylinder brass rod was attached. The specially designed MRI-compatible 3-D fiber optic force sensor [21] was attached beneath the slider. An MRI compatible RFA needle was attached to the force sensor to measure the needle insertion forces in the MRI. The position of the needle was measured with the optical encoder (LIN-500-10-N, EM1-0-500, US Digital) and the encoder signal was transmitted through a long shielded cable that passed through the filter panel of MRI room with cable driver (PC5-H10, US Digital). The pneumatic cylinder had 152.4mm (6 in) stroke and was made of non-magnetic anti-stiction material (AC-13270-3, Airpot^®). The only metal, brass (Alloy 360), was used to make the rod, and we tested the cylinder in the MRI and saw no significant image artifacts. The two pneumatic transmission lines were 9 meters in length with 3.175mm (1/8 in) inner diameter (ID). The two Piezo pressure proportional valves were purchased from Hoerbiger^™(Tecno plus), with nominal reaction time of less than 10ms. The total mass load of the pneumatic system including cylinder piston-rod, slider, force sensor, optical encoder and RFA needle is about 0.675Kg. All measurements were sampled through the Sensoray data acquisition (DAQ) card (Model 626) and the controller was implemented in a Linux PC (Intel^® P4 1.8GHz CPU and 512MB Memory) with 500Hz sampling rate.

B. 3-D Fiber-Optic Force Sensor

Force sensor was included in this system to sense the force of needle insertion so that haptic feedback can help the surgeon perform the needle insertion tasks. Due to the working principle of MRI, a number of conventional force sensors are not compatible. Hence, a 3-D MRI-compatible fiber optic force sensor is designed and developed for this application [21]. Light is transmitted via optical cables to and back from the force sensor. A force acting on the force sensor will cause a deformation in the elastic frame structure and by monitoring the change in the reflected light intensity, the force can be computed. All the non-MRI compatible equipment is located in the control room and will not affect the MR image quality.

The force sensor consists of three prismatic joints, with a pair of elastic frame structures attached to each prismatic joint, as shown in the right of Figure 1. A normal process of developing the elastic frame structure usually starts with the designing of the mechanism, followed by simulation like finite element analysis before the prototype is built. The initial design phase is often the most challenging and depends greatly on experience and creativity. It is desired that there is a systematic way of designing the elastic frame structure and hence, a topology optimization technique that is able to aid the designing process is used. Maximizing the output-input displacement gain is also incorporated in the objective function too. This will result in better resolution, higher stiffness (less movement at the loading point), and larger bandwidth.

In the prototype that was developed, plastic material (ABS, Acrylonitrile Butadiene Styrene) is used for the elastic frame structure. Plastic materials, while ideal for MRI, are known for their hysteretic force-deformation characteristic. To account for this hysteretic effect, Prandtl-Ishlinskii play operator is used to model the hysteresis. All the details on the 3-D fiber optic force sensor design, development, and evaluation are presented in [21].

III. Model of the Pneumatic Actuation System

To design and evaluate controllers for the pneumatic actuation system, a model has to be developed. The model of the system was comprised of four parts: valve model, transmission line model, piston-load model, and friction model.

A. Valve model

The valves we used in our system were pressure proportional valves. Compared to mass flow rate proportional valves, pressure valves avoid not only the nonlinearity of orifice mass flow rate, but also the requirement of pressure sensor or pressure observer for cylinder chamber pressure information. Since the inner mechanism of the valve is unknown, we approximated the valve as a first order system based on experimental data. The valve model is thus given by:

$$\frac{P_v(s)}{u(s)}=\frac{0.8s+50}{s+50}$$ (1)

where P_v is the valve output pressure and u is the valve input voltage. This model gives good approximation of real valve step response, as shown in Figure 2.

Fig. 2.

Actual and model step response comparison for valve and 9 meters pneumatic transmission line

B. Transmission line model

As mentioned in [15], the basic differential equations governing the air flow in the tube was first derived in [22] as:

$$\frac{\partial P}{\partial l}=-R_{t}v-\rho \frac{\partial v}{\partial t}$$ (2)

$$\frac{\partial v}{\partial l}=-\frac{1}{\rho c^2}\frac{\partial P}{\partial t}$$ (3)

where P, v and ρ are the air pressure, velocity and density distribution along the transmission line direction l at time t, respectively; R_t is the tube resistance; and c is the speed of sound. A schematic of the pneumatic transmission line is shown in Figure 3.

Fig. 3.

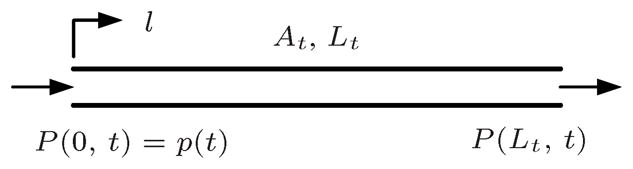
Schematic of the pneumatic transmission line

After some algebraic manipulation, we can show that both P and v satisfy the following second order partial differential equation about z = {v, P}:

$$\frac{{\partial }^{2}z}{\partial l^2}-\frac{1}{c^2}\frac{{\partial }^{2}z}{\partial t^2}-\frac{R_t}{\rho c^2}\frac{\partial z}{\partial t}=0$$ (4)

but with different initial values and boundary conditions.

This is the famous telegraph equation and significant work has been done in this area to get the solution to the above equation under different initial and boundary conditions. In 1950s, Goldstein [23] found two analytical solutions to the telegraph equation by studying the physical phenomenon of diffusion with discontinuous movements. The two solutions have same zero initial condition but with different boundary conditions: one is with a step function as the boundary condition and the other is with a pulse function. This is quite similar to studying the pressure dynamics of transmission lines, but both solutions are so complicated that it is difficult to evaluate them analytically or numerically. Numerical algorithms have been developed by some researchers but none of them give solutions simple enough to be used for controller design or simulation purposes [24], [25]. Furthermore, the solution to the telegraph equation does not necessarily characterize the dynamics of pressure in the transmission line, due to three factors: Firstly, the telegraph equation characterizes pressure dynamics for open end transmission line with fixed boundary conditions. In the real pneumatic system, the boundary condition at the end of the transmission line changes as the pressure builds up in the cylinder chamber. Secondly, the air density, ρ, is a function of both time t and the location x, and is included in the coefficients of the telegraph equation. Thus, the dynamics of the pressure along the transmission line is the solution to the telegraph equation with time varying boundary conditions and varying coefficients in the partial differential equation that are dependent on the solution itself. Finally, the derivation of telegraph equation is based on the assumption that there is no reflection or resonance in the transmission line, which is not the case for a transmission line connected to a closed volume as in our experimental system.

Due to the above challenges, we approximated the 9 meters transmission line dynamics as a first order system with time delay, which represents the pressure build up process at the end of the transmission line and the pressure propagation along the transmission line, respectively. This is given by:

$$\frac{P_o(s)}{P_i(s)}=\frac{0.25s+32}{s+32}{e}^{-0.0265s}$$ (5)

where P_o is the output pressure and P_i is the input pressure. The time delay is determined as the ratio of the transmission line length and the speed of sound, i.e. L_t/c. This model closely characterizes the actual transmission line step response, as is shown in Figure 2.

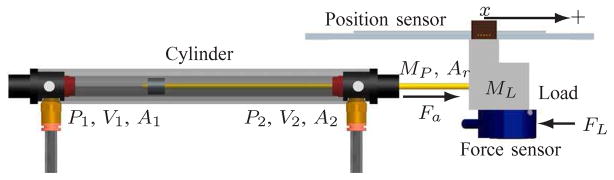
C. Piston-load model

The structure of the cylinder is shown in Figure 4, and the dynamics of the cylinder was modeled as:

$$M\ddot{x}=P_1{A}_1-P_2{A}_2-P_a{A}_r+F_L+F_f$$ (6)

where M is the total mass of the piston-rod, the slider, the needle, and the force sensor; x is the position of the slider; P₁, A₁ and P₂, A₂ are the pressure and the effective cross sectional area of both chambers; P_a is the atmosphere pressure; A_r is the effective cross-sectional area of the rod; F_L is the external force, and F_f is the total frictional force.

Fig. 4.

Schematic representation of the piston-load subsystem

Since we are using proportional pressure valves, we can directly use the two chamber pressures P₁ and P₂ as the control variables. Hence the desired position was the only command input variable, and we simplified the problem by assuming that the pressure in both chambers is 275.8 kPa (40 psi) at steady state and we used the pressure deviation as control input, i.e., P₁ = 275.8 + u and P₂ = 275.8 − u. Thus, we can rewrite the above equation as:

$$M\ddot{x}=(A_1+A_2)u+(275.8-P_a)A_r+F_L+F_f$$ (7)

Since the external force F_L can be measured by a force sensor, and (275.8 − P_a)A_r is a known constant, the model can be further simplified as:

$$M\ddot{x}=(A_1+A_2)u^{\prime }+F_f$$ (8)

where u′ = u+u₀, and u₀ = [(275.8 − P_a)A_r + F_L]/(A₁ + A₂) is known.

D. Friction model

Friction is an interacting force between objects in contact with relative motion and it directly affects the system stability and position accuracy. A detailed discussion on friction can be found in [26]. Friction is generally considered as a combination of seven elements, namely: static friction, coulomb friction, viscous friction, Stribeck friction, rising static friction, frictional memory, and Dahl effect. The friction observed in our device has static friction significantly higher than that when in motion. This makes the system less likely to be stable when precise position accuracy is desired and hence it should be treated with care. Although a combination of commonly used friction models, namely, static friction, coulomb friction and viscous friction can be used to characterize this effect, Stribeck friction was used in our modeling because Stribeck friction models the friction force transient at low velocities while static friction characterizes friction only at zero velocity. Since we were limited by the available experimental apparatus to measure friction (unlike the sophisticated equipment available for measuring friction in tribology), we chose the following friction model:

$$F_f=1.1sgn(\stackrel{.}{x})+0.2\stackrel{.}{x}+0.5e^{-{(\stackrel{.}{x}/0.04)}^2}sgn(\stackrel{.}{x})$$ (9)

to approximate the observed friction force. The sign function represented the Coulomb friction, the proportional term corresponded to viscous friction and the exponential term characterized the friction profile in the low velocity region. The parameters were roughly estimated so that (9) gave similar friction effect as in our application. This friction model can be used in simulation to verify the effectiveness of the controllers, but not necessarily accurate enough to describe the actual friction force. The discrepancy can in some way test the robustness of the controller against the uncertain friction force.

IV. Design of Controllers

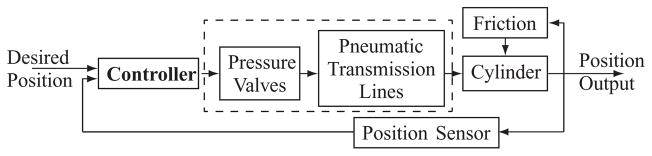
The full pneumatic system model is comprised of eqs. (1), (5) and (8), and is hence a fourth order system. Since no pressure sensor can be placed inside the MRI, we cannot measure pressure at the inlet of the cylinder chambers. Consequently, we cannot use a feedback loop to improve the response of the valve-transmission line subsystem. The control diagram of the pneumatic system with only position feedback is shown in Figure 5. In this section, the controller block is designed using sliding mode control (SMC) techniques; valve-transmission line dynamics were neglected in the design and the controller parameters were chosen in such a way that the slider moved slowly, so that the system can be controlled with a relatively slow response of valve-transmission line with time delay.

Fig. 5.

Control diagram of the pneumatic system

The goal of the controllers is to overcome the influence of friction with slow actuators. The approach pursued here was to treat the friction as an uncertain term, and design controllers accordingly, such that certain performance can be achieved in the presence of friction. This was the sliding mode control approach with the advantage of being robust to uncertainties; thus, the controller will be designed without consideration of the valve transmission line dynamics and the system model was simplified to be a second order system, described by (8). This greatly simplifies the design of controller, since friction can now be cancelled directly with the control law output.

The idea of sliding mode control is to drive the system states onto the designed sliding surface on which the system performance can be ensured and it is independent of system uncertainty.

A. SMC I

If we take e = x_d − x as the position error, then we can shift the system equilibrium point to the origin and the system model in eq. (8) can be rewritten in the state space form as:

$$\stackrel{.}{e}=v$$ (10)

$$\stackrel{.}{v}=\frac{1}{M}[(A_1+A_2)u^{\prime }+F_f]$$ (11)

and the sliding surface can be designed as s = e+av = 0. The motion on this sliding surface is described as ė = −e/a, and e = 0 is an asymptotically stable point by choosing a > 0, and the convergence rate can be controlled with the choice of a.

To determine the control law that drives the system states onto the sliding surface and maintains them there, the derivative of s is taken as:

$$\stackrel{.}{s}=\stackrel{.}{e}+a\stackrel{.}{v}=v+\frac{a}{M}[(A_1+A_2)u^{\prime }+F_f]$$ (12)

By choosing u′ = −β(e, v)sgn(s), where

$$\beta (e,v)\ge \left|\frac{Mv+{aF}_f}{a(A_1+A_2)}\right|$$ (13)

and sgn(·) as a sign function, the system stability and performance can be ensured. With a stable system, the range of the velocity v is bounded and so is the friction force. Thus, the right term in (13) has an upper bound denoted by β₀ and the control law can be further simplified to: u = −β₀sgn(s).

Such control law will induce chattering due to the slow response of the valve-transmission line. A common way to address this problem is to replace the sign function with the saturation function and hence the control law is given by:

$$u^{\prime }=-{\beta }_0\text{sat}\left(\frac{e+av}{\epsilon }\right)$$ (14)

This turns out to be a PD controller with saturation. By appropriately choosing a, the rate of convergence can be controlled, which in turn limits the maximum speed of the needle. The reciprocal of parameter ε behaves as the proportional gain of the PD controller when the system states remain on the boundary layer {|s| ≤ ε}, and can determine the system position accuracy. The saturation amplitude β₀ should be chosen large enough to account for the system uncertainty, i.e., the friction force; but it should not be too large, because the control law is more vulnerable to slow valve-transmission line response and can lead to system instability.

B. SMC II

As mentioned in the design of SMC I, large saturation amplitude makes the system more vulnerable to slow valve-transmission line response and it should be avoided. The saturation amplitude used in SMC I is the upper bound of β(x, v). It is observed in the device that the friction force while in motion is significantly smaller than that in steady state. Thus, we can use the following saturation amplitude instead to improve the performance of the system:

$$\beta =\{\begin{array}{cc}{\beta }_1,& \mid v\mid \le v_0\\ {\beta }_2,& \mid v\mid >v_0\end{array}$$ (15)

where β₂ < β₁.

C. SMC III

An alternative approach to reduce the saturation limit is to divide the control into continuous and switching components. Taking

$$u^{\prime }=-\frac{F_c}{A_1+A_2}-\frac{M}{a(A_1+A_2)}v+U$$ (16)

where F_c is of the form of coulomb friction with friction force smaller than the minimum friction observed, we get:

$$\stackrel{.}{s}=\frac{1}{M}[(A_1+A_2)U+(F_f-F_c)]$$ (17)

with an upper bound for $\mid (F_f-F_c)/(A_1+A_2)\mid ={\beta }_0^{\prime }<{\beta }_0$. And the modified sliding mode control law can be written as:

$$u^{\prime }=-\frac{F_c}{A_1+A_2}-\frac{M}{a(A_1+A_2)}v-{\beta }_0^{\prime }\text{sat}\left(\frac{x+av}{\epsilon }\right)$$ (18)

V. Experimental Results

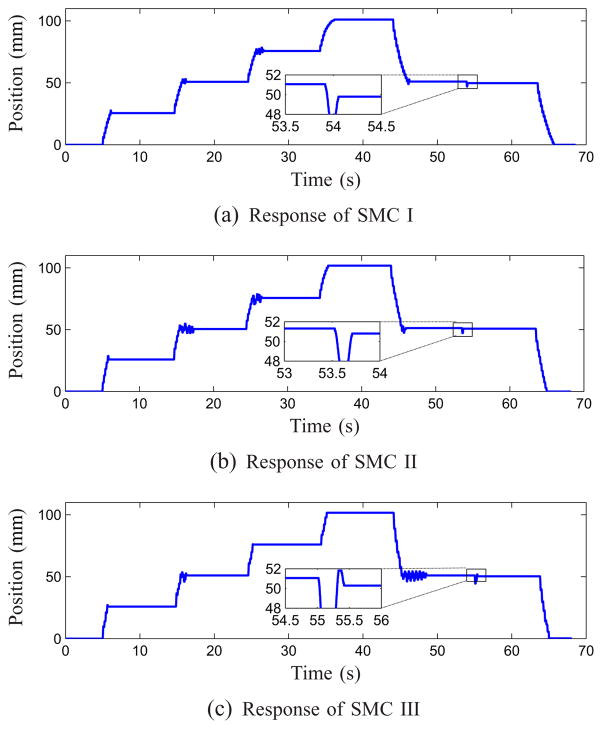
After verifying the effectiveness of the controllers in simulation, actual experiments were conducted. All three versions of sliding mode controllers gave very good performance to step input after tuning the controller parameters as shown in Figure 6. By choosing the appropriate saturation amplitude, the maximum acceleration of the slider was limited and the slider moved slow enough for the actuator to respond. The position accuracy of 1mm was achieved easily considering the 1mm position resolution in the MR images. Better accuracy can be acquired with fine parameter tuning. For all three controllers, the experiments started at zero position and then the desired position was set to 25.4, 50.8, 76.2 and 101.6 mm, and then back to 50.8, and 0mm. Before the final zero position was set, a 1mm step command was given at the 50.8mm location to verify the desired 1mm resolution. As can be seen in Figure 6, the step response curves vary slightly at different positions. For example, in Figure 6(a), the step response from 0 to 25.4mm motion exhibited a small overshoot while the step response of 25.4mm to 50.8mm and 50.8mm to 76.2mm exhibited two and three cycles of oscillation, respectively, and the step response of 76.2mm to 101.6mm approached the 101.6mm position slowly without overshoot. This was because of the presence of non-uniform friction along the guide rods. Since the friction around the 50.8mm to 76.2mm position was low, the system moved quickly and hence it induced oscillations. Friction around the 101.6mm position was high, so the system moved slowly and hence overshoot was avoided. These showed the robustness of the SMCs. At the cost of dynamic response (overshoots and oscillations), the controllers gave stable and accurate position control over varying friction force/external disturbance. As can be seen from the plots, stick-slip behavior was observed and it was consistent with the simulation results, namely, small amplitude oscillations occurred at the desired location because the SMCs behaved as a stiff PD controller. The peak to peak amplitude of the oscillations before stabilization at the target location were within acceptable limits (less than 2.5mm for SMC I, and 5mm for both SMC II and SMC III). Experimental data shows that the system can have a position accuracy of less than 1mm. Among all three sliding mode controllers, SMC I performed best, since it gave more uniform step response with smaller amplitude oscillation.

Fig. 6.

Experimental results for all three sliding mode controllers. The commands given to all three controllers were similar, i.e., start from 0 position to 25.4, 50.8, 76.2, 101.2mm, and back to 50.8 and 0. An additional 1mm amplitude step signal was given at about 55 s to show that the movement would be initialized and the desired position would be reached within 1mm error. Each sub-figure has a zoom-in plot for such step response.

VI. MRI-Compatibility Test

MRI test was conducted using a 3.0 T SIEMENS^® MRI unit, to verify the MRI-compatibility of the system as well as its performance under MRI environment.

A. Pneumatic Actuation in MRI

The device was put into the MRI bore and actuated without MR scanning and with MR scanning during part of the actuation process. Same step response as in Figure 6 was acquired and we observed that the performance of the pneumatic actuation system was not affected by the strong magnetic field as well as the varying magnetic field generated during scanning.

Phantom test was then conducted to show both the device MRI-compatibility as well as the system position accuracy as shown in Figure 7. The phantom is made of a mixture of 200ml boiling water with 7.2 g gelatin powder (Knox gelatin, Kraft Foods Global Inc.). Figure 7(a) – Figure 7(c) were high resolution images with long scanning time for static imaging, while Figure 7(d) was low resolution image with very short scanning time for continuous imaging (5 frames per second). No image distortion from the device was observed in the MR images as shown in the figures. We observed some blobs near the needle tip. This is because we were using RFA needle, which contains multiple sharp needles inside, and it is known that these sharp edges will create artifacts in the MR images. Signal noise ratio (SNR) was computed for all four images as 65.58, 66.77, 64.42 and 20.17, respectively, using the region of interest (ROI) definition for the signal and the noise as defined in Figure 7(a). The SNR of Figure 7(d) is significantly lower than the other three because of its short scanning time. The images in Figure 7(a) – Figure 7(c) were taken when the needle was at the initial position, 12.7mm position and 25.4mm position. The positions measured from the MR images matched our commanded positions. This further shows that the device is fully MRI-compatible and can work without any interference inside the MRI.

Fig. 7.

Device position accuracy under MRI

B. Force Sensor in the MRI

Experiments were also conducted to demonstrate the MRI-compatibility of the 3-D fiber-optic force sensor that was attached at the base of the needle in the needle driver robot. We initially used a commercially available force sensor that was claimed to be MRI compatible. However, experiments showed that the reading from the strain-gauge based force sensor is affected by the MR scanning sequence. The force sensor was mounted onto the 1-DOF pneumatic system and moved inside the MRI bore without any load. Figure 8(a), 8(c) and 8(e) show clearly the offset along all three axes that was observed during the motion of the sensor inside the magnet during scanning (without any interaction of the needle with an object). In addition, offset value changed as the sensor moved. The motion profile can be found in Figure 8(g). This experiment demonstrated that the readings from the strain-gauge based force sensor were affected during MR imaging. Although the commercial force sensor was developed with MRI-compatible materials, some of the components were metallic. We suspect that the eddy currents induced in the metal parts lead to the peculiar offset in the force values.

Fig. 8.

Comparison of a commercial MR compatible force sensor and 3-D fiber-optic force sensor under MR imaging

The commercial force sensor was then replaced with our 3-D fiber-optic force sensor. A phantom was also placed about 65mm from the needle’s initial position and Figure 8(b), 8(d) and 8(f) show the readings from the optical force sensor during a typical needle insertion task with motion profile shown in Figure 8(h). From the plots, it is seen that the force sensing along the z-axis is observed when the needle penetrates the phantom tissue (see Fig. 8(f)). The MR imaging started at time t = 35s, and no offset in the force readings was observed due to imaging.

VII. Conclusion

In this paper, an MRI-compatible 1-DOF pneumatic system using long transmission lines has been developed and various sliding mode controller designs have been implemented. Due to the unknown structure of the pressure valves, they were approximated as a first order system based on the experimental observations. The long transmission lines were modeled as a first order system with time delay because the equation that governs the dynamics of long transmission lines is a varying coefficient telegraph equation with varying boundary conditions and is extremely difficult to solve. Sliding mode controllers based on the developed model were designed and evaluated. The sliding mode controllers gave very good results in actual experiments, with position error less than 1mm. Experiments were also conducted to demonstrate the MRI-compatibility of the entire system with a 3-D fiber-optic force sensor attached at the base of the needle in the needle driver robot.

Future work will focus on improving the performance of sliding mode controller by including the actuator-transmission line dynamics in the controller design and developing MRI-compatible fiber optic pressure senor for cylinder pressure sensing as well as building a multiple degree-of-freedom MRI compatible robot for use in breast biopsy and radio-frequency ablation of breast tumor under continuous MRI.