Reference-free particle selection enhanced with semi-supervised machine learning for cryo-electron microscopy

Abstract

Reference-based methods have dominated the approaches to the particle selection problem, proving fast and accurate on even the most challenging micrographs. A reference volume, however, is not always available and building a set of reference projections from the data itself requires significant effort to attain the same level of accuracy. We propose a reference-free method to quickly extract particles from the micrograph. The method is augmented with a new semi-supervised machine-learning algorithm to accurately discriminate particles from contaminants and noise.

Introduction

1. Importance of automated particle selection

Existing computer algorithms automate nearly every step in single-particle reconstruction of macromolecules captured by cryo-electron microscopy (cryo-EM). These steps include data collection, classification and reconstruction; yet, the general problem of selecting particles from a micrograph in an objective way remains unsolved. A researcher may spend weeks to months, painstakingly hand-picking low-contrast particles among contaminants, which include images of ethane/propane bubbles, ice crystals and noise, in order to obtain a single high-resolution three-dimensional reconstruction. Furthermore, the trend in cryo-EM is moving away from characterizing a single conformation, toward giving an inventory of multiple conformational states all coexisting within a heterogeneous sample. This change in agenda substantially increases the amount of effort going into particle selection and motivates the current interest in seeking better automation of this important step.

2. A particle selection framework

Before outlining prior efforts in particle selection, we note the main obstacles to be overcome by a successful particle selection algorithm. Such an algorithm must (1) precisely locate the position of particles in the micrograph, (2) accurately discriminate particles from contaminants and noise while (3) minimizing the amount of manual intervention. As becomes apparent in the review of prior efforts, the solution to the first problem is independent of the second and third as long as a reference is available. However, if a reference is not available, current approaches require a fair amount of intervention just to locate a particle in the micrograph; e.g., by hand-tuning specific parameters or selecting initial references from the micrograph itself. The second problem remains unsolved in all but the easiest cases with high contrast.

3. Prior efforts in automated particle selection

Particle selection techniques can be divided into reference-based and reference-free methods. A reference can be obtained either from a known three-dimensional structure, if available, or by selecting example particles in a micrograph. Initial approaches to particle selection relied on a referenced-based approach called template-matching (see Nicholson and Glaeser (2001) for an in-depth review). Roseman (2003) improved template matching by adopting a method to account for changes in local variance efficiently in Fourier space. Sigworth (2004) and Wong et al. (2004) noted that cross-correlation with a template assumes Gaussian white noise, and developed new template-matching methods that take different approaches to incorporate a generic noise model learned from the existing data. Other approaches have experimented with reduced representations (Volkmann, 2004) and hierarchical scoring functions (Chen and Grigorieff, 2007).

Another reference-based approach to particle selection utilizes recent advances in machine learning, namely detection cascades (Viola and Jones, 2001), to discriminate between particles and contaminants/noise. Sorzano et al. (2009) and Mallick et al. (2004) apply a classifier cascade to perform cost-sensitive learning, a learning methodology that minimizes the number of false positives. Ogura and Sato (2004b) developed a pyramidal neural network algorithm to both characterize and discriminate particles from contaminants/noise. While these approaches utilize a more general model, they cannot directly incorporate a reference and thus, require the user to manually pick particles in each micrograph or defocus group.

Reference-free approaches leverage the observation that images of physical objects, such as particles in a micrograph, have limited complexity and, from an information-theoretic point of view, can be described by a compact representation (Wang, 2001). While these approaches do not require a reference, they are not free of user intervention. Image segmentation-based approaches either require the user to follow a certain protocol and modify it to fit the problem at hand (Adiga et al., 2005; Umesh Adiga et al., 2004; Yu and Bajaj, 2004) or to optimize a set of parameters (Voss et al., 2009; Woolford et al., 2007a; Woolford et al., 2007b).

Other approaches utilize more generic models at the expense of increasing computational complexity. Singh et al. (2004) explored a more general approach called hidden Markov random fields; this is an undirected graphical model that can utilize dependencies between individual pixels to characterize a particle. Ogura and Sato (2004a) proposed a Monte Carlo search that moves windows randomly across the micrograph, looking to optimize a score related to the class average of data within windows distributed across the micrograph.

Finally, there are approaches that combine both reference-based and reference-free methods; these approaches use a clustering algorithm to deal with the false positives generated by template matching. Hall and Patwardhan (2004) utilized a self-organizing map, by employing an unsupervised neural network, to recognize and remove false positives. Likewise, Shaikh et al. (2008) performed a 2D alignment to cluster and average a set of views; one can then traverse a hierarchy of averaged views to annotate particles.

4. Outline of paper

We will introduce a simplified particle extraction tool, which only requires knowledge of the particle size, or size range. We will then propose a new, more efficient design, which operates in Fourier space for large images. Since the primary purpose of our proposed algorithm is to provide extracted data windows to a later algorithm, we will show how the extracted data windows may serve as references to both the established template-matching algorithm, SPIDER’s LFCPick (Rath and Frank, 2004), and a new semi-supervised machine-learning algorithm, proposed in this work, which we call AffinityRank. Finally, we apply the proposed algorithms on an established benchmark dataset as well as a dataset related to our own interests, the ribosome.

Method

1. Design of DoGLFC

The proposed reference-free particle selection algorithm builds on the Scripps Institute’s DoG Picker (Voss et al., 2009), a fast method to segment particles in a micrograph. The difference of Gaussian (DoG) algorithm creates a peak map similar to template matching with cross-correlation. However, Spider’s peak selection algorithm (Rath and Frank, 2004) finds only a subset of the peaks on the DoG map at the center of a particle: see Figure 1 for several illustrative DoG peaks (center column) with their corresponding particle (left column). These peaks tend to resemble a uniform disk having a radius proportional to the corresponding particle. To create peaks compatible with the requirements of a peak selection algorithm, we cross-correlate the DoG map with a uniform disk (see resulting peaks in the right column of Figure 1). This simple modification results in a reference-free particle selection algorithm requiring only the particle size, or size range, which we call DoGLFC.

Figure 1.

Three example particles (left column) with corresponding 1D difference of Gaussian peaks (center) column and 1D DoGLFC peaks (right column). Note that the DoG peaks correspond to the particles selected with the DoGLFC peaks. The x-axis of the peak plots corresponds to the image pixel position in row-major order and the y-axis is the corresponding pixel value in either the DoG map (center) or DoGLFC map (right). The center pixel in the window corresponds to the center of this graph. The graphs represent roughly 12,000 pixels values that oscillate quickly giving the appearance of an area plot. The first row shows an example where peak-picking algorithm would have missed the particle. The second row would have resulted in a poorly centered particle. The third row shows a good particle found with the DoG map. The ribosomes shown were collected at 300 kV at a defocus of 2 µm to illustrate the difficulty of this dataset.

The DoGLFC algorithm as outlined in Figure 2 requires a single tunable parameter or set of parameters based on the particle radius or range of expected radii, which can be derived from prior knowledge or from a small set of reference projections. Execution of the algorithm returns a list of 3-tuples describing the location of the particle (x and y coordinate) and the peak height. The algorithm starts by calculating an initial Gaussian blur, ${\mathrm{\Psi }}_{\mathit{\text{xy}}}^0$, with sigma parameter:

$${\sigma }_0=r·\sqrt{(k^2-1)/(2k^2·\text{ln}(k))}$$

The difference of Gaussian (DoG) width, k, is set to 1.2 for a single object of radius, r, or to the start of the radius range (Figure 2). Then, for each object radius, a Gaussian blur of the previous blur is calculated (scaled by the DoG width), and the difference is taken between both the current and previous blurs. Next, the current DoG map is correlated with a uniform disk of radius, r, scaled by the DoG width to give the current object radius. Finally, Spider’s peak search algorithm is applied to the peak map, Π_x, and the resulting peaks are merged with the previous peak list, P^i-1. The motivation and derivation for the DoG width and sigma parameters are described in (Voss et al., 2009).

Figure 2.

Pseudocode describing the DoGLFC algorithm. The left column states the input and output of the algorithm; it also defines each symbol in the notation. The right column contains the Pseudocode describing the algorithm. PeakSearch describes both the peak picking and merging algorithms found in Spider (Rath and Frank, 2004).

2. Implementation for Large images

While the real-space implementation of the Gaussian filter can be faster in practice, it only holds up to a certain particle size (Voss et al., 2009). We present a theoretical extension to this algorithm that allows for a single Fourier transform of the original input image and a set of inverse Fourier transforms, one for each radius, to create the real-space peak map for peak picking. The two convolutions, Gaussian blur and uniform disk, will be multiplications in Fourier space by means of the convolution theorem. The difference of Gaussian blur is also a difference in Fourier space since the Fourier transformation is linear. The following equation provides the Fourier transform of a uniform disk of radius, r:

$$A(f)=\frac{\sqrt{3r}}{4f}{\mathrm{J}}_1(2\pi \mathit{\text{fr}})$$

where J₁ is the Bessel function.

3. Improved ranking of extracted particles

The DoGLFC algorithm captures potential particles (or objects) of a specific size and, thus has less discriminative power than a reference-based technique such as template matching (Rath and Frank, 2004), which can make use of more detailed information – when a good reference is available. We propose a new semi-supervised machine-learning algorithm, AffinityRank, to improve the ranking of particle windows as illustrated in Figure 3. The AffinityRank algorithm is given three inputs:

1. A matrix of image windows, W_i,t, where each row is an image (i=1…n) of size d by d and each column is a pixel (t=1…d²).

2. Maximum size for the reduced image, m, which is much smaller than d².

3. Two reference sets of image windows chosen from the data (subsets of W_i,t); the positive set, containing the putative particle (P), and negative set, not containing the putative particle (N).

Figure 3.

Pseudocode of the AffinityRank algorithm. The algorithm takes three inputs: the set of images, the maximum dimension of each Eigenvector and two sets of indices indicating which windows should be used as positive or negative references. The output of the algorithm is a ranking score on each window where the higher the rank the more likely the window contains a particle.

The output of the algorithm is a ranking score, R_i, for each of the n given image windows.

The AffinityRank algorithm starts in Figure 3 Step 1 by compressing the image windows, W_i,t, containing candidate particles to a small set of eigenvectors in matrix, M_i,k, with a non-linear dimensionality reduction technique called diffusion maps (Coifman et al., 2005; Zelnik-manor and Perona, 2004). The diffusion maps algorithm is similar to multi-dimensional scaling (MDS) in that it performs eigendecomposition on the pairwise distances between images, rather than on the images themselves. Unlike MDS, the diffusion maps algorithm applies a non-linear mapping, A_i,j=exp(D_i,j/σ), to the pairwise distances, D_i,j, where σ is a scaling parameter, and subsequently performs PCA on the graph Laplacian of the row-normalized affinity matrix, A_i,j. This non-linear mapping of the pairwise distances is known as a kernel, and thus, the diffusion maps algorithm is a member of the kernel-PCA family. This step both implicitly denoises the image windows and increases the efficiency of the later steps.

In steps 2–5 of Figure 3, the AffinityRank algorithm pre-calculates the affinity matrix, A_i,j while selecting the optimal number of eigenvectors. It starts by calculating the pairwise distances among image windows embedded in this new space (Step 2, Figure 3), and converts the distance matrix, D_i,j, to a Gaussian affinity matrix, A_i,j, using the same normalization as the diffusion maps algorithm (Step 3, Figure 3), as suggested by Zelnik-manor and Perona (2004). These steps are repeated to determine (Step 5, Figure 3) the optimal number of dimensions in the diffusion space, which is measured by the separation between the positive and negative sets as defined by the score in Step 4, Figure 3, which estimates the average maximum affinity between positive examples and subtracts this values from the mean affinity between negative examples. In practice, we start with a single dimension and terminate when the separation started to decrease, which occurred in less than five iterations.

In steps 6–10 of Figure 3, the AffinityRank algorithm performs iterative re-ranking of each window with respect to the positive and negative sets, which grow with each successive iteration. The re-ranking starts at Step 6 in Figure 3 by calculating a ranking score for each window, the affinity rank, which measures the maximum affinity to a window in the positive set, P, minus the mean affinity to all windows in the negative set, N. Then, the top- or bottom-ranked windows not already in the positive and negative sets are added to those sets, respectively (Steps 7–10 in Figure 3). This procedure is repeated until every window belongs to either the positive or negative set. This is the most time-consuming step in the re-ranking procedure; it scales with O(n³) where n is the number of images.

The AffinityRank algorithm is versatile in that it does not require an explicit set of references. Since the DoGLFC algorithm provides an initial ranking for the extracted windows as measured by the cross-correlation peak, this algorithm can utilize a subset of windows taken from both the top and bottom of the initial ranking. It can then iteratively improve this ranking. As described in the results section, we apply two variations of the AffinityRank algorithm: one with manually selected references for the KLH dataset and one with references derived from the initial DoGLFC ranking.

4. Experiment and Performance

We will benchmark the DoGLFC and AffinityRank algorithms on a dataset available from Scripps Institute (http://ami.scripps.edu/prtl_data) (Zhu et al., 2003), the KLH I (Zhu et al., 2004) dataset, as well as a ribosome dataset related to our own work. Each dataset poses a unique challenge to the DoGLFC algorithm and allows a consistent comparison between past and future algorithms.

We use manually annotated particles as ground truth in both datasets; for KLH I, we use a set of side view coordinates picked by Mouche (Zhu et al., 2004), and for the ribosome, we use a set of coordinates picked by Pallesen with the aid of SPIDER’s LFCPick (Rath and Frank, 2004). Both sets of manually selected particle images resulted in publication-quality three-dimensional reconstructions. Since our algorithm will not produce precisely the same coordinates as Mouche’s or Pallesen‘s manually chosen particles, we allow the comparison to vary by no more than 15% of the window size. Note that the use of LFCPick to aid in Pallesen’s particle picking biases the resulting score pessimistically; this problem will be treated in the Discussion section.

We will use the following three criteria to assess the performance of DoGLFC:

1. 1-Precision (previously called the false positive rate) and FNR (1-recall)

2. Area under the precision recall curve (APR); see supplemental material Figures 1 and 2 for the corresponding plots of the precision recall curve.

3. Three-dimensional reconstruction (along with Fourier Shell Correlation)

In previously published works (Hall and Patwardhan, 2004; Huang and Penczek, 2004; Mallick et al., 2004; Ogura and Sato, 2004b; Rath and Frank, 2004; Roseman, 2004; Sigworth, 2004; Singh et al., 2004; Umesh Adiga et al., 2004; Volkmann, 2004; Wong et al., 2004), the 1-recall was correctly referred to as the false negative rate (FNR), FN/(TP+FN), yet the 1-precision, (FP/(FP+TP), was incorrectly referred to as the false positive rate, which measures FP/(FP+TN). We calculate the same metrics (as near as we can tell) as the previous papers, yet refer to them by their proper names and further define them to avoid ambiguity. More details covering the pervasiveness and implications stemming from this incorrect use of terminology is covered in (Langlois and Frank, 2011).

The precision and recall measure the consistency between the algorithm and the picker (or truth) in terms of the positive (particle-containing) windows only. One minus the precision (or 1-recall) simply measures the mistakes rather than the successes. Most particle-picking algorithms find more windows than there are particles, and to limit the number of false positives (at the expense of true positives) a cutoff is used, e.g. minimum cross-correlation coefficient or maximum number of windows. The APR measures the overall trade-off between the precision and recall over the effective range of a cutoff. The three-dimensional reconstruction and corresponding FSC is performed in the case where results of DoGLFC deviate significantly from benchmark results to examine whether the discrepancy between algorithm and benchmark is significant and, thus, pernicious.

Results and discussion

We demonstrate the effectiveness of the proposed DoGLFC algorithm augmented with AffinityRank on two very different datasets: the keyhole limpet hemocyanin (Mouche et al., 2003) and the ribosome dataset. Figure 1 (first column) and Figure 4a illustrate the differences between the two datasets with example images, which result from different experimental conditions, imaging conditions and samples. While both datasets pose unique challenges, it is clear from the example micrographs that picking experimental ribosome projections, due to their lack of distinct geometrical features, presents a more difficult problem for both human and machine.

Figure 4.

Illustration of a) keyhole limpet hemocyanin (KLH) micrograph and b) corresponding difference of Gaussian map. Note the DoG peaks occur at the edge of the KLH particle rather than the center as in the ribosome data.

1. Keyhole limpet hemocyanin benchmark

The Keyhole Limpet Hemocyanin (KLH) dataset was established as a benchmark by the 2004 particle selection bakeoff (Zhu et al., 2004), and has been used in testing algorithms developed since (Chen and Grigorieff, 2007; Woolford et al., 2007a; Woolford et al., 2007b). This dataset provides an extensive comparison with twelve other particle-picking algorithms as summarized in Table 1.

Table 1.

Benchmarking DoGLFC over both the Keyhole Limpet Hemocyanin Dataset (top) and Ribosome Dataset (bottom) with an extensive comparison to previously published works. The first column describes the algorithm with reference, the second column the year of publication, the third and forth columns the performance in terms of percent 1-Precision and the false negative rate (FNR). The (400) following Spider LFCPick and DoG LFC indicates the metrics were calculated over the first 400 windows ranked by highest cross-correlation.

	Year	1-Precision (%)	FNR (%)
Keyhole Limpet Hemocyanin Dataset
DogLFC	2010	92.0	3.2
DogLFC + AffinityRank	2010	20.3	14.3
Naïve Bayes Boosting (Sorzano et al., 2009)	2009	10.7	36.6
SwarmPS (Woolford et al., 2007b)	2007	15*	9
Signature (Chen and Grigorieff, 2007)	2007	12.9**	9.8
Sigworth (Sigworth, 2004)	2004	4.5	23.2
Mallick (Mallick et al., 2004)	2004	11.7	14.2
Volkmann (Volkmann, 2004)	2004	12.2	27.4
Wong (Wong et al., 2004)	2004	16.2	23.8
Roseman (Roseman, 2004)	2004	16.6	2.4
Hall and Patwardhan (Hall and Patwardhan, 2004)	2004	22	27.4
Yu and Bajaj (Yu and Bajaj, 2004)	2004	24.7	7.3
Huang and Penczek (Huang and Penczek, 2004)	2004	30.7	46.8
Zhu (Zhu et al.2003)	2003	13.7	9.7
Ludtke (Ludtke et al.1999)	1999	23.7	43.4
Ribosome Dataset
Spider LFCPick (400)	2010	66.9	0.4
DogLFC	2010	85.9	6.0
DogLFC (400)	2010	73.8	21.8
DogLFC + AffinityRank	2010	65.7	19.1

^*It is unclear whether the same dataset was used

^**It is unclear how this metric was calculated but it is most likely 1-Precision

The difference-of-Gaussian map of a KLH micrograph (Figure 4b) has peaks around the boundary of a particle rather than the center as in the ribosome micrographs, Figure 1. This seems to be unique to the KLH particles and seems to be related to the intensity variation of the particle, which is highest around the boundary of the particle. The subsequent disk cross-correlation on the DoG map improves this centering; however, a subset of the resulting windows of the DoGLFC algorithm will still center at a corner of a subset of particles, resulting in a particle that is partially cut off. This problem can be corrected with iterative center refinement. Nevertheless, some particles are still missed because the iterative center refinement fails to center the particle on a small subset of the data. To overcome this problem, we took the top 30 windows from DoGLFC and created rotational averages (similar to EMAN Boxer (Ludtke et al., 1999)) and used these templates for fast locally normalized cross-correlation. Finally, to reduce the number of false positives, we applied the AffinityRank algorithm with particle views found by DoGLFC, which overlap coordinates picked by Mouche from the first micrograph only: this results in 15 windows with particles in side-views and ~100 windows that do not contain particle side-views. Note that in this task it is necessary to use manual selections in order to avoid selecting the overrepresented top views, which were ignored by Mouche for the bakeoff.

Table 1 reports the performance of each algorithm, both those compared in the bakeoff and those developed since bakeoff, according to the corresponding publication, and compares the algorithms in terms of the false positive rate (1-precision) and the false negative rate (FNR). Table 2 presents a new metric to compare particle picking algorithms, the area under the precision/recall curve (APR). The precision/recall curve plots the algorithm performance over all cutoffs, comparing algorithms without regard to how the final cutoff was chosen. In other words, the APR compares the ability of the particle picker to rank particles over contaminants and noise.

Table 2.

Comparison between DoGLFC, DoGLFC + AffinityRank and Spider’s LFCPick over both the Ribosome Dataset (top) and Keyhole Limpet Hemocyanin Dataset (bottom) in terms of Ranking Performance measured by the percent area under the precision-recall curve (%APR).

	DoGLFC (Orig.)	DoGLFC (AffinityRank)	LFCPick
Ribosome dataset	49.2	55.9α	61.2
KLH dataset	20.7β	82.0β	80.3β

^αNo manually selected references used

^βMeasures the APR based on 1042 total positives, not detected positives

The 1-precision measures the proportion of non-particle windows falsely labeled as particles; the results in Table 1 demonstrate that DoGLFC + AffinityRank performs competitively to previously published techniques even with minimal supervision using only particles picked from a single micrograph. From the bakeoff only Roseman’s, Mallik’s and Zhu’s techniques perform substantially better whereas from later techniques only Signature performs better. To attain the results in Table 1, the classification cascades, Naïve Bayes Boosting (Sorzano et al., 2009) and Mallick (2004), as well as the template-based methods, Signature (Chen and Grigorieff, 2007) and Roseman’s (2004) method, require at least 3–5 micrographs to properly train their methods. In contrast, DoGLFC + AffinityRank only requires a single micrograph.

Table 1 also compares DoGLFC to DoGLFC + AffinityRank. The DoGLFC algorithm was run with no supervision, returning the maximum number of windows for each micrograph. It missed about 3% of the particles and included a substantial number of false positives. AffinityRank reduces the number of false positives to nearly the same level as many of the bakeoff algorithms. It misses an additional 11% of the particles. Table 2 further shows that the improvement of AffinityRank results from a general improvement (by more than 4 times) in ranking particles over contaminants and noise. AffinityRank does not require any parameter tuning or threshold selection; these results reflect only the first 13 particles picked from the first micrograph.

Of the methods in the bakeoff, Roseman’s method is the most similar to DoGLFC, it is also one of the best performing methods in the bakeoff, and it is the standard particle selection method in SPIDER. For these reasons, a further experiment was performed comparing both methods with a minimal amount of user intervention.

Roseman’s protocol was followed strictly except for the final hand tuning, which is unnecessary for this comparison and was skipped. Table 2 compares both methods using the area under the precision/recall curve (APR). The original DoGLFC algorithm performs quite poorly (20.7%): without a reference, the top-views contaminate this result. However, the performance improves ~4 times when the AffinityRank method is used, and performs competitively with Roseman’s method (82.0% versus 80.3%). The precision recall curves (Supplemental Figure 1) further illustrate the superior performance of AffinityRank, which dominates Spider’s LFCPick over the entire plot.

2. Ribosome dataset

The ribosome dataset presents a more realistic task. It presents a tougher challenge than the KLH complex dataset because it has a lower contrast as it was collected at 300 KV, whereas the KLH complex was collected at 120 kV. The ribosome micrographs were collected at −180°C on SO163 film using a Tecnai F30 Polara electron microscope equipped with a field emission gun at 300 kV. The objective aperture was 100 µm, and the magnification was 59,000. Micrographs were digitized with a step size of 7 µm on a ZI Imaging Scanner, for more details see (J. Pallesen and J. Frank, Structure of the Ribosome with Factors RF1/RF3, 2011, In preparation).

Unlike the KLH complex, the peaks in the difference-of-Gaussian map correspond better to the centers of the ribosomes (see Figure 1). This greatly simplifies the particle-picking protocol since neither iterative centering nor re-extracting windows with fast local cross-correlation are required. Thus, we ran the difference of Gaussian algorithm with a single particle radius of 110 pixels and an allowed overlap of 20%. We also took the first 1000 windows since we only expected about 100 ribosomes on each micrograph. For AffinityRank, we divided the micrographs by defocus into 22 groups where each group had 30 micrographs, and ~30,000 windows. We used the top and bottom 10% of each micrograph (~3000 positive ~3000 negative windows) as the starting positive and negative windows, respectively. No reference or manual intervention was used to achieve the reported results in Table 1 and Table 2.

Table 1 compares DoGLFC and its variants to Roseman’s local fast cross-correlation (LFCPick in SPIDER) using the same criteria as the particle-picking bakeoff. When we use a 400 window cutoff, the DoGLFC (alone) algorithm performs about 20% worse than LFCPick in terms of false positives (85.9 versus 66.9) whereas it performs substantially worse in terms of false negatives (21.8 versus 0.4).

Manual inspection of the micrographs yielded several reasons for this discrepancy in performance. First, DoGLFC simply found different particles than LFCPick, e.g. when two particles overlapped, LFCPick chose one and DoGLFC the other. Second, DoGLFC ranked a substantial number of particles so low they were lost by the 400-window cutoff; this accounts for 15 percentage points (see Table 1). Third, DoGLFC missed particles in close proximity to a contaminant. In this case, the peak for the particle became indistinguishable from the peak for the contaminant.

The AffinityRank algorithm enhances the performance of DoGLFC by improving the ranking of particles, outside the 3,000-window cutoff, such that far more positive windows fall in the first 400. As shown in Table 1, AffinityRank decreases the FNR by about 2 percentage points, from 21.8% to 19.1%; it also decreases the 1-precision by nearly 9 percentage points, thus becoming competitive with SPIDER’s LFCPick. In order to get a similar result with LFCPick, one would have to derive templates from multiple micrographs, then cluster and average them in some way. This is not only computationally more intensive but is also potentially less accurate. Thus, DoGLFC + AffinityRank is an excellent alternative when a reference is not available.

Table 2 compares the ranking performance of DoGLFC (and the AffinityRank variant) with fast locally normalized cross-correlation in terms of the area under the precision/recall curve. The DoGLFC algorithm used alone performs about 12% worse than LFCPick whereas DoGLFC + AffinityRank performs only about 5% worse. The precision recall curves (Supplemental Figure 2) illustrate that AffinityRank has higher precision at lower sensitivity and Spider’s LFCPick at higher sensitivity. This result serves to illustrate that a good reference improves the accuracy in particle picking.

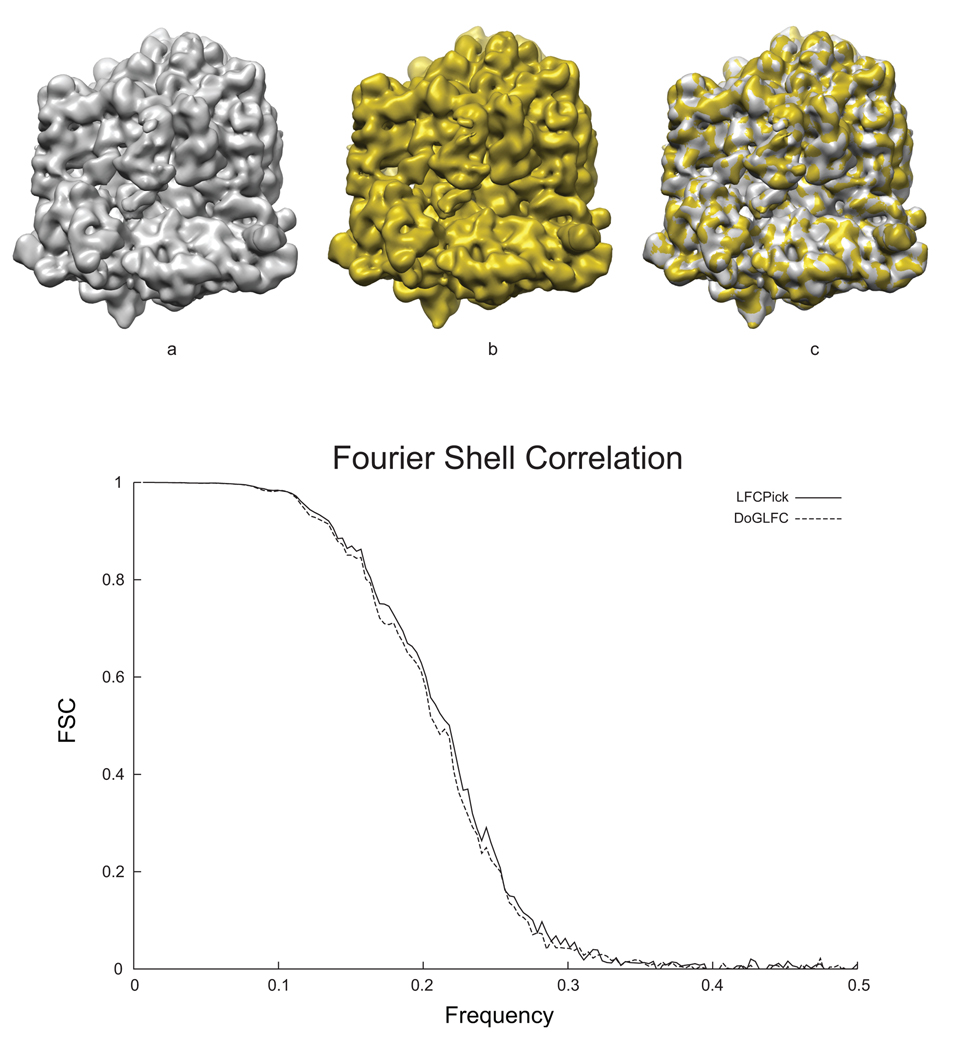
To investigate whether a loss of 20% of likely good particles is detrimental to the final reconstruction, we performed a reconstruction with the good windows (the windows that overlap with Pallesen’s picks with LFCPick) and compared to a reconstruction of the gold standard, i.e., Pallesen’s picks using LFCPick, see Figure 5. The DoGLFC reconstruction is shown in Figure 5a, the LFCPick reconstruction in Figure 5b, and their overlay in Figure 5c. Qualitatively, these reconstructions are essentially the same. The Fourier-shell correlation, Figure 5d, further confirms this assessment, with less than a half-angstrom difference using the FSC = 0.5 criterion.

Figure 5.

Reconstruction of our ribosomal dataset. (a) refined volume from manually verified particles selected by DoGLFC; (b) refined volume from manually verified particles selected by LFCPick; (c) an overlay of both volumes (a and b) illustrating they are identical for all practical purposes and d) an overlaid plot of the Fourier Shell Correlations for the volumes shown in a and b. The FSC curves are almost identical.

3. Discussion

In this work, we introduced a new reference-free particle-picker, called DoGLFC, which requires only knowledge of the particle size or range of sizes. While this algorithm performs quite well given its reference handicap, it really serves as a stepping-stone to building a better reference-free algorithm. To this end, we demonstrate how a new template-matching algorithm, AffinityRank can utilize DoGLFC to create both a reference-based and reference-free algorithm that achieves competitive results on a standard benchmark and a ribosome dataset.

Reference-free algorithms such as the DoGLFC algorithm work because physical objects have limited complexity, and thus can be described by a compact representation. Specifically, particles on a micrograph have a narrow range of size variation and can be located by a narrow band of low-frequency components. This feature gives DoGLFC an advantage over Roseman’s method, in that, it naturally avoids many contaminants based on size: contaminants make up the highest-ranked windows in a template-based method. A combination of these methods would produce an algorithm much like Signature (Chen and Grigorieff, 2007), which eliminates contamination using the spectrum correlation function to filter particles based on size.

DoGLFC is also more efficient than Roseman’s method, even on large images. This large image implementation, introduced in Methods, raises an interesting interpretation of the DoGLFC algorithm. The difference of Gaussian is the difference of two low-pass Gaussian filters and can be viewed as a band pass filter. Similarly, cross-correlation with a template can be seen as a special case of the box filter. The DoGLFC algorithm simply stacks a unique Bessel filter (acting as a box filter) on the difference of Gaussian filter to yield sharper peaks. This can be viewed as a new type of filter that goes beyond locating the edges of objects, and instead locates their centers of mass.

The AffinityRank algorithm was introduced to discriminate between views in the KLH dataset and improve the ranking on the ribosome dataset. It can be thought of as a template-matching (it even uses a similar measure (Lewis, 1995)) algorithm taking a data-driven approach rather than the model-based approach taken by other template-matching algorithms. A standard template-matching algorithm usually starts with a volume (a model), deriving reference projections for template matching. If no volume exists, then the user must select a number of particles and average them (essentially yielding the same projections as the volume); e.g. Roseman (2004) averaged views of the KLH particles, then generated rotational templates, and Ludtke (1999) created rotational averages of picked particles. AffinityRank takes a bottom-up approach (more data driven) where examples are simply the experimental projections without special pre-processing. The denoising effect of embedding the data into a diffusion map makes this approach feasible and reduces the computational cost.

The AffinityRank algorithm is a semi-supervised (transductive) classifier (Sindhwani et al., 2005). Unlike Sorzano et al. (2009) where “semi-supervised” is intended to mean interacting with the user, “semi-supervised” is used here in the traditional machine learning sense, where the learning algorithm uses un-picked particles to help improve the final model or ranking. By utilizing the underlying distribution of the unpicked particles, AffinityRank requires far fewer training samples than most other proposed algorithms; e.g. the method in (Sorzano et al., 2009) requires 50 to 100 picked references to achieve the desirable performance. AffinityRank makes use of the unpicked particles in both the diffusion map and iterative ranking refinement steps.

It is important to note that the performance scores obtained for the ribosome dataset are pessimistic due to the use of Roseman’s method (SPIDER’s LFCPick) to create the benchmark. This potentially introduces two types of bias: one toward the reference used in template matching and the second toward the algorithm itself. While the reference bias may be negligible, the bias toward template matching ensures that any comparison between the scores will be pessimistic. That is, DoGLFC may find new particles, which have been missed by template matching, and thus mislabeled by this approach (see Figure 6 for an illustrative example).

Figure 6.

Example illustrating algorithm bias. a) Three good particles on the micrograph; b) Two particles found by LFCPick and manually verified as correct, giving 100% sensitivity; c) Two particles found by DoGLFC, which were verified as correct since they overlap with the windows verified in (b); in other words, not by a separate manual verification. Here DoGLFC has made two errors, (i) locating an unverified particle and (ii) missing a verified one. This toy example illustrates why the score of the DoGLFC performance is pessimistic.

In future work, the DoGLFC algorithm will only be the first stage in a more extensive machine-learning protocol that will provide intelligent interaction with the user. One step in this direction will be to explore modifications to the AffinityRank algorithm and alternatives to better incorporate manual annotation of particles. In this way, a user can more quickly discover the bulk of the particles within a dataset. We will also explore better ways to include prior knowledge such as related references as well as models built from previously picked datasets.

In sum, a new unsupervised particle detection algorithm, DoGLFC, was developed to extract potential particle windows from a micrograph without the benefit of a reference. This algorithm is both effective and simple, requiring a single parameter, the particle size or size range. The windows extracted by the DoGLFC method can then serve as examples to a subsequent learning algorithm; e.g. the AffinityRank method. AffinityRank is a semi-supervised learning algorithm that utilizes manifold learning to improve the ranking of particle windows; it has the advantage that it does not require an explicit reference, i.e. it can use the initial ranking produced by the DoGLFC algorithm. When combined, the combination of DoGLFC and AffinityRank performs competitively when compared with existing template-based methods.