Signal enhancement for the sensitivity-limited solid state NMR experiments using a continuous, non-uniform acquisition scheme

Abstract

We describe a sampling scheme for the two-dimensional (2D) solid state NMR experiments, which can be readily applied to the sensitivity-limited samples. The sampling scheme utilizes continuous, non-uniform sampling profile for the indirect dimension, i.e. the acquisition number decreases as a function of the evolution time (t1) in the indirect dimension. For a beta amyloid (Aβ) fibril sample, we observed overall 40 ~ 50% signal enhancement by measuring the cross peak volume, while the cross peak linewidths remained comparable to the linewidths obtained by regular sampling and processing strategies. Both the linear and Gaussian decay functions for the acquisition numbers result in similar percentage of increment in signal. In addition, we demonstrated that this sampling approach can be applied with different dipolar recoupling approaches such as radiofrequency assisted diffusion (RAD) and finite-pulse radio-frequency-driven recoupling (fpRFDR). This sampling scheme is especially suitable for the sensitivity-limited samples which require long signal averaging for each t1 point, for instance the biological membrane proteins where only a small fraction of the sample is isotopically labeled.

Introduction

The two-dimensional (2D) NMR spectroscopy has been widely applied to determine the molecular structure of large biomolecules such as amyloid fibrils and membrane proteins.[1,2] A regular 2D NMR dataset contains a series of time-domain free induction decays (FIDs) with a uniform increment in the evolution period in the indirect dimension (t1), and each FID is usually acquired with the same acquisition numbers. The number of FIDs is determined by the total evolution period as well as the maximum t1 increment. The total evolution period is chosen so that the cross peaks in 2D spectrum have comparable linewidths along the direct and indirect dimensions after the Fourier transformation (FT). The maximum t1 increment is related to the designed frequency range in the indirect dimension. For the sensitivity-limited samples, certain types of window functions such as the Gaussian window are often applied to both the direct and indirect dimensions when processing the 2D spectra in order to achieve the acceptable signal-to-noise ratio. The application of Gaussian windows in the indirect dimension is equivalent to the addition of a weighing factor to the entire 2D dataset, i.e., the information from the FIDs acquired with longer t1 are diminished even though they contribute to the total experimental time. In the present work, we describe an alternative sampling scheme with the acquisition number decreases continuously as a function of t1, while keeping the maximum t1 period and the total experimental time the same as for the regular sampling scheme. This sampling scheme essentially spent most of the experimental time on the FIDs with greater signal comparing with the noise. Processing such 2D datasets requires no window function along the indirect dimension since the acquisition profiles themselves have the similar effect. We will show that this sampling scheme applied on a selectively labeled beta amyloid (Aβ) fibril sample induces 40 ~ 50 % overall increase in the cross peak volumes with comparable linewidths as those obtained with the regular sampling scheme. This will result in a reduction of the experimental time by the factor of 2 for acquiring a 2D spectrum with similar quality.

Experimental Section

Samples

All experiments were conducted on an Aβ fibril sample with ¹³C, ¹⁵N-uniform labeling on the residues Phe20, Asp23, Val24, Lys28, Gly29, Ala30 and Ile31. The peptide synthesis and the preparation of the sample have been described previously.[3]

NMR experiments

All experiments were performed at 9.4 T (100.4 MHz ¹³C NMR frequency) with a Varian InfinityPlus spectrometer and a Varian 3.2 mm magic angle spinning (MAS) probe. The 2D ¹³C-¹³C correlation experiments were initialized with 70 kHz π/2 radiofrequency (rf) pulse on the ¹H channel, which was followed by 50 kHz cross polarization (CP) with adiabatic ramp on the ¹³C channel. For the rf-assisted diffusion (RAD), the MAS speed was 10 kHz, the mixing period was 10 ms and the ¹H rf amplitude was set to ~ 60 kHz during CP. For the finite-pulse radiofrequency-driven recoupling (fpRFDR),[4] the sample was spinning at 20 kHz, the mixing period was 1.6 ms and ~ 69 kHz ¹H rf was used during CP. The finite π pulses during the RFDR mixing period were 15.0 μs, and for both experiments, a 105 kHz ¹H decoupling field was applied during the evolution, mixing and acquisition periods. For both RAD and fpRFDR experiments, the t1 increment was set to 36.8 μs and the maximum t1 was 3.5 ms with 96 real and image FIDs in the indirect dimension.

The acquisition profiles for 2D experiments were set up as follows: Initially, a one-dimensional (1D) ¹³C CP spectrum was acquired and the intrinsic line width was determined by measuring the full-width at the half maximum (FWHM) of several distinct peaks. The maximum t1 time was then estimated according to literature with a designed indirect dimension linewidths,[5] and the number of t1 points was determined from the maximum t1 time and the designed frequency range for the indirect dimension. The maximum t1 time was fixed for all the acquisition profiles. The acquisition numbers for each t1 point were setup according to Figure 1 to satisfy the criteria that the total experimental time was constant for all profiles, i.e. the area below each curve was the same. Practically, the acquisition number was first calculated according to linear or Gaussian function, and then rounded to the nearest integer. To determine the effect of acquisition profiles, we measured the indirect dimension ¹³C FWHM and the cross peak volumes. The cross peak volume was measured by integrating a 10 pts × 10 pts region around the center of the selected peak using nmrPipe software. For RAD experiments, the selected peaks were F20 Cα/Cβ, D23 Cα/Cβ, V24 Cα/Cβ, K28 Cα/Cγ, G29 Cα/C, A30 Cα/Cβ, I31 Cα/Cβ and I31 Cα/Cγ1. For fpRFDR experiments, the selected peaks were V24 Cα/Cβ, G29 Cα/C, A30 Cα/Cβ and I31 Cα/Cβ. These peaks were selected because they were clearly distinct from other signals in the spectra.

Figure 1.

The (A) linear and (B) Gaussian acquisition profiles for the continuous, non-uniform sampling scheme. For each plot, the horizontal axis was the index of t1 points and the vertical axis was the acquisition numbers. The linear and Gaussian profiles were chosen in such that the total number of t1 points and the areas under the profiles were kept constant. For the curves in panel (A), the nomination such as “linear 50%” means that the number of scans decays to 50% (i.e. 32 scans) comparing with the “square” profile. For the curves in panel (B), the “Gaussian 30” means that the width of the Gaussian curve was set to 30% of the total t1.

Results

The indirect dimension linewidths can be restored by using linear or Gaussian acquisition profiles with slow decay

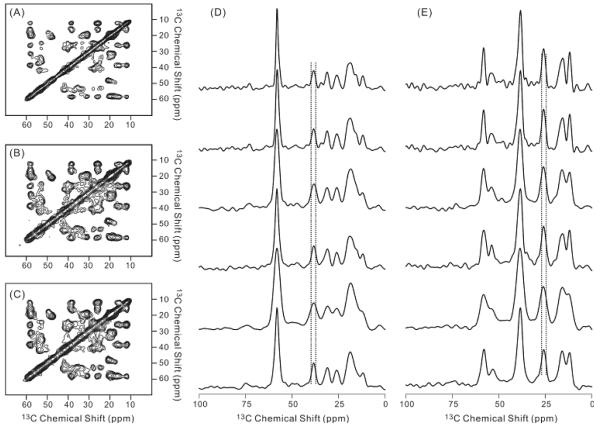
Figure 2(A)-(C) showed the 2D contour plots for the RAD experiments with the acquisition profiles “square”, “linear 50%” and “Gaussian 50”, respectively. It is clear that the spectrum features were retained by using the non-uniform sampling scheme. The 1D slice in figure 2(D)-(E) showed the change of linewidths in the indirect dimension for different acquisition profiles. The top two slices showed the linewidths from regular acquisition with and without additional line broadening during the processing. The following slices showed the spectra linewidths using “linear 100%”, “linear 50%”, “Gaussian 30” and “Gaussian 50” profiles, respectively. The profiles “linear 100%” and “Gaussian 30” generated cross peak linewidths that were considerably larger comparing with the “square” profile; however, the linewidths could be restored by using slower decay profiles such as “linear 50%” and “Gaussian 50”. The FWHM for the “linear 50%” or “Gaussian 50” spectra were comparable to the FWHM for the “square” spectrum with additional line broadening, while ~ 20% broader than the linewidths for without line broadening. This result suggested that the weighing factor applied during the acquisition had similar effect as the weighing factor applied during the processing in terms of the spectral resolution. The 1D slices shown in figure 2(D) and 2(E) also indicated that the corresponding peaks in the contour plots 2(A-C) had comparable linewidths. Since these plots were presented with the same first contour level height and contour level factor,[6] the fact that the peaks in figure 2(B) and 2(C) looked broader then the corresponding peaks in figure 2(A) suggested qualitatively that the spectra obtained by “linear 50%” or “Gaussian 50” profiles had higher peak intensities comparing with the “square” spectrum, with the assumption that all peaks had the same line shape.

Figure 2.

The panels (A)-(C) showed the 2D RAD contour plots for the spectra acquired using “square”, “linear 50%” and “Gaussian 50” acquisition profiles, respectively. The spectrum (A) was processed with 100 Hz Gaussian line broadening in both direct and indirect dimensions. The spectra (B) and (C) were processed with 100 Hz Gaussian line broadening in the direct dimension, but no line broadening in the indirect dimension. All spectra were shown with the same cut-off contour level in the nmrpipe software. The panels (D)-(E) displayed two sets of representative 1D slices along 58.3 ppm and 38.5 ppm in the direct dimension, respectively. The acquisition profiles used to obtain the 1D spectrum were “square” (processed with zero line broadening in the indirect dimension), “square” (processed with 100 Hz line broadening in the indirect dimension), “linear 100%”, “linear 50%”, “Gaussian 30” and “Gaussian 50” from top to bottom. The vertical dashed lines were used to show the FWHM in the top 1D spectrum (i.e. “square” acquisition profile) for the corresponding peak in each panel.

There is an overall 40~50 % signal enhancement using the continuous, non-uniform sampling schemes

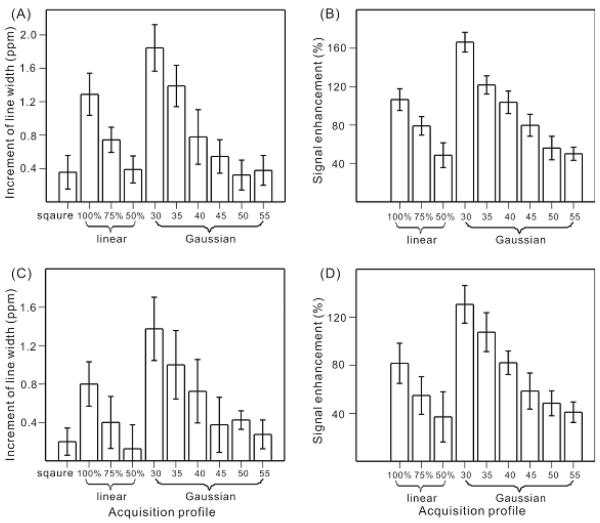
Figure 3 displays a quantitative analysis to the change of the indirect dimension linewidths and cross peak volumes for different acquisition profiles. For the particular amyloid fibril sample with ~ 2 ppm intrinsic linewidths, there was a ~ 0.4 ppm additional line broadening in the indirect dimension due to the applying of the Gaussian window functions. Practically, this 20 % line broadening will be present for the sensitivity-limited sample as the trade-off between a reasonable signal-to-noise ratio and an acceptable spectra resolution. Figure 3(A) showed that the same amount of line broadening in the indirect dimension can be achieved using “linear 50%” or “Gaussian 50” acquisition profiles with no additional Gaussian window function during processing. Quantitatively, there were 87 ± 16 %, 65 ± 12 %, 36 ± 14 %, 25 ± 9 %, 15 ± 8 % and 18 ± 9 % increments in the linewidths comparing with the 2 ppm intrinsic linewidth for this sample by applying “gaussian 30”, “gaussian 35”, “gaussian 40”, “gaussian 45”, “gaussian 50” and “guassian 55” profiles, respectively. Figure 3(A) also indicated that there was a broad range of linewidth increment using the non-uniform sampling scheme. One possible explanation was that different labeled sites in the sample have different relaxation rate. Therefore, the truncation effect due to the acquisition profiles was not uniform for all labeled sites. As shown in figure 3(B), while the linewidths was comparable, the non-uniform sampling schemes resulted in 40~50 % increase in the cross peak volume. The signal enhancement was due to the fact that most of the experimental time has been distributed to the FIDs with short t1 and stronger signal, as well as the fact that all the experimental data was retained during the processing of the FIDs. The similar amount of linewidths increment and signal enhancement were observed for 2D ¹³C/¹³C correlation experiment using fpRFDR mixing (Figure 3(C) and 3(D)), which suggested that the modification on acquisition was robust and may be applied with different mixing pulse sequences. The combination of figure 3(A) and 3(C) suggested that the increment of linewidths did not change significantly for the gaussian profiles 45, 50 and 55, although figure 3(A) seemed to indicate a slightly larger linewidth increment for 55 comparing with 50. However, the signal enhancement seemed to be smaller with larger gaussian profile widths, as shown in figure 3(B) and 3(D). Therefore, the optimized gaussian acquisition profile may have half width at half maximum (HWHM) around 1.8 ms, as calculated for the gaussian 45 profile.

Figure 3.

Plots of the increment in the indirect dimension linewidths (A and C) and the signal enhancement (B and D) by applying the non-uniform sampling schemes to the 2D-RAD (A and B) and 2D-fpRFDR (C and D) experiments. The linewidths increment was calculated by comparing the FWHM of the selected cross peaks (specified in the experimental section) in the corresponding spectrum to the calculated linewidths according to the literature method.[5] The signal enhancement was determined by comparing the cross peak volumes obtained by linear or Gaussian acquisition profiles to the ones by the regular profile. In plots A and C, the spectra with “square acquisition profile” were processed with 100 Hz Gaussian line broadening in both direct and indirect dimension. The error bars represented the standard deviation of the same analysis for several cross peaks.

In order to assess the change in the signal-to-noise (S/N) ratio due to the modification of acquisition profiles, we performed analysis on the spectra noise by integrating over 10 different regions in each spectrum where there was no cross peak. The average and standard deviation of the absolute values of the 10 independent measurements was reported in Table1. The results indicated that the change of average noise over different acquisition profiles was within ± 20%. Comparing with the relatively large standard deviation for the 10 independent measurements, it was reasonable to assume that the spectrum noise was not affected significantly by using non-uniform acquisition profiles. Figure 3(B) and 3(D) then illustrated that the S/N ratio should decrease as a function of the widths of the Gaussian acquisition profiles. Therefore, the present sampling scheme was in principle different from the “matched filter” approach in which the S/N ratio reaches the maximum value when the applied weighing function matches the intrinsic linewidth in the original spectrum.

Table 1.

Noise analysis for the spectra acquired using non-uniform sampling schemes.^a

Acquisition Profiles	Average	Standard deviation	Difference from the square profiled (%)
Square (no LB)b	5.2e7	4.1e7	-----
Square (100 LB)c	4.8e7	4.4e7	−9.2
Linear 100%	5.9e7	3.6e7	11.1
Linear 75%	4.4e7	4.0e7	−18.6
Linear 50%	4.5e7	2.6e7	−15.9
Gaussian 30	6.6e7	3.9e7	21.2
Gaussian 35	4.5e7	2.8e7	−16.0
Gaussian 40	5.5e7	2.6e7	5.4
Gaussian 45	4.3e7	2.3e7	−21.1
Gaussian 50	5.6e7	3.1e7	7.0
Gaussian 55	5.3e7	3.8e7	1.3

^aAnalysis has only been performed for 2D-RAD experiments.

^bSquare acquisition profile with 100 Hz Gaussian line broadening along t2 and zero line broadening along t1.

^cSquare acquisition profile with 100 Hz Gaussian line broadening along t1 and t2 dimensions.

^dPercentage of change in the average noise comparing with square (no LB).

Discussion

Depending on the nature of the NMR samples, the data collection approaches are generally classified into two categories: the “sampling-limited” regime and the “sensitivity-limited” regime. In the “sampling-limited” regime where 3D or higher dimensional experiments are often involved, a variety of sampling methods including reduced dimensionality, projective reconstruction, covariance NMR and filter diagonalization have been proposed to reduce the experimental time.[7-11] In the “sensitivity-limited” regime, the concept of using the non-uniform acquisition numbers for each t1 point to achieve signal enhancement in 2D spectroscopy was first mentioned by Levitt and coworkers in 1984.[12] However, most of the studies have been focused on the exponential discrete sampling which requires complicated data processing methods such as maximum entropy reconstruction algorithm.[13-16] The present work demonstrated experimentally that the concept of “non-uniform sampling” can be implemented in a simpler way as far as the sampling is in the “sensitivity-limited” regime. Using the optimized linear or Gaussian acquisition profiles, the proposed continuous non-uniform sampling scheme resulted in 40~50 % enhancement in the cross peak volume, and therefore could potentially shorten the experimental time by the factor of 2. Comparing with the discrete non-uniform sampling methods, the present scheme resulted in similar salvage of sampling time but with more straightforward data processing approach.[17] For instance, the sampling scheme is suitable for the membrane protein systems where the isotope-labeled proteins were diluted by the unlabeled phospholipids vesicles. Due to the restriction of the total sample volume in solid state NMR experiments, those samples are usually in the “sensitivity-limited” regime. Although the Aβ fibril samples had ~ 2 ppm linewidths, the application of the scheme should not be restricted by the linewidths because it essentially only changes the distribution of acquisition numbers within different t1 points while the maximum t1 number was “intrinsically” determined by the linewidths. The same idea may also be applied to 3D or 4D experiments as far as the experiment is in the “sensitivity-limited” regime and this will in principle shorten the experimental time by the factor of 4 or 8, respectively. In addition, the sampling scheme is not limited to the ¹³C/¹³C correlation experiments. The application on ¹⁵N/¹³C correlation sequences resulted in similar degree of signal enhancement. The scheme may also be applied to the 2D CHHC or NHHC experiments where the signal to noise was usually low.[18] However, the number of scans may need to be set to the integers of four to fulfill the complete phase cycling.

Conclusion

The present work showed that 40~50 % signal enhancement can be achieved in 2D spectrum for a sensitivity-limited Aβ fibril sample by using the continuous, non-uniform sampling scheme, where the acquisition numbers decay as a function of the t1 period. This approach simply spent most of the experimental time on the FIDs with short t1 which contributed stronger signals. Both linear and Gaussian decay curves resulted in similar amount of signal enhancement when the slope of the linear function or the width of the Gaussian function was appropriately adjusted. For the Aβ fibril sample, we demonstrated that the optimized results were obtained when the width of the decay profiles was equivalent to one half of the entire t1 period. This sampling scheme can be in principle applied to all “sensitivity-limited” multidimensional NMR experiments where each FID in the indirect dimension required large acquisition numbers.