Insect hygroreceptor responses to continuous changes in humidity and air pressure

Abstract

The most favored model of humidity transduction views the cuticular wall of insect hygroreceptive sensilla as a hygromechanical transducer. Hygroscopic swelling or shrinking alters the geometry of the wall, deforming the dendritic membranes of the moist and dry cells. The small size the sensilla and their position surrounded by elevated structures creates technical difficulties to mechanically stimulate them by direct contact. The present study investigated hygroreceptors on the antennae of the cockroach and the stick insect. Accurately controlled, homogeneous mechanical input was delivered by modulating air pressure. Both the moist and dry cells responded not only to changes in air pressure, but also in the opposite direction, as observed during changes in air humidity. The moist-cell’s excitatory response to increasing humidity and increasing air pressure implies that swelling of the hygroscopic cuticle compresses the dendrites, and the dry-cell’s excitatory response to decreasing humidity and decreasing air pressure implies that shrinking of the hygroscopic cuticle expands the dendrites. The moist and dry cells of the stick insect are more sensitive to pressure changes than those of the cockroach, but the responses to air pressure are generally weaker than to humidity. Therefore, the hygroreceptive sensilla differ in their physical properties and constitutions. Furthermore, the mechanical parameters associated with homogeneous changes in air pressure on the sensillum surface can only partially account for the responses of the moist and dry cells of both species to humidity stimulation.

Introduction

The mechanisms underlying the impressive ability of many insect species to react behaviorally to humidity gradients are still poorly understood. Experiments on humidity transduction present many technical difficulties beyond those involved in the electrophysiological study of the function of the dual system (i.e. moist cells and dry cells) of hygroreceptors. The various notions concerning the transduction process have been summed up in three models (Tichy and Loftus 1996). The first model is based on a mechanical mode of action similar to a hair hygrometer in which activity is initiated by swelling and shrinking of hygroscopic sensillum structures. The second model holds that hygroreceptors operate as psychrometers in which the degree of cooling due to evaporation of water from the sensillum surface is used to measure the humidity (or the dryness) of the air. In the third model, humidity affects the electrolyte concentration just outside the dendritic processes of the hygroreceptive cells. The drier the air, the greater the evaporation rate of water out of the sensillum, and the greater the quantitative changes in the electrolyte concentration.

The mechanical hygrometer model, most favored in the literature, was developed based on the close association of the sensillum wall with the dendritic membranes (Fig. 1A,B; Altner et al. 1983). Supporting evidence for a mechanical action came from moving the electrode minimally during the electrophysiological recordings (in the cockroach, Yokohari 1978; in the cricket, Itoh et al 1984) or from applying external pressure on the sensillum tip (in the moth, Becker 1978). Both can influence the firing rate of the moist and dry cells. These findings contradict related attempts to modulate the discharge rates of the hygroreceptive cells in a reversible manner by slight lateral movements of the recording electrode in both the cockroach (Loftus 1976) and the stick insect (Tichy 1979). A more quantitative approach to demonstrate swelling and shrinking of the sensillum wall involved high-resolution scans of the fine surface structures of the apical region of hygroreceptive sensilla in the honey bee using atomic force microscopy (Resch et al 1998). However, no change in the dimensions of the sensillum wall became apparent when ambient humidity was set at different levels.

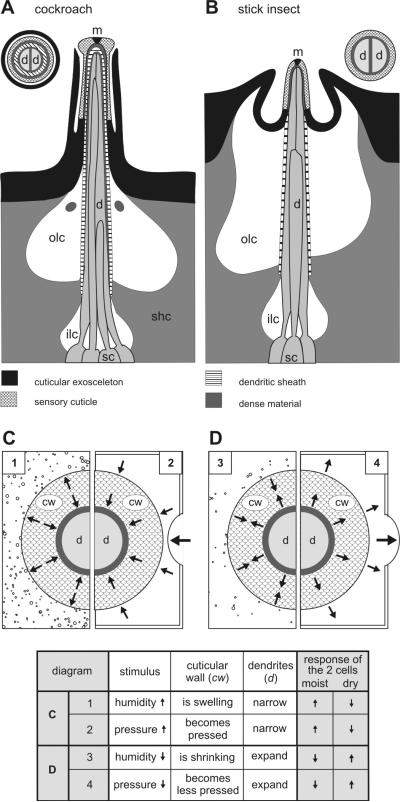
Fig. 1.

A-D: Diagram of the hygroreceptive sensilla on the cockroach and stick insect antenna and proposed effects of changes in humidity and air pressure. A and B: the cuticular processes, cellular associations and lymph cavities in longitudinal section. The main feature common to both insects is a thin-walled sensillum cuticle that lacks a pore system to connect the lumen of the dendritic sheath with outside. The molting pore (m) at the tip is plugged by dense material. Of the three or four sensory cells innervating the sensillum, two possess unbranched outer dendritic segments (d) extending up to the apex of the cuticular peg. The dendritic terminals entering the narrow lumen allow only a small space to separate them from the dendritic sheath and from each other. Dense material accumulates in the space towards the apex of the peg. Farther inside, below the base of the peg, the space opens out to form the small inner receptor lymph cavity (ilc). This cavity encloses the central portion of the dendrites between their inner and outer segments, and is surrounded by sheath cells (shc). Outside the sheath there is a more voluminous space, the outer receptor lymph cavity (olc) (after Tichy and Loftus 1996). C and D: proposed effects of changes in humidity (left side in both diagrams) and changes in air pressure (right side in both diagrams) on the cuticular wall (cw) and the dendritic processes (d) of the moist and dry cell. Swelling or expanding of the sensory cuticle, due to its tendency to take up water, increases the discharge rate of the moist cell and decreases that of the dry cell (Tichy 1987; Fig. 1C); conversely, shrinking or contracting of the cuticular wall, due to its tendency to lose water, increases the discharge rate of the dry cell and decreases that of the moist cell (Fig. 1D). The internal pressure increase during swelling is imitated by increasing air pressure (Fig. 1C), and the internal decrease in pressure during shrinking is imitated by decreasing air pressure (Fig. 1D)

The present study therefore opted to provide accurately controlled mechanical input to the dendritic membranes while avoiding direct contact with the sensillum wall. We developed equipment that delivered precisely timed and dosed changes of the air pressure on the preparation. To facilitate the comparison with the method of changes in humidity, we applied slow and continuous pressure changes at different rates. We investigated two morphological types of hygroreceptive sensilla, one on the antennae of the cockroach (Yokohari 1978; Tominaga et al 1982) and the other on the stick insect (Altner et al 1978). We found that the moist and dry cells respond oppositely to continuous changes in air pressure, as to changes in humidity. Nevertheless, the responses are weaker to air pressure than to humidity. Furthermore, both cell types are more sensitive to pressure changes in the stick insect than in the cockroach. Our data suggest that the hygroreceptive sensilla differ in their physical properties and constitutions. They also suggest that the mechanical parameters associated with homogeneous changes in air pressure can only partially account for the responses of the moist and dry cells of both species to humidity stimulation.

Sensillum structures and possible effects of humidity and pressure stimulation

Understanding the first event in the stimulation of hygroreceptive cells requires understanding the sensillum structures and how deformations of the dendritic membranes of the two cell types are caused by cuticular wall swelling and shrinkage due to humidity changes and to the forces imposed on the wall due to air pressure changes.

Externally, hygroreceptive sensilla can be described as small, peg-like cuticular structures with a cap like a mushroom or with a rounded tip (Altner et al. 1983). The first type includes the sensillum capitulum of the cockroach (Fig. 1A; Yokohari 1978; Tominaga et al. 1982), the second type the stick insect’s peg-in-pit sensillum (Fig. 1B; Altner et al. 1978). Their position on the antennae appears to be a trade-off between exposure and protection. While the occurrence on a body appendage enhances the contact with ambient air, abrasion by encountered objects demands protection by elevated surrounding structures. The cockroach’s sensillum capitulum projects from the antenna surface but is overtowered by neighboring hairs. A tightly fitting protection wall encloses the mushroom-shaped stem, so tight that it can be taken for a thin outer wall of the sensillum with a ring-shaped opening just under the cap (Fig. 1A). In the stick insect, on the other hand, the peg-in-pit sensillum is located in a cavity and surrounded by an inflated collar (Fig. 1B).

The sensillum wall typically lacks pores, except for a single terminal molting pore plugged by electron-dense material. The wall consists of cuticle and is discarded at molt together with the exuvium. Thickness varies but is generally < 1 μm – in the cockroach 0.3 μm (Fig. 15 in Yokohari 1981) and in the stick insect 0.6 μm (Fig. 2 in Tichy 2007). The dendrites of two of the three or four sensory cells are quite long, closely adjoining, and extend far out into the peg. The third dendrite branches and sends numerous slender extensions into the peg (cockroach, Fig. 1A) or is folded and terminates below the cuticle (stick insect, Fig. 1B). Two sensory cells have been identified as hygroreceptive (a moist and a dry cell) and one as thermoreceptive (a cold cell). Their total of three dictates that at least one of the two long dendrites is a hygroreceptor. However, the two long dendrites probably have similar function and belong to the two hygroreceptors. Consequently, the third is considered to be thermoreceptive.

A dendritic sheath encloses the dendrites in a small lumen filled with finely granular lymph. In the cockroach, the sheath extends up to the sensillum tip, where it narrows to form an apex just inside the tip (Fig. 1A). In the stick insect, the sheath terminates deeper, near the base of the cuticular peg. Here, the sheath merges with the inside of the peg wall so that the outer region of the dendrites seems to be enclosed directly within the wall rather than within the sheath (Fig. 1B). The dendritic membranes need to be intimately associated with the wall. Too much lymph in between could cushion the volume changes in the wall and impede their effect on the dendrites. But if the wall is so hygroscopic that it withdraws sufficient water vapor from the air to produce a graded effect on the dendrites, it could as well withdraw water from the inside. We suggested that the dendritic sheath provides waterproofing to the side (Tichy and Loftus 1996). Studying the resolving power of the stick-insect’s moist and dry cells for steady-state humidity revealed that both cell types withstood several 6-min periods of adaptation in an air stream of 0% relative humidity (Tichy 1978). Since the air stream traveled at 2.5 ms⁻¹ and the sensillum diameter was < 25 μm, the dry air flowed at more than 10⁶ sensillum diameters per second. Relative to the sensillum, the mass of air contacting it per second is very great. Lack of effective insulation would have immediately dried the sensilla out.

The cuticular wall swells or expands due to its tendency to take up water. This, in turn, increases the discharge rate of the moist cell and decreases that of the dry cell (Fig. 1C); conversely, the cuticular wall would shrink or contract because it tends to lose water. This increases the discharge rate of the moist cell and lowers that of the dry cell (Fig. 1D). The effects of swelling and shrinking cannot be realized from moist and dry cell responses during humidity changes. Swelling of the cuticular wall would be expected to increase the internal pressure (Fig. 1E), shrinking to decrease it (Fig. 1F). Just as the forces caused by swelling and shrinking stimulate the moist and dry cells, we propose that the internal pressure changes due to external changes in air pressure have similar effects on the discharge rates of both types of cells. Note, however, that the mechanical model considers the thin cuticular wall (< 1 μm) to be hygroscopic, thereby balancing out its moisture content with the surrounding air. In both insects, the moist and dry cells respond with transient discharge rates when an adapting air stream aimed at the sensillum was replaced within 15 ms by another air stream having a different humidity (Tichy 1978; Tichy and Loftus 1990). Other hygroscopic materials like human hair (average width 50 μm) or wood, when exposed to a new humidity, will exchange humidity considerably slower as indicated by their slow change in dimensions. Such materials are therefore hardly useful to imitate the effects of swelling and shrinking by changing air pressures.

Methods

Animals and location of hygroreceptive sensilla

We used adult cockroaches (Periplaneta americana) and stick insects (Caurausius morosus) from our laboratory cultures. In the cockroach, the hygroreceptive sensilla are located on the distal half of the antennae, only on the ventral side near or even directly beneath a segment’s most distal and thickest bristles. They are often located on alternating segments, about 20 per antenna and rarely more than one per segment. In the stick insect, on the other hand, only one hygroreceptive sensillum is present on the antenna: on the 12^th antennal segment in a field of about 50 olfactory and mechanoreceptive sensilla.

Electrophysiology

Following anaesthesia with CO₂, the animals were immobilized on a Plexiglas holder using strips of adhesive tape. One antenna was fastened with dental cement (Harvard Cement) on a narrow Plexiglas support for unobstructed stimulation with an air stream of changing humidity. Action potentials were recorded between two electrolytically sharpened tungsten wires, one inserted at an angle of about 45° into the sensillum base, and the other lengthwise about 2 mm into the tip of the antenna. After amplification, the band pass (0.1 – 3 kHz) filtered signals were passed through an AD-converter (1401 plus, Cambridge Electronic Design; 12-bit; 10 kHz) and fed into a PC for online recording. Data were stored on a hard disk and analyzed off-line using the Spike 2 software (Cambridge Electronic Design). Spike detection and classification was done by tools based on the spike waveform shape in combination with the template waveform matching system. It allows classification by a template setting dialog and by continuously controlling the template forming process. Selected periods can be run again with different template parameters and data can be reclassified either automatically or manually.

Humidity stimulation

Quantitative stimulation was provided by an air stream continuously flowing over the antenna. Compressed air was cleaned, dried and split into two streams. Their flow rates were equalized by matching the rates in mass flow meters. The first stream was bubbled out through many openings in a polyethylene tube firmly anchored in a tank containing ion-exchange water at constant depth and a temperature of 42°C. The second stream was conducted through the tank in a spiral tube and remained dry as it was warmed to 42°C. The temperature of the two streams was then set at 22°C by driving them through a further self-made thermostatically controlled heat exchanger. After emerging from the heat exchanger, the two air streams passed through electrical proportional valves (KWS 3/4, Kolvenbach) and then were combined to a single stream. The water vapor pressure of this stream was sinusoidally modulated by mixing the two streams in a ratio determined by the proportional valves. To hold the flow rate of the mixed air constant at 2.5 ms⁻¹, the control voltages (AD-converter, 1401 plus, Cambridge Electronic Design) of the proportional valves were phase shifted by 180°. The mixed air was divided into two streams. For stimulation, the first stream was directed towards the antenna by way of a Plexiglas tube 7 mm in diameter. The hygroreceptive sensillum was 5 mm away from the outlet of the tube. By passing the second stream through a 1-cm³ detection chamber of a UV-absorption hygrometer (K 20, Campbell Scientific), water vapor density was measured at a high rate of 100 Hz. Based on the water vapor density and temperature, as determined by a fine-wire thermocouple (wire diameter 13 μm, Type E, Campbell Scientific) positioned within the air stream, the relative humidity was determined.

A simple, non-quantitative form of humidity stimulation utilized hand-operated 25 ml polyethylene syringes filled with moist glass wool or desiccant material (silica gel). The syringe was positioned a few millimetres away from the antenna with the opening directed to the hygroreceptive sensillum. By moving down the piston the moist or dry air was expelled from the syringe. The time course of the air puff was not measured.

Pressure stimulation

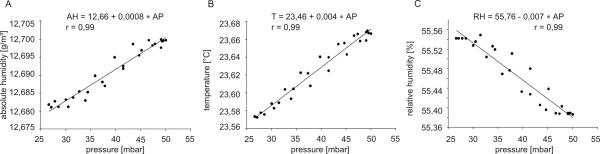
The recording setup was mounted on a platform inside a see-through Plexiglas box which could be lifted in order to insert the recording electrode and test the stability of the hygroreceptor’s activity under atmospheric pressure. Then the box was lowered on a sealing band and sealed airtight by weighing it down. Air pressure inside the box was slightly increased by adding air with an aquarium pump, yielding a flat pressure value between 10 and 20 mbar above atmospheric pressure. By moving a piston of a cylinder that was connected on both sides with the box, the flat pressure value was slowly and continuously modulated in a sinusoidal fashion. Positive air pressure changes were achieved by pushing air in and negative air pressure changes by pulling it out. Air pressure was measured by a gauge pressure sensor (Honeywell) positioned outside the box but connected by a nylon tube with the box. The gauge pressure sensor was calibrated to measure the pressure relative to the atmospheric pressure at the laboratory. A pressure gauge reading of 0 mbar at sea level actually represents 1013 mbar with reference to vacuum; at the Vienna city centre, at an altitude of 171 m, the pressure value actually represents 1009 mbar. The relative humidity was determined by connecting the airtight box with a 1-cm³ detection chamber of a UV-absorption hygrometer (K 20, Campbell Scientific) and another containing a fine-wire thermocouple (wire diameter 13 μm, Type E, Campbell Scientific). Changing the air pressure changed both the absolute humidity and the temperature (Fig. 2). As indicated by the slope of the regression lines, boosting the air pressure by 1 mbar increases the absolute humidity by 0.0008 g/m³ (Fig. 2A) and the temperature by 0.004 °C (Fig. 2B). Accordingly, an increasing air pressure by 1 mbar drops the relative humidity by 0.007 % (Fig. 2C). Although the absolute humidity increases, the relative humidity decreases due to the increase in temperature. Thus, increasing the relative humidity by 1 % requires decreasing the air pressure by 142 mbar. This value is almost three times greater than the 50-mbar pressure changes tested here. In a previous study the resolving power of the stick-insect’s moist and dry cells was found to be 5% relative humidity (Tichy 1978). Thus, the changes in relative humidity produced by changing air pressure are quite below the detection limit of the moist cells and the dry cells.

Fig. 2.

A-C: Effects of changes in air pressure on the absolute humidity, the temperature and the relative humidity inside the pressure chamber. A: absolute humidity plotted as function of air pressure. B: temperature plotted as function of air pressure. C: relative humidity determined from values in A and B as function of air pressure. Relationships approximated by linear regressions, AH absolute humidity, RH relative humidity, r correlation coefficient, T temperature

Air pressure and humidity

Relative humidity is defined as the relationship between the saturated water vapor pressure and the air’s partial water vapor pressure at a given temperature. Since saturation water vapor pressure increases with temperature, the relative humidity decreases with increasing temperature if the actual amount of water vapor stays the same (Fig. 3). In the temperature range between 20 and 30°C, any value from 0 and 100% relative humidity can be produced by adjusting the water vapor pressure between 0 and 40 mbar water vapor. In order to avoid producing physiologically excessive pressures inside the pressure chamber, the upper limit of air pressure was 50 mbar. The various humidity parameters were calculated by the Vaisala Humidity Calculator, a web-based software tool.

Fig. 3.

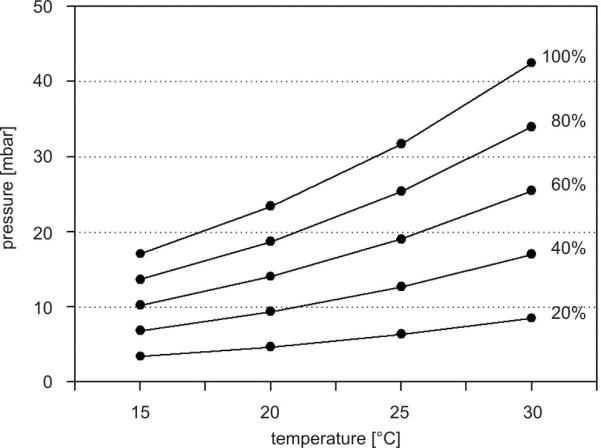
Calculated values of the relative humidity for different water vapor pressures and temperatures

Response magnitude and differential sensitivity

Impulse frequency (imp s⁻¹) was determined by the number of impulses over a time span of 0.5 s. The differential sensitivity is the mean change in impulse frequency for each unit change in stimulus magnitude. The quantity is given by the slope of the function that approximates the relation between stimulus parameters and response. Approximation was done with regression lines in 2-D plots or regression planes in 3-D plots using the least squares method.

Results

Identification

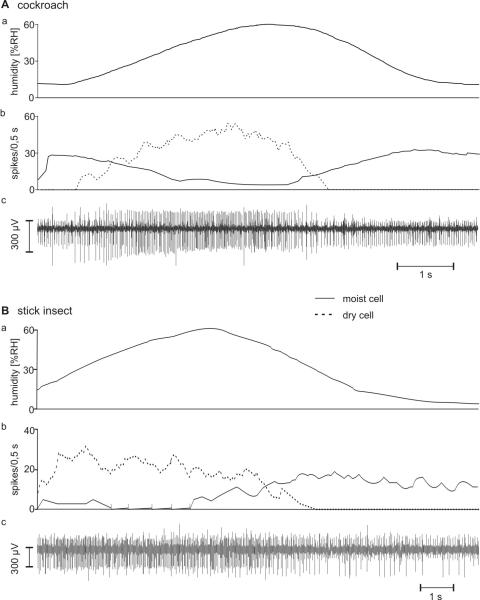
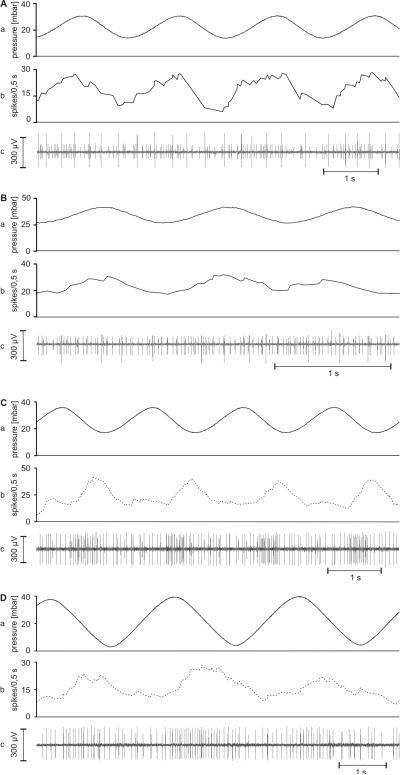
The two antagonistic hygroreceptive sensory cells (moist and dry) occur together with one thermoreceptive sensory cell (cold) forming a triad in a single sensillum on the antennae of the cockroach and the stick insect. Identification of the moist and dry cells was provided by their opposite responses to changes in humidity at constant temperatures. Responses to slow and continuous changes in humidity are shown in Fig. 4A,B. When the humidity of the air stream was increased, the moist cells responded with rising impulse frequency, the dry cells with lowered frequency. Upon reverse stimulation (humidity of air stream decreased) the dry cells responded with increasing impulse frequency, the moist cells with decreased frequency. The form of the impulses, however, varied. Their amplitudes differed from one recording to another and often tended to decrease during changes in humidity, but the ratio of the amplitudes of the moist and dry cells was constant. Some recordings revealed the activity of a third sensory cell, which displayed the largest amplitudes (Fig. 4Bc). Decreasing humidity caused this cell to slightly increase the discharge rate, but the response was less pronounced than in the dry cell. The strong reactions to falling temperature indicated a cold cell; such a cell has been demonstrated to occur together with the moist and dry cells in the same sensillum on the antennae of cockroaches (Loftus 1968; Yokohari 1978) and stick insects (Tichy 1979, 1978; Tichy and Loftus 1987).

Fig. 4.

A and B: Responses of the moist and dry cells to slow and continuous humidity changes. A: cockroach. B: stick insect. a time course of the relative humidity; b time course of the mean frequency (bin width, 0.5 s) of the moist cell (solid line) and the dry cell (dotted line); c extracellular recorded activity. In the cockroach, the moist cell displays larger impulse amplitudes than the dry cell; in the stick insect, impulses from the cold cell tend to be the largest; the moist-cell’s impulses are medium sized and those from the dry cell are the smallest

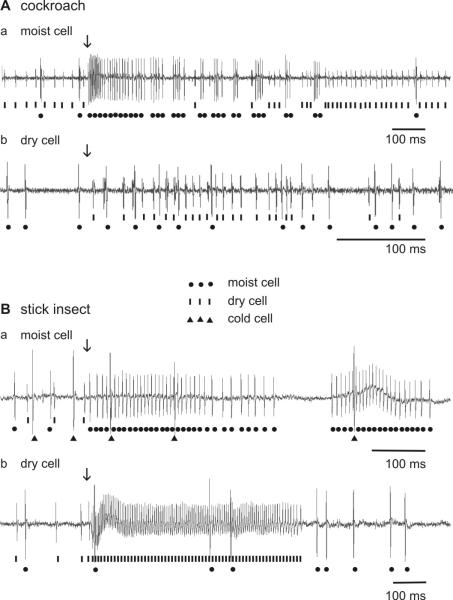
The same qualitative antagonistic responses of the moist and dry cells to slow and continuous changes in humidity can also be elicited by expelling air from syringes containing either moist glass wool or silica gel. In these situations, the discharge rate of one unit rose while that of the other remained unchanged or fell. The moist cells produced excitatory responses to puffs of moist air (in the cockroach, Fig. 5Aa; in the stick insect, Fig. 5Ba), and conversely, the dry cells to puffs of dry air (in the cockroach, Fig. 5Ab; in the stick insect, Fig. 5Bb). Upon termination of the air puffs, the discharge dropped at once to frequencies much lower than before stimulation.

Fig. 5.

A and B: Examples of the responses of the moist and dry cells to puffs of moist and dry air. A: cockroach. B: stick insect. a stimulus: moist air puff; b stimulus: dry air puff. Lines, impulses of moist cells; dots, impulses of dry cells; triangles, impulses of the cold cell. Arrows mark stimulus onset

Slowly changing humidity

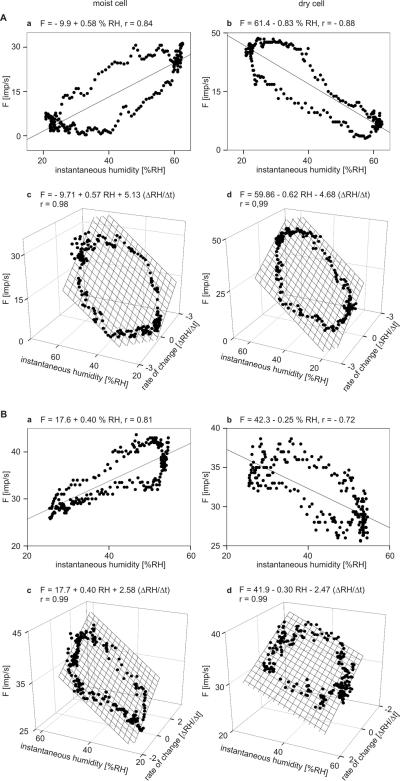
During oscillating changes in humidity at low rates between −2% and +2% RH s⁻¹ and at peak-to-peak amplitudes < 50% RH, the discharge rates of the moist cells and the dry cells of both the cockroach and the stick insect might be interpreted as the response to instantaneous humidity, i.e., the succession of humidities at particular instants in time (Fig. 4A,B). However, impulse frequencies of both types of cells did not depend exclusively on instantaneous humidity. Fig. 6Aab,Bab shows the responses of the moist and dry cells of both insects during a single “oscillation” period plotted as function of the humidities values passed through. The dependence of impulse frequency on instantaneous humidity is quite linear but the frequency curves for rising and falling values of instantaneous humidity did not coincide. The frequency curves approached closed figures that coarsely resemble an ellipse. This relationship emphasized that in each cell the same value of humidity can be accompanied by more than one value of frequency and that the sequence of frequency values is too orderly to attribute frequency differences at any given humidity simply to random variation in the response. Moreover, such closed curves are reminiscent of a Lissajous figure, in which two oscillating magnitudes are plotted one as a function of the other. The shape of the figures produced is determined by the ratio of the frequencies of the two oscillations, the ratio of their amplitudes and their phase differences. Of the possible parameters that might explain the Lissajous figures is the first differential of instantaneous humidity, the rate of humidity change.

Fig. 6.

A and B: Impulse frequency of the moist and dry cells as function of instantaneous humidity, and as function of both instantaneous humidity and rate of humidity change. A: cockroach. B: stick insect. a impulse frequency of a single moist plotted against instantaneous humidity. b impulse frequency of a single dry cell plotted against instantaneous humidity. Stimulus-response functions approximated by linear regressions (F = a + bRH; where F is the impulse frequency, a the height of the regression line, and b the slope of function indicating the mean change in impulse frequency for each percent change in instantaneous humidity). c impulse frequency of the same moist cell as in a plotted against instantaneous humidity and its rate of change. d impulse frequency of the same moist cell as in b plotted against instantaneous humidity and its rate of change. Multiple regressions which utilize 3-dimensional planes (F = a + bRH + c dRH/dt; where F is the impulse frequency, and a the height of the regression plane) are calculated to determine the simultaneous effects of instantaneous humidity (b-slope) and the rate of humidity change (c-slope) on the response frequencies of both cells. RH relative humidity, r correlation coefficient

To estimate the simultaneous effects of instantaneous humidity and the rate with which humidity changes, impulse frequency of each cell was plotted as a function of instantaneous humidity and its rate of change in Fig. 6Acd for the cockroach and in Fig. 6Bcd for the stick insect. Multiple regressions (F = a + b RH + c ΔRH/Δt; where F is the impulse frequency, and a the height of the regression plane) were then calculated to determine the differential sensitivities of impulse frequency for instantaneous humidity (b-slope) and the rate of humidity change (c-slope). The slopes demonstrate the two properties that characterize these cells: the sign of the slopes is positive for the moist cell and negative for the dry cell, i.e., an increase in both instantaneous humidity and the rate of humidity change led to a frequency increase in the moist cell but to a frequency decrease in the dry cell. These cells are typical for the 20 moist cells and the 20 dry cells examined in the cockroach and the stick insect. Basic data are summarized in Table 1.

Table 1.

Summary of data used to determine differential sensitivities of the moist and dry cells in cockroaches and stick insects

Type of receptors	Moist cell of cock- roach	Dry cell of cockroach	Moist cell of stick insect	Dry cell of stick insect
Stimulus: humidity
Range in which humidity oscillated, % RH	0 to 50	0 to 50	0 to 50	0 to 50
Range of the rate of humidity change, % RH s−1	−2 to +2	−2 to +2	−2 to +2	−2 to +2
Units tested extensively	38	40	42	38
Units used for multiple regressions	20	20	20	20
Number of multiple regressions	62	66	58	60
Number of points per multiple regression	< 175	< 175	< 175	< 175
Mean correlation coefficient, r	0.94 ± 0.19	0.93 ± 0.17	0.95 ± 0.18	0.96 ± 0.17
Mean differential sensitivity to instantaneous   humidity, imp s−1 / % RH	+ 0.52	−0.60	+0.42	−0.31
Mean differential sensitivity to the rate of hu-   midity change, imp s−1 / % RH s−1	+5.11	−4.62	+2.51	−2.41
Stimulus: pressure
Range in which pressure oscillated, mbar	5 to 45	5 to 45	5 to 45	5 to 45
Range of the rate of humidity change, mbar s−1	−10 to +10	−10 to +10	−10 to +10	−10 to +10
Units tested extensively	32	34	46	44
Units used for multiple regressions	20	20	20	20
Number of multiple regressions	60	60	68	68
Number of points per multiple regression	< 80	< 80	< 80	< 80
Mean correlation coefficient, r	0.98 ± 0.09	0.98 ± 0.09	0.97 ± 0.12	0.98 ± 0.11
Mean differential sensitivity to instantaneous   humidity, imp s−1 / mbar	+0.14	−0.16	+0.77	−0.45
Mean differential sensitivity to the rate of hu-   midity change, imp s−1 / mbar s−1	+0.15	−0.18	+0.52	−0.38

In the cockroach, mean sensitivity to instantaneous humidity (b-slope) was +0.5 (imp s⁻¹)/% RH for the moist cell (Fig. 6Ac) and −0.6 (imp s⁻¹)/% RH for the dry cell (Fig. 6Ad); mean sensitivity to the rate of humidity change (c-slope) was +5.1 (imp s⁻¹)/(% RH s⁻¹) for the moist cell (Fig. 6Ac) and −4.6 (imp s⁻¹)/(% RH s⁻¹) for the dry cell (Fig. 6Ad). Thus, in the moist cell an increase of 1 imp s⁻¹ can be elicited either by increasing instantaneous humidity +2 % RH, provided the rate of change is constant, or by increasing the rate of humidity change +0.1 % RH s⁻¹. In the dry cell, the corresponding values are −1.6 % RH and −0.2 % RH s⁻¹.

In the stick insect, mean sensitivity to instantaneous humidity (b-slope) was +0.4 (imp s⁻¹)/% RH for the moist cell (Fig. 6Bc) and −0.3 (imp s⁻¹)/% RH for the dry cell (Fig. 6Bd); mean sensitivity to the rate of humidity change (c-slope) was +2.5 (imp s⁻¹)/(% RH s⁻¹) for the moist cell (Fig. 6Bc) and −2.4 (imp s⁻¹)/(% RH s⁻¹) for the dry cell (Fig. 6Bd). Thus, in the moist cell an increase in 1 imp s⁻¹ can be elicited either by increasing instantaneous humidity +2.5% RH, provided the rate of change is constant, or by increasing the rate of humidity change +0.4 % RH s⁻¹. In the dry cell, of the corresponding values are −3.3% RH and −0.4 % RH s⁻¹.

Slowly changing air pressure

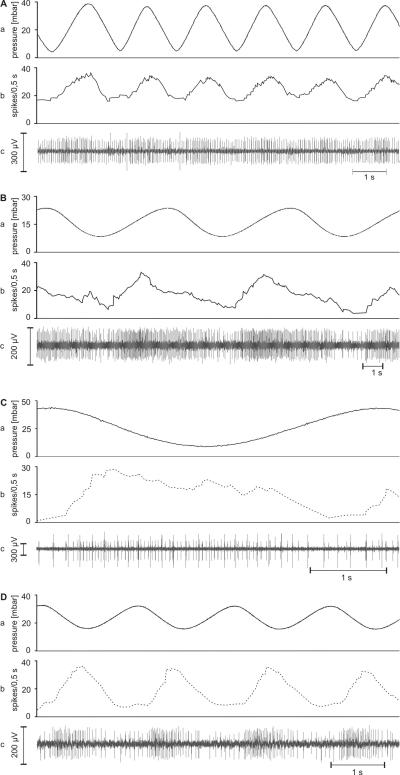
A different set of moist and dry cells from a total of 40 sensilla (20 each of the cockroach and the stick insect) were subjected to several series of oscillating changes in air pressure at low rates between −10 and +10 mbar s⁻¹. The range of air pressure covered was roughly 25 mbar between 5 and 45 mbar. Figures 7 and 8 clearly show that the moist and dry cells are modulated by such slow and continuous changes in air pressure. In the cockroach, however, oscillations with amplitudes smaller than 20 mbar hardly affected the discharge rates of either cell (Fig. 7), but in the stick insect, both cell types responded to oscillating pressure changes even at such small amplitudes (Fig. 8). It turned out that in both insects the discharge rate of the moist cells increased while air pressure rose and decreased as air pressure fell (Fig. 7AB; Fig. 8AB), and, conversely, the discharge rate of the dry cells increased by lowering air pressure and decreased by raising it (Fig 7CD; Fig. 8CD). Several recordings contained both types of cells distinguishable by the amplitude and form of their impulses, but the antagonistic responses observed during slow changes in humidity did not occur during slow changes in air pressure. Only one cell – either the moist or the dry one – changed its impulse frequency.

Fig. 7.

A-D: Examples of the responses of the cockroach’s moist and dry cells to slow and continuous pressure changes. A and B: moist cells from different recordings responding to increasing pressure. C and D: dry cells from different recordings responding to decreasing pressure. a time course of the air pressure; b time course of the mean frequency (bin width, 0.5 s) of the moist cell (solid line) and the dry cell (dotted line); c extracellular recorded activity

Fig. 8.

A-D: Examples of the responses of the stick insect’s moist and dry cells to slow and continuous pressure changes. A and B: moist cells from different recordings responding to increasing pressure. C and D: dry cells from different recordings responding to decreasing pressure. a time course of the air pressure; b time course of the mean frequency (bin width, 0.5 ms) of the a moist cell (solid line) and the dry cell (dotted line); c extracellular recorded activity

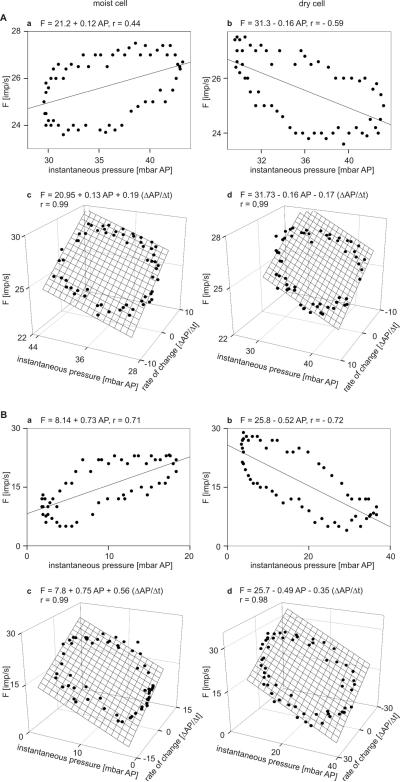
In Fig. 9Aab and Bab the responses of moist and dry cells of both the cockroach and the stick insect during a single “oscillation” period were plotted to give the dependence on instantaneous air pressure. The course of the points approaches an ellipse indicating that in addition to instantaneous air pressure the rate with which air pressure was changing affects impulse frequency. Multiple regressions (F = a + b RH + c ΔRH/Δt; where F is the impulse frequency, and a the height of the regression plane) were calculated to determine the simultaneous influence of air pressure and its rate of change (Fig. 9Acd,Bcd). The slopes indicate the differential sensitivity to instantaneous air pressure (b-slope) and low rate of pressure change (c-slope). In both insects, the sign of the slopes was positive for the moist and negative for the dry cells. Accordingly, increasing instantaneous pressure and its rate of change raised the impulse frequency of the moist cell and lowered it in the dry cell. Conversely, decreasing instantaneous pressure and its rate of change raised the impulse frequency of the dry cell and lowered it in the moist cell. Furthermore, the slopes were steep for both cells in the stick insect (Fig. 9Bcd) but flat in the cockroach (Fig. 9Acd). Thus, changes in instantaneous pressure or in the rate of pressure change had relatively small effects on cockroach cell activity but somewhat larger effects in the stick-insect.

Fig. 9.

A and B: Impulse frequency of the moist and dry cells as function of instantaneous pressure, and as function of both instantaneous pressure and rate of pressure change. A: cockroach. B: stick insect. a impulse frequency of a single moist cell plotted against instantaneous pressure. b impulse frequency of a single dry cell plotted against instantaneous pressure. Stimulus-response functions approximated by linear regressions (F = a + bAP; where F is the impulse frequency, a the height of the regression line, and b the slope of function indicating the mean change in impulse frequency for each percent change in instantaneous pressure). c impulse frequency of the same moist cells as in a plotted against instantaneous pressure and its rate of change. d impulse frequency of the same moist cells as in b plotted against instantaneous pressure and its rate of change. Multiple regressions which utilize 3-dimensional planes (F = a + b AP + c dAP/dt; where F is the impulse frequency, and a the height of the regression plane) are calculated to determine the simultaneous effects of instantaneous pressure (b-slope) and the rate of pressure change (c-slope) on the response frequencies of both cells. AP air pressure, r correlation coefficient

The four cells in Fig. 9 are typical for the 20 moist and 20 dry cells examined in both the cockroach as well as the stick insect. In each cell, 5 to 6 oscillation periods were tested. The mean values obtained for all cells are shown in Tab. 1. In the cockroach, mean sensitivity to instantaneous pressure (b-slope) was +0.14 (imp s⁻¹)/mbar for the moist cell (Fig. 9Ac) and −0.16 (imp s⁻¹)/mbar for the dry cell (Fig. 9Ad); mean sensitivity to the rate of pressure change (c-slope) was +0.15 (imp s⁻¹)/(mbar s⁻¹) for the moist cell (Fig.9Ac) and −0.18 (imp s⁻¹)/(mbar s⁻¹) for the dry cell (Fig. 9Ad). Thus, in the moist cell an increase of 1 imp s⁻¹ can be elicited either by a 7.1 mbar increase in instantaneous pressure (provided the rate of change is constant), or by a pressure change rate of 6.6 mbar s⁻¹. In the dry cell, the corresponding values were −6.2 mbar and −5.5 mbar s⁻¹.

In the stick insect, mean sensitivity to instantaneous pressure (b-slope) was +0.77 (imp s⁻¹)/mbar for the moist (Fig. 9Bc) and −0.45 (imp s⁻¹)/mbar for the dry cell (Fig. 9Bd) ; mean sensitivity to the rate of pressure change (c-slope) was +0.52 (imp s⁻¹)/(mbar s⁻¹) for the moist (Fig. 9Bc) and −0.38 (imp s⁻¹)/(mbar s⁻¹) for the dry cell (Fig. 9Bd). Thus, the moist cell increased its discharge by 1 imp s⁻¹ either at an instantaneous pressure increase of +1.3 mbar (constant rate of change) or at a rate of pressure change increase of +1.9 mbar s⁻¹. The dry cell values were −2.2% mbar and −2.6 mbar s⁻¹.

Discussion

The notion of a mechanical mechanism underlying humidity transduction originally arose from the dependence on the relative humidity, which indicates a hygroscopic material that absorbs and releases moisture, and from the mechanical sensitivity, as summarized in the Introduction. Necheles (1925) was first to demonstrate that the humidity behavior of mosquitoes is correlated with relative humidity rather than with the saturation deficit of the air. Based on the mosquito’s behavioral responses to relative humidity, he suggested that the antennal hairs function as hair hygrometers. Pielou (1940) demonstrated that the “pit peg” sensilla on the antennae of the mealworm beetle are hygroreceptors. He found that the dead cuticle is hygroscopic and absorbs water. The observation that the degree of swelling depends on the relative humidity led him to propose a hygrometrical function. Nijhaut and Sheffield (1979) observed that the cuticular hairs on the antennae of male mosquitoes can be erected by regulating the water content of a swelling, proteinaceous material at the hair base. Yokohari (1978) demonstrated the mechanical sensitivity of moist and dry cells in cockroach’s sensillum capitulum by laterally moving the recording electrode and elaborated the mechano-hygrometer model. According to Yokohari, the mushroom-shaped stem is the hygroscopic structure that takes on and gives off water until it reaches equilibrium with the surrounding air (Fig. 1A). Later, Itoh et al (1984) tested the effect of electrode movements on hygroreceptive sensilla in crickets. Contrary to the cockroach, where moist cell activity was increased by electrode pull and that of the dry cell by electrode push, in the cricket the moist-cell’s activity increased by electrode push and that of the dry cell by electrode pull. No attempt was made to explain this difference.

Support for a hygrometric mode of action of hygroreceptive cells came from an electrophysiological study on the cockroach: it revealed a correlation of the response magnitudes of both moist and dry cells with the relative air humidity, even when air temperature was changed (Yokohari and Tateda 1976). In the stick insect’s moist cell, relative humidity adequately explains the responses no matter how humidity was changed, either by changing the partial pressure of water vapor at constant temperature or by changing the temperature at constant vapor pressure (Tichy and Loftus 1990). So far, there is no direct evidence that a hygroscopic mechanism is responsible for stimulus transmission in hygroreceptors. In stick insects, however, Tichy (2007) demonstrated that the cold cell of the hygroreceptive sensilla responded with a brief increase in activity when the partial pressure of water vapor was suddenly lowered without changing ambient temperature. No temperature change would occur in the sensillum if its surface were dry. The most plausible explanation for the cold-cell’s response to a drop in humidity was that evaporation of hygroscopically bound water from the sensillum surface lowers enthalpy.

In the present study, mechanically stimulate the hygroreceptive cells was provided by changes in air pressure. Pressurization was positive as well as negative, and by avoiding direct contact with the sensillum surface there was no local compaction or physical impediment. During slow and continuous changes in air pressure, the moist and dry cells displayed opposite responses. In both the cockroach and the stick insect, the discharge rate of the moist cell was increased by raising air pressure and decreased by lowering it, and the discharge rate of the dry cell was increased by lowering air pressure and decreased by raising it. These observations indicate that the forces applied by changing air pressure are transmitted from the sensillum surface throughout the thin cuticular wall (> 1 μm) to the dendritic membranes. The moist-cell’s excitatory response to both increasing humidity and increasing air pressure implies that swelling of the hygroscopic cuticle compresses the dendrites; the dry-cell’s excitatory response to both decreasing humidity and decreasing air pressure means that a shrinking hygroscopic cuticle expands the dendrites (Fig. 1C,D). In the cockroach, however, responsiveness to pressure changes is much weaker than in the stick insect. However, differences in the responsiveness may not reflect differences in hygroscopic cuticle properties. Pressure sensitivity may well depend on the size of the surface area that receives pressure changes. In the cockroach’s sensillum capitulum, the hygroscopic stem is enclosed by a tightly fitting cuticular wall protecting from contact with the air and restricting expansion across the width (Fig. 1A). Thus, air pressure may only act on the hemispherical sensillum tip (Fig. 15, Yokohari 1978). In the stick insect, on the other hand, the peg-shaped sensillum is surrounded by an open cavity, so that the whole peg receives the pressure change (Fig. 1B). In order to determine the surface areas over which air pressure acts, we utilized the formula of a hemisphere for the cockroach’s sensillum (A = 2r²π; r = 3 μm; Fig. 15, Yokohari 1978) and that of a cone for the stick-insect’s sensillum (A = rπs, r = 0.7 μm, s = 6.4 μm; Fig. 2D, Tichy 2007). The values are 56.6*10⁻¹⁴ m² for the cockroach and 1.4*10⁻¹¹ m² for the stick-insect. Hence, the mechanical forces that air pressures between 20 and 40 mbar (2,000 and 4,000 hPa) produced on the receptive surface areas were in the range of 1.1 to 2.3 nN for the cockroach’s sensillum capitulum and 28 to 57 nN for the stick-insect’s peg-in-pit sensillum. This simple calculation shows that different fractions of the applied pressure may act on the hygroreceptive cells in the cockroach and the stick insect.

The pressure exerted by the air is actually the sum of the partial pressures of the gaseous components of air, including water vapor. The earth’s surface air pressure is roughly 1,000 mbar at sea level (1,009 mbar in central Vienna) and the water vapor pressure ranges from 0 to 40 mbar, depending on humidity, wind and thermal cycling. At a given temperature and water vapor pressure, the relative humidity indicates how close the air is to saturation. The curves in Fig. 3 show that at temperatures between 20°C and 25°C, a 1% change in relative humidity can be achieved by changing water vapor pressure from 0.2 to 0.3 mbar. If the internal pressure changes produced by swelling and shrinking of the hygroscopic sensillum wall do actually imitate humidity stimulation, one would assume that the frequency spectrum for coding humidity changes between 0 to 100 % RH will be covered by pressure changes between 0 to 40 mbar, depending on air temperature. Strictly speaking, the sensitivity of the moist and dry cells for a 1%-change in humidity should be in the sensitivity range for pressure change between 0.2 to 0.3 mbar. But this is not the case. In the cockroach, the mean differential sensitivity for humidity changes was 0.5 imp/s per %RH for the moist cell and −0.6 imp/s per %RH for the dry cell, compared to the mean differential sensitivity for air pressure changes, in which the corresponding values were 0.1 imp/s per mbar and −0.1 imp/s per mbar (Tab. 1). Thus an increase of 1 imp/s in the moist cell can be elicited either by increasing humidity by 2% RH or air pressure by 10 mbar; or in the dry cell by a decrease of 1.6% RH or 10 mbar. Compared to physics, where in the 20 to 30°C range a change in air pressure by 1 mbar changes humidity by 2.3 to 4.3% RH, in the cockroach’s moist and dry cells a pressure change of 1 mbar has the same effect as a humidity change of roughly 0.2% RH. This means that only 10% of the humidity responses can be elicited by pressure changes.

In the stick insect, the mean differential sensitivity for changes in humidity was 0.4 imp/s per %RH for the moist cell and −0.3 imp/s per %RH for the dry cell, whereas the mean differential sensitivity for air pressure changes was 0.7 imp/s per mbar for the moist and −0.5 imp/s per mbar for the dry cell (Tab. 1). Producing a 1 imp/s increase in the moist cell requires either an increase in humidity of 2.5% RH or in air pressure of 1.4 mbar; and in the dry cell a decrease of 3.3% RH or 2.0 mbar. While in physics a 1 mbar pressure change produces humidity changes between 2.3 to 4.3%, in the stick-insect’s moist and dry cells a 1 mbar pressure change has the same effect as a humidity change of roughly 1.6% RH. Depending on air temperature, between 40 and 70% of the responses to changing humidity can be attributed to mechanical forces caused by air pressure changes.

The experiments show that the discharge rates of the hygroreceptive cells in both insect species can be modulated by the mechanical forces acting on the sensillum surfaces during air pressure changes. However, the responses to mechanical stimulation by pressure changes are generally weaker than to humidity stimulation. Explanations may be sought in the manner in which humidity affects the mechanical properties of the sensillum wall. The effects of hygroscopic swelling and shrinking depend on many factors including not only the rate and amount of water exchanged with the air but also on structural properties of the sensillum wall. Hygroscopic changes of wall structures may be restricted to discrete hygroscopic zones in which the absorbed water becomes concentrated. If local hygroscopic irregularities are present, the mechanical stimuli produced by swelling and shrinking of the cuticular wall were locally distributed. Since the mechanical stimulation induced by the pressure changes acted from all sides they cannot adequately imitate the mechanical effect of swelling and shrinking.

No single convincing hypothesis can be advanced to explain the observation that either the moist or the dry cell was activated by changes in air pressure but never both cells in the same recording. Usually both cells were encountered in a single sensillum and distinguished by the amplitude and form of their impulses. When closing the air-tight chamber and increasing the pressure to the level that was thereafter modulated in a sinusoidal fashion, impulse amplitudes diminished and noise increased. However, the ratio of the amplitudes of the moist and dry cell remained constant. Perhaps a small movement of the recording electrode relative to the sensillum base during pressure change may reduce recording quality. Different coupling mechanisms together with a local hygroscopic heterogeneity in the sensillum wall may decrease sensitivity of one cell. Or an individual sensory cell may no longer have been functional.

The weak responses of the moist and dry cells to mechanical stimulation, on the other hand, could simply arise as by-product of the transduction process. For example, the cuticular wall may not be sealed against the dendritic processes. In contradiction with the hygrometer model, water may flow continuously from the lymph and the dendrites through the cuticular wall, where it is exposed to controlled evaporation in the ambient air. The air humidity may produce an evaporation rate that would quantitatively change the chemical concentration, osmotic pressure or mechanical stress in the sensory cells (Tichy and Loftus 1996). While water moves in either direction in the mechanical hygrometer – from the air into the sensillum (inward) or the reverse (outward) – in the evaporation rate detector, water passes only in one direction, from a high concentration inside the sensillum to a low concentration outside. Mechanical deformations of the cuticular wall due to changes in the evaporation rate will exert forces on the dendritic membranes and inadequately modulate the discharge rates of moist or dry cells. A hygroscopic material would be unnecessary. The lymph flow would have to be small enough to allow humidity to influence the concentration, but at the same time great enough to keep the concentration from being physiologically excessive under conditions normally encountered by the insects.

In a different type of hygroreceptive sensillum on the antennae of the bombycid moth, Steinbrecht and Müller (1991) demonstrated that prolonged exposure to dry air reversibly affects the volume of the dendritic processes of moist and dry cells. They become shorter and thinner. A “low-density matrix” appears within the open space between the dendritic membranes and the cuticular wall. The volume of this matrix increases at the same rate as the volume of the dendritic processes decreases. Thus the “low-density matrix” swells or expands in dry air and shrinks or contracts in moist air, precisely opposite to the hygroscopic cuticular wall as proposed by the hygrometer model. Perhaps the “low-density matrix” provides a link between the dendritic membranes and the sensillum wall. Steinbrecht and Müller did emphasize, however, that the dendrites shortened by the withdrawal of water due to evaporation on the sensillum surface. The water may be supplied from the dendrites of the moist and dry cells, the lymph cavity and supporting cells. These authors suggested the hygroreceptors function as psychrometers that measure the humidity by means of evaporative cooling.

In the present study, the moist and dry cells of the cockroach and the stick insect have been shown to respond antagonistically not only to changes in humidity but to changes in air pressure as well. These responses are of interest because of the mechanical transduction mechanism favored in the literature. Results here rule out this possibility only as an adequate and exclusive explanation and highlight the need for further research into the possible functions of evaporation detector or psychrometer.