Block urn design - a new randomization algorithm for sequential trials with two or more treatments and balanced or unbalanced allocation

Abstract

Permuted block design is the most popular randomization method used in clinical trials, especially for trials with more than two treatments and unbalanced allocation, because of its consistent imbalance control and simplicity in implementation. However, the risk of selection biases caused by high proportion of deterministic assignments is a cause of concern. Efron’s biased coin design and Wei’s urn design provide better allocation randomness without deterministic assignments, but they do not consistently control treatment imbalances. Alternative randomization designs with improved performances have been proposed over the past few decades, including Soares and Wu’s big stick design, which has high allocation randomness, but is limited to two-treatment balanced allocation scenarios only, and Berger’s maximal procedure design which has a high allocation randomness and a potential for more general trial scenarios, but lacks the explicit function for the conditional allocation probability and is more complex to implement than most other designs. The block urn design proposed in this paper combines the advantages of existing randomization designs while overcoming their limitations. Statistical properties of the new algorithm are assessed and compared to currently available designs via analytical and computer simulation approaches. The results suggest that the block urn design simultaneously provides consistent imbalance control and high allocation randomness. It can be easily implemented for sequential clinical trials with two or more treatments and balanced or unbalanced allocation.

1. Introduction

Selection bias is the most devastating factor in clinical trials. In sequential comparative trials, deterministic assignments post risks for selection bias, especially when the trial is not double blinded. Our recent search of the www.clinicaltrials.gov shows that more than 53% of a total of 5097 currently recruiting phase III interventional trials are either open label or single blind. On the other hand, the most commonly used permuted block design (PBD) has the highest proportion of deterministic assignments^1–3, and the risk of selection bias associated with the PBD has been a concern for decades.^4–6 Suspicious selection biases have been reported in trials using the PBD stratified by clinical sites.^7,8 Commonly used randomization methods with better allocation randomness include Efron’s biased coin design⁹ and Wei’s urn design.¹⁰ However, both of these two designs do not provide consistent imbalance control and may cause time related biases in study results. Several modified randomization algorithms have been proposed based on Efron’s biased coin design and Wei’s urn design, including Wei’s adaptive biased coin design¹¹, Soares and Wu’s big stick design¹², Smith’s generalized biased coin design¹³, Chen’s biased coin design with imbalance tolerance¹⁴, Chen’s Ehrefest urn design¹⁵, and Antognini’s symmetric extension of Ehrenfest urn design and asymmetric extension of Ehrenfest urn design¹⁶. Quantitative comparisons of these randomization designs under two-treatment balanced allocation scenarios indicate that the big stick design (BSD) has the most favorable overall performance measured by the combination of treatment balance and allocation randomness,¹⁷ but it applies to balance two-treatment trials only.

Berger et al. proposed the maximal procedure (MP) in 2003, placing a uniform distribution on all feasible randomization sequences under the pre-specified sample size and the maximum tolerated imbalance (MTI).¹⁸ The algorithm for the generation of the MP randomization sequences was proposed by Salama et al. in 2008,¹⁹ where a directed acyclic graph accommodating all possible allocation sequences under the MTI is created, from which the transition probabilities from the last node to the first node are calculated with a backward procedure based on the condition that these sequences have the same probability. The original MP method applies to two arm balanced trial. Salama’s algorithm allows MP to be applicable in two arm balanced and unbalanced trial. Recently, Kuznetsova and Tymofyeyev proposed the brick tunnel randomization method, which was considered as a generalized form of MP for trial with unbalanced allocation and two or more treatment groups, but the distribution of its candidate sequence is not uniform any more.²⁰ The MP, the PBD and the BSD all use the MTI restrictions, but in different formats. The MP and the BSD use deterministic assignments only when imbalances reach the MTI, while PBD uses deterministic assignments more frequently in order to enforce perfect balance within each completed block. The BSD uses pure random assignments when treatment imbalance is smaller than the MTI, while the MP has conditional probabilities targeting the uniform distribution for all feasible sequences.

The implementation of randomization designs in sequential clinical trials involves the calculation of the conditional allocation probability. Most randomization designs provide an explicit function to calculate the conditional allocation probability based on the number of subjects previously assigned to each treatment, which is independent of the allocation history. This is also called Markov chain property. Furthermore, for some randomization designs, such as PBD and BSD, the Markov chain holds a steady-state property so that the conditional allocation probability can be expressed as an explicit function of a set of finite discrete status of treatment imbalance. The total number of these imbalance statuses depends on study design parameters, such as the number of treatments, the allocation ratio and the MTI, and is independent from the length of the randomization sequence. The MP does not ensure the steady-state Markovian property. The algorithm proposed by Salama et al. for generation of the MP randomization sequence¹⁹ for two-arm trial and the algorithm proposed by Kuznetsova and Tymofyeyev for the generation of the brick tunnel randomization sequence for two or more arms trial²⁰ is more complex than most explicit conditional allocation probability functions of other randomization designs.

In this paper, we propose a block urn design (BUD) that overcomes the weaknesses of currently available randomization designs and simultaneously provide the following favorable feathers: 1) consistent imbalance control under the MTI; 2) lower probabilities of deterministic assignments and correct guesses; 3) generally applicable to trials with two or more treatments and balanced or unbalanced allocation; and 4) explicit function for conditional allocation probability which is easy for implementation. The algorithm of the BUD is presented in Section 2. In Section 3, statistical properties of the BUD are assessed based on the conditional allocation probability and the steady-state probability. The performance of the BUD (in terms of proportion of deterministic assignments and the correct guess probability) is compared to those of PBD, BSD, and MP under two-treatment scenarios in Section 4. The comparison is extended to scenarios with more than two treatments and unbalanced allocation in Section 5. Discussions and conclusions are provided in Section 6.

2. Algorithm of the block urn design

Consider a sequential clinical trial comparing m treatments with a target allocation w₁: w₂: · · ·: w_m, where all w s are integers with the greatest common divisor of 1. The minimal number of assignments satisfying exact balance is $W={\sum }_{j=1}^m{w}_j$, with w_j assignments for treatment j (j = 1, 2, · · ·, m). These W assignments are considered as a minimal balanced set. Let b = λW be the block size, and λ be the number of minimal balanced sets in each block.

The block urn design (BUD) uses an active urn and an inactive urn. The generation procedure of the BUD randomization sequence can be described as follows:

1. Starts from a block of λW balls, with λw_j color coded balls for treatment j (j = 1, 2, · · ·, m) in the active urn. The inactive urn is empty at this time.

2. Allocates a subject to a treatment based on the color of a ball randomly drawn from the active urn.

3. After each treatment allocation, the selected ball is placed in the inactive urn.

4. Repeat steps 2 and 3 until a minimal balanced set is collected in the inactive urn. These W balls are returned to the active urn immediately. Other balls, if any, stay in the inactive urn.

5. Repeat steps 2 through 4 until the last subject is randomized.

Rosenberger and Lachin indicated that the PBD can be considered as a repeated random rule.²¹ In other words, each block works in an urn model without replacement. The difference between the BUD and the PBD is the ball return rule. In PBD, λW balls of a whole block are returned together, while in the BUD, W balls of a minimal balanced set are returned when they are cumulated in the inactive urn. When the block contains only one minimal balanced set, i.e. λ = 1, the BUD is identical to PBD. Like the PBD, the BUD procedure works for trials with two or more treatments and balanced or unbalanced allocation ratios. Table 1 provides an example of the urn model of the BUD randomization process for two-treatment balanced allocation scenarios.

Table 1.

Urn model of the block urn design procedure (Two-treatment balanced allocation with block size b = 6)

i	Prior randomization		Randomization		Post randomization
	Active urn	Pr(Ti = A)	Random number	Subject allocation	Na	Nb	|Na-Nb|	Inactive urn	Balls return to active urn
1	AAABBB	0.5	0.4026	A	1	0	1	A
2	AABBB	0.4	0.5654	B	1	1	0	AB	AB
3	AAABBB	0.5	0.0927	A	2	1	1	A
4	AABBB	0.4	0.3080	A	3	1	2	AA
5	ABBB	0.25	0.7758	B	3	2	1	AAB	AB
6	AABBB	0.4	0.9219	B	3	3	0	AB	AB
7	AAABBB	0.5	0.6115	B	3	4	1	B
8	AAABB	0.6	0.8604	B	3	5	2	BB
9	AAAB	0.75	0.4848	A	4	5	1	ABB	AB
10	AAABB	0.6	0.7746	B	4	6	2	BB
11	AAAB	0.75	0.2345	A	5	6	1	ABB	AB
12	AAABB	0.6	0.8507	B	5	7	2	BB
13	AAAB	0.75	0.0661	A	6	7	1	ABB	AB
14	AAABB	0.6	0.2630	A	7	7	0	AB	AB

T_i: treatment allocation for subject i.

Random number: computer generated random number with a uniform distribution on (0,1).

N_a: total number of subjects allocated to treatment A.

N_b: total number of subjects allocated to treatment B.

3. Statistical properties of the block urn design

3.1. Conditional allocation probability

Let N_ij be the number of allocation to treatment j among the i subjects, let P_ij be the probability for subject i to be assigned to treatment j under the condition of previous treatment allocation distribution N_i–1,j (j = 1, 2, · · ·, m). For all randomization designs using urn models, the conditional allocation probability is:

$$p_{ij}=\frac{\text{number}\text{of}\text{balls}\text{in}\text{the}\text{active}\text{urn}\text{for}\text{treatment}j}{\text{total}\text{number}\text{of}\text{balls}\text{in}\text{the}\text{active}\text{urn}}$$ (1)

For the BUD with a block size b = λW, the conditional allocation probability is:

$$P_{ij}=\frac{w_j\lambda +w_j{k}_{i-1}-N_{i-1,j}}{W\lambda +{Wk}_{i-1}-(i-1)},\text{where}{k}_{i-1}=\underset{1\le j\le m}{min}int{N}_{i-1,j}/w_j$$ (2)

Here k_i-1 represents the number of minimal balanced sets in previous assignments. Function int(x) returns the greatest integer less than or equal to x. For example, for a two-arm trial with w₁ = 2, w₂ = 3, and λ = 2. When the 13^th subject is ready for randomization, 5 subjects were previously allocated to treatment A and 7 to treatment B. We have

$$\begin{array}{l}{k}_{16}=min\left[int5/2,int(11/3)\right]=min2,3=2\\ p_{17,1}=\frac{2\times 2+2\times 2-5}{5\times 2+5\times 2-16}=\frac{3}{4}\\ p_{17,2}=\frac{3\times 2+3\times 2-11}{5\times 2+5\times 2-16}=\frac{1}{4}\end{array}$$

For trials with a balanced allocation w_j = 1, (j = 1, 2, · · ·, m), the conditional allocation probability is:

$$P_{ij}=\frac{\lambda +k_{i-1}-N_{i-1,j}}{m\lambda +{mk}_{i-1}-(i-1)},\text{where}{k}_{i-1}=\underset{1\le j\le m}{min}{N}_{i-1,j}$$ (3)

Furthermore, for two-treatment balanced trials, we have:

$$P_{i1}=\frac{\lambda +min(N_{i-1,1},N_{i-1,2})-N_{i-1,1}}{2\lambda +min(N_{i-1,1},N_{i-1,2})-(i-1)},P_{i2}=1-P_{i1}$$ (4)

Similarly, using an urn model, the PBD randomization sequence can be generated based on the following conditional allocation probability:

$$P_{ij}=\frac{w_j\lambda +w_j\lambda k_{i-1}^{\ast }-N_{i-1,j}}{b+{bk}_{i-1}^{\ast }-(i-1)},\text{where}{k}_{i-1}^{\ast }=int\left(\frac{i-1}{b}\right)$$ (5)

Where $b=\lambda W=\lambda {\sum }_{j=1}^m{w}_j$ is the block size. The similarity between equations (2) and (5) indicates that the randomization sequence generation and the implementation of the BUD is as simple as those of the PBD, although the BUD offers better allocation randomness. Table 2 compares the randomization sequence generation processes between the BUD and the PBD under a multiple treatment unbalanced scenario.

Table 2.

Comparison of conditional allocation probabilities of the BUD and PBD (Three-treatment unbalanced allocation w₁:w₂:w₃=1:2:2 Block size = 10)

i	Randi	Block urn design (BUD)							Permuted block design (PBD)
		Ni-1,1	Ni-1,2	Ni-1,3	ki-1	Pi1	Pi2	$T_i^{\&}$	Ni-1,1	Ni-1,2	Ni-1,3	Pi1	Pi2	$T_i^{\&}$
1	0.8290	0	0	0	0	2/10	4/10	3	0	0	0	2/10	4/10	3
2	0.4852	0	0	1	0	2/9	4/9	2	0	0	1	2/9	4/9	2
3	0.7767	0	1	1	0	2/8	3/8	3	0	1	1	2/8	3/8	3
4	0.0069	0	1	2	0	2/7	3/7	1	0	1	2	2/7	3/7	1
5	0.9145	1	1	2	0	1/6	3/6	3	1	1	2	1/6	3/6	3
6	0.5337	1	1	3	0	1/5	3/5	2	1	1	3	1/5	3/5	2
7	0.7652	1	2	3	1	2/9§	4/9§	3	1	2	3	1/4	2/4	3
8	0.1473	1	2	4	1	2/8	4/8	1	1	2	4	1/3	2/3	1
9	0.2346	2	2	4	1	1/7	4/7	2	2	2	4	0/2	2/2	2*
10	0.0684	2	3	4	1	1/6	3/6	1	2	3	4	0/1	1/1	2*
11	0.9372	3	3	4	1	0/5	3/5	3	2	4	4	2/10§	4/10§	3
12	0.8102	3	3	5	1	0/4	3/4	3	2	4	5	2/9	4/9	3
13	0.6827	3	3	6	1	0/3	3/3	2*	2	4	6	2/8	4/8	2
14	0.3290	3	4	6	2	1/7§	4/7§	2	2	5	6	2/7	3/7	2
15	0.6940	3	5	6	2	1/6	3/6	3	2	6	6	2/6	2/6	3
16	0.6481	3	5	7	2	1/5	3/5	2	2	6	7	2/5	2/5	2
17	0.9090	3	6	7	3	2/9§	4/9§	3	2	7	7	2/4	1/4	3
18	0.4940	3	6	8	3	2/8	4/8	2	2	7	8	2/3	1/3	1
19	0.3266	3	7	8	3	2/7	3/7	2	3	7	8	1/2	1/2	1
20	0.1690	3	8	8	3	2/6	2/6	1	4	7	8	0/1	1/1	2*
21	0.4618	4	8	8	4	2/10§	4/10§	2	4	8	8	2/10§	4/10§	2
22	0.4423	4	9	8	4	2/9	3/9	2	4	9	8	2/9	3/9	2

^&T_i = iif (Rand_i < P_i1, 1, iif (Rand_i < (P_i1 + P_i2), 2, 3))

^*: Deterministic assignment.

^§The active urn is updated by returning balls from the inactive urn.

Compared to the PBD, which starts a new block every 10 assignments, the BUD updates the active urn more frequent, giving the randomization sequence a lower proportion of deterministic assignment and a lower correct guess probability. In the PBD, the last assignment in each block is always deterministic, like assignments #10 and #20 shown in Table 2. This fixed pattern makes the deterministic assignments easy to predict. With the BUD, deterministic assignment could occur, like assignment #13 in Table 2, but the timing of such occurrences is random, making correct prediction less likely occur.

3.2. Steady-state probabilities

With an urn model, the conditional probability depends solely on the contents in the active urn. In the BUD, the active urn is complementary to the inactive urn which contains only the unbalanced part of the randomization sequence. In other words, the conditional allocation probability of the BUD is a function of the treatment imbalance status which composes a Markov process with steady-state probabilities. For a given trial design with m treatments, a target allocation of w₁: w₂: · · ·: w_m, and a block size of $b=\lambda {\sum }_{j=1}^m{w}_j$, the number of steady-states is:

$$Q=\prod _{j=1}^m(\lambda w_j+1)-\prod _{j=1}^m(\lambda -1)w_j+1$$ (6)

For the example shown in Table 2, with m = 3, w₁: w₂: w₃ = 1: 2: 2, and λ=2, the Q = 57. Formula (6) is simplified to Q = (λ + 1)^m − λ^m if the trial has a balanced allocation, and can be further simplified to Q = 2λ + 1 when the balanced trial has two treatments. In this scenario, the transition probability and steady-state probability of the BUD Markov chain are not difficult to obtain.

Let D_i–1 = N_i–1,1 − N_i–1,2 be the treatment imbalance before the randomization of subject i, the conditional allocation probability (4) can be written as:

$$P_{i1}=\frac{1}{2}-\frac{D_{i-1}}{4\lambda -2\mid D_{i-1}\mid },P_{i2}=1-P_{i1}$$ (6)

Since the absolute treatment imbalance can only change by one unit after each assignment and is capped by λ, the sequence |D| = {|D₁|, |D₂|, · · ·, |D_n|} forms a Markov process with (λ + 1) steady-states: 0, 1, · · ·, λ − 1, and λ. The transition probabilities across these states are:

$$\begin{array}{l}Pr\mid D_i\mid =\mid D_{i-1}\mid =Pr\mid D_i\mid <\mid D_{i-1}\mid -1=Pr\mid D_i\mid >\mid D_{i-1}\mid +1=0\\ Pr\mid D_i\mid =1\mid \mid D_{i-1}\mid =0=1\\ Pr\mid D_i\mid =\mid D_{i-1}\mid -1=\frac{1}{2}+\frac{\mid D_{i-1}\mid }{4\lambda -2\mid D_{i-1}\mid }\\ Pr\mid D_i\mid =\mid D_{i-1}\mid +1=\frac{1}{2}-\frac{\mid D_{i-1}\mid }{4\lambda -2\mid D_{i-1}\mid }\end{array}$$

These results give the transitional probability matrix for the Markov chain |D|:

$$\mathbf{P}(\mid \mathbf{D}\mid )=\left[\begin{array}{cccccccc}0& 1& 0& 0& \cdots & 0& 0& 0\\ \frac{\lambda }{2\lambda -1}& 0& \frac{\lambda -1}{2\lambda -1}& 0& \cdots & 0& 0& 0\\ 0& \frac{\lambda }{2\lambda -2}& 0& \frac{\lambda -2}{2\lambda -2}& \cdots & 0& 0& 0\\ 0& 0& \frac{\lambda }{2\lambda -3}& 0& \cdots & 0& 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& 0& \cdots & 0& \frac{2}{\lambda +2}& 0\\ 0& 0& 0& 0& \cdots & \frac{\lambda }{\lambda +1}& 0& \frac{1}{\lambda +1}\\ 0& 0& 0& 0& \cdots & 0& 1& 0\end{array}\right]$$

The steady-state probability vector π = {π₀, π₁, π₂, · · ·, π_λ} for this Markov chain can be obtained by using the mathematical induction approach (see Appendix A):

$${\pi }_{\lambda }=\frac{1}{2}{\left(\sum _{i=0}^{\lambda -1}\frac{{\lambda }^i}{i!}\right)}^{-1}$$ (8)

$${\pi }_{\lambda -i}=\left(\frac{{\lambda }^i}{i!}+\frac{{\lambda }^{i-1}}{(i-1)!}\right){\pi }_{\lambda }(i=1,2,\cdots ,\lambda -1)$$ (9)

$${\pi }_0=\frac{\lambda }{2\lambda -1}\left(\frac{{\lambda }^{\lambda -1}}{(\lambda -1)!}+\frac{{\lambda }^{\lambda -2}}{(\lambda -2)!}\right){\pi }_{\lambda }=\frac{{\lambda }^{\lambda -1}}{(\lambda -1)!}{\pi }_{\lambda }$$ (10)

Table 3 lists the steady-state probabilities for scenarios with varying from 1 to 8.

Table 3.

Steady-state probability of BUD randomization sequence Two-treatment balanced allocation scenarios

λ	π0	π1	π2	π3	π4	π5	π6	π7	π8
1	0.500	0.500
2	0.333	0.500	0.167
3	0.265	0.441	0.235	0.059
4	0.225	0.394	0.254	0.106	0.021
5	0.199	0.359	0.255	0.134	0.046	0.008
6	0.180	0.330	0.250	0.150	0.067	0.019	0.003
7	0.166	0.308	0.243	0.159	0.083	0.032	0.008	0.001
8	0.154	0.289	0.236	0.164	0.095	0.043	0.015	0.003	3.7E-4

The steady-state probabilities can be used to quantify the statistical probabilities of the randomization sequence. For example, π_λ is the asymptotic probability of achieving the state of |D| = λ, which is equivalent to the probability of deterministic assignment. For scenarios with more than two treatments or unbalanced allocation, computer simulations can be used to estimate the steady-state probabilities.

4. Randomness comparison under two-treatment balanced allocation scenarios

The trade-off between treatment imbalance and allocation randomness exists for all randomization designs. The proposed block urn design (BUD) aims to a consistent imbalance control. Efron’s biased coin design and Wei’s urn design do not yield consistent treatment imbalance control. The absolute value of treatment imbalance in these two designs can increase as the sample size increases. Therefore, the performance comparison will be limited to the PBD, the BSD, and the MP, because all these designs follow the same rule of the maximum tolerated imbalance (MTI), and focusing on the allocation randomness measured by the proportion of deterministic assignment (DA) and the correct guess (CG) probability. A treatment assignment T_i is deterministic if only one treatment is available for the randomization of subject i under the conditional allocation probability. The concept of CG is based on the convergent guessing strategy given by Blackwell and Hodges, which is to guess the next treatment allocation as the least represented treatment arm.²² Under two-treatment balanced allocation scenarios, the probabilities of DA and CG for the BUD can be obtained from the steady-state probabilities:

$${DA}_{\mathit{BUD}}(\lambda )={\pi }_{\lambda }$$ (11)

$${CG}_{\mathit{BUD}}(\lambda )={\pi }_0\frac{1}{2}+\sum _{\delta =1}^{\lambda }{\pi }_{\delta }Pr\mid D_i\mid =\delta -1\mid \mid D_{i-1}\mid =\delta$$ (12)

The probabilities of DA and CG for the PBD with a block size b = 2λ are provided by Matts and Lachin,⁴

$${DA}_{\mathit{PBD}}(\lambda )=\frac{1}{\lambda +1}$$ (13)

$${CG}_{\mathit{PBD}}(\lambda )=\frac{1}{2}+\frac{1}{2\lambda }\left(\frac{2^{2\lambda -1}}{C_{2\lambda }^{\lambda }}-\frac{1}{2}\right)$$ (14)

Where $C_n^m=n!/m!/(n-m)!$ is the number of ways choosing m from n objects. For the BSD with an imbalance limit of λ, the probabilities of DA and CG are given by Kundt²³ and Chen¹⁵ respectively:

$${DA}_{\mathit{BSD}}(\lambda )=\frac{1}{2\lambda }$$ (15)

$${CG}_{\mathit{BSD}}(\lambda )=\frac{1}{2}+\frac{1}{4\lambda }$$ (16)

For the MP, there are no analytical results currently available for the probabilities of DA and CG. Numerical estimates can be obtained by computer simulations based on the randomization sequence generation algorithm given by Salama et al.¹⁹ Figure 1 shows the comparison results. The randomness of the PBD, the BSD and the BUD are not affected by the sample size. Therefore, analytical results based on formulas (11–16) are used in Figure 1. The MP is affected by the sample size. In order to minimize this effect, a large sample size (N=300) is used for computer simulation with 10,000 replicated runs.

Figure 1.

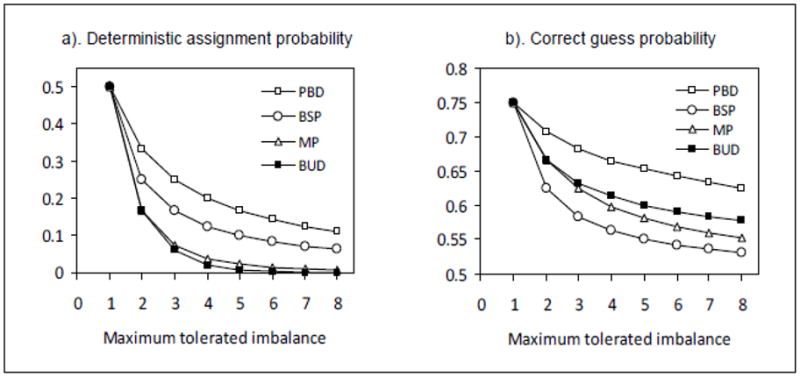
As shown in Figure 1, with the same MTI, the DA probabilities for the BUD and MP are much lower than those for the PBD. The BSD has the lowest CG probability. The MP has a lower CG probability than the BUD. Both the MP and the BUD have CG probabilities lower than the PBD. The commonly used PBD has the highest (worst) probabilities in both DA and CG. If the CG probability is weighted more than the DA probability, the Soares and Wu’s big stick design (BSD) is the best choice for trials with two treatments and balanced allocation. Otherwise, the MP and BUD are better options. The generation of the MP randomization sequence requires a special algorithm, which is more complex than the explicit conditional probability function for the BUD. Combining the considerations of allocation randomness and implementation, the block urn design (BUD) is a more favorable selection than the other three designs.

5. Randomness comparison under general scenarios

Based on the availabilities of implementation algorithms, the comparison under two-treatment unbalanced allocation scenarios will be limited to the BUD, the PBD and the MP, the comparison under multiple treatment scenarios will be limited to the BUD and the PBD only. All comparisons of randomness are based on the same level of treatment imbalances, which is quantified by the block size $b=\lambda {\sum }_{j=1}^m{w}_j$ for the PBD and the BUD, and the MTI for the MP. For two-treatment balanced trials, MTI is equivalent to parameter λ. For general scenarios with m treatments and allocation w₁: w₂: · · ·: w_m, the treatment imbalance restriction for the PBD is:

$$\underset{1\le j\le m}{max}\left(\frac{N_{ij}}{w_j}-k_i\right)\le \lambda ,\text{where}{k}_i=\underset{1\le j\le m}{min}\left(int\left(\frac{N_{ij}}{\lambda w_j}\right)\right)$$ (17)

Here λw_j is the number of assignments for treatment j in a complete block; integer k_i is the number of blocks currently completed. For the BUD, a complete block consists λ minimal balanced sets, and the imbalance restriction is:

$$\underset{1\le j\le m}{max}\left(\frac{N_{ij}}{w_j}-k_i^{\ast }\right)\le \lambda ,\text{where}{k}_i^{\ast }=\underset{1\le j\le m}{min}\left(int\left(\frac{N_{ij}}{w_j}\right)\right)$$ (18)

Here integer $k_i^{\ast }$ is the number of currently completed minimal balanced sets. If the integer requirement for $k_i^{\ast }$ is released, there is:

$$\underset{1\le j\le m}{max}\left(\frac{N_{ij}}{w_j}-k_i^{\ast \ast }\right)\le \lambda ,\text{where}{k}_i^{\ast \ast }=\underset{1\le j\le m}{min}\left(\frac{N_{ij}}{w_j}\right)$$ (19)

Restriction (19) applies to the MP. Consider a two-treatment trial with allocation w₁: w₂, assuming 1 ≤ w₁ ≤ w₂, condition (19) becomes:

$$\left|\frac{N_{i1}}{w_1}-\frac{N_{i2}}{w_2}\right|<\lambda ,\text{or}\left|N_{i1}-\frac{w_1}{w_2}{N}_{i2}\right|<\lambda w_1=\mathit{MTI}$$ (20)

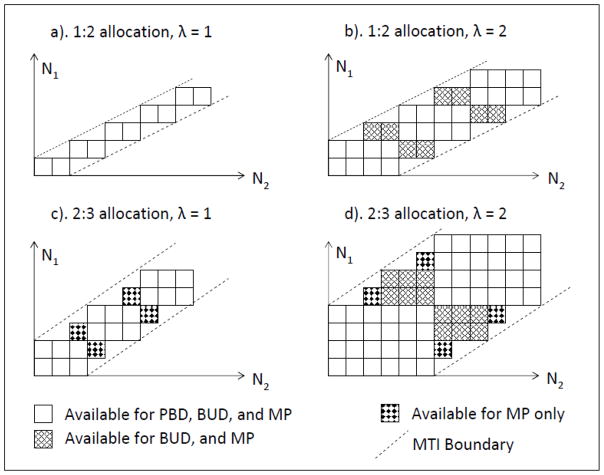
Condition (20) is identical to the formula (1) in Salama’s paper¹⁹ used to determine feasible MP sequences. Formula (20) indicates that the MTI for the MP is equivalent to the λw₁ in the PBD and the BUD. Based on (18–20), feasible randomization sequences for the PBD, the MP and the BUD under two-treatment scenarios are plotted in Figure 2. Starting from the original point (0,0), one unit vertical or horizontal forward movement represents an assignment to treatment 1 or 2 respectively. A node (N₁, N₂) represent a treatment distribution with N₁ and N₂ subjects in treatment 1 and 2 respectively. A movement is deterministic if and only if it is on the upper or right edges of the feasible path area. When λ = 1, and w₁=1, the three designs have the same feasible sequences, because there is no other paths between the two boundaries other than those for the PBD, as shown in scenario a) in Figure 2. When λ > 1, and w₁=1, there are extra minimal balanced sets exist between the PBD paths and the two MTI boundaries. These paths are available to both BUD and MP, as shown in scenario b) in Figure 2. For example, under the BPD, (N₁, N₂) Both paths (2, 2) → (2,3) and (1,3) → (2,3) are deterministic. For the BUD and the MP, there are feasible paths (2, 2) → (3, 2), (2, 2) → (2, 3), (1, 3) → (1, 4) and (1, 3) → (2, 3) available.

Figure 2.

Comparison of feasible allocation sequences

When λ = 1, and w₁>1, the BUD is identical to the PBD. There are extra paths between the complete blocks and the boundaries. These paths are available to the MP only, as shown in scenario c). For example, there is only one path (2, 2) → (2, 3) for both the PBD and the BUD, yielding a deterministic assignment. For the MP, there are (2, 2) → (2, 3) and (2, 2) → (3, 2) available. When λ > 1, and w₁>1, there are extra paths for the BUD and the MP, and additional paths for MP alone as shown in scenario d) of Figure 2. In general, having more feasible sequence paths indicates lower probabilities of CG and DA. However, same number of feasible sequences does not necessarily mean the same level of allocation randomness, because the transition probabilities associated with each step in the sequence could be different. Computer simulation results comparing the PBD, the MP and the BUD under two-treatment scenarios are presented in Table 4. Compared to the PBD, using either the MP or the BUD for trials with λ > 1 will result in a substantial reduction in deterministic assignments as well as about 10% reduction in correct guesses. For cases with w₁>1 and λ = 1, the MP offers the highest allocation randomness, as illustrated in scenario c) of Figure 2. This benefit disappears when λ > 1. In most cases, the MP has a lower CG, and the BUD has a lower DA. However, the differences between the two designs are small.

Table 4.

Comparison of randomness among PBD, MP and BUD (sample size = 300, simulation replication = 10,000)

Randomization Design		Deterministic assignment probability			Correct guess probability
Allocation	λ	PBD	MP	BUD	PBD	MP	BUD
w1 = 1 w2 = 2	1	0.4443	0.4444	0.4444	0.7780	0.7779	0.7778
	2	0.2891	0.1208	0.1206	0.7444	0.7080	0.7079
	3	0.2126	0.0481	0.0338	0.7268	0.6840	0.6884
	4	0.1706	0.0244	0.0097	0.7168	0.6741	0.6792
	5	0.1412	0.0142	0.0027	0.7097	0.6676	0.6745
	6	0.1163	0.0095	0.0008	0.7030	0.6632	0.6716
w1 = 2 w2 = 3	1	0.3002	0.1636	0.2999	0.7198	0.6899	0.7200
	2	0.1772	0.0310	0.0312	0.6838	0.6274	0.6428
	3	0.1258	0.0108	0.0032	0.6658	0.6092	0.6234
	4	0.0978	0.0052	0.0003	0.6546	0.6004	0.6143
	5	0.0798	0.0032	0.0000	0.6469	0.5940	0.6094
	6	0.0670	0.0023	0.0000	0.6416	0.5898	0.6065
w1 = 1 w2 = 2 w3 = 2	1	0.2400	Not available	0.2399	0.6065	Not available	0.6068
	2	0.1364		0.0202	0.5589		0.5120
	3	0.0956		0.0017	0.5346		0.4826
	4	0.0734		0.0002	0.5187		0.4674
	5	0.0597		0.0000	0.5069		0.4584
	6	0.0502		0.0000	0.4985		0.4520

PBD: Permuted block design

MP: Maximal procedure

BUD: Block urn design

MTI: Maximum tolerated imbalance

Correct guess uses convergent strategy

For trials comparing more than two treatments with unbalanced allocation, the PBD was the only method previously available with consistent imbalance control. The proposed BUD has made noticeable improvements in both DA and CG, as seen in table 5.

6. Discussion and Conclusion

The proposed block urn design (BUD) consistently demonstrates advantages over the commonly used permuted block design (PBD) across all trial scenarios. While both designs share the same favorable features of consistent imbalance control, simple implementation and applicability to all trial scenarios, the BUD significantly reduces the probability and the timing predictability of deterministic assignments.

The proposed BUD and Berger’s maximal procedure (MP) have similar performance regarding the trade-off between treatment imbalance and allocation randomness. The MP has a uniform distribution for all feasible sequences, which the BUD does not have. The BUD holds a stationary Markovian property that the MP holds only for balanced allocation with λ = 1 or 2, or unbalanced allocation with λ = 1. The practical advantage of the BUD over the MP comes from simplicity in implementation and applicability for all treatment number and allocation ratio scenarios.

As a randomization design without a uniform distribution for all feasible randomization sequences, the proposed BUD could be challenged when a randomization-model is desired for the analysis of the trial results. For small trials, when all feasible randomization sequences can be listed by a computer program and the probability associated with each sequence is calculated, a randomization model based permutation test could be performed with the consideration of the unequal probabilities associated with different sequences. For trials with a large sample size, this could be difficult because of the total number of feasible sequence for BUD will be prohibitively large. Computer simulation could be considered to repeatedly sample the randomization sequence using the BUD algorithm for randomization-model based analysis. Further works are needed to exam this issue. In practice, the likelihood based analysis using the population model can be performed regardless of the randomization procedure.^{20, 24}

Some limitations of the BUD have been noticed. By using the urn model, the BUD cannot control treatment imbalance below the value of w₁. For example, if the target allocation is 5:7, the minimal balanced set will include 12 assignments. Treatment imbalances in any subsets of these 12 assignments could occur. Cases like N₁−N₂ = 5 or N₁−N₂ = −7 may exceed the investigator’s tolerable limit. With the MP, the MTI can be smaller than w₁.

In conclusion, the proposed block urn design combines the high allocation randomness of the maximal procedure and the simplicity of the permuted block design. It can be used in clinical trials where both treatment imbalances and deterministic assignments are seriously concerned.

Appendix. Steady-state probability of block urn design randomization sequence

When the block urn design (BUD) with a block size of b = 2λ is applied to a two-treatment balanced allocation trial, the transitional probability matrix for the Markov chain of the absolute treatment imbalance |D| is:

$$\mathbf{P}(\mid \mathbf{D}\mid )=\left[\begin{array}{cccccccc}0& 1& 0& 0& \cdots & 0& 0& 0\\ \frac{\lambda }{2\lambda -1}& 0& \frac{\lambda -1}{2\lambda -1}& 0& \cdots & 0& 0& 0\\ 0& \frac{\lambda }{2\lambda -2}& 0& \frac{\lambda -2}{2\lambda -2}& \cdots & 0& 0& 0\\ 0& 0& \frac{\lambda }{2\lambda -3}& 0& \cdots & 0& 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& 0& \cdots & 0& \frac{2}{\lambda +2}& 0\\ 0& 0& 0& 0& \cdots & \frac{\lambda }{\lambda +1}& 0& \frac{1}{\lambda +1}\\ 0& 0& 0& 0& \cdots & 0& 1& 0\end{array}\right]$$ (1)

The steady-state probability vector π = {π₀, π₁, π₂, · · ·, π_λ} for this Markov chain is given by:

$${\pi }_0=\frac{\lambda }{2\lambda -1}{\pi }_1$$ (2)

$${\pi }_1={\pi }_0+\frac{\lambda }{2\lambda -2}{\pi }_2$$ (3)

$${\pi }_i=\frac{\lambda -i+1}{2\lambda -i+1}{\pi }_{i-1}+\frac{\lambda }{2\lambda -i-1}{\pi }_{i+1}(i=2,3,\cdots ,\lambda -1)$$ (4)

$${\pi }_{\lambda }=\frac{1}{\lambda +1}{\pi }_{\lambda -1}$$ (5)

From (4) and (5), we have

$${\pi }_{\lambda -1}=(\lambda +1){\pi }_{\lambda }=\left(\frac{{\lambda }^1}{1!}+\frac{{\lambda }^0}{0!}\right){\pi }_{\lambda }$$ (6)

$${\pi }_{\lambda -2}=\frac{\lambda +2}{2}{\pi }_{\lambda -1}-{\pi }_{\lambda }=\left(\frac{{\lambda }^2}{2!}+\frac{{\lambda }^1}{1!}\right){\pi }_{\lambda }$$ (7)

Using the mathematical induction strategy, assume ${\pi }_{\lambda -h}=\left(\frac{{\lambda }^h}{h!}+\frac{{\lambda }^{h-1}}{(h-1)!}\right){\pi }_{\lambda }$ and ${\pi }_{\lambda -(h-1)}=\left(\frac{{\lambda }^{h-1}}{(h-1)!}+\frac{{\lambda }^{h-2}}{(h-2)!}\right){\pi }_{\lambda }$. It works for h = 2. Let i = λ − h, based on (4),

$$\begin{array}{l}{\pi }_{\lambda -h}=\frac{\lambda -(\lambda -h)+1}{2\lambda -(\lambda -h)+1}{\pi }_{\lambda -(h+1)}+\frac{\lambda }{2\lambda -(\lambda -h)-1}{\pi }_{\lambda -(h-1)}\\ \left(\frac{{\lambda }^h}{h!}+\frac{{\lambda }^{h-1}}{(h-1)!}\right){\pi }_{\lambda }=\frac{h+1}{\lambda +h+1}{\pi }_{\lambda -(h+1)}+\frac{\lambda }{\lambda +h-1}\times \left(\frac{{\lambda }^{h-1}}{(h-1)!}+\frac{{\lambda }^{h-2}}{(h-2)!}\right){\pi }_{\lambda }\\ {\pi }_{\lambda -h}=\frac{\lambda +h+1}{h+1}\times \left[\frac{{\lambda }^h}{(\lambda +h-1)h!}\lambda -1+\frac{{\lambda }^h}{(\lambda +h-1)(h-1)!}\right]{\pi }_{\lambda }\\ =\frac{\lambda +h+1}{(\lambda +h-1)(h+1)}\times \left[\frac{{\lambda }^{h+1}}{h!}+\frac{{\lambda }^h}{h!}(h-1)\right]{\pi }_{\lambda }\\ =\frac{(\lambda +h+1){\lambda }^h}{(h+1)!}{\pi }_{\lambda }=\left[\frac{{\lambda }^{h+1}}{(h+1)!}+\frac{{\lambda }^h}{h!}\right]{\pi }_{\lambda }\end{array}$$

This proves that for i = 1, 2, · · ·, λ − 1,

$${\pi }_{\lambda -i}=\left(\frac{{\lambda }^i}{i!}+\frac{{\lambda }^{i-1}}{(i-1)!}\right){\pi }_{\lambda }(i=1,2,\cdots ,\lambda -1)$$ (8)

Set i = λ − 1 for (8), we have

$${\pi }_1=\left(\frac{{\lambda }^{\lambda -1}}{(\lambda -1)!}+\frac{{\lambda }^{\lambda -2}}{(\lambda -2)!}\right){\pi }_{\lambda }$$ (9)

Based on (2) and (9),

$${\pi }_0=\frac{\lambda }{2\lambda -1}\left(\frac{{\lambda }^{\lambda -1}}{(\lambda -1)!}+\frac{{\lambda }^{\lambda -2}}{(\lambda -2)!}\right){\pi }_{\lambda }=\frac{{\lambda }^{\lambda -1}}{(\lambda -1)!}{\pi }_{\lambda }$$ (10)

Under the condition of ${\displaystyle \sum _{i=0}^{\lambda }}{\pi }_i=1$,

$$\begin{array}{l}\left[\frac{{\lambda }^0}{0!}+(\frac{{\lambda }^1}{1!}+\frac{{\lambda }^0}{0!})+(\frac{{\lambda }^2}{2!}+\frac{{\lambda }^1}{1!})+\dots +\left(\frac{{\lambda }^{\lambda -1}}{(\lambda -1)!}+\frac{{\lambda }^{\lambda -2}}{(\lambda -2)!}\right)+\frac{{\lambda }^{\lambda -1}}{(\lambda -1)!}\right]{\pi }_{\lambda }=1\\ {\pi }_{\lambda }=\frac{1}{2}{\left(\sum _{i=0}^{\lambda -1}\frac{{\lambda }^i}{i!}\right)}^{-1}\end{array}$$ (11)

For a given value of λ, the steady-state probability vector π = {π₀, π₁, π₂, · · ·, π_λ} can be obtained from (11), (10) and (8).