Mercedes–Benz water molecules near hydrophobic wall: Integral equation theories vs Monte Carlo simulations

Abstract

Associative version of Henderson-Abraham-Barker theory is applied for the study of Mercedes–Benz model of water near hydrophobic surface. We calculated density profiles and adsorption coefficients using Percus-Yevick and soft mean spherical associative approximations. The results are compared with Monte Carlo simulation data. It is shown that at higher temperatures both approximations satisfactory reproduce the simulation data. For lower temperatures, soft mean spherical approximation gives good agreement at low and at high densities while in at mid range densities, the prediction is only qualitative. The formation of a depletion layer between water and hydrophobic surface was also demonstrated and studied.

INTRODUCTION

The investigation of the structure and properties of liquid water near solid surfaces is a subject of great fundamental and technological interest in electrochemical and biological processes, ecological and geochemical sciences, corrosion and heterogeneous catalysis, and many other studies. Since it is difficult to obtain molecular level information from experiments, microscopic studies based on statistical-mechanical treatments play essential roles. For the last decades, the different microscopical models for water and surface were proposed for the description of surface-water interface by computer simulation and integral equation techniques. There are usually three types of models for water molecules used for this aim. In first of them water molecules are modeled by hard spheres with embedded multipoles. This model was used for the description of the structure of water and aqueous solutions at surfaces using the reference hypernetted chain theory.^{1, 2, 3, 4} In second type of models, so-called rigid models, water molecules are considered as steric molecular frames of potential centers with partial charges such as simple point charge (SPC) model. This model was used for the description of the structure of water and aqueous solutions at surfaces by means of reference interaction site model (RISM)^{5, 6} and the 3D reference interaction site model (3D RISM) integral equation theories.^{7, 8} In the third type of models, so-called flexible models, water molecules are considered as 2:1 binary mixture of hydrogen and oxygen atoms with partial charges. In result, this type of model can be handled by integral equation theories for spherical particles.^{9, 10} The modeling of solid surface can be done in different way from structureless noncharged or charged hard walls to different more or less realistic lattice models.^{6, 8}

However, in spite of intensive investigation of water and aqueous solutions near surface, even for simple structureless hydrophobic surface, our microscopic understanding is not complete. One of the open questions is the roles of hydrogen bonding near surface. The main relevant result for the behavior of water at a solid nonpolar interface is that with decreasing curvature of the surface water molecules close to the surface sacrifice one hydrogen bond and flip over, in contrast to small nonpolar surfaces where water conserves hydrogen bonds by pointing those bonds in directions that straddle the solute. This effect was observed in computer simulations on realistic models^{11, 12} and on surface vibrational spectroscopy experiments.¹³ The hydrogen bond contribution also plays an important role in the formation of microscopically thin depletion layer with low water density between hydrophobic surface as was suggested by Stillinger.¹⁴ The effect of drying water molecules from the nonpolar surface was predicted more recently also by Lum, Chandler, and Weeks.¹⁵ Since the hydrogen bonding can be considered as some type of association phenomena at the presence of hydrophobic surface, the formation of this layer has the similar nature as in the case of dimerising,¹⁶ chain,¹⁷ and network forming fluids¹⁸ near surface.

In order to separate the hydrogen bonding effect from others, it will be more convenient to use some simplified model than realistic ones. The realistic models include many geometrical details and types of interactions, including electrostatic, hydrogen bonding, and van der Waals interactions, which creates the difficulties in computational treatment and interpretation of obtained results. One of the simplest model for water is the so-called Mercedes–Benz (MB) model originally proposed by Ben-Naim 40 years ago.^{19, 20, 21} MB is a 2D model in which each water molecule is modeled as a disk that interacts with other such waters through: (1) a Lennard–Jones (LJ) interaction and (2) an orientation-dependent hydrogen bonding interaction through three radial arms arranged as in the MB logo. The hydrogen bonding interaction is a Gaussian function of angle and distance. Bulk water has previously been studied in this model using NPT Monte Carlo simulations^{21, 22, 23, 24, 25} and thermodynamic perturbation and integral equation techniques.^{26, 27, 28} Those studies have shown that the MB model qualitatively gives many properties of real water, including the density anomaly, the minimum in the isothermal compressibility as a function of temperature, the large heat capacity and the experimental trends for the thermodynamic properties of non-polar solvation.²¹ MB model was also applied in NPT Monte Carlo simulations for studies of mechanism of hydrophobic solvation which depends once on solute radius.²³ It was founded a very different mechanism for aqueous solvation of large nonpolar solutes (much larger than a water) than for smaller solutes in total agreement with simulations on realistic models and experiment.^{11, 12, 13} Two advantages of the MB model, compared to more realistic water models, are: (1) that well-converged computer simulations of thermodynamic properties can be obtained in a reasonable amount of time,^{21, 23} and (2) the underlying physical principles can be more readily communicated and visualized in 2Ds.

In a recent paper,^{26, 27, 28, 29, 30} Wertheim's theory for associating fluids^{31, 32} was applied to the MB model of water through a thermodynamic perturbation theory (TPT),^{31, 32, 33, 34} and an integral equation theory (IET).^{31, 35, 36} We found that both of these analytical approaches are in semi-quantitative agreement with the Monte Carlo simulation results for the molar volumes, isothermal compressibility, thermal expansion coefficient, and heat capacity. IET also gives good prediction for the pair correlation functions of MB model waters. The advantage of the TPT and IET theories is that they require much less computer time than the Monte Carlo simulations. Our interest in using the MB model is that it serves as one of the simplest models of an orientationally dependent liquid, so it can serve as a testbed for developing analytical theories that might ultimately be useful for more realistic models.

In this paper, we describe a more analytical approach for the description of water near hydrophobic surface in framework of MB model for water molecules. For this aim, we used Henderson–Abraham–Barker (HAB) approach³⁷ which establishes the direct relation between bulk and surface properties. Holovko and Vakarin¹⁶ generalized this approach for the description of associating fluids near the wall. The associative HAB was developed by inserting a non-associative giant single particle into an associating fluid and using Wertheim-Ornstein-Zernike (WOZ) equation. In the infinite dilution, WOZ split up into two independent equations: the first for the associative fluid and the second for fluid near surface. The second uses the bulk fluid properties as input. We should mention that the considering approach is enough general and does not put any restrictions on the considering model. The interaction between the giant particle and fluid molecules is totally independent from fluid-fluid interaction and in the limit of infinite large giant particle should be taken in the form of interaction between fluid particle and wall. The associative version HAB theory was applied for the description of dimerising fluid near hard wall¹⁶ and near charged wall³⁸ for chain and network forming fluids.^{17, 18} The associative version of HAB theory was also generalized for the description of different types of associative fluids near crystalline wall.^{39, 40, 41}

The perspectives of this article are as follows: After the above-given introduction, we briefly review the model in Sec. 2. Following this, we present used theories in Sec. 3. Theoretical and simulation results are reported, compared, and discussed in Sec. 4. The last section highlights the main conclusions of this work.

THE MODEL

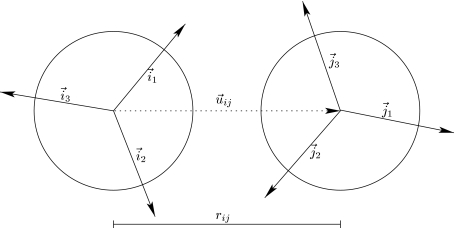
We study MB water that is close to nonpolar plane. Each MB water molecule is a 2D Lennard–Jones disk with three arms separated by an angle of 120° (see Fig. 1).^{19, 21} The interaction potential between two MB particles is a sum of two parts, a Lennard–Jones term and a hydrogen-bonding (HB) term

$$U(\overrightarrow{X_i},\overrightarrow{X_j})=U_{\text{LJ}}\left(r_{ij}\right)+U_{\text{HB}}(\overrightarrow{X_i},\overrightarrow{X_j}),$$ (1)

where r_ij is the distance between centers of particles i and j, and $\overrightarrow{X_i}$ denotes the vector representing the coordinates and the orientation of the ith particle. The Lennard–Jones part of the potential is defined as

$$U_{\text{LJ}}\left(r_{ij}\right)=4{\varepsilon }_{\text{LJ}}\left({\left(\frac{{\sigma }_{\text{LJ}}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{\text{LJ}}}{r_{ij}}\right)}^6\right),$$ (2)

where ɛ_LJ is the well-depth and σ_LJ is the contact parameter. The hydrogen bonding part of the interaction potential is

$$U_{\text{HB}}(\overrightarrow{X_i},\overrightarrow{X_j})=\sum _{k,l=1}^3{U}_{\text{HB}}^{kl}(r_{ij},{\theta }_i,{\theta }_j),$$ (3)

where $U_{\text{HB}}^{kl}$ describes the interaction between two arms of different molecules

$$\begin{array}{c}\hfill U_{\text{HB}}^{kl}(r_{ij},{\theta }_i,{\theta }_j)={\varepsilon }_{\text{HB}}G(r_{ij}-r_{\text{HB}})G(\overrightarrow{i_k}\overrightarrow{u_{ij}}-1)G(\overrightarrow{j_l}\overrightarrow{u_{ij}}+1).\end{array}$$ (4)

By writing down the scalar products explicitly, we obtain the following form of the HB potential

$$\begin{array}{ccc}\hfill U_{\text{HB}}^{kl}(r_{ij},{\theta }_i,{\theta }_j)& =& {\varepsilon }_{\text{HB}}G(r_{ij}-r_{\text{HB}})\hfill \\ & & \times G\left(\cos \left({\theta }_i+\frac{2\pi }{3}(k-1)\right)-1\right)\hfill \\ & & \times G\left(\cos \left({\theta }_j+\frac{2\pi }{3}(l-1)\right)+1\right),\hfill \end{array}$$ (5)

where k and l stands for the different arms and G(x) is an unnormalized Gaussian function

$$G\left(x\right)=\exp \left(-\frac{x^2}{2{\sigma }^2}\right).$$ (6)

Further, ɛ_HB=−1 is an energy parameter and r_HB=1 is a characteristic hydrogen bond length. $\overrightarrow{u_{ij}}$ is the unit vector along $\overrightarrow{r_{ij}}$ and $\overrightarrow{i_k}$ is the unit vector representing the kth arm of the ith particle, where θ_i is the orientation of the ith particle. The strongest hydrogen bond occurs when an arm of one particle is collinear with the arm of another particle and the two arms point in opposing directions. The LJ well-depth ɛ_LJ is 0.1 times, the HB interaction energy ɛ_HB and the Lennard–Jones contact parameter σ_LJ is 0.7r_HB.

Figure 1.

Two molecules of MB water (i and j), separated by the distance r_ij. Each molecule has three bonding vectors denoted by $\overrightarrow{i_k}$ (or $\overrightarrow{j_l}$); k, l = 1, 2, 3.

In the present work, we model the interactions between the MB molecules and the walls as

$$\phi \left(z\right)=4{\varepsilon }_w\left({\left(\frac{{\sigma }_w}{z}\right)}^9-{\left(\frac{{\sigma }_w}{z}\right)}^3\right),$$ (7)

where ɛ_w=ɛ_LJ and σ_w=σ_LJ are the parameters of the Lennard–Jones (9,3) wall-particle potential.

THEORY

Monte Carlo simulations

Computer simulations for MB water close to Lennard–Jones adsorbing surfaces were performed in the (N, V, T) ensemble. Simulations were made for MB water between two parallel plates with such distance between plates that we have bulk phase in middle. Therefore, the two walls did not interfere with each other.

In N, V, T, we simulated from 500 to 1000 MB particles between two walls. At each step, one randomly chosen water molecule is moved. We used periodic boundary conditions and the minimum image convention. The starting configuration of each phase point was selected at random, and the first 1 × 10⁶ moves were discarded as the system equilibrated. Statistics were gathered over the next 1 × 10⁷ moves. In these simulations, the liquid water density was fixed at bulk density at a particular temperature. The point of doing these simulations at constant density is simply to study the water structures at different densities.

Integral equation theory

Application of the integral equation approach to a description of the interface is based on the associative HAB integral equation^{16, 17, 37, 38}

$$h_{\alpha w}\left(r\right)=c_{\alpha w}\left(r\right)+\int c_{\alpha \mu }^{bulk}\left(r^{\prime }\right){\sigma }_{\mu \nu }{h}_{\nu w}\left(\right|\vec{r}-{\vec{r}}^{\prime }\left|\right)d{\vec{r}}^{\prime },$$ (8)

where h_αw(r) and c_αw(r) are the partial total and direct wall-particle correlation functions and the values σ_μν are the density parameters which correspond to different bonded states of MB molecules. The $c_{\alpha \mu }^{bulk}\left(r\right)$ are the bulk partial direct correlation functions which are calculated using the following procedure.²⁶ The multidensity OZ equation for bulk is expressed as

$$\widehat{\mathbf{h}}\left(k\right)=\widehat{\mathbf{c}}\left(k\right)+\widehat{\mathbf{c}}\left(k\right)\mathbf{\rho }\widehat{\mathbf{h}}\left(k\right),$$ (9)

where $\widehat{\mathbf{h}}\left(k\right)$ and $\widehat{\mathbf{c}}\left(k\right)$ are the matrices whose elements are the Fourier transforms of the partial correlation functions $h_{ij}^{bulk}\left(r\right)$ and $c_{ij}^{bulk}\left(r\right)$. We use partial correlation functions which remain finite upon decrease of the temperature.²⁶ In Eq. 9, ρ represents the matrix which replaces the Wertheim's density parameters σ and contains the partial number densities. Here we restrict ourselves to the so-called “ideal network” approximation.^{35, 36} This means that we neglect the component of the correlation that is responsible for formation of the ring-like structures.³⁶ The OZ equation involves the matrices c, h, and ρ of dimensionality 5 × 5. By taking into account the equivalence of the bonding arms we obtain

$$\widehat{\mathbf{z}}\left(k\right)=\left(\begin{array}{cc}\hfill {\widehat{z}}_{00}\left(k\right)& \hfill {\widehat{z}}_{01}\left(k\right)\\ \hfill {\widehat{z}}_{10}\left(k\right)& \hfill {\widehat{z}}_{11}\left(k\right)\end{array}\right),\mathit{\rho }=\left(\begin{array}{cc}\hfill {\rho }^{bulk}& \hfill 3{\rho }^{bulk}\\ \hfill 3{\rho }^{bulk}& \hfill 6{\rho }^{bulk}\end{array}\right),$$ (10)

where lower indices denote the state of the MB molecules (0 for unbonded and 1 for bonded). In Eq. 10, z denotes either the h or c correlation function. The coefficients 3 and 6 in ρ result from the reduction of the dimensionality of the OZ equation.²⁶ In order to solve the OZ equation, an additional relation between the h and c correlation functions is needed. In the present study, we choose the polymer PY closure³¹ in the form

$$\begin{array}{ccc}\hfill c_{ij}^{bulk}\left(r\right)& =& f_{\text{LJ}}\left(r\right)\left(t_{ij}^{bulk}\left(r\right)+{\delta }_{i0}{\delta }_{j0}\right)\hfill \\ & & +{\delta }_{i1}{\delta }_{j1}{\left(x_1^{bulk}\right)}^2{\overline{f}}_{\text{HB}}\left(r\right)e_{\text{LJ}}\left(r\right)\left[t_{00}^{bulk}\left(r\right)+1\right],\hfill \end{array}$$ (11)

where $t_{kl}^{bulk}\left(r\right)=h_{kl}^{bulk}\left(r\right)-c_{kl}^{bulk}\left(r\right)$, $x_1^{bulk}$ is the fraction of MB particles not bonded at one arm, f_LJ(r)=e_LJ(r)−1, and e_LJ(r)=exp[−U_LJ(r)∕k_BT]. Furthermore, ${\overline{f}}_{\text{HB}}\left(r\right)$ is the orientationally averaged Mayer function for the hydrogen bond potential (Eq. 3) and $x_1^{bulk}$ follows from mass-action law as³¹ in the form

$$x_1^{bulk}=\frac{1}{1+3{\rho }^{bulk}{x}_1^{bulk}\Delta }.$$ (12)

Δ is defined by ³¹

$$\Delta =2\pi \int g_{00}^{bulk}\left(r\right){\overline{f}}_{\text{HB}}\left(r\right)rdr.$$ (13)

The total pair distribution function g^bulk(r) is calculated via the relation

$$\begin{array}{c}\hfill g^{bulk}\left(r\right)=g_{00}^{bulk}\left(r\right)+3g_{01}^{bulk}\left(r\right)+3g_{10}^{bulk}\left(r\right)+9g_{11}^{bulk}\left(r\right).\end{array}$$ (14)

The associative HAB integral equation can be in same formalism as for bulk written as

$$h_{iw}\left(r\right)=c_{iw}\left(r\right)+\int c_{ij}^{bulk}\left(r^{\prime }\right){\rho }_{jk}{h}_{kw}\left(\right|\vec{r}-{\vec{r}}^{\prime }\left|\right)d{\vec{r}}^{\prime }.$$ (15)

To solve HAB equation, we must write also closure condition for water-wall and in this work, we used PY type of equation written in the form

$$c_{iw}\left(z\right)=f_w\left(z\right)(t_{iw}\left(z\right)+{\delta }_{i0}),$$ (16)

where f_w(z) = exp [ − ϕ(z)/k_BT] − 1. Solving the HAB integral equation, supplemented by the closure condition, we get the t_iw(z) functions and then the usual density profile

$$\rho \left(z\right)={\rho }^{bulk}(g_{0w}\left(z\right)+3g_{1w}\left(z\right)).$$ (17)

We also calculated the surface density excess Γ which is defined as

$$\Gamma ={\int }_a^{\infty }\left(g\right(z)-1)dx,$$ (18)

where g(z) = ρ(z)/ρ^bulk and a is smallest distance where g(z) is equal to 1.

Other closures are also possible. Here, we also tried the polymer soft mean-spherical approximation (PSMSA). In this closure, we divide the LJ potential into a short-range reference part U₀(r) and a long-range perturbation part U₁(r) as suggested elsewhere^{28, 42}

$$U_{\text{LJ}}\left(r\right)=U_0\left(r\right)+U_1\left(r\right),$$ (19)

where

$$\begin{array}{c}\hfill U_0\left(r\right)=\left\{\begin{array}{cc}\hfill U_{\text{LJ}}\left(r\right)+{\varepsilon }_{\text{LJ}}& \hfill r\ge r_m\\ \hfill 0& \hfill r<r_m\end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill U_1\left(r\right)=\left\{\begin{array}{cc}\hfill -{\varepsilon }_{\text{LJ}}& \hfill r\ge r_m\\ \hfill U_{\text{LJ}}\left(r\right)& \hfill r<r_m\end{array}\right..\end{array}$$

The distance r_m that separates these two components is chosen to be the position of a minimum of the LJ part of the potential function, i.e., r_m=2^1∕6σ_LJ. We obtain the PSMSA closure relation by substituting f_LJ(r) with

$$f_0\left(r\right)=\exp \left[-\frac{U_0\left(r\right)}{k_{B}T}\right]-1,$$ (20)

and e_LJ(r) with

$$e_0\left(r\right)=f_0\left(r\right)+1,$$ (21)

into Eq. 11. Then, only the one term for which i = 0 and j = 0 has a different form

$$c_{00}\left(r\right)=f_0\left(r\right)(t_{00}\left(r\right)+1)-(f_0\left(r\right)+1)\frac{U_1\left(r\right)}{k_{B}T}.$$ (22)

MB particle wall potential ϕ(z) was also divided into a short-range reference part ϕ₀(z) and a long-range perturbation part ϕ₁(z)

$$\phi \left(z\right)={\phi }_0\left(z\right)+{\phi }_1\left(z\right),$$ (23)

where

$$\begin{array}{c}\hfill {\phi }_0\left(z\right)=\left\{\begin{array}{cc}\hfill \phi \left(z\right)+\frac{8\sqrt{3}}{9}{\varepsilon }_w& \hfill z\ge z_m\\ \hfill 0& \hfill z<z_m\end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill {\phi }_1\left(z\right)=\left\{\begin{array}{cc}\hfill -\frac{8\sqrt{3}}{9}{\varepsilon }_w& \hfill z\ge z_m\\ \hfill \phi \left(z\right)& \hfill z<z_m\end{array}\right..\end{array}$$

The distance z_m that separates these two components is chosen to be the position of a minimum of the ϕ(z) part of the potential function, i.e., z_m = 3^1/6σ_w. We obtain the PSMSA closure relation by substituting f_w(r) with

$$f_{w0}\left(z\right)=\exp \left[-\frac{{\phi }_0\left(z\right)}{k_{B}T}\right]-1,$$ (24)

into Eq. 16. Then, only the one term for which i = 0 has a different form

$$c_{0w}\left(z\right)=f_{w0}\left(z\right)(t_{0w}\left(z\right)+1)-(f_{w0}\left(z\right)+1)\frac{{\phi }_1\left(z\right)}{k_{B}T}.$$ (25)

RESULTS AND DISCUSSION

All the results are shown in reduced units: the energy and temperature are normalized to the HB energy parameter ɛ_HB (A^*=A∕|ɛ_HB|,T^*=k_B*T∕|ɛ_HB|) and the distances are scaled to the hydrogen bond characteristic length r_HB (r^*=r∕r_HB).

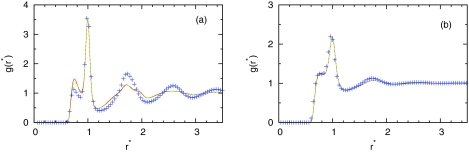
For HAB theory, it is important to have good results for bulk. Figure 2 shows the bulk water-water radial distribution functions, g(r*), calculated for high T* = 0.36 and low T* = 0.18 temperature at density obtained at simulation. In particular, Fig. 2 compares the IET with PY (red solid line) and SMSA (green dashed line) closures and the MC results (symbols).^{21, 23} This figure shows that SMSA gives slightly better result at smaller distances for low temperatures.

Figure 2.

The water-water radial distribution function, g(r*), at (a) T* = 0.18, P* = 0.19 and (b) T* = 0.36, P* = 0.19. The MB model Monte Carlo result²³ is presented by symbols, the PY results by red continuous line, and the SMSA results by green dashed line.

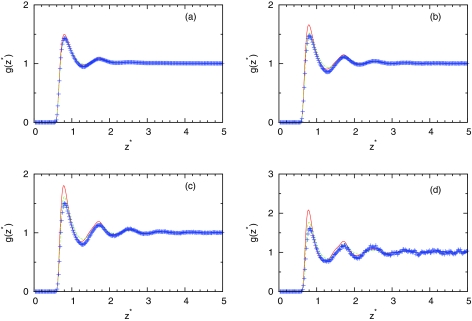
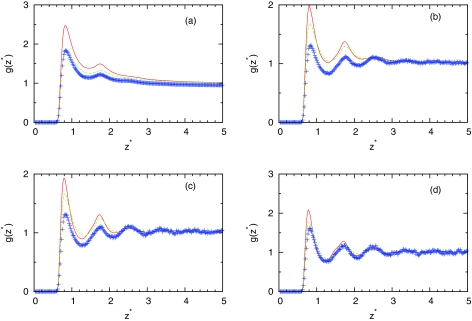
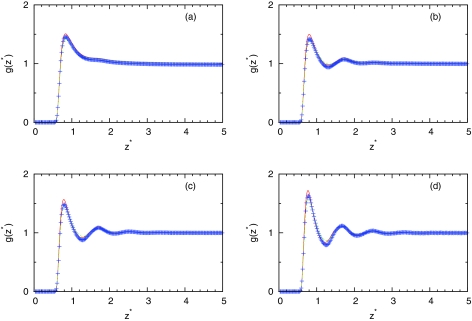
Figures 345 show the computed profiles of water density close to plane. Figure 3 shows how theory can predict structure at different temperatures at fixed simulation pressure. We can see that IET with SMSA closure gives good prediction in all temperature range while results of IET with PY closure are slightly worse. Figures 45 show density dependence of profiles at different temperatures. At higher temperature (T* = 0.36), theory gives excellent prediction of results. For lower temperatures, SMSA gives good agreement at low and high densities while in at mid range densities, the theories do not predict the structure correctly. At these ranges of densities, we are noticing dewetting due to angle dependence of water-water interaction which is neglected on IET level. The obtained results need in some comment. The fact that IET with SMSA closure gives good agreement with the simulations at high temperatures is not surprise. This is consistent with other studies that use the mean spherical approximation.^{43, 44} At high densities and low temperatures, the SMSA results are also reasonable due to renormalization of long-range interactions.⁴⁴ What is unexpected, however, that the SMSA is successful also for low densities and low temperatures. This success can be explained by the hydrogen bonding contributions to profiles of water density near surface. As we can see from Fig. 4, at low temperature for the intermediate densities ρ* = 0.534 and ρ*= 0.741, SMSA overestimates the value of profile. The SMSA gives higher values than computer simulations. Since SMSA is the linear theory about long-range interaction, we can predict that for the density lower than ρ* = 0.1, the result of computer simulations will be higher than the result of SMSA. In this region, SMSA as usually the mean spherical approximation fails to give the second virial coefficient correctly at low temperatures.

Figure 3.

Density profile of MB water close to LJ plane. The MB model Monte Carlo result is presented by symbols, the PY results by red continuous line, and the SMSA results by green dashed line for pressure p* = 0.19 and (a) T* = 0.36, ρ* = 0.534, (b) T* = 0.28, ρ* = 0.741, (c) T* = 0.24, ρ* = 0.870, and (d) T* = 0.18, ρ* = 0.990.

Figure 4.

Same as Fig. 3, results are for T* = 0.18 and (a) ρ* = 0.1, (b) ρ* = 0.534, (c) ρ* = 0.741, and (d) ρ* = 0.990.

Figure 5.

Same as Fig. 4, results are for T* = 0.36.

From density profiles, we calculated some other surface quantities. This way we can have possibility to check the quality of proposed theory and to discuss other specific surface properties of water in framework of this model. First we checked the contact theorem for MB model of water near surface. Usually the contact theorem is formulated for fluids near hard wall.^{45, 46} For soft wall, considering in this paper, this theorem can be presented approximately in the form

$$\rho \left(z_m\right)=\beta p-\beta {\int }_0^{\infty }\rho \left(z\right)\frac{\partial \phi \left(z\right)}{\partial z}dz,$$ (26)

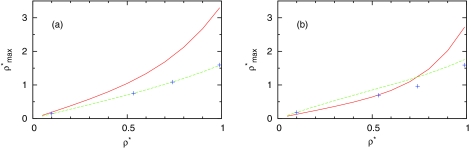
where p is the water bulk pressure, β inverse temperature, and z_m corresponds to the value of the first peak in profile ρ(z). Figure 6 shows the density dependence contact value of ρ(r_m) at high and low temperatures calculated from Eq. 26 and from IET and computer simulation. As we can see we have good correlation between results obtained from Eq. 26 and from IET and computer simulations.

Figure 6.

Dependence of maximum density of MB water close to LJ plane on density. The SMSA results from Eq. 26 are presented by red solid line and from IET by green dashed line and from Monte Carlo simulations by symbols for (a) T* = 0.36 and (b) T* = 0.18.

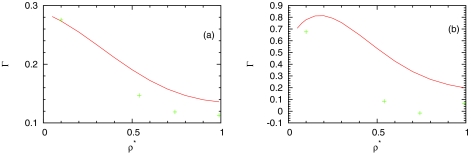
The surface density excess is connected with the adsorption coefficient Γ which can be calculated from Eq. 18. The results for Γ as a function of density at different temperatures are plotted in Fig. 7. We have compared our results also with MC data. It is necessary to note that the Γ calculated within the SMSA approximation is quantitatively correct at low densities and high temperatures only. At higher densities, deviations are seen. At low temperatures, the deviations are high mainly due to approximation of orientationally averaging in the theory. IET and MC results demonstrate qualitatively the same tendencies. With increasing density, the surface density excess decreases. This feature is similar as for other associative fluids.^{16, 17, 18} In the presence of hydrophobic surface, water molecules form smaller number of hydrogen bonds than in bulk. The surface repulses water molecules away from surface into the bulk phase. This tendency is opposite to the case of simple liquids where due to packing effect the density of molecules near surface is larger than in bulk. As a result, the adsorption coefficient Γ for simple liquids increases with increasing density.

Figure 7.

Dependence of absorption coefficient of MB water close to LJ plane on density. The MB model Monte Carlo result is presented by symbols and the SMSA results by red solid line for (a) T* = 0.36 and (b) T* = 0.18.

For better understanding of water behavior near surface, we calculated the number of hydrogen bonds of water molecules as function of distance from hydrophobic wall. This was done using the following approximation. First we calculated ratio of nonbonded MB molecules at distance z from wall from mass action law as

$$x_1\left(z\right)=\frac{2}{1+\sqrt{12\rho \left(z\right)\Delta \left(z\right)}},$$ (27)

where ρ(z) is density around hydrophobic wall from HAB and Δ(z) is defined as integral from center at distance z from wall

$$\Delta \left(z\right)=\int g_{00}^{bulk}\left(r\right){\overline{f}}_{\text{HB}}\left(r\right)d\mathbf{r}.$$ (28)

Equations 27, 28 are generalization of Eqs. 12, 13 for bulk. Each molecule has three arms. The probability that a hydrogen bond is formed at one arm is (1 − x₁(z)). We now get the following equations for average number of hydrogen bonds per molecule at distance z:

$$n\left(z\right)=3(1-x_1\left(z\right)).$$ (29)

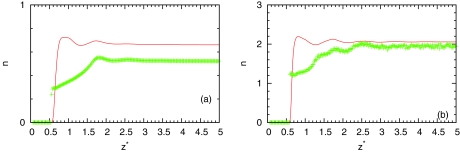
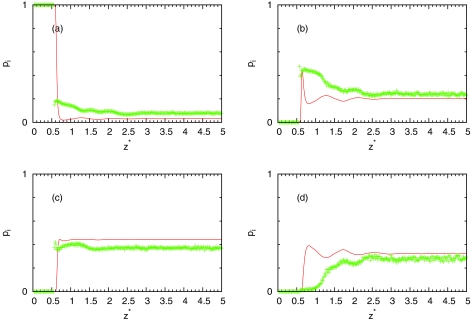
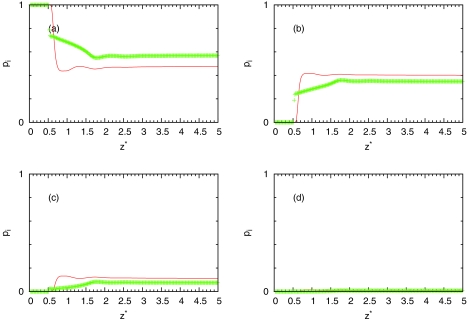
The results for the bulk water are presented in Table 1. From this table, we can see overestimation of number of hydrogen bonds from IET approximately to 0.1 at high and low temperatures. Average number of hydrogen bonds of MB water as a function of distance from hydrophobic wall is presented in Fig. 8. We can see that theory overestimates averaged number of hydrogen bonds at all distances at high and low temperatures. We can also see that at small distances from wall theory predict that water can still form same number of hydrogen bonds as in bulk. Probably this is the main defect of IET with considering closures. The reason is that orientationally averaging is equivalent to arms being randomly distributed and water close to surface can still form three hydrogen bonds which is different than in simulation. However, as we can see from Fig. 8, computer simulations show correct prediction. Average number of hydrogen bonds near surface is smaller than in bulk. Figures 910 show populations of nonbonded ($p_0\left(z\right)=x_1^3\left(z\right)$), once bonded ($p_1\left(z\right)=3x_1^2\left(z\right)(1-x_1\left(z\right))$), twice bonded (p₂(z) = 3x₁(z)(1 − x₁(z))²), and triple bonded (p₃(z) = (1 − x₁(z))³) water molecules. From these results, we can see same conclusions about accuracy of IET as from average number of hydrogen bonds.

Table 1.

Hydrogen bonds distribution in bulk water. Comparison of IET results with computer simulation results for pressure p* = 0.19 for high and low temperature.

	T* = 0.36, ρ* = 0.534		T* = 0.18, ρ* = 0.99
	IET	MC	IET	MC
n	0.66	0.52	2.05	1.93
p0	0.47	0.57	0.03	0.08
p1	0.40	0.35	0.20	0.25
p2	0.11	0.073	0.44	0.38
p3	0.010	0.007	0.33	0.29

Figure 8.

Average number of hydrogen bonds per MB water molecule depending on distance from LJ plane. The MB model Monte Carlo result is presented by symbols and the SMSA results by red solid line for pressure p* = 0.19 and (a) T* = 0.36, ρ* = 0.534 and (b) T* = 0.18, ρ* = 0.990.

Figure 9.

Population p_i of (a) nonbonded, (b) once bonded, (c) twice bonded, and (d) triple bonded MB water molecule depending on distance from LJ plane. The MB model Monte Carlo result is presented by symbols and the SMSA results by red solid line for pressure p* = 0.19 and T* = 0.18, ρ* = 0.990.

Figure 10.

Same as Fig. 8, results are for T* = 0.36, ρ* = 0.534.

The obtained results for the dependence of number of hydrogen bonds of water molecules of the distance from a hydrophobic surface (especially calculated from computer simulations) are in qualitative agreement obtained recently from 3D water model using the probabilistic hydrogen bonds approach.^{47, 48} In this approach, it was assumed that the water-water hydrogen bonds have a binomial character. This assumption corresponds to ideal network approximation³⁶ used in IET. Djikaev and Ruckenstein^{47, 48} calculated the populations p_i(z) as

$$\begin{array}{ccc}\hfill p_0\left(z\right)& =& p_0{K}_0\left(z\right),p_1\left(z\right)=p_1{K}_1\left(z\right),\hfill \\ \hfill p_2\left(z\right)& =& p_2{K}_2\left(z\right),p_3\left(z\right)=p_3{K}_3\left(z\right),\hfill \end{array}$$ (30)

where p₀, p₁, p₂, and p₃ are corresponding values for bulk water as presented in Table 1. The coefficient-functions K_i(z) were evaluated by using geometrical constrains by averaging orientations of water molecules near surface. Though the results of Djikaev and Ruckenstein^{47, 48} are correct, the approach used is semiphenomenological and does not give possibility to describe microscopic structure between water and surface.

CONCLUSIONS

We use the simple 2D MB model of water to study the properties of water near nonpolar wall. We have calculated the structure and adsorption of the MB water molecules by means of the PY and SMSA approximation of the associative HAB integral equation. We have compared our results with MC simulation data. We concluded that prediction of HAB is in quantitative agreement with MC at high temperatures and is qualitatively correct for cold water. The virtue of employing this approach is that it gives physical insights and is analytical, and so is much more efficient computationally than Monte Carlo simulations model.

We found the desorption of water molecules near hydrophobic surface which is more stronger at lower temperatures. This phenomenon leads to the formation of depletion layer between water and surface. The developed IET approach has two general defects. It includes only orientational-averaged functions. Due to this, orientational correlation effects are neglected. For the description of such effect, IET should be expanded for orientational-dependent IET similar as was done in previous work²⁷ for bulk case. The second defect is connected with the associative version of HAB approach which uses the bulk fluid properties as input. In result, the degree of association x₁ is determined by the solution for bulk fluid. For the improvement of IET, we can use the inhomogeneous version of Wertheim-Ornstein-Zernike equation (WOZ2) similar as was done for dimerising fluid in work of Henderson et al.⁴⁹ Such programme of improvement of IET will be considered in our future work.