Three-dimensional impedance map analysis of rabbit liver

Abstract

Three-dimensional impedance maps (3DZMs) are computational models of acoustic impedance of tissue constructed from histology images. 3DZMs can be analyzed to estimate model-based quantitative ultrasound parameters such as effective scatterer diameter (ESD). In this study, 3DZMs were constructed from normal and fatty rabbit livers. Estimates of ESD were made using the fluid-filled sphere scattering model. Weighting toward smaller scatterer sizes produced ESD estimates of 7.5 ± 1.3 and 7.0 ± 0.3 μm for normal and fatty liver, respectively, approximately the size of a liver cell nucleus. This suggests the nucleus could be a primary source of scattering in liver.

Introduction

Ultrasound imaging is safe, portable, and inexpensive when compared to other imaging modalities such as x-ray, computed tomography, and magnetic resonance imaging.1 These advantages make ultrasound an active area of research to expand the capabilities and diagnostic function of medical ultrasound. Conventional B-mode imaging provides a mainly qualitative description of tissue macrostructure and contains only part of the information available in the echo signal. Quantitative ultrasound (QUS) seeks to utilize frequency-dependent details available from radio-frequency (RF) echo signals to determine properties of tissue microstructure.2 Several QUS parameters, particularly the effective scatterer diameter (ESD), can be estimated to provide information about acoustic scattering sites.3

Three-dimensional impedance maps (3DZMs) are computational models of acoustic impedance and are a powerful tool in studying small-scale acoustic scattering in biological tissue.4 3DZMs are created from a series of adjacent histological images that have been aligned to one another to form a three-dimensional (3D) volume. Each voxel of the reconstructed 3D volume is assigned a value of acoustic impedance. The 3DZM can be related to ultrasonic backscatter through the use of intensity form factors, which are scattering models for different scatterer geometries.3 The form factor is related by the Fourier transform of the 3D spatial autocorrelation of the acoustic impedance distribution.5 Equivalently the form factor can be computed as the squared magnitude of the 3D spatial Fourier transform, or power spectrum, of the impedance distribution due to the Wiener-Khintchine theorem.6 Thus form factors are proportional to the power spectrum of an impedance distribution, making 3DZMs a useful tool in determining a link between histological features and ultrasonic backscatter data to elucidate the scattering structures in tissue.

Methods

Lobes of normal and fatty liver from New Zealand white rabbits were excised. The fat content of the fatty liver was measured to be 14.6% using a modification of the Folch method.7 The fat content of the normal liver of the specific rabbit used in this experiment was not available, but for rabbits of the same species fed on a high-fiber diet, the average fat content was 1.7%. The liver samples were chemically fixed in formalin, sliced into 3 μm sections, stained with hematoxylin and eosin (H&E), and prepared as standard histology slides. Each slide was digitized using a NanoZoomer HT slide scanner (Hamamatsu, Hamamatsu City, Japan) at a pixel resolution of 0.46 μm. A typical histologic slide image was around 23 000 × 18 000 pixels or roughly 10 500 μm × 8 000 μm.

The series of images were then aligned using a novel method of computer registration.8 The first stage of registration occurs at the global level to provide a rough alignment using highly decimated images. This stage also serves to exclude any missing slides or images of tissue that may have been damaged in the histology processing. A set of rigid registration parameters (rotation and translation) that represent best global alignment are found using a correlation metric. At the local registration stage, a set of affine transformations (now including stretching and shearing) are found that best optimize an intensity mean-squared error metric. To increase computational efficiency and robustness, the affine registration begins using decimated versions of the images.9 Once a suitable set of transformations is found, the initial transforms are passed to the next stage where more image information is used. The stages are repeated with more image information each time until the last stage when the undecimated images are registered.

This process is performed image by image with the transforms applied in cascade to create an aligned series of histology images. The image intensity and saturation values are then normalized to account for varying degrees of dye uptake between histology slices. Missing histologic sections are replaced computationally using cubic Hermite interpolation along each column of pixels, which is done independently for each color field (RGB). Finally, acoustic impedance values are assigned to each pixel based on the H&E’s color value.10, 11 The final product is a 3D volume of acoustic impedance, the 3DZM, that closely mimics the structure of the tissue slides from which it was created (Sarwate is a board-certified pathologist) (Fig. 1).

Figure 1.

(Color online) Three-dimensional histologic maps (a) and (c) and three-dimensional impedance maps (b) and (d) for a normal liver (a) and (b) and a fatty liver (c) and (d). The size of the four maps is 300 × 300 × 300 μm³.

A total of 48 3DZMs were constructed, 24 from the sample of fatty liver and 24 from the sample of normal liver. The regions from which 3DZMs were created were chosen to be independent of one another and to avoid high-level tissue structure to maximize the homogeneity of the section. The 3DZMs represent the acoustic impedance of a 300 × 300 × 300 μm³ volume of tissue (650 × 650 × 100 pixels), and have a voxel size of 0.46 × 0.46 × 3 μm³.

Estimation of the ESD from the 3DZM was performed by fitting the power spectrum of the volume with the fluid-filled sphere intensity form factor,6, 12 which is a theoretical model of acoustic scattering,

$$F(k,d)={\left(\frac{3j_1\left(\mathit{kd}\right)}{\mathit{kd}}\right)}^2$$ (1)

where j₁ is the first order spherical Bessel function of the first kind, k is the acoustic wave number, and d is the scatterer diameter. In this case, the form factor F models the simple geometry of a sphere of uniform impedance embedded in a background material of differing impedance. The Fourier transform of the 3D autocorrelation of the relative impedance function, or equivalently the squared magnitude of its Fourier transform6 was computed,

$$R_u(k_x,k_y,k_z)=\frac{1}{k^2}{|\frac{1}{\mathit{MNP}}·\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}\sum _{z=0}^{p-1}\frac{z(x,y,z)-z_0}{z_0}{e}^{-j(k_{x}x+k_{y}y+k_{z}z)}|}^2$$ (2)

where z is the spatial function of impedance, z₀ is the background impedance, M, N, and P are the number of data points in the x, y, and z directions, respectively, and k_x, k_y, and k_z are the components of the acoustic wave number k such that $k_x^2+k_y^2+k_z^2=k^2$. Two different methods of power spectral estimation were used. The first method uses the formula for the power spectrum given above, and the second is a weighted estimation which removes the 1∕k² from the standard formula

$$R_w(k_x,k_y,k_z)={\left|\frac{1}{\mathit{MNP}}\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}\sum _{z=0}^{p-1}\frac{z(x,y,z)-z_0}{z_0}{e}^{-j(k_{x}x+k_{y}y+k_{z}z)}\right|}^2.$$ (3)

The fitting was performed on a 3D function of k; hence the 1D form factor equation was transformed into a 3D function. This was trivially done by calculating the value of the form factor at each data point (k_x, k_y, k_z) using the magnitude k of the data point.

The purpose of using the weighted method is that it places a higher emphasis of the ESD estimation on higher frequencies. The reason for this is that when the power spectrum is calculated, the number of points calculated for any spatial frequency of magnitude k is proportional to k². Thus, more data points corresponding to higher spatial frequencies are calculated. By weighting the fitting at each data point by 1∕k², every spatial frequency contributes equally towards the ESD estimation. Removing the 1∕k² weighting term introduces an implicit weighting of the estimation towards smaller ESD sizes.

Results

For the standard power spectral method of the 3DZMs given by Eq. 2, the ESD was estimated to be (mean ± standard deviation) 114 ± 43 μm for the normal liver and 94 ± 53 μm for the fatty liver. These mean values are roughly the size of a cluster of several hepatocyte cells. The large standard deviations (approximately 37% and 56%) suggest that these estimates are not tied to a single scatterer size.

The weighted estimation given by Eq. 3 produced an ESD of 7.5 ± 1.3 μm for the normal liver and 7.0 ± 0.3 μm for the fatty liver. This smaller size is the result of placing more weight on the high frequencies of the form factor when performing the fitting. The mean values near 7 μm correspond closely to the size of the nucleus (Fig. 2). The smaller standard deviations (approximately 18% and 4%) suggest that these are better fits for most of the 3DZMs that were created for both the normal and fatty liver samples.

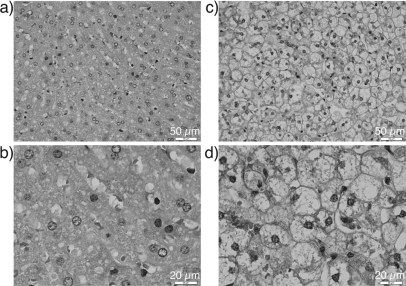
Figure 2.

(Color online) Histology images of normal rabbit liver at 40× (a) and 100× (b) magnification. Fat content of normal liver is typically between 1.5% and 2%. Histology images of fatty liver at 40× (c) and 100× (d) magnification. Fat content of the fatty liver pictured was measured to be 14.6%. Scale bars of (a) and (c) are 50 μm and scale bars of (b) and (d) are 20 μm. Dark circular-like structures are the cell nuclei.

Discussion

3DZMs have shown themselves to be useful in studying ultrasound scattering from tissue microstructure.13, 14 The relative homogeneity of liver compared to other tissues makes it an almost ideal sample on which to perform the 3DZM analysis. Unlike ultrasound transducers which have a fixed bandwidth, 3DZMs are bandlimited only by the resolution of the images, which was not a limiting factor in analyzing scattering in liver tissue. The ability to choose the analysis bandwidth with the 3DZMs makes them quite versatile in exploring details of tissue microstructure over multiple scales.

Because the regions chosen to create 3DZMs were selected to avoid higher-order structures and maximize tissue homogeneity, the ESD estimation weighted toward larger scatterer sizes did not consistently detect a specific size. The weighting of the ESD estimation toward smaller scatterer sizes proved to be useful in obtaining estimates with a low variance. The mean ESD values of 7.5 and 7.0 μm closely correspond to the actual diameter of the liver cell nuclei as illustrated in Fig. 2. The ability to link QUS parameters and histology information makes 3DZMs a useful tool in understanding and identifying ultrasound scattering on the micro scale and motivates further research using this method.