Calcium and Stretch Activation Modulate Power Generation in Drosophila Flight Muscle

Abstract

Many animals regulate power generation for locomotion by varying the number of muscle fibers used for movement. However, insects with asynchronous flight muscles may regulate the power required for flight by varying the calcium concentration ([Ca²⁺]). In vivo myoplasmic calcium levels in Drosophila flight muscle have been found to vary twofold during flight and to correlate with aerodynamic power generation and wing beat frequency. This mechanism can only be possible if [Ca²⁺] also modulates the flight muscle power output and muscle kinetics to match the aerodynamic requirements. We found that the in vitro power produced by skinned Drosophila asynchronous flight muscle fibers increased with increasing [Ca²⁺]. Positive muscle power generation started at pCa = 5.8 and reached its maximum at pCa = 5.25. A twofold variation in [Ca²⁺] over the steepest portion of this curve resulted in a two- to threefold variation in power generation and a 1.2-fold variation in speed, matching the aerodynamic requirements. To determine the mechanism behind the variation in power, we analyzed the tension response to muscle fiber-lengthening steps at varying levels of [Ca²⁺]. Both calcium-activated and stretch-activated tensions increased with increasing [Ca²⁺]. However, calcium tension saturated at slightly lower [Ca²⁺] than stretch-activated tension, such that as [Ca²⁺] increased from pCa = 5.7 to pCa = 5.4 (the range likely used during flight), stretch- and calcium-activated tension contributed 80% and 20%, respectively, to the total tension increase. This suggests that the response of stretch activation to [Ca²⁺] is the main mechanism by which power is varied during flight.

Introduction

The ability to fly is a major reason for the amazing ecological and evolutionary diversification of insects. Many small flying insects, including Diptera, have evolved remarkable adaptations for flight powered by small wings that require high wing beat frequencies (WBFs), up to 1000 Hz, to generate sufficient aerodynamic lift and power (1). High frequencies have required specialized adaptations of the flight muscles that power wing beating, including the fastest kinetics of any muscle myosin cross-bridge cycle (2), indirect linkage of flight muscles to wings (hence the term “indirect flight muscle” (IFM)) to take advantage of the resonance and elastic properties of the thorax (3), and a relatively short length excursion of the muscle (4). High speed would also greatly increase the cost of activation-relaxation cycling if each wing beat required cyclic release and ATP-driven reuptake of calcium, as is typical for regulation of synchronous striated muscles whose action cycles are synchronized with spikes or volleys of neural input that trigger pulses of elevated myoplasmic calcium (5,6). Many insect flight muscles, especially those of small insects, have been spared the high cost of beat-to-beat calcium pumping thanks to ancestors that evolved asynchronous flight muscles, which instead depend instead on highly enhanced properties of stretch activation and shortening deactivation. In Drosophila, the motor neuron that innervates the asynchronous IFMs fires at ∼5 Hz, well below the ∼200 Hz muscle length (ML) excursion frequency at room temperature (7), and calcium is not released into and removed from the myoplasm during each contraction relaxation cycle. Instead, the required tension levels for positive work and power production are enabled by stretch activation and shortening deactivation, which require only steady maintenance of myoplasmic [Ca²⁺] above a critical threshold (1,8,9). A small stretch or shortening of an active muscle fiber is followed by a delayed increase or decrease, respectively, in tension. The timing of these delays in tension change enables positive work and power generation for each muscle contraction-relaxation cycle because during sequential contraction cycles, the tension is higher during muscle shortening than during muscle lengthening. In contrast, a muscle without substantial stretch activation or shortening deactivation would produce higher tension during lengthening than during shortening, and hence would absorb work and not generate power.

The myofilament [Ca²⁺] has been presumed to be held relatively constant during flight, with its only role being to enable initiation and maintenance of wing beating until it is decreased to stop wing beating and terminate flight (10). However, a recent study strongly suggested that [Ca²⁺] may regulate power generation by Drosophila IFM during flight, rather than just turning the muscle fibers on and off to initiate and end flight (7). This study found a correlation between motor nerve stimulation frequency, calcium levels, WBF, and aerodynamic power generation that suggests an active power-regulating role for [Ca²⁺]. Calcium was found to vary ∼2-fold during flight. To efficiently increase aerodynamic power by varying calcium, the IFM power and optimum ML oscillation speed for power generation would need to meet the increased aerodynamic requirements over a twofold variation in [Ca²⁺]. Gordon and Dickinson (7) found no evidence for differential recruitment of IFM fibers. Thus, rather than recruiting more muscle fibers for higher power generation, as do species with multiple motor units that are sequentially recruited (11), Drosophila IFM might regulate its IFM power output by varying myoplasmic [Ca²⁺].

Stretch-activated tension (F_SA) has been shown to vary with myoplasmic [Ca²⁺] (12–14). However, the general relationship between [Ca²⁺] and F_SA is controversial. Linari et al. (12) and Agianian et al. (14) reported maximum F_SA from Lethocerus IFM at intermediate [Ca²⁺] (pCa ∼ 6.0), where the calcium-activated isometric tension (F₀) reaches only ∼20% of its maximum value. Raising [Ca²⁺] stepwise from pCa ∼ 6.0 to pCa = 4.5 did not change the total tension (F₀ + F_SA), because as isometric tension increased, F_SA was proportionally reduced. At pCa = 4.5, F_SA was only ∼10% of total tension. Thus, they proposed that the two activation modes are complementary and competitive, recruiting from the same limited pool of myosin motors. In contrast, Iwamoto et al. (13) observed in Lethocerus IFM that F₀ and F_SA both saturated at pCa = 4.5, but with the proportions reversed: F₀ reached only 5–10% of total (F₀ + F_SA) tension, whereas F_SA accounted for 90–95%, with the two components summing additively but not competitively.

To determine how the [Ca²⁺] in Drosophila IFM influences muscle power and speed, we used the work loop technique to measure in vitro power generation. We found that IFM power and muscle kinetics increased with increasing [Ca²⁺]. If calcium varies twofold during flight between pCa = 5.7 and 5.4, then IFM power would vary ∼2-fold during flight and muscle kinetics would vary by 1.2-fold, matching the changes in aerodynamic power and WBF observed by Gordon and Dickinson (7). To determine the influence of stretch-activated and isometric calcium tensions on power modulation, we measured tension responses to very fast muscle-lengthening steps at various levels of [Ca²⁺]. F_SA increased proportionally with isometric calcium tension but reached its maximum value at a slightly higher [Ca²⁺] than calcium tension and had a fourfold greater influence on total tension over the pCa range that produced the greatest change in power. This suggests that the change in power during flight comes predominantly from calcium modulating F_SA. Thus, Drosophila is likely varying [Ca²⁺] within fibers as a mechanism to modulate muscle power, rather than sequentially recruiting fibers, to meet the aerodynamic demands of small-insect flight.

Materials and Methods

Muscle mechanics

Dissection of IFM fibers from 2- to 3-day-old Oregon-R Drosophila and the initial setup of fibers on the mechanics apparatus were performed as previously described (2,15). Briefly, IFM fibers were removed from the thorax while it was in a dissection solution (pCa 8.0, 5 mM MgATP, 1 mM free Mg²⁺, 0.25 mM phosphate, 5 mM EGTA, 20 mM N,N-bis(2-hydroxyethyl)-2-aminoethanesulfonic acid (BES, pH 7.0), 175 mM ionic strength, adjusted with Na methane sulfonate, 1 mM DTT, 50% glycerol, and 0.5% Triton X-100) at 4°C. Both ends of the isolated fiber were secured with aluminum T-clips and mounted on a muscle mechanics apparatus with one end connected to a force gauge and the other end connected to a servo motor. The fiber was stretched until just taut, the fiber length between the clips was measured, and the fiber was lengthened by 5% in a relaxing solution (pCa 8.0, 5 mM MgATP, 8 mM phosphate, 15 mM creatine phosphate, 300 U/ml creatine phosphokinase, 1 mM free Mg²⁺, 5 mM EGTA, 20 mM BES (pH 7.0), 200 mM ionic strength, adjusted with Na methane sulfonate, 1 mM DTT). We measured the fiber length again, along with the fiber cross-sectional area, using a 10× objective on the apparatuses' inverted microscope and video analysis software (Ion Optix, Milton, MA). We determined the cross-sectional area using the formula for an ellipse, and the two required fiber diameters (one measured from below and the other from the side) using a rectangular prism. The fiber was activated to pCa = 5.0 with activating solution (the same as the relaxing solution except for calcium concentration) and subjected to sinusoidal analysis (see below). The fiber was stretched by 2% ML increments until the power output, as determined by sinusoidal analysis at 0.125% ML change, was maximized. Fibers that did not produce power > 40 W/m³ were discarded. Isometric tension, step analysis, work loop, and sinusoidal analysis protocols were subsequently performed at this optimal length at 15°C.

Work loop power measurements

A high [MgATP] relaxing solution (pCa 8.0, 12 mM MgATP, 30 mM creatine phosphate, 600 U/ml creatine phosphokinase, 1 mM free Mg²⁺, 5 mM EGTA, 20 mM BES (pH 7.0), 200 mM ionic strength, adjusted with Na methane sulfonate, 1 mM DTT) was exchanged into the muscle chamber because we previously determined that maximum IFM fiber kinetics and power require >10 mM MgATP (2). The fiber was activated by incrementally exchanging high [MgATP] activating solution (the same as the high [MgATP] relaxing solution but with pCa = 4.0). The fiber was oscillated through a sinusoidal waveform at 75 Hz, 100 Hz, 125 Hz, 150 Hz, 175 Hz, and 200 Hz, and amplitudes of 0.75%, 1%, 1.25%, and 1.5% ML at pCa = 6.25, 6.0, 5.8, 5.75, 5.5, 5.0, and 4.5. Ten identical consecutive sinusoids were applied to the muscle, and both tension and ML change traces were recorded at a sampling frequency of 8 kHz. The oscillatory pattern of the ML change started at the base of the sinusoidal waveform. Thus, the tension level starts at the calcium-activated tension level for that pCa and increases. We determined positive work and negative work by calculating the area under the tension curve during shortening and lengthening, respectively, for each cycle (Fig. 1) using the equation Work = ∫FdL, where F is tension and dL is fiber length change. Negative work was subtracted from positive work to calculate net work, and net work was multiplied by oscillation frequency to calculate power. We used the work and power values from the eighth cycle because by the sixth or seventh cycle, the power reached a constant value. We did not exhaustively optimize power generation at each [Ca²⁺], because we wanted to focus on the effects of calcium rather than vary every possible parameter to maximize power.

Figure 1.

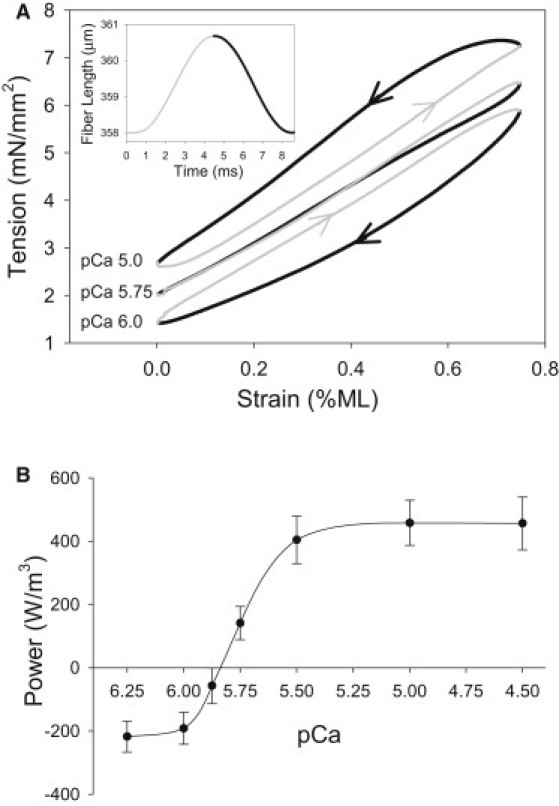
Influence of [Ca²⁺] on power generation. (A) Representative work loop traces from one fiber show the tension response to a 0.75% ML change. The inset shows that the same fiber was symmetrically oscillated through a sinusoidal waveform at 125 Hz. The oscillatory pattern of the ML change started at the base of the sinusoidal waveform. Thus, the tension level starts at the F₀ level for that pCa and increases. Wide black traces show fiber shortening, and thin gray traces show fiber lengthening. Arrows also indicate shortening and lengthening. (B) Maximum power was determined at seven [Ca²⁺] by optimizing strain amplitude with 0.25% increments, and frequency with 25 Hz increments for each [Ca²⁺] using the work loop technique. The data are fit with a Hill curve, as described in the legend of Fig. 3. N = 7 fibers; values are mean ± SE.

Sinusoidal analysis

We used sinusoidal analysis to determine whether [Ca²⁺] influenced the frequency at which maximum power was generated (f_max). The fiber was subjected to a series of calcium concentrations by partial exchanges of the high [MgATP] relaxing or activating solution. After each exchange, the solution was thoroughly mixed around the fiber, and the fiber was incubated in the solution for 2 min to allow complete diffusion before mechanical evaluation was performed. At each [Ca²⁺], 0.25% peak-to-peak strain amplitude and frequencies ranging from 0.5 to 650 Hz were applied to the fiber, and power and f_max were determined as previously described (2,15). Experiments were performed at 15°C. Statistical analysis, Student's t-test (p < 0.05), or one-way analysis of variance (p < 0.05) was performed with the use of either Microsoft Excel or SPSS.

Stretch-activation analysis

The tension response to a muscle-lengthening step was measured at 10 [Ca²⁺] in a high [MgATP] bathing solution. For each [Ca²⁺], steps were applied to fibers after the Ca²⁺-dependent isometric tension reached its maximum for that pCa. A lengthening step of 1% ML over 0.5 ms and a 2.5% ML step over 1.5 ms were applied to IFM fibers at each pCa level. After 300 ms, the fibers were slowly returned to their original length over 500 ms. Isometric tension was measured before and after each stretch at every Ca²⁺ concentration. If isometric tension decreased by >10% after a single stretch, the data from that fiber were discarded. Control experiments starting at low instead of high pCa were performed to ensure that the order of pCa testing did not influence the results. We measured the amplitude of the stretch-activated force (F_SA) after the lengthening step by subtracting the total Ca²⁺-activated isometric tension (immediately before the step) from the peak value of the delayed force increase (phase 3 (16)) after stretch. We corrected this tension level to show only active components (F_SA) by subtracting passive tension (P_SA) measured at pCa = 8.0 (Fig. 2). P_SA was measured at the same time point after the step as the phase 3 peak amplitude at pCa = 4.5. To determine the rate of phase 3 (r₃), the tension response after the initial spike, Huxley and Simmon's phases 2–4 (16), was fit to the sum of three exponential curves: $a_1\text{exp}\left(-k_{1}t\right)+a_2\text{exp}\left(-k_{2}t\right)+a_3\left(1-\text{exp}\left(-k_{3}t\right)\right)+\text{offset}$, where k₃ is r₃.

Figure 2.

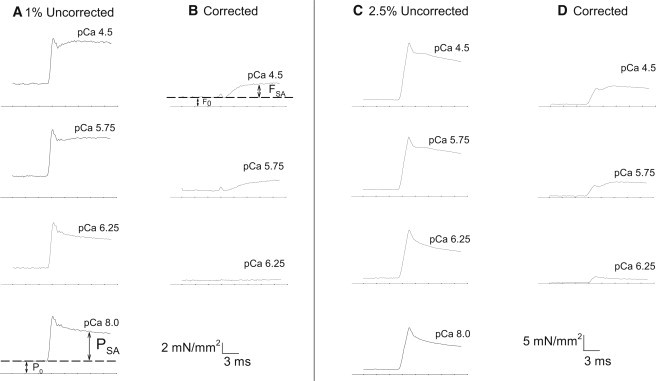
Tension response to calcium and stretch activation. Examples of force traces from step increases in length. (A) Tension response to a 1% ML step over 0.5 ms at five [Ca²⁺] selected from the 10 recorded (shown in Fig. 3). Arrows indicate the time points at which the four tension values were measured. The P_SA and F_SA measurements were taken at the same time point after the step. The P_SA time point was chosen based on the typical time it takes for F_SA to reach its maximum value. (B) Corrected tension traces after subtracting the pCa = 8.0 passive tension trace (P₀ and P_SA, bottom panel of A) to show only the influence of active force-generating muscle components. (C) Tension response to a 2.5% ML, 1.5 ms step increases in length at five [Ca²⁺] selected from the 10 recorded (shown in Fig. 3.) (D) Corrected tension traces after subtracting the 2.5% pCa = 8.0 passive tension trace (P₀ and P_SA, bottom panel of C). The bottom line in each panel indicates zero tension.

Isometric tension

We used an independent set of IFM fibers for isometric tension experiments because measuring isometric tension in conjunction with the step experiments introduced higher variability into the isometric tension data. High-[MgATP] activating solution (pCa = 4.0) was exchanged into the chamber to sequentially increase the Ca²⁺ concentration. Immediately after each exchange, the solution was mixed around the fiber. After 2 min, isometric tension was measured. Isometric tension was measured at the same Ca²⁺ concentrations as the stretch-activation experiments. Passive tension (P₀) was subtracted from isometric tension to calculate calcium-activated tension (F₀; Fig. 2). Tension versus [Ca²⁺] plots were fitted with the Hill equation, $f=\text{a}/\left(1+{10}^{{\text{b}}^{\ast }\left(\text{x}-\text{c}\right)}\right)$.

Results

Power generation

To investigate the influence of [Ca²⁺] on IFM power generation, we employed the work loop technique (17) to enable measurements under length change conditions similar to those estimated to be used by Drosophila during flight (18,19) (Fig. 1 A, inset). Drosophila IFM work loops rapidly produce high tension levels as lengthening progresses (thin gray line) at all calcium concentrations, due to the high stiffness of passive components of the IFM sarcomere (Fig. 1 A). This results in a high amount of work absorption by the fiber. To generate positive work and power at high calcium concentrations, the stretch-activation mechanism elevates tension levels after lengthening so that tension is higher during shortening (pCa = 5.0; Fig. 1 A, thick black line) than during lengthening.

Power production was measured under maximum power generating conditions for each [Ca²⁺]. The conditions that generated maximum power were 0.75% ML at all calcium concentrations, 100 Hz oscillation frequency at lower calcium concentrations, and 125 Hz at higher calcium concentrations. At low [Ca²⁺], IFM fibers absorbed work and power (pCa = 6.0; Fig. 1 A). Fibers did not produce positive work and power until pCa ∼ 5.8 (Fig. 1 B). Power increased with rising [Ca²⁺] ∼3-fold, from pCa = 5.75 to pCa = 5.0. The maximum power, measured at pCa = 4.5, was 456 ± 83 W/m³. We tested whether decreasing the resting tension by starting the work loop run at a shorter ML would increase power, as this should decrease tension during lengthening and negative work. Lower P₀ did decrease negative work, but positive work production decreased even more than negative work, resulting in lower net work and power generation. Changing the ML strain and frequency from optimal conditions influenced power generation, but did not alter the general trend of power increasing with [Ca²⁺].

Tension response of IFM fibers to lengthening steps

To determine the relationship between cytosolic [Ca²⁺] and stretch activation, we applied quick muscle-lengthening steps of 1% and 2.5% to skinned IFM fibers at 10 different [Ca²⁺]. Tension responses from Drosophila IFMs at pCa = 4.5 showed the classic stretch-activation response composed of an immediate tension rise concomitant with stretch (phase 1); a quick tension decay (phase 2); a slower, delayed increase in tension (phase 3 or stretch activation); and a very slow decay in tension (phase 4; Fig. 2) (16).

The ML change and speed of the step caused slight differences in the uncorrected tension responses. A 2.5% ML step increase over 1.5 ms at pCa = 4.5 generated a larger phase 1 amplitude than a 1% ML step over 0.5 ms, relative to their phase 3 amplitudes (Fig. 2, A and C). Our previous stretch response measurements with Drosophila IFMs obtained at pCa = 4.5 using a shorter ML step (0.5%) displayed a less prominent phase 1 amplitude compared with this study (20,21). Thus, for Drosophila IFM, as step length increases, phase 1 amplitude also increases relative to the phase 3 amplitude. This is likely due to the very high passive tension of Drosophila IFM as seen at pCa = 8.0 in Fig. 2.

To quantify the tension response to lengthening steps, we separated total Drosophila IFM tension into two components, F₀ and F_SA, after correcting for the imposed passive elastic component of isometric tension (P₀) and the elicited passive elastic component of stretch-activated tension (P_SA; Fig. 2). P₀ was measured at pCa = 8.0 after the muscle's optimal power-producing length was determined (see Materials and Methods). P_SA, which is the total tension minus P₀ after a step-length increase, was also measured at pCa = 8.0 (Fig. 2 B). P₀ is 68% of isometric tension at pCa = 4.5 (Table 1). P_SA accounts for 79% of the delayed increase in active tension after a 1% ML step, and 86% after a 2.5% ML step.

Table 1.

Isometric and stretch-activated properties of IFM

Step (ML, ms)	pCa = 8.0		pCa = 4.5
	P0 mN/mm2	PSA mN/mm2	F0 mN/mm2	FSA mN/mm2
Isometric	1.7 ± 0.2	NA	0.8 ± 0.2	NA
1.0%, 0.5	NA	5.5 ± 0.5	NA	1.5 ± 0.2
2.5%, 1.5	NA	11.4 ± 1.1∗	NA	1.8 ± 0.2

Abbreviations: F₀, calcium-activated tension; F_SA, stretch-activated tension (see Fig. 3 for labeled tension traces); NA, not applicable; P₀, passive isometric tension; P_SA, passive stretch tension after a lengthening step. N = 8 fibers for isometric data and N = 11 fibers for P_SA and F_SA data.

^∗Significantly different from 1.0%, 0.5 (Student's t-test, p < 0.05).

Ca²⁺-activated tension

Isometric tension of wild-type Drosophila IFMs increased with increasing [Ca²⁺]. Tension started increasing above P₀ at pCa ∼ 6.25, and maximum tension was reached at pCa ∼ 5.75 (Fig. 3). At pCa = 4.5, the total isometric tension was 2.5 ± 0.3 mN/mm². When P₀ was subtracted, this resulted in F₀ equal to 0.8 ± 0.2 mN/mm² (Table 1). Fitting the normalized F₀ curve resulted in a Hill coefficient of 2.6 ± 0.2 and pCa₅₀ of 6.1 ± 0.01 (Fig. 3 and Table 2).

Figure 3.

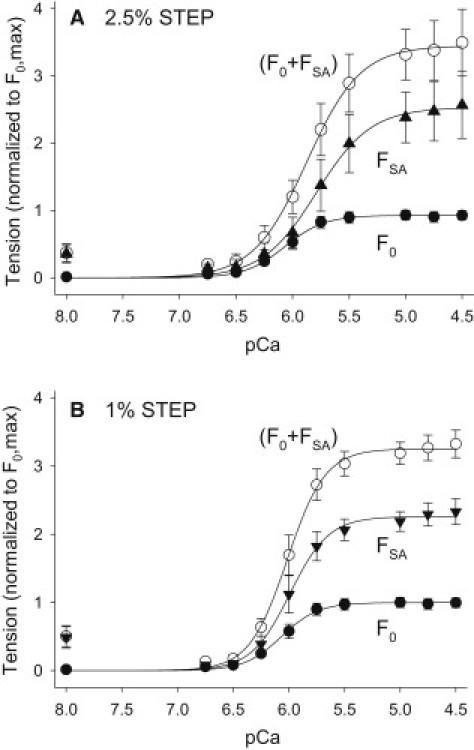
Effect of [Ca²⁺] on F₀, F_SA, and F₀+F_SA. (A) Tension response to 2.5% ML step over 1.5 ms. (B) Tension response to 1% ML length step over 0.5 ms. Data are normalized to each fiber's maximum isometric tension (F₀,_max) which was measured at pCa = 4.5 after the optimal ML was determined (see Materials and Methods). Data were fit with the Hill equation, $f=\text{a}/\left(1+{10}^{\text{b}\left(\text{x}-\text{c}\right)}\right)$. The F₀ data are the same for both A and B and are from a separate set of fibers (N = 8) than was used to determine 1% and 2.5% F_SA (N = 11). Measuring isometric tension levels and step responses versus pCa from the same fiber introduced more variability into the isometric data than measuring only isometric tension versus pCa. Values are mean ± SE.

Table 2.

pCa₅₀ and Hill coefficients for F₀ and F_SA

	F0	1.0% FSA	2.5% FSA
pCa50	6.10 ± 0.01	6.02 ± 0.04∗	5.88 ± 0.07∗
Hill coefficient	2.62 ± 0.18	2.53 ± 0.45	1.87 ± 0.22∗

Values are mean ± SE.

^∗Significantly different from F₀ (one-way analysis of variance, p < 0.05); N = 11 fibers for F₀ and N = 8 for F_SA.

Stretch-activated tension

Significant F_SA occurred over a pCa range of 6.0–4.5 in fibers subjected to a 2.5% stretch (Figs. 2 D and 3 A). F_SA was first apparent at pCa ∼ 6.25 and reached its maximum value of 2.28 ± 0.38 mN/mm² at pCa = 5.0. F_SA stayed constant from pCa = 5.0–4.5. We determined a pCa₅₀ of 5.88 ± 0.07 and a Hill coefficient of 1.87 ± 0.22 by fitting the normalized 2.5% F_SA curve (Fig. 3 A and Table 2).

The 1% F_SA showed no major differences compared with 2.5% F_SA in response to [Ca²⁺] (Fig. 3 B). Both increased with [Ca²⁺] and produced ∼2-fold greater tension than F₀ at pCa = 4.5 (Table 1). Variations in ML, passive tension, amplitudes higher or lower than 2.5% and 1.0%, and different speeds of stretch did not alter the general relationship of F_SA increasing with [Ca²⁺] and reaching its maximum value at pCa ∼ 5.0.

A comparison of the F₀ and F_SA curves and their pCa₅₀ values shows that F_SA reaches its maximum value at slightly higher [Ca²⁺] compared with F₀ (Fig. 3 and Table 2). The maximum F₀ value occurs over a slightly wider pCa range compared with that of F_SA (Fig. 3). At pCa = 4.5, F_SA accounts for ∼70% of total active tension (F₀ + F_SA), whereas F₀ contributes ∼30% to total active tension.

Influence of [Ca²⁺] on muscle kinetics

To determine the influence of [Ca²⁺] on cross-bridge and muscle kinetics, we measured the rate (r₃) of the delayed force increase (phase 3) after a lengthening step and the frequency at which maximum small-amplitude power was generated (f_max). The r₃ was 1747 ± 117 s⁻¹ 5 for 2.5% ML steps and 1363 ± 34 s⁻¹ for 1% ML steps at pCa = 4.5. The rate decreased with decreasing [Ca²⁺] (Fig. 4). Similarly, f_max increased with increasing [Ca²⁺], spanning most of the pCa = 5.7–5.4 range, within which Fig. 1 B shows that flight power generation rises twofold with a twofold rise in [Ca²⁺]. However, like power output, f_max does not increase significantly for [Ca²⁺] above pCa = 5.5. A maximum value for f_max occurs at 177 ± 5 Hz at pCa = 4.5 (Fig. 4). At [Ca²⁺] less than pCa = 6.0, f_max was not measurable, because power was not generated and stretch activation was not prominent enough to determine r₃.

Figure 4.

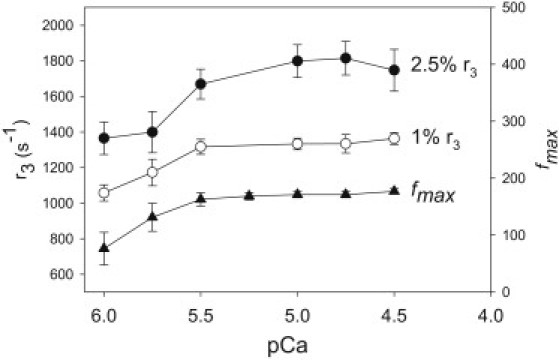
Effect of [Ca²⁺] on cross-bridge and muscle kinetics. The relative speed of cross-bridge cycling at six calcium concentrations was estimated by measuring the rate of phase 3 (stretch-activated) tension redevelopment (r₃) after a 2.5% and a 1% ML stretch. The r₃-value was measured by fitting the tension response to the sum of three exponential curves (see Materials and Methods). The data were obtained from 11 fibers. The dependence of muscle speed on [Ca²⁺] was measured by determining the frequency at which maximum power was generated (f_max) using small-amplitude sinusoidal analysis. The data were obtained from seven fibers. Values are mean ± SE.

Discussion

Power for flight

We found that in vitro power generation by Drosophila IFM increased with [Ca²⁺], thus establishing a calcium-based mechanism that Drosophila could be using in vivo to modulate muscle power generation during flight. Drosophila IFM is composed of 12 dorsal longitudinal muscle fibers and 14 opposing dorsoventral muscle fibers. The fibers are innervated by five motor units for the dorsal longitudinal muscle and three for the dorsoventral muscle, driven by a set of four loosely coupled central pattern generators (22). However, no evidence of differential recruitment of motor units was found when pairwise recordings of fibers were taken during tethered flight (7). The mechanism of motor unit recruitment, i.e., increasing the number of active fibers within a muscle to increase power output (23), may not be practical in small insects. The small number of muscle fibers may preclude the use of fiber recruitment for fine-tuning power. Also, the thoracic flight system may need all fibers to be active and contributing to thoracic stiffness for the flight resonance system (thorax, IFM, and wings) to oscillate over the required WBF range that supports flight. Instead, a method of modulating power when all fibers are already active, varying [Ca²⁺], is most likely the main mechanism for IFM power modulation. In this respect, IFM is similar to mammalian cardiac muscle, where all myocytes are active during every beat, so power is modulated by force-frequency and force-length effects on myoplasmic [Ca²⁺] and myofilament sensitivity to Ca²⁺.

Gordon and Dickinson (7) found that [Ca²⁺] varied ∼2-fold inside IFM during tethered Drosophila flight and correlated with changes in aerodynamic power and IFM motor nerve firing frequency. If this twofold variation occurs from pCa = 5.7 to 5.4 (2.0–4.0 μM free calcium), a range in which IFM power generation is highly influenced by [Ca²⁺] and includes the [Ca²⁺] that produces maximum power (Fig. 1), Drosophila IFM power output would also vary ∼2-fold. Shifting the range to slightly lower calcium concentrations would increase the power variation (up to threefold) that a twofold change in [Ca²⁺] would cause, but this would probably include concentrations where power is minimal and hence not enough is generated to support flight. Unfortunately, Gordon and Dickinson (7) were only able to measure the relative and not the actual variation in IFM [Ca²⁺] during flight. However, the aerodynamic power changes that occurred during tethered flight were measured to be ∼2-fold, so a two- to threefold change in muscle power would match the aerodynamic requirements.

Varying [Ca²⁺] also has a significant impact on muscle and cross-bridge kinetics. The r₃-value, an indicator of cross-bridge cycling rate (16,24), increased 1.2-fold over the pCa range we postulate is used during flight (pCa = 5.7–5.4). Similarly f_max, the optimal muscle speed for power generation, also increased 1.2-fold over the same range. For maximum muscle power generation during flight, muscle kinetic changes should correlate with changes in WBF. WBF has been measured to vary in Drosophila from ∼190 Hz to 230 Hz at 23–25°C to modulate aerodynamic power generation (25). Thus, the 1.2-fold change in WBF matches our observed ∼1.2-fold change in muscle and myosin cycling kinetics.

Role of calcium- and stretch-activated tensions

Our study reveals at least part of the mechanism whereby changes in [Ca²⁺] modulate work and power generation by Drosophila IFM. Increasing [Ca²⁺] increases the amount of F_SA produced by IFM. The pCa ranges in which F_SA and F₀ increase with [Ca²⁺] are very similar. Both start at the same pCa, suggesting that a minimum F₀ may be required for stretch activation to function. However, F₀ reaches maximum tension at a slightly lower [Ca²⁺] than F_SA, and has a higher pCa₅₀ than F_SA. Over the [Ca²⁺] range likely to be used during flight (pCa = 5.7–5.4), F_SA would contribute ∼80% to the increase in tension and F₀ would contribute only 20%. Thus, F_SA variation is critical for modulating power during flight.

We found that in Drosophila IFM, F_SA is continuously additive to F₀, in contrast to a study of Lethocerus IFM that found the two tensions competing for complementary shares of the maximum tension ceiling that occurs over the pCa range of ∼6.35–4.5 (12). Drosophila F_SA is 2.4-fold higher than F₀ when F₀ is at its maximum. At low F₀ levels, F_SA is proportionally lower. In contrast, Linari et al. (12) found that Lethocerus F_SA decreased with increasing F₀. The different effects of [Ca²⁺] on F_SA between the two species cause different work and power responses to calcium. Krzic et al. (26) found that work and power generation by Lethocerus flight muscle is maximal at pCa = 6.1, where F_SA is near maximum and F₀ is very low (12). Work drops precipitously at [Ca²⁺] above pCa = 6.0, correlating with increasing F₀ and decreasing F_SA. The lower pCa for maximum work suggests that Lethocerus should operate its muscle at pCa = 6.1 for maximum power. Lethocerus could potentially modify how much muscle power it is generating by increasing or decreasing [Ca²⁺] around its 6.1 maximum. However, there may be less need for this to occur in Lethocerus than in Drosophila, because Lethocerus has ∼1000-fold more IFM fibers and a smaller fiber diameter size (27), which would make fiber recruitment a more feasible mechanism.

Other recent work also supports the idea that insects have evolved variations in the response of their stretch-activation mechanisms to [Ca²⁺]. Iwamoto et al. (13) found that F₀ was relatively large and F_SA was modest for Bombus and Ctenacroscelis at saturating [Ca²⁺], pCa = 4.0–4.5. In contrast, Lethocerus had relatively low F₀ and high F_SA at saturating [Ca²⁺]. Although our results and those of Iwamoto et al. (13) make it clear that there are species differences, there are conflicting results concerning the response of Lethocerus IFM to varying [Ca²⁺]. Iwamoto et al.'s (13) results for Lethocerus are almost the opposite of those obtained by Linari et al. (12) and Krzic et al. (26) at saturating [Ca²⁺], which indicated low F_SA and high F₀ at pCa = 4.5. Results from an earlier study agree with those of Iwamoto et al. (13), showing that Lethocerus F_SA was twice as high as F₀ at high [Ca²⁺] (27). Thus, further investigation is required to clarify how Lethocerus IFM responds to [Ca²⁺].

Recent stretch-activation investigations have suggested a thin-filament-based cross-bridge recruitment mechanism (13,14,28). The stress or strain on the thin filaments from lengthening a fiber under load may cause a greater number of myosin-binding sites to become available on the thin filament than are initially made available by calcium binding to a minor fraction of all available troponin complex sites. This mechanism (if correct) together with our findings would lead us to conclude that Drosophila modulates IFM power output during flight by varying the number of cycling cross-bridges rather than the number of active fibers.