Focal Adhesion Kinase Stabilizes the Cytoskeleton

Abstract

Focal adhesion kinase (FAK) is a central focal adhesion protein that promotes focal adhesion turnover, but the role of FAK for cell mechanical stability is unknown. We measured the mechanical properties of wild-type (FAKwt), FAK-deficient (FAK−/−), FAK-silenced (siFAK), and siControl mouse embryonic fibroblasts by magnetic tweezer, atomic force microscopy, traction microscopy, and nanoscale particle tracking microrheology. FAK-deficient cells showed lower cell stiffness, reduced adhesion strength, and increased cytoskeletal dynamics compared to wild-type cells. These observations imply a reduced stability of the cytoskeleton in FAK-deficient cells. We attribute the reduced cytoskeletal stability to rho-kinase activation in FAK-deficient cells that suppresses the formation of ordered stress fiber bundles, enhances cortical actin distribution, and reduces cell spreading. In agreement with this interpretation is that cell stiffness and cytoskeletal stability in FAK−/− cells is partially restored to wild-type level after rho-kinase inhibition with Y27632.

Introduction

Cells that adhere to an extracellular matrix form an architecturally highly complex cytoskeleton. A major component of the cytoskeleton is force-generating actomyosin stress fibers that connect to focal adhesions (FAs). The interplay of actomyosin stress fibers and FAs defines to a large part the mechanical behavior of cells, such as their motility, morphology, and contractility (1–6).

Focal adhesion kinase (FAK) is a central protein of FAs and is known to regulate several cytoskeletal and other focal adhesion proteins. FAK interacts with integrins (7), paxillin (8), p130Cas (9), α-actinin (10), and other proteins that link FAs to the actin cytoskeleton (4). The molecular details of these interactions have not been fully characterized, but it is generally agreed that FAK promotes a high FA turnover through a rho-kinase (ROCK)-dependent pathway (11–14). FAK knockout cells show high rhoA-kinase and ROCK activity (12,13,15). Because ROCK inactivates myosin light chain phosphatase, phosphorylates myosin light chain, and therefore promotes actomyosin contractility, it has been hypothesized that contractile tension in the cytoskeleton is altered in FAK-deficient cells (10,14–18). Direct measurements of traction forces, however, showed no difference between wild-type and FAK-deficient fibroblasts (19).

With regard to the mechanical stability of cells, the role of FAK is similarly unclear. Because FAK promotes high FA turnover and high cell motility (12,13,19), it could be expected that the cytoskeleton in FAK-deficient cells is less dynamic and more rigid compared to FAK-expressing cells. However, FAK-deficient cells show a rounded cell morphology with a smaller spreading area, pronounced cortical distribution of the actin cytoskeleton, and a loss of actomyosin stress fibers (12,13), all of which are signs of reduced cell stiffness. Treatment of FAK-deficient cells with the ROCK-inhibitor Y27632 leads to a larger spreading area and a reformation of stress fibers (13), which is puzzling as this inhibitor induces the complete opposite behavior in wild-type fibroblasts (20).

The aim of this work was first to directly measure the impact of FAK on cell mechanics in mouse embryonic fibroblasts (MEFs), and second to characterize how rho-kinase contributes to the mechanical changes in wild-type and FAK-deficient cells. Our results show that FAK is important for maintaining cell rigidity (stiffness) through promoting a static and highly aligned contractile cytoskeleton. FAK knockout leads to a pronounced speedup of cytoskeletal dynamics, which is independent of any decreased FA turnover in these cells. We hypothesize that the effects of FAK on cytoskeletal dynamics and organization are, to a large extent, mediated through a compensatory activation of ROCK in FAK knockout cells. In support of this hypothesis, we find that treatment with the ROCK-inhibitor Y27632 has opposite effects on cell rigidity and cytoskeletal dynamics in FAK wild-type versus knockout cells.

Materials and Methods

Cells and cell culture

FAK-deficient (FAK−/−) and FAK wild-type (FAKwt) mouse embryonic fibroblasts (MEFs) were purchased from American Type Culture Collection (FAK−/−, cat. No. CRL-2644; FAKwt, cat. No. CRL-2645; ATCC, Manassas, VA). FAKwt and FAK−/− cells from ATCC are reported to carry a p53 knockout mutation (11). Moreover, FAK−/− cells overexpress PYK2, a homologous protein of FAK (21). PYK2 overexpression has no effect on cell mechanics (22), but p53 overexpression may have a small effect (23). To rule out any of these secondary effects, we performed siRNA downregulation experiments on differently derived MEF cells (obtained from Dr. W. H. Ziegler, University of Leipzig, Leipzig, Germany) with normal PYK2 and p53 expression levels. All cell lines were maintained in low glucose (1 g/L) Dulbecco's modified Eagle's medium supplemented with 10% fetal calf serum, 2 mM L-glutamine, and 100 U/ml penicillin-streptomycin (i.e., Dulbecco's modified Eagle's medium complete medium). This medium was also used during measurements except where stated otherwise. siRNA against FAK (siFAK) was targeted against both splice variants of murine FAK (gene accession numbers NM_007982.2 and NM_001130409.1). The sequence was sense: R(GGG ACA UUG CUG CUC GGA A)dTdT; antisense: R(UUC CGA GCA GCA AUG UCC C)dTdG. siRNA was 3′AlexaFluor546-labeled to assess transfection efficiency. As a control (siControl), we used Alexa-Fluor546-labeled Allstar siRNA (Qiagen, Hilden, Germany), a nonsilencing siRNA with no homology to any known mammalian gene. Transfection of 100,000 MEFs was performed in 35-mm wells using 6 μl HiPerFect transfection reagent (Qiagen) with 20 nM siRNA.

Magnetic tweezer microrheology

Magnetic tweezer rheology exerts a mechanical shear stress to the cell by applying lateral forces to magnetic beads that are connected to the cytoskeleton through adhesion contacts on the apical cell surface (24). This technique reports the passive mechanical properties of the cytoskeleton, such as the elastic modulus and its time (or frequency) dependency. In brief, superparamagnetic, epoxylated beads (4.5 μm, Dynabeads; Invitrogen, Carlsbad, CA) were coated with fibronectin (5 μg per 1 × 10⁷ beads; Roche, Pleasanton, CA) at 4°C for 24 h. Before measurements, the beads were sonicated, 2 × 10⁵ beads were added to ∼10⁵ subconfluent cells in a 35-mm dish, and cells were incubated with the beads for 30 min at 5% CO₂ and 37°C. Thereafter, the medium was exchanged with fresh, prewarmed medium to remove unbound beads. Measurements were performed on a heated inverted microscope stage at 40× magnification (NA 0.6) without CO₂. The measuring time was limited to 30 min per dish. A solenoid with a sharp-tipped steel needle core was used to generate a defined force on the bead.

When a step force f was applied to a cell-bound bead, it moved with a displacement d(t) toward the tweezer needle tip (Fig. 1). Following Kasza et al. (25) and Kollmannsberger et al. (26), we estimate the typical strain γ(t) as d(t) divided by the bead radius r, and the typical stress σ as the applied force divided by the bead cross-sectional area, r²π. The creep compliance J(t) in units of Pa⁻¹ is then given by γ(t)/σ and is fit to the equation J(t) = J₀(t/t₀)^b with time normalized to t₀ = 1 s. The prefactor, J₀, and the power-law exponent, b, were both force-dependent. The value J₀ is the creep compliance at t₀ = 1 s and corresponds, apart from a negligible correction factor (the Gamma function, Γ, at 1−b) to the inverse magnitude of the cell's dynamic shear modulus evaluated at a radian frequency ω₀ = 1 rad/s (27,28),

$$\left|G^{\prime }\left({\omega }_0\right)+i{G}^{″}\left({\omega }_0\right)\right|=\frac{1}{J_0}\Gamma \left(1-b\right).$$

The power-law exponent b reflects the dynamics of the force-bearing structures of the cell that are connected to the bead (27). A power-law exponent of b = 0 is indicative of a purely elastic solid, and b = 1 is indicative of a purely viscous fluid. In cells, the power-law exponent usually falls in the range between 0.1 and 0.5, whereby higher values have been linked to a higher turnover rate of cytoskeletal structures (27).

Figure 1.

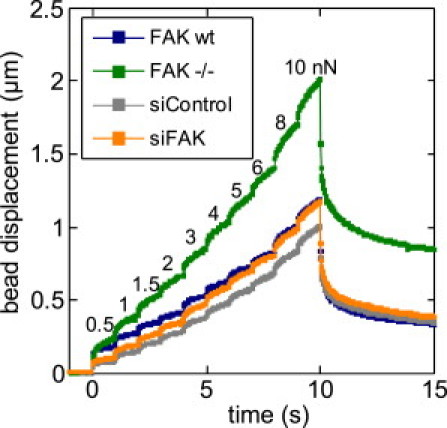
Magnetic tweezer microrheology. Bead displacement (geometric mean from >74 cells) versus time during force steps with increasing force magnitude. Each step lasted 1 s. Numbers above the curve indicate the lateral pulling force (in units of nN). After 10 s, the force was reduced to zero. The differential cell stiffness (see Fig. 4A) and the exponent of the creep modulus (see Fig. 4B) was computed as described in Kollmannsberger et al. (26).

Atomic force microscopy

Atomic force microscopy (AFM) is used as an alternative method to measure cell stiffness. A nonfunctionalized sharp tip that is in contact with the cell for <1 s serves as a probe. The measurements are therefore not influenced by focal adhesion formation between the probe and the cell. Cells were seeded on fibronectin-coated (50 μg/ml) cell culture dishes (Nalge Nunc, Rochester, NY) in CO₂-independent medium (Leibovitz L-15 medium, with L-Glutamine; Gibco, Invitrogen, Carlsbad, CA) for 12 h before and during measurements. Measurements were performed on a MFP-3D Stand Alone AFM (Asylum Research, Goleta, CA) as described previously (22). The spring constants of the cantilevers (Bio-Lever; Olympus, Melville, NY) were determined before cell measurements using the thermal noise method (29) and were in the range of 5.9–7.7 pN/nm. The force mapping mode with 260-pN maximum indentation force (indentation depth between 30 and 100 nm) was used to measure cell stiffness and sample height (Fig. 2 A). Force versus z-piezo extension curves (Fig. 2 C) were acquired on different positions on the sample surface. The local shear moduli (Fig. 2 B) were obtained by fitting the extended Hertz model to each force versus z-piezo extension curve in the force map (30). In the extended Hertz model for a conical indenter, the relationship between the applied force F and the resulting sample indentation δ is given by

$$F=\frac{2}{\pi }\frac{E}{1-{\nu }^2}{\delta }^2\text{tan}\left(\alpha \right),$$

where E is the Young's modulus, ν is the Poisson's ratio, and α is the opening half-angle of the conical cantilever tip (30,31). We assumed an incompressible sample with a Poisson's ratio of ν = 0.5. Therefore, the shear modulus G is related to the Young's modulus E by G = E/[2·(1+ ν)] = E/3. A region of 80 × 80 μm was scanned to obtain 10 × 10 or 20 × 20 force curves. To reduce the influence of the underlying substrate, only regions of the cell that were at least 60% of the maximum cell height were analyzed.

Figure 2.

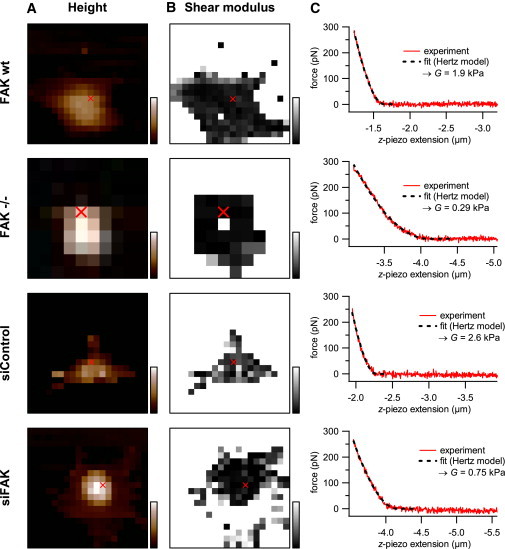
AFM force mapping. (A) Height. Scan range: 80 μm × 80 μm. Color-bar range (black to white): 0–5 μm. (B) Corresponding shear modulus. Grayscale range (black to white): 0–20 kPa. (C) Force versus z-piezo extension data at the position indicated (red cross) in panels A and B. A fit of the Hertz model to the data gives the local shear modulus at this position.

Nanoscale particle tracking

This method is used to quantify internal remodeling processes of the cytoskeleton. Fibronectin-coated fluorescent beads (4.5 μm) are bound to confluent cells via integrins (32,33). The spontaneous movement of the beads was tracked for 5 min. The mean-squared displacement (MSD) of bead movements followed a power-law with time (t) according to MSD = D·(t/t₀)^β (Fig. 3). The value t₀ was set to 1 s, D reflects an apparent diffusivity, equivalent to the square of the distance traveled during a 1 s interval, and the power-law exponent β is a measure of the persistence, with β = 1 for randomly moving beads and β = 2 for directed, ballistic motion along a straight path (32).

Figure 3.

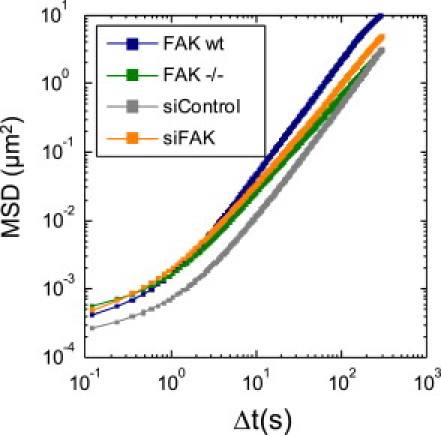
Nanoscale particle tracking. Cytoskeletal remodeling dynamics was estimated from the apparent diffusivity and the power-law exponent (see Fig. 4, E and F) of the mean-squared bead displacement (geometric mean of >611 beads) versus time.

Immunofluorescence of focal adhesions and the actin cytoskeleton

A quantity of 10,000–50,000 cells was seeded on 5 μg/ml fibronectin-coated glass slides and incubated overnight at 37°C and 5% CO₂. Adherent cells were fixed for 20 min with 3% paraformaldehyde and lysed for 5 min with 0.2% Triton-X-100. Cells were then blocked for 1 h in 0.5% BSA and PBS at room temperature. Primary antibodies (1:10⁶ vinculin/hVIN-1; Sigma, St. Louis, MO) and secondary antibodies (μl:200, FITC-coupled anti-mouse IgG; Jackson ImmunoResearch, West Grove, PA) were both diluted in 0.5% BSA and PBS at given ratios and incubated for 1 h at room temperature each. Alexa-Fluor546-Phalloidin (Molecular Probes, Eugene, OR) was added simultaneously with the second antibody for actin staining. Samples were mounted with Mowiol (Sigma) solution. Microscopy was carried out on a DMI6000 microscope with a 63×/1.3 NA objective (Leica Microsystems, Wetzlar, Germany). Images were acquired with a charge-coupled device camera (ORCA ER; Hamamatsu, Hamamatsu City, Japan).

Traction microscopy

This technique measures the forces that cells exert on their surroundings by observing the displacements of beads embedded in a flexible gel substrate on which the cells are cultured (32,34). Traction measurements were performed with 6.1% acrylamide/bisacrylamide (19:1) gels with 0.5-μm green fluorescent beads. The Young's modulus of the gels was 12.8 ± 0.8 kPa as measured from the linear extension of a cylinder of gel (16-mm diameter, 50-mm length) under force. Gels were coated with 50-μg bovine collagen G (Biochrom AG, Berlin, Germany) diluted in 50 mM HEPES overnight at 4°C. 10⁴ cells were seeded on the gels and incubated under normal growth conditions. During the measurements, the cells were maintained at 37°C and 5% CO₂ in a humidified atmosphere. Cell tractions were computed from an unconstrained deconvolution of the gel surface displacement field (32,35) measured before and after cells were detached from the substrate with a cocktail of 80-μM cytochalasin D and 0.25% trypsin.

Statistical evaluation

FAK knockout and FAK silencing experiments were performed on MEF cells derived from two different cell isolations. Therefore, for statistical evaluation, we only compared FAKwt with FAK−/− cells, and siControl cells with siFAK cells. Statistical significant differences were calculated using a Student's unpaired t-test, assuming unequal variances. Results were considered to be significant and marked with an asterisk for p < 0.05. All data are expressed as arithmetic mean ± standard error of the mean, except for bead detachment experiments (expressed as cumulative probability) and for data that show a log-normal distribution, namely cell stiffness measured with magnetic tweezers and AFM, and apparent diffusivity (32,36). These data are expressed as geometric mean ± geometric standard error of the mean. Number of measurements is between 46 and 184 cells for traction measurements, between 85 and 144 cells for adhesion strength measurements, between 611 and 1031 beads for nanoscale particle tracking experiments, between 10 and 30 cells for AFM measurements, and between 74 and 129 cells for magnetic tweezer measurements.

Results and Discussion

MEF cells, regardless of FAK expression levels, behave mechanically similar to other cells: they stiffen when probed at high forces (Fig. 4 A). Measurements with magnetic tweezers show that cell stiffness was approximately twofold higher in FAKwt versus FAK−/− cells. Those differences were significant (p < 0.05) at all force levels. A similar trend was observed in siControl versus siFAK knockdown cells, although the differences were less pronounced and were not consistently significant at all force levels.

Figure 4.

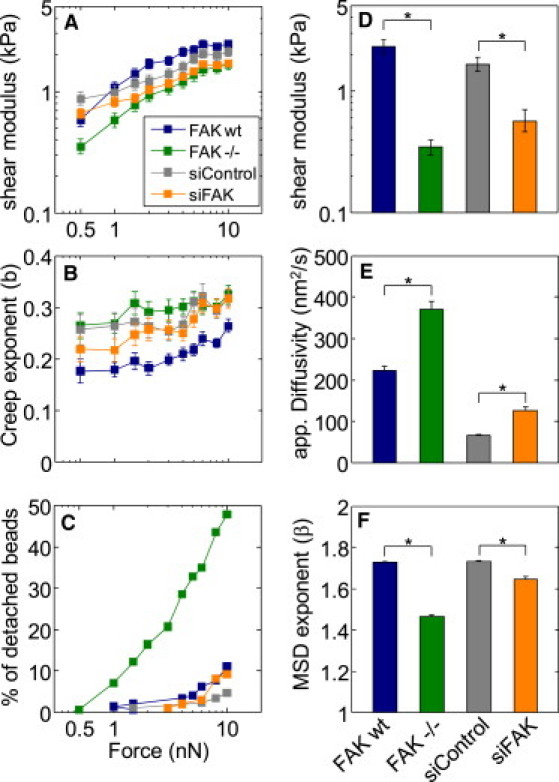
FAK increases cell stiffness and adhesion strength, and reduces cytoskeletal dynamics. Cell stiffness (magnitude of the shear modulus) (A) and exponent of the creep modulus (B) measured with magnetic tweezer microrheology at different forces. (C) Adhesion strength of fibronectin-coated beads expressed as percentage of detached beads versus pulling force. (D) Cell stiffness (shear modulus) measured with an uncoated AFM-tip. Apparent diffusivity (E) and power-law exponent of the mean-squared displacement (F) of spontaneous movements of FN-coated beads attached to the cell surface. (Bars) Standard error. (Asterisk) Significant (p < 0.05) differences.

To test whether these differences are attributable to the mechanical behavior of the cytoskeleton, as opposed to differences in FAK-mediated adhesion properties of the fibronectin-coated magnetic beads, we performed stiffness measurements using an atomic force microscope (AFM) (Fig. 4 D). Because the cantilever tip of the AFM was not functionalized and was in contact with the cell surface for <1 s, these measurements are not influenced by specific adhesion between the cell and the probe. The AFM measurements confirm our results obtained with magnetic tweezers, with a notable exception that the differences between FAK-expressing and FAK-deficient cells were even larger than those measured by magnetic tweezers.

The shear modulus magnitude from AFM measurements approximately matched the values obtained with magnetic tweezers (Fig. 4, A and D). Differences are attributable to the uncertainty in the geometric factor that is needed to convert forces to stress, and displacements to strain (27,37). Moreover, the shear modulus magnitude from magnetic tweezer measurements reflects the combined elastic and dissipative cell properties at a timescale of 1 s, whereas the fit of the Hertz-model to the AFM force-indentation data was performed under the assumptions of a purely elastic response and a Poisson's ratio of 0.5. These assumptions are reasonable because the cell's elastic properties dominate over dissipative properties, the timescale of the AFM indentation measurements was also approximately 1 s, and the Poisson's ratio has only a moderate effect on the result.

In the magnetic tweezer experiments, the creep compliance increased with time according to a power-law with exponent b that was significantly increased by ∼50% in FAK−/− cells compared to FAKwt cells (Fig. 4 B). A similar trend was also seen in siControl versus siFAK cells, although the differences were not always significant at all force levels. The larger creep exponent in the FAK-deficient cells indicates that the cytoskeletal structures that are connected to the magnetic beads remodel more rapidly and show a higher turnover compared to FAK-expressing cells. This finding is somewhat unexpected, as the focal adhesion complex, which is part of the structure probed by the magnetic beads, has been previously reported to be more stable in FAK-deficient cells (11,14). As a plausible hypothesis, we suggest that not so much the focal adhesion complex, but the connected cytoskeletal structures are more dynamic and unstable in FAK-deficient cells.

To test this hypothesis, we used the nanoscale particle tracking technique. Fibronectin-coated fluorescent beads are connected to the cytoskeleton via integrin-type cell surface receptors, and their movements are followed over time for several minutes. Although the type of probe is the same as in the magnetic tweezer experiments, the properties being measured are not. The magnetic beads are actively forced and thus report the passive mechanical properties of the cytoskeleton, such as elastic modulus and its time (or frequency) dependency. In the particle tracking experiments, the beads are passive in the sense that they are not externally forced (except thermally) and report the active material properties of the cytoskeleton. This is because the beads act as fiducial markers of the cytoskeleton and move only if the cytoskeletal structures to which they are bound also move, for instance due to cytoskeletal remodeling events (38), including those that lead to an overall cell movement, and contractile force fluctuations (32). We find an increased apparent diffusivity of the cytoskeleton-bound beads in the FAK-deficient cells (Fig. 4 E), which is in agreement with our hypothesis that the cytoskeleton of FAK-deficient cells is less stable and more dynamic.

Additional support for this hypothesis comes from the finding that nearly 50% of the magnetic beads attached to FAK−/− cells detach at forces of 10 nN, as opposed to only 10% of the beads that detach from FAKwt cells (Fig. 4 C). Although we do not know whether the bead detachment occurred due to a rupture of protein bonds in the focal adhesion complex or due to a rupture of protein bonds in the associated cytoskeleton, previous reports of a more stable adhesion complex in FAK-deficient cells (11,12,14) point to the cytoskeleton as the weakest link.

We noted that the fibronectin-coated fluorescent beads moved more persistently and with a significantly larger exponent β when attached to FAK-expressing cells as compared to FAK-deficient cells (Fig. 4 F). The β characterizes the time evolution of the MSD of the beads and was closer to a ballistic behavior in FAK-expressing cells, as opposed to a more random behavior in FAK-deficient cells. Because the beads generally follow and move along a path that is determined by the cytoskeletal architecture, the straighter and more persistent movement of the beads attached to FAK-expressing cells suggests a more aligned cytoskeleton, whereas the more random bead movement in FAK-deficient cells in turn suggests a more isotropic arrangement of the cytoskeleton.

Passive and active cytoskeletal properties are intricately linked by universal scaling laws (39,40): a stiffer cytoskeleton is usually less frequency- or time-dependent (the power-law exponent b tends toward zero) (27), remodels more slowly on short timescales (the apparent diffusivity D is smaller) (38) but more persistently (the MSD-exponent β at longer timescales is higher) (32). A comparison of the magnetic tweezer and particle tracking data (Fig. 4) shows that FAK−/− and FAKwt cells obey these scaling laws.

Fluorescent images confirm, in agreement with previous reports (12,15), that FAKwt cells have a highly ordered and aligned actin cytoskeleton with prominent stress fibers, whereas FAK−/− cells show a more pronounced cortical actin cytoskeleton (Fig. 5 A). Such differences are not visible in siControl versus siFAK cells, which is consistent with the smaller differences that we found in all of the mechanical parameters between these cells (Fig. 4). We attribute these smaller mechanical differences and the lack of any discernible differences in the cytoskeletal architecture between siControl and siFAK cells to an incomplete FAK knockdown, with expression levels of ∼10% of baseline FAK in the siRNA-silenced cells (data not shown). In this regard, FAK may behave similarly to other focal adhesion proteins. For example, a downregulation of the focal adhesion protein vinculin to ∼10% of control level is sufficient for proper focal adhesion formation and mechanical coupling (41,42), and only cells with full vinculin knockout show substantial mechanical impairment.

Figure 5.

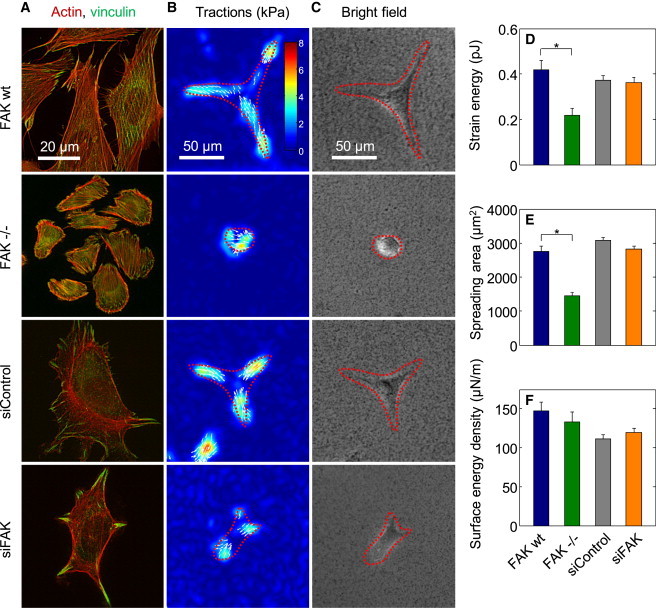
Traction force magnitude is not affected by FAK. (A) Fluorescence images (actin, red; vinculin, green) of cells plated on glass. (B) Traction maps and corresponding (C) bright-field images of cells on polyacrylamide gels. (Red-dashed line) Cell outlines. Strain energy (D) and spreading area (E) are reduced in FAK−/− cells, but the average traction force magnitude and strain energy normalized to the spreading area (F) are not dependent on FAK expression levels.

It is known that cell stiffness scales linearly with cytoskeletal prestress, which in turn depends on the contractile activation, cell area (both spreading area and cross-section area), and cytoskeletal alignment (43). To test whether the stiffness differences in cells with different FAK expression levels are attributable to altered prestress, we measured the traction forces of these cells (Fig. 5, B and C). As a scalar value of cell tractions, we computed the elastic strain energy that is stored in the matrix below the cell (35). Strain energy was twofold decreased in FAK−/− cells (Fig. 5 D), but this was solely due to a diminished spreading area of the FAK−/− cells (Fig. 5 E). When strain energy was normalized to spreading area (corresponding to an average surface energy density) (Fig. 5 F), no difference could be seen between FAKwt and FAK−/− cells. Consistent with this finding, the maximum tractions and average traction magnitude in all cells types were similar (Fig. 5 B), which is also in line with previous reports (44,45). Moreover, siControl and siFAK cells, which did not differ in their spreading area (Fig. 5 E), showed no difference in strain energy (Fig. 5 D). Taken together, these findings suggest that the smaller stiffness of FAK-deficient cells was the result of a reduced prestress (26,46), which in turn was predominantly caused by a decreased spreading area and therefore increased cross-sectional area. Note that this interpretation rests on the assumption of a similar cell volume in FAK-expressing and FAK-deficient cells.

Decreased stress fiber expression and a more pronounced cortical organization in the actin cytoskeleton of FAK−/− cells have been reported to result from rho-kinase, which is known to be overactive in FAK−/− cells (12,13,15). We confirmed, in line with previous reports (13), that treatment of the FAK−/− cells with 10 μM of the ROCK-inhibitor Y27632 for 30 min reestablishes a more wild-type fibroblast cell morphology (data not shown). Y27632-treatment not only affected the organization of the actomyosin cytoskeleton, but it partially rescued the mechanical properties of the FAK−/− cells toward a FAK wild-type phenotype. The spontaneous motion of beads bound to FAK−/− cells became significantly less diffusive and more directed after Y27632-treatment, and the cell stiffness measured by AFM increased (Fig. 6 A). Remarkably, FAKwt cells responded to ROCK-inhibition with Y27632 with the exact opposite behavior: lower cell stiffness and more diffusive, less directed bead motion.

Figure 6.

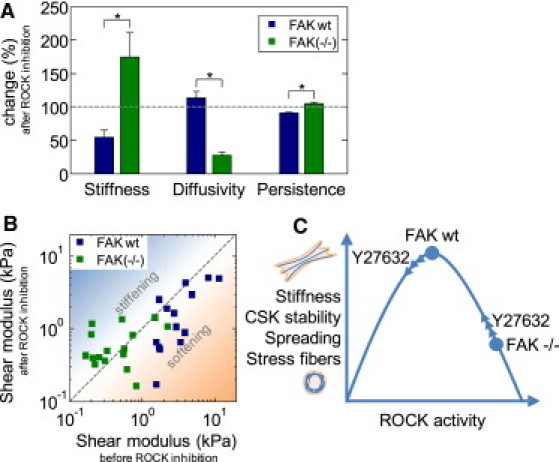
ROCK-inhibitor has diverging effects on cell mechanical behavior in FAKwt versus FAK−/− cells. (A) Change in cell stiffness, bead diffusivity, and persistence of bead motion after ROCK inhibition with 10 μM Y27632 for 30 min (relative to untreated cells, dashed line). (B) Stiffness of individual cells measured with AFM before and after ROCK inhibition with Y27632. (Shaded-dashed line) Line of identity. (C) Schematic representation of the proposed molecular pathway: FAK exerts its influence on cytoskeletal stiffness, stability, and morphology through modulation of the expression and activity level of ROCK. (Arrowheads) Expected changes of cell stiffness and cytoskeletal properties after ROCK-inhibition with Y27632 along a specific trajectory.

On a cell-by-cell basis, the stiffness change in FAK−/− cells after Y27632-treatment was highly correlated (r² = 0.51) with the stiffness before Y27632-treatment (Fig. 6 B, and see Fig. S1 in the Supporting Material). Soft cells stiffened after treatment with the ROCK-inhibitor Y27632, whereas stiff cells softened. FAKwt cells, which were generally stiffer than FAK−/− cells, tended to soften after ROCK inhibition regardless of baseline stiffness (Fig. 6 B, and see Fig. S1). This observation, together with the fact that ROCK is more active in FAK−/− cells, suggests that cytoskeletal architecture, mechanics, and dynamics can change in response to altered ROCK activity only along a specific trajectory, as conceptually outlined in Fig. 6 C. Accordingly, cell stiffness, stress fiber formation, cytoskeletal stability, and spreading area are highest at an intermediate ROCK activity level as is present in normal (FAKwt) cells. At lower or higher levels of ROCK activity, all those parameters decrease. The question then arises how FAK and ROCK are connected such that they alter cytoskeletal architecture and mechanics only along a specific trajectory.

ROCK is activated by rhoA-kinase, which in turn is regulated by FAK via rho-GEFs (activator) and rho-GAPs (inactivator) (18). This gives FAK a dual role that is crucial for the spatiotemporal regulation of rhoA-kinase and ROCK activity (3,4,18). ROCK is known to regulate intermediate filament assembly, actin polymerization via LIM-kinase, cortical actin distribution via adducin (47), and actomyosin contraction via myosin light chain (MLC) phosphatase inhibition and direct MLC phosphorylation (48–50).

In our experiments, it was expected that inhibition of rho-kinase by Y27632 decreases MLC-dependent contractility and, therefore cell stiffness. FAKwt cells behaved as expected, but FAK−/− cells did not. The restructuring of the cytoskeleton toward a more mesenchymal phenotype in FAK−/− cells after ROCK inhibition seemed to dominate over any decrease in actomyosin contractility. We speculate that this may be because ROCK activates the trans-membrane actin binding proteins ezrin, radixin, and moesin (ERM) that are important for the cortical distribution of actin (51–53). Because ROCK is overactive in the FAK−/− cells, it could induce an overactivation of the ERM proteins and thereby induce the binding of cortical actin bundles to the plasma membrane. To validate the involvement of ERM proteins, however, further work is needed.

Regardless of the molecular mechanisms, our data show that FAK stabilizes the actin cytoskeleton through a ROCK-mediated pathway.