Characterization of Mg²⁺ Inhibition of Mitochondrial Ca²⁺ Uptake by a Mechanistic Model of Mitochondrial Ca²⁺ Uniporter

Abstract

Ca²⁺ is an important regulatory ion and alteration of mitochondrial Ca²⁺ homeostasis can lead to cellular dysfunction and apoptosis. Ca²⁺ is transported into respiring mitochondria via the Ca²⁺ uniporter, which is known to be inhibited by Mg²⁺. This uniporter-mediated mitochondrial Ca²⁺ transport is also shown to be influenced by inorganic phosphate (Pi). Despite a large number of experimental studies, the kinetic mechanisms associated with the Mg²⁺ inhibition and Pi regulation of the uniporter function are not well established. To gain a quantitative understanding of the effects of Mg²⁺ and Pi on the uniporter function, we developed here a mathematical model based on known kinetic properties of the uniporter and presumed Mg²⁺ inhibition and Pi regulation mechanisms. The model is extended from our previous model of the uniporter that is based on a multistate catalytic binding and interconversion mechanism and Eyring's free energy barrier theory for interconversion. The model satisfactorily describes a wide variety of experimental data sets on the kinetics of mitochondrial Ca²⁺ uptake. The model also appropriately depicts the inhibitory effect of Mg²⁺ on the uniporter function, in which Ca²⁺ uptake is hyperbolic in the absence of Mg²⁺ and sigmoid in the presence of Mg²⁺. The model suggests a mixed-type inhibition mechanism for Mg²⁺ inhibition of the uniporter function. This model is critical for building mechanistic models of mitochondrial bioenergetics and Ca²⁺ handling to understand the mechanisms by which Ca²⁺ mediates signaling pathways and modulates energy metabolism.

Introduction

Ca²⁺ is a key regulatory ion and has multiple roles in mitochondrial function and dysfunction (1–5). Ca²⁺ is known to mediate signaling pathways between cytosol and mitochondria and modulate mitochondrial energy metabolism. Alteration of mitochondrial Ca²⁺ homeostasis can lead to mitochondrial dysfunction and mitochondria-mediated cellular injury and apoptosis. Mg²⁺ is another key regulatory ion and the intracellular concentration of free Mg²⁺ varies significantly in vivo (0.2–2 mM) under various physiological and pathological conditions (e.g., hormonal stimulation, myocardial ischemia) (6–8). Alteration of cytosolic Mg²⁺ homoeostasis is known to influence mitochondrial substrate and cation (e.g., Ca²⁺) transport systems and bioenergetics (e.g., Mg²⁺ is a cofactor for the operation of F₁F₀-ATPase and adenine nucleotide translocase; Mg²⁺ regulates many key enzymes in mitochondria, such as pyruvate dehydrogenase; Mg²⁺ also inhibits mitochondrial Ca²⁺ uptake via the Ca²⁺ uniporter (6–8)). Therefore, it is essential to mechanistically characterize the biophysical and kinetic mechanisms associated with the transport of Ca²⁺ into mitochondria and how variations in cytosolic Mg²⁺ influence this Ca²⁺ transport.

Ca²⁺ uniporter is the primary influx pathway for Ca²⁺ in respiring mitochondria, and hence is an important regulator of mitochondrial Ca²⁺. This uniporter-mediated mitochondrial Ca²⁺ uptake is known to be influenced by inorganic phosphate (Pi), in addition to the inhibition by Mg²⁺ (9–13). Thus, the kinetics of Ca²⁺ uptake not only depends on the catalytic properties of the uniporter and the electrochemical gradient of Ca²⁺ across the inner mitochondrial membrane (IMM), but also on the mechanisms of Mg²⁺ inhibition and Pi regulation of the uniporter function. This has been extensively investigated in many experimental (8,9,11–16) and modeling (17–22) studies. Early initial velocity studies of Ca²⁺ uptake in rat heart and liver mitochondria suggest that Mg²⁺ is a competitive inhibitor of Ca²⁺ uptake where it induces a sigmoid kinetics and the degree of sigmoidicity (K_m of Ca²⁺ for the uniporter) increases with increase in [Mg²⁺], without altering the maximal activity of the uniporter (9,14,15).

However, subsequent study on the kinetics of Ca²⁺ uptake in rat liver mitochondria reported a noncompetitive type of Mg²⁺ inhibition of Ca²⁺ uptake by increasing the K_m of Ca²⁺ and decreasing the maximal activity of the uniporter, with increase in [Mg²⁺] (11). Furthermore, the Ca²⁺ uptake is shown to be regulated by Pi (9,10). Specifically, the kinetic study of Crompton et al. (9) on Ca²⁺ uptake in rat heart mitochondria shows significant differences in the initial Ca²⁺ uptake, when measured with 0 and 1 mM Pi in the buffer. Though the regulatory roles of Pi on oxidative phosphorylation (23,24) and matrix Ca²⁺ buffering through Ca²⁺-Pi complex formation (25) are well recognized, it is not understood how Pi can modulate Ca²⁺ uptake via the uniporter. Furthermore, though the mechanisms of extramatrix Ca²⁺ and membrane potential (ΔΨ) dependencies of Ca²⁺ uptake have been well-described mathematically (17–22), the kinetic mechanism by which Mg²⁺ inhibits and Pi regulates the uniporter function has not been well characterized in terms of a mechanistic model. The need for such a model is critical for developing mechanistic integrated models of mitochondrial bioenergetics and Ca²⁺ handling that can be helpful in understanding the mechanisms by which Ca²⁺ plays a role in mediating signaling pathways and modulating energy metabolism under normal and pathological conditions.

Previously, we introduced a mechanistic mathematical model of Ca²⁺ uniporter (20) that satisfactorily describes the available data on the kinetics of Ca²⁺ uptake, measured in respiring mitochondria isolated from rat hearts and rat livers under diverse experimental preparations (14–16). This model was developed based on a multistate catalytic binding and interconversion mechanism and Eyring's free-energy barrier theory for interconversion (26–28). In addition, the model accounts for the allosteric cooperative binding of Ca²⁺ to the uniporter, observed experimentally (14,15). In a recent work, this model is further improved to accurately characterize the mechanism of ΔΨ-dependency of Ca²⁺ uptake (22). An interesting prediction of this improved model is that the Ca²⁺-binding sites on the uniporter are located at equal and negligible distances from the bulk phase on either side of the IMM and the binding affinities of the uniporter to both cytosolic and matrix Ca²⁺ are the same. This alternate model is shown to be more robust with minimal number of model parameters that accurately describes the available data (14–16). Furthermore, this alternate model is insensitive to physiological variations in matrix [Ca²⁺]. Though these models are able to characterize the possible mechanisms of both the extramatrix Ca²⁺ and ΔΨ dependencies of Ca²⁺ uptake, they do not account for the effects of Mg²⁺ and Pi on the kinetics of Ca²⁺ uptake. Furthermore, there exists no mathematical model in the literature that characterizes the inhibitory effect of Mg²⁺ and regulatory role of Pi on the uniporter-mediated Ca²⁺ uptake in mitochondria.

In this article, we develop a mechanistic mathematical model of Ca²⁺ uniporter that improves the existing models (17–22) and provides a biophysical basis for the inhibitory effect of Mg²⁺ and regulatory role of Pi on the uniporter-mediated Ca²⁺ uptake. The model, extended from our previous models (20,22), is thermodynamically balanced and adequately describes a large number of independent data sets on both Mg²⁺-dependent and Mg²⁺-independent Ca²⁺ uptake via the uniporter (8,9,11,12,14–16). The model accurately depicts the inhibitory effect of Mg²⁺ on Ca²⁺ uptake in which the kinetics of Ca²⁺ uptake is hyperbolic in the absence of Mg²⁺ and sigmoid in the presence of Mg²⁺. A mixed type Mg²⁺ inhibition mechanism is shown to be consistent with the available data.

Mathematical Formulation

Experimental data for model formulation

The kinetic mechanisms associated with the Mg²⁺ inhibition and Pi regulation of mitochondrial Ca²⁺ transport is not well established. However, experimental studies in respiring isolated mitochondria (9,11,14–16) and intact permeabilized myocytes (8) provide adequate information about the influences of Mg²⁺ and Pi on the initial rates of Ca²⁺ transport into mitochondria. The initial rate data from isolated mitochondria describe the kinetics of extramatrix Ca²⁺- and ΔΨ-dependent mitochondrial Ca²⁺ uptake at various extramatrix [Mg²⁺] and [Pi]. The initial rate data from permeabilized cells demonstrate the nature of mitochondrial Ca²⁺ uptake in response to physiological variations of cytosolic [Mg²⁺] and [Ca²⁺]. Therefore, these kinetic data are appropriate for building kinetic models of the Ca²⁺ uniporter to characterize the mechanisms by which Mg²⁺ and Pi regulate the uniporter-mediated mitochondrial Ca²⁺ transport.

The kinetic studies of Scarpa and colleagues (14,15) report the initial rates of Ca²⁺ uptake with variations in extramatrix [Ca²⁺] (0–200 μM), measured in isolated mitochondria from rat livers and rat hearts, in the presence of 2 and 5 mM Mg²⁺ and 5 and 2 mM Pi in the buffer. These studies reveal a sigmoid kinetics of the extramatrix Ca²⁺-dependent Ca²⁺ uptake in the presence of Mg²⁺ and Pi. The kinetic study of Crompton et al. (9) reports the initial rates of Ca²⁺ uptake with variations in extramatrix [Ca²⁺] (0–35 μM), measured in isolated mitochondria from rat hearts, both in the absence and presence of 1 mM Mg²⁺ and Pi in the buffer. Although this study reveals a similar sigmoid kinetics of the extramatrix Ca²⁺-dependent Ca²⁺ uptake in the presence of 1 mM Mg²⁺ and 1 mM Pi, the kinetics was shown to become hyperbolic in the absence of Mg²⁺ with 0 and 1 mM Pi present in the buffer. These studies suggest that Mg²⁺ is a competitive inhibitor of Ca²⁺ uptake that alters only the K_m of Ca²⁺ for the uniporter. The kinetic study of Bragadin et al. (11) reports the initial rates of Ca²⁺ uptake with variations in extramatrix [Ca²⁺] (0–300 μM), measured in isolated mitochondria from rat livers, both in the absence and presence of 2 and 5 mM Mg²⁺ with 2 mM Pi in the buffer. This study reveals a similar sigmoid kinetics of the extramatrix Ca²⁺-dependent Ca²⁺ uptake in the presence of 2 and 5 mM Mg²⁺, and the kinetic was shown to become hyperbolic in the absence of Mg²⁺.

However, this study indicates a noncompetitive type of Mg²⁺ inhibition of Ca²⁺ uptake that significantly alters both the K_m of Ca²⁺ and the maximal activity of the uniporter. The kinetic study of Wingrove et al. (16) reports the initial rates of Ca²⁺ uptake with variations in ΔΨ (90–200 mV) for different levels of extramatrix Ca²⁺ ([Ca²⁺]_e = 0.5, 1.0, and 1.5 μM), measured in isolated mitochondria from rat livers, in the absence of Mg²⁺ with 0.2 mM Pi present in the buffer. This study reveals a nonlinear, Goldman-Hodgkin-Katz-type ΔΨ-dependency of Ca²⁺ uptake. The regulatory effect of Pi on Ca²⁺ uptake seems to be prominent only at low Pi levels (0–1 mM), which is evident from the study of Crompton et al. (9): Pi was shown to increase both the K_m of Ca²⁺ and the maximal activity of the uniporter; Pi did not appreciably affect the kinetics of Ca²⁺ uptake at higher levels of Pi ([Pi] > 1 mM). This kinetic model of Ca²⁺ uniporter is developed based on basic physical-chemical principles of ion transport across biomembranes and is parameterized to adequately reproduce these diverse experimental data sets in isolated mitochondria as well as the data sets of Szanda et al. (8) in permeabilized cells.

Proposed mechanism of Mg²⁺ inhibition of Ca²⁺ uniporter

Fig. 1 schematizes the proposed kinetic mechanism of Mg²⁺ inhibition of the uniporter-mediated Ca²⁺ transport into mitochondria. The uniporter functional unit is assumed to have two binding sites for Ca²⁺ and two distinct allosteric sites for Mg²⁺, facing either the external (cytosolic) side or the internal (matrix) side depending on the state of the uniporter (Fig. 1 A). In the forward process, an ionized Ca²⁺ from the cytosolic side binds to the uniporter T to form the complex T2Ca²⁺_e, which further favors the binding of second ionized Ca²⁺ (cooperative binding) to form the complex T2Ca²⁺_e. The complex T2Ca²⁺_e then undergoes conformational changes forming the complex 2Ca²⁺_xT in the matrix side. In the reverse process, the complex 2Ca²⁺_xT dissociates in two steps to form two free Ca²⁺ ions and the unbound uniporter T in the matrix side (Fig. 1 B).

Figure 1.

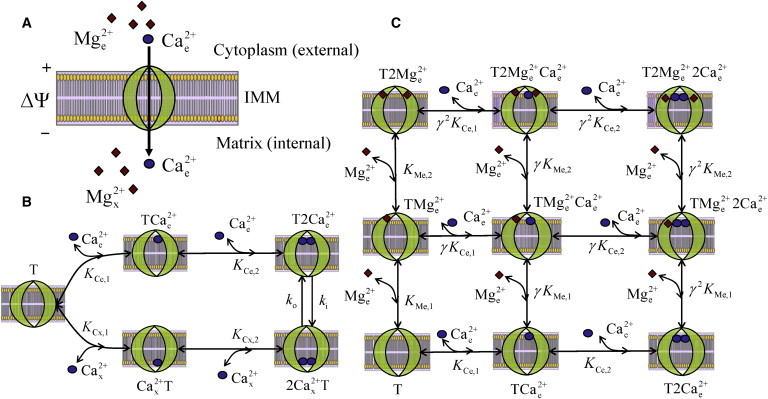
Proposed kinetic mechanism of Mg²⁺ inhibition of mitochondrial Ca²⁺ uptake via the Ca²⁺ uniporter. (A) Schematics of the Ca²⁺ uniporter, driven by the electrochemical gradient of Ca²⁺ (circle) across the IMM, exposed to Mg²⁺ ions (diamond). (B) Schematics of different Ca²⁺-bound uniporter states during translocation of Ca²⁺ across the IMM. (C) Schematics of different Ca²⁺- and Mg²⁺-bound uniporter states in the cytoplasmic side in a linear mixed-type inhibition mechanism for Mg²⁺ inhibition of mitochondrial Ca²⁺ uptake. In the matrix side, the Ca²⁺-Mg²⁺ interaction is symmetrical to that in the cytoplasmic side. K_Ce,1, K_Ce,2, K_Me,1, and K_Me,2 are the dissociation constants associated with the binding of first and second cytoplasmic Ca²⁺ and Mg²⁺ to the uniporter; 1 ≤ γ ≤ ∞ is a parameter that controls the binding affinity of Ca²⁺ and Mg²⁺ to the uniporter. The translocation of Ca²⁺ across the IMM (T2Ca_e²⁺ ↔ 2Ca_x²⁺2) is limited by two rate constants k_i and k_o, which are dependent on ΔΨ.

We consider a general, linear mixed-type inhibition mechanism for Mg²⁺ inhibition of the uniporter function. In this scheme, the interactions of Mg²⁺ and Ca²⁺ with the uniporter in the cytosolic side can be described by Fig. 1 C. Here, in one process, two Mg²⁺ ions cooperatively bind to the uniporter states E₁ (T, TCa_e²⁺, T2Ca_e²⁺) in two different steps to form the complexes

$${\text{E}}_1{\text{Mg}}_{\text{e}}^{2+}\left({\text{TMg}}_{\text{e}}^{2+},{\text{TMg}}_{\text{e}}^{2+}{\text{Ca}}_{\text{e}}^{2+},{\text{TMg}}_{\text{e}}^{2+}{2\text{Ca}}_{\text{e}}^{2+}\right)$$

and

$${\text{E}}_1{2\text{Mg}}_{\text{e}}^{2+}\left({\text{T}2\text{Mg}}_{\text{e}}^{2+},{\text{T}2\text{Mg}}_{\text{e}}^{2+}{\text{Ca}}_{\text{e}}^{2+},{\text{T}2\text{Mg}}_{\text{e}}^{2+}{2\text{Ca}}_{\text{e}}^{2+}\right).$$

In another process, two ${\text{Ca}}^{2+}$ ions cooperatively bind to the uniporter states E₂ (T, TMg_e²⁺, T2Mg_e²⁺) in two different steps to form the complexes

$${\text{E}}_2{\text{Ca}}_{\text{e}}^{2+}\left({\text{TCa}}_{\text{e}}^{2+},{\text{TMg}}_{\text{e}}^{2+}{\text{Ca}}_{\text{e}}^{2+},{\text{T}2\text{Mg}}_{\text{e}}^{2+}{\text{Ca}}_{\text{e}}^{2+}\right)$$

and

$${\text{E}}_2{2\text{Ca}}_{\text{e}}^{2+}\left({\text{T}2\text{Ca}}_{\text{e}}^{2+},{\text{TMg}}_{\text{e}}^{2+}{2\text{Ca}}_{\text{e}}^{2+},{\text{T}2\text{Mg}}_{\text{e}}^{2+}{2\text{Ca}}_{\text{e}}^{2+}\right).$$

In the matrix side, the Ca²⁺-Mg²⁺ interaction is symmetrical to that in the cytoplasmic side. The complete kinetic scheme for the Mg²⁺ inhibition of the uniporter function is shown in Fig. S1 of Appendix SA in the Supporting Material. Except for the 2Ca²⁺-bound uniporter complexes T2Ca²⁺_e and 2Ca²⁺_xT, the other uniporter complexes are assumed not to undergo any conformational changes that give rise to Ca²⁺ translocation across the IMM.

The translocation of Ca²⁺ via the uniporter is limited by the interconversion rate constants k_i and k_o, which are dependent on ΔΨ. K_Ce and K_Cx (K_Me and K_Mx) are the dissociation constants for the binding of cytosolic and matrix Ca²⁺ (Mg²⁺) to the uniporter. It is assumed that the binding of Mg²⁺ affects the binding of Ca²⁺ and vice versa. In this regard, the binding affinities of Ca²⁺ to the Mg²⁺-bound uniporter states and Mg²⁺ to the Ca²⁺-bound uniporter states decrease with increase in the number of Ca²⁺ and Mg²⁺ binding, which is mainly determined by the control parameter γ (1 ≤ γ ≤ ∞). Note that the parameter γ defines the type of Mg²⁺ inhibition of the uniporter function. For example, γ = 1 represents a noncompetitive inhibition, γ = ∞ represents a competitive inhibition, and 1 < γ < ∞ represents a mixed-type inhibition mechanism.

Ca²⁺ uniporter flux expression

Based on the proposed mechanism of Mg²⁺ inhibition of mitochondrial Ca²⁺ transport (Fig. 1) and the assumption of quasi-steady-state flux and rapid equilibrium binding of Ca²⁺ and Mg²⁺, the net Ca²⁺ transport flux via the uniporter (J_CU) can be expressed as (see Appendix SA in the Supporting Material):

$$J_{\text{CU}}=\frac{{\left[\text{T}\right]}_{\text{tot}}}{D}\left(k_i\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}^2}{K_{\text{Ce}}^2}-k_o\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}^2}{K_{\text{Cx}}^2}\right),$$ (1)

where [T]_tot represents the total uniporter concentration, and

Model 1

$$D=D_1=1+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}^2}{K_{\text{Ce}}^2}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}^2}{K_{\text{Cx}}^2}+\frac{{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}^2}{K_{\text{Me}}^2}+\frac{{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}^2}{K_{\text{Mx}}^2}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}^2{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}^2}{{\gamma }^4{K}_{\text{Ce}}^2·K_{\text{Me}}^2}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}^2{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}^2}{{\gamma }^4{K}_{\text{Cx}}^2·K_{\text{Mx}}^2}.$$ (2a)

Model 2

$$D=D_2=1+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}}{K_{\text{Ce}}}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}^2}{K_{\text{Ce}}^2}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}}{K_{\text{Cx}}}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}^2}{K_{\text{Cx}}^2}+\frac{{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}}{K_{\text{Me}}}+\frac{{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}^2}{K_{\text{Me}}^2}+\frac{{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}}{K_{\text{Mx}}}+\frac{{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}^2}{K_{\text{Mx}}^2}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}}{\gamma ·K_{\text{Ce}}·K_{\text{Me}}}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}^2}{{\gamma }^2·K_{\text{Ce}}·K_{\text{Me}}^2}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}^2{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}}{{\gamma }^2·K_{\text{Ce}}^2·K_{\text{Me}}}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}^2{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}^2}{{\gamma }^4·K_{\text{Ce}}^2·K_{\text{Me}}^2}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}}{\gamma ·K_{\text{Cx}}·K_{\text{Mx}}}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}^2}{{\gamma }^2·K_{\text{Cx}}·K_{\text{Mx}}^2}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}^2{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}}{{\gamma }^2·K_{\text{Cx}}^2·K_{\text{Mx}}}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}^2}{{\gamma }^4·K_{\text{Cx}}^2·K_{\text{Mx}}^2}.$$ (2b)

Model 3

$$D=D_3=1+2\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}}{K_{\text{Ce}}}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}^2}{K_{\text{Ce}}^2}+2\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}}{K_{\text{Cx}}}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}^2}{K_{\text{Cx}}^2}+2\frac{{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}}{K_{\text{Me}}}+\frac{{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}^2}{K_{\text{Me}}^2}+2\frac{{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}}{K_{\text{Mx}}}+\frac{{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}^2}{K_{\text{Mx}}^2}+4\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}}{\gamma ·K_{\text{Ce}}·K_{\text{Me}}}+2\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}^2}{{\gamma }^2·K_{\text{Ce}}·K_{\text{Me}}^2}+2\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}^2{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}}{{\gamma }^2·K_{\text{Ce}}^2·K_{\text{Me}}}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}^2{\left[{\text{Mg}}^{2+}\right]}_{\text{e}}^2}{{\gamma }^4·K_{\text{Ce}}^2·K_{\text{Me}}^2}+4\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}}{\gamma ·K_{\text{Cx}}·K_{\text{Mx}}}+2\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}^2}{{\gamma }^2·K_{\text{Cx}}·K_{\text{Mx}}^2}+2\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}^2{\left[{\text{Mg}}^{2+}\right]}_{\text{x}}}{{\gamma }^2·K_{\text{Cx}}^2·K_{\text{Mx}}}+\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}^2{[{\text{Mg}}^{2+}]}_{\text{x}}^2}{{\gamma }^4·K_{\text{Cx}}^2·K_{\text{Mx}}^2}.$$ (2c)

Note that for γ > 1, the higher-order terms in the uniporter flux expression becomes smaller and smaller compared to the leading order terms, because the concentrations of Ca²⁺ and Mg²⁺ bound uniporter states become smaller and smaller. Model 1, Model 2, and Model 3 represent, respectively, the full cooperative, partial cooperative, and no-cooperative binding of Ca²⁺ and Mg²⁺ to the uniporter (see Appendix SA in the Supporting Material). The kinetic parameters K_Ce, K_Cx, k_i, and k_o are constrained by the equilibrium relationship

$$K_{\text{eq}}=\frac{k_i}{k_o}·\frac{K_{\text{Cx}}^2}{K_{\text{Ce}}^2}={\left(\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{x}}^2}{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}^2}\right)}_{\text{eq}},$$ (3)

where K_eq is the equilibrium constant for transport of 2Ca²⁺ via the uniporter.

ΔΨ-dependency of the kinetic parameters

We follow a similar approach to that of our previous cation transporter models (20,22,29) to describe the ΔΨ-dependency of the kinetic parameters. Because Mg²⁺ and Ca²⁺ have identical valence, similar assumptions and biophysical parameters are used to describe the ΔΨ-dependency of Mg²⁺ and Ca²⁺ binding constants for the uniporter. We only summarize below the final equations that are used to express the kinetic parameters K_eq, K_Ce, K_Cx, K_Me, K_Mx, k_i, and k_o in terms of ΔΨ:

$$K_{\text{eq}}=\text{exp}\left(2\Delta \Phi \right),\Delta \Phi =\frac{\text{Z}F\Delta \Psi }{RT},$$ (4)

$$\begin{array}{l}{K}_{\text{Ce}}=K_{\text{Ce}}^0\text{exp}\left(-{\alpha }_{\text{e}}\Delta \Phi \right),K_{\text{Cx}}=K_{\text{Cx}}^0\text{exp}\left(+{\alpha }_{\text{x}}\Delta \Phi \right),\\ K_{\text{Me}}=K_{\text{Me}}^0\text{exp}\left(-{\alpha }_{\text{e}}\Delta \Phi \right),K_{\text{Mx}}=K_{\text{Mx}}^0\text{exp}\left(+{\alpha }_{\text{x}}\Delta \Phi \right),\end{array}$$ (5)

$$k_{\text{i}}=k_{\text{i}}^0\text{exp}\left(+2{\beta }_{\text{e}}\Delta \Phi \right),k_{\text{o}}=k_{\text{o}}^0\text{exp}\left(-2{\beta }_{\text{x}}\Delta \Phi \right),$$ (6)

$$\begin{array}{l}{\beta }_{\text{e}}=\frac{1}{2}\left[1+\frac{nH}{\Delta \Phi }\text{ln}\left\{\frac{\left(\frac{\Delta \Phi }{nH}\right)}{\text{sinh}\left(\frac{\Delta \Phi }{nH}\right)}\right\}\right]-{\alpha }_{\text{e}},\\ {\beta }_{\text{x}}=\frac{1}{2}\left[1-\frac{nH}{\Delta \Phi }\text{ln}\left\{\frac{\left(\frac{\Delta \Phi }{nH}\right)}{\text{sinh}\left(\frac{\Delta \Phi }{nH}\right)}\right\}\right]-{\alpha }_{\text{x}}.\end{array}$$ (7)

Here Z = 2 is the valence of Ca²⁺ or Mg²⁺; F, R, and T denote the Faraday's constant, ideal gas constant, and absolute temperature, respectively (F = 96484.6 J/mol/mV and R = 8.3145 J/mol/K); α_e (α_x) is the ratio of the potential difference between Ca²⁺ or Mg²⁺ bound to the site of the uniporter facing the external (internal) side of the IMM and Ca²⁺ or Mg²⁺ in the bulk phase to the total membrane potential; and β_e (β_x) is the displacement of external (internal) Ca²⁺ from the coordinate of maximum potential barrier. The ΔΨ-dependency of k_i and k_o are derived based on a nonlinear Goldman-Hodgkin-Katz type formalism by expressing β_e and β_x as functions of ΔΨ (22); nH is an arbitrary number that determines the degree of deviation from the linear Goldman-Hodgkin-Katz formalism.

Substituting Eq. 4 for K_eq, Eq. 5 for K_Ce and K_Cx, and Eq. 6 for k_i and k_o into Eq. 3, the following kinetic and thermodynamic constraints were obtained:

$$\left(\frac{k_{\text{i}}^0}{k_{\text{o}}^0}\right).{\left(\frac{K_{\text{Cx}}^0}{K_{\text{Ce}}^0}\right)}^2=1\text{and}{\alpha }_{\text{e}}+{\alpha }_{\text{x}}+{\beta }_{\text{e}}+{\beta }_{\text{x}}=1.$$ (8)

From our previous analyses of the ΔΨ-dependency of mitochondrial Ca²⁺ uptake (22), it is apparent that the Ca²⁺ (Mg²⁺) binding sites on the uniporter are located at equal and negligible distances from the bulk phase on either side of the IMM (i.e., α_e = α_e ≈ 0) and the binding affinities of the uniporter to both cytosolic and matrix Ca²⁺ (Mg²⁺) are the same (K⁰_Ce = K⁰_Cx and K⁰_Me and K⁰_Mx). The kinetic constraint in Eq. 8, then, provides k_i⁰ = k_o⁰ and the biophysical constraint in Eq. 8 is automatically satisfied. The estimate nH = 2.65 was found to well describe the ΔΨ-dependencies of the biophysical parameters β_e and β_x. We followed similar assumptions for binding of Ca²⁺ and Mg²⁺ to the uniporter and translocation of Ca²⁺ via the uniporter, so that α_e = α_e = α ≈ 0, K⁰_Ce = K⁰_Cx = K⁰_C, K⁰_Me = K⁰_Mx = K⁰_M, k_i⁰ = k_o⁰ = k⁰, and nH = 2.65. With this, the number of unknown parameters for estimation in this model is further reduced from ten to four (k⁰, K⁰_C, K⁰_M, and γ).

Pi-dependency of the kinetic parameters

Low extramatrix Pi levels have been shown to modulate the kinetics of Ca²⁺ uniporter in isolated rat heart mitochondria. Specifically, the kinetic study of Crompton et al. (9) shows changes in both the K_m of Ca²⁺ and the maximal activity of the uniporter at 0 and 1 mM Pi, in the presence and absence of extramatrix Mg²⁺. However, other initial rate studies with higher concentrations of Pi (>1 mM) do not show any significant effect of Pi on the kinetics of Ca²⁺ uniporter (11,14,15). In view of these experimental observations, we incorporate the Pi effect on the uniporter function by exclusively modifying the apparent K_m of Ca²⁺ and Mg²⁺ for the uniporter (K⁰_C and K⁰_M) as

$$K_{\text{C}}^0=K_{\text{C}}^0·(1+\frac{\left[\text{Pi}\right]}{(K_{\text{Pi}}+\left[\text{Pi}\right]})$$

and

$$K_{\text{M}}^0=\frac{K_{\text{M}}^0}{(1+\frac{\left[\text{Pi}\right]}{(K_{\text{Pi}}+\left[\text{Pi}\right]})},$$ (9)

where K_Pi is the Pi binding constant for the uniporter; K⁰_C and K⁰_M on the right side of Eq. 9 are the true (intrinsic) dissociation constants of Ca²⁺ and Mg²⁺ for the uniporter. Further justification for the proposed mechanism of Pi regulation of the kinetic parameters K⁰_C and K⁰_M is given in Appendix SB in the Supporting Material. With negligible pH gradient across IMM, Pi can quickly equilibrate across the IMM via the Pi-H⁺ cotransporter (23,24,30). Therefore, we assumed that [Pi]_e = [Pi]_x = [Pi]. With this modification, the total number of unknown parameters for estimation in this uniporter model becomes five$(k_0,K_{\text{C}}^0,K_{\text{M}}^0,K_{\text{Pi}}\text{and}\gamma )$.

Parameter estimation and sensitivity analysis

To estimate the unknown kinetic parameters $\varphi =(k_0,K_{\text{C}}^0,K_{\text{M}}^0,K_{\text{Pi}},\gamma )$ of the model, a combined least-squares estimation technique was used in multiple steps to fit the model-simulated outputs to the available experimental data,

$$\underset{\varphi }{\text{min}}E\left(\varphi \right),E\left(\varphi \right)=\sum _i^{N_{\text{exp}}}\sum _j^{N_{\text{data}}}\frac{1}{N_{\text{data}}}{\left(\frac{\left(J_{\text{CU},j}^{\text{data}}-J_{\text{CU},j}^{\text{model}}\left(\varphi \right)\right)}{\max \left(J_{\text{CU},j}^{\text{data}}\right)}\right)}^2,$$ (10)

where N_exp is the number of experiments and N_data is the number of data points in a particular experiment, $J_{\text{Uni},j}^{\text{data}}$ are the experimental data and $J_{\text{CU},j}^{\text{model}}\left(\varphi \right)$ are the corresponding model simulated outputs, and $\max \left(J_{\text{CU},j}^{\text{data}}\right)$ is the maximum value of $J_{\text{CU},j}^{\text{data}}$. The accuracy and robustness of the model fitting to the data for a particular model are assessed based on the value of mean residual error E(ϕ) and its sensitivities to perturbations in the optimal parameter estimates.

The model sensitivity to infinitesimal changes in the parameter values can be computed by

$$S_{{\varphi }_i}^E=\left|\frac{\partial \text{ln}E}{\partial \text{ln}{\varphi }_i}\right|=\frac{{\varphi }_i}{E}\left|\frac{\partial E}{\partial {\varphi }_i}\right|\approx \left|\frac{E\left({\varphi }_i+0.001{\varphi }_i\right)-E\left({\varphi }_i-0.001{\varphi }_i\right)}{0.002E\left({\varphi }_i\right)}\right|\text{;}{S}_{\varphi }^E=\sum _i^{N_p}\left|S_{{\varphi }_i}^E\right|,$$ (11)

where ϕ_i is the i^th parameter; $S_{{\varphi }_i}^E$ denotes the normalized sensitivity index for the parameter ϕ_i, whereas S_ϕ^E denote the combined normalized sensitivity index for all parameters together. A higher sensitivity index indicates that a small change in a given parameter (or all parameters) can result in a significant change in the model output. The most accurate model and parameters can have higher $S_{{\varphi }_i}^E$ and S_ϕ^E with lower least-squared error E(ϕ).

Results

In this section, we provide the detailed parameterization and independent validation of the three versions of the kinetic model of mitochondrial Ca²⁺ uniporter. The three kinetic models (Model 1, full cooperativity; Model 2, partial cooperativity; Model 3, no cooperativity) are simulated to exclusively fit the available data sets (9,11,14–16) on the kinetics of extramatrix Ca²⁺- and ΔΨ-dependent mitochondrial Ca²⁺ uptake measured both in the absence and presence of different amounts of Mg²⁺ and Pi in the buffer. The model fittings of these data sets are demonstrated through Fig. 2. The dashed, solid, and dotted lines represent the fittings for Model 1, Model 2, and Model 3, respectively. The model is further validated by comparing the model predictions to another data set (8) on the kinetics of mitochondrial Ca²⁺ uptake measured in permeabilized cells with physiological variations in cytosolic [Ca²⁺] and [Mg²⁺], which is demonstrated in Fig. 3. The estimated parameter values associated with these three variant models are provided in Table 1. Additional model simulations describing the nature of extramatrix Ca²⁺ and ΔΨ dependencies and the nature of Mg²⁺ inhibition of mitochondrial Ca²⁺ uptake are demonstrated through Fig. S3, Fig. S4, and Fig. S5 of Appendix SC in the Supporting Material.

Figure 2.

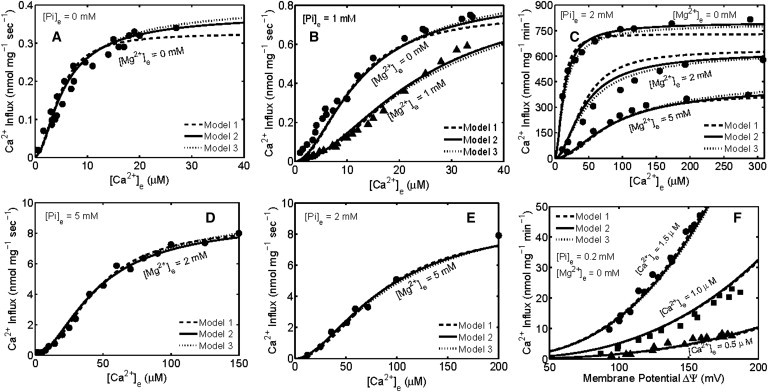
Comparison of the Ca²⁺ uniporter models (lines) to the experimental data (points) on the extramatrix Ca²⁺ and ΔΨ-dependencies of mitochondrial Ca²⁺ uptake measured both in the presence and absence of extramatrix Mg²⁺. Shown are the fittings of three different versions of the kinetic model (Model 1, Model 2, and Model 3) to the kinetic data of (A and B) Crompton et al. (9) in which the initial rates of Ca²⁺ influx in response to variations in extramatrix [Ca²⁺] were measured in energized mitochondria of rat hearts suspended (A) in a medium containing 0 mM Mg²⁺ and 0 mM Pi and (B) in a medium containing 0 and 1 mM Mg²⁺ and 1 mM Pi; (C) Bragadin et al. (11) in which the initial rates of Ca²⁺ influx in response to variations in extramatrix [Ca²⁺] were measured in energized mitochondria of rat livers suspended in a medium containing different levels of Mg²⁺ ([Mg²⁺]_e = 0, 2, and 5 mM) and 2 mM Pi; (D) Vinogradov and Scarpa (14) in which the initial rates of Ca²⁺ influx in response to variations in extramatrix [Ca²⁺] were measured in energized mitochondria of rat livers suspended in a medium containing 2 mM Mg²⁺ and 5 mM Pi; (E) Scarpa and Graziotti (15) in which the initial rates of Ca²⁺ influx in response to variations in extramatrix [Ca²⁺] were measured in energized mitochondria of rat hearts suspended in a medium containing 5 mM Mg²⁺ and 2 mM Pi; and (F) Wingrove et al. (16) in which the initial rates of Ca²⁺ influx as a function of ΔΨ were measured in energized mitochondria of rat livers suspended in a medium containing three different levels of Ca²⁺ ([Ca²⁺]_e = 0.5, 1.0, and 1.5 μM), with 0 mM Mg²⁺ and 0.2 mM Pi present in the medium. The models were fitted to these data sets by setting ΔΨ at 140 mV for the data corresponding to 0 mM Pi (A) and 190 mV for the data corresponding to ≥ 1 mM Pi (B–E). Matrix [Ca²⁺] was fixed at 250 nM and matrix [Mg²⁺] was fixed at 0.4 mM.

Figure 3.

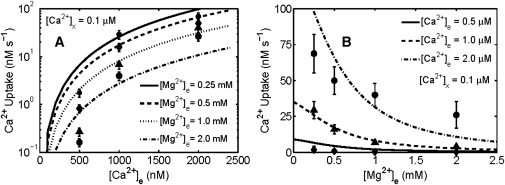
Comparison of the Ca²⁺ uniporter model (lines) to the experimental data (points) on the cytosolic Ca²⁺ and Mg²⁺ dependencies of mitochondrial Ca²⁺ uptake measured in permeabilized cells by Szanda et al. (8). Shown are the simulations and comparisons of Model 2 of the uniporter to the kinetic data in which the initial rates of Ca²⁺ uptake were measured (A) as a function of cytosolic [Ca²⁺] (logarithmic y axis) with four different levels of cytosolic Mg²⁺ ([Mg²⁺]_e = 0.25, 0.5, 1, and 2 mM), and (B) as a function of cytosolic [Mg²⁺] (linear y axis) with three different levels of cytosolic Ca²⁺ ([Ca²⁺]_e = 0.5, 1.0, and 2.0 μM). Model simulations were done using ΔΨ = 190 mV, matrix [Ca²⁺] = 0.1 μM, and matrix [Mg²⁺] = 0.4 mM. The rate constant k⁰ was found to be 5.96 nM/s (0.006 × 10⁻³ nmol/mg/s), as 1 mg mitochondrial protein = 1 μL mitochondrial volume.

Table 1.

Estimated parameter values and the corresponding normalized sensitivity coefficients for the kinetic model of mitochondrial Ca²⁺ uniporter

Parameters(ϕi)	Model 1		Model 2		Model 3		References
	Value	$S_{{\varphi }_i}^E$	Value	$S_{{\varphi }_i}^E$	Value	$S_{{\varphi }_i}^E$
k0 (nmol/mg/s)	1.27 × 10−3	0.0671	1.49 × 10−3	0.2692	1.58 × 10−3	0.3302	(9)
	20.32 × 10−3	0.0671	22.35 × 10−3	0.2692	22.12 × 10−3	0.3302	(11)
	16.51 × 10−3	0.0671	19.37 × 10−3	0.2692	20.54 × 10−3	0.3302	(14)
	27.94 × 10−3	0.0671	30.55 × 10−3	0.2692	29.23 × 10−3	0.3302	(15)
	63.5 × 10−3	0.0671	62.58 × 10−3	0.2692	60.04 × 10−3	0.3302	(16)
K0C (M)	3.965 × 10−6	0.1131	2.786 × 10−6	0.4946	1.955 × 10−6	0.7319	All
K0M (M)	0.655 × 10−3	0.0564	0.542 × 10−3	0.1725	0.403 × 10−3	0.4218	All
γ (Unitless)	3.9	0.1784	5.7	0.1739	9.2	0.1412	All
KPi (M)	0.2 × 10−3	0.0319	0.2 × 10−3	0.1678	0.2 × 10−3	0.2696	All
Eϕ; SEϕ	0.077; 0.447		0.058; 1.278		0.053; 1.895		Eqs. 10 and 11

Rate constant k⁰ is redefined as k⁰ = [T]_tot · k⁰. Note that the apparent values of K⁰_C and K⁰_M calculated using Eq. 9 for different [Pi] matches well with the estimates in Table S1 of Appendix SB in the Supporting Material, obtained without considering the Pi regulation mechanism of K⁰_C and K⁰_M.

We followed a multistep modular approach for parameterization of the model:

• Step 1.

  The kinetic parameters k⁰ and K⁰_C were estimated based on the Pi- and Mg²⁺-independent data ([Pi]_e = 0 mM; [Mg²⁺]_e = 0 mM) of Crompton et al. (9) (Fig. 2 A). The values of the kinetic parameters K_Pi, K⁰_M, and γ were reasonably chosen (fixed) to fit this data set, because these parameters are insensitive to this data set. The ΔΨ was set at 140 mV, corresponding to 0 mM Pi, based on a 2003 study by Bose et al. (23).

• Step 2.

  The Pi-dependent data of Crompton et al. (9) (Fig. 2 B) both with and without Mg²⁺ ([Pi]_e = 1 mM; [Mg²⁺]_e = 0 and 1 mM) were used to estimate K_Pi, K⁰_M, and γ, as these data sets are suitable to estimate the Pi and Mg²⁺ binding constants. In this step, the values of k⁰ and K⁰_C remained the same, as estimated in the first step. The ΔΨ was set at 190 mV, corresponding to a typical state-2 respiration with Pi ≥ 0.2 mM (23,24,30).

• Step 3.

  The five parameters k⁰, K⁰_C, K⁰_M, K_Pi and γ were further optimized and fine-tuned to jointly fit the model to the three data sets of Crompton et al. (9), along with the kinetic data of Bragadin et al. (11) ([Pi]_e = 2 mM; [Mg²⁺]_e = 0, 2, and 5 mM, see our Fig. 2 C); Vinogradov and Scarpa (14) ([Pi]_e = 5 mM; [Mg²⁺]_e = 2 mM, see our Fig. 2 D); Scarpa and Graziotti (15) ([Pi]_e = 2 mM; [Mg²⁺]_e = 5 mM, see our Fig. 2 E); and Wingrove et al. (16) ([Pi]_e = 0.2 mM; [Mg²⁺]_e = 0 mM, see our Fig. 2 F).

The parameter k⁰ was allowed to vary among data sets from different groups to account for different tissue types (i.e., mitochondria from rat livers versus rat hearts) and diverse experimental preparations that affect the overall uniporter activity (e.g., heterogeneity of mitochondrial population and differential energization or ΔΨ). The biophysical parameter α_e = α_e = α was set at zero and nH was set at 2.65, based on our previous uniporter model (22). Matrix [Ca²⁺] was set at 250 nM; matrix [Mg²⁺] was set at 0.4 mM, a value within the physiological range, based on the extensive work of Jung et al. (31); and ΔΨ was set at 190 mV for Pi ≥ 0.2 mM (9,23). We note here that, this extended uniporter has all the characteristics of our previous uniporter model (20,22). The model is insensitive to physiological variations in matrix [Ca²⁺], which is demonstrated in Fig. S3, A and B, in Appendix SC in the Supporting Material. Hence, the parameter estimates would depend neither on matrix [Ca²⁺], nor on Ca²⁺ buffering and Ca²⁺-Pi complex formation in the matrix.

One of the key observations from the model analyses of the data (fitting) is that, the fitting is able to provide unique and accurate estimates of the kinetic parameters K⁰_C, K⁰_M, K_Pi, and γ for all the available data sets (Table 1), irrespective of the amounts of Mg²⁺ and Pi present in the buffer. Furthermore, the fitting gives a unique and accurate estimate of k⁰ for all the data sets obtained from the same source (e.g., k⁰ is same for all the data curves of Crompton et al.). The fitting is able to provide a unique and accurate estimate of the parameter K_Pi (K_Pi ≈ 0.2 mM) that governs the Pi-dependencies of the kinetic parameters (K⁰_C and K⁰_M). Most importantly, Pi only seems to modulate the K⁰_C and K⁰_M in low Pi range (0–1 mM); for [Pi]_e > 1 mM; it does not alter K⁰_C and K⁰_M significantly, which is consistent with the available data.

Another important observation from the fitting is that this estimated value of K⁰_C is found to be much lower (e.g., K⁰_C ≈ 4.14 μM using Model 1 for all data sets) compared to our previously estimated values (20,22) (e.g., K⁰_C = 46 μM and 88 μM using Model 1 from the data sets of Scarpa and colleagues (14,15)). This is due to the presence of 2 and 5 mM Mg²⁺ and 5 and 2 mM Pi in their buffer, which significantly modifies the apparent K_m of Ca²⁺ for the uniporter; this was not accounted for in our previous uniporter models (20,22). Even in the presence of 2 or 5 mM Pi, the apparent K_m of Ca²⁺ becomes ∼9 μM, which is still much lower than that of the previous estimates. A small K_m value indicates that Ca²⁺ uptake attains saturation for a lower level of extramatrix Ca²⁺, compared to our previous uniporter models (20,22), which is demonstrated in Fig. S4, A and B, of Appendix SC in the Supporting Material. Overall, this uniporter model accurately depicts the kinetics of mitochondrial Ca²⁺ uptake over a wide range of experimental conditions, in which the kinetics of Ca²⁺ uptake is hyperbolic in the absence of Mg²⁺, sigmoid in presence of Mg²⁺, and the degree of sigmoidicity increases with increase in [Mg²⁺], which is depicted in Fig. S4, C and D, of Appendix SC in the Supporting Material.

From the fittings of the models to the data (Fig. 2), it is apparent that both Model 2 and Model 3 adequately explain the available data compared to Model 1. This is also evident from the combined least-square error (E_ϕ) and normalized sensitivity coefficients for individual parameters and all parameters together ($S_{{\varphi }_i}^E$ and S^E_ϕ) (Table 1). Specifically, E_ϕ is higher and S^E_ϕ is lower for Model 1, whereas E_ϕ is lower and S^E_ϕ is higher for Model 2 and Model 3. Additional statistical test based on the Akaike's Information Criterion (AIC) is also conducted to verify the goodness of the fits. The computed value of AIC (AIC = N_dataln(E_ϕ) + 2N_ϕ) was found to be higher for Model 1 compared to Model 2 and Model 3. This is obvious because the number of unknown parameters (N_ϕ) is the same in all three models. Therefore, AIC is strictly dependent on E_ϕ for a given model. From model parameterization and sensitivity analyses (Table 1) it is made clear that the kinetic parameters K⁰_C, K⁰_M, and γ are very accurate and consistent over a wide variety of experimental preparations at physiological levels of Pi. The estimated values of these parameters varied between different versions of the model due to the nature of binding assumptions. Therefore, either of the models (Model 2 or Model 3) can be considered as the most accurate model of the uniporter that best describes the available data compared to Model 1.

Based on these estimated values of the kinetic parameters (K⁰_C, K⁰_M, K_Pi, γ) and the previously estimated values of the biophysical parameters (α, nH), we further validated the uniporter model by simulating the extramatrix Ca²⁺ and Mg²⁺ dependencies of mitochondrial Ca²⁺ uptake in permeabilized cells (8). Fig. 3 A shows the model comparisons (logarithmic y axis) to the data as a function of cytosolic [Ca²⁺] for four different cytosolic [Mg²⁺] values ([Mg²⁺]_e = 0.25, 0.5, 1, and 2 mM; [Pi]_e = 1 mM), whereas Fig. 3 B shows the model comparisons (linear y axis) to the data as a function of cytosolic [Mg²⁺] for three different cytosolic [Ca²⁺] values ([Ca²⁺]_e = 0.5, 1, and 2 μM; [Pi]_e = 1 mM). We used one of the most accurate models of the uniporter (Model 2) for these model simulations. The value of the rate constant k⁰ was first converted from the units of nmol/mg/s to the units of nM/s by using the conversion factor 1 mg protein = 3.7 μL, then modified until the model predictions closely match the data. Matrix [Ca²⁺] was set at 250 nM, matrix [Mg²⁺] was set at 0.4 mM, and ΔΨ was set at 190 mV. Considering that no other kinetic parameter was adjusted, the model is able to adequately predict the data and the nature of Mg²⁺ inhibition of mitochondrial Ca²⁺ uptake in intact permeabilized cells (8), under physiological variations of cytosolic [Ca²⁺] and [Mg²⁺], supporting the accuracy of the model. Similar model predictions on % Mg²⁺ inhibition of Ca²⁺ uptake as a function of extramatrix [Ca²⁺] and [Mg²⁺] are demonstrated through Fig. S5 of Appendix SC in the Supporting Material.

From the model analyses of the available data (Figs. 2 and 3), it is evident that this uniporter model is able to explain adequately the extramatrix Pi-, Mg²⁺-, Ca²⁺-, and ΔΨ-dependent kinetics of mitochondrial Ca²⁺ uptake in a wide variety of experimental preparations. To further validate the proposed mechanisms of Mg²⁺ inhibition of the uniporter function, we integrated this uniporter model and our recently developed 3Na⁺-1Ca²⁺ antiporter model (29) to our previously developed model of mitochondrial Ca²⁺ handling and bioenergetics (19). The integrated model is used to simulate the experimental data of Cox and Matlib (32) and McCormack et al. (12) on matrix free [Ca²⁺] as a function of extramatrix free [Ca²⁺], [Mg²⁺], and [Na⁺]. Detailed analyses and fittings of the integrated model to these data sets are described in Appendix SD (Figs. S6 and S7) in the Supporting Material. The model appropriately described these data sets, further signifying the accuracy and robustness of this uniporter model and the proposed Mg²⁺ and Pi regulation mechanisms.

Discussion

The work reported in this article provides the detailed development of a mechanistic mathematical model of mitochondrial Ca²⁺ uniporter that characterizes the kinetic mechanisms by which cytosolic Mg²⁺ inhibits and Pi regulates the uniporter-mediated Ca²⁺ transport into mitochondria. The model is extended from our previous models of the uniporter (20,22) and developed based on a similar multistate catalytic binding and interconversion mechanism for carrier-mediated facilitated transport and Eyring free energy barrier theory for interconversion and electrodiffusion (26–28). The model is parameterized and validated by comparing the model-simulated outputs to a large number of independent data sets on the kinetics of extramatrix Ca²⁺- and ΔΨ-dependent Ca²⁺ uptake via the uniporter, obtained in respiring mitochondria isolated from rat hearts and livers (9,11,14–16) and intact permeabilized myocytes (8) both in the absence and presence of different amounts of extramatrix Mg²⁺ and Pi. The model precisely describes the inhibitory effect of extramatrix Mg²⁺ and the regulatory role of Pi on the uniporter-mediated mitochondrial Ca²⁺ uptake, observed in these experiments.

Although this uniporter model has all the characteristics of our previous uniporter models (20,22), it significantly differs from the earlier models in that it mechanistically characterizes the inhibitory effect of Mg²⁺ and regulatory role of Pi on the uniporter function. It identifies the most plausible Mg²⁺ inhibition and Pi regulation mechanisms based on a large number of experimental data sets (8,9,11,12,14–16). This uniporter model clarifies the earlier contradictory results on the type of Mg²⁺ inhibition of the uniporter function. Particularly, whereas the kinetic studies of Crompton et al. (9) and Scarpa and colleagues (14,15) showed a competitive type of Mg²⁺ inhibition, the later kinetic study of Bragadin et al. (11) showed a noncompetitive type of Mg²⁺ inhibition of Ca²⁺ uptake. Our model suggests a mixed-type mechanism for Mg²⁺ inhibition of Ca²⁺ uptake, in which the kinetics of Ca²⁺ uptake is hyperbolic in the absence of Mg²⁺ and sigmoid in the presence of Mg²⁺. This is manifested by a marked increase in the apparent K_m of Ca²⁺ for the uniporter and decrease in the maximal activity of the uniporter with increasing extramatrix [Mg²⁺]. Furthermore, the degree of sigmoidicity increases with increase in extramatrix [Mg²⁺], which is consistent with experimental observations.

This uniporter model also accurately explains the regulatory effect of cytosolic Pi on mitochondrial Ca²⁺ uptake, typically seen at low Pi levels (0–1 mM) in the kinetic study of Crompton et al. (9). Accordingly, the K_m of Ca²⁺ and Mg²⁺ for the uniporter (K⁰_C and K⁰_M) were expressed in terms of Pi, in which Pi is shown to increase the value of K⁰_C and decrease the value of K⁰_M, and the Pi effect is shown to be negligible at higher Pi concentrations ([Pi] > 1 mM), consistent with the available data. On the other hand, without considering the Pi regulation mechanism, the model did not fit to the available data with unique K⁰_C and K⁰_M values for all data sets. This is apparent from the detailed model analyses presented in Appendix SB in the Supporting Material, which justifies this formulation of Pi regulation of K⁰_C and K⁰_M parameters. However, additional kinetic data at submillimolar Pi concentrations may be necessary to mechanistically evaluate the precise regulatory effect of Pi on the uniporter function.

Despite significant technical advances, the structure and composition of mitochondrial Ca²⁺ uniporter and the regulation mechanisms of the uniporter function by divalent cations (e.g., Mg²⁺) and metabolites (e.g., Pi) are still largely unknown. Our present uniporter model is based on the assumption that there exist at least two binding sites for Ca²⁺ ions and two separate allosteric sites for Mg²⁺ ions on the uniporter (Fig. 1). We explored three possible Ca²⁺ and Mg²⁺ binding schemes (Model 1, full cooperativity; Model 2, partial cooperativity; and Model 3, no cooperativity) to resolve the most likely Ca²⁺ and Mg²⁺ binding mechanism that can explain the observed kinetics of mitochondrial Ca²⁺ uptake under diverse experimental preparations (8,9,11,12,14–16). With our model analyses of the available data, though we are not able to fully distinguish between the three versions of the kinetic model, Model 2 and Model 3 seem to describe the data most accurately compared to Model 1. Alternatively, by assuming 1), two binding sites for Ca²⁺ ions and one separate allosteric site for Mg²⁺ ions on the uniporter or 2), two binding sites for Ca²⁺ ions and Mg²⁺ ions competing for the Ca²⁺ binding sites, we were not able to fit the two reduced models to any of the available data sets (see Figs. S8–S10 and Appendix SE in the Supporting Material).

In this mixed-type Mg²⁺ inhibition scheme for the Ca²⁺ uniporter, we consider binding of two Ca²⁺ ions and two Mg²⁺ ions to the uniporter, and the order of Ca²⁺ and Mg²⁺ binding does not affect the uniporter conformational states. In addition, the translocation of Ca²⁺ across the IMM occurs only via the conformational changes of the 2Ca²⁺-bound uniporter complexes T2Ca²⁺_e and 2Ca²⁺_xT (Fig. 1); other Mg²⁺ and Ca²⁺-bound uniporter states do not undergo any conformational changes. However, alternate mechanisms are possible, in which the Mg²⁺-bound uniporter states can undergo conformational changes, leading to Mg²⁺ influx via the Ca²⁺ uniporter. This is not considered here because it not only introduces additional parameter, but also there is lack of experimental evidence and data available on the kinetics of Mg²⁺ transport via the Ca²⁺ uniporter. Another salient feature of this uniporter model is that, using a single control parameter γ, the model can display all possible types of Mg²⁺ inhibition mechanisms (e.g., γ = 1, noncompetitive inhibition; γ = ∞, competitive inhibition; and 1 < γ < ∞, a mixed-type inhibition). Consequently, by analyzing a large number of experimental data sets (8,9,11,12,14–16), the model confirmed that a mixed-type inhibition mechanism is most viable for the operation of the Ca²⁺ uniporter.

Another important feature of this uniporter model is that it provides a unique and consistent estimates of the kinetic parameters associated with the binding of Ca²⁺, Mg²⁺, and Pi to the uniporter (K⁰_C, K⁰_M, K_Pi, and γ) over a large number of experimental data sets (9,11,14–16). Most importantly, the estimate of K_m of Ca²⁺ for the uniporter (K⁰_C) is found to be much lower compared to that reported in our earlier studies (20,22), and is unique over all the available data sets, irrespective of the amounts of extramatrix Mg²⁺ and Pi and the tissue types (hearts versus livers). For example, in this uniporter model, K⁰_C is found to be ∼4.14 μM using Model 1 for all the available data sets, whereas Model 1 of our previous uniporter models (20,22) estimated a much higher value of K⁰_C, at ∼44 μM for rat liver mitochondria (14) and 88 μM for rat heart mitochondria (15), due to the presence of different amount of Mg²⁺ and Pi in the buffer. In this model, this effect is attributed to changes in the binding affinities of Ca²⁺ for the uniporter with different amount of extramatrix Mg²⁺ and Pi. Accordingly, Ca²⁺ uptake reaches saturation at a much lower level of extramatrix Ca²⁺ (≈30 μM) in the absence of extramatrix Mg²⁺ compared to our previous uniporter models (20,22), when simulated over the entire ΔΨ-range; in the presence of 2 mM Mg²⁺, a higher level of extramatrix Ca²⁺ (≈100 μM) is required for the Ca²⁺ uptake to attain saturation (see Fig. S4, A and B, of Appendix SC in the Supporting Material).

Though the pathways of mitochondrial Ca²⁺ transport have been known for last three decades, their functional consequences are becoming increasingly clear in recent years in relation to the cell physiology and pathophysiology. Most importantly, mitochondrial Ca²⁺ uptake plays a substantial role in shaping cytosolic Ca²⁺ signals in many cell types and regulating local Ca²⁺ concentration in cellular microdomains (3,33,34). It is also apparent that mitochondria can considerably alter the kinetics of intracellular Ca²⁺ oscillations and waves generated by Ca²⁺ release from the endoplasmic reticulum (35). A decline in mitochondrial Ca²⁺ uptake can have significant effect on the spatiotemporal characteristics of cellular Ca²⁺ signaling and mitochondrial energy metabolism.

Considering its significance in tuning Ca²⁺-mediated cellular responses, it is important to understand each factor that modulates mitochondrial Ca²⁺ transport. In this regard, Mg²⁺ is known to be a key regulator of mitochondrial cation and substrate transport systems, and inhibition of mitochondrial Ca²⁺ uptake by physiological elevations of cytosolic Mg²⁺ has been well recognized in many experimental studies (8,9,11). However, the consequences of this inhibition are poorly understood at cellular levels and it is largely unknown whether Mg²⁺ has any potential role in modifying cellular Ca²⁺ signals. Therefore, this model of Ca²⁺ uniporter is very useful for building biophysically based integrated models of mitochondrial and intracellular Ca²⁺ handling, to understand the mechanisms by which Ca²⁺ plays a critical role in the signal transduction processes and modulates mitochondrial and cellular energy metabolisms.