Abstract
The association of specific events with the context in which they occur is a fundamental feature of episodic memory. However, the underlying network mechanisms generating what–where associations are poorly understood. Recently we reported that some hippocampal principal neurons develop representations of specific events occurring in particular locations (item-position cells). Here, we investigate the emergence of item-position selectivity as rats learn new associations for reward and find that before the animal's performance rises above chance in the task, neurons that will later become item-position cells have a strong selective bias toward one of two behavioral responses, which the animal will subsequently make to that stimulus. This response bias results in an asymmetry of neural activity on correct and error trials that could drive the emergence of particular item specificities based on a simple reward-driven synaptic plasticity mechanism.
The hippocampus is critically involved in the acquisition of new episodic memories (Scoville and Milner 1957; Eichenbaum 2000). In particular, the formation of associations between events and the context where they occur, a fundamental feature of episodic memory, depends on hippocampal function (Manns and Eichenbaum 2006; Eichenbaum et al. 2007).
We have recently shown that some hippocampal principal neurons develop representations of specific events occurring in particular locations (Komorowski et al. 2009). In this study, animals learned which of two stimulus items (what) was rewarded depending on the environmental context (where) in which the items were presented (Rajji et al. 2006; Manns and Eichenbaum 2009). On each trial, a rat initially explored one of the two contexts, after which the two stimulus items were placed into different positions (corners) of the context (Fig. 1A); the animal then investigated the items (scented flower pots), and should learn to dig (Go response) for a buried food reward in the appropriate pot for that context or not dig (NoGo) at pots where no reward was buried. All animals performed at no better than chance (50%) for the first 30 trials, then acquired the what–where associations, reaching an average accuracy of 86% in the last 30 trials of the training session (Fig. 1B).
Figure 1.
Hippocampal principal cells that develop conjunctive what–where representations are behavior-selective cells. (A) Task scheme. Animals have to learn to associate contexts to items (scented pots) for reward. A 40-sec period of context exploration is allowed before items presentation. An item is considered “chosen” when the rat digs its pot searching for reward. (B) Average task performance accuracy during the first, middle, and last block of 30 trials. (*) P < 0.01 (t-test) when compared with chance performance (50% in this task). (C, left) Mean IP cell firing rates during sampling of the preferred and nonpreferred items in the same position before learning (left set of bars) and after learning (right sets of bars). (Other panels) Mean firing rates during the sampling of the rewarded and nonrewarded item are shown for the two types of IP cells (as labeled) separately and for P cells. (*) P < 0.01 (t-test). (D) Mean firing rates of IP and P cells on item samplings occurring preceding Go and NoGo responses before and after learning. (*) P < 0.01 (t-test).
In this paradigm, we previously indentified principal neurons showing differential firing during the sampling of one of the two stimulus items when located in the same position (Fig. 1C, left), which we called as item-position (IP) cells (Komorowski et al. 2009). IP cell responses did not distinguish the items during the first 30 trials of the learning session, but did fire during item sampling at particular locations. Subsequently, we showed that many IP cells increased firing during the sampling of an item-position combination in parallel with learning (Fig. 1C, left). Importantly, we observed approximately equivalent selectivity for rewarded and nonrewarded item-position combinations (Fig. 1C, middle). We also identified principal neurons that were active during item sampling in a particular position, but without distinguishing the items at any time; these cells were referred to as P cells (Fig. 1C, right).
The mechanisms leading to the formation of particular associations by hippocampal neurons remain largely unknown. What determines whether a neuron will signal one association rather than another, and why do some neurons not develop an association? To better understand the emergence of IP cells, we have further analyzed recordings previously collected (Komorowski et al. 2009). We hypothesized that reward should influence in shaping neuronal activity during learning, and we sought to determine whether cells that eventually become IP cells have differential activity during trials that end or not in reward consumption before behavioral learning takes place.
We find that prior to both task acquisition and the appearance of item-position selectivity, IP cells that will later prefer a rewarded item are strongly selective for Go behavioral responses, whereas IP cells that will later prefer a nonrewarded item are strongly selective for NoGo behavioral responses. This behavioral bias consequently leads to different firing rates associated with correct (rewarded) and error (nonrewarded) trial outcomes. We propose a simple model in which item-position cell specificity emerges through synaptic modifications of inputs carrying item information based on the presence or absence of reward following decision-making.
Results
In order to understand the evolution of item selectivity in IP cells, as well as the lack of selectivity in P cells, we compared the firing patterns of these cells in the first 30 trials, when task performance was at chance level and item-position selectivity had not developed, with patterns in the middle and last 30 trials, when performance had raised above chance and reached its peak, respectively. In the first 30 trials, we found that IP cells that would later prefer a rewarded item-position combination (rewarded IP cells) fired at much higher rates on sampling events followed by a Go response than events that ended in a NoGo response (Fig. 1D, left middle panel). Conversely, during the first 30 trials, IP cells that would eventually prefer a nonrewarded item-position combination (nonrewarded IP cells) fired at much higher rates on sampling events. followed by a NoGo response (Fig. 1D, right middle panel). The behavior-selective bias by IP cells persisted in the last 30 trials. On the other hand, P cells had no behavioral response bias, either early or late in training (Fig. 1D, right). In Figure 2 we show rasters and peri-event histograms of IP and P cells for item-sampling events preceding Go and NoGo responses. Thus, the IP cells that eventually come to prefer rewarded and nonrewarded stimulus items can be characterized as “Go cells” and “NoGo cells,” respectively. This behavioral selectivity also exists while the animals’ performance is at chance (Fig. 1D; Table 1) and, therefore, before the appearance of item-position preferences (Fig. 1C). How do these Go and NoGo cells develop item preferences?
Figure 2.
Examples of IP and P cells. Shown are spike rasters (top) and peri-event histograms (middle) for stimulus sampling events preceding Go and NoGo responses, along with the mean spike frequency (bottom) during sampling of the rewarded and nonrewarded item in the first 30 trials (“First Trials”) and all other trials (“Last Trials”). The red bar in the peri-event histograms corresponds to the time period between 0 and 1 sec, which is the time period used for the statistical analyses shown in this and all other figures.
Table 1.
Mean spike frequency of IP and P cells (M ± SEM)a
We knew from our previous study (Komorowski et al. 2009) that IP cell responses are higher on correct than on error trials after learning (Fig. 3A). Based on the above results, however, we reasoned that selective Go and NoGo firing patterns should also result in differential firing rates for the different items during sampling on trials that subsequently ended with a reward (correct trials) vs. trials that ended without reward (errors), even before learning has taken place. This expectation was confirmed in that, during the first 30 trials, neurons that would later become IP cells preferring the rewarded stimulus fired at higher rates preceding correct Go responses when the rewarded item was presented, and at higher rates preceding incorrect Go responses to the nonrewarded item (Fig. 3B, top, middle). Conversely, neurons that would later become IP cells preferring the nonrewarded item fired at higher rates preceding correct NoGo responses when a nonrewarded item was presented, and preceding incorrect NoGo responses when a rewarded item was presented (Fig. 3B, bottom middle panel). P cells were similarly active on correct and error trials (Fig. 3B, right panel).
Figure 3.
Item-position cells present differential firing rates on correct and error trials before learning. (A) Mean spiking frequency of IP cells in their preferred position on correct and error trials during the first (left set of bars) and last (right set of bars) 30 trials of the learning session. (*) P < 0.01 (t-test). (B, left) Mean firing rates of IP cells on correct and error trials for the later preferred and nonpreferred item in the same position during the first 30 trials of the session (i.e., during chance performance). (Other panels) Mean firing rates on correct and error trials during samplings of the rewarded and nonrewarded item before learning is shown for the two types of IP cells separately and for P cells. (*) P < 0.05 (two-way ANOVA interaction of item type with trial outcome).
The firing rate asymmetries in rewarded and nonrewarded trials suggest that mechanisms of reward-driven synaptic strengthening and weakening of connections between sensory inputs from the item stimuli and IP cells could lead to the observed item selectivity of these cells. To better understand this, we have elaborated a simple computational model of decision-making in this task. In this model we begin with the Go and NoGo cells in the network and assume that they compete with each other (Fig. 4A). Therefore, Go cells fire at higher rates and suppress the NoGo cells during item sampling prior to a Go response, and NoGo cells fire at higher rates and suppress the Go cells during item sampling prior to NoGo responses. The probability of a Go or a NoGo response following each item sampling event is modeled as dependent on the relative synaptic strength of sensory inputs from the item stimuli to the Go and NoGo cells. For example, when sampling item X, the probability of digging (Go) will be higher than withholding digging (NoGo) if the connection strength from item X sensory inputs to the Go cell population is higher than that to the NoGo cell population (see Fig. 4B). Finally, we make the assumption of two plasticity mechanisms acting following the Go/NoGo response: (1) Reward following a correct response leads to a strengthening of the synaptic connections between sensory afferents carrying information about the item and cells that were active (see below) during item sampling, whereas (2) nonreward leads to a weakening of these synaptic connections. These synaptic changes are modeled as proportional to the firing rate of the cell during item sampling. Therefore, cells that were firing at a low rate during item sampling are subjected to low plasticity effects, whereas cells firing at a higher rate are subjected to a greater level of plasticity (Fig. 4C).
Figure 4.
Model scheme. (A) Afferents carrying sensory information from each stimulus (just one stimulus is depicted in this figure) impinge on a population of Go and NoGo cells, which compete with each other for determining behavior. (B) The probability of a Go action upon sampling of item X (P(Go|X)) is dependent on the relative synaptic weights from item X sensory stimuli to the cell populations. The probability of a NoGo action is given by P(NoGo|X) = 1 − P(Go|X), and similar formulas hold for P(Go|Y) and P(NoGo|Y). (C) Shown are possible outcomes following Go (top) and NoGo (bottom) responses to an item. A strengthening of connections between the stimulus and the cell population determining behavior occurs if the behavior led to reward; otherwise, a weakening of these connections occurs.
The details of the model implementation are as follows: The choice between a Go (digging) or a NoGo response (withhold digging) after each item sampling event in the same position is modeled as a random variable following conditional probabilities; P(Go|X) is the probability of digging given item X is examined, P(NoGo|X) is the probability of withhold digging given item X is examined, and similarly for P(Go|Y) and P(NoGo|Y). The probability of a Go response following item X sampling is given by P(Go|X) = f(WX,Go/(WX,Go + WX,NoGo)), where WX,Go and WX,NoGo denote the synaptic weights from item X sensory afferents to the Go and NoGo cells, respectively (see Fig. 4B). The function f:[0,1] → [0,1] is a sigmoid function7 defined by f(x) = 1./(1 + exp(−8(x − 0.5)). Similar formulas hold for the other conditional probabilities (notice that P(Go|X) + P(NoGo|X) = P(Go|Y) + P(NoGo|Y) = 1). The firing rate of each cell population during item sampling is modeled as proportional to the synaptic weight of afferents carrying information from that item: FCellType = εWItem,CellType + η, with the subscripts Item standing for X or Y, CellType denotes Go or NoGo cells, and η represents Gaussian noise with mean 0 and variance 1. The factor ε denotes a gain (εgain > 1) or a suppression (εsuppression < 1) factor: associated with Go responses, ε = εgain for Go cells and ε = εsuppression for NoGo cells, with the opposite happening associated with NoGo responses. Synaptic weights are subject to changes after each response, with the following 2 equations being responsible for the update of the synaptic weights: WItem,CellType = WItem,CellType + Δ if the correct (rewarded) behavioral response for that item was emitted, and WItem,CellType = WItem,CellType − Δ for the error (nonrewarded) response. Finally, the increment/decrement factor Δ is proportional to the firing rate during item sampling: Δ = δ FCellType, with δ > 0.
We ran simulations starting with the connections from either item (X or Y) to either cell population (Go or NoGo cells) having the same weight. On each trial, item X (rewarded item in the model) or Y (nonrewarded item) is randomly presented. Following each response, synaptic weights are updated dependent on whether a Go (correct for item X; error for item Y) or a NoGo (error for item X; correct for item Y) response was emitted. Model performance simulated both the course of behavioral learning (Fig. 5A) and the development of item selectivity in Go and NoGo cells (Fig. 5B, top), which showed behavioral response bias before and after learning (Fig. 5B, bottom).
Figure 5.
Computational model of reward-dependent synaptic plasticity is able to account for the development of item specificity in behavior-selective cells. (A) Network performance for item sampling events occurring before and after learning (labeled as “first” and “last trials”). (B, top) Mean firing rates of model Go and NoGo cells before and after learning for the rewarded and nonrewarded item. (Bottom) Mean firing rates associated with Go and NoGo responses. (C) Mean firing rates of model Go and NoGo cells on correct and error trials for the rewarded and nonrewarded items during item sampling events occurring before learning. (D) Mean synaptic weights (WItem,CellType) changes as a function of the item sampling event number. G = Go cells; NG = NoGo cells. Results represent the mean over 100 simulations.
The model is based on reward-based plasticity rules and the differential firing rates associated with correct and erroneous responses. Thus, Go cells become IP cells that will later prefer the rewarded stimulus because the high firing rate associated with Go responses to that item will be followed by reward, leading to a strengthening of the synaptic connections from the stimulus item to this cell (Fig. 5C,D). Conversely, when the nonrewarded item is presented and the rat emits a Go response, the high firing rate by Go cells to that item will not be followed by a reward, leading to a weakening of synaptic connection strength from the item to the cell (Fig. 5C,D). Also, when either stimulus item is presented and the animal emits a NoGo response, the firing rate of Go cells is relatively low, and therefore the effect of plasticity mechanisms is modest in this condition. This accounts for why the synaptic connections from the rewarded item to the Go cell are only slightly weakened following an error after sampling of this item, while the connections from the nonrewarded item to this cell also remain largely unchanged following a correct response (in both cases, a NoGo response is emitted). A complementary combination of mechanisms accounts for NoGo cells, which are the IP cells that eventually prefer the nonrewarded item. Notice that it is assumed that the high firing rate during correct NoGo responses to the nonrewarded stimulus is associated with a delayed reward, which occurs after the animal digs the correct item in the other position of the arena (see Discussion).
The model predicts that Go and NoGo cells should develop differential firing rates preceding the same behavioral responses, depending on which item is examined (Fig. 6A). Namely, upon learning, Go (NoGo) cells should exhibit a higher firing rate during samplings of their preferred rather than nonpreferred items that end with a Go (NoGo) response. In Figure 6B we show that this prediction is in fact confirmed: After learning, IP cells coding for the rewarded item spike more during sampling of the rewarded than the nonrewarded item preceding Go responses, while IP cells coding for the nonrewarded item spike more during sampling of this item preceding NoGo responses. Notice that this result also means that even though IP cells start out as pure Go/NoGo cells, they do develop a genuine item preference even after controlling for the behavioral response emitted; that is, after learning, Go/NoGo-place responses can be separated from item-position coding. According to the model, this is due to the fact that an increased activity during sampling of the later preferred item early in training was associated with reward signals, while an increased activity during sampling of the later nonpreferred item was not (Figs. 3B, 5C): The proposed plasticity rules predict that this asymmetry leads to a specific increase of the synaptic connections from the later preferred item (Fig. 5D). Curiously, since the firing rate is modeled as proportional to the synaptic weights (i.e., F ∼ εW), the higher the W, the higher the firing rate, even when the cells are suppressed (that is, when ε = εsuppression). Therefore, the model also predicts that Go (NoGo) cells should spike more to the rewarded (nonrewarded) item preceding NoGo (Go) responses after learning (Fig. 6A). In accordance with this model prediction, IP cells coding for the rewarded item also come to spike more during samplings of the rewarded than nonrewarded item preceding NoGo responses (Fig. 6B, top). However, IP cells coding for the nonrewarded item did not spike differentially during item samplings of either item preceding Go responses (Fig. 6B, bottom). We speculate that this different characteristic between the two types of IP cells may be due to different temporal proximity of reward following Go and NoGo responses (see Discussion).
Figure 6.
IP cells present item selectivity with learning even after controlling for the behavioral response emitted. (A, top) Mean firing rates of model Go cells for the rewarded and nonrewarded items during item sampling events preceding Go and NoGo responses occurring before and after learning. (Bottom) Similar as before, but for model NoGo cells. (B) Similar as in A, but for actual IP cells. (*) P < 0.01 (t-test).
In contrast to the patterns of activity in IP cells, P cells fired at equal rates on item sampling events that precede Go and NoGo responses (Fig. 1D, right) and end in reward and nonreward (Fig. 3B, right). We considered two hypotheses about why P cells would not become item specific with learning: P cells might not develop specificity for an item because they lack the reward asymmetry seen in behavior-selective cells (Fig. 3B). Alternatively, P cells might not follow the plasticity rules because they do not receive inputs about the stimuli and/or reward. We tested these hypotheses by adding a P-cell population into the model. P cells were modeled as not influencing the behavior, but they followed the same plasticity rules as Go and NoGo cells. We found that the model P-cell population does not develop item selectivity with learning (Fig. 7A), in accordance with experimental results. This is because, as expected, P cells fire at the same rate on correct and error trials following the sampling of either the rewarded or the nonrewarded item (Fig. 7B). Hence, the plasticity mechanisms act similarly in connections carrying inputs from either item. However, in this model P cells increase their firing rate to both items with learning (Fig. 7A). This nonselective increase occurs because correct responses are emitted more often following the sampling of either item after learning; hence, the model dictates that the reward-based plasticity should increase the synaptic connections from both items to the P cells (Fig. 7C). Since we did not observe such an increase in firing rates for P cells (Fig. 1C, right; Table 1), our results suggest that P cells are not subjected to the same plasticity effects as the IP cells, either because they do not receive item information, and/or because they do not receive reward signals.
Figure 7.
Model P cells do not develop item specificity with learning, but increase firing rates to both items. (A) Mean firing rate of model P cells before and after learning for the rewarded and nonrewarded item (left) and associated with Go and NoGo responses (right). (B) Mean firing rate of model P cells on correct and error trials for the rewarded and nonrewarded items during item sampling events occurring before learning. (C) Mean synaptic weights changes. Same simulations as in Figure 5.
Discussion
The present findings suggest that firing patterns associated with different behavioral responses leading to asymmetrical firing rates on rewarded and nonrewarded events could underlie the development of specific item-position coding. Current theories in reward-based reinforcement learning are compatible with these findings. In particular, the influence of reward in shaping neuronal activity has been well demonstrated by a number of studies (Huang and Kandel 1995; Okatan 2009). The required feedback of trial outcomes to the hippocampus may be provided by dopaminergic inputs. Indeed, activation of D1/D5 receptors can increase the duration of Schaffer collateral LTP in response to a stimulus (Huang and Kandel 1995) and, in turn, modulate place cell stability (Kentros et al. 2004). Of note, a recent study using monkeys reported the existence of hippocampal cells able to signal trial outcome (Wirth et al. 2009). Although their findings differ from ours because such cells were found following trial outcome, and not preceding it, they provide important evidence that the hippocampus has information about the trial outcome.
Our results are in accordance with previous reports showing that different hippocampal cells can code for different sensory and behavioral features of events (Ranck 1973; Berger et al. 1976; Wiener et al. 1989; Wood et al. 1999). In our data set, we found that early in training some cells did not present spatial coding, other cells exhibited pure spatial coding, while others coded for both position and behavioral responses. Cells of the latter type also came to code for a specific item in parallel with behavioral learning, thus becoming IP cells. On the other hand, cells that presented pure position coding during the first trials remained only position selective throughout the learning session, and were thus denoted as P cells. Since P cells did not present behavioral bias, they lacked the reward asymmetry (see Fig. 3B) required by our model for the emergence of item coding. It remains to be established why and how different cells are endowed with different coding properties (more below).
We showed that a simple model of reward-dependent synaptic plasticity is able to account for the development of item specificity by cells whose activity correlates with the behavioral response emitted. Importantly, animals are not rewarded for correct or erroneous NoGo responses, so many sampling events are not followed by immediate feedback. Nevertheless, a correct NoGo response to the nonrewarded item in one position of the arena can lead to reward consumption at the end of the trial if the animal decides to dig the rewarded item located in the other position of the arena. In this case, we postulate that the same reward signal reinforces both the connections from the rewarded stimulus to the Go cells and from the nonrewarded stimulus to the NoGo cells. The requirement of changing synaptic weights after a cell is active (in this case, the NoGo cells) and the sensory stimuli are no longer present (in this case, the nonrewarded item) is a long standing problem in reinforcement-based learning theory, and has been called the “distal reward problem” (Izhikevich 2007) or “credit assignment problem” (Schultz et al. 1997; Sutton and Barto 1998; Jin et al. 2009). This problem is solved by some theories hypothesizing that under certain conditions some synapses would become “tagged” or “eligible” for subsequent modifications should reinforcement/punishment signals later arrive (Sutton and Barto 1998; Izhikevich 2007; Redondo and Morris 2011). The present model incorporates such a distal reward mechanism to explain the reinforcement (or punishment) of connections arriving at the NoGo cells.
The model assumes that neurons conveying information about the items project to the hippocampus, and, in particular, to Go and NoGo cells. This assumption is in accordance with a wealth of evidence showing that the hippocampus is indirectly connected to sensory areas in the cortex (Witter et al. 1989; Burwell et al. 1995; Burwell and Amaral 1998; Lavenex and Amaral 2000; Brown and Aggleton 2001; Pereira et al. 2007). Sensory information from multiple modalities and associational areas arrive at the hippocampus after a relay in postrhinal and perirhinal cortices and in the entorhinal cortex (Witter et al. 1989; Burwell et al. 1995; Burwell and Amaral 1998; Lavenex and Amaral 2000). The sensory information reaching the hippocampus is therefore already highly processed and likely to convey higher order attributes, such as those required for object identity, as postulated by the model.
In our model, two units (Go and NoGo cell populations) compete with one another through mutual inhibition, and only one unit wins the competition on each item-sampling event. This feature is similar to those used in competitive learning algorithms (Rumelhart and Zipser 1985; Grossberg 1987; McClelland and Rumelhart 1988); in fact, this part of our model can be regarded as a competitive learning network composed of a single cluster with two units. However, simple competitive learning networks cannot model our results, since the assignment of units in the cluster to the input patterns is a random process (i.e., the Go cell unit could be randomly assigned to the nonrewarded item). This is because competitive learning networks perform unsupervised learning, in which there is no feedback from the environment. The plasticity in our model, on the other hand, relies on error and reward signals, which are responsible for assigning each unit to the appropriate item. Therefore, in our model the assumption of mutual inhibition is required to set the winner of the competition (as in competitive learning), while feedback from the environment is required for allowing the plasticity to occur at the appropriate synapses (as in reinforcement learning).
We note that even though the model successfully accounts for the development of item selectivity, it does not explain all of the findings: In particular, the model predicts symmetric changes in firing rate of Go and NoGo cells (Figs. 5, 6A), which was not always observed experimentally (Figs. 1D, 6B). Thus, the firing rate of actual NoGo cells prior to the emission of NoGo responses does not increase as much with learning as the firing rate of actual Go cells prior to Go responses (Figs. 1D, 6B). Moreover, actual NoGo cells contradict the model's prediction of increased firing during samplings of the nonrewarded item prior to Go responses after learning (Fig. 6). The asymmetry of firing rate changes in actual Go and NoGo cells may be related to the different temporal proximity of reward following Go and NoGo responses: While reward immediately follows a correct Go response, reward consumption occurs a few seconds after a correct NoGo response. Therefore, the “synaptic eligibility trace” (Sutton and Barto 1998) would have a higher decay in NoGo than Go cells when reward signals arrive (see Izhikevich 2007), making the synaptic reinforcement less prominent in NoGo cells, which would account for the lack of symmetry in firing pattern changes between Go and NoGo cells. In accordance with this scenario, asymmetric changes in firing rates can be simulated by modification of the model to selectively reduce the magnitude of the synaptic plasticity after NoGo responses (data not shown).
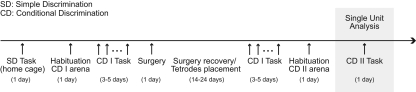
Although spatial coding (place cells) is considered a hallmark of hippocampal activity (O'Keefe and Dostrovsky 1971), there is also strong evidence that hippocampal neurons code for other types of information (Eichenbaum et al. 1999). Starting with Ranck (1973), several experiments have identified firing patterns of hippocampal neurons related to nonspatial stimuli, as well as cognitive and behavioral events (Ranck 1973; Berger et al. 1976; Wiener et al. 1989; Wood et al. 1999). Among the clearest of these are single hippocampal neurons that fire predicting eye-blink responses in a classical conditioning paradigm (Berger et al. 1983). A more recent striking example is hippocampal neurons that code for a “jump” response in a conditioned avoidance task (Lenck-Santini et al. 2008). Hippocampal neurons that fire associated with specific behavioral actions were also recently reported in humans (Mukamel et al. 2010). These previous results are consistent with our current findings that identified hippocampal neurons whose activity predict Go and NoGo behavioral responses. It is yet to be determined, however, whether these behavioral correlates pre-exist, develop during training before the implantation surgery (see Fig. 8; Materials and Methods), or develop exceedingly quickly early in learning the item-context problem analyzed here. Moreover, it also remains to be determined whether the behavioral selectivity is originated from place field representations, which are likely formed during context habituation (Fig. 8). Regardless of the source of these initial behavioral correlates, these findings and others suggest that hippocampal cells code for the conjunction of “what,” “where,” and “what to do.”
Figure 8.
Experimental timeline.
In summary, the present results suggest mechanisms underlying the emergence of neural coding for specific what–where representations. The proposed mechanisms are based on a combination of asymmetric initial conditions that vary among cells and are consequences of behavioral biases, while the animal was at chance performance, along with simple plasticity rules dependent on the presence or absence of reward following the animal's response. Such mechanisms could also be responsible for the formation of a range of firing specificities observed in neurons in higher order areas of the brain.
Materials and Methods
Training and data acquisition
Behavioral training and electrophysiology recording methods are described in full detail in Komorowski et al. (2009). Figure 8 shows the experimental timeline. Briefly, six male Long-Evans rats weighing 400–450 g were maintained at a minimum of 85% of normal body weight. Rats first learned to dig in 10-cm-tall, 11-cm-wide terra cotta pots filled with common playground sand for one-quarter Froot Loop (Kellogg's) pieces. Next, animals were trained on a simple discrimination between two pots filled with sand and scented with different oil fragrances (aloe vs. clove) placed side by side simultaneously in the home cage. The positions of the two stimuli were pseudorandomized, although they were never located in the same positions on more than three consecutive trials. The rat could dig in the aloe-scented pot for one-quarter of a Froot Loop, but digging in the clove-scented pot resulted in a 5-sec timeout. Rats achieved a performance criterion of eight correct of 10 consecutive trials in this simple discrimination task within a single session.
During the next days, rats were then trained on a first conditional discrimination task in a two-sided arena (each side is referred to as a context) (Fig. 1A). A detailed description of this task is provided in the next section. Briefly, rats should learn which of two stimuli (or items) is the correct choice depending on in which context they are located. The items were scented pots as in the simple discrimination task; the same two items were used in each trial, which occurred in one of the two contexts in a pseudorandom order. Rats learned this first conditional discrimination task in 3–5 d (∼80 trials per day).
After reaching the performance criterion, rats were implanted with a recording headstage above the left dorsal hippocampus centered at +3.6 mm posterior and +2.9 mm lateral to bregma. The headstage contained 12–18 independently movable tetrodes aimed at CA1 and CA3. Each tetrode was composed of four 12.5-μm nichrome wires with the tips plated with gold to bring the impedance to 200 kΩ at 1 kHz. Animals recovered for 7–10 d, after which the tetrodes were moved down slowly over the course of 1–2 wk, until the tips reached the pyramidal cell layer of CA1 or CA3. The locations of these tetrodes was estimated in vivo using driver turn counts to determine electrode depth as well as electrophysiological events, including the appearance of complex spikes, θ modulated spiking, as well as the presence of θ and high-frequency ripples in the local field potentials. Electrode location was confirmed by passing a 25-µA current for 20 sec through each tetrode immediately before perfusion to create a lesion visible after histological processing with Nissl stain.
After surgery and placement of tetrodes, rats continued to perform the first conditional discrimination task (Fig. 8) until their performance had exceeded 80% for three consecutive previous days. Finally, the animals were introduced to a novel arena with the same general configuration, but with new flooring and new wallpaper defining each context. After habituation to this environment (15–20 min), animals were tested on a second conditional discrimination problem using pots with new scented oils and digging media. Rats learned this second conditional discrimination task within a single recording session (Fig. 1B). All results shown in the present work were obtained from the analysis of this latter learning session.
During all recording sessions, spike activity was amplified (10,000×), filtered (600–6000 Hz), and saved for offline analysis using the software Spike (written by Loren Frank, University of California, San Francisco). Single-unit waveforms recorded from each tetrode during a ∼2-h recording session were isolated offline and determined to be stable through their clustering as identified using three-dimension projections of spike peak, valley, principal components, and timestamps using Offline Sorter software (Plexon). Thus, neuronal waveforms fit the same cluster parameters in the first, middle, and last 30 trial blocks. In addition, behavior was recorded with digital video (30 frames/sec) that was synchronized with the acquisition of neural data. The animal's location was tracked with one or two light-emitting diodes located on the recording head stages. The onset of stimulus (or item) sampling was defined by scanning the video and manually marking the frame on which the rat's nose crossed the rim of the pot; this timestamp corresponds to time 0 in the peri-event histograms shown in Figure 2. Mean spike frequencies shown in Figures 1, 3, and 6 were calculated during the stimulus-sampling period, which was defined from 0 to 1 sec following the onset of stimulus sampling. Rare cases of stimulus sampling events occurring <1 sec apart were excluded from the analysis. Timestamps for the onset of stimulus sampling and for spikes were imported into MATLAB for subsequent data analyses. The results reported here were obtained from the data of the same five rats investigated in Komorowski et al. (2009), plus one additional animal.
Conditional discrimination task
The environment consisted of two 37 × 37 cm boxes connected by a central alley that allowed the rat to shuttle between them (Fig. 1A). Before the task, rats were first habituated to the environment for 15–20 min and were allowed to forage for scattered food on the floor. The entrance to the central alley could be closed with dividers at each end of the alley to block the animal within either box. Each box differed substantially in contextual cues, which included different flooring (wood vs. black paper) and different wallpaper (white paper vs. black paper). Rats were trained to alternate between the two contexts by traversing the central alleyway when the dividers were lifted. On each trial of the conditional discrimination task, the rat was allowed to enter a context, after which a divider would close, and the animal was permitted to explore the contextual cues for 40 sec (Fig. 1A). The animal was then blocked within one side of the context using another divider and two items were placed in different corners of the context. In this work, each of the four possible corners (two per context) is referred to as a “position.” Both items were common terra cotta flowerpots, each scented with a different odor (e.g., grapefruit and geranium) and filled with a different digging media (e.g., white foam and purple beads). The positions of the items were pseudo-randomized such that they appeared in each position equally, but never in the same position on more than three consecutive trials. In Context A, Item X (i.e., grapefruit-white foam) would contain the Froot Loop reward, whereas in Context B, Item Y (i.e., geranium-purple beads) would contain the reward. Notice that while there is one correct item per context, there are two rewarded and two nonrewarded item-position combinations associated to each context (e.g., item X in either position [top or bottom left corner] of Context A is a rewarded item-position combination). Digging in the correct pot yielded the buried reward, but digging in the incorrect pot resulted in the removal of both pots and a 5-sec time-out. The next trial immediately followed the previous one.
Data analysis
All analyses were done with built-in and custom-written routines in MATLAB. The identification of IP cells was based on a significant interaction (P < 0.05) between item and position during the last 30 trials of the session, as assessed by ANOVA. As in our previous study (Komorowski et al. 2009), we did not find differences in the firing patterns of CA1 and CA3 neurons, which were therefore combined for the analyses. A total of 22 IP cells was found across all animals (n = 6). A total of 12 IP cells showed item selectivity in only one position, eight IP cells showed item selectivity in two positions, one IP cell showed item-selectivity in three positions, and one IP cell showed item selectivity in all four positions. Nine IP cells coded for the rewarded item, and nine IP cells coded for the nonrewarded item. Four IP cells coded for the rewarded item in one position, and for the nonrewarded item in another position. A total of 23 P cells were identified. Table 2 depicts the distribution of cells in each animal.
Table 2.
Cell distribution
The spiking data from all IP cells were pooled; the bar graphs shown in the figures represent mean spiking frequency ±SEM over individual item sampling events across all cells of the relevant type in each panel (e.g., in Figs. 1C,D and 3B, the left panel was obtained from the pool of 22 IP cells, the middle panels from the pool of 13 IP cells, the right panel from the pool of 23 P cells). The number of item samplings events in each pool is displayed in the figures. In Table 1 we show that our main result holds when analyzing the mean spike frequency over each cell activity.
Computational model
The model simulates the appearance of item coding on top of an already existent position coding. The model is phenomenological and based on a competition between two cell populations for action selection. One cell population codes for a “dig” action (Go cells), whereas the other population codes for a “withhold digging” action (NoGo cells). Notice, therefore, that the position selectivity and the selectivity for a behavioral response are assumed from the start and their development is not explicitly modeled (see Discussion). We modeled only one context and one position. We assume that this position corresponds to a position where the cell is active (i.e., a “preferred position”) (see Table 1). As cells were typically not active in their “nonpreferred positions” (Table 1), no plasticity effects would occur in these locations (see plasticity rules below). Therefore, there is no loss of generality in modeling just one position. In cases of cells that are active in more than one position, we assume that the development of item coding in each position is independent from each other and can be treated separately.
The rewarded item was chosen to be X, so that there was only one rewarded (X) and one nonrewarded (Y) stimulus in the model. All model equations are described in detail in the Results section (see also Fig. 4 for a model scheme). Briefly, we assume that Go and NoGo cells receive sensory inputs carrying information about each stimulus. These connections start with the same strength in both cell populations, but are subjected to plasticity depending on trial outcome. On each item-sampling event, Go and NoGo cells compete with each other, and one population is able to suppress the other and drive behavior. The competition is modeled as a random process with probability dependent on the relative synaptic weights from the stimulus afferents to the cells. Although we do not explicitly model the network mechanism underlying the competition between Go and NoGo cells, we think of it as being mediated by inhibition. We speculate that the specific pattern of network connections leading to the reciprocal inhibition between Go and NoGo cell populations emerges during training prior to surgery (see Fig. 8). On each simulated trial, we assume that the cell population that is most active recruits a pool of interneurons and inhibits the other cell population by feedforward lateral inhibition. Therefore, the stronger the synaptic connections from a stimulus to a given cell population relative to the other, the higher the chance of this cell population to determine the behavioral response to that stimulus. Of note, there is evidence to suggest that “winner-takes all” processes of this kind exist in the hippocampus (Klausberger and Somogyi 2008; Klausberger 2009). If Go cells win the competition, we consider that the rat digs the sampled item. If NoGo cells win the competition, it is assumed that the rat digs the other item in the other position of the context (not explicitly modeled). Note, therefore, that NoGo actions can also lead to (delayed) reward signals (see also Discussion). Synaptic plasticity is modeled to occur following trial termination depending on the presence or absence of reward and is proportional to the firing rate of the cells during item sampling. In a practical way, this means that only connections to the cells that determined behavior (which fired at increased rate and suppressed the others) are subjected to major plasticity effects. Therefore, upon trial termination, the presence of reward leads to reinforcement between afferent connections carrying stimulus information and the population that determined the behavioral response for that stimulus, while the absence of reward decreases the strength of these synapses.
The model was implemented in MATLAB. We assumed that the synaptic weights (W) saturate at 5. We used as initial conditions W = 2.5 for Go/NoGo cells, and W = 3.5 for P cells. Model parameters were δ = 0.02, εsuppression = 0.5, εgain = 1.5. See the Results section for model equations.
Acknowledgments
This work was supported by National Institutes of Health/National Institute of Mental Health Grants (MH051570 and MH71702 to H.E.) and Conselho Nacional de Desenvolvimento Científico e Tecnológico, Brazil (to A.B.L.T.).
Footnotes
During the writing of this work, it came to our attention that a very similar model of decision-making based on a sigmoidal probability curve also dependent on synaptic weights was used before in Fusi et al. (2007).
References
- Berger TW, Alger B, Thompson RF 1976. Neuronal substrate of classical conditioning in the hippocampus. Science 192: 483–485 [DOI] [PubMed] [Google Scholar]
- Berger TW, Rinaldi PC, Weisz DJ, Thompson RF 1983. Single-unit analysis of different hippocampal cell types during classical conditioning of rabbit nictitating membrane response. J Neurophysiol 50: 1197–1219 [DOI] [PubMed] [Google Scholar]
- Brown MW, Aggleton JP 2001. Recognition memory: What are the roles of the perirhinal cortex and hippocampus? Nat Rev Neurosci 2: 51–61 [DOI] [PubMed] [Google Scholar]
- Burwell RD, Amaral DG 1998. Cortical afferents of the perirhinal, postrhinal, and entorhinal cortices of the rat. J Comp Neurol 398: 179–205 [DOI] [PubMed] [Google Scholar]
- Burwell RD, Witter MP, Amaral DG 1995. Perirhinal and postrhinal cortices of the rat: A review of the neuroanatomical literature and comparison with findings from the monkey brain. Hippocampus 5: 390–408 [DOI] [PubMed] [Google Scholar]
- Eichenbaum H 2000. A cortical-hippocampal system for declarative memory. Nat Rev Neurosci 1: 41–50 [DOI] [PubMed] [Google Scholar]
- Eichenbaum H, Dudchenko P, Wood E, Shapiro M, Tanila H 1999. The hippocampus, memory, and place cells: Is it spatial memory or a memory space? Neuron 23: 209–226 [DOI] [PubMed] [Google Scholar]
- Eichenbaum H, Yonelinas AP, Ranganath C 2007. The medial temporal lobe and recognition memory. Annu Rev Neurosci 30: 123–152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fusi S, Asaad WF, Miller EK, Wang XJ 2007. A neural circuit model of flexible sensorimotor mapping: Learning and forgetting on multiple timescales. Neuron 54: 319–333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossberg S 1987. Competitive learning: From interactive activation to adaptive resonance. Cognitive Science 11: 23–63 [Google Scholar]
- Huang YY, Kandel ER 1995. D1/D5 receptor agonists induce a protein synthesis-dependent late potentiation in the CA1 region of the hippocampus. Proc Natl Acad Sci 92: 2446–2450 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM 2007. Solving the distal reward problem through linkage of STDP and dopamine signaling. Cereb Cortex 17: 2443–2452 [DOI] [PubMed] [Google Scholar]
- Jin DZ, Fujii N, Graybiel AM 2009. Neural representation of time in cortico-basal ganglia circuits. Proc Natl Acad Sci 106: 19156–19161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kentros CG, Agnihotri NT, Streater S, Hawkins RD, Kandel ER 2004. Increased attention to spatial context increases both place field stability and spatial memory. Neuron 42: 283–295 [DOI] [PubMed] [Google Scholar]
- Klausberger T 2009. GABAergic interneurons targeting dendrites of pyramidal cells in the CA1 area of the hippocampus. Eur J Neurosci 30: 947–957 [DOI] [PubMed] [Google Scholar]
- Klausberger T, Somogyi P 2008. Neuronal diversity and temporal dynamics: The unity of hippocampal circuit operations. Science 321: 53–57 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komorowski RW, Manns JR, Eichenbaum H 2009. Robust conjunctive item-place coding by hippocampal neurons parallels learning what happens where. J Neurosci 29: 9918–9929 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavenex P, Amaral DG 2000. Hippocampal-neocortical interaction: A hierarchy of associativity. Hippocampus 10: 420–430 [DOI] [PubMed] [Google Scholar]
- Lenck-Santini PP, Fenton AA, Muller RU 2008. Discharge properties of hippocampal neurons during performance of a jump avoidance task. J Neurosci 28: 6773–6786 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manns JR, Eichenbaum H 2006. Evolution of declarative memory. Hippocampus 16: 795–808 [DOI] [PubMed] [Google Scholar]
- Manns JR, Eichenbaum H 2009. A cognitive map for object memory in the hippocampus. Learn Mem 16: 616–624 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClelland JL, Rumelhart DE 1988. Explorations in parallel distributed processing: A handbook of models, programs, and exercises. MIT Press, Cambridge, MA [Google Scholar]
- Mukamel R, Ekstrom AD, Kaplan J, Iacoboni M, Fried I 2010. Single-neuron responses in humans during execution and observation of actions. Curr Biol 20: 750–756 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okatan M 2009. Correlates of reward-predictive value in learning-related hippocampal neural activity. Hippocampus 19: 487–506 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Keefe J, Dostrovsky J 1971. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res 34: 171–175 [DOI] [PubMed] [Google Scholar]
- Pereira A, Ribeiro S, Wiest M, Moore LC, Pantoja J, Lin SC, Nicolelis MA 2007. Processing of tactile information by the hippocampus. Proc Natl Acad Sci 104: 18286–18291 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajji T, Chapman D, Eichenbaum H, Greene R 2006. The role of CA3 hippocampal NMDA receptors in paired associate learning. J Neurosci 26: 908–915 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranck JB Jr 1973. Studies on single neurons in dorsal hippocampal formation and septum in unrestrained rats. I. Behavioral correlates and firing repertoires. Exp Neurol 41: 461–531 [DOI] [PubMed] [Google Scholar]
- Redondo R, Morris R 2011. Making memories last: The synaptic tagging and capture hypothesis. Nat Rev Neurosci 12: 17–30 [DOI] [PubMed] [Google Scholar]
- Rumelhart DE, Zipser D 1985. Feature discovery by competitive learning. Cognitive Science 9: 75–112 [Google Scholar]
- Schultz W, Dayan P, Montague PR 1997. A neural substrate of prediction and reward. Science 275: 1593–1599 [DOI] [PubMed] [Google Scholar]
- Scoville WB, Milner B 1957. Loss of recent memory after bilateral hippocampal lesions. J Neurol Neurosurg Psychiatry 20: 11–21 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton RS, Barto AG 1998. Reinforcement learning: an introduction. The MIT Press, Cambridge, MA [Google Scholar]
- Wiener SI, Paul CA, Eichenbaum H 1989. Spatial and behavioral correlates of hippocampal neuronal activity. J Neurosci 9: 2737–2763 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wirth S, Avsar E, Chiu CC, Sharma V, Smith AC, Brown E, Suzuki WA 2009. Trial outcome and associative learning signals in the monkey hippocampus. Neuron 61: 930–940 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witter MP, Groenewegen HJ, Lopes da Silva FH, Lohman AH 1989. Functional organization of the extrinsic and intrinsic circuitry of the parahippocampal region. Prog Neurobiol 33: 161–253 [DOI] [PubMed] [Google Scholar]
- Wood ER, Dudchenko PA, Eichenbaum H 1999. The global record of memory in hippocampal neuronal activity. Nature 397: 613–616 [DOI] [PubMed] [Google Scholar]