Abstract
Models of Response to Intervention (RTI) include parameters of assessment and instruction. This study focuses on assessment with the purpose of developing a screening battery that validly and efficiently identifies first-grade children at risk for reading problems. In an RTI model, these children would be candidates for early intervention. We examined accuracy, fluency, growth, and teacher rating measures as predictors of child status (at risk, not at risk) at the end of the school year based on an unselected sample of 243 children. The prediction model that best fit our selection criteria included 2-word fluency measures and a teacher rating of reading problems. Word-fluency growth was an equally plausible choice statistically, but, because the measure would require an additional data point, it was not the most efficient choice. The receiver-operator characteristic curve analysis yielded an area-under-the-curve index of .96, which indicates the selected 3-variable model is highly accurate.
The most current reauthorization of the Individuals with Disabilities Education Improvement Act (IDEIA, 2004) allows for the incorporation of Response to Intervention (RTI) to identify children with specific learning disabilities. This approach may be used instead of a discrepancy model in which students’ scores on intelligence and achievement tests are compared. The typical RTI model includes three to four stages, or tiers, of assessment and instruction. In the domain of reading, Tier 1 usually involves (a) universal screening (i.e., screening of all students) to identify those at risk for reading problems, (b) general education instruction that is founded on scientifically based reading research, and (c) progress monitoring to identify any students who are not growing in reading skills at an expected rate (Berkeley, Bender, Peaster, & Saunders, 2009; McKenzie, 2009; Shinn, 2007). Students who are at risk for reading problems and do not show a positive response to general education instruction, including growth at expected rates, are selected to receive increasingly intense and focused instruction in subsequent tiers.
Although many school districts are already using RTI as a means to identify and provide services to at-risk children, there is limited research on fully implementing each stage of RTI. Most work focuses on children’s response to specific supplemental instruction (i.e., Tier 2) and intensive intervention (i.e., Tier 3) protocols primarily in the domain of reading (e.g., Fuchs, Compton, Fuchs, Bryant, & Davis, 2008; Hatcher et al., 2006; Ryder, Tunmer, & Greaney, 2008). There is considerably less work on assessment, especially assessment batteries used for universal screening. The focus of this article is on the development and evaluation of a universal screening battery that may be effective in the identification of first-grade children at risk for reading problems. The importance of early identification is elevated due to the explosion of scientific evidence on successful intervention methods for young, normally developing readers and children who struggle in the initial stages of reading development (e.g., Fuchs et al., 2001; Hatcher, Hulme, & Ellis, 1994; Torgesen et al., 1999). Given validated methods of addressing early reading problems, it becomes critical to develop procedures that identify children who will benefit from intervention.
Essential Characteristics of Universal Screening
Two essential characteristics of universal screening are efficiency and validity. To assess all children, a screening battery must be quick and easy to administer (i.e., efficiency). Given that instructional time is a precious commodity, screening batteries must minimize the amount of time for children’s screening as opposed to instruction. It also must measure the critical variables and have high classification accuracy (i.e., validity). High classification accuracy results when the screen identifies most of the children who would ultimately experience a reading problem (true positive cases). Over identification (false positive cases) and under identification (false negative cases) are classification errors that work against accuracy. The implications of both types of errors need consideration. False positive errors result in providing additional services to children who ultimately will not experience problems, whereas false negative errors result in not providing services to children who will experience reading difficulties. The decision on which error is more acceptable is often based on available resources: how many children can be served?
Early identification efforts often target kindergarten as the screening window from which to predict reading failure in later years, but screening this early results in many classification errors (Scarborough, 1998). Classification accuracy is improved considerably when screening occurs at the beginning of first grade (e.g., O’Connor & Jenkins, 1999), but even in first grade the accuracy of screening measures has not been ideal. For example, O’Connor and Jenkins reported 0% false negatives and 70% false positives for their briefest battery (35 min.) in fall of first grade, and .01% false negatives and 47% false positives for their longest fall battery (50–65 min.). The improvement in the false positive rate, while still high, comes at the cost of doubling assessment time. Compton, Fuchs, Fuchs, and Bryant (2006), predicting from the beginning of first grade to the end of second grade, identified a promising screening battery that produced 10%–13.6% false negative cases and 17.2%–17.3% false positive cases, depending on how poor reading was defined at the end of second grade, based on logistic regression results.
It is likely that first-grade screening may be more accurate than kindergarten screening, because in first grade children are beginning to exhibit behaviors more proximal to word and connected-text reading (i.e., phonological, phonetic, and orthographic skills) and these behaviors can be reliably measured (Fuchs, Fuchs, & Compton, 2004). An abundance of correlational and experimental evidence demonstrates strong relationships between word reading and phonological awareness (segmentation and blending), sublexical units (letter names, letter sounds, digraphs, rimes), orthography (pseudowords, real words, spellings), and vocabulary (e.g., Catts, Fey, Zhang, & Tomblin, 1999; Compton, 2000, 2003; Ehri & Soffer, 1999; Pennington & Lefly, 2001; Riedel, 2007). Although most early screening batteries rely on test performance, we included the perspective that teacher ratings also provide valuable information. For example, children’s attention to task- and work-related behaviors predicts achievement and response to intervention (e.g., Gijsel, Bosman,& Verhoeven, 2006; McKinney, Mason, Perkerson, & Clifford, 1975; Stage, Abbott, Jenkins, & Berninger, 2003; Torgesen, Wagner, Rashotte, Rose, et al., 1999).
Thus, a screening battery might comprise measures of sublexical, word, and language skills as well as teacher ratings of children’s skills. Despite strong relationships with reading, questions about the measurement of these skills remain. For example, should accuracy (untimed) or fluency (timed) measures of these skills be used? Are measures of growth in these skills over time important? Do teachers’ evaluations of the skills add to the prediction of reading problems? For the sake of efficiency, fluency measures would be preferable to accuracy measures; growth measures, which require additional assessment time points, would be unfavorable; and teacher ratings, which do not require any child assessment time, would be advantageous. However, efficiency must be balanced against validity. A discussion of accuracy and fluency measures, growth, and teacher ratings follows.
Accuracy and Fluency Measures
Previous research on screening batteries relied on measures of children’s accuracy in reading skills (e.g., Foorman et al., 1998). In accuracy measures, the number of items correct is the variable under consideration. The resurgence of theoretical and empirical interest in word and passage reading fluency and its connection to comprehension (e.g., Kame’enui & Simmons, 2001; National Reading Panel, 2000) has led to research using fluency measures of various aspects of reading in screening. In these measures, the number of items correct in a limited time frame (e.g., a minute) is the variable of concern. These measures assess accuracy and rate. From the perspective of practice, many schools nationwide have adopted Dynamic Indicators of Basic Early Literacy Skills (DIBELS, 2001; Good, Simmons, & Kame’enui, 2001), which are fluency-based measures of phonological, decoding, and text reading skills derived from curriculum-based measurement research (Deno, 1985). Thus, fluency measures have become a part of the early reading assessment landscape for creating benchmarks and evaluating progress.
Screening research focused only on fluency measures in first grade has not yielded desirable accuracy indexes (Jenkins, Hudson, & Johnson, 2007; Johnson, Jenkins, Petschur, & Catts, 2009; Riedel, 2007). Recently, the National Center on Response to Intervention (2011) posted evaluations of a number of screening instruments. Of the 14 reading or related tools, only four were rated as providing “convincing evidence” on classification accuracy. The positive results obtained by Compton et al. (2006) at the end of second grade cited earlier were based on language measures as well as word fluency. Ritchey and Speece (2006) found different roles for accuracy and fluency measures in kindergarten. For example, an accuracy measure of phonemic awareness was a unique predictor of word reading, but its fluency counterpart was not. However, both measures were unique predictors of spelling skill, as was letter-sound accuracy and growth in letter-sound fluency. The authors suggested that, for word reading, young children need to gain the insight that words are composed of sounds, but the speed with which they could do so was not relevant. On the other hand, accurate spelling requires not just accurate but also rapid access to both phonemes and letter sounds. Thus, accuracy and fluency measures may have different yet equally important roles to play in early identification, and need to be compared in the same battery of measures. To investigate this possibility, accuracy measures can be supplemented with curriculum-based measures (CBM) that are designed to measure fluency at text, word, and sublexical levels with brief (1 to 2 min.) probes and that have demonstrated reliability and validity (Deno, 1985; Fuchs & Fuchs, 1998; Marston, 1989). CBM measures are sensitive to child growth, can be administered repeatedly, do not exhibit ceiling effects, and tap a theoretically important aspect of literacy development—fluency (Kame’enui & Simmons, 2001; LaBerge & Samuels, 1974; Logan, 1988, 1997). These well-developed procedures provide an avenue to explore the relative importance of fluency in early identification in conjunction with accuracy measures.
Growth
With respect to growth, there is accumulating evidence that measures of learning over time may be a key to early identification efforts (Byrne, Fielding-Barnsley, & Ashley, 2000; Compton et al., 2006; Deno, Fuchs, Marston, & Shin, 2001; Speece & Case, 2001). Growth in RTI contexts generally refers to children’s performance over time in relation to instruction, so the use of growth as a screening measure is a relatively novel application. Byrne et al. (2000) reported that the number of phonological awareness training sessions needed by preschoolers to demonstrate perfect performance differentiated disabled and nondisabled readers in elementary school and contributed significant unique variance (8% to 21%) to fifth-grade literacy performance beyond the contribution of phonological awareness. Deno et al. (2001) found that first-grade students in general education demonstrated more than twice the growth in oral reading fluency compared to their counterparts in special education; this discrepancy held when intercepts were controlled. More recently, Compton et al. (2006) demonstrated improvement in accurate identification from first to second grade by including growth in word reading fluency. These findings suggest that screening batteries may be improved by capturing children’s response to classroom instruction. We know that children grow over time; the important issue is whether the amount of growth predicts future reading status. Indexing growth through multiple measurements may improve screening precision compared to single-point estimates. The trade-off is in efficiency. Growth estimates require at least two data points, necessitating more cost and time in identifying children who are at risk.
Teacher Ratings
Other variables that may be important for prediction of academic achievement include teacher ratings of student behavior and academic achievement (DiPerna & Elliott, 1999; DuPaul et al., 2004; Taylor, Anselmo, Foreman, Schatschneider, & Angelopoulos, 2000). For example, Stage et al. (2003) showed that ratings of children’s attention to task and work-related behaviors predict achievement and response to intervention. Furthermore, Speece and Ritchey (2005) reported that ratings of academic competence uniquely predicted end-of-year reading skill in a multivariate model that included reading, reading-related variables, and intelligence. More recently, Speece et al. (2010) found that teacher ratings of reading problems were a significant predictor of at-risk status in fourth-grade children. Teacher ratings may add to predictive validity because teachers have intimate knowledge of children’s reading behaviors that may not be captured in discrete measures of accuracy, fluency, or growth. Teacher ratings are efficient in that they do not take any instructional time away from children and can likely be completed in less time than required of individual assessments.
Defining At-Risk Status
Finding the most efficient and valid screening battery hinges on the critical issue of how a potential reading problem is defined. One approach is to simply choose a cut point on a single measure or on separate multiple measures (e.g., 1 standard deviation below the mean or below the 30th percentile on a word-identification task and a word-attack task) and declare that any children who are below that cut point have a reading problem (e.g., Nelson, 2008; Riedel, 2007; Torgesen, 2000). Measures used for cut points typically have national norms, so the cut point is based on means and standard deviations generalizable to the nation’s schoolchildren. Another approach to defining a reading problem is to use factor scores derived from multiple measures and then determine a cut point to identify children with reading problems. The former method is easier to reproduce in practice, but the latter may be more desirable because it takes into account how children do on a combination of measures weighted for their importance rather than single or multiple measures used separately to define a reading problem. Other methods in use rely on local or sample test norms to define cut-off scores on level, slope, or both (e.g., Fuchs et al., 2004; McMaster, Fuchs, Fuchs, & Compton, 2005; Speece & Case, 2001). These methods typically use curriculum-based measures that are not nationally normed in the same manner as commercial products.
Present Study
The purpose of the present study was to identify an efficient and valid screening battery that could be used for universal screening within an RTI framework for first-grade children. We focused on two research questions that remain unanswered in the screening literature: (a) Within each type of measure (accuracy, fluency, teacher ratings, growth), which variables capture the most variance in predicting reading status (i.e., at risk vs. not at risk) at the end of the school year? and (b) When the best predictors from each group are combined, what is the best final set of predictors in predicting reading status? We used factor analysis of multiple measures of reading to determine our criterion for reading problems and logistic regression to model risk of reading problems.
Method
Participants
The sample included 257 first-grade children from 11 parochial schools and 16 classrooms located in a major mid-Atlantic city and nearby suburban communities. All first-grade students (N = 367) attending the participating schools were invited to join the investigation via parent letter and permission form; 70% of the parents granted permission. School size ranged from 166 to 715 students with a median of 483 students. Only children with complete data were included in the analysis, resulting in a sample of 243 children. The median percentage of children eligible for free and reduced-price meals at the school level was 5% (ranging from 0% to 75%).
The analysis sample included 114 female (47%) and 129 male (53%) children with a mean age of 6.56 years (SD = .32) prior to the beginning of data collection. Parents reported students’ race and/or ethnicity. Nearly 80% of the sample was Caucasian, 7% African American, 7% Asian, 3% Hispanic, and less than 1% American Indian, and approximately 2% reported more than one race. The majority of the students spoke English as their first language (96%). Schools provided data on the number of extra services provided to children (i.e., additional reading or math instruction, counseling, or speech/language instruction; or those who were referred for special education evaluation, had an individual education plan [IEP], and/or received other service). Of the 242 children on whom we had data, 22.7% received at least one service. Six children (2.5%) had an IEP, and eight children (3.3%) were referred for special education consideration. For mother’s level of education, less than 1% had no high school degree, 35% had a high school degree, 44% had a college degree, and 21% had graduate or professional training.
Measures
Students were individually tested with measures of sublexical, word-level, and language skills in four waves across the school year. Data from waves 1, 2, and 3 (fall/winter) were used to develop the screening battery. Growth variables were defined as the difference between wave 3 and wave 1 scores. Data from wave 4 (spring) were used to define the criterion for at-risk status. In addition to the student assessments, teachers completed ratings of reading, academic competence, social skills, and problem behaviors after November 1, which allowed teachers time to gain familiarity with the children’s skills.
Sublexical skills
Letter-Sound Fluency (LSF; Elliott, Lee, & Tollefson, 2001; Ritchey, 2002; Speece & Case, 2001)
LSF measures the number of correct letter sounds children identify in 1 minute. Lowercase letters are randomly arranged on a standard-size page, and students are required to give the sound of consonants (including either the hard or soft sound of c and g) and short vowels. The resulting score reflects the number of sounds correctly produced in 1 minute. Alternate-forms reliability (r = .82–.93) and predictive criterion-related validity (r = .58 –.75) with the Basic Reading Cluster score of the Woodcock Johnson Psychoeducational Battery—Revised (WJ-R; Woodcock & Johnson, 1989) is adequate (Elliott et al., 2001; Speece & Case, 2001).
Phonemic Segmentation Fluency (PSF; DIBELS, 2001)
This measure requires the child to segment an orally presented word into individual phonemes. The final score is the number of correct segments produced in 1 minute. Alternate-forms reliability (r = .60–.90; DIBELS, 2001; Kaminski & Good, 1996; Ritchey, 2002) and predictive and concurrent criterion-related validity with reading, spelling, and reading-related skills are adequate (r = .54 –.68; DIBELS, 2001; Kaminski & Good, 1996; Ritchey, 2002).
Graphophonemic Fluency (GPF; Speece, DaDeppo, Hines, & Walker, 2005)
GPF is a timed measure that evaluates phonetic skills. A graphophoneme is two or more letters representing one or more phonemes (e.g., ch, gr, ea); however, any actual words are excluded. The resulting list includes 66 graphophonemes that are randomly arranged on each probe. Two probes were administered, and the average number of graphophonemic units pronounced in 1 minute was used in analysis. Psychometric data show high test/retest/parallel forms reliability of .90 to .92. In addition, there is solid evidence for both concurrent validity (r = .72) with the Basic Skills Cluster score from the Woodcock Reading Mastery Test/Normative Update (WRMT/NU) and predictive validity (r = .79) with word-identification fluency.
Comprehensive Test of Phonological Processing (CTOPP; Wagner, Torgesen, & Rashotte, 1999)
The CTOPP Rapid Digit Naming subtest measures the speed with which students name six numbers randomly repeated 12 times in a visual array. The CTOPP Rapid Letter Naming subtest is identical; however, six letters are randomly displayed throughout the array. The resulting score for CTOPP Rapid Digit Naming and Rapid Letter Naming is the amount of time in seconds that students require to say the items on the page averaged over two probes. Reliability coefficients for alternate forms on Rapid Digit Naming and Rapid Letter Naming (r = .87 and .82) and test-retest (r = .91 and .97), respectively, demonstrate acceptable technical adequacy. There is established criterion-related validity with word-analysis and word-identification subtests of the WRMT-R (r = .66–.70).
Word-level skills
Test of Word Reading Efficiency (TOWRE; Torgesen, Wagner, & Rashotte, 1999)
The TOWRE is a norm-referenced measure that consists of two subtests. The Sight Word Efficiency (SWE) subtest comprises real words, and students are instructed to read as many words as possible during a 45-second time period. The Phonemic Decoding Efficiency (PDE) subtest requires students to decode nonsense words. The resulting raw score for each subtest is the number of words read correctly in 45 seconds. The authors report high alternate-form reliability (r ≥ .93) for both subtests. In addition, there is established concurrent validity for the PDE with the Word Attack subtest from the WRMT-R (r = .85) and the SWE with the Word Identification subtest of the WRMT-R (r = .87).
Woodcock Reading Mastery Test/Normative Update (WRMT/NU; Woodcock, 1998)
Two subtests were administered. The Word Attack subtest evaluates ability to decode nonsense words. The raw score is the number of words correctly decoded. The Word Identification subtest evaluates students’ ability to read printed words. The resulting raw score is based on the number of words read correctly. Woodcock (1998) used subtests from the Woodcock-Johnson Reading Tests, such as Word Comprehension (r = .77) and Passage Comprehension (r = .71), to establish concurrent validity with first-grade children. In addition, split-half reliability is .98 for first-grade children (Woodcock, 1998).
Word Identification Fluency (WIF)
To evaluate students’ speed and accuracy identifying printed words, two WIF probes (D. Compton, personal communication, 2003) were administered. Each probe consists of 50 words that are arranged in increasing difficulty. The raw score is the number of words read correctly in 1 minute. Speece et al. (2005) found high test-retest/parallel form reliability (r = .95) and strong validity (r = .85) with the WRMT-R Word Identification subtest.
Passage Reading Fluency (PRF; Fuchs, Hamlett, & Fuchs, 1990)
PRF is a CBM assessment that evaluates oral reading fluency in connected text. Children are given 1 minute to orally read a passage at the first-grade reading level and are given two probes. The raw score is the number of words students read accurately in 1 minute, averaged across two trials. There is high test-retest/alternate form reliability (r ≥ .90) and strong criterion-related validity from several studies (e.g., Deno, 1985; Fuchs & Fuchs, 1998; Marston, 1989).
Comprehensive Reading Assessment Battery (CRAB; Fuchs, Fuchs, & Hamlett, 1989)
Students read two 400-word folktales written at the 1.5 grade level during a 3-minute period and then answer 10 comprehension questions. The resulting scores are the average number of words read accurately per minute (fluency) and questions answered correctly (comprehension) during two trials. The fluency and comprehension scores show excellent test-retest reliability (r ≥ .90) and concurrent criterion-related validity of .91 to .92 with the Stanford Achievement Test (SAT) (Fuchs, Fuchs, & Maxwell, 1988).
Spelling Fluency (SF)
SF is a CBM assessment modified from the Word Spelling Test (WST; Deno, Mirkin, Lowry, & Kuehnle, 1980, as cited in Fuchs, Fuchs, Hamlett, & Allinder, 1991). Students are asked to spell a new word every 10 seconds for 2 minutes. The words are randomly drawn, with replacement, from the Harris-Jacobson grade-level list. The measure of interest is the mean number of correct letter sequences (CLS) per minute based on two trials. The WST has a strong test-retest reliability of .92 and criterion validity based on the PIAT-Spelling and the SAT-Spelling (r = .73 and .99, respectively).
Language skills
CTOPP Elision (Wagner et al., 1999)
The CTOPP Elision subtest is a norm-referenced assessment of phonological awareness that measures students’ ability to delete syllables and phonemes from an orally presented word and then to pronounce the resulting word. The raw score is made up of the number of sounds deleted correctly. Authors report test-retest reliability of .88 and strong criterion-related validity of .73 and .74 with the Word ID and Word Analysis subtests of the WRMT-R, respectively.
Woodcock-Johnson Psychoeducational Battery—Revised (WJ-R; Woodcock & Johnson, 1989; Woodcock & Mather, 1989, 1990)
The Oral Vocabulary–Synonyms and Antonyms subtest of the WJ-R was administered. This subtest assesses students’ ability to provide one-word synonyms and antonyms. The examiner displays a printed word in front of the student and states, “tell me another word for …” or “tell me the opposite of….” The two subtests consist of 20 synonyms and 24 antonyms; administration of each subtest is discontinued after four consecutive incorrect answers. Student responses are categorized as correct or incorrect, and the resulting number correct is used in analysis. Psychometric data show strong split-half reliability (r ≥ .90) and adequate construct validity for first-grade students.
Teacher ratings
The Social Skills Rating System—Teachers (SSRS; Gresham & Elliott, 1990)
Classroom teachers completed the Academic Competence (nine items), Social Skills Rating (30 items) and Problem Behavior Rating (18 items). Academic Competence is assessed through a 5-point Likert scale with questions regarding reading and math achievement, cognitive function, parental involvement, and level of motivation. Social Skills and Problem Behaviors items are evaluated on a 3-point Likert scale, and higher scores indicate less positive evaluations. The sum of items values for each subtest was used in data analysis. Test-rest reliability coefficients range from .84 to .93 for the three subtests. Criterion-related validity is supported, with correlations from .59 to .81 on another child behavior scale completed by teachers. Independent reviewers (Benes, 1995; Furlong & Karno, 1995) report high internal consistency (r ≥ .80) and strong criterion-related, construct, content, and social validity.
Reading Rating Form
Teachers rated students’ overall reading ability using a 5-point Likert scale (Reading Rating–Overall Rating, RROR) on this researcher-developed measure. A score of 1 or 2 represented performance below grade level, while scores of 3–5 indicated achievement at or above grade level. If a child received a rating of 1 or 2, teachers were asked to indicate a specific area or areas of reading difficulty (i.e., decoding, fluency, vocabulary, comprehension, and/or motivation). The sum of the number of problems checked produced a score for Reading Rating–Problems (RRPR). Concurrent validity with the current sample was established using reading measures (i.e., TOWRE SWE; WRMT Word ID and Word Attack). The validity coefficients range from .61 to .69 for the RROR and −.39 to −.50 for the RRPR.
Procedures
Data collection
As previously noted, data were obtained from four waves of testing during the academic year. The median dates for each wave were December 14, January 31, March 22, and May 9, respectively. To the extent possible, children were tested in the same order within wave to preserve spacing of approximately 6 weeks between assessment waves. Table 1 lists the measures administered by wave. Prior to beginning data collection, graduate research assistants were trained on all measures and met an accuracy criterion of 90% for administration and scoring. In addition, unannounced fidelity checks were conducted during each testing wave.
Table 1.
Tests Administered During the Longitudinal Investigation by Wave
| Wave 1 | Wave 2 | Wave 3 | Wave 4 | |
|---|---|---|---|---|
| CRAB (Comprehension) | ● | |||
| CRAB (Fluency) | ● | |||
| CTOPP Elision | ● | |||
| CTOPP Rapid Digits | ● | |||
| CTOPP Rapid Letters | ● | |||
| Graphophonemic Fluency | ● | ● | ● | |
| Letter-Sound Fluency | ● | ● | ● | |
| Passage Reading Fluency | ● | ● | ||
| Phonemic Segmentation Fluency | ● | ● | ● | |
| Reading Rating Form (Teachers) | ● | |||
| Spelling Fluency (CLS) | ● | ● | ● | |
| SSRS (Teachers) | ● | |||
| TOWRE Sight Word Efficiency | ● | |||
| TOWRE Phonemic Decoding Efficiency | ● | |||
| WIF | ● | ● | ● | |
| WJ-R Oral Vocabulary–Synonyms and Antonyms | ● | |||
| WRMT Word Attack | ● | ● | ||
| WRMT Word ID | ● | ● |
Note.—CTOPP = Comprehensive Test of Phonological Processing; CLS = Correct Letter Sequences; SSRS = Social Skills Rating System; TOWRE = Test of Word Reading Efficiency; WIF = Word Identification Fluency; WJ-R = Woodcock-Johnson Psychoeducational Battery—Revised; WRMT = Woodcock Reading Mastery Test; CRAB = Comprehensive Reading Assessment Battery.
Data analysis
There were several steps in the data analysis of this study. First, we needed to identify those students who exhibited poor reading performance at the end of first grade. The following measures of comprehension, word recognition, and decoding (collected at wave 4) were used to define the reading criterion: CRAB Fluency, CRAB Comprehension, WRMT Word Attack, WRMT Word Identification, SF, GPF, and WIF. These measures were subjected to an exploratory principal axis factor analysis to increase the reliability and reduce the number of criterion variables. Once the factors were estimated, we identified criteria for the factor scores, which were then used to classify students as at-risk or not-at-risk readers.
Measures used as predictor variables in the all-subsets regression analysis included assessments of reading and related skills (collected at waves 1 and 2), estimates of growth on several predictors (collected at wave 3), and teacher ratings. We recognized that large correlations among the predictor variables can have a serious impact on the standard errors and regression weights associated with each predictor in a regression model. Although our regression strategy of inspecting that total R2s of various models does not rely on the standard errors (and significance tests) of any of the predictors, we nevertheless used the variance inflation factor (VIF) as a diagnostic tool to see if multicollinearity was operating among our predictors in each of the five all-subsets regressions that were conducted. Using a rule of thumb of VIF greater than 10 as an indication that multicollinearity was a serious issue (Cohen, Cohen, West, and Aiken, 2003), we observed that none of the VIFs for the predictors in any of the models reached this level.
Four regressions were performed to identify the best accuracy (WRMT Word Attack and Word Identification, CTOPP Elision, WJ-R Oral Vocabulary), fluency (TOWRE SWE and PDE, GPF, PSF, LSF, SF, WIF, CTOPP Rapid Digits and Rapid Letters), growth (GPF, LSF, PSF, SF, WIF), and teacher ratings (SSRS Problem Behaviors, Social Skills, and Academic Competence, Reading Ratings–Overall, and Reading Ratings–Problems). The best predictors from these four analyses were then entered into another regression to identify the subset of the most efficient predictors. These predictors were used in a logistic regression model to assess the overall classification accuracy of these variables and the risk probability values associated with specific performances on the predictor variables.
Results
Descriptive Statistics
Table 2 provides sample descriptive statistics on all measures organized by criterion and predictor variables. This table also provides data by the at-risk and not-at-risk subgroups identified by our definition of the criterion described in the next section. Tables 3 and 4 provide correlations among the predictor and criterion variables, respectively.
Table 2.
Descriptive Statistics for Total Sample and by Reader Group
| Total Sample | Not-At-Risk Readers | At-Risk Readers | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | N | Mean | SD | N | Mean | SD | N | |
| Predictor measures: | |||||||||
| CTOPP Elision | 10.77 | 2.69 | 243 | 11.12 | 2.60 | 198 | 9.20 | 2.53 | 45 |
| CTOPP Rapid Digits–Time | 25.89 | 6.98 | 243 | 24.48 | 5.67 | 198 | 32.09 | 8.68 | 45 |
| CTOPP Rapid Letters–Time | 29.56 | 8.98 | 243 | 27.59 | 6.71 | 198 | 38.20 | 12.19 | 45 |
| Graphophonemic Fluency | 18.87 | 14.59 | 243 | 21.82 | 14.50 | 198 | 5.90 | 4.25 | 45 |
| Graphophonemic Fluency growth | 12.11 | 9.59 | 243 | 13.06 | 9.99 | 198 | 7.96 | 6.08 | 45 |
| Letter-Sound Fluency | 50.46 | 16.02 | 243 | 52.71 | 15.88 | 198 | 40.57 | 12.62 | 45 |
| Letter-Sound Fluency growth | 15.11 | 16.73 | 243 | 15.80 | 17.53 | 198 | 12.04 | 12.29 | 45 |
| Phonemic Segmentation Fluency | 33.78 | 13.60 | 243 | 34.45 | 13.06 | 198 | 30.80 | 15.56 | 45 |
| Phonemic Segmentation Fluency growth | 11.03 | 13.36 | 243 | 10.68 | 12.73 | 198 | 12.57 | 15.91 | 45 |
| Spelling (CLS) | 22.54 | 10.70 | 243 | 24.74 | 10.35 | 198 | 12.84 | 5.66 | 45 |
| Spelling (CLS) growth | 9.74 | 7.66 | 243 | 10.28 | 8.04 | 198 | 7.36 | 5.12 | 45 |
| SSRS Academic Competence | 95.71 | 10.85 | 243 | 98.24 | 9.91 | 198 | 84.60 | 7.30 | 45 |
| SSRS Problem Behaviors | 93.49 | 10.99 | 243 | 92.25 | 10.01 | 198 | 98.96 | 13.35 | 45 |
| SSRS Social Skills | 110.13 | 13.67 | 243 | 111.77 | 13.32 | 198 | 102.93 | 12.93 | 45 |
| Teacher Reading Rating (overall rating) | 3.25 | .96 | 243 | 3.48 | .84 | 198 | 2.24 | .80 | 45 |
| Teacher Reading Rating (total problems) | .62 | 1.39 | 243 | .27 | .91 | 198 | 2.18 | 1.95 | 45 |
| TOWRE Sight Word Efficiency | 106.86 | 12.58 | 243 | 109.87 | 11.35 | 198 | 93.58 | 8.49 | 45 |
| TOWRE Phonemic Decoding Efficiency | 107.27 | 10.66 | 243 | 109.06 | 10.29 | 198 | 99.38 | 8.58 | 45 |
| WJ-R Oral Vocabulary–Synonyms and Antonyms | 11.93 | 3.69 | 243 | 12.46 | 3.46 | 198 | 9.60 | 3.80 | 45 |
| Word ID Fluency | 24.77 | 23.78 | 243 | 28.94 | 24.47 | 198 | 6.46 | 2.97 | 45 |
| Word ID Fluency growth | 11.18 | 11.69 | 243 | 12.45 | 12.51 | 198 | 5.59 | 3.37 | 45 |
| WRMT Word Attack | 108.00 | 13.12 | 243 | 111.00 | 10.98 | 198 | 94.80 | 13.70 | 45 |
| WRMT Word ID | 110.94 | 10.27 | 243 | 113.67 | 8.50 | 198 | 98.93 | 8.68 | 45 |
| Criterion measures: | |||||||||
| CRAB Comprehension | 4.09 | 2.30 | 243 | 4.77 | 1.96 | 198 | 1.09 | .80 | 45 |
| CRAB Fluency | 68.37 | 36.65 | 243 | 78.93 | 32.05 | 198 | 21.91 | 8.82 | 45 |
| Graphophonemic Fluency | 35.64 | 17.46 | 243 | 40.34 | 15.64 | 198 | 14.99 | 6.85 | 45 |
| Passage Reading Fluency | 65.66 | 38.44 | 243 | 76.06 | 34.93 | 198 | 19.92 | 6.16 | 45 |
| Spelling (CLS) | 36.61 | 12.23 | 243 | 39.64 | 11.02 | 198 | 23.27 | 7.44 | 45 |
| Word ID Fluency | 48.33 | 27.54 | 243 | 55.63 | 25.22 | 198 | 16.22 | 5.55 | 45 |
| WRMT Word Attack | 110.60 | 11.83 | 243 | 113.78 | 9.68 | 198 | 96.64 | 10.32 | 45 |
| WRMT Word ID | 110.84 | 8.94 | 243 | 113.54 | 7.06 | 198 | 98.98 | 6.32 | 45 |
Note.—CTOPP = Comprehensive Test of Phonological Processing; CLS = Correct Letter Sequences; SSRS = The Social Skills Rating System; TOWRE = Test of Word Reading Efficiency; WJ-R = Woodcock-Johnson Psychoeducational Battery—Revised; WRMT = Woodcock Reading Mastery Test; CRAB = Comprehensive Reading Assessment Battery.
Table 3.
Correlations among the Predictor Variables
| Measures | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. CTOPP Elision | 1.00 | ||||||||||||||||||||||
| 2. CTOPP Rapid Digits–Time | −.25 | 1.00 | |||||||||||||||||||||
| 3. CTOPP Rapid Letters–Time | −.27 | .86 | 1.00 | ||||||||||||||||||||
| 4. Graphophonemic Fluency | .50 | −.49 | −.52 | 1.00 | |||||||||||||||||||
| 5. Graphophonemic Fluency growth | −.08 | −.09 | −.06 | −.31 | 1.00 | ||||||||||||||||||
| 6. Letter-Sound Fluency | .23 | −.51 | −.54 | .54 | .02 | 1.00 | |||||||||||||||||
| 7. Letter-Sound Fluency growth | .13 | −.02 | −.01 | .02 | .20 | −.29 | 1.00 | ||||||||||||||||
| 8. Phonemic Segmentation Fluency | .20 | −.13 | −.20 | .20 | −.14 | .33 | −.13 | 1.00 | |||||||||||||||
| 9. Phonemic Segmentation Fluency growth | −.03 | .10 | .16 | −.15 | .13 | −.27 | .23 | −.59 | 1.00 | ||||||||||||||
| 10. Spelling (CLS) | .49 | −.50 | −.54 | .77 | −.15 | .47 | .04 | .16 | −.10 | 1.00 | |||||||||||||
| 11. Spelling (CLS) growth | .02 | −.10 | −.10 | −.01 | .27 | .05 | .04 | .11 | .00 | −.15 | 1.00 | ||||||||||||
| 12. SSRS Academic Competence | .40 | −.43 | −.49 | .53 | .01 | .25 | .04 | .13 | −.08 | .50 | .13 | 1.00 | |||||||||||
| 13. SSRS Problem Behaviors | −.21 | .20 | .23 | −.21 | −.06 | −.30 | −.02 | −.19 | .09 | −.29 | .11 | −.38 | 1.00 | ||||||||||
| 14. SSRS Social Skills | .26 | −.18 | −.20 | .28 | −.03 | .25 | .06 | .22 | −.06 | .30 | .13 | .42 | −.69 | 1.00 | |||||||||
| 15. Teacher Reading Rating (overall rating) | .41 | −.43 | −.46 | .62 | −.06 | .33 | .05 | .12 | −.04 | .57 | .11 | .74 | −.10 | .26 | 1.00 | ||||||||
| 16. Teacher Reading Rating (total problems) | −.32 | .46 | .45 | −.38 | −.14 | −.33 | −.04 | −.16 | .06 | −.42 | −.12 | −.62 | .26 | −.28 | −.67 | 1.00 | |||||||
| 17. TOWRE Sight Word Efficiency | .51 | −.54 | −.58 | .86 | −.14 | .41 | .07 | .11 | −.08 | .78 | .00 | .61 | −.23 | .33 | .68 | −.47 | 1.00 | ||||||
| 18. TOWRE Phonemic Decoding Efficiency | .51 | −.45 | −.48 | .86 | −.14 | .41 | .11 | .17 | −.10 | .71 | .06 | .54 | −.18 | .26 | .62 | −.41 | .85 | 1.00 | |||||
| 19. WJ-R Oral Vocabulary–Synonyms and Antonyms | .42 | −.23 | −.22 | .37 | −.07 | .21 | .11 | .22 | −.03 | .35 | −.07 | .26 | −.25 | .23 | .25 | −.19 | .38 | .32 | 1.00 | ||||
| 20. Word ID Fluency | .46 | −.41 | −.45 | .85 | −.29 | .28 | .10 | .12 | −.08 | .71 | −.05 | .53 | −.13 | .26 | .62 | −.33 | .90 | .83 | .36 | 1.00 | |||
| 21. Word ID Fluency growth | .01 | −.04 | −.04 | −.14 | .56 | .08 | .11 | −.02 | .03 | −.13 | .33 | .03 | −.04 | −.05 | −.01 | −.14 | −.12 | −.05 | −.01 | −.37 | 1.00 | ||
| 22. WRMT Word Attack | .57 | −.43 | −.49 | .79 | −.14 | .40 | .08 | .19 | −.10 | .71 | .05 | .59 | −.25 | .35 | .60 | −.38 | .79 | .84 | .40 | .78 | −.08 | 1.00 | |
| 23. WRMT Word ID | .58 | −.49 | −.54 | .84 | −.15 | .38 | .06 | .15 | −.08 | .79 | .01 | .61 | −.24 | .36 | .67 | −.49 | .94 | .84 | .42 | .88 | −.13 | .83 | 1.00 |
Note.—CTOPP = Comprehensive Test of Phonological Processing; CLS = Correct Letter Sequences; SSRS = The Social Skills Rating System; TOWRE = Test of Word Reading Efficiency; WJ-R = Woodcock-Johnson Psychoeducational Battery—Revised; WRMT = Woodcock Reading Mastery Test.
Table 4.
Correlations among the Criterion Variables
| Measures | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1. CRAB Comprehension | 1.00 | |||||||
| 2. CRAB Fluency | .83 | 1.00 | ||||||
| 3. Graphophonemic Fluency | .69 | .80 | 1.00 | |||||
| 4. Passage Reading Fluency | .81 | .95 | .78 | 1.00 | ||||
| 5. Spelling (CLS) | .57 | .71 | .71 | .68 | 1.00 | |||
| 6. Word ID Fluency | .78 | .93 | .83 | .92 | .74 | 1.00 | ||
| 7. WRMT Word Attack | .64 | .71 | .75 | .70 | .68 | .75 | 1.00 | |
| 8. WRMT Word ID | .78 | .86 | .78 | .84 | .73 | .87 | .84 | 1.00 |
Note.—CRAB = Comprehensive Reading Assessment Battery; CLS = Correct Letter Sequences; WRMT = Woodcock Reading Mastery Test.
Principal Component Analysis of the Criterion Assessments and the Identification of At-Risk Readers
A maximum-likelihood principal components analysis was conducted using raw scores for all seven criterion measures. Kaiser’s rule of retaining all factors with eigenvalues greater than one indicated a one-factor solution would account for 80% of the variance in the criterion variables (with an eigenvalue of 5.6 for the first component and eigenvalues less than .5 for the remaining components). All seven variables displayed high loadings on the factor (all above .82), with the WRMT Word Identification subtest, CRAB Fluency, and WIF having the highest loadings (above .94). A factor score for each student was computed based upon the factor weights.
To identify students with poor reading skills at the end of the school year, we employed the following strategy: sample-based percentile scores were computed from the previously obtained factor score, and a reading problem was defined as scoring below the 25th percentile on this factor score and also below a raw score of 30 on Passage Reading Fluency. The latter cutoff represents the 25th percentile on norms reported by Hasbrouck and Tindal (2006) based on over 19,000 first-grade students in 23 states. The second condition was necessary because the sample performed above the national normative mean on several tests (see Table 1). Thus, a score below the 25th percentile on the factor derived from the sample may not indicate poor reading on an absolute basis, whereas requiring a low factor score and a low passage-reading-fluency score would likely reflect at-risk status. Our goal was to identify a pool of likely poor readers to evaluate the accuracy of our screening battery; we do not suggest that 25% of first-grade children require Tier 2 intervention. The issue of selecting a cut point is a substantive one; the 25th percentile is one often used in research, but practitioners would likely base their cutoff on the number of children they can serve given available resources. Our procedure yielded 45 at-risk children. The low-factor-score criterion identified 57 children; adding the low-PRF condition resulted in dropping 12 of the low-factor children, resulting in a final at-risk sample of 45 children. All children who met the low-PRF condition also met the low-factor-score criterion.
Predicting Reading Status in First Grade by Predictor Subsets
In order to address our questions regarding the usefulness of accuracy, fluency, growth, and teacher predictors of reading status, we conducted four separate all-subsets regression analyses1 (Miller, 2002). While there are many variations on an all-subsets regression strategy, they all begin by computing all possible R2s for all possible combinations of predictors of every possible predictor set size. Then, the obtained R2 values can be rank ordered from highest to lowest within a given set size. Our particular strategy was to examine the highest R2 values for each set size and to look for a point of “diminishing returns” such that going from the best set of predictors of size n to the best set of predictors of size n + 1 would not provide an important increase in the overall R2 value, which we arbitrarily chose to be an increase of less than 3% additional variance accounted for in reading status. In support of this decision, we note that Cohen (1988) defined a small effect in multiple regression as one that accounts for 2% of the variance (a medium effect accounts for 13% of the variance). Once it was determined that we could not increase the variance accounted for in reading status (by 3% or more) by adding an additional predictor, we then examined the different possible combinations of predictors that made up that set. Because there would possibly be a number of potential combinations of predictors within each set that could account for a similar amount of variance, we examined all the models within that set that were within 3% of the variance accounted for from the best-fitting model from that set. Acknowledging that there was no statistical justification to select a particular model from this subset, the actual selection of a particular model from among the best-fitting models was based on practical grounds (i.e., time to administer each task).
All-subsets regression of the accuracy predictors
WRMT Word Identification, WRMT Word Attack, WJ-R Oral Vocabulary, and the CTOPP Elision subtest were entered into an all-subsets regression predicting reading status. The best-fitting models of predictor set sizes 1 (each predictor alone) to 4 (all predictors in the model) yielded R2 values of .29, .30, .30, and .30, respectively. These values begin to show diminishing increase in R2 values after set size 1. For example, increasing the predictor set size from 1 to 2 would only have increased the overall R2 value by 1%, so we chose to examine all four models that had only one predictor. WRMT Word Identification accounted for 29.4% of the variance, WRMT Word Attack accounted for 18% of the variance, WJ-R Oral Vocabulary accounted for 9.1% of the variance, and CTOPP Elision accounted for 9% of the variance in reading status. None of the other variables came within 3% variance accounted for from the best-fitting model, so we concluded that the model that included WRMT Word ID as the sole predictor of reading status was the best model of the accuracy predictor set.
All-subsets regression of the fluency predictors
The nine variables representing the fluency predictors were entered into an all-subsets regression predicting reading status. The total R2s from the best-fitting models of predictor set size 1 to 3 are .31, .40, and .41, respectively. The R2 values begin to show a diminishing increase after predictor set size 2, with the best model of three predictors accounting for only an additional .13% of the variance in reading status. Of the best-fitting models, the model with WIF and TOWRE SWE together accounts for 39.6% of the variance in reading status, and the next best set of two predictors (CTOPP Rapid Letter Naming and TOWRE SWE) accounts for 5.9% less variance than the best two-predictor model. From this, we concluded that the two-predictor model of WIF and TOWRE SWE was the best model of the fluency predictor set.
All-subsets regression of the teacher ratings
The five variables representing the teacher ratings were entered into an all-subsets regression predicting reading status. The total R2s from the best-fitting models of predictor set size 1 to 3 are .29, .34, and .34, respectively. These values begin to show a diminishing increase in R2 values after predictor set size 2, with the best model of three predictors accounting for only an additional increase of .8% in the variance in reading status. Using our criterion of only considering the models that are within 3% of the variance accounted for by the best model, two models with two predictors were examined. The model with the highest R2 value (.34) had Reading Rating–Problems and SSSR–Academic Competence as the predictors, while the next best model (R2 = .32) used Reading Rating–Problems and Reading Rating–Overall as predictors. Since there is no statistical reason to select one model over the other, we chose the second model (Reading Rating–Problems and Reading Rating–Overall) because both of these variables come from the same rating form, making it easier and faster for teachers to complete.
All-subsets regression of the growth measures
The five variables representing the growth measures were entered into an all-subsets regression predicting reading status. The total R2s from the best-fitting models of predictor set size 1 to 3 are .05, .06, and .07, respectively. The R2 values begin to show a diminishing increase after predictor set size 1, with the best model of two predictors accounting for only an additional increase of .9% in the variance in reading status. Using our criterion of considering the models with one predictor that are within 3% of the variance accounted for by the best model, only the top two models were examined. The model with the highest R2 value (.05) used WIF Growth as the predictor, and the model with the second highest R2 value (.04) had GPF Growth as a predictor. Again, since there is no statistical reason to select one of these models over the other, and the fact that both of these measures are similar in time to administer, we chose the first model (WIF Growth). In addition, WIF Growth replicates other findings (Compton et al., 2006) and is a skill more proximal to important reading outcomes than GPF Growth.
All-subsets regression using the variables from the best models
Six variables (WRMT Word Identification, TOWRE SWE, WIF, Reading Rating–Problems, Reading Rating–Overall, and WIF Growth) from the previously selected models were entered into an all-subsets regression. The total R2s from the best-fitting models of predictor set size 1 to 4 are .31, .40, .46, and .47, respectively. The increase in R2 values diminishes after predictor set size 3, with the best model of four predictors accounting for a small increase of 1.3% in additional variance accounted for in reading status. Using our criterion of considering the models that are within 3% of the variance accounted for by the best model, only the top three models with three predictors were examined. The model with the highest R2 value (.46) comprised TOWRE SWE, Reading Rating–Problems, and WIF Growth. The model with the next highest R2 value (.46) had TOWRE SWE, WIF, and Reading Rating–Problems as predictors, and the third highest model (R2 = .45) included WRMT Word Identification, Reading Rating–Problems, and WIF Growth. Of these three potential models, we chose the second model because the measures from that model do not require a second assessment to assess growth.
Determining Probability of Reading Problems
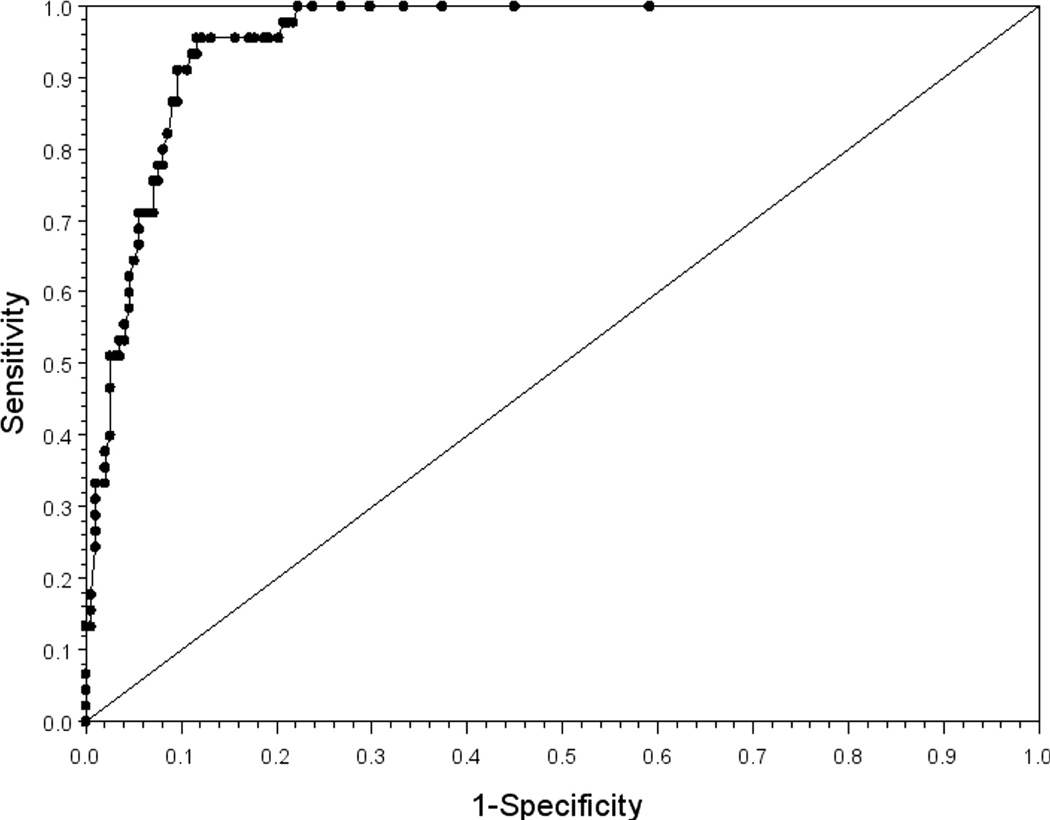
Using the three predictor variables selected above, we performed a logistic regression and a receiver-operator characteristic (ROC) curve analysis (Swets, 1986) to fit a model that predicts which students will be identified as at risk for a reading problem. ROC curves provide a useful tool for examining the utility of a screening battery in predicting the presence or absence of a problem. ROC curves allow for an inspection of potential cut points for a screening battery that may be chosen to optimize sensitivity, specificity, or minimize a certain type of error (false positives or false negatives). A standard ROC curve will have sensitivity on the y-axis and 1-specificity (false positives) on the x-axis. The area under the curve (AUC) of an ROC curve is a probability index that ranges from .50, which means the screening battery does no better than chance, to 1.0, which means perfect prediction. The value of the AUC can also be thought of as the probability that the screening battery will correctly classify a pair of randomly selected individuals where one has the problem and the other does not.
The ROC curve analysis yielded an AUC value of .96 (see Fig. 1). This exceeds the value of .85 used by the National Center on Response to Intervention (2011) to evaluate screening tools. From this graph, one could select a point along the curve (which would represent a potential cut point on a linearized combination of the three independent variables) that could be investigated for an acceptable level of sensitivity and specificity. For example, this graph indicates that if we chose a sensitivity level of .80 (false negative rate = .20), the corresponding specificity rate would be .92 (false positive rate = .08). If a desired sensitivity level was .90 (false negative rate = .10), the corresponding specificity level would be around .90 (false positive rate = .10).
Figure 1.
ROC curve predicting reading status.
Discussion
The purpose of this study was to identify a screening battery that accurately and efficiently identifies first-grade children at risk for reading problems. Given scarce resources and the desire to intervene as early as possible to prevent reading failure, the identification of an efficient and valid screening procedure is critical. This is not a new problem in education, but it continues to be vexing. As Jenkins et al. (2007) pointed out, screening studies are difficult to compare because different measures are used to define the screen and the outcome, and different statistical techniques are used to identify predictors and to define reading problems. Further, different types of samples are recruited, which would influence the distributional properties of the measures. However, with the addition of greater numbers of screening studies like the one described here, the research community can begin to converge on a set of predictors appropriate for screening batteries early in elementary school. For example, it has been shown across studies that sublexical, word-level, and language measures predict reading status for first-grade children (e.g., Compton et al., 2006; Foorman et al., 1998). Our results build on this foundation.
Our study adds to the literature by investigating not only what variables to measure but also how to measure them to ultimately identify a valid screening battery chosen for optimal efficiency. The questions about the kinds of measures to include centered on the relative strength of accuracy and fluency measures, whether growth measures are necessary, and whether teacher ratings should be included in a screening battery. Our methodology was designed to identify the best accuracy, fluency, growth, and teacher-rating variables in separate analyses and then examine the identified predictors from each of these categories to determine which were most important for predicting reading status. We privileged measures that were efficient if they were as valid as other less efficient measures.
With regard to accuracy and fluency predictors, the best accuracy predictor was word identification (WRMT Word Identification) and the best fluency predictors were two-word-identification fluency tasks (TOWRE Sight Word Efficiency and Word Identification Fluency), suggesting the importance of word identification in the screening battery. In the final models that comprised three variables, we found that the accuracy and fluency measures were equally predictive. Thus, the fluency measures could be privileged in screening batteries to maximize efficiency. It is interesting to note that the two word identification fluency tasks added uniquely to the prediction of reading status despite their correlation of .90 (see Table 2). The Word Identification Fluency task added 8.9% variance to the 31% accounted for by TOWRE Sight Word Efficiency. We speculate that the reason may relate to how the measures are constructed. The TOWRE measure is designed to differentiate children across a broad age range, whereas the Word Identification Fluency task is designed to differentiate children within a grade. Thus, the additional variance contributed by Word Identification Fluency may be linked to its sensitivity to differences exhibited by children within a smaller developmental window. Based on this finding, it may be necessary to include measures in screening batteries that discriminate children both within and across developmental levels for greatest predictive power.
In examining growth variables, we found that the best predictor was growth in Word Identification Fluency, again suggesting the importance of word identification in early screening. The finding that Word Identification Fluency growth was the best predictor from the growth set replicates Compton et al. (2006). However, it also extends the finding because our study included an unselected sample (i.e., a sample that represented the full range of achievement) and a wider range of measures. In selecting the best final model, we did not include the growth measure, as it did not improve prediction over similarly strong models without measures requiring a second measurement point.
It is interesting that none of the accuracy, fluency, or growth measures representing sublexical and language skills added to the prediction of reading problems. This finding is in contrast to findings from several studies of first-grade children. For example, Foorman et al. (1998) and O’Connor and Jenkins (1999) identified either letter sounds or letter names and a phonemic awareness skill in their prediction batteries. Compton et al. (2006) also identified a phonemic task and oral vocabulary. Several differences between these studies and our investigation may account for the differences. Due to difficulties in getting started in the schools, our data-collection schedule began later in the fall than other studies. Additionally, we used a broader measurement net and an unselected sample that, on average, performed above national norms. It may be that the sublexical and phonological skills are important when screening earlier in the first-grade year when the sample consists of poorer readers (Compton et al., 2006) or children from more diverse backgrounds (Foorman et al., 1998).
Among the teacher-rating variables, we found that teacher ratings of overall reading and teacher ratings of reading problems were the most important. In the final prediction model, the number of reading problems for children reading below grade level (i.e., decoding, fluency, vocabulary, comprehension) contributed uniquely to the screening battery. Collecting teacher ratings data does not take any instructional time and capitalizes on teachers’ firsthand knowledge of students’ reading ability. While teacher ratings have been shown to be correlated with direct measures of reading, these ratings are not often used as part of screening. This study suggests that including teacher ratings as part of a screening battery may add to both the efficiency and validity of the screening battery. It is interesting that within the Reading Rating instrument, the number of problems selected by teachers was more predictive than the overall rating, suggesting it is capturing the severity of reading problems experienced by children reading below grade level. This is a plausible explanation given that we were predicting status (at risk, not at risk) and not a continuous outcome. Given the validity coefficients reported in the Method section for these two ratings in which the coefficients were higher for the Overall Reading Rating than the number-of-problems rating, we would expect the overall rating to better distinguish children across a broader range of reading skill as would be seen in a continuous measure of reading skill.
The end result of our analysis was a screening battery that accounted for almost half of the variance in reading status. We determined that the models beyond a three-variable set did not add appreciable variance. Within the possible three-variable sets, we selected the one that was most efficient because there was no statistical reason to choose from among the top models that accounted for, essentially, the same amount of variance. The most efficient model included TOWRE Sight Word Efficiency, Word Identification Fluency, and Reading Rating–Problems. This battery would take, at most, 10 minutes to administer and score per child in addition to teacher time associated with the reading ratings. Thus, the screening criterion of efficiency was accomplished. Regarding validity, the ROC curve analysis yielded an AUC value of .96, which is quite high. One could select a cut point that yielded sensitivity and specificity indexes of .90, which compares favorably to other studies (Jenkins et al., 2007).
It is important to consider the other variables within the final three-variable sets that accounted for a similar amount of variance in the criterion. We selected the variable set that was most efficient from a practical perspective. However, using a different lens would have led to selection of a screen that included Word Identification Fluency growth and/or WRMT Word Identification. We are not making an argument that accuracy and growth variables are not important within an RTI context, only that the additional time involved in collecting these measures is not offset by an increase in the variance accounted for in the criterion. In all the models considered viable, the Reading Rating (of number of) Problems was included. Thus, including this teacher rating or a similar measure is recommended for future screening research.
It is also important to discuss how it was determined that children were at risk for a reading problem in this study, because the screening batteries identified across studies may differ depending on the criterion used. We conducted a factor analysis of the measures given to children at the end of first grade, which yielded one factor that explained 80% of the variance in the criterion measures. Because, on average, our sample performed above the normative mean, we chose a conservative approach to defining our criterion. We determined that children with reading problems were those who scored below the 25th percentile on the factor based on the sample and below 30 words per minute on passage-reading fluency, which corresponded to the 25th percentile on national norms. This procedure identified 45 children as at risk (18.5%). Percentages of at-risk children identified across first-grade studies reviewed by Jenkins et al. (2007, Table 2) ranged from 8% to 48% with a median value of 23%. Thus, the proportion of children identified by our procedures is slightly lower than the midpoint for extant studies. The procedures we used in this screening study should be applied in other samples to determine the generalizability of our findings.
Limitations
Our results are qualified primarily by the timing of the assessment waves. It is unknown whether the same results would obtain if the assessments began earlier in the year and if the period for assessing growth was from September to January rather than December to March. Ideally, screening measures would be administered earlier in the school year to begin interventions as soon as possible. Given that our assessments began in late fall, the screening battery may be appropriate as a benchmark after initial exposure to the general education curriculum. Another issue is the partial overlap between the predictor and criterion measures. Although collecting data at two time points and the use of factor analysis to define the criterion as a dichotomous variable (at risk, not at risk) mitigates shared method variance to some extent, it is certainly possible that independent measures at the two time points would yield different results. Finally, our sample was drawn from parochial schools representing middle-class families for the most part and, as such, the results may not generalize to other populations that have different characteristics. We would point out, however, that the children identified as at risk experienced rather severe problems on the fall level and growth measures compared to their not-at-risk peers. The not-at-risk children read over four times as many words on the fall Word Identification Fluency measure (29 wpm vs. 6.5 wpm) and experienced twice as much growth (12.5 wpm vs. 5.6 wpm). Moreover, the not-at-risk children scored approximately a standard deviation higher on the nationally norm-referenced tests.
Implications
A basic principle of RTI is universal screening to identify children at risk for reading problems. In this study, a quick screen that included measures of word-reading fluency and teacher ratings was sufficient to accurately identify children at risk for reading problems at the end of first grade. The word-fluency result replicates recent findings by other investigators using different methods and samples and thus appears to be a durable finding. That teacher ratings of number of reading problems ascended as a powerful predictor is not surprising given that teachers have multiple opportunities to observe students and make judgments on their skill levels. What perhaps is surprising is that most investigators do not tap this important source of information. Further investigation of what teacher judgments can add to the identification of children at risk is warranted, and we note that the same measure was predictive in a study of older readers (Speece et al., 2010). This study shows that it is possible to establish an efficient and valid screen that adequately identified children at risk for reading problems. As practice and policy move forward with efforts to implement response to intervention, studies such as this one can guide decisions about measures to include in universal screening.
Acknowledgments
This work was funded by the National Institute of Child Health and Human Development (grant no. R01HD46758) and the U.S. Department of Education (grant no. H325D070082).
Footnotes
As an alternative to running four separate all-subsets regressions, we also performed a single all-subsets regression with all predictor variables. Our final chosen model remained the same, but we felt that presenting four separate regressions provided more information regarding the predictors within each category.
Contributor Information
Deborah L. Speece, University of Maryland
Christopher Schatschneider, Florida State University.
Rebecca Silverman, University of Maryland.
Lisa Pericola Case, University of Maryland.
David H. Cooper, Elon University
Dawn M. Jacobs, University of Maryland
References
- Benes KM. Review of Social Skills Rating System. In: Conoley JC, Impara JC, editors. The twelfth mental measurements yearbook. Lincoln: University of Nebraska–Lincoln, Buros Institute of Mental Measurements; 1995. pp. 965–967. [Google Scholar]
- Berkeley S, Bender W, Peaster LG, Saunders L. Implementation of response to intervention: A snapshot of progress. Journal of Learning Disabilities. 2009;42:85–95. doi: 10.1177/0022219408326214. [DOI] [PubMed] [Google Scholar]
- Byrne B, Fielding-Barnsley R, Ashley L. Effects of preschool phonemic identity training after six years: Outcome level distinguished from rate of response. Journal of Educational Psychology. 2000;92:659–667. [Google Scholar]
- Catts HW, Fey ME, Zhang X, Tomblin JB. Language basis of reading and reading disabilities: Evidence from a longitudinal investigation. Scientific Study of Reading. 1999;3:331–361. [Google Scholar]
- Cohen J. Statistical power analysis for the behavior sciences. 2nd ed. New York: Academic Press; 1988. [Google Scholar]
- Cohen J, Cohen P, West SG, Aiken LS. Applied multiple regression/correlational analysis for the behavioral sciences. 3rd ed. Hillsdale, NJ: Erlbaum; 2003. [Google Scholar]
- Compton DL. Modeling the growth of decoding skills in first-grade children. Scientific Studies of Reading. 2000;4:219–259. [Google Scholar]
- Compton DL. Modeling the relationship between growth in rapid naming speed and decoding skill in first-grade children. Journal of Educational Psychology. 2003;95:225–239. [Google Scholar]
- Compton DL, Fuchs D, Fuchs LS, Bryant JD. Selecting at-risk readers in first grade for early intervention: A two-year longitudinal study of decision rules and procedures. Journal of Educational Psychology. 2006;98:394–409. [Google Scholar]
- Deno SL. Curriculum-based measurement: The emerging alternative. Exceptional Children. 1985;52:219–232. doi: 10.1177/001440298505200303. [DOI] [PubMed] [Google Scholar]
- Deno SL, Fuchs LS, Marston D, Shin J. Using curriculum-based measurement to establish growth standards for students with learning disabilities. School Psychology Review. 2001;30:507–524. [Google Scholar]
- DIBELS: Dynamic Indicators of Early Literacy Skills. 2001 Retrieved from http://www.dibels.uoregon.edu/measures.
- DiPerna JC, Elliott SN. Development and validation of the academic competence evaluation scales. Journal of Psychoeducational Assessment. 1999;17:207–225. [Google Scholar]
- DuPaul GJ, Volpe RJ, Jitendra AK, Lutz JG, Lorah KS, Gruber R. Elementary school students with AD/HD: Predictors of academic achievement. Journal of School Psychology. 2004;42(2):285–301. [Google Scholar]
- Ehri LC, Soffer AG. Graphophonemic awareness: Development in elementary students. Scientific Studies of Reading. 1999;3:1–30. [Google Scholar]
- Elliott J, Lee SW, Tollefson N. A reliability and validity study of the Dynamic Indicators of Early Literacy Skills—Modified. School Psychology Review. 2001;30:33–49. [Google Scholar]
- Foorman BR, Fletcher JM, Frances DJ, Carlson CD, Chen D, Mouszaki A, Taylor RH. Technical Report: Texas Primary Reading Inventory. 1998 ed. Houston: Center for Academic and Reading Skills and University of Houston; 1998. [Google Scholar]
- Fuchs D, Compton DL, Fuchs LS, Bryant J, Davis GN. Making “secondary intervention” work in a tier-three Responsiveness-to-Intervention model: Findings from the first-grade longitudinal reading study of the National Research Center on Learning Disabilities. Reading and Writing. 2008;21(4):413–436. [Google Scholar]
- Fuchs D, Fuchs LS, Compton DL. Identifying reading disabilities by responsiveness-to-instruction: Specifying measures and criteria. Learning Disabilities Quarterly. 2004;27:216–227. [Google Scholar]
- Fuchs D, Fuchs LS, Thompson A, Al Otaiba S, Yen L, Yang NJ, O’Connor R. Is reading important in reading-readiness programs? A randomized field trial with teachers as program implementers. Journal of Educational Psychology. 2001;93:251–267. [Google Scholar]
- Fuchs LS, Fuchs D. Treatment validity: A unifying concept for reconceptualizing the identification of learning disabilities. Learning Disabilities Research and Practice. 1998;13(4):204–219. [Google Scholar]
- Fuchs LS, Fuchs D, Hamlett CL. Monitoring reading growth using student recalls: Effects of two teacher feedback systems. Journal of Educational Research. 1989;83:103–111. [Google Scholar]
- Fuchs LS, Fuchs D, Hamlett CL, Allinder RM. Effects of expert system advice within curriculum-based measurement on teacher planning and student achievement in spelling. School Psychology Review. 1991;20:49–66. [Google Scholar]
- Fuchs LS, Fuchs D, Maxwell L. The validity of informal reading comprehension measures. Remedial and Special Education. 1988;9:20–29. [Google Scholar]
- Fuchs LS, Hamlett CL, Fuchs D. Monitoring basic skills progress. Austin, TX: Pro-Ed; 1990. [Google Scholar]
- Furlong M, Karno M. Review of Social Skills Rating System. In: Conoley JC, Impara JC, editors. The twelfth mental measurements yearbook. Lincoln: University of Nebraska–Lincoln, Buros Institute of Mental Measurements; 1995. pp. 967–969. [Google Scholar]
- Gijsel MA, Bosman AM, Verhoeven L. Kindergarten risk factors, cognitive factors, and teacher judgments as predictors of early reading in Dutch. Journal of Learning Disabilities. 2006;39:558–571. doi: 10.1177/00222194060390060701. [DOI] [PubMed] [Google Scholar]
- Good RH, Simmons DC, Kame’enui EJ. The importance of decision-making utility of a continuum of fluency-based indicators of foundational reading skills for third-grade high stakes outcomes. Scientific Studies of Reading. 2001;5(3):257–288. [Google Scholar]
- Gresham F, Elliott S. Social Skills Rating System manual. Circle Pines, MN: American Guidance Service; 1990. [Google Scholar]
- Hasbrouck J, Tindal GA. Oral reading fluency norms: A valuable assessment tool for reading teachers. Reading Teacher. 2006;59(7):636–644. [Google Scholar]
- Hatcher PJ, Hulme C, Ellis AW. Ameliorating early reading failure by integrating the teaching of reading and phonological skills: The phonological linkage hypothesis. Child Development. 1994;65:41–57. [Google Scholar]
- Hatcher PJ, Hulme C, Miles JN, Carroll JM, Hatcher J, Gibbs S, Snowling MJ. Efficacy of small group reading intervention for beginning readers with reading-delay: A randomized controlled trial. Journal of Child Psychology and Psychiatry. 2006;47:820–827. doi: 10.1111/j.1469-7610.2005.01559.x. [DOI] [PubMed] [Google Scholar]
- Individuals with Disabilities Education Improvement Act of 2004, Pub. L. No. 108-446, § 601, Stat. 2004. p. 2647. [Google Scholar]
- Jenkins JR, Hudson RF, Johnson ES. Screening for at-risk readers in a Response to Intervention framework. School Psychology Review. 2007;36:582–600. [Google Scholar]
- Johnson ES, Jenkins JR, Petschur Y, Catts HW. How can we improve the accuracy of screening instruments? Learning Disability Research & Practice. 2009;24:174–185. [Google Scholar]
- Kame’enui EJ, Simmons DC. Introduction to this special issue: The DNA of reading fluency. Scientific Studies of Reading. 2001;5:203–210. [Google Scholar]
- Kaminski RA, Good RH. Towards a technology for assessing basic early literacy skills. School Psychology Review. 1996;25:215–227. [Google Scholar]
- LaBerge D, Samuels J. Towards a theory of automatic information processing in reading. Cognitive Psychology. 1974;6:293–323. [Google Scholar]
- Logan GD. Toward an instance theory of automatization. Psychological Review. 1988;95:492–527. [Google Scholar]
- Logan GD. Automaticity and reading: Perspectives from the instance theory of automatization. Reading and Writing Quarterly. 1997;13(2):123–146. [Google Scholar]
- Marston DB. A curriculum-based measurement approach to assessing academic performance: What it is and why do it. In: Shinn MR, editor. Curriculum-based measurement. New York: Guilford; 1989. pp. 18–78. [Google Scholar]
- McKenzie R. Obscuring vital distinctions: The oversimplification of learning disabilities within RTI. Learning Disabilities Quarterly. 2009;32:203–215. [Google Scholar]
- McKinney JD, Mason J, Perkerson K, Clifford M. The relationship between classroom behavior and academic achievement. Journal of Educational Psychology. 1975;67:198–203. [Google Scholar]
- McMaster KL, Fuchs D, Fuchs LS, Compton DL. Responding to nonresponders: An experimental field trial of identification and intervention methods. Exceptional Children. 2005;71:445–463. [Google Scholar]
- Miller AJ. Subset selection in regression. 2nd ed. New York: Chapman & Hall; 2002. [Google Scholar]
- National Center on Response to Intervention. Screening tools chart. 2011 Retrieved from http://www.rti4success.org/chart/screeningTools/screeningtoolschart.html.
- National Reading Panel. Report of National Reading Panel: Teaching children to read: An evidence-based assessment of the scientific research literature on reading and its implications for reading instruction. Report of the subgroups. Washington, DC: National Institutes of Child Health and Human Development; 2000. [Google Scholar]
- Nelson JM. Beyond correlational analysis of the Dynamic Indicators of Basic Early Literacy Skills (DIBELS): A classification validity study. School Psychology Quarterly. 2008;23:542–552. [Google Scholar]
- O’Connor RE, Jenkins JR. Prediction of reading disabilities in kindergarten and first grade. Scientific Studies of Reading. 1999;3:159–197. [Google Scholar]
- Pennington BF, Lefly DL. Early reading development in children at risk for dyslexia. Child Development. 2001;72:816–833. doi: 10.1111/1467-8624.00317. [DOI] [PubMed] [Google Scholar]
- Riedel BW. The relation between DIBELS, reading comprehension, and vocabulary in urban first-grade students. Reading Research Quarterly. 2007;42:546–562. [Google Scholar]
- Ritchey KD. The prediction of growth in reading subskills and the relationship of growth to literacy outcomes in kindergarten (Unpublished doctoral dissertation) College Park: University of Maryland; 2002. [Google Scholar]
- Ritchey KD, Speece DL. From letter names to word reading: The nascent role of sublexical fluency. Contemporary Educational Psychology. 2006;31:301–327. [Google Scholar]
- Ryder JF, Tunmer WE, Greaney KT. Explicit instruction in phonemic awareness and phonemically based decoding skills as an intervention strategy for struggling readers in whole language classrooms. Reading and Writing. 2008;21(4):349–369. [Google Scholar]
- Scarborough HS. Early identification of children at risk for reading disabilities: Phonological awareness and some other promising predictors. In: Shapiro BK, Accardo PJ, Capute AJ, editors. Specific reading disability: A view of the spectrum. MD: York: Timonium; 1998. pp. 75–107. [Google Scholar]
- Shinn M. Identifying students at risk, monitoring performance, and determining eligibility within response to intervention. School Psychology Review. 2007;6:601–617. [Google Scholar]
- Speece DL, Case LP. Classification in context: An alternative approach to identifying early reading disability. Journal of Educational Psychology. 2001;93:735–749. [Google Scholar]
- Speece DL, DaDeppo L, Hines S, Walker C. Graphophonemic fluency study. Unpublished raw data. 2005 [Google Scholar]
- Speece DL, Ritchey KD. A longitudinal study of the development of oral reading fluency in young children at risk for reading failure. Journal of Learning Disabilities. 2005;38:387–399. doi: 10.1177/00222194050380050201. [DOI] [PubMed] [Google Scholar]
- Speece D, Ritchey K, Silverman R, Schatschneider C, Walker C, Andrusik K. Identifying children in middle childhood who are at risk for reading problems. School Psychology Review. 2010;39:258–276. [PMC free article] [PubMed] [Google Scholar]
- Stage SA, Abbott RD, Jenkins JR, Berninger VW. Predicting response to early reading intervention from verbal IQ, reading-related language abilities, attention ratings, and verbal IQ-word reading discrepancy: Failure to validate discrepancy method. Journal of Learning Disabilities. 2003;36:24–33. doi: 10.1177/00222194030360010401. [DOI] [PubMed] [Google Scholar]
- Swets JA. Indices of discrimination or diagnostic accuracy: Their ROCs and implied models. Psychological Bulletin. 1986;99:100–117. [PubMed] [Google Scholar]
- Taylor H, Anselmo M, Foreman AL, Schatschneider C, Angelopoulos J. Utility of kindergarten teacher judgments in identifying early learning problems. Journal of Learning Disabilities. 2000;33:200–210. doi: 10.1177/002221940003300208. [DOI] [PubMed] [Google Scholar]
- Torgesen JK. Individual differences in response to early interventions in reading: The lingering problem of treatment resisters. Learning Disabilities Research and Practice. 2000;15:55–64. [Google Scholar]
- Torgesen JK, Wagner RK, Rashotte CA. Test of Word Reading Efficiency: Examiner’s manual. Austin, TX: Pro-Ed; 1999. [Google Scholar]
- Torgesen JK, Wagner RK, Rashotte CA, Rose E, Lindamood P, Conway T, Garvin C. Preventing reading failure in young children with phonological processing disabilities: Group and individual responses to instruction. Journal of Educational Psychology. 1999;91:579–593. [Google Scholar]
- Wagner RK, Torgesen JK, Rashotte CA. Comprehensive Test of Phonological Processing: Examiner manual. Austin, TX: Pro-Ed; 1999. [Google Scholar]
- Woodcock RW. Woodcock Reading Mastery Test—Revised/Normative Update. Circle Pines, MN: American Guidance Service; 1998. [Google Scholar]
- Woodcock RW, Johnson MB. Woodcock-Johnson Psychoeducational Battery—Revised. Allen, TX: DLM; 1989. [Google Scholar]
- Woodcock RW, Mather N. WJ-R Tests of Achievement: Examiner’s manual. In: Woodcock RW, Johnson MB, editors. Woodcock-Johnson Psychoeducational Battery—Revised. Chicago: Riverside: 1989, 1990. [Google Scholar]