Abstract
There is a need to develop multiscale models of vascular adaptations to understand tissue level manifestations of cellular level mechanisms. Continuum based biomechanical models are well suited for relating blood pressures and flows to stress-mediated changes in geometry and properties, but less so for describing underlying mechanobiological processes. Discrete stochastic agent based models are well suited for representing biological processes at a cellular level, but not for describing tissue level mechanical changes. We present here a conceptually new approach to facilitate the coupling of continuum and agent based models. Because of ubiquitous limitations in both the tissue- and cell-level data from which one derives constitutive relations for continuum models and rule-sets for agent based models, we suggest that model verification should enforce congruency across scales. That is, multiscale model parameters initially determined from data sets representing different scales should be refined, when possible, to ensure that common outputs are consistent. Potential advantages of this approach are illustrated by comparing simulated aortic responses to a sustained increase in blood pressure predicted by continuum and agent based models both before and after instituting a genetic algorithm to refine 16 objectively bounded model parameters. We show that congruency-based parameter refinement not only yielded increased consistency across scales, it also yielded predictions that are closer to in vivo observations.
Keywords: Agent Based Model (ABM), Constrained Mixture Model (CMM), Growth and Remodeling, Model Verification
INTRODUCTION
Pioneering work in the 1960s and 1970s revealed the fundamental importance of mechanical stimuli in arterial wall biology, something now studied widely in the allied fields of vascular mechanics and mechanobiology. For example, via comparative studies across species, Wolinsky and Glagov1 showed that the increased thickness of the aortic wall in larger mammals correlates well with the increased luminal radius that is necessary to accommodate the increased volumetric blood flows, with wall tension per lamellar unit remaining nearly constant at ~ 2 N/m. It thus became apparent that the normal aortic wall grows (changes mass) and remodels (changes microstructure) during development and maturation so as to achieve and maintain nearly constant a preferred value of the mean circumferential stress (σθ = Pa/h, where P is pressure, a the luminal radius, and h the wall thickness).2,3 This general finding is also consistent with an idea that emerged in hemodynamics during the same period, namely, that the aortic wall grows, remodels, and adapts so as to maintain nearly constant the mean wall shear stress (τw = 4μQ/πa3, where μ is viscosity and Q the volumetric flow rate,2,4 with the particular target value of stress varying along the vascular tree and across species).5 Wolinsky6 suggested further that thickening of the aortic wall in response to hypertension is consistent with the concept that mean circumferential stress is maintained nearly constant, a finding that has been confirmed by others.7,8
Continuum biomechanical models are now capable of describing and predicting many salient features of arterial adaptations to altered hemodynamics,9-11 including hypertension, yet it is becoming increasingly apparent that there is a need for integrative multiscale models that can capture both the molecular and cellular mechanisms and their associated manifestations at the tissue level.11-14 Toward that end, we suggested that coupling discrete stochastic agent based models (ABMs) of cell level processes with continuum based constrained mixture models (CMMs) of tissue level phenomena promises to increase our understanding of the biology and physiology in health and disease.15 Whereas continuum based models employ phenomenological constitutive relations, agent based models simulate interactions of autonomous agents (e.g., individual cells) with each other and with their environment based on a literature-derived set of rules.16
We now suggest further that effective coupling of such different types of models across scales necessitates a new level of model verification. Although it is typically assumed that lower scale data and models are inherently more reliable because the experiments are better controlled, they need not be physiologically relevant. In contrast, higher scale data and models can be physiologically relevant, but it is often difficult to identify, and therefore model, all contributors to the observed behavior. In other words, ubiquitous limitations in either the data or their interpretation exist at all scales. We thus suggest that increased confidence in models built from data collected at different scales can be achieved by ensuring that select outputs common to the different models are inherently self-consistent. Therefore, notwithstanding our ultimate goal of building multiscale models that increase our understanding of vascular adaptations and disease progression, the primary goal of this paper is to introduce a conceptually new approach to verification in multiscale modeling. As an illustrative example, we show that achieving congruency between ABM and CMM predictions of time-dependent aortic adaptations to a sustained increase in pressure not only increases consistency across scales, it can also yield overall model predictions that are closer to in vivo reports. As it will be seen, the predicted arterial responses arise from growth (changes in mass) and remodeling (changes in structure and thus tissue properties) processes, which in turn result from changes in the production and removal of both structurally and non-structurally significant constituents (e.g., collagen and smooth muscle cells as well as vasoactive molecules, growth factors, and matrix metalloproteinases) that are driven by changes in hemodynamically induced stresses. Hence, this example also reinforces the need for integrative models of molecular, cellular, and tissue level changes.
METHODS
A comprehensive bio-chemo-mechanical model of arterial growth and remodeling will ultimately need to account for the effects of hundreds of biochemically active molecules and their mechanical consequences on the arterial wall, and vice versa. Toward this end, and for illustrative purposes, we begin by focusing on seven vasoactive, mitogenic / synthetic, and proteolytic molecules that are particularly important to arterial adaptations in mild hypertension: NO (nitric oxide), ET-1 (endothelin-1), TGF-b (transforming growth factor-beta1), PDGF-AB (platelet derived growth factor - AB), and MMP-1, -2 and -9 (matrix metalloproteinase-1, -2 and -9). Moreover, we consider a simple canonical problem wherein a thin-walled, cylindrical artery (mouse aorta) remains axisymmetric during adaptation and its luminal radius remains essentially unchanged due to a modest perturbation in blood pressure in the absence of a change in flow. In this special case, the CMM and the ABM can be run independently and their outputs can be compared. Such comparisons are essential prior to coupling the different models tightly via information exchanges during a single simulation.
Constrained Mixture Model (CMM)
The concept of a CMM of soft tissue growth and remodeling was introduced by Humphrey and Rajagopal.17 This theoretical framework enforces full mixture equations of mass balance for both structurally significant (insoluble) and structurally insignificant (soluble or insoluble) constituents, but enforces the classical equation of linear momentum balance quasi-statically in terms of a rule-of-mixtures relation for the stress response (i.e., individual strain energy functions are assumed to be additive). Individual structurally significant constituents are allowed to exhibit different natural (stress-free) configurations, rates of turnover, and material properties despite being constrained to deform together with the tissue as a whole. Over the past few years, CMMs of arterial adaptations have been verified via numerical hypothesis testing and parametric sensitivity studies,14,18 and they have been shown to capture salient features of diverse vascular adaptations and disease processes.11,12,19
Mathematical details and descriptions of the data-driven formulations can be found elsewhere,11 but note here that three classes of constitutive relations are needed for each of the K = 1,2,…, n structurally significant constituents: stored energy functions (energy per surface area in a thin-walled formuation) that describe elastic responses of individual constituents, rates of mass density production (mass per surface area per time) that mathematically account for cell proliferation and matrix synthesis, and survival functions (non-dimensional and bounded from 0 to 1) that account for cell apoptosis / necrosis and matrix degradation. Herein, we consider n = 3 primary structural constituents, amorphous elastin, fibrillar collagens (types I and III combined), and smooth muscle that can exhibit active and passive mechanical behaviors. Whereas classical relations have proven useful for prescribing individual stored energy functions (e.g., neo-Hookean for elastin or exponential for collagen and passive smooth muscle), first order approximations have been employed for both the mass density production and survival functions. For example, mass density production has commonly been assumed to deviate from its basal value in proportion to differences in intramural and wall shear stress from target values, namely
| (1) |
where is the basal rate of production and and are dimensionless gain-type parameters that scale the stress-mediated changes in production at each growth and remodeling time s. Differences in a scalar metric of intramural stress from baseline are denoted by , where the subscript h denotes the homeostatic target value, and similarly for differences in wall shear stress Ωτw. In this way, it is possible for individual constituents to increase their contribution to loading bearing when stresses exceed target values; conversely, if stresses equal their target values, then the production rate equals its basal value as it should. This “lumped parameter” relation is based on considerable tissue level data that suggest sigmoidal relations between changes in the cellular production of diverse effector molecules and changes in stress.13 For example, increased production of TGF-b by stressed smooth muscle cells increases their production of collagen whereas increased endothelial production of NO (at high wall shear stress) or ET-1 (at low wall shear stress) decrease and increase, respectively, the production of collagen by smooth muscle cells. The assumed linearity of Eq. (1) thus approximates the sigmoidal mechanical dose responses when differences in stress from target are modest (noting, for example, that homeostatic values in the mouse aorta are on the order of 100 kPa for intramural circumferential stress and 10 Pa for wall shear stress). Copious tissue level data suggest further that apoptosis and the degradation of extracellular constituents by matrix metalloproteinases (MMPs) both tend to follow first-order type kinetics.20-24 Hence, a commonly used form for the survival function is
| (2) |
where is a rate-type parameter (having units of inverse days) and denotes differences between the current tension, at time s, and its homeostatic value, at time τ when the constituent was synthesized and incorporated within the extant matrix. Note that if is zero and is constant, then one recovers a first order kinetic decay. The tension dependency is meant to capture some of the complexity of MMPs in stressed tissues, noting that MMP production and activity can increase with increased stress on a cell while degradation rates can decrease for collagen at higher stresses. Functional vascular elastin is unique in that it tends to be deposited during the perinatal period and its half-life tends to be on the order of the lifespan of the organism (e.g., 40 years in humans).25-28 Hence, one need not prescribe kinetic functions for elastin under normal conditions in maturity.
Agent Based Model (ABM)
Individual cells, or agents, are identified in ABMs by their pixel location within a prescribed computational grid and by the behaviors they are endowed with based on prescribed cell specific rule-sets. For example, smooth muscle cells (SMCs) are allowed to proliferate, migrate (move from one pixel to another), and synthesize and secrete diverse proteins, including growth factors (PDGF-AB and TGF-b), extracellular matrix proteins (e.g., collagen type I), and proteases (e.g., MMP-1). As noted earlier, the rates and extents of production of many of these factors by an individual SMC are regulated in part by the circumferential stress that the cell experiences at a particular time. Endothelial cells (ECs) are similarly capable of producing vasoactive molecules (e.g., ET-1 and NO), growth factors, and MMPs. Soluble molecules, such as NO, ET-1, PDGF-AB, TGF-b, MMP-1, 2, and 9, can diffuse throughout the computational domain based on a pixel-based algorithm that approximates Fick’s second law of diffusion.29
A detailed description of procedures used to identify rule-sets for different types of vascular cells and effector molecules of interest can be found elsewhere, and so too a listing of many specific rules and parameter values.15 Here, therefore, we simply discuss two illustrative examples. Data suggest that the production of TGF-b by smooth muscle cells in response to changes in circumferential stress30,31 can be modeled via a simple linear rule (cf. Eq (1) for the CMM), namely
where m (pg/kPa) and b (pg) are parameters required to fit the data. Note that the basal production is obtained when the circumferential stress is at its homeostatic target value. In contrast, the rate of production of MMP-2 by smooth muscle cells in response to changes in circumferential stress32,33 appears to demand a more complex rule,
where M is the maximum rate of production (e.g., 0.018 ng/cell/6 hrs), and δ, α, κ and n are parameters required to fit the data. Given that MMPs are often produced in latent form (as proMMPs), the parameter A further allows this relation to yield that percentage of the MMP that is active. Regarding activity, note for example that the amount of active MMP-1 (pg) at a particular pixel will degrade collagen I at that pixel proportional to enzyme present. Similarly, the amount of PDGF-AB (in pg) at a particular pixel will cause the SMC at that discrete location to proliferate accordingly, which in turn will contribute to overall arterial growth via a radial increase in wall thickness. Consequences of the other 5 key molecules are also modeled similarly. In summary, we reiterate that our ABM rule-sets have been subjected to a formal confidence scoring as well as numerical testing of their ability to yield both homeostatic stability and insensitivity to transient changes in stimuli.15 In other words, we have previously required comparable levels of model verification for the ABM and the CMM separately.
Illustrative Simulation
We adopted the models of arterial adaptation reported by Valentin et al.11 for the CMM and Thorne et al.15 for the ABM. Both models were prescribed herein to have the same initial geometry and mass fractions of solid constituents for an abdominal aorta from the mouse: an initial pressurized inner radius of 230 μm, wall thickness of about 30 μm, and SMC, elastin, and collagen mass fractions of 0.28, 0.28, and 0.44, respectively. Note that the ABM also included a monolayer of ECs, but they did not play any role in the problem studied because of the assumed near constancy of wall shear stress in the presence of a constant blood flow. Constituent mass was distributed uniformly in the CMM. In contrast, SMC mass was distributed in the ABM via approximately 3 layers of cells (Fig. 1), with each 10 μm × 10 μm pixel patch containing a SMC agent in addition to matrix (i.e., collagen and elastin) and non-space occupying biochemical factors. The total mass of the ABM vessel due to the simulated SMCs at each time point, i, was thus calculated as
| (3) |
where Vi was the current vessel volume (i.e., total number of pixels multiplied by a fixed volume per pixel patch (1.0E-9 cm3/patch), ρ the mixture density of the artery (1.05 g/cm3), and and Emass the current mass of collagen and elastin, respectively. Hence, although there was only one SMC agent at each pixel, the mass and size of that SMC could evolve (i.e., hypertrophy or atrophy) depending on the mass of the other constituents at that pixel. The average wall thickness of the vessel was calculated from the area of each pixel patch, where
| (4) |
with rl denoting the constant luminal radius (230 μm) and Ai the current vessel area or number of patches multiplied by the area for each pixel.
FIGURE 1.
Graphical display of an ABM model of a mouse abdominal aorta (a) before and (b) after a simulated hypertension (defined herein as a sustained 30% increase in mean pressure).
The response of the CMM to changes in pressure was determined by material parameters for the aforementioned passive behavior of elastin (modeled as neo-Hookean) and collagen (modeled as exponential), the active behavior of the smooth muscle (modeled using a Rachev – Hayashi relation18), and growth and remodeling parameters for cell turnover and matrix deposition and degradation (Tables 1 and 2). For example, muscle activation parameters included the circumferential stretch at which contraction was maximum or minimum plus the net ratio of constrictors to dilators. Most of these parameters are well known or well bounded18. The behavior of each agent within the ABM was similarly determined by a selected set of 17 rules governed by 37 parameters15 (Tables 1 and 2). Note that EC production of NO, ET-1, and PDGF-AB in response to shear stress were fixed in these simulations because of the constancy of flow and because inner radius did not change appreciably in the ABM. The rules governing the removal of cleaved collagen and elastin by gelatinases (i.e., MMP-2 and MMP-9) were also fixed based on pilot parameter sensitivity studies. In summary, for the illustrative problem considered, only 4 parameters in the CMM and 12 parameters in the ABM were deemed to be less well determined and thus required further refinement (Table 2) via our proposed congruency check. Bounds for these parameters were prescribed based on our prior parameter sensitivity studies (Table 2).15,18
TABLE 1.
Values of model parameters used in the ABM and CMM to simulate the bio-chemo-mechanical response of a mouse abdominal aorta to altered blood pressure. These values were inferred from the literature and deemed either to be reliable or to be reasonable based on prior parameter sensitivity studies; hence, they were fixed and not optimized in the minimization procedure to increase congruency. For detailed information on the constitutive relations or rules in which the parameters occur, please see the original papers15,18.
| Prescribed (Fixed) Parameters | |
|---|---|
| CMM | References |
| Prestretches and Elastic Parameters | |
| , , | [12] |
| ce = 58.8 KPa, , , , | |
| Muscle Activation and Shear-Constrictor Ratio | |
| TM = 150 KPa, λM = 1.6, λ0 = 0.83 | [36] |
| CB = 0.68 | [18] |
| Initial Mass Fractions and Half-lives | |
| ϕc(0) = 0.44, ϕe(0) = 0.28 ϕm(0) = 0.28 | [37,38] |
| , | [2,39] |
|
| |
| ABM | |
|
| |
| Growth Factors | |
| δPDGF = 0.15, αPDGF = 0.84, ΚPDGF = 0.42, nPDGF = 1.24 | [40,41] |
| MPDGF = 0.78 pg cell−1 6hr−1 | |
| Vasoactive Factors | |
| δET−1 = 0.60, αET−1 = 0.40, κET−1 = 3.63, nET−1 = 1.68 | [42,43] |
| MET−1 = 0.01 pg cell−1 6hr−1 | |
| Removal Factors | |
| δMMP−2 = 0.03, αMMP−2 = 0.52, κMMP−2 = 2.0E – 06, nMMP−2 = 2.84 | [32,33] |
| MMMP−2 = 1 pg cell−1 6hr−1, DMMP−2 = 99, AMMP−2 = 0.001 | |
| δMMP−9 = 0.04, αMMP−9 = 0.44, κMMP−9 = 4.0E – 06, nMMP−9 = 2.88 | [32,44] |
| MMMP−9 = 0.002 pg cell−1 6hr−1, DMMP−9 = 87, AMMP−9 = 0.003, DMMP−1 = 80.6 | |
TABLE 2.
Listed are both the initial values of the parameters and the bounds that defined the search space used in the genetic algorithm to improve congruency between ABM and CMM predictions of smooth muscle and collagen mass via Eq. (5). Note that 16 parameters were allowed to vary: CMM (top 4 rows) and ABM (bottom 12 rows). See Eqs. (1) and (2), the Appendix, and Table 1 in Thorne et al.15 for associated constitutive equations, definitions, or rules. Also listed are the final values of the parameters following minimization.
| Parameter | Initial Value | Lower Bound | Upper Bound | After Genetic Algorithm |
|---|---|---|---|---|
| 1 | 0.1 | 10 | 1.11 | |
| 10 | 0.1 | 10 | 3.85 | |
| 1 | 0.1 | 10 | 2.85 | |
| 10 | 0.1 | 10 | 8.75 | |
|
| ||||
| MMP-10 | 2.69E-04 | 2.69E-05 | 2.69E-03 | 9.47E-04 |
| MMP-1%A | 0.39 | 0.039 | 3.93 | 1.04 |
| C0 | 0.009 | 0.0009 | 0.09 | 0.07 |
| CTGF | 114.94 | 11.49 | 1149.42 | 134.57 |
| Mp | −1.45E+09 | −1.45E+10 | −9.69E+08 | −1.53E+09 |
| M0 | 80000 | 53333.33 | 120000 | 6.12E+04 |
| Ma1 | 71020 | 7102 | 106530 | 9.89E+04 |
| Ma2 | 100 | 66.66 | 1000 | 223.21 |
| PDGFσθ | 4.79E-07 | 3.19E-07 | 7.19E-07 | 7.03E-07 |
| PDGF0 | 4.17E-05 | 4.17E-06 | 6.25E-05 | 6.17E-05 |
| TGFβσθ | 1.65E-06 | 1.65E-07 | 1.65E+05 | 7.87E-06 |
| TGFβ0 | 1.03E-04 | 1.03E-05 | 1.03E-03 | 3.69E-04 |
Model Congruency
A strategy common in multiscale modeling is to let the lower scale models sequentially inform the higher scale models, which ultimately should lead to tissue- or organ-level behaviors of clinical importance. The tacit assumption underlying such a strategy is that the lower scale models, or associated data, are more reliable. We suggest that this need not be the case. Rather, all data are inherently limited and it is preferable to ensure model congruency across scales by requiring outputs common to the models to be self-consistent.
We used predicted collagen and smooth muscle mass as outputs common to the ABM and the CMM suitable for congruency checking. Whereas the CMM is designed to satisfy the condition of tissue maintenance automatically (i.e., no net changes under conditions of balanced turnover in unchanging configurations), this need not always be the case for the ABM because of its inherent stochasticity and because data are generally collected separately for production and removal. Moreover, the prior parameter sensitivity study for the ABM was one-dimensional15; small changes to multiple ABM parameters that favor a particular action (e.g. proliferation) could potentially lead to an unsteady response even under normal conditions. Hence, we sought to ensure congruency for both the problem of tissue maintenance over a 56 day simulation (i.e., normotension, or, NT) and the problem of a long-term aortic adaptation to a sustained 30% increase in pressure (i.e., hypertension, or, HT) that began on day 2 of a 500 day simulation. The durations of study for NT and HT were motivated by prior results using a CMM11 and were not too computationally expensive.
Mathematically, therefore, to increase congruency between the ABM and CMM, we sought to minimize the following objective function,
| (5) |
where C denotes mass of collagen present during each 6 hour time step j for either the ABM or the CMM, and M likewise denotes the mass of smooth muscle predicted by either the ABM or the CMM. Because of the lack of information otherwise, we did not weight the minimization to favor either the ABM or CMM; that is, both were deemed to be equally uncertain in general. When additional data become available, the minimization could be weighted accordingly. Regardless, a genetic algorithm (GA) heuristic in MATLAB was used to find optimal values of the 16 parameters by minimizing the value of e. Genetic algorithms are based on concepts of natural selection and are well suited for stochastic or highly nonlinear objective functions. Basically, the GA generates parameter sets (called populations) derived from a parent set (i.e., set of parameters that gave the lowest value of e). The number of parameter sets (population size) for each generation herein was set to 40, and the process was repeated for 25 generations. Due to the stochastic nature of the ABM, each population was simulated at least 10 times and these outputs (M and C) averaged before comparison with the outputs from the CMM.
RESULTS
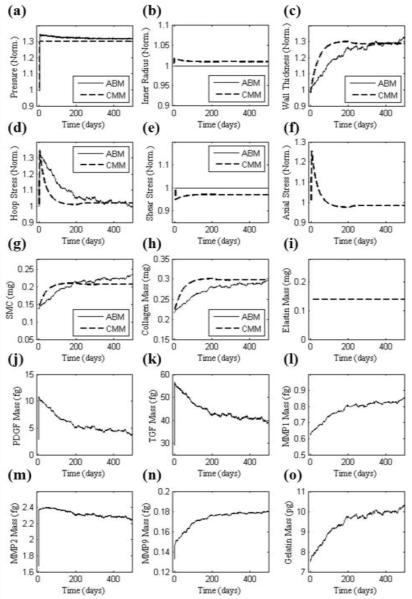
Aortic responses to increased blood pressure (HT), defined herein as an abrupt but sustained 30% increase in mean arterial pressure from 96.4 to 125.3 mmHg34, was simulated independently by the CMM and ABM. The CMM predicted an initial increase in circumferential and axial stress and a decrease in wall shear stress due to the abrupt increase in pressure and the associated elastic distension (increase in inner radius) and isochoric thinning of the wall. Consistent with Eq. (1), the increased intramural stress and decreased wall shear stress worked together to hasten an increase in both SMC and collagen mass, which in turn thickened the wall and restored intramural stresses toward normal over time (Fig. 2). Note that there was no change in elastin mass although all mass fractions changed accordingly, and a rapid vasoconstriction returned the luminal diameter back toward its original value. The ABM also responded to the sudden increase in circumferential stress, which was estimated solely by the higher pressure at a constant radius by the aforementioned Laplace’s equation, which in turn caused an associated increase in SMC production of PDGF-AB, TGF-b, and each of the MMPs. Whereas PDGF-AB led to an increase in SMC mass, TGF-b led to an increase in collagen production, which initially outpaced degradation. Note that the amount of collagen tended to reach steady state around day 220 when both TGF-b and MMP-1 also tended to plateau. Hence, the arterial wall also thickened in the ABM (Fig. 2). The expected 30% thickening13 was achieved by both models, albeit over different time courses. This thickening is illustrated visually in Fig. 1 for the ABM, which shows actual screen-shots that contrast the mouse abdominal aorta in normotensive (Fig. 1a) and hypertensive conditions after 500 days of elevated blood pressure (Fig. 1b). The endothelial layer is shown in yellow and the media in red, with the inner radius and number of ECs kept fixed.
FIGURE 2.
Illustrative results, before parameter refinement via the genetic algorithm, for a 30% increase in mean luminal pressure using initial parameters (Table 2). CMM (dashed line) and ABM (solid line) predictions of (a) pressure and (d,e,f) stresses normalized with respect to the homeostatic values, (b) luminal diameter and (c) thickness normalized with respect to original values, (g-i) intramural constituents, and (j-o) soluble molecular masses. Elastin mass, but not mass fraction, is constant in the CMM and currently not predicted by the ABM. Axial stress cannot be estimated by the ABM and was not considered within the CMM to alter turnover rates in this illustrative simulation.
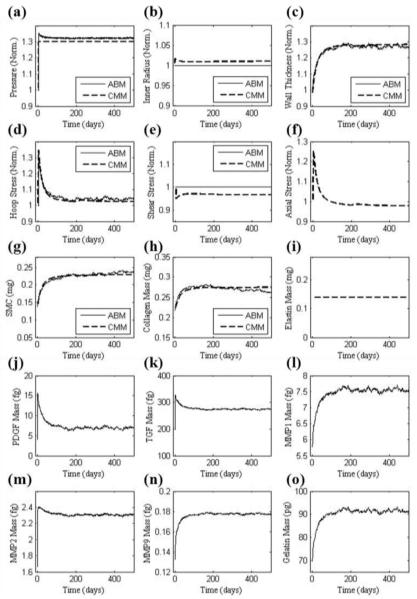
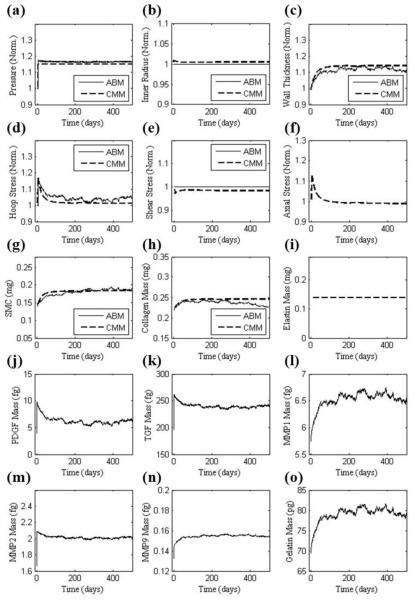
The outputs in Fig. 2 resulted when using parameter values (initially determined directly from data in the literature) corresponding to the two separate scales (i.e. tissue and cellular). Given the different time courses for the two predictions, we sought to increase congruency across the scales by simultaneously refining the less reliable parameters in each model (4 for the CMM and 12 for the ABM). This refinement was accomplished using the genetic algorithm to minimize the objective function in Eq. 5 based on two common outputs, predicted SMC and collagen mass. Table 2 shows both the initial and the refined parameter values. The hypertensive simulation of Fig. 2 was then repeated with the refined parameters (Fig. 3). Whereas all prior responses were preserved qualitatively, note the improved agreement between the models throughout the time course of changing SMC and collagen mass. For example, the percent difference between SMC and collagen mass, as predicted by the CMM and ABM, was only 4.3%. Agreement was also improved between the models for both wall thickness and circumferential stress. In particular, the refined parameter values allowed the ABM to predict a faster increase in growth factors, metalloproteinases, and gelatin mass. The sustained increase in SMC and collagen mass corresponded well with the sustained increase in wall thickness after the artery remodeled in a new state within ~120 days. Fig. 4 shows a similarly good agreement between models for the case of a 15% increase in blood pressure using the parameters from Table 2 and Fig. 3, which were based on the required congruency for a 30% increase in pressure. This figure thus shows that advantages of this simple verification step apply more broadly than for the single case examined.
FIGURE 3.
Similar to Figure 2 (for 30% increase in pressure) except based on values of the parameters (Table 2) that increased congruency between ABM and CMM model predictions of collagen and smooth muscle mass; these parameters were determined by minimizing Eq. (5) using the genetic algorithm.
FIGURE 4.
Similar to Figure 3 except for a 15% increase in pressure. Note, however, that the parameter values were the same as used in Figure 3, which were found to increase congruency between the ABM and CMM for the case of a 30% increase in pressure. Hence, this result shows the broader applicability of the minimization procedure.
Finally, as shown in Supplemental Figure S1, note that geometry and mass did not deviate significantly from baseline values in a 500 day simulation of normotension using the refined parameter values. This finding resulted, in part, because parameter refinement sought congruency under both normotensive and hypertensive conditions and the CMM has been shown previously to be stable under homeostatic conditions for long periods18. Ensuring balanced turnover (biological stability) is important because data informing the models often come from studies wherein production (e.g, matrix synthesis) or removal (e.g., MMP activity) are considered independently. Ensuring numerical stability is equally important for it confirms that computational inaccuracies do not affect the results.
DISCUSSION
A common fallacy in multiscale modeling is that data at lower scales are necessarily more reliable. Rather, we emphasize that whereas experiments conducted at lower scales are often better controlled, which gives rise to data that are easier to interpret, the associated experimental conditions (e.g., experiments on isolated cells cultured on 2-D membranes) tend to render the cellular environment, and thus response, different from physiological. Hence, one must often question the in vivo relevancy, and thus overall utility, of lower scale assays. In contrast, experiments conducted at higher levels of biological scale (e.g., in vivo studies) are, by definition, physiologically relevant, yet the plethora of uncontrolled effects (hormonal or neural, artifacts induced by anesthesia, and so forth) render the interpretation of the associated results difficult. Given our ultimate desire to understand tissue level phenomena based on molecular and cellular level mechanisms, we must find ways to overcome inherent limitations in the available data. In this paper, we suggest that multiscale modeling may provide one logical means for extracting the best information from the inherently limited data that are collected at different scales.
We suggest that multiscale modeling should not be viewed simply as a means to pass lower scale information to higher scale models in order to ultimately address pathophysiologic conditions. Rather, multiscale modeling can also be used to increase the utility of, and thus confidence in, otherwise inherently limited information. Because there should always be some overlap in the inputs or outputs of models at successive scales, it should be possible to identify simple canonical problems for the purpose of evaluating congruency across scales when the models act independently. Indeed, ensuring such congruency via parameter refinement may help obviate the propagation of uncertainty in the original data to the model.
In our illustrative example, the ABM was built on cell-level data whereas the CMM was built based largely on tissue-level data. Hence, one should not expect the two models initially to predict the same values of common outputs, as, for example, the proliferation of particular cells (e.g., SMCs) or production of particular molecules (e.g., collagen) by the ABM and the associated accumulation of mass due to such cells or molecules by the CMM. Indeed, this was borne out by the initial simulations (Fig. 2). Yet, there should be a unique production / accumulation in any actual situation independent of the models used. As we showed (Fig. 3), minimizing differences in common outputs (i.e., collagen and SMC mass) allowed an iterative refinement of parameters in both models, which in turn led to increased congruency in other predictions.
In summary, it is increasingly realized that multiscale models will be essential for integrating information from the tissue / organ level, at which diseases such as atherosclerosis and aneurysms present and can be treated clinically (e.g., stents or endografts), with information at the molecular / cell level, at which underlying mechanisms exist and can be treated (e.g., pharmacologically). In Thorne et al.15, we showed that agent based models can be subjected to verification tests that have proven useful for continuum mixture models, including numerical stability that allows one to simulate long-term homeostasis and insensitivity to transient perturbations that are not expected to affect long-term remodeling. In this way, models at two scales are rendered internally consistent and more amenable to linking in a multiscale sense. In this paper, we extended the requirement of internal consistency to include an additional level of congruency. That is, we suggest that, albeit for different reasons, experimental data are inherently limited at all scales and the associated modeling parameters should similarly be expected to be limited. By identifying appropriate canonical problems, outputs common to models at multiple scales can be compared for the same simulations; when these outputs differ, an iterative process can be used to increase model congruency. To illustrate the potential utility of this multiscale congruency approach, we simulated cell-mediated large artery adaptation to a sustained increase in blood pressure. Both models initially predicted characteristic observations of aortic adaptations to hypertension; that is, the arterial wall thickened proportional to the increase in pressure, due in large part to increased SMC and fibrillar collagen mass, and thereby restored circumferential stress toward normal while maintaining a constant inner radius and thus wall shear stress. Nevertheless, parameter refinement via the congruency checks brought these characteristic predictions into much closer agreement over the period of interest. Moreover, both predictions also appeared to come into closer agreement with data in the literature.
Wolinsky showed in a series of Goldblatt hypertension studies (systolic pressure increase of ≥ 24%) in rats that wall stress in the aorta is significantly greater than control at 70 days but returns to normal by 140 days.35 Matsumoto and Hayashi similarly showed in Goldblatt hypertensive (systolic pressure increase of ≥ 30%) rats that circumferential stress in the aorta did not return to normal until 126 days.8 The ABM alone, governed primarily by experimental data from cell culture studies, predicted a delayed remodeling response wherein circumferential stress did not return to within 1% of its target value until day 350. In contrast, the CMM, when governed primarily by data from tissue-level turnover rates plus stored energy functions for normal structurally significant constituents, predicted a faster remodeling response, returning hoop stress to within 1% of its target value by day 70. Following parameter refinement via the congruency check, both models predicted a recovery within 1% of the target circumferential stress by day 125 (Fig. 3b), which is closer to that measured experimentally in the two rodent models discussed. Although there remains a need for new experiments both to formulate improved constitutive relations for CMMs and rule-sets for ABMs and to validate single- and multi-scaled models, we submit that ensuring congruency in models across scales may help correct uncertainties that are otherwise inherent to data and models built on single-scale studies alone.
Supplementary Material
ACKNOWLEDGMENTS
This work was supported, in part, via NIH grants HL-082838 (to SMP) and HL-86418 (to JDH).
APPENDIX
| Symbol (units) | Classification | Definition |
|---|---|---|
| CMM: Bounded |
Gain parameter governing circumferential-stress mediated rate of production of collagen. See Eq. (1) |
|
| CMM: Bounded |
Gain parameter governing circumferential-stress mediated rate of production of smooth muscle. See Eq. (1) |
|
| CMM: Bounded |
Gain parameter governing shear-stress mediated rate of production of collagen. See Eq. (1) |
|
| CMM: Bounded | Gain parameter governing shear-stress mediated rate of production of smooth muscle. See Eq. (1) |
|
| MMP-10 (pg) | ABM: Bounded | Baseline mass of MMP-1 |
| MMP-1%A (%) | ABM: Bounded | Percent of MMP-1 that is active |
| C0 (pg) | ABM: Bounded | Baseline mass of collagen |
| CTGF | ABM: Bounded | Rate parameter governing TBFb mediated rate of production of collagen (pg of collagen per pg of TGFb) |
| Mp | ABM: Bounded |
Rate parameter governing PDGF mediated SMC proliferation rate (pg of SMC per pg of PDGF) |
| M0 (pg) | ABM: Bounded | Baseline SMC proliferation rate (pg) |
| Ma1 | ABM: Bounded | Apoptosis chance for SMC (1) |
| Ma2 | ABM: Bounded | Baseline apoptosis chance for SMC (2) |
| PDGFσθ(pg/kPa) | ABM: Bounded |
Rate parameter governing hoop stress mediated rate of production of PDGF (pg of PDGF per kPa of stress) |
| PDGF0 (pg) | ABM: Bounded | Baseline mass of PDGF |
| TGFβσθ (pg) | ABM: Bounded |
Rate parameter governing hoop stress mediated rate of production of TGFb (pg of TGFb per kPa of stress) |
| TGFβ0 (pg) | ABM: Bounded | Baseline mass of TGFb |
| CMM: Observed | Homeostatic stretch when elastin is deposited | |
| CMM: Observed | Homeostatic stretch when collagen is deposited | |
| CMM: Observed | Homeostatic stretch when SMC is deposited | |
| Ce (kPa) | CMM: Calculated |
Neo-Hookean material parameter for the stored energy of elastin |
| CMM: Calculated |
Fung-type exponential material parameter for the stored energy of collagen (1) |
|
| CMM: Calculated | Fung-type exponential material parameter for the stored energy of SMC (1) |
|
| CMM: Observed |
Fung-type exponential material parameter for the stored energy of collagen (2) |
|
| CMM: Observed |
Fung-type exponential material parameter for the stored energy of SMC (2) |
|
| Tm(kPa) | CMM: Observed | Maximum stress generated by SMC |
| λM | CMM: Observed | Circumferential stretch where active stress is maximum |
| λ0 | CMM: Observed | Circumferential stretch where active stress is zero |
| CB | CMM: Observed |
Material parameter for the ratio of constrictor concentration to dilator concentration |
| CS | CMM: Observed |
Scaling parameter for shear stress induced change in constrictor concentration scaling factor |
| ϕc(0) | CMM: Observed | Initial mass fraction of collagen in the arterial wall |
| ϕe(0) | CMM: Observed | Initial mass fraction of elastin in the arterial wall |
| ϕm(0) | CMM: Observed | Initial mass fraction of SMC in the arterial wall |
| CMM: Observed | Half-life of SMC | |
| CMM: Observed | Half-life of collagen | |
| NO0 (pg) | ABM: Observed | Baseline mass of NO |
| NOτw | ABM: Observed |
Rate parameter governing shear stress mediated rate of production of NO (pg of NO per kPa of stress) |
|
δPDGF (pg) αPDGF κPDGF(kPa−1) nPDGF MPDGF |
ABM: Observed | Parameters of the sigmoid function: PDGF = M (δ + α(1 – e−kxn)) Maximum rate of PDGF production |
|
δET–1 (pg) αET–1 κET–1 (kPa−1 nET–1 MET–1 |
ABM: Observed |
Parameters of the sigmoid function: ET1 = M (δ + α(1 – e−kxn)) Maximum rate of ET-1 production |
|
δMMP–2 (pg) αMMP–2 κMMP–2 (kPa−1) nMMP–2 MMMP–2 AMMP–2 (%) |
ABM: Observed | Parameters of the sigmoid function: MMP2 = A (M (δ +α(1 – e−kxn))) Maximum rate of MMP-2 production Percent of MMP-2 Active |
| DMMP–2 | ABM: Observed | Degradation rate of MMP-2 |
|
δMMP–9 (pg) αMMP–9 κMMP–9 (KPa−1 nMMP–9 MMMP–9 AMMP–9 (%) |
ABM: Observed | Parameters of the sigmoid function: MMP9 = A (M (δ +α(1 – e−kxn))) Maximum rate of MMP-9 production Percent of MMP-9 Active |
| DMMP–9 | ABM: Observed | Degradation rate of MMP-9 |
| DMMP–1 | ABM: Observed | Degradation rate of MMP-1 |
Note: Parameters within the ABM or CMM are classified as observed, bounded, or calculated. Observed parameters were either cited elsewhere or obtained via direct measurements or fits to experimental data. Bounded parameters are less well known, but are expected to fall within specified range. Lastly, calculated parameters include those that are needed to satisfy equilibrium under homeostatic conditions.
Footnotes
Conflicts: None
REFERENCES
- 1.Wolinsky H, Glagov S. A lamellar unit of aortic medial structure and function in mammals. Circ Res. 1967;20:99–111. doi: 10.1161/01.res.20.1.99. [DOI] [PubMed] [Google Scholar]
- 2.Langille BL. Remodeling of developing and mature arteries: endothelium, smooth muscle, and matrix. J Cardiovasc Pharmacol. 1993;21(Suppl 1):S11–17. doi: 10.1097/00005344-199321001-00003. [DOI] [PubMed] [Google Scholar]
- 3.Lehoux S, Levy BI. Collateral artery growth: making the most of what you have. Circ Res. 2006;99:567–569. doi: 10.1161/01.RES.0000243585.97392.95. [DOI] [PubMed] [Google Scholar]
- 4.Li S, Huang NF, Hsu S. Mechanotransduction in endothelial cell migration. J Cell Biochem. 2005;96:1110–1126. doi: 10.1002/jcb.20614. [DOI] [PubMed] [Google Scholar]
- 5.Greve JM, Les AS, Tang BT, Draney Blomme MT, Wilson NM, Dalman RL, Pelc NJ, Taylor CA. Allometric scaling of wall shear stress from mice to humans: quantification using cine phase-contrast MRI and computational fluid dynamics. Am J Physiol Heart Circ Physiol. 2006;291:H1700–1708. doi: 10.1152/ajpheart.00274.2006. [DOI] [PubMed] [Google Scholar]
- 6.Wolinsky H. Effects of hypertension and its reversal on the thoracic aorta of male and female rats. Morphological and chemical studies. Circ Res. 1971;28:622–637. doi: 10.1161/01.res.28.6.622. [DOI] [PubMed] [Google Scholar]
- 7.Hu JJ, Baek S, Humphrey JD. Stress-strain behavior of the passive basilar artery in normotension and hypertension. J Biomech. 2007;40:2559–2563. doi: 10.1016/j.jbiomech.2006.11.007. [DOI] [PubMed] [Google Scholar]
- 8.Matsumoto T, Hayashi K. Mechanical and dimensional adaptation of rat aorta to hypertension. J Biomech Eng. 1994;116:278–283. doi: 10.1115/1.2895731. [DOI] [PubMed] [Google Scholar]
- 9.Taber LA. A model for aortic growth based on fluid shear and fiber stresses. J Biomech Eng. 1998;120:348–354. doi: 10.1115/1.2798001. [DOI] [PubMed] [Google Scholar]
- 10.Rachev A, Stergiopulos N, Meister JJ. Theoretical study of dynamics of arterial wall remodeling in response to changes in blood pressure. J Biomech. 1996;29:635–642. doi: 10.1016/0021-9290(95)00108-5. [DOI] [PubMed] [Google Scholar]
- 11.Valentin A, Cardamone L, Baek S, Humphrey JD. Complementary vasoactivity and matrix remodelling in arterial adaptations to altered flow and pressure. J R Soc Interface. 2009;6:293–306. doi: 10.1098/rsif.2008.0254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Baek S, Valentin A, Humphrey JD. Biochemomechanics of cerebral vasospasm and its resolution: II. Constitutive relations and model simulations. Ann Biomed Eng. 2007;35:1498–1509. doi: 10.1007/s10439-007-9322-x. [DOI] [PubMed] [Google Scholar]
- 13.Humphrey JD. Vascular adaptation and mechanical homeostasis at tissue, cellular, and sub-cellular levels. Cell Biochem Biophys. 2008;50:53–78. doi: 10.1007/s12013-007-9002-3. [DOI] [PubMed] [Google Scholar]
- 14.Valentin A, Humphrey JD. Evaluation of fundamental hypotheses underlying constrained mixture models of arterial growth and remodelling. Philos Transact A Math Phys Eng Sci. 2009;367:3585–3606. doi: 10.1098/rsta.2009.0113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Thorne BC, Hayenga HN, Humphrey JD, Peirce SM. Towards a multi-scale computational model of arterial adaptation in hypertension: verification of a multi-cell agent-based model. Frontiers in Computational Physiology and Medicine. 2011;2:1–12. doi: 10.3389/fphys.2011.00020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Thorne BC, Bailey AM, DeSimone DW, Peirce SM. Agent-based modeling of multicell morphogenic processes during development. Birth Defects Research Part C: Embryo Today: Reviews. 2007;81:344–353. doi: 10.1002/bdrc.20106. [DOI] [PubMed] [Google Scholar]
- 17.Humphrey JD, Rajagopal KR. A constrained mixture model for arterial adaptations to a sustained step change in blood flow. Biomech Model Mechanobiol. 2003;2:109–126. doi: 10.1007/s10237-003-0033-4. [DOI] [PubMed] [Google Scholar]
- 18.Valentin A, Humphrey JD. Parameter sensitivity study of a constrained mixture model of arterial growth and remodeling. J Biomech Eng. 2009;131:101006. doi: 10.1115/1.3192144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Baek S, Rajagopal KR, Humphrey JD. A theoretical model of enlarging intracranial fusiform aneurysms. J Biomech Eng. 2006;128:142–149. doi: 10.1115/1.2132374. [DOI] [PubMed] [Google Scholar]
- 20.Cho A, Courtman DW, Langille BL. Apoptosis (programmed cell death) in arteries of the neonatal lamb. Circ Res. 1995;76:168–175. doi: 10.1161/01.res.76.2.168. [DOI] [PubMed] [Google Scholar]
- 21.Gelman RA, Williams BR, Piez KA. Collagen fibril formation. Evidence for a multistep process. J Biol Chem. 1979;254:180–186. [PubMed] [Google Scholar]
- 22.Kao WW, Berg RA, Prockop DJ. Kinetics for the secretion of procollagen by freshly isolated tendon cells. J Biol Chem. 1977;252:8391–8397. [PubMed] [Google Scholar]
- 23.Niedermuller H, Skalicky M, Hofecker G, Kment A. Investigations on the kinetics of collagen-metabolism in young and old rats. Exp Gerontol. 1977;12:159–168. doi: 10.1016/0531-5565(77)90001-8. [DOI] [PubMed] [Google Scholar]
- 24.Gelman RA, Poppke DC, Piez KA. Collagen fibril formation in vitro. The role of the nonhelical terminal regions. J Biol Chem. 1979;254:11741–11745. [PubMed] [Google Scholar]
- 25.Langille BL. Arterial remodeling: relation to hemodynamics. Can J Physiol Pharmacol. 1996;74:834–841. [PubMed] [Google Scholar]
- 26.Shapiro SD, Endicott SK, Province MA, Pierce JA, Campbell EJ. Marked longevity of human lung parenchymal elastic fibers deduced from prevalence of D-aspartate and nuclear weapons-related radiocarbon. J Clin Invest. 1991;87:1828–1834. doi: 10.1172/JCI115204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Davis EC. Stability of elastin in the developing mouse aorta: a quantitative radioautographic study. Histochemistry. 1993;100:17–26. doi: 10.1007/BF00268874. [DOI] [PubMed] [Google Scholar]
- 28.Humphrey JD. Cardiovascular Solid Mechanics: Cells Tissues and Organs. 1 ed. Springer; New York: 2002. [Google Scholar]
- 29.Robertson SH, Smith CK, Langhans AL, McLinden SE, Oberhardt MA, Jakab KR, Dzamba B, DeSimone DW, Papin JA, Peirce SM. Multiscale computational analysis of Xenopus laevis morphogenesis reveals key insights of systems-level behavior. BMC Syst Biol. 2007;1:46. doi: 10.1186/1752-0509-1-46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mata-Greenwood E, Grobe A, Kumar S, Noskina Y, Black SM. Cyclic stretch increases VEGF expression in pulmonary arterial smooth muscle cells via TGF-beta1 and reactive oxygen species: a requirement for NAD(P)H oxidase. Am J Physiol Lung Cell Mol Physiol. 2005;289:L288–289. doi: 10.1152/ajplung.00417.2004. [DOI] [PubMed] [Google Scholar]
- 31.Morishita R, Gibbons GH, Horiuchi M, Kaneda Y, Ogihara T, Dzau VJ. Role of AP-1 complex in angiotensin II-mediated transforming growth factor-beta expression and growth of smooth muscle cells: using decoy approach against AP-1 binding site. Biochem Biophys Res Commun. 1998;243:361–367. doi: 10.1006/bbrc.1997.8012. [DOI] [PubMed] [Google Scholar]
- 32.Kim YS, Galis ZS, Rachev A, Han HC, Vito RP. Matrix metalloproteinase-2 and -9 are associated with high stresses predicted using a nonlinear heterogeneous model of arteries. J Biomech Eng. 2009;131:011009. doi: 10.1115/1.3005163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Okuno T, Andoh A, Bamba S, Araki Y, Fujiyama Y, Fujiyama M, Bamba T. Interleukin-1beta and tumor necrosis factor-alpha induce chemokine and matrix metalloproteinase gene expression in human colonic subepithelial myofibroblasts. Scand J Gastroenterol. 2002;37:317–324. doi: 10.1080/003655202317284228. [DOI] [PubMed] [Google Scholar]
- 34.Guo X, Kassab GS. Variation of mechanical properties along the length of the aorta in C57bl/6 mice. Am J Physiol Heart Circ Physiol. 2003;285:H2614–2622. doi: 10.1152/ajpheart.00567.2003. [DOI] [PubMed] [Google Scholar]
- 35.Wolinsky H. Long-term effects of hypertension on the rat aortic wall and their relation to concurrent aging changes. Morphological and chemical studies. Circ Res. 1972;30:301–309. doi: 10.1161/01.res.30.3.301. [DOI] [PubMed] [Google Scholar]
- 36.Rachev A, Hayashi K. Theoretical study of the effects of vascular smooth muscle contraction on strain and stress distributions in arteries. Ann Biomed Eng. 1999;27:459–468. doi: 10.1114/1.191. [DOI] [PubMed] [Google Scholar]
- 37.Fischer GM, Llaurado JG. Collagen and elastin content in canine arteries selected from functionally different vascular beds. Circ Res. 1966;19:394–399. doi: 10.1161/01.res.19.2.394. [DOI] [PubMed] [Google Scholar]
- 38.Faury G, Pezet M, Knutsen RH, Boyle WA, Heximer SP, McLean SE, Minkes RK, Blumer KJ, Kovacs A, Kelly DP, et al. Developmental adaptation of the mouse cardiovascular system to elastin haploinsufficiency. J Clin Invest. 2003;112:1419–1428. doi: 10.1172/JCI19028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Stenmark KR, Mecham RP. Cellular and molecular mechanisms of pulmonary vascular remodeling. Annu Rev Physiol. 1997;59:89–144. doi: 10.1146/annurev.physiol.59.1.89. [DOI] [PubMed] [Google Scholar]
- 40.Ma YH, Ling S, Ives HE. Mechanical strain increases PDGF-B and PDGF beta receptor expression in vascular smooth muscle cells. Biochem Biophys Res Commun. 1999;265:606–610. doi: 10.1006/bbrc.1999.1718. [DOI] [PubMed] [Google Scholar]
- 41.Li Z, Moore S, Alavi MZ. Mitogenic factors released from smooth muscle cells are responsible for neointimal cell proliferation after balloon catheter deendothelialization. Exp Mol Pathol. 1995;63:77–86. doi: 10.1006/exmp.1995.1032. [DOI] [PubMed] [Google Scholar]
- 42.Dancu MB, Berardi DE, Vanden Heuvel JP, Tarbell JM. Asynchronous shear stress and circumferential strain reduces endothelial NO synthase and cyclooxygenase-2 but induces endothelin-1 gene expression in endothelial cells. Arterioscler Thromb Vasc Biol. 2004;24:2088–2094. doi: 10.1161/01.ATV.0000143855.85343.0e. [DOI] [PubMed] [Google Scholar]
- 43.Ziegler T, Bouzourene K, Harrison VJ, Brunner HR, Hayoz D. Influence of oscillatory and unidirectional flow environments on the expression of endothelin and nitric oxide synthase in cultured endothelial cells. Arterioscler Thromb Vasc Biol. 1998;18:686–692. doi: 10.1161/01.atv.18.5.686. [DOI] [PubMed] [Google Scholar]
- 44.Garcia-Lopez G, Vadillo-Ortega F, Merchant-Larios H, Maida-Claros R, Osorio M, Soriano-Becerril D, Flores-Herrera H, Beltran-Montoya J, Garfias-Becerra Y, Zaga-Clavellina V. Evidence of in vitro differential secretion of 72 and 92 kDa type IV collagenases after selective exposure to lipopolysaccharide in human fetal membranes. Mol Hum Reprod. 2007;13:409–418. doi: 10.1093/molehr/gam025. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.