Abstract
In this paper, we propose a novel method to reduce the magnitude of 4D CT artifacts by stitching two images with a data-driven regularization constrain, which helps preserve the local anatomy structures. Our method first computes an interface seam for the stitching in the overlapping region of the first image, which passes through the “smoothest” region, to reduce the structure complexity along the stitching interface. Then, we compute the displacements of the seam by matching the corresponding interface seam in the second image. We use sparse 3D features as the structure cues to guide the seam matching, in which a regularization term is incorporated to keep the structure consistency. The energy function is minimized by solving a multiple-label problem in Markov Random Fields with an anatomical structure preserving regularization term. The displacements are propagated to the rest of second image and the two image are stitched along the interface seams based on the computed displacement field. The method was tested on both simulated data and clinical 4D CT images. The experiments on simulated data demonstrated that the proposed method was able to reduce the landmark distance error on average from 2.9 mm to 1.3 mm, outperforming the registration-based method by about 55%. For clinical 4D CT image data, the image quality was evaluated by three medical experts, and all identified much fewer artifacts from the resulting images by our method than from those by the compared method.
1. Introduction
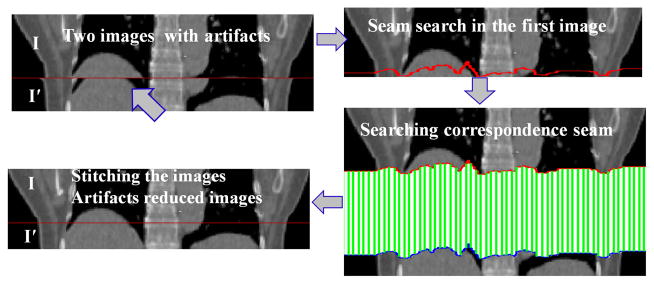
The spatial accuracy of reconstructed medical images is critically important in radiation therapy, both for tumors and for the surrounding normal tissue. Four dimensional computed tomography (4D CT) provides a way of reducing the uncertainties caused by respiratory motion. With 4D CT images one can assess the three dimensional (3D) position of the tumor and avoidance structures at specified phases of the respiratory cycle and directly incorporate that information into treatment planning. The fundamental problem in 4D CT image reconstruction is to stitch two image stacks from the “same” phase of two consecutive breathing cycles to form a coherent image (Fig. 1 ). However, due to the variability of the respiratory motion, those two image stacks may not come from exactly the same phase, which substantially complicates the reconstruction problem. In recent years, a great amount of efforts have been devoted on improving 4D CT imaging, including (1) using breathing training to improve the respiratory regularity [18]; (2) improving the sorting algorithms [17]; (3) using internal anatomical features instead of external surrogates [15]; and (4) post-scan processing [3, 4 ]. However, the problem remains very challenging. In fact, a recent study [21, 5] shows that all current 4D CT acquisition and reconstruction methods frequently lead to spatial artifacts and those artifacts occur with an alarmingly high frequency and spatial magnitude. Hence, significant improvement on reducing the artifacts is needed in 4D CT imaging.
Figure 1.
The fundamental problem in this paper.
One way to solve this image stitching problem is to use deformable registration [3] to account for the respiratory motion. However, general deformable registration methods may not be structure-aware, causing structure inconsistency and further producing visual artifacts. The most closely related work of our approach is the optimal seam-based method [6]. Our method shares a similar framework. One drawback of that method is, again, the lack of the capability of making use of the rich structures of the lung CT images. It does not explicitly align the anatomical structures while stitching two image stacks, causing anatomical inconsistence.
In this paper, we proposed a novel method based on graph algorithms for solving the 4D CT artifacts reduction problem. Our method is of structure-awareness and has the capability of substantially reducing the misalignment of the anatomy structures. In our method, we first compute an interface seam for stitching in the overlapping region of the first image, which passes through the “smoothest” region to reduce the structure complexity along the stitching interface. Then, the corresponding seam is obtained while mapping the first interface seam to the overlapping region of the second image stack, which is essentially to solving a multiple-label problem in Markov Random Fields. We use sparse 3D features as the structure cues to guide the seam mapping, in which a regularization term is incorporated to enforce the structure consistency. The displacements of the second seam are propagated to the rest of second image and the two images are stitched along the interface seams based on the computed displacements field.
1.1. 4D CT Artifacts Problem
Due to current spatio-temporal limitation of CT scanners, the entire body can not be imaged in a single respiratory period. One widely used method in clinic to acquire 4D CT images of a patient is to use the CT scanner in the helical mode, that is, image data for adjacent couch positions are continuously acquired sequentially. To obtain time-resolved image data with periodic motion, multiple image slices must be reconstructed at each couch position for a time interval equal to the duration of a full respiratory period, which can be achieved in the helical mode with a very low pitch (i.e., the couch moves at a speed low enough so that a sufficient number of slices can be acquired for a full respiratory period). The image slices acquired at each couch position form an image stack, which is associated with a measured respiratory phase and covers only part of the patient’s body. In the post-processing stage, the stacks from all the respiratory periods associated with a same specific measured respiratory phase are stacked together to form a 3D CT image of the patient for that phase. A 4D CT image is then reconstructed by temporally viewing the 3D phase-specific datasets in sequence. However, due to the variability of respiratory motion, image stacks from different respiratory periods could be misaligned, causing the resulting 4D CT data does not accurately represent the anatomy in motion [21, 5].
In this paper, we focus on the basic step in 4D CT image reconstruction, that is, how to stitch two image stacks Ii and Ij that partially overlap in anatomy, to obtain a spatio-temporally coherent data set, further reducing the artifacts. The reason that we only consider the case of anatomy overlap is that anatomy gap is fundamentally avoidable. For example, We are able to control either the pitch (couch translation speed and/or X-ray tube rotation speed) or the patient’s respiratory rate (increasing breaths per minute by training) to guarantee the overlaps between two stacks from adjacent couch positions. Another possible way to resolve the anatomy gapping problem is to utilize a bridge stack Ib acquired from another respiratory phase which overlaps with both image stacks, Ii and Ij. We then perform the following stitching operations: first stitch Ii with Ib to obtain an intermediate stack Iib, which overlaps with Ij; and then stitch Iib with Ij, resulting in an artifact-reduced stack Iibj. Thus, the fundamental problem is to stitch two partially overlapping stacks. However, in this case we need to be aware of the deformation errors induced by using the bridge stack from a different phase.
2. The Method
2.1. Overview of the Method
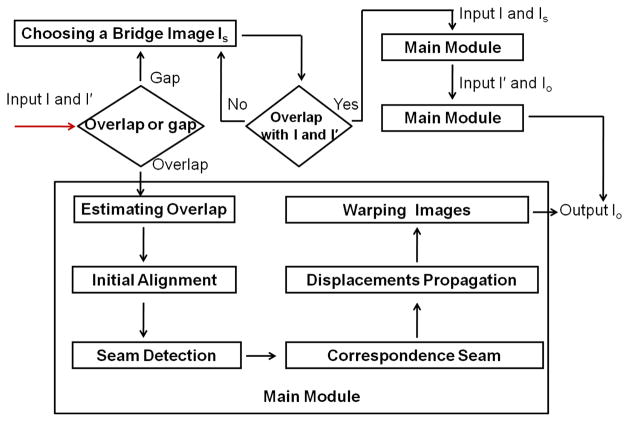
Given two image stacks, I and I′, with a partial overlap in anatomy, we want to stitch them together to generate a spatially coherent image, i.e., to minimize the artifacts in the resulting image as much as possible. Assume that Ω ⊂ I overlaps with Ω′ ⊂ I′. We call I (resp., I′) the fixed (resp., moving) image. Our method consists of the following six steps (the main module in Fig. 2):
Figure 2.
Method overview.
-
Step 1
Overlap estimation. The purpose of this step is to define the overlapping regions Ω in I and Ω′ I′. We use a “bridge” image stack that comes from the other respiratory phase, which overlaps with both I and I′. The overlapping regions Ω and Ω′ are computed by matching I and I′ to the bridge image using normalized cross correlation (NCC).
-
Step 2
Initial alignment. Initially align I with I′ by a general registration method to reduce the stitching errors due to the large displacements.
-
Step 3
Seam detection. Computing an interface seam in the fixed image for stitching. To reduce the alignment ambiguity, the interface seam for stitching is required to pass through the “smoothest” region in Ω with minimum structure complexity. We model this problem as an optimal seam detection problem by the graph searching method [14], which are widely used in many problems in computer vision field [8, 7, 20, 19].
-
Step 4
Matching correspondence seam. Matching the correspondence interface seam in the moving image. Intuitively, we hope to “move” the interface seam in the fixed image to the moving image to find the “best” one that can be perfectly aligned with the one in the fixed image. To be structure-aware, ideally, the two seams should cut the same anatomical structures at the same locations and should be well aligned at those locations. We formulate the problem as a multiple-label problem with an additional term in the energy function to enforce the structure consistency.
-
Step 5
Displacement propagation. Propagating the displacements to the rest of the moving image. The displacement vectors of the voxels in the rest of the moving image can be computed by solving a Laplace equation with Dirichlet boundary condition [11].
-
Step 6
Warping image. Warping the images and getting an artifact-reduced image. Two imaged are stitched and the misalignments and visual artifacts caused by respiratory motion are reduced.
The whole process of our method is shown in Fig. 2. In the following of the paper, we mainly focus on the main steps 3, 4 and 5.
2.2. Computing the Optimal Interface Seam in Ω
The Interface Seam
Recall that Ω (x, y, z) denotes the overlapping region of the fixed image I. Assume that the size of Ω is X × Y × Z, and the two image stacks, I and I′, are stitched along the z-dimension. Thus, the interface seam S in Ω is orthogonal to the z-dimension and can be viewed as a function S(x, y) mapping (x, y) pairs to their z-values. To ease the stitching, we certainly hope the interface seam itself is smooth enough. We thus specify the maximum allowed changes in the z-dimension of a feasible seam along each unit distance change in the x- and y-dimensions. More precisely, if Ω(x, y, z′) and Ω(x, y + 1, z″) (resp., Ω(x, y, z′) and Ω(x + 1, y, z″)) are two neighboring voxels on a feasible seam and δy and δx are two given smoothness parameters, then |z′ − z″| ≤ δy (resp., |z′ − z″| ≤ δx).
The Energy Function enforces the interface seam passing through the region of Ω with less structure complexity. Two factors should be considered: (1) The gradient smoothness in Ω which prevents the seam from breaking anatomy edges; and (2) the similarity between the neighboring voxels in the overlapping region of the fixed image (Ω) and that of the moving image (Ω′). Let Cs(p) denote the gradient smoothness cost of the voxel at p(x, y, z) 1 and Cd(p) be the dissimilarity penalty cost of voxel p under the neighborhood setting
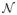 . Denote S a feasible interface seam. The energy function is defined with the following equation:
. Denote S a feasible interface seam. The energy function is defined with the following equation:
| (1) |
where α is used to balance Cs(p) and Cd(p) and
| (2) |
and
| (3) |
Optimization
The problem of finding in Ω an optimal interface seam S while minimizing the objective function
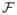 (S) is in fact an optimal single surface detection problem, which can be solved by computing a minimum-cost closed set in the constructed graph from Ω [14].
(S) is in fact an optimal single surface detection problem, which can be solved by computing a minimum-cost closed set in the constructed graph from Ω [14].
2.3. Matching the Correspondence Seam with Anatomy Structure Awareness
The optimal interface seam in the moving image (actually, in the overlapping region Ω′ of the moving image) is computed by solving a multiple-label problem in Markov Random Fields (MRFs), in which we use sparse 3D features as the guidance for the structure awareness.
Seam Matching with Graph Labeling
Intuitively, we want to “move” the interface seam in the fixed image to the moving image to find the corresponding one, which is the “best” match with the one in the fixed image. We model it as a multiple labeling problem. A label assignment lp to a voxel p(x, y, z) on the seam S is associated with a vector dp = (dx, dy, dz), called the displacement of p. That is, we map p(x, y, z) ∈ Ω in the fixed image to p′(x + dx, y + dy, z + dz) ∈ Ω′ in the moving image. Thus, the problem is modeled as a multiple labeling problem, where each node corresponds to exactly one voxel p of the seam S with its label denoted by lp. The energy E(
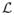 ) of a labeling
) of a labeling
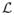 is the log-likelihood of the posterior distribution of an MRF [2]. E(
is the log-likelihood of the posterior distribution of an MRF [2]. E(
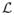 ) is composed of a data term Ed and a spatial smoothness term Es,
) is composed of a data term Ed and a spatial smoothness term Es,
| (4) |
| (5) |
where
represents the average values in a local neighborhood at the voxel p. We used a 3 × 3 × 3 neighborhood to compute the data term. Ed(lp) is in fact the block matching score between p ∈ Ω and its corresponding voxel in Ω′. Assume that nodes p(x, y, z) and q(x′, y′, z′) are adjacent on seam S under the neighborhood setting
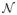 . The spatial smoothness of their labels is defined as,
. The spatial smoothness of their labels is defined as,
| (6) |
Preserving the Topology Structure with Feature Guide
Eq (4) presents a way to match the seam in the moving image to one in the fixed image. However, this function only makes sure that the seam in the moving image has the best alignment with the seam in the fixed image. There is no guarantee that both seams cut the same anatomy structures at the same locations. Simply removing the visual artifacts may “hide” the real anatomy structure misalignment, resulting in a visually attractive result, but producing wrong structures of anatomy. Thus, the essential step is to make sure both seams cut the same anatomy structures at the same locations, preserving the structure consistency. We propose to use sparse 3D features to form a structure topology around each node on the seams to guide the structure alignment while mapping the seam in the fixed image to one in the moving image. For each node p ∈ S, we generate k nearest-neighbors feature points, denoted as
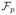 . These points form a structure topology that help to find the structure-aware matching. We introduce a new regularization term to Eq.(4) to enforce the structure consistency to form the new energy function Eq.(7)
. These points form a structure topology that help to find the structure-aware matching. We introduce a new regularization term to Eq.(4) to enforce the structure consistency to form the new energy function Eq.(7)
| (7) |
For feature point q in I, its correspondence in I′ is denoted corr(q). Thus the term Er(lp) is expressed as,
| (8) |
where
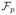 is the k nearest feature points of p ∈ S. k = 2 is used in our current study. In Fig. 3, we show how to use the features to guide the seam matching.
is the k nearest feature points of p ∈ S. k = 2 is used in our current study. In Fig. 3, we show how to use the features to guide the seam matching.
Figure 3.
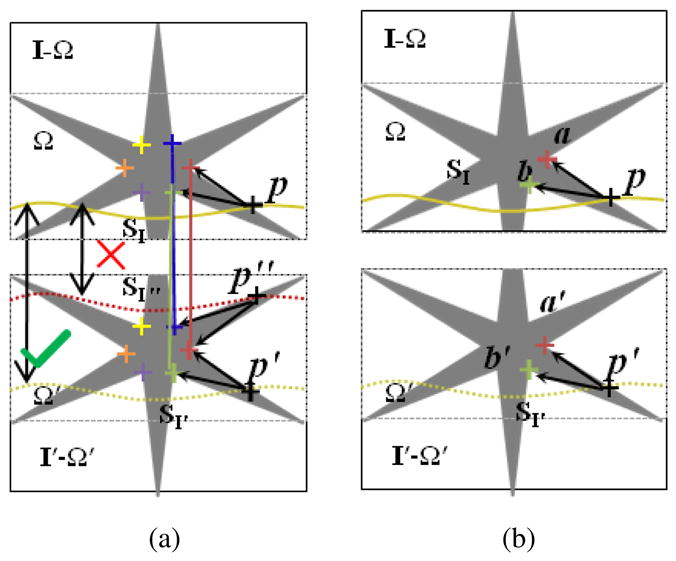
Feature-guided seam matching in the moving image. The correspondences in I and I′ are shown with the colored crosses. From (a) we can see the seams SI″ and SI′ may have same cost values due to the similar structure they passed. Obviously, SI″ is not correct. We can use the matched features to guide the seam matching. For the point p ∈SI, the features in a local region form a structure topology of p that help to reject incorrect matching. An example matched seam in the moving image is showed in (b). where
 denotes the neighboring system and β is the parameter to balance the two terms. Suppose label lp is defined by the displacement dp. let ΔII′ be (I(p − I′(p + dp))2. The data term for each node on the interface seam S is defined, as follows.
denotes the neighboring system and β is the parameter to balance the two terms. Suppose label lp is defined by the displacement dp. let ΔII′ be (I(p − I′(p + dp))2. The data term for each node on the interface seam S is defined, as follows.
Approximation by Graph Cuts
The function defined in Eq. (7) leads to an energy minimization problem in MRF, which is computationally intractable (NP-hard). However, it has been shown that an approximate solution can be found that typically produces good results using the multiple label graph cuts method[2].
2.4. Displacements Propagation
Once the optimal seam displacement vectors d are computed on S, the displacements need to be propagated to the rest of the moving image I′. To smoothly propagate the displacements d, we minimize the following Laplace equation with Dirichlet boundary condition [11] to obtain the propagation displacements d*.
| (9) |
where ∇ is a gradient operator. The problem can be discretized and solved by the conjugate gradients method.
Using the propagation displacements d* in I′, we perform a warping with a bilinear interpolation in I′, resulting an artifact-reduced image [11].
3. Implementation
3.1. Feature Detection and Matching
We use a structure-tensor-based 3D Föorstner operator which were used in Ref.[9]. The 3D Förstner feature operator assigns a response to each voxel p, denoted by R(p). After we compute the response R for every voxel, we extract feature points as the subset of image voxels whose R-value is a local maximum within a local neighborhood of size 7 × 7 × 7. The feature descriptor used in study is a revised SURF descriptor [9]. First, we take a 8 × 8 × 8 neighborhood for each detected feature point, and further divide into sixty-four 2 × 2 × 2 sub-regions. And then, for each subregion, a six-dimensional description vector f is computed to characterize the local intensity structure:
| (10) |
The sub-region descriptors are then connected together to form a 384-dimensional feature vector, which is further normalized to a unit vector to get the final descriptor for each feature point.
We use two steps to match the 3D features. The correspondences between two input images are established by finding nearest-neighbors (NNs) in the 384-dimensional vector space. As suggested in [16]. First, a distance ratio r is computed after the NN search, which is the ratio of the smallest distance value to the second-smallest. A match is accepted if r is smaller than a given threshold ( we use 0.5 is our study). Second, a symmetric criterion is applied, which performs the NN search in two directions and a matched pair (p, p′) is kept only if it satisfies the NN-optimality in both directions. After the first step, we can reject most of the wrong correspondences. In the second step, we use RANSAC [10] to reject outliers. It was shown that a local affine transform could handle complex articulated deformations [13]. Thus, we formulate the deformation transform in a local neighborhood as the affine transform, which is model used in RANSAC. To measure the affine transform, we need s = 4 points and all the 4 points must not be co-plane. Let w be the probability that any correspondence is an inlier, p be the probability that at least one random correspondence is free from outliers. We set w = 0.8 and p = 0.99. Thus, the number of feature points N is computed as . Thus, for each feature point, we select 9 neighborhood points including itself and use RANSAC to reject wrong correspondences. In our experiments, in the first step, we got about 230–280 correspondences. The final correspondences after the second step was about 150–200.
3.2. Parameters Setting
In this paper, we apply the graph searching method [14] to detect an optimal interface seam in the fixed image. In our experiments the smoothness parameters were set δx = δy = 3. In Eq.(1), α was set to 0.5. In Eq.(7), we set λ = 1, β = 0.3 and γ = 0.1. To reduce the computation complexity in Eq.(7), we used a hierarchical approach with three levels pyramid. The displacements resolution of each voxel on S were (−4, −2, 0, 2, 4) mm, (−2, −1, 0, 1, 2) mm and (−1, −0.5, 0, 0.5, 1) mm along each dimension from 3th pyramid level to 1th pyramid level. The number of labels at each level was 53 = 125 for 3D image.
4. Experimentation and Results
4.1. Experimentation on Simulated Data
Evaluation Method
To generate synthesized test datasets, clinical CT images with no artifacts were each divided into two sub-images partially overlaps each other. Then, known motion deformation vectors were applied to one sub-image to produce the corresponding moving image. In order to make the deformation fields more realistic, we selected an image has the same locations from another phase and the deformation fields were computed between two images. Some 3D feature points were identified as the landmarks. The landmarks distance errors (LDE) between the resulting artifact-reduced images and the original images were computed as the metric. Our experiments studied the following aspects of the method: (1) the average and standard deviation of LDE; and (2) the sensitivity of the displacement propagation.
Seven lung 3D CT images without artifacts were used. Each CT image consisted of 40 slices with a resolution of 0.98mm×0.98mm×2mm. While dividing the 3D CT image into two sub-images, we set the overlap between the two sub-images to be 20 slices, which indicated that there was 40 mm displacement along z-dimension between the fixed and the moving images. We further upsampled the image along the z-dimension with a resolution of 0.98mm×0.98mm×1mm. The size of the image was then 512 × 512 × 80. The number of landmarks identified for the measure of LDE was ten in each 3D CT image, which uniformly spread over the moving images.
Results
The results were summarized in Table 1 showing the average (avg) and standard deviation (std) of LDE’s. We showed the LDE’s for each of the seven synthesized datasets (1) while no registration operation was applied, i.e., simply stacking the two sub-images; (2) after initial registration; (3) using the method without feature guidance [6](i.e., with no feature-based regularization term); and (4) using the proposed method with the feature guidance (i.e., with the feature-based regularization term). In our method, the combined affine and B-Spline registration were used as the initial registration method. We used the elastix tools [12] in our experiments. From Table 1, we can see that the LDE’s were significantly reduced after initial registration. While after applying our method, the LDE’s were further decreased by 55% from 2.9 mm to 1.3 mm on average. The standard deviation was also further decreased from 1.7 mm to 1.0 mm. Compared with the method without feature guidance, we can see the LDE’s decreased by 32% from 1.9 mm to 1.3 mm. Especially for Dataset 5, the method without feature guidance failed and the LDE’s increased from 3.6 mm to 4.0 mm. While applying our method, the feature correspondences successfully guide the interface seam matching to well align the anatomical structures, and the average LDE was decreased from 3.6 mm to 1.7 mm. This example demonstrated the usefulness of the feature guidance.
Table 1.
Landmarks distances errors (LDE) (avg±std mm).
| Method | Data 1 | Data 2 | Data 3 | Data 4 | Data 5 | Data 6 | Data 7 | Avg |
|---|---|---|---|---|---|---|---|---|
| Before registration | 45.2 ±5.5 | 43.1±3.8 | 37.5± 3.4 | 42.5±2.7 | 47.6±6.4 | 36.4±4.7 | 44.3± 3.8 | |
| After registration | 2.5±2.0 | 2.6±1.5 | 1.7±1.1 | 2.4±1.4 | 3.6±2.7 | 2.9±1.9 | 2.1±1.4 | 2.9±1.7 |
| Without regulation ([6]) | 1.8±1.6 | 1.7±1.0 | 1.0±0.6 | 1.5±1.1 | 4.0±3.6 | 2.3±1.4 | 1.2±0.9 | 1.9±1.5 |
| With regulation (our method) | 1.6±1.3 | 1.1±0.6 | 1.0±0.6 | 1.6±1.1 | 1.7±1.5 | 1.4±1.0 | 1.0±0.7 | 1.3±1.0 |
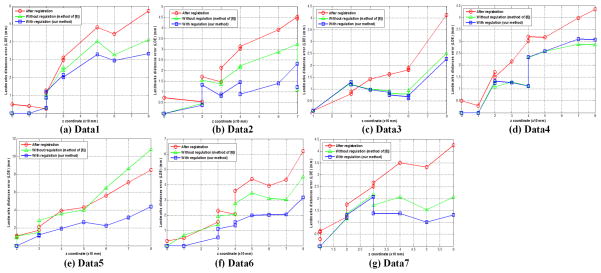
The displacement estimation in the non-overlapping region of the moving image is challenging due to the nature of non-rigid deformation. To analyze the propagation behaviors of the seam displacements to the rest of the moving image, we plotted the LDE’s of all the landmarks based on their z-coordinates (note that a large z-coordinate indicates that the landmark is far away from the interface seam for stitching). For each data set, we compared three results: (1) the results after initial registration; (2) the results by the method without the feature guidance [6]; and (3) the results by the proposed method with the feature guidance term. Figure 4 showed that the average LDE’s were not large in the overlapping regions (i.e., the z-coordinates of the landmarks were smaller than 40 mm). The largest LDE observed in the non-overlapping regions in our experiment was about 4.4 mm (Fig. 4(e)). We observed that the LDE increased as the distance of the landmark from the interface seam increased For the clinical 4D CT images, no method can guarantee the computed deformation field is correct for the non-overlapping region of the moving image, especially, when the non-overlapping region is large. Fortunately, one image stack at a certain phase of a breathing period commonly consists of about 20 slices in our clinical helical 4D CT images. Thus, our results indicate that the method is robust in the clinical setting.
Figure 4.
LDE with respect to the z coordinate for seven data.
4.2. Experimentation on Clinical Data
Evaluation Method
For the clinical test datasets, we used the images acquired by a 40-slice multi-detector CT scanner (Siemens Biograph) operating in the helical mode. The amplitude of the respiratory motion was monitored using a strain belt with a pressure sensor (Anzai, Tokyo, Japan). The respiratory phase at each time point was computed by the scanner console software via renormalization of each respiratory period by the period-specific maxima and minima of the amplitudes. The Siemens Biograph 40 software was used to sort the raw 4D CT images retrospectively into respiratory phase-based bins to form a sequence of phase-specific 3D CT images. We tested on six 4D CT data set with each having 10 phases and each phase consisting of about 120 to 190 slices. The number of image stacks depends on the breathing periods. In general, there were about 10 to 20 periods for each phase and in each phase there were about three pairs of image stacks presenting obvious artifacts. Thus, the total number of cases we studied was about 6 × 10 × 3 = 180.
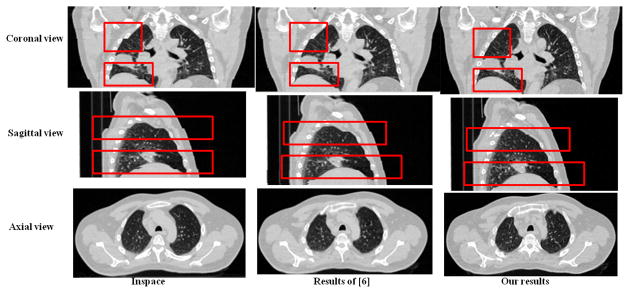
For the 4D CT images acquired in the helical mode, to the best of our knowledge, there are few methods designated to reduce the reconstruction artifacts. We thus compared the artifact-reduced results by our method with those obtained by the commercial Inspace software [1] and by the method in [6]. The Inspace software directly stacks two adjacent image stacks. The method in [6] shared our general framework, but it did not enforce the structure consistency. The quality of the results was judged by three medical experts.
Results
All observers identified much fewer artifacts in the images produced by the proposed method than those output by the Inspace. As to the comparison to the method in [6], if the interface seams in the overlapping regions were correctly matched, our method produced slightly better results. However, without the feature guidance, the method in [6] frequently failed to obtain structure-consistent alignment of the two interface seams. Example results were shown in Fig. 5.
Figure 5.
The comparisons of the proposed method with Inspace [1] and the method in [6]. Please enlarge the images for details.
4.3. Running time
All experiments were conducted on an Intel (2.4GHz) Dual CPU PC with 4 GB of memory running Microsoft Windows. We show the average execution times over all experiments for the main steps.
5. Discussion
The experiments demonstrated the promise of the method to improve the quality of 4D CT. Several limitations need further efforts to improve the method. The proposed method may not well handle the images with small overlapping regions (along the z-dimension). In that case, the interface seams are difficult to be detected. The second limitation is that the propagation of the displacements to the non-overlapping region of the moving image is unsupervised due to the lack of a priori knowledge. A common approach to resolve that problem is to use interpolation, which needs some known control points scattering over the image. Unfortunately, such control points are not available in our problem. Thirdly, if the overlapping regions are quite homogeneous, the method may fail to discover meaningful features to guide the alignment of the interface seams, which makes the alignment being structure-aware very challenge. Finally, if the patient has an abruptly changed breathing pattern, resulting in large magnitude of artifacts in 4D CT, the initial registration may not be able to capture those artifacts, leading to the failure of our method. Arguably, in that situation, it is better to re-acquire the 4D CT images or re-sorting the images rather than to “fix” it by a post-processing method.
6. Conclusion
Reducing artifacts in 4D CT is a very challenge problem. It is especially important to preserve the structure consistency while reducing the artifacts. In this paper, we developed a novel structure-aware method to achieve that goal for the helical 4D CT imaging. The main contribution is to model the structure-awareness as an additional regularization to enforce the structure consistency using the guidance of 3D features. The presented method was evaluated on simulated data with promising performance. The results on clinical 4D CT images were compared to other methods, and all three medical experts identified much fewer artifacts in the resulting images obtained by the proposed method. In conclusion, the reported method effectively reduces the artifacts directly from the reconstructed images and is promising to improve the quality of 4D CT.
Table 2.
The average runnting time for the main steps. I: Seam detection; II: Feature extraction; III: Feature matching; IV: Seam matching V: Displacements propagation.
| Step | I | II | III | IV | V |
|---|---|---|---|---|---|
| Running Time | 4 s | 76 s | 35 s | 132 s | 62 s |
Acknowledgments
This research was supported in part by the NSF grants CCF-0830402 and CCF-0844765, and the NIH grants R01 EB004640 and K25 CA123112.
Footnotes
p(x, y, z) denotes a point at (x, y, z) and compacted as p. p = (x, y, z) denotes a vector with three elements, which is denoted as p.
Contributor Information
Dongfeng Han, Email: handongfeng@gmail.com.
John Bayouth, Email: john-bayouth@uiowa.edu.
Qi Song, Email: qi-song@uiowa.edu.
Sudershan Bhatia, Email: sudershan-bhatia@uiowa.edu.
Milan Sonka, Email: milan-sonka@uiowa.edu.
Xiaodong Wu, Email: xiaodong-wu@uiowa.edu.
References
- 1.Inspace. Vol. 6. Siemens Medical Solutions; Malvern, PA: p. 7. [Google Scholar]
- 2.Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts. PAMI. 2001;23(11):1222–1239. 3, 4. [Google Scholar]
- 3.Ehrhardt J, Werner R, Saring D, Frenzel T, Lu W, Low D, Handels H. An optical flow based method for improved reconstruction of 4D CT data sets acquired during free breathing. Medical Physics. 2007;34:711. 1. doi: 10.1118/1.2431245. [DOI] [PubMed] [Google Scholar]
- 4.Georg M, Souvenir R, Hope A, Pless R. CVPRW’08. IEEE; 2008. Manifold learning for 4D CT reconstruction of the lung; pp. 1–8.pp. 1 [Google Scholar]
- 5.Han D, Bayouth J, Bhatia S, Sonka M, Wu X. Characterization and Identification of Spatial Artifacts during 4D-CT Imaging. Medical Physics. 2011;38:1–2. doi: 10.1118/1.3553556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Han D, Bayouth J, Bhatia S, Sonka M, Wu X. Motion Artifact Reduction in 4D Helical CT: Graph-Based Structure Alignment. Medical Computer Vision. Recognition Techniques and Applications in Medical Imaging. 2011:63–73. 1, 5, 6, 7. [Google Scholar]
- 7.Han D, Sonka M, Bayouth J, Wu X. Optimal multiple-seams search for image resizing with smoothness and shape prior. The Visual Computer. 2010;26(6):749–759. 2. [Google Scholar]
- 8.Han D, Wu X, Sonka M. Optimal multiple surfaces searching for video/image resizing-a graph-theoretic approach. 2009 IEEE 12th International Conference on Computer Vision; IEEE; 2009. pp. 1026–1033.pp. 2 [Google Scholar]
- 9.Han X. Feature-constrained Nonlinear Registration of Lung CT Images. MICCAI EMPIRE 2010. 2010;4:5. [Google Scholar]
- 10.Hartley R, Zisserman A. Multiple view geometry in computer vision. Cambridge Univ Pr; 2003. p. 5. [Google Scholar]
- 11.Jia J, Tang CK. Image stitching using structure deformation. PAMI. 2008;30(4):617–631. 3, 4. doi: 10.1109/TPAMI.2007.70729. [DOI] [PubMed] [Google Scholar]
- 12.Klein S, Staring M, Murphy K, Viergever M, Pluim J. Elastix: a toolbox for intensity based medical image registration. IEEE Transactions on Medical Imaging. 2010:5. doi: 10.1109/TMI.2009.2035616. in press. [DOI] [PubMed] [Google Scholar]
- 13.Li H, Kim E, Huang X, He L. CVPR 2010. IEEE; 2010. Object matching with a locally affine-invariant constraint; pp. 1641–1648.pp. 5 [Google Scholar]
- 14.Li K, Wu X, Chen DZ, Sonka M. Optimal surface segmentation in volumetric images-a graph-theoretic approach. PAMI. 2006;28(1):119–134. 2, 3, 5. doi: 10.1109/TPAMI.2006.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Li R, Lewis J, Cerviño L, Jiang S. 4D CT sorting based on patient internal anatomy. Physics in Medicine and Biology. 2009;54:4821. 1. doi: 10.1088/0031-9155/54/15/012. [DOI] [PubMed] [Google Scholar]
- 16.Lowe D. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision. 2004;60(2):91–110. 5. [Google Scholar]
- 17.Lu W, Parikh P, Hubenschmidt J, Bradley J, Low D. A comparison between amplitude sorting and phase-angle sorting using external respiratory measurement for 4D CT. Medical Physics. 2006;33:2964. 1. doi: 10.1118/1.2219772. [DOI] [PubMed] [Google Scholar]
- 18.Neicu T, Berbeco R, Wolfgang J, Jiang S. Synchronized moving aperture radiation therapy (SMART): improvement of breathing pattern reproducibility using respiratory coaching. Physics in Medicine and Biology. 2006;51:617. 1. doi: 10.1088/0031-9155/51/3/010. [DOI] [PubMed] [Google Scholar]
- 19.Song Q, Wu X, Liu Y, Haeker M, Sonka M. Simultaneous searching of globally optimal interacting surfaces with shape priors. CVPR. 2010:2.
- 20.Song Q, Wu X, Liu Y, Smith M, Buatti J, Sonka M. Medical Computer Vision. Recognition Techniques and Applications in Medical Imaging (MICCAI 2009) 2009. Optimal graph search segmentation using arc-weighted graph for simultaneous surface detection of bladder and prostate; pp. 827–835.pp. 2 [DOI] [PubMed] [Google Scholar]
- 21.Yamamoto T, Langner U, Loo BW, et al. Retrospective analysis of artifacts in four-dimensional CT images of 50 abdominal and thoracic radiotherapy patients. International Journal of Radiation Oncology. 2008;72(4):1250–1258. 1, 2. doi: 10.1016/j.ijrobp.2008.06.1937. [DOI] [PMC free article] [PubMed] [Google Scholar]