Double-clad fiber with a tapered end for confocal endomicroscopy

Abstract

We present a double-clad fiber coupler (DCFC) for use in confocal endomicroscopy to reduce speckle contrast, increase signal collection while preserving optical sectioning. The DCFC is made by incorporating a double-clad tapered fiber (DCTF) to a fused-tapered DCFC for achromatic transmission (from 1265 nm to 1325 nm) of > 95% illumination light trough the single mode (SM) core and collection of > 40% diffuse light through inner cladding modes. Its potential for confocal endomicroscopy is demonstrated in a spectrally-encoded imaging setup which shows a 3 times reduction in speckle contrast as well as 5.5 × increase in signal collection compared to imaging with a SM fiber.

1. Introduction

Endomicroscopy is an emerging medical imaging technique combining the flexibility of endoscopy with the advantages of confocal microscopy, namely micrometric resolution and optical sectioning. The technology is currently being investigated for its diagnostic potential in the field of gastroenterology for assessing colorectal lesions [1], colon polyps [2] and Barrett’s esophagus [3]. Its potential was also demonstrated in vivo for cervical precancerous lesion detection [4, 5] and preliminary studies on an animal model showed promise towards oral lesion identification [6].

Endomicroscopes can be broadly classified into two main groups, according to the type of optical fiber used. The first group includes most commercially available endomicroscopes and is based on fiber bundles. This solution is relatively easy to implement but suffers from low pixel density (≈ 30,000 pixels for a 1 mm of diameter [7]) and high back reflections from the bundle tip [8]. The second group uses a single optical fiber but requires a scanning mechanism at its distal end. It allows high pixel density [9] in small flexible probes [10, 11] void of pixelation artifacts.

The added diagnostic value of confocal endomicroscopes lies in the capability of performing optical sectioning through spatial filtering of reemitted light using pinholes (table top systems) or single mode (SM) optical fibers (endoscopes). This, in addition to dramatically reducing signal levels, yields images that suffer from speckle noise. Conventional confocal microscopes resolve both these issues by using two pinholes (one for illumination and one for detection) with different diameters. For single fiber based systems, this translates into using double-clad fibers (DCFs) where the SM core transmits illumination light and the inner cladding acts as a larger collection aperture. This speckle reduction technique was successfully implemented in wide field endoscopy [12]. However, for confocal endomicroscopy, diameter ratios must be carefully chosen to preserve sectioning.

The gain associated with using a DCF depends on the ability to efficiently (and robustly) couple light in and out while separating core and inner cladding modes. We showed in a previous article [13] that double-clad fiber coupler (DCFC) allowed quasi-lossless integration of DCF in a wide field endoscopy setup. The challenges of realizing a DCFC with core/inner cladding diameters ratios compatible with confocal microscopy are however much greater as the appropriate diameter ratio required for optical sectioning is very small and results in losses at the fused junction.

We herein present a method for using DCFs in confocal endomicroscopy for preserving the optical sectioning while benefiting from signal increase and speckle reduction. This is done by adding an achromatic double-clad tapered fiber (DCTF) at the imaging branch of a DCFC which allows precise adjustment of the collection to illumination ratio for single fiber confocal endomicroscope. We describe the fabrication and characterize the DCTF combined with the previously described DCFC [13]. Finally, we test this device for imaging of biological tissue in a spectrally-encoded confocal microscopy setup.

2. Confocal endomicroscopy with a double clad fiber

Wilson et al. described the effect of enlarging the collection aperture on lateral resolution and on optical sectioning [14]. In this section, we expand the development to partially coherent imaging systems using Gaussian illumination in order to choose the optimal ratio of inner cladding diameter to core mode field diameter (MFD) of the DCF.

2.1. Partially coherent imaging

We begin our description by examining optical sectioning in partially coherent confocal imaging systems for different detector sizes. A wavelength independent imaging theory can be expressed by defining normalized optical coordinates (u and ν) [15] in the axial and radial directions, respectively:

$$u=4k{z}_s{\text{sin}}^2(\alpha /2),$$ (1)

and

$$\nu =k{r}_s\text{sin}(\alpha ),$$ (2)

where k = 2π/λ, λ is the wavelength, z_s and r_s are the axial and radial coordinates at the sample plane and α is the half-angle supported by the objective lens.

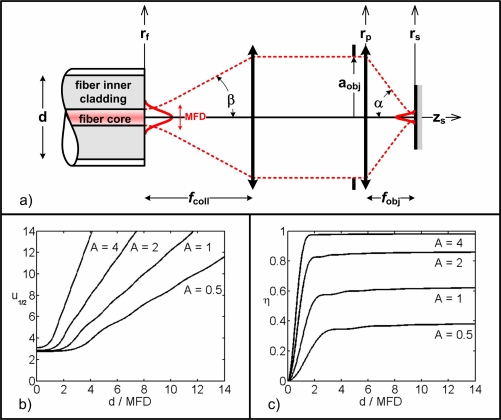
Figure 1(a) shows the general configuration for confocal imaging using a DCF. Illumination of the sample comes from the DCF core mode and collection is performed through the inner cladding propagating a large number of orthonormal modes. Because of the orthonormality of the inner cladding modes [16], confocal imaging using a DCF can be considered as an incoherent sum of multiple coherent detection systems (one for each inner cladding mode) [17]. If the number of modes is large enough, the base can be considered complete and imaging can be approximated as being partially coherent [15]. In this partially coherent imaging scheme the intensity measured at the detector’s plane is given by integrating light reflected back from the sample onto the fiber’s plane over the inner cladding collection area. Following Gu’s work [15], we define the axial plane response of the system as

$$I(u)\propto {\int }_0^{{\nu }_p}{\left|{\int }_0^1{P}_1(\rho )P_2(\rho )\text{exp}(iu{\rho }^2)J_0(\nu \rho )\rho d\rho \right|}^2\nu d\nu ,$$ (3)

where I(u) is the collected intensity as a function of defocus for different values of ν_p, the normalized radius of the DCF inner cladding at the plane of the fiber. ν_p is given by

$${\nu }_p=k\frac{d}{2}\text{sin}(\beta ),$$ (4)

where d is the diameter of the DCF’s inner cladding and β is the reciprocal half-angle at the fiber plane. P_1,2 are illumination and collection pupil functions at the objective plane, respectively, expressed as a function of a normalized radial coordinate ρ, defined as

Fig. 1.

Confocal imaging with a DCF. (a) Light propagation schematic. Illumination light originates from the core of the DCF defined by its MFD (taken at the 1/e² intensity point) and numerical aperture (illumination half-angle β). It is collimated with a lens of focal length f_coll and fills an objective lens (of focal length f_obj, aperture 2a_obj, illumination cone half-angle α). Light collection is performed through the inner cladding of the DCF (of diameter d). Light propagates along the z-axis and r_f, r_p and r_s define the radial coordinates at the fiber, objective lens pupil and sample planes, respectively. (b) Optical sectioning (u_1/2) for a perfect plane reflector as a function of the ratio d/MFD for different values of the pupil filling factor A. c) Excitation efficiency (η) for a perfect plane reflector at focus (u = 0) as a function of the ratio d/MFD for different values of A.

$$\rho =\frac{r_p}{a_{\text{obj}}},$$ (5)

where r_p is the radial coordinate at the objective lens pupil plane and a_obj is the radius of the pupil. J₀ is a Bessel function of the 1st kind and 0th order.

The amplitude of the field at the pupil plane P₁(ρ) is obtained by examining the illumination pattern. Illumination amplitude, E_ill(r_f), from the SM core is function of the radial coordinate r_f (at the fiber plane) and may be approximated by a Gaussian profile [16]

$$E_{\text{ill}}(r_f)=\frac{a_{\text{ill}}}{\sqrt{N_f}}\text{exp}\left[-{\left(\frac{2r_f}{\text{MFD}}\right)}^2\right],$$ (6)

where a_ill is the complex amplitude of the fundamental mode. MFD is the mode field diameter which is defined by the diameter at which the intensity drops by a factor 1/e². N_f is an energy normalization factor given by

$$N_f=2\pi {\int }_0^{\infty }{\left|\text{exp}\left[-{\left(\frac{2r_f}{\text{MFD}}\right)}^2\right]\right|}^2{r}_{f}d{r}_f=\frac{\pi {\text{MFD}}^2}{8}.$$ (7)

As was done by Gu et al. [18], we define a filling factor A, to take into account the possible under or over filling of the microscope objective pupil:

$$A={\left(k\frac{a_{\text{obj}}}{f_{\text{coll}}}\frac{\text{MFD}}{2\sqrt{2}}\right)}^2.$$ (8)

As seen from Eq. (8), the filling factor depends on the MFD (itself a function of the fiber core diameter and numerical aperture) and the focal length of the collimating lens, f_coll.The amplitude of the Gaussian illumination field falls at e^−A/2 of its peak value at the edge of the objective lens aperture of radius a_obj. When the objective lens respects the Abbe condition, the filling factor becomes

$$A={\left(kM\text{sin}(\alpha )\frac{\text{MFD}}{2\sqrt{2}}\right)}^2,$$ (9)

where M is the system’s magnification given by

$$M=\frac{f_{\text{obj}}}{f_{\text{coll}}}=\frac{\text{sin}(\beta )}{\text{sin}(\alpha )}.$$ (10)

Assuming that the diameter of the collimating lens is much greater than the beam diameter, we may express the field at the objective lens pupil as

$$E_{\text{ill}}(r_p)=\frac{a_{\text{ill}}}{\sqrt{N_p}}\text{exp}\left[-{\left(\frac{r_p\sqrt{A}}{a_{\text{obj}}\sqrt{2}}\right)}^2\right],$$ (11)

where N_p is a normalization factor given by

$$N_p=2\pi {\int }_0^{\infty }{\left|\text{exp}\left[-{\left(\frac{r_p\sqrt{A}}{a_{\text{obj}}\sqrt{2}}\right)}^2\right]\right|}^2{r}_{p}d{r}_p=\frac{\pi a_{\text{obj}}^2}{A}.$$ (12)

With Eq. (5) and Eq. (11), we obtain an expression for the illumination pupil (P₁(ρ)) [15]:

$$P_1(\rho )=\text{exp}\left[-{\left(\frac{\rho \sqrt{A}}{\sqrt{2}}\right)}^2\right].$$ (13)

The detection pupil P₂(ρ) is simply given by

$$P_2(\rho )=1.$$ (14)

Finally, using Eq. (9), we rewrite ν_p as a function of the ratio d/MFD as

$${\nu }_p=\frac{d}{\text{MFD}}\sqrt{2A}.$$ (15)

2.2. Optical sectioning

Using Eq. (3), we compute I(u) for different values of d/MFD and A. Results are plotted in Fig. 1(b) and show the value of defocus for which the intensity drops by a factor 2 (i.e. u_1/2). This development is a crude approximation of a real confocal imaging system with a DCTF, but has the advantage of giving normalized results for any type of DCTF as long as its fundamental mode is nearly Gaussian and the inner cladding is highly MM. It also provides insight on how to optimize a confocal imaging system to balance the signal collection and axial resolution.

2.3. Signal collection

Another important criterion to consider in confocal endomicroscopy is light efficiency. Depending on the application, one may wish to favor axial resolution and overfill the objective’s pupil (with A ≈ 0.5) or one may favor a more parsimonious use of photons (with A > 1) at the expense of a slightly lower resolution. The system’s efficiency (defined as the ratio of detected power over input power), η, is function of the illumination (η₁) and collection (η₂) efficiencies. The transmitted energy through the objective pupil depends on the filling factor as

$${\eta }_1=1-e^{-A}.$$ (16)

For a perfect plane reflector at focus (u = 0), the ratio of power detected by a circular detector of radius ν_p over the incident power at the detection plane is given by

$${\eta }_2=\frac{{\int }_0^{{\nu }_p}{\left|{\int }_0^1\text{exp}\left[-{\left(\frac{\rho \sqrt{A}}{\sqrt{2}}\right)}^2\right]J_0(\nu \rho )\rho d\rho \right|}^2\nu d\nu }{{\int }_0^{\infty }{\left|{\int }_0^1\text{exp}\left[-{\left(\frac{\rho \sqrt{A}}{\sqrt{2}}\right)}^2\right]J_0(\nu \rho )\rho d\rho \right|}^2\nu d\nu }.$$ (17)

Under these conditions, the system’s efficiency is simply given by [15]

$$\eta ={\eta }_1{\eta }_2.$$ (18)

Figure 1(c) shows η for different values of ratio d/MFD and various filling factors A. For a perfect planar reflector at focus, η rapidly stabilizes around its maximal value for d/MFD ratios larger than 2, but, in most in vivo biomedical applications, the sample is a bulk diffusive medium incorporating optically smooth reflective surfaces. In this type of samples, η will continue to grow for ratios d/MFD larger than 2 because of the out of plane diffused and reflected signals.

2.4. Speckle contrast

Another limitation for the use of single fiber endomicroscopy in the clinical world is speckle contrast. Speckle noise creates patterns in images that can be misinterpreted by clinicians. When light is reflected by a diffusing sample, a speckle pattern is formed at the fiber plane. If a SM fiber is used for illumination and collection, and if the sample properties are such that it creates a fully developed speckle pattern, the fundamental mode of the fiber will be excited following a Gaussian probability function in amplitude. The intensity image formed by scanning the diffusive sample will then have a speckle contrast of 1. If a MM fiber (or the inner cladding of a DCTF) is used for detection, each orthogonal mode will independently be excited by the speckle pattern following a Gaussian probability function in amplitude. The mean intensity of each orthogonal mode will depend on the speckle pattern’s coherence area A_c at the fiber plane and on the mode’s profile. If the detector at the end of the fiber is larger than the field coming from the fiber, each mode will be detected independently and the resulting intensity image will have a lower speckle contrast. In this case, the speckle contrast C_MM is given by [19]

$$C_{\text{MM}}=\frac{{\sigma }_s}{I_s}=\frac{\sqrt{{\mathrm{\Sigma }}_{n=1}^N{\overline{I}}_n^2}}{{\mathrm{\Sigma }}_{n=1}^N{\overline{I}}_n},$$ (19)

where σ_s is the standard deviation of the detected intensity, Ī_s is the mean of the detected intensity, N is the number of modes and I_n is the mean of the intensity coupled in mode n of the inner cladding.

Another way to explain the reduction in speckle contrast is to consider the set of orthogonal modes to be complete (highly MM fiber). With this approximation, imaging becomes partially coherent and the highly MM fiber can be approximated as a circular detector of diameter d sensitive to the intensity of the field at the fiber plane. In this case, we are in the presence of an integrated speckle statistic [19]. For a circular detector of perfect intensity sensitivity of 1 and area A_d, in the approximation that A_d ≫ A_c, the speckle contrast C_d is given by

$$C_d\approx \sqrt{\frac{A_c}{A_d}}\propto \frac{\sqrt{A_c}}{d}.$$ (20)

Therefore, when the speckle spot size at the detection plane is smaller than the detection area, increasing the detection diameter d will result in integrating the speckle pattern over a larger area thus reducing the speckle contrast.

2.5. Discussion

Figure 1(c) shows that an efficient use of the laser intensity requires a filling factor A greater than 1. Taking this into account, a comparison between Figs. 1(b) and 1(c) shows that a right balance between signal collection and optical sectioning may be obtained using a ratio d/MFD ≈ 5 and a filling factors A ≈ 1 which should lead, according to Eq. (19) or Eq. (20), to an appreciable speckle contrast reduction.

In the following section we demonstrate that the use of a DCTF allows the ratio d/MFD to vary from 5 to 10 while being compatible with a previously published DCFC [13].

3. Double-clad fiber coupler for confocal endomicroscopy

Benefits from DCF in a clinical environment are only obtained when coupled to robust fiber couplers. An ideal DCFC for confocal endomicroscopy consists of a null coupler for the core mode to avoid illumination losses and to ensure achromatic coupling of the inner cladding modes. Additionally, splitting of inner cladding modes should favor the detection branch. However, a lossless symmetrical coupler may transmit at best 50% of the MM energy. Achromaticity of the inner cladding coupling is ensured by the coupling statistics of a high number of modes.

3.1. Limitations of current DCFCs

Previously reported DCFCs made with large d/MFD ratios (≥ 10) showed great promise for imaging techniques not requiring optical sectioning such as wide field endoscopy or nonlinear imaging techniques not requiring a detection pinhole to obtain optical sectioning [20–22]. Their fabrication methods (such as side polishing [23, 24], twisting [25] and fusing and tapering [13, 26]) are however not suitable for DCF having smaller d/MFD ratios (such as 5) required to preserve confocal sectioning. The major limitation is that light propagating in a DCFC made of, for example, a 9 : 45 : 125 μm DCF would couple significant power in the outer cladding modes of the side polished, twisted or fused structure. These modes are then lost at the output of the DCFC, making such a coupler very inefficient.

3.2. DCTF propagation

We propose herein to use a DCFC previously designed for endoscopy and taper down its illumination branch until the optimal ratio d/MFD is obtained (see Fig. 2(a)). Fabrication, characterization as well as light propagation within such a DCTF are described in the following sections.

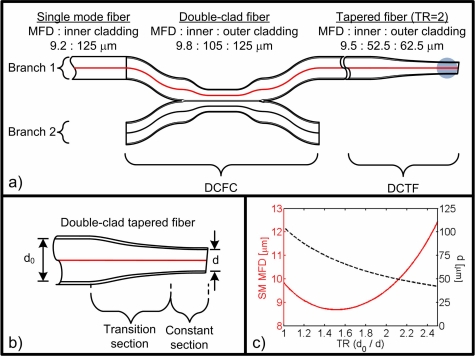
Fig. 2.

Double-clad tapered fiber (DCTF). (a) Schematic of the DCFC with a tapered end, the gray area representing a high index gel drop to diminish back reflections. (b) Schematic of the tapered end. (c) MFD (solid red line) and inner cladding diameter d (dotted black line) as a function of the taper ratio.

Figure 2(b) presents a down-tapered double-clad fiber. The DCF used is an all-silica commercial fiber (Nufern, East Granby, CT, SM-9-105-125). The core is germanium-doped, with a numerical aperture of 0.12, a diameter of 9 μm and a cutoff wavelength of 1250 nm. The inner cladding is made of pure silica, with a numerical aperture of 0.20 and a diameter of 105 μm. The outer cladding is fluorine-doped and has a diameter of 125 μm.

Figure 2(c) shows the evolution of the SM illumination MFD and the MM inner cladding diameter d as a function of the taper ratio (TR) (defined as the fiber reduction factor d₀/d). The MFD of the fundamental mode initially decreases with higher TR but eventually increases as the mode diffracts out of the smaller core. As TR varies from 1 to 2.5, the core mode MFD which has a minimal value of 9 μm increases up to 12 μm. The MM inner cladding collection diameter, however, decreases as TR increases following an inversely proportional law. A wide range of MM detection diameter over SM illumination ratios are thus easily obtainable by varying the TR.

Tapered fibers are easily fabricated such that the evolution of the core mode is adiabatic, i.e., with no coupling of the fundamental core mode to higher-order modes [27]. This ensures that SM illumination is lossless and achromatic, allowing simple implementations of spectral encoding [28] and interferometric imaging [29].

3.3. Fabrication and characterization

The tapering setup consists of a propane-oxygen micro-torch mounted on a three axis motorized stage, two translation motorized stages for stretching the fiber, a microscope for fiber inspection, a broadband source and an optical spectrum analyzer for spectral characterization of the core transmission through the DCTF [30].

The fabrication of the DCFT begins by splicing the DCF with two SM fibers connected with the broadband source and the optical spectrum analyzer. The two splices ensure that only transmission in the core mode is characterized. The fiber is then stripped over the length to be tapered and cleaned with acetone. The adiabaticity criterion is met by heating the DCF over 8 mm with a traveling flame during tapering. Tapering is stopped when the fiber reaches a TR of 2. The fiber is angled cleaved at the center of the taper and inspected on a splicing station (Vytran, Morganville, NJ, FFS-2000) (see Figs. 3(d) and 3(e)). This final inspection allows measuring the final TR of the DCFT by comparison with the original cross-section of the DCF (see Figs. 3(c)) and to appreciate the quality of the angle cleave.

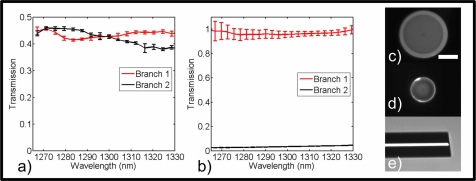
Fig. 3.

Characterization of the down tapered DCFC. (a) Spectral response of the MM inner cladding transmission. (b) Spectral response of the SM core transmission. (c) Cross section of the original DCF. (d) Cross section of the DCTF. (e) Side view of the angle cleaved DCTF. Scale bar: 50 μm. Error bars represent 1 standard deviation.

Angle cleaving by 7.2° allows illumination light to be backreflected into the inner and outer cladding modes instead of into the core mode. Because of the high index difference between the outer cladding and air most of the back reflected light couples into the outer cladding modes. These outer cladding back reflections are attenuated by using a higher index gel drop in the constant section of the DCTF (see Fig. 2(a)).

After the SM spectral characterization and inspection of the DCTF cleave, the DCTF is spliced with the DCFC. Spectral characterization of the SM transmission of the full device (DCFC and DCTF) (see Fig. 3(b)) is done by multiplying the SM spectral response of the DCTF with the SM spectral response of the DCFC [13]. Spectral characterization of the MM transmission of the full device (see Fig. 3(a)) is done by using a wavelength-swept source [31] and a diffuser [13]. The diffuser allows the excitation of lower and higher order modes of the DCTF and the wavelength-swept source allows the characterization of the transmission of the full DCF device with a photodetector large enough to collect all the light at the output of the DCF instead of using an optical spectrum analyzer that spatially filters the input light.

4. Confocal imaging with a down tapered DCFC

Confocal imaging using the down tapered DCFC was demonstrated on a spectrally encoded confocal microscopy setup. Spectral encoding (SE) [28] allows rapid imaging with a high number of resolvable points (up to 1000 × 1000 points) of reflective [32] and fluorescent [33] samples and was shown to be compatible with endoscopy [10] and confocal endomicroscopy [34].

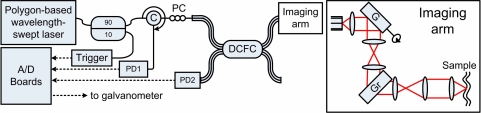
Figure 4 summarizes the imaging setup which consists of a polygon based wavelength-swept laser (λ₀ = 1310 nm, Δλ = 80 nm, sweep rate = 8.9 kHz) [31] coupled to the core of the DCFC for illumination of the sample through a standard SE imaging arm. The SM output of the laser is spliced to a SM fiber circulator itself spliced to the SM core of the DCFC for quasi lossless illumination of the sample. SE confocal imaging is achieved by using a galvanometer-mounted mirror for the slow axis scan (Cambridge Technology, Lexington, MA) and a holographic transmission grating (Wasatch Photonics, Logan, UT, 1125 ln/mm) for the fast axis. A high NA microscope objective (Olympus, Tokyo, Japan, LUMFLN 60XW, NA= 1) is used to illuminate and collect light from the sample. A pupil filling factor of A = 1.2 was obtained by enlarging the collimated beam (f_collimator = 11mm, Thorlabs, Newtown, NJ, C220THE-C) through telecentric telescopes made from achromatic lenses (f_1,1 = 50 mm, f_1,2 = 150 mm, f_2,1 = 75 mm, f_2,2 = 150 mm, Edmund, Barrington, NJ, NT45-803, NT47-380 and NT45-805) arranged in a 4 – f configuration. Coherent light backscattered from the sample is collected by the core of the DCTF and sent to an InGaAs photo-detector (New Focus, 2117-FC) through the circulator. Diffuse backscattered light is collected by the inner cladding of the DCTF and sent via the second branch of the DCFC to another identical photo-detector. Inner cladding light sent to the first branch is lost at the splice between the DCFC and the SM fiber leading to the circulator. A rapid digitizer simultaneously acquires single- and multi-mode signals for comparison. The galvanometer is controlled by a separate A/D board.

Fig. 4.

Spectrally encoded confocal microscopy setup used to demonstrate imaging with the tapered-fiber DCFC. SE is achieved using a polygon-based wavelength-swept laser fiber coupled to an acquisition triggering mechanism and to an imaging arm through a circulator (C) spliced to the tapered-fiber DCFC. The imaging arm consists of a collimating lens, a galvanometer mounted mirror (G), two telecentric telescopes, a transmission grating (GR) and an objective lens. InGaAs photo-detectors (PD) collect coherent and partially coherent light. PC : polarization controllers.

The axial resolution was measured using a mirror mounted on a piezo-electric translation stage (Burleigh, Mississauga, Canada, PCS-5000). The axial 50:50 plane response for the SM signal is 3.4 ± 0.1 μm comparatively to 1.3 μm for a SM fiber based confocal microscope with a filling factor A of 1.2 [18]. The axial 50:50 plane response for the MM signal is 5.8 ± 0.1 μm comparatively to 4 μm for a partially coherent SM confocal microscope with a filling factor A of 1.2 and a d/MFD ratio of 5.5 (see Fig. 1(b)). The lateral resolution was measured using a resolution target (Edmund Optics, Barrington, NJ, U.S. Airforce 1951). The 90:10 edge response for the SM signal is 0.76 ± 0.03 μm comparatively to 0.6 for a perfect confocal microscope while the 90:10 edge response for the MM signal is 1.18 ± 0.04 μm. The difference between theoretical and experimental values for the axial and lateral resolutions may be explained by the use of the scalar paraxial approximation, the use of an objective designed for wavelengths in the visible part of the spectrum and by various aberrations.

The speckle contrast and the intensity collected were measured using a 20% solution of intralipid. The SM signal speckle contrast is 0.7 ± 0.2. The MM signal speckle contrast is 0.23 ± 0.08. The intensity increase between the MM signal comparatively to the SM signal is 5.5.

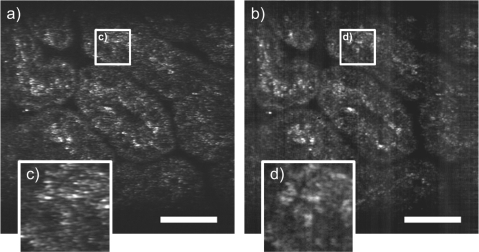
Finally, to show the potential of the DCTF for confocal imaging of biological samples we imaged a 7 day old mouse embryo fixed in a solution of 4% of paraformaldehyde (see Fig. 5). Figure 5(a) is a 20 frame average of the SM signal and Fig. 5(b) is a 20 frame average of the MM signal. SM and MM 1024 × 1024 images were acquired simultaneously at 10 MHz resulting in an 8.8 fps imaging for each signal. SM and MM images were normalized independently to allow visualization of structures in both images despite the increase in MM signal. Zooming in the same region of the SM and MM images (see Figs. 5(c) and 5(d) allows visualization of speckle reduction on 3 round structures in the MM signal not seen in the SM image because of the higher speckle contrast. The vertical bands visible on Fig. 5(b) reveal a slight achromaticity of the DCFC that would not affect piezo based single fiber confocal endomicroscopes [11].

Fig. 5.

Simultaneously acquired images of a 7 day old mouse embryo fixed in a solution of 4% of paraformaldehyde. (a) Average of 20 images of the SM signal (scale bar of 50 μm). (b) Average of 20 images of the MM signal (scale bar of 50 μm). (c) Zoom of the SM image. (d) Zoom of the MM image. Intensity scale of the SM and MM images were normalized independently.

5. Conclusion

We demonstrated the design, the fabrication, the characterization and the application of an achromatic (from 1265 nm to 1325 nm) passive all-fiber device for confocal endomicroscopy. This device allows SM illumination of the sample and simultaneous SM and MM detection. The DCTF allows d/MFD ratios varying from 5 to 10. This flexibility of the different illumination and collection schemes allows many compromises between optical sectioning, collected intensity and speckle contrast.

The final device has a transmission of the illumination core mode of > 95% and a collection of > 40% of the inner cladding MM signal and a d/MFD ratio of 5.5. In a spectrally encoded confocal microscopy setup at 1310 nm with a water immersion objective (NA = 1), the MM 50:50 axial plane response of 5.8 ± 0.1 μm is 1.5 time larger than the SM 50:50 axial plane response, the intensity collected comparatively to the SM signal is increased by a factor 5.5 and the MM signal speckle contrast is 3 times lower than the SM signal speckle contrast. Moreover, the comparison of the SM core and MM inner cladding signals showed, in biological samples, structures in the MM inner cladding signal not identifiable in the SM core signal due to higher speckle contrast.

This device allows imaging with higher signal, lesser speckle noise with limited loss in axial and lateral resolution compared to traditional SM fiber based confocal microscopes. It is easily transferable to existing clinical endomicroscopes using SM fibers. It can be manufactured using commercially available fibers and is inherently achromatic. The all-fiber technology also provides stable, alignment-free systems that can be used in any environment.