Spectroscopic-speckle variance OCT for microvasculature detection and analysis

Abstract

We propose and studied optical coherence tomography (OCT) combining spectroscopic (SOCT) and speckle variance (svOCT) functions to effectively detect locations of microvasculatures and assess blood oxygen saturation level. Chorioallantoic membrane of a chick embryo was imaged in vivo to perform the analysis of the system. We also studied the effect of speckle in spectral domain using experimental data and performed time-averaging to reduce speckle noise locally. We combined SOCT and svOCT images using hue, saturation and value (HSV) color map to show the localized spectroscopic property of blood. Results show distinct spectroscopic properties between arterial blood and capillary blood.

1. Introduction

The ability to image retinal microvasculatures and assess oxygen saturation level accurately with high spatial resolution is important in a wide range of medical diagnoses and treatments for eye diseases including diabetic retinopathy, which is one of the major causes of blindness [1,2]. However, retinal microvasculatures are hard to image due to their small sizes. Moreover, it is difficult to measure retinal blood oxygen saturation level (SO₂) accurately. One reason for this is the layered structure of the retina which makes the extraction of the absorption properties difficult. Another difficulty in accurate SO₂ assessment using a conventional retinal oximeter is due to the unknown optical-path-length [3].

Recent advances in optical coherence tomography (OCT) such as dual beam OCT have made OCT a competitive modality in terms of retinal microvasculature imaging [4–6]. One type of functional OCT called spectroscopic OCT (SOCT) that extracts localized wavelength dependent properties of the sample, has been considered a promising technique for accurate measurement of SO₂ since its first advent [7]. SOCT can simultaneously measure the spectral modulation induced by blood absorption and photon optical path lengths; therefore, SOCT may provide an accurate SO₂ assessment with high spatial resolution. There have been several demonstrations of SOCT for SO₂ assessment using ex vivo samples and blood phantoms [8–13].

One difficulty associated with SOCT's application in blood SO₂ assessment comes from the prevalent existence of speckle in OCT images obtained from in vivo or in situ biological samples. Speckle is the result of the coherent summation of light waves with random path lengths [14] and it is often considered as a noise source which degrades the quality of OCT images [15–17]. Various methods have been developed to reduce speckle in spatial domain, such as angle compounding, spectral compounding, and strain compounding [18–20]. In addition to adding “salt-and-pepper-like” noise to OCT images, speckle also induces random modulation to interferometric spectra [21], which significantly reduces SOCT contrast. However, the role of speckle in SOCT has not been extensively investigated.

In spite of being a noise source, speckle also carries information. For example, laser speckle imaging (LSI) technique has been used in imaging blood vessel networks in brain and retina since the 1990s [22–24]. As for OCT, the speckle phenomenon has been used in speckle variance OCT (svOCT) for the visualization of microvasculature [25,26].

In this study, we propose to combine SOCT and svOCT for the detection of microvasculature and assess the blood SO₂. svOCT images accentuate blood vessels because speckle patterns in areas with flowing blood vary rapidly and are uncorrelated between frames. This also implies that speckle induced random spectral modulation in spectral domain varies rapidly and becomes uncorrelated in different frames. Therefore, performing spectroscopic analysis on multiple OCT images and averaging the resultant SOCT signals may effectively reduce the speckle noise within blood vessels and lead to an unambiguous SOCT signal. To acquire data for the proposed analysis, we performed Fourier domain OCT (FD OCT) imaging of the chorioallantoic membrane (CAM) of a chick embryo in vivo. CAM is a commonly used model tissue for surgical retinal research and simulation [27]. We have obtained svOCT images that highlight blood vessels, and studied speckle statistics at areas with or without blood vessels. We also performed time-frequency analysis to obtain SOCT signal, studied speckle phenomena in spectral domain, and demonstrated that in the areas with blood vessels, averaging SOCT signal can significantly reduce speckle-induced random spectral modulation. Finally, we extracted a relative SO₂ map and combined SOCT and svOCT images using hue, saturation, and value (HSV) color map to show localized spectroscopic property of blood vessels.

2. Theory

FD OCT measures spectral interferogram S (k) = η[|E_R(k)|² + |E_S(k)|² + 2Re(〈E_R(k) E_S*(k)〉)]. Here η is the responsive coefficient of the system; k = 2π/λ is wavenumber; E_R and E_S are electrical fields from reference and sample arm; * denotes complex conjugate; 〈 〉 denotes time average; Re() refers to the real part of a complex signal. The interference signal S_OCT (k) is the third term in the expression of S(k). As shown in Eq. (1), A-scan I_OCT(z) can be obtained from inverse Fourier transform of S_OCT (k), which is the cross spectral density created by interference between spectra from sample and reference arm:

$$I_{OCT}\left(z\right)={\mathbb{F}}^{-1}\left[S_{OCT}(k)\right]$$ (1)

In Eq. (1), z indicates the distance between the reference plane and the sample plane sliced. Here, I_OCT(z) is the complex amplitude of OCT signal. It is worth mentioning that the measured interferometric spectra have to be converted to k space through a re-sampling procedure [28].

2.1 Blood SO₂ and absorption coefficient

Blood oxygen saturation level, SO₂, is defined as the ratio between the concentration of oxygenated hemoglobin (HbO₂) and total hemoglobin, shown as Eq. (2). In Eq. (2), $C_{Hb{O}_2}$ and C_Hb indicate the concentration of oxygenated and de-oxygenated hemoglobin:

$$S{O}_2=\frac{C_{Hb{O}_2}}{C_{Hb{O}_2}+C_{Hb}}$$ (2)

Considering that oxygenated hemoglobin (HbO₂) and deoxygenated hemoglobin (Hb) are the only chromophores in blood, we can express blood absorption coefficient as

$$\alpha =C_{Hb}{\epsilon }_{Hb}+C_{Hb{O}_2}{\epsilon }_{Hb{O}_2}$$ (3)

In Eq. (3), ${\epsilon }_{Hb{O}_2}$ and ε_Hb indicate the extinction coefficients of HbO₂ and Hb.

Equation (3) can be rewritten as Eq. (4), where $C=C_{Hb{O}_2}-C_{Hb}$:

$$\alpha =C\left[{\epsilon }_{Hb}+S{O}_2\left({\epsilon }_{Hb{O}_2}-{\epsilon }_{Hb}\right)\right]$$ (4)

Since the extinction coefficient of Hb and HbO₂ have different wavelength dependencies as shown in Fig. 1 [29], the wavelength dependency of blood absorption can be used in the assessment of blood SO₂. In Fig. 1, the blue curve indicates the extinction coefficient of Hb and the red curve indicates the extinction coefficient of HbO₂. In this study, we compared the spectroscopic properties of OCT signal in long and short wavelength range (as indicated in Fig. 1) for the SO₂ assessment.

Fig. 1.

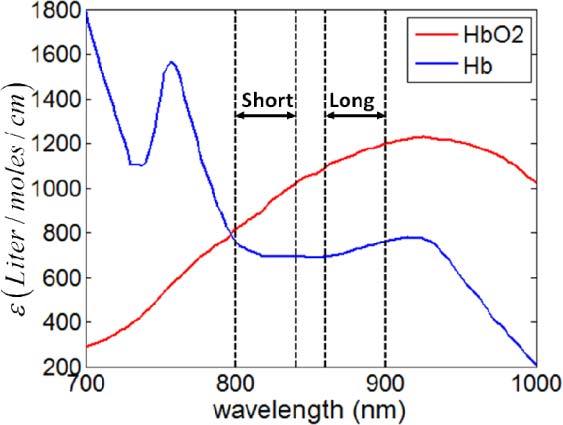
Molar extinction coefficient spectra of Hb (blue) and HbO₂ (red).

2.2 Spectroscopic OCT (SOCT) for blood SO₂ assessment

SOCT is used to assess blood SO₂ based on the attenuation properties of the blood in different wavelength ranges. There are different ways to extract SO₂-dependent blood spectroscopic properties from FD OCT data, one of which is to apply Short Time Fourier Transformation (STFT) to complex-valued OCT data in spatial domain (A-Scan) to acquire a localized spectrum, and afterwards compare local spectral intensities in short and long wavelength ranges [7]. The other method for SO₂ assessment is to directly obtain OCT image using spectral interferograms in long and short wavelength ranges, respectively, and then compare the two OCT images acquired from them [11]. For the convenience of narration, we refer to the first method as the STFT method and the second method as two-wavelength (TW) method.

In STFT method, STFT is applied to I_OCT(z), the complex amplitude of OCT signal. Without considering the randomness of OCT signal due to speckle, S_OCT can be expressed as Eq. (5):

$$\begin{array}{l}{S}_{OCT}(k)={\displaystyle \int S_0(k)M\left(k,z\right)\cos \left(2kz\right)dz}\\ ={\displaystyle \int U\left(k,z\right)\cos \left(2kz\right)dz}\end{array}$$ (5)

In Eq. (5), S₀(k) indicates the envelope of interferometric pattern detected by spectrometer with a spectrally flat specimen; M(k,z) denotes the spectral modulation induced by sample.

An estimation of U at location z₀ can be obtained by applying STFT to I_OCT(z) using Gaussian window [7,13]:

$$V(k,z_0)=\left|\mathbb{F}\left\{I_{OCT}\left(z\right)\exp \left[-4\ln 2\frac{{\left(z-z_0\right)}^2}{L^2}\right]\right\}\right|$$ (6)

In Eq. (6), z₀ is the center of the Gaussian window; L indicates the full width half maximum (FWHM) of the Gaussian window which determines the spatial resolution of this analysis; F indicates Fourier transform. Please note that a tradeoff exists between spatial and spectral resolution in such time-frequency analysis, and the spectral resolution is inversely proportional to L.

To assess SO₂ using spectrum obtained from Eq. (6), we calculated γ by comparing spectral intensities in long and short wavelength range (I_long and I_short), as shown in Eq. (7). I_long and I_short are obtained from averaging the amplitude of localized spectrum V(k,z₀)in long and short wavelength ranges. Therefore, I_long and I_short are functions of spatial coordinate z. Similarly, each pixel in OCT image corresponds to one localized spectrum from STFT and thus corresponds to one γ value which is a function of spatial coordinate. Values of γ are assigned to corresponding pixels to form SOCT image to represent the relative SO₂:

$$\gamma \left(z\right)=\log \left(\frac{I_{short}}{I_{long}}\right)=\log \left(I_{short}\right)-\log \left(I_{long}\right)$$ (7)

In TW method, Gaussian windows, G_long and G_short, are applied to each spectral interferogram. As shown in Eq. (8) and Eq. (9), I_long and I_short are real valued amplitudes of OCT signal obtained from spectral interferograms in long and short wavelength ranges. In Eqs. (8) and (9), | | indicates the absolute value of a complex number:

$$I_{long}\left(z\right)=\left|{\mathbb{F}}^{-1}\left[S_{OCT}(k)G_{long}(k)\right]\right|$$ (8)

$$I_{short}\left(z\right)=\left|{\mathbb{F}}^{-1}\left[S_{OCT}(k)G_{short}(k)\right]\right|$$ (9)

Similarly, we compared I_long and I_short obtained from TW method to extract spectroscopic property related to SO₂, as shown in Eq. (7).

Let us assume that the attenuation follows Beer-Lambert’s law, and the attenuation coefficients at the centers of short and long wavelength bands are α_long and α_short, respectively. Therefore we have I_long = I_0,longe^-zαlong and I_short = I_0,shorte^-zαshort. z here indicates the interaction length between light and blood. Further using Eq. (4) for α_long and α_short, we may express γ as Eq. (10), which clearly shows how γ depends on blood SO₂:

$$\gamma \left(z\right)=\log \left(\frac{I_{0,long}}{I_{0,short}}\right)+zC\left[\Delta {\epsilon }_{Hb}+S{O}_2\left(\Delta {\epsilon }_{Hb{O}_2}-\Delta {\epsilon }_{Hb}\right)\right]$$ (10)

In Eq. (10), Δε_HbO2 = ε_HbO2,long-ε_HbO2,short and Δε_Hb = ε_Hb,long-ε_Hb,short.

The advantage of the STFT method is the high spectral resolution which enables us observation of local spectroscopic features. However the method depends on the FWHM of the Gaussian window used. Thus high spectral resolution can only be obtained at the expense of reduced spatial resolution. Therefore, we used the STFT method to study the effect of speckle in SOCT signal. However, the STFT method is much more time consuming compared to the TW method. According to Eqs. (6), (8) and (9), γ at each spatial location is obtained through FFT in STFT method. Therefore, it requires N²log₂N operations to obtain an A-scan of SOCT from OCT signals. Here N indicates the number of pixels in one A-scan. On the other hand, one only needs to perform FFT twice from the raw spectral data to obtain γ values in an A-scan of SOCT from the TW method, which indicates only 2Nlog₂N operations are required. As a result, the STFT method takes O(N) times more operations compared to TW method. Using GPU processing developed in our laboratory, it takes less than 1 millisecond to obtain one B mode frame of SOCT signal using TW method.

2.3 Speckle in OCT and speckle variance OCT (svOCT) for blood vessel detection

Speckle prevalently exists in OCT images and has been extensively studied in the literatures [14–17]. |I_OCT|, the amplitude of OCT signal with fully developed speckle, is a random variable that follows a Rayleigh distribution shown in Eq. (11):

$$\rho \left(\left|I_{OCT}\right|\right)=\frac{\left|I_{OCT}\right|}{{\sigma }_{OCT}^2}\exp \left(-\frac{\left|I_{OCT}^2\right|}{2{\sigma }_{OCT}^2}\right)$$ (11)

In Eq. (11), σ_OCT² is the variance and σ_OCT² = 2〈|I_OCT|〉²/π for fully developed speckle in OCT images.

Speckle pattern forms due to the coherent superposition of random phasors. As a result of speckle, the OCT signal becomes random in an area that is macroscopically uniform. If the sample under imaging is static, the speckle pattern is temporally stationary. However, when photons are backscattered by moving particles, such as red blood cells in flowing blood, the formed speckle pattern will change rapidly over time. In this study, speckle patterns at areas with flowing blood have a large temporal variation, which can be quantified by inter-frame speckle variance. Speckle variance OCT (svOCT) calculates inter-frame speckle variance using N₀ B-mode OCT images with Eq. (12) [25,26]:

$$S{V}_{jm}=\frac{1}{I_{mean,jm}}\sqrt{\frac{1}{N_0}{\displaystyle \sum _{i’=0}^{N_0-1}{\left(I_{i\text{'}jm}-I_{mean,jm}\right)}^2}}$$ (12)

In Eq. (12), j and m are lateral and depth pixel indices of the B-Scan; i' indicates the index of frame which is also a dummy variable; I_i'jm is the signal intensity at pixel (j, m) in the i'^th frame. I_mean,jm is the averaged signal over the same set of pixels, which is calculated by Eq. (13):

$$I_{mean,jm}=\frac{1}{N_0}{\displaystyle \sum _{i‘=0}^{N_0-1}{I}_{i\text{'}jm}}$$ (13)

In conventional temporal LSI, areas with increased blood flow have blurred speckle patterns, because the camera has a finite exposure time and effectively averages rapidly changing speckle pattern. The speckle contrast in LSI is extracted in a similar way as Eq. (12) [22,24]. However, it calculates the variance of signal in a given window in spatial domain, unlike svOCT which calculates the variance of signal of the same pixel acquired at different frames. Therefore, the spatial resolution of temporal LSI is determined by the window size used in signal processing which extracts speckle contrast, while the spatial resolution of svOCT is determined by the optics in OCT system. It is also worth mentioning that blood vessels appear bright in svOCT due to its large temporal variation and appear dark in LSI due to small spatial variation associated with a long camera exposure.

2.4 Speckle in SOCT

Considering speckle as a multiplicative noise which causes random spectral modulation, it is more appropriate to express V_measure,i, the localized interferometric spectrum obtained from STFT at the i^th frame as the product of the deterministic term V, as shown in Eq. (6) and the speckle noise term N_s,i, as in Eq. (14):

$$V_{measure,i}\left(k,z_0\right)=N_{s,i}\left(k,z_0\right)V\left(k,z_0\right)$$ (14)

Equation (14) implies that the random speckle term N_s,i impedes effective extraction of macroscopic spectroscopic properties. As a result, it is critical to minimize speckle to obtain a SOCT signal that correlates with blood SO₂ level. Fortunately, due to the constantly moving scatterers in the flowing blood, speckle pattern in OCT image decorrelates in different frames for areas with blood flow. The Bienaymé formula states that the variance of the sum of uncorrelated random variables equals the sum of variances of the random variables [30]. Therefore, averaging V_measure from N₀ frames as shown in Eq. (15) may reduce the variance of the multiplicative noise term N_s to be σ²/ N₀, assuming random variable N_s,i has a variance of σ². As a result, it is possible to reduce speckle in these areas through extensive time-averaging and to obtain an unambiguous estimation of SO₂ based on an accurate measurement of V(k,z₀).

$$\frac{1}{N_0}{\displaystyle \sum _{i=0}^{N_0-1}{V}_{measure,i}\left(k,z_0\right)}=\frac{1}{N_0}\left[{\displaystyle \sum _{i=0}^{N_0-1}{N}_{s,i}\left(k\right)}\right]V\left(k,z_0\right)=N_{s}V\left(k,z_0\right)$$ (15)

3. Experiment and signal processing

The FD OCT system for raw data acquisition is very similar to our previous work [31,32]. A 12-bit, 70kHz, 2048 pixel CCD line-scan camera (EM4, e2v, USA) was used in the home-built OCT engine. The superluminescence diode (SLED) light source had 105nm effective bandwidth and centered at 845nm (Superlum Ireland, SN: T-870-HP). A Dell T7500 workstation was used to host a high-speed frame grabber (NI PCI-1424) and the captured raw spectra were buffered in a host memory block and finally saved onto the hard drive. A pair of high-speed galvanometers were used to perform raster scanning. The scanning spot size was approximately 13µm assuming Gaussian beam. Graphics processing unit (GPU) based high-speed processing and display was used to facilitate alignment and real-time monitoring. The data acquisition, processing, display, and buffering were realized on a multi-thread, CPU-GPU real-time heterogeneous computing system [31,32]. We took in vivo images of a mature chorioallantoic membrane (CAM) from a chick embryo which had been incubated for 12 days. The thickness of CAM is usually about 100µm. In mature CAM, there are three distinct layers: primary stratum, capillary plexus, and a thin stratum composed primarily of specialized chorionic epithelial cells [27]. Figure 2 shows a chick embryo with a portion of its inner shell membrane peeled so that blood vessels at CAM can be seen clearly. As shown in Fig. 2, CAM is a relatively transparent thin membrane and, therefore, blood vessels at CAM are easily accessible. We peeled the inner shell membrane before imaging. In this study, OCT images were taken at a speed of 25 000 line-per-second or 50 frames-per-second with each B-scan containing 500 A-scans. We repetitively took OCT images of the CAM with blood vessels at the same slice. Spectral data for 500 frames of OCT images was acquired and post-processed. In our OCT images, a pixel with the same lateral and axial indices represents the same location in 3D space since we imaged the same slice. However, an OCT signal at the same pixel takes different values in different frames, due to the existence of noise including speckle.

Fig. 2.

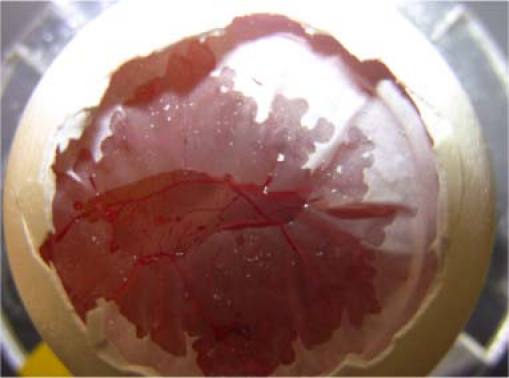
A chick embryo with part of its inner shell membrane peeled

When extracting localized spectra using the STFT method in Eq. (6), we chose a Gaussian window with FWHM of 20μm, i.e., L = 20μm. I_short and I_long were calculated by averaging the intensity from local spectra obtained in long (860nm-900nm) and short wavelength range (800nm-840nm) as shown in Fig. 1. In the TW method, we used Gaussian window G_short and G_long centering at 820nm and 880nm respectively. The FWHM of G_short and G_long are both 15nm, which implies an axial resolution of approximately 20μm. Considering the refractive index of tissue (~1.4), the axial resolution of our spectroscopic analysis is approximately 14μm.

4. Results

4.1. Speckle properties of OCT signal

Figure 3 (a) and Fig. 3 (b) show B-Scan of the CAM obtained without averaging and with averaging 500 frames. The scale bar in Fig. 3 (a) represents 100μm in length. Figure 3 shows the primary stratum and the thin stratum. Moreover, a major blood vessel is clearly visible in Fig. 3. The result in Fig. 3 is in good agreement with the histologic cross-section of mature chick CAM [27]. The shape of the vessel lumen is a well-defined oval, which indicates the large blood vessel is an artery. This is because arteries have a large amount of muscle in their walls to constrict and dilate to control blood flows and bear the powerful force generated by the heart. Conversely, veins usually have collapsible walls and change their shape depending on the surrounding tissue conditions. It is worth mentioning that all images in Figs. 3 and 4 and in Figs. 7, 8 (a), (b), and (c) below have the same dimensions which are 3mm (lateral) X 500μm (axial).

Fig. 3.

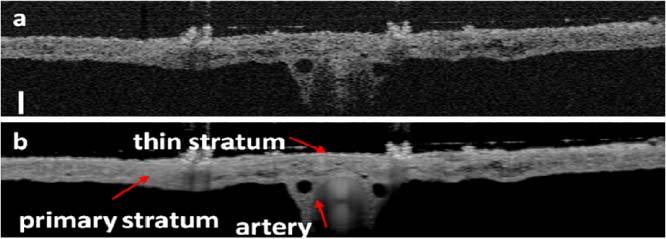
(a) B-mode OCT image without averaging; (b) B-mode OCT image obtained by averaging 500 frames

Fig. 4.

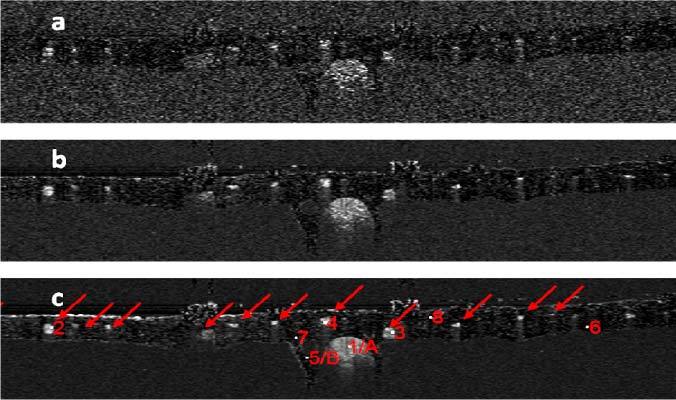
svOCT images obtained by using 10 (a), 100 (b) and 500 (c) frames of OCT images to calculate the speckle variance.

We obtained svOCT image through Eq. (12) using 10, 100, and 500 frames of OCT images and show the results in Figs. 4 (a), (b) and (c). There are blood vessels located in the primary stratum of the CAM, as indicated by red arrows in Fig. 4 (c). According to the anatomy of CAM, blood vessels scattering in the primary stratum are capillary vessels [27]. Figure 4 (c) also shows points of interest (POI) which will be used in the analysis of temporal speckle properties and spectral domain speckle noise. POIs are indicated by numbers 1 - 8, and letters A and B. Points 1 (A), 2, 3, 4 are within the blood vessel; while points 5 (B), 6, 7, 8 are not. Vessels in Fig. 4 are located in depths ranging from 20μm to 100μm from the thin stratum. While in human retina, radial peripapillary capillaries and inner capillaries are also located less than 100μm in depth [6]. As to the dimension of blood vessels, the large vessel in which Point 1 is located has a diameter of 270μm; and other selected vessels (Points 2, 3 and 4) have diameters ranging from 50μm to 60μm which are also similar to that of human retina. Therefore, the similarity between the anatomical structure of CAM and retina makes CAM an appropriate tissue to validate svOCT and SOCT techniques toward the study of retinal microvasculatures and SO₂. Figure 4 also shows that by using more frames of OCT image to calculate the svOCT image, the svOCT images can achieve better contrast. This is because in our experiment the sample had negligible bulk movement during data acquisition and the same lateral location was scanned [26].

To show different temporal speckle statistics for areas with or without blood, we studied the probability distribution of OCT signals at Points 1 - 8. Unlike conventional laser speckle imaging (LSI) techniques which study the statistical property of speckle pattern in a region of interest, we are interested in speckle statistics of the same pixel at different time of svOCT, because svOCT uses interframe variance to extract speckle contrast, as shown in Eq. (12). Therefore, we selected Points 1 to 4 to represent the statistics for signal from pixels inside of blood vessels and Points 5 to 8 to represent the statistics for signal from pixels outside of blood vessels. According to Eq. (11), |I_OCT| at areas with flowing blood (Points 1, 2, 3 and 4) exhibit Rayleigh distribution. On the other hand, |I_OCT| at areas without blood (Points 5, 6, 7 and 8) exhibit distribution similar to Gaussian due to the summation of random factors such as optical or electrical noise in the system and bulk movement of the sample during data acquisition. Assume the random OCT signal is ergodic. For a given pixel, we may calculate the histogram of the signal intensities using OCT data acquired in different frames and use this histogram as an experimental estimation of |I_OCT|’s probability distribution at the pixel due to the ergodicity. For each selected pixel (Points 1 to 8), we normalized the intensities to their standard deviations σ_OCT, calculated the histograms of the normalized signal and show the resultant histograms corresponding to Points 1 - 8 in Figs. 5(a)–(h) . In Figs. 5 (a)–(d) and Figs. 5 (e)–(h), we also plot the Rayleigh and Gaussian probability density functions with a variance equal to 1, which are the red curves and are in good agreement with the experimentally acquired histograms. Results in Figs. 5 (a)–(d) verify that the amplitude of the OCT signal within the blood vessel is ergodic and its speckle statistics follows Eq. (11), as we stated before. In addition, as we normalized the signals to their standard deviations for the convenience to compare experimentally obtained probability distributions with the standard Rayleigh and Gaussian distributions shown as red curves in Fig. 5. All the histograms in Fig. 5 appear to have similar width. However, the signal variance of the static tissue was much smaller than the blood vessel, therefore the speckle contrast can be obtained to highlight blood vessels.

Fig. 5.

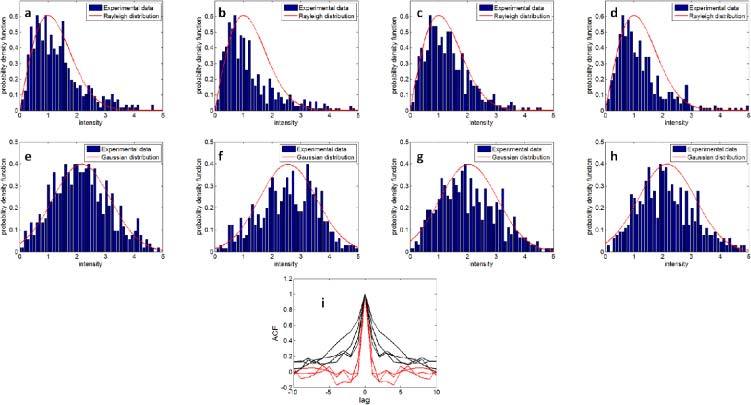
(a)–(h) Histogram of signal intensity at Pixels 1–8; (i) autocorrelation function of signal intensity obtained from points 1–4 (red curves) and obtained from points 5–8 (black curves).

To show that OCT signals at areas with flowing blood decorrelate at different frames, we calculated the autocorrelation functions (ACF) of OCT signal at Points 1-8 and show the results in Fig. 5 (i). Figure 5(i) shows the remarkable difference between ACF obtained from Points 1 – 4 (red curves) and ACF obtained from Points 5 – 8 (black curves). ACFs in Fig. 5 (i) show that signals obtained from blood vessel have shorter decorrelation time compared to signals obtained from non-blood tissue. In other words, signals at Points 1 – 4 decorrelate at adjacent frames, while there exist residual correlation at points 5 – 8 at adjacent frames. For pixels within blood vessels, the decorrelation of OCT signals in different frames also allows us to reduce speckle noise in spatial and spectral domain through extensive time averaging, as we demonstrate in Eq. (15).

4.2. Speckle and its reduction in SOCT

To show the random spectral modulation induced by speckle in SOCT signal, we used the STFT method and extracted localized spectra V_A(λ) and V_B(λ) using Eq. (6) from one complex-valued B-Scan. V_A(λ) and V_B(λ) correspond to Point A(x_a, y_a) and B(x_b, y_b), shown in Fig. 4 (c). Point A is located inside of the major artery and Point B is in the primary stratum. We also studied the localized spectra obtained from the vicinity of Points A and B at (x_a,y_a ± 5μm), (x_b,y_b ± 5μm), (x_a ± 10μm,y_a) and (x_b ± 10μm, y_b). Spectra obtained in the vicinity of Point A and B are shown in Figs. 6 (a) and (b) , respectively. Due to the existence of speckle, spectra in Figs. 6 (a) and (b) have random intensity fluctuation which does not depend on spatial coordinate. Results in Figs. 6 (a) and (b) indicate that the SOCT signal not only depends on macroscopic optical properties of the specimen such as scattering and absorption coefficients, but also strongly depends on the microscopic distribution of scatterers if there is speckle. This severely impedes the effective extraction of spectroscopic information. To reduce speckle, we applied STFT to extract localized spectrum from each OCT image. Therefore, for each point in 3D space, we obtained 500 localized spectra, averaged their intensities to obtain V(λ) with reduced speckle noise. The averaged spectra at the vicinity of Point A and B are shown in Figs. 6 (c) and (d), respectively. Spectra in Fig. 6 (c) have significantly reduced speckle compared to Fig. 6 (a) and their spectral shapes are similar. On the other hand, spectra in Fig. 6 (d) still have residual random modulation. Results in Fig. 6 (c) implies that temporal averaging can effectively remove speckle in SOCT signal obtained from areas with flowing blood, because speckle pattern changes at different measurements. As a result, the SOCT signal with reduced speckle may be correlated with the specimen’s macroscopic optical property to extract blood SO₂ information.

Fig. 6.

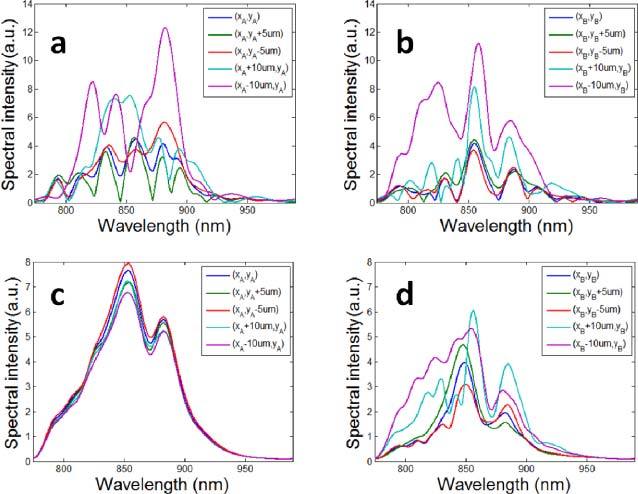
(a) Localized spectra obtained in the vicinity of Point A without averaging; (b)Localized spectra obtained in the vicinity of Point B without averaging; (c)Localized spectra obtained in the vicinity of Point A obtained by averaging 500 spectra; (d)Localized spectra obtained in the vicinity of Point B obtained by averaging 500 spectra.

4.3. Combining SOCT and svOCT

Using STFT method, we were able to obtain localized spectrum for each pixel of a complex-valued B-Scan image. Afterwards, we calculated the γ value corresponding to each pixel using Eq. (7) and the result formed a SOCT image shown as Fig. 7 (a) . Due to speckle induced random spectral modulation, Fig. 7 (a) suffers from overwhelming noise and the blood vessels are not discernable. To reduce speckle, we obtained 10 localized spectra for each pixel from 10 frames of complex-valued OCT images, averaged the intensity of the 10 spectra, and calculated γ using Eq. (7). The result is shown in Fig. 7(b) which still suffers from severe speckle noise. Using the same method, we obtained SOCT images from 100 and 500 frames of complex-valued OCT images and show results in Figs. 7 (c) and (d). Due to reduced speckle in areas with blood, the SOCT signal appears smoother with extensive averaging. We also used the TW method to obtain SOCT images. We obtained I_short and I_long from spectral data acquired in one frame and used Eq. (7) to calculate the SOCT signal. The result is shown in Fig. 7 (e). We also used 10 frames of spectral data to calculate 10 frames of I_short and 10 frames of I_long. Afterwards, we averaged I_short and I_long for the calculation of γ. The result is shown in Fig. 7 (f). When I_short and I_long are acquired from 100 and 500 frames of data, we obtained SOCT images in Figs. 7 (g) and (h) using TW method. To enhance contrast of images in Fig. 7, we normalized γ to their maximum values, and then mapped the normalized result to new values such that 1% of data is saturated at low and high intensities of the image

Fig. 7.

SOCT images obtained from the STFT method using 1 (a), 10 (b), 100 (c), 500 (d) frames of OCT data; SOCT images obtained from the TW method using 1 (e), 10 (f), 100 (g), 500 (h) frames of OCT data.

In Figs. 7 (c), (d), (g), and (h), areas without flowing blood still have granular texture even after extensive averaging. This is because in those areas speckle patterns are stationary and averaging over time does not remove speckle-induced spectral modulation, which is consistent with results shown in Fig. 5 (i) and Fig. 6 (d). Due to the noisy nature of the spectroscopic signal in the areas without blood flow, it is possible that both I_long and I_short take very small values (close to 0). As a result, with speckle noise, γ can vary greatly since it is the logarithm of the ratio between I_long and I_short. On the other hand, with the reduced speckle noise, γ at areas with flowing blood have smoother texture and vary within a relatively smaller range. In Fig. 7, γ values corresponding to the whole image are mapped to a grey scale. Due to the limited dynamic range of a digital image, γ within blood vessels represent a very small fraction of the dynamic range. Therefore, it is hard to see spatial variation of γ within blood vessels in Fig. 7.

To show spectroscopic properties of blood more clearly, we combined svOCT image and SOCT image together. In areas with flowing blood, the SOCT signal is of interest and svOCT signal is large. To highlight the blood vessels, we applied thresholding to the svOCT image in Fig. 4 (c) to determine whether a pixel is within a blood vessel. This thresholded svOCT also indicates where the SOCT signal can be used for SO₂ assessment. The result after thresholding is shown in Fig. 8 (a) . To overlay the SOCT image with thresholded svOCT image, we used a HSV (H, hue; S, saturation; V, value) color map. If a pixel is within a blood vessel according to the thresholded svOCT image, the V component is 1; otherwise, the V component is 0. As to the H component which determines the color, we tabulated SOCT signals at pixels which were identified to be within a blood vessel, performed histogram equalization to the SOCT signals, and assigned the signal after histogram equalization as the H component of the corresponding pixel. SOCT signals shown in Figs. 7 (d) and (h) are used as H component in the combined images due to their minimum speckle noise. Besides, the S component of every pixel is 1. Figures 8 (b) and (c) show the combined SOCT and svOCT images when Figs. 7 (d) and (h) are combined with the thresholded svOCT image using an HSV colormap. Color at the bottom of the colorbar (red) in Figs. 8 (b) and (c) represents a smaller γ compared to color at the top of the colorbar (purple). Figures 8 (b) and (c) not only show the locations and dimensions of blood vessels, but also exhibit the spectroscopic property of blood. For a clearer demonstration, Figs. 8 (d) and (e) show the zoom-in svOCT and SOCT image in the vicinities of Points 1, 2, 3 and 4, corresponding to Figs. 8 (b) and (c). Spatial variation of γ can be visualized in Figs. 8(b)–(e), because pixels outside of blood vessels were excluded in this mapping and the SOCT signal with significantly reduced speckle noise is represented by the full dynamic range of the digital image in Figs. 8 (b)–(e) in terms of hue. We also studied γ(z) within a blood vessel along the A-scans where Points 1, 2, 3 and 4 are located. γ(z) obtained from STFT method are shown in Fig. 8 (f), corresponding to Point 1 to 4, from left to right. Similarly, γ(z) obtained from TW method are shown in Fig. 8 (g). For a more explicit demonstration, we performed linear fitting to γ(z) and show the corresponding fitting results as red curves in Figs. 8 (f) and (g).

Fig. 8.

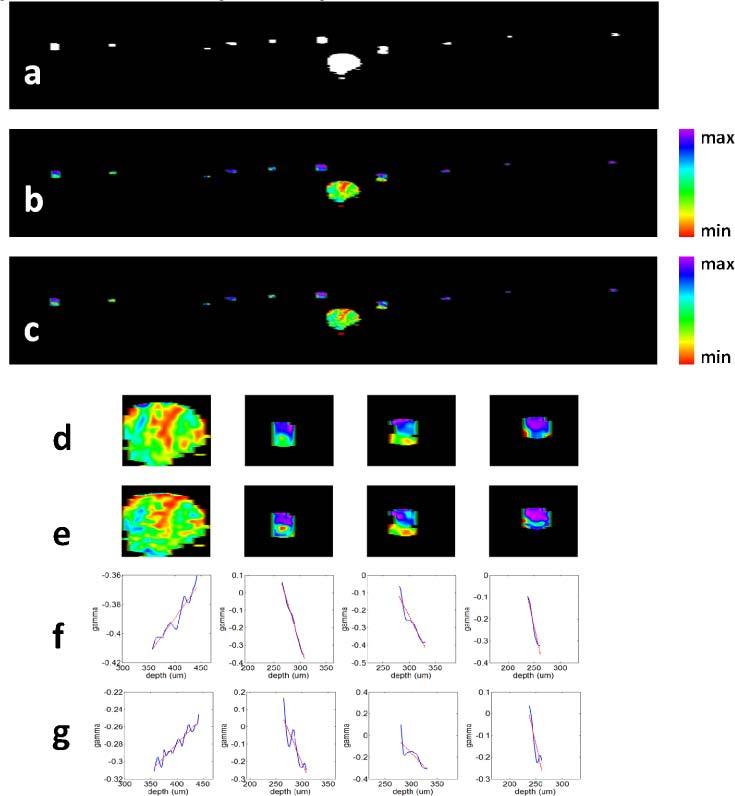
(a) Thresholded svOCT image that highlights blood vessels; (b) combined svOCT image and SOCT image obtained from STFT method; (c) combined svOCT image and SOCT image obtained from TW method; (d) the vicinities of Points 1, 2, 3 and 4 in the combined svOCT and SOCT image from STFT method; (e) the vicinities of Points 1, 2, 3 and 4 in the combined svOCT and SOCT image from TW method; (f) and (g) shows γ(z) obtained, corresponding to Point 1 to 4, from STFT method and TW method, respectively.

As shown in Eq. (10), SOCT signal γ depends on blood SO₂, as well as Δε_HbO2 and Δε_Hb. In our spectroscopic analysis, the central wavelengths for short and long wavelength bands are 820nm and 880nm respectively, in both the STFT and TW method. For these two central wavelengths, ε_HbO2,short and ε_HbO2,long are approximately 916 liter/cm/Mol and 1154 liter/cm/Mol. ε_Hb,short and ε_Hb,long are approximately 693 liter/cm/Mol and 726 liter/cm/Mol [29]. Therefore, Δε_HbO2 = 238 liter/cm/Mol and Δε_Hb = 33 liter/cm/Mol. According to Eq. (10), γ varies as l at a slope proportional to blood SO₂.

Seen from Figs. 8 (b) and (c), or even more clearly from Figs. 8 (d) and (e), γ gets larger as increasing imaging depth in the artery while the opposite trend is shown in capillaries. As shown in Fig. 8 (f), it is clear that γ(z) corresponding to the artery has a positive slope while γ(z) corresponding to capillaries have negative slopes. Figure 8 (g) can lead to the same observation. Therefore, γ has a smaller slope in capillary blood than in arterial blood. The fact that this method can show distinctive differences between the absorption properties of blood with different oxygenation level shows that the method could be used to quantitative assess blood SO₂ level. The difference between Figs. 8 (b) and (c) may derive from the slightly different spatial resolutions and noise in the final SOCT image achieved by the STFT method and the TW method. Although SOCT images acquired from STFT method and TW method are slightly different, they both clearly show spectroscopic properties of the blood. It is worth mentioning that although histogram equalization maps signal amplitude to a new value and make direct quantitative estimation of SO₂ from Fig. 8 difficult, the mapping function is monotonic, which means if one pixel has a larger signal than another before equalization, it is so afterwards. As a result, the slope of γ has the same sign before and after histogram equalization.

5. Discussion

Based on Eq. (10) which considers only absorption, γ should have increased with l regardless of the SO₂ level, because both Δε_HbO2 and Δε_Hb for the selected wavelength ranges are larger than 0. However, Fig. 8 shows γ within the capillaries decreases as l, indicating a negative slope. Such result can be explained by considering wavelength dependent scattering coefficient of blood in the NIR range [33,34]. If the Beer-Lambert law holds, OCT signal attenuates as

$$I_{OCT}=I_0{e}^{-\left({\alpha }_s+{\alpha }_a\right)z}$$ (16)

In Eq. (16) α_s is the reduced scattering coefficient of blood.

When scattering is considered, m, the slope of γ becomes

$$m=C\left[\Delta {\epsilon }_{Hb}+S{O}_2\left(\Delta {\epsilon }_{Hb{O}_2}-\Delta {\epsilon }_{Hb}\right)\right]+\left({\alpha }_{s,long}-{\alpha }_{s,short}\right)$$ (17)

In Eq. (17), α_s,short and α_s,long are the reduced scattering coefficients of blood in short and long wavelength ranges. It is known that the scattering coefficient decreases approximately as λ^-1.7 for wavelengths above 500 nm [34]. This indicates that α_s,long is smaller than α_s,short and thus the second term in Eq. (17) becomes negative. As a result, although the first term in Eq. (17) is always positive, m can be negative when the effect of scattering is included, which explains the results in Fig. 8.

Quantitative assessment of blood SO₂ using SOCT requires extracting signal attenuation due to absorption, which is challenging because in OCT both absorption and scattering cause the signal to attenuate. Some encouraging results have been acquired in previous studies. For example, C. Xu et al developed a least-squares algorithm for SOCT to separate absorption and scattering [35]. Recently, F. E. Robles et al proposed to use the real and imaginary parts of the refractive index obtained from SOCT measurement to separate scattering and absorption [36].

To show that we can obtain a quantitative value of SO₂ using this method, we obtained a SO₂ level of the artery at Point 1 using the following quantitative analysis. We selected the A-scan that contains Point 1, corresponding to the center of the large artery as indicated by Fig. 4 (c), and we calculated I_short and I_long for each pixel in this A-scan from the result of the STFT method. As the scattering coefficient decreases approximately as λ^-1.7 in the wavelength range of our study, we can use exact values of the scattering coefficient at wavelength λ₀ = 810nm (α_s,λ0) and the corresponding anisotropy factor (g) from literatures to calculate the reduced scattering coefficient α_s,λ [33,34] Using the result in Reference [33], we obtained reduced scattering coefficients at 820nm and 880nm, corresponding to the centers of short and long wavelength bands. The resultant α_s,short and α_s,long, are 6.6cm⁻¹ and 7.4cm⁻¹, respectively. With these α_s,short and α_s,long, we calculated the ratio between the logarithm of normalized signal amplitude in short and long wavelength ranges that include the effects of scattering which is found to be 1.03 and this corresponds to a SO₂ value of 96%. We are performing a detailed analysis of the quantitative SO₂ assessment and this will be the topic of our future publication.

6. Conclusion

In this paper, we took in vivo OCT images of the CAM from a chick embryo to study the effectiveness of the spectroscopic-speckle variance OCT. We obtained a cross-sectional svOCT image which highlighted microvasculatures. We also studied the probability distribution of speckle in the areas with or without blood flow. Furthermore, the role of speckle in spectral domain was investigated. Finally, SOCT and svOCT images were combined to show localized spectroscopic property of blood. Our results showed distinct spectroscopic differences between arterial blood and capillary blood, which verifies the effectiveness of our method.