Abstract
Optical coherence tomography (OCT) has recently been used to produce 3D angiography of microvasculature and blood flow maps of large vessels in the rodent brain in-vivo. However, use of this optical method for the study of cerebrovascular disease has not been fully explored. Recent developments in neurodegenerative diseases has linked common cardiovascular risk factors to neurodegenerative risk factors hinting at a vascular hypothesis for the development of the latter. Tools for studying cerebral blood flow and the myogenic tone of cerebral vasculature have thus far been either highly invasive or required ex-vivo preparations therefore not preserving the delicate in-vivo conditions. We propose a novel technique for reconstructing the flow profile over a single cardiac cycle in order to evaluate flow pulsatility and vessel compliance. A vascular model is used to simulate changes in vascular compliance and interpret OCT results. Comparison between atherosclerotic and wild type mice show a trend towards increased compliance in the smaller arterioles of the brain (diameter < 80μm) in the disease model. These results are consistent with previously published ex-vivo work confirming the ability of OCT to investigate vascular dysfunction.
OCIS codes: (110.4500) Optical coherence tomography
1. Introduction
Aging, hypertension and Alzheimer’s disease (AD) are major determinants of cognitive impairment. Moreover, risk factors for AD and other neurodegenerative diseases are strongly correlated to cardiovascular risk factors leading to increased interest in studying the impact of cardiovascular disease on brain vasculature [1, 2, 3, 4]. Evidence is emerging that vascular dysfunction is an early biomarker of ensuing neuronal dysfunction but the link between vascular dysfunction and neuronal deficits remain difficult to study in vivo. The development of new tools to assess vascular health in vivo are necessary to bridge the gap between ex vivo studies and in vivo function.
In animals, the emergence of new optical imaging techniques has provided unprecedented access to vascular anatomy and tissue perfusion [5]. Two photon microscopy (TPM) using labelled markers allows high resolution imaging of vascular networks. Recent work with this technique has showed the measurement of blood flow and longitudinal studies of vascular network remodelling after stroke [6, 7]. However, TPM of the neuro-vascular network is highly invasive as it requires the use of labeled markers and a cranial window. The preparation of the cranial window leads to temporary loss of intra-cranial pressure which may be detrimental to the measurement of vascular function.
Optical coherence tomography (OCT) offers an interesting alternative to study vascular health as it has recently been used to produce 3D angiography of cerebral microvasculature (CMV) in the rodent brain in vivo and blood flow maps of large vessels. Many groups have developed techniques for producing angiography images of the CMV [8, 9, 10, 11]. These techniques can be used to decipher flow in small vessels down to 10 μm diameter. With reduced oversampling, blood flow in larger vessels can be measured with good temporal resolution opening the door for functional studies [12].
The genetically altered (LDLR−/− hApoB+/+) mice spontaneously develop atherosclerotic plaques and can be used as a model of CMV dysfunction. In the main carotid arteries, atherosclerosis is known to cause a decrease of compliance [13]. However, recent evidence show that this effect is reversed in resistance arteries due to a possible compensatory reaction [14]. The aim of this study was to verify whether OCT can be used to corroborate these effects in vivo.
In this work we develop a technique to gate Doppler OCT acquisitions and reconstruct the blood flow profile across a single cardiac cycle in arterioles using an electrocardiography (ECG) signal. We then use this gating technique to compare the changes of blood flow and vessel diameter across a cycle in wildtype (WT) and atherosclerotic (ATX) mice, the latter expected to exhibit changes in vascular function. Our results are then analyzed using a simple model to derive an estimate of vascular compliance and interpreted using a recently developed vascular anatomical network model. Compliance estimations from OCT data were derived but displayed lower Signal to Noise Ratio (SNR) than pulsatility measures. We confirm that Doppler OCT has enough sensitivity to quantify blood flow changes across a cardiac cycle and show that these changes can be used to provide estimators of vascular properties in mice.
2. Materials and methods
2.1. Animals and preparation
The procedures and protocols were performed in accordance with our institutional guidelines and the Guide for the Care and Use of Laboratory Animals of Canada. Animals were kept under standard conditions (24C; 12:12hr light/dark cycle). We used 6 month-old (m/o) C57Bl/6 male mice (WT, bodyweight of 34.8 ± 4.2g, n = 6; Charles River Laboratories, St-Constant, QC, Canada) and atherosclerotic mice (ATX, bodyweight of 34.3 ± 6.3g, n = 6); the latter are knockout mice for the LDL receptor but express the human apolipoprotein B-100 gene (LDLR−/− hApoB+/+). The founders of the colony of ATX mice were generously provided by Dr Hobbs (University of Texas Southwestern, Dallas, TX). All mice were fed with a normal standard diet (Harlan Laboratories, Tecklad 2014S, Montreal, QC, Canada) since ATX mice develop spontaneous atherosclerotic lesions.
For imaging, the mice were anesthetized with 10% weight/volume urethane in PBS (200 μL/10 g) and placed in a stereotaxic stage (Harvard Apparatus) with a heating pad to maintain body temperature. Animal temperature and heart rate were monitored throughout the experiment to ensure proper anaesthesia. Skin was removed from the top of the head and imaging was performed directly through the parietal bone over the somatosensory cortex.
2.2. Quantification of basal CBF
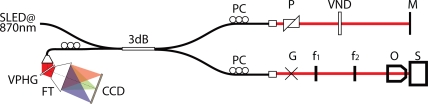
Imaging was performed using a frequency domain Doppler OCT System. The system is based on an infrared Super Light Emitting Diode (Exalos EXS8710-2411, Langhorne, PA) with a center wavelength of 870 nm, a spectral width of 65 nm and a typical output power of 5mW providing 2.5 mW of power on the sample. This light source yields a theoretical axial resolution of 5 μm. A custom built spectrometer is used as the detector with a high-speed 2048 pixel line camera (Basler Sprint spL2048 -140k, Exton, PA). The maximum acquisition speed of the camera is 67k A-lines per second but hard drive writing limits acquisition to 15k A-lines per sec. At this acquisition rate the maximum detectable Doppler blood flow speed without phase wrapping is 3 mm/s but could be increased with phase unwrapping. The depth of field is approximately 1.5mm in air. Light is collimated from the fiber using dual 16mm achromats with 2mm spacing. Scanning on the sample is performed using a dual galvanometer system (Thorlabs, Newton, NJ) imaged using a telescope (f1 = 75mm and f2 = 150mm) on the back aperture of a 10X (Olympus UMPLFLN 10XW, Markham, Ontario) infinity corrected objective yielding a lateral resolution of 10 μm. Fig. 1 shows a schematics of the system. Two stages allow positioning of the light on the rotation axis of the galvanometer mirrors to eliminate Doppler shifts created by scanning. This was optimized to reduce Doppler shifts when scanning the fast galvanometer which corresponds to the X direction.
Fig. 1.
Schematic of OCT system design, SLED : Super Luminescent Diode, PC : Polarization controllers, P : Dispersion compension prisms, VND : Variable Neutral Density Filter, M : Reference Mirror, G : Dual galvanometer scanners, f : sample arm telescope lenses, O : Objective, S : Sample, VPHG : Volume Phase Holographic grating, FT : F-Theta Lens, CCD : CCD Line Camera.
Image reconstruction was done in Matlab. Spectral shaping of the interference signal using a Hanning window was used to eliminate side lobes in the final image at the expense of broadening axial resolution to ∼ 7 μm. Automatic dispersion compensation to the second and third order dispersion imbalance was implemented according to the procedure described in [15]. The optimization criteria was set to increase image contrast by maximizing the structural image derivative. Optimization was done on the first frame of each acquisition to obtain the dispersion coefficients which were then applied to the rest of the acquisition. Reconstruction of flow speed is based on a moving-scatterer-sensitive reconstruction technique adapted from [12, 16] which uses the Kasai Autocorrelator [17]. A digital high pass filter is used to remove the stationary scattering components from the OCT image. The measured sensitivity of the system was 106 dB with a dynamic range of 76 dB.
Prior to the in vivo studies, the system was validated for its ability to quantify flow. A liquid phantom was syringe pumped through a glass capillary embedded in a silicone solid phantom. Both phantoms contained scattering and absorbing particles in quantities creating tissue like optical properties. The capillary had a 200 μm interior diameter and was subjected to 8 different flow speeds distributed between 8.33 and 167 nL/s range. In order to obtain Doppler signal, the capillary was placed diagonally in respect to the incoming light. For each flow value, 10 volume acquisitions were done, reconstructed and averaged. Taking a horizontal slice of the resulting volume, it is possible to calculate the quantitative phantom flow by summing the vertical Doppler speeds over the capillary cross section [12]. Flow was overestimated by 39% for an imposed flow of 8.33 nL/s, this is an expected result of the application of the digital high pass filter which causes distortion of low Doppler frequencies. Reconstruction of flow speeds over 100 nL/s exhibited phase wrapping of the Doppler signal due to vertical speeds being greater then 3 mm/s. Phase unwrapping allowed to recover the correct speed direction in the center of capillary but not an accurate flow measurement as even after unwrapping flow was respectively underestimated by 16% and 30%. The minimal error on flow measurements was between 33 and ∼ 83 nL/s with errors ranging from 4 to 13%. For a 200 μm diameter capillary, these speeds represent average liquid speeds of ∼ 1 to 2.5 mm/s. This range is the one expected in small arteries in vivo giving confidence in the ability of the system to accurately measure blood flow.
Series of volume acquisitions were done on each mouse with scan dimensions of 800 μm by 800 μm. Arteries were found directly between the skull and the surface of the brain. Light penetration enabled imaging of structures as deep as 500 μm. According to the procedure outlined in [12], quantitative blood flow (nL/s) was calculated in each mouse on plunging arteries found in each 3D volume data set. An average of 5 distinct arteries were measured per animal. Vessel diameter was estimated as the smallest cross section of the vessel crossing the horizontal imaging plane. Diameters obtained ranged from 50 to 160 μm. Blood flow was then estimated by integrating speed over a region of interest.
2.3. ECG coregistered OCT acquisition
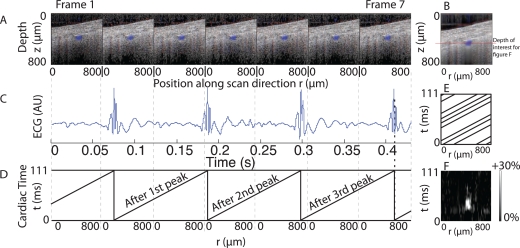
For each main artery imaged on the animals, two perpendicular single slice scans were performed. These slices had dimensions of 800 μm (X or Y axis) by ∼ 1.7 mm (Z axis) and were scanned 400 times at a rate of ∼ 16Hz (one slice each 945x65 μs). For each A-line acquired, an ECG signal was coregistered yielding an ECG acquisition rate of > 15kHz therefore giving sufficient sampling to accurately identify QRS peaks in the signal. A value of time after QRS peak was given to each A-line (cardiac cycle time). After reconstruction, each A-line was placed in a 3D matrix with regards to position and cardiac time enabling a reconstruction of the arterial cross-section at each time point in the cardiac cycle. Fig. 2 depicts the reconstruction process for the first 7 frames of an acquisition and the placement of their A-lines in the 3D matrix. Fig. 2F depicts the observed cardiac cycle change of blood speed on a line that crosses the vessel. A change of 30% from the minimum Doppler speed value is observed at cardiac time 30 ms at the position where the blood vessel is present, this corresponds to the arrival of the blood pulse from the heart. Animal placement in the stereotaxic stage was sufficiently stable to avoid important physiological movement that could interfere with the data and therefore no movement correction was necessary for ECG gated reconstructions.
Fig. 2.
Reconstruction of the cardiac profile of an artery on a WT mouse. A : The first 7 reconstructed frames over the same line. B : Average of all 400 frames showing blood vessel underneath the cranium. Decorrelation causes blurring underneath the main blood vessel and reveal the position of other smaller vessels in the frame. C : The corresponding ECG signal from these frames. D : The time after ECG peak is used to place each A-line of a frame in a 3D matrix by using it’s position and time value. E : Superimposition of the 7 frames in the reconstructed matrix, with 400 frames and with proper desynchronized condition, the matrix is filled. F : After reconstruction and placement of all 400 frames, the full 3D matrix was obtained. A slice was taken at the depth indicated by the red line on figure B, this slice had dimensions of 800 μm (position along r axis) by 111 ms (time in cardiac cycle). The percent change of Doppler speed from the minimum for each position was then plotted on figure F. For the positions where the vessel was present a change up to 30% high can be observed (white spot on figure) when the blood pulse arrives from the heart. A corresponding increase in Doppler speed is also observed at the same cardiac time at other positions on the line albeit to a weaker extent, this suggests the presence of smaller vessels.
Each arterial cross section was identified and a value of blood speed at each cardiac cycle time point was obtained by the sum of the Doppler vertical speeds in a Region of Interest (ROI). Arterial cross section area for each time point was evaluated using a threshold of 10% above the maximum speed value in a data set.
2.4. Compliance evaluation
A simple tube geometry was used to derive an expression for a compliance estimator where all necessary data can be obtained from OCT measurements. The tube is defined by a radius r and a length L in which a flow Φ is flowing. The pressure gradient between the edges of the tube is denoted δP. The flow is given by the Hagen-Poiseuille (Eq.(1)) where η is the fluid viscosity.
| (1) |
At steady state, the arterial tree can be estimated as a resistive network with fixed vessel diameters determining flow resistance. In this steady-state network, the pressure in each artery is a fraction of the main aortic pressure. The combined effect of compliance of all vessels C, is to add a non-linearity 𝒜(C) under pressure changes. At steady-state, the local arteriolar pressure PA can be expressed as proportional to the systemic pressure P.
| (2) |
Likewise, at steady-state, the pressure gradient between the edges of a vessel can be expressed as proportional to the systemic pressure. Thus, both the pressure gradient and the local arteriolar pressure are proportional to the systemic pressure and therefore to each other. A parameter α can be defined to establish the proportionality between these two values. This parameter is different for each arteriole at a particular position in the vascular network. Similar arterioles will have similar α values.
| (3) |
Equating Eq.(1) and Eq.(3) gives a link between the pressure inside an artery and the flow of blood within it at steady-state.
| (4) |
Compliance, is the change in vessel volume, ΔV, for a certain change in arterial pressure, ΔPA. Inherent physiological change of these values is between systolic peak and diastolic valley of systemic pressure which are noted respectively s and d. Define the systole to be the steady-state. Then at the diastole, the relations above will hold up to a small correction from the non-linearities introduced by systemic compliance contributions:
| (5) |
where 𝒜(CI) is assumed to be a small change to the relations above (Eq.(1) and Eq.(3)) due to non-linearities attributed to the integrated compliance for the network CI. To first order, neglecting 𝒜(CI), the local compliance can be estimated by
| (6) |
Replacing the expressions for volume and local pressure into Eq.(6), the compliance dependant terms are eliminated.
| (7) |
where A is the vessel cross-sectional area. Define the change from the diastole to the systole of the vessel cross-section by δA = As/Ad, the blood flow change by δΦ = Φs/Φd. The average blood speed in a vessel v̄ is related to the flow and area by Φ = Av̄, therefore a change in blood speed is δv̄ = δΦ/δA. Replacing these expressions in Eq.(7) yields
| (8) |
| (9) |
In this last equation, Ĉ is a local compliance evaluator that can be obtained with the vessel area and blood flow at the diastole (Ad and Φd) and the change in blood flow and vessel diameter between the diastole and the systole (δΦ and δA). The second expression uses the change in average blood speed instead of the change in flow. Blood viscosity, η, is calculated for each vessel as it is dependent on vessel diameter and hematocrit level. When comparing vessels with the same diameter and the same location in different animals, we assumed their vascular position was similar and α values to be close. This and neglecting 𝒜(CI) are the limitations of this estimator.
2.5. Angiography acquisition
For each animal a high density low scanning speed acquisition was done to obtain high resolution CMV images. The angiography was done outside of regions with large arteries in order to obtain smaller vessels. The scanned area had a surface of 800 × 800 μm composed of 400 slices containing 32 760 A-lines each. The spacing between two A-lines was ∼ 0.024 μm which for a 10 μm lateral resolution represents an oversampling factor of ∼ 400. A correction was applied to the reconstructed data to remove physiological movement artefacts as angiography measurements were extremely sensitive to small displacements of the animal. This correction was done by removing the average Doppler value obtained from the first 30 μm underneath the surface of the cranium. This depth sample corresponds to the skull where no vessels are expected and a Doppler value would only be a product of bulk tissue movement.
2.6. Vascular Anatomical Network modelling
Along with the compliance estimator previously presented a second method is used to interpret blood speed changes over the cardiac cycle. We constructed a model of the microvasculature using a stylized vascular anatomical network (VAN) based on previous work [18]. Blood speed is calculated in the different arterial segments of the model. By individually modifying the compliance parameter of the arteries in the model it is possible to interpret which compliance change situation better describes the observed differences in cardiac cycle profile in animal measures.
The VAN used below contains a diverging series of arterioles that are connected to capillaries, which further converge to a single veinule (Fig. 7A below). Each segment is characterized by its vascular properties (Length l, diameter d and hematocrit Hct), which are then used to calculate its resistance according to the Hagen-Poiseuille Law, . The parameter η(d,Hct,t) is a parametrization of the blood viscosity based on [19]. Hematocrit for all vascular segments was fixed at Hct = 15%. The other vascular properties used in the VAN modeled are summarized in table 1. Defining ΔP(t) to be the change in pressure across a segment and Q(t) the flow in the same segment, the flow-pressure relationship is given by:
| (10) |
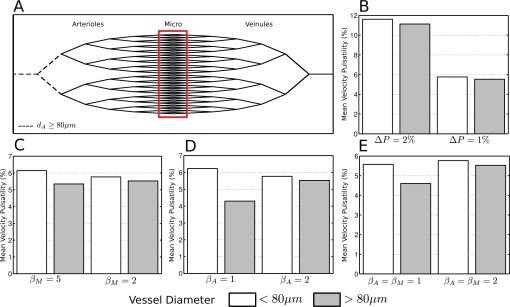
Fig. 7.
A. Vascular anatomical network simulated. The dotted lines and the red box represent respectively the larger and the smaller vessels. These are the vascular segments for which the compliance parameter is modified during the simulation. B. Effect of changes in pressure wave amplitude at the entry of the VAN. small and large vessels change their pulsatility proportionally. C. Effect of lowering the compliance (increasing the parameter βM) of small vessels while leaving the larger vessels at βA = 2, D. Effect of increasing the compliance of larger vessels (βA = 1) while leaving smaller vasculature intact. E. Effect of increasing compliance of both larger and smaller vessels (βA = βM = 1)
Table 1.
Vascular segment parameters
| Branch - # segments | Input
|
Function of input
|
|||
|---|---|---|---|---|---|
| Length (μm) | Diameter (μm) | Volume (nL) | Viscosity (cP) | Resistance (mmHg s / μL) | |
| A1-1 | 200 | 100 | 1.57 | 2.78 | 1.70 |
| A2-2 | 200 | 80 | 1.00 | 2.75 | 4.11 |
| A3-4 | 200 | 64 | 0.64 | 2.72 | 9.89 |
| A4-8 | 200 | 51.2 | 0.41 | 2.67 | 23.75 |
| A5-16 | 200 | 41.0 | 0.26 | 2.62 | 56.82 |
| A6-32 | 200 | 32.8 | 0.17 | 2.56 | 135.56 |
| C-64 | 250 | 30 | 0.18 | 2.53 | 238.82 |
| V6-32 | 200 | 36.0 | 0.20 | 2.58 | 93.54 |
| V5-16 | 200 | 45.1 | 0.32 | 2.64 | 39.16 |
| V4-8 | 200 | 56.3 | 0.50 | 2.69 | 16.35 |
| V3-4 | 200 | 70.4 | 0.78 | 2.73 | 6.80 |
| V2-2 | 200 | 88 | 1.25 | 2.77 | 2.82 |
| V1-1 | 200 | 110 | 1.90 | 2.79 | 1.17 |
All vascular properties can then be calculated using the nodal pressures distribution and the oriented incidence matrix A, which represents the VAN topology. Vessels non-linear compliance is integrated into the model by a pressure-volume relationship :
| (11) |
where is the average pressure at the center of the ith vessel, Vi(t) is its volume, PIC is the intra-cranial pressure, β is the compliance parameter and is a constant characterizing the initial state of the VAN. For an increase in pressure from time td to time ts. The pressure change can be estimated by expanding the expression for small volume changes:
| (12) |
| (13) |
By comparing this last equation to Eq.(6) we obtain a relation between both compliance parameters.
| (14) |
Therefore an increase in vessel flexibility is expressed by a higher compliance parameter C or a decreased parameter β.
To simulate the VAN’s dynamic response to vascular perturbations such as arteriolar dilation or input pressure variations, nodal pressures are first computed, assuming that vascular properties and VAN topology are given at equilibrium. Then, at each time step tn, compliant volume changes are calculated given the previous state nodal pressures Pn−1 and arteriolar pertubation. These modifications lead to a variation of vascular resistances across the VAN, and new nodal pressures Pn are calculated.
Since atherosclerotic mice are expected to develop high blood pressure and have rigid large arteries, simulations below studied changes in blood pressure at input of the VAN to simulate measures of blood flow change during a single ECG cycle. To evaluate how the change of blood flow pulsatility is modulated by microvasculature compliance, we simulated various configurations to assess their impacts on end results. These simulations where then used to form an interpretation of the results.
3. Results
3.1. Flow pulsatility measurement
Reconstruction of the flow over the cardiac cycle yielded blood speed variation profiles for each measured artery. The reconstructed profiles consisted of 100 time frames equally spaced between two QRS peaks giving a time resolution of approximately 1.5 ms for an animal with a 400 beat per minute heart rate. These profiles were reconstructed using 400 scans over 25 seconds therefore covering approximately 100 heart beats or 1 heart beat for every four scans. The asynchronous condition of scanning and heart rate ensured good coverage of the 3D reconstructed space with less then 0.1% missing A-lines. Coverage of the reconstructed space depended on heart rate where a lower heart rate was more likely to produce an incomplete data set. Filtering was done in the transverse direction and in time to fill in the missing A-line positions with the importance of each position weighted by the amount of A-lines averaged in it.
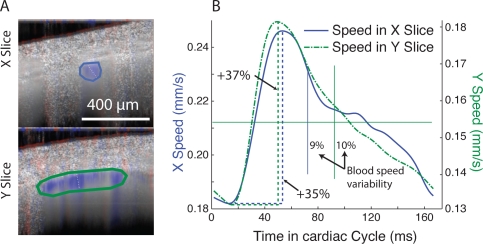
The profiles were low pass filtered using a 10 ms FWHM Hanning window and the boundary condition was set to ensure continuous blood speed between the end and the start of the cycle. Two different pulsatility metrics were used. The first was the percent blood speed increase from the minimum to the maximum blood speed. The second metric was the standard deviation of the speed values divided by the mean. For each vessel the X and Y slices were compared and only vessels where both flow profiles and pulsatility measurements matched were retained for the study. Discarded vessels include possible veins and vessels where the blood speed was too small to discern a clear cardiac trend. On some vessels one slice was retained while the other was discarded if it presented a clear cardiac profile while it’s paired slice did not. Fig. 3 shows two slices on a retained vessel and the flow profiles measured for each slice. The maximum value of the blood speed was associated with the arrival of the systolic pressure wavefront (which travels much faster then the blood itself). The minimum value was associated with the return to diastolic pressure.
Fig. 3.
Calculation of flow pulsatility in a single artery on a WT mouse. A. Two perpendicular slices of the artery are measured. The images present the average flow over the whole cardiac cycle. The flow is in red-blue overlaid on the grayscale structure. The artery is directly underneath the cranium and the region of interest is circled. B. Filtered blood speed profile in the region of interest. The Doppler speed is averaged in the region of interest for each time point in the cardiac cycle. The average speed is ∼ 0.21mm/s in the X slice region of interest. The average speed in the Y slice is ∼ 73% of the speed in the X slice due to different ROI coverages. The cardiac cycle profile is identical in both slices confirming the variation is due to cardiac activity. Variation between the maximum speed (systolic) and the minimum speed (diastolic) is calculated. Variability (solid vertical lines) is the standard deviation divided by the mean.
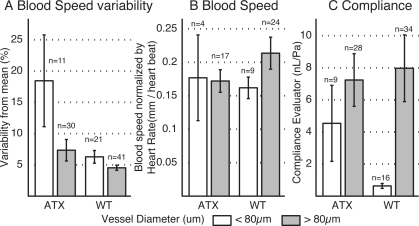
Total number of retained slices was 41 in the ATX group (11 slices < 80 μm) and 62 in the WT group (21 slices < 80 μm). Artery diameter was hand measured between the zero crossing points at the top and the bottom of the artery. The maximum on minimum flow change (not shown) and the pulsatility metric (Fig. 5A) both show a trend towards increased flow pulsatility in the ATX group with regards to the WT group which was larger for vessels smaller than 80 μm. However this trend was not statistically significant.
Fig. 5.
Blood speed change over the cardiac cycle. Only slices where the X and Y cardiac cycle profiles matched were retained. A. Variability of the blood speed over the cardiac cycle. B. Normalized blood speed change between the maximum and minimum value in the cardiac cycle. C. Compliance estimator. Error bars = SEM.
3.2. Basal CBF
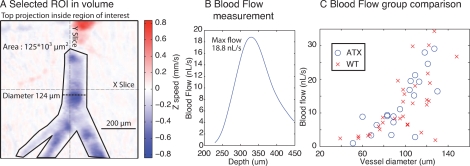
Basal CBF was evaluated for each measured artery using the 3D volume scans. Fig. 4A presents a typical region of interest selected on a plunging artery from a WT animal. For each artery the diameter was measured.
Fig. 4.
Example of blood flow measurement in a branching artery A. Top projection of the measured volume presenting a branching artery, diameter is 124 μm. The artery is only slightly tilted from the horizontal plane. B. Flow passing through the selected area at different depths. The maximum flow is where the artery is completely contained within the area and corresponds to it’s quantitative flow C. Blood flow as a function of vessel diameter, results from 20 ATX and 31 WT vessels, vessels larger then 150 μm not shown. No significant difference in the blood flow distribution is observed between the two groups.
For sharply plunging vessels, the flow vs depth profile remained mostly constant and flow estimations were direct. For some vessels, measurement of blood flow through a region of interest presented a depth dependent flow value. Fig. 4B shows such a profile. These vessels were almost horizontal and presented a peak in their flow vs depth profile which indicated the depth at which the vessel cross section was completely contained within the region of interest, these were kept for the analysis by choosing the depth at which the cross-section was completely contained in one plane. Horizontal vessels however did not present a clear maximum flow value as they would cross the same plane many times in opposite directions. The latter were rejected. Veins, associated with non-pulsatile flow as identified by the cardiac cycle reconstruction were also rejected. Fig. 4C presents the flow results from 20 ATX vessels and 31 WT vessels.
To allow further comparison of blood flow between the different animals and vessel dimensions, the quantitative blood flow was normalized by the vessel area obtained from it’s diameter and by the heart rate of the animal. This effectively gave a measure of blood speed per heart beat in each vessel. Data was separated between vessels with diameter less than or greater than 80 μm. Results of normalized blood flow measurements are presented in Fig. 5B. Average heart rate for the WT group was 477.9±46.1 beats per minute (bpm) and 542.6±31.9 bpm for the ATX group yielding a non significant trend towards higher heart rate in the ATX group.
3.3. Compliance estimation
The compliance was evaluated for the arteries that were retained for both measurements of pulsatility and flow. Considering each volume acquisition was coupled to two slice ECG gated acquisitions, each artery yielded on average two estimations of compliance. Eq.(9) was used with the diastolic area and flow (Ad and Φd) approximated by their cycle averaged value from the volume reconstructions. The results for both animal types and vessel diameter groups are presented in Fig. 5C. High variances are due to the combination of measures each having individual errors used in the estimator.
3.4. Vascular anatomy
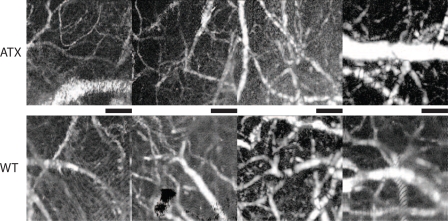
For completeness, Fig. 6 presents maximum intensity projection angiography results from 8 different animals. Results are displayed with similar structures and vessel sizes in both animal types aligned vertically. Smallest measurable vessel size was ∼ 10 μm and maximum vessel depth was 300 μm below the surface of the skull. Although each angiography presents a different structure, no major structural difference were observed between the two animal types.
Fig. 6.
Angiography results from 8 different animals. First row ATX animals and second row WT animals. The black bar has length of 200 μm. The results are displayed in a log scale. Similar vessel sizes are compared between the two groups.
3.5. Flow pulsatility modelling
Simulations were performed by varying the arteriole pressure Part at the input of the VAN. The ECG pulse modeled was a Gaussian function of the form
| (15) |
where is the arteriole pressure, ΔP is the relative pressure variation of the pulse, σT = 15 ms is its temporal width and Toffset = 50 ms is its temporal offset. The VAN response to this pulse was simulated over a period of ΔT = 100 ms, which corresponds to a heart beat frequency of f = 600 bpm. The ’normal’ case is represented by the pressure wave amplitude ΔP = 1% and by the compliance parameter β = 2 for all vascular segments.
Fig. 7 is a summary of the different effects of input pressure and compliance changes. Fig. 7A shows the simulated stylized model. As was done in measurements, vessels were separated by size in two categories with conventions identical to experimental results above. Fig. 7B shows the effect of increasing the blood pressure variation ΔP on measures of pulsatility. We observe that for both vessel size groups, pulsatility increases with blood pressure proportionally. This is in line with the trend observed in experimental results, Fig. 5A, where we observe overall increased pulsatility in ATX mice compared to WT. Figs. 7C, D respectively show the impact of varying compliance at the level of smaller (< 80 μm) and larger (> 80 μm) vessels or both respectively. In Fig. 7C, only the smaller vasculature compliance was modified by making them more rigid (β = 5) than our ’normal’ value β = 2 trying to simulate experimental observation by a decrease of compliance naively expected in atherosclerosis. This simulation did lead to changes in pulsatility mimicking the experimental observations (i.e. variations between small and large vessels) but a large change of the compliance parameter was required to create a small pulsatility difference between smaller and larger vasculature. On the other hand, if the compliance of larger vessels (> 80 μm) is increased (smaller β value), we observe the same trend, coherent with observations Fig. 5A, but amplified (Fig. 7D). Finally, Fig. 7E shows the results of the simulation when both compliances were decreased, again we observe trends similar to that of experimental results. Other simulations were done but did not follow the experimental trend.
4. Discussion
4.1. ECG gated reconstructions
OCT was used to study blood flow and its pulsatility in CMV. This work shows that reconstruction of the flow over the cardiac cycle can be used to estimate blood speed variation profiles for individual vessels. Cardiac cycle reconstruction yielded flow change estimations in under 10 minutes in intact preparations. This fast and non-invasive technique would therefore be able to study the acute effect of drugs on the cerebro-vascular myogenic tone. Besides direction, the flow pulsatility or lack thereof was used as an indicator of vessel function as arterioles are expected to have pulsatility while veinules are not.
4.2. Basal CBF
The normalized blood speed result showed a trend in the >80 μm vessels where flow was higher in the WT group. This trend was the same as the one previously reported [20]. However, for the < 80 μm vessels we did not see a similar trend which might be due to low SNR in the measures.
It is also of interest to note that the anesthetic used in this study (Urethane) differs from the one used in the previous work (Somnotol). The current anesthetic maintained a higher heart rate (almost twofold) than previously measured under Somnotol. This change may render the effect size smaller in the comparisons performed here and further work will have to be performed controlling for both blood pressure and heart rate to understand its impact
As expected blood speed was higher in larger vessels, however this alone did not allow to have a better measurement of blood flow in those vessels. Smaller vessels were usually diving branch offs from larger vessels and the region where they cross the horizontal imaging plane was relatively small and well defined giving a straightforward measurement of flow. Larger vessels were however positioned at the surface of the brain and were mostly horizontal. Their orientation rendered the definition of a horizontal crossing region more difficult. Moreover if that region extended beyond the dimensions of the imaged region, the exact blood flow could not be calculated and the latter vessels were rejected.
4.3. Compliance evaluation
The local pulsatility of blood speed is partly a result of the combined effect of compliance of all upstream feeding vessels. Our results showed an increase in the blood speed pulsatility of smaller vessels for the ATX group compared to the WT group. This result alone, however, did not enable to distinguish the changes in vessel compliance at the different arterial levels. OCT evaluation of compliance through the estimator Ĉ showed a trend towards an increase in small vessel compliance (< 80 μm) for ATX mice compared to WT mice while differences were smaller for larger vessels.
The use of the VAN model allowed additional interpretation of the data. Three compliance change scenarios yielded a similar change in blood pulsatility as the one observed between the two groups. Based on the compliance estimation of smaller arteries and ex vivo data, the most likely scenario involves an increased vascular compliance in all arteries at this level for the ATX group.
Observations on the angiography of arterioles in the cortex of both models did not reveal dramatic differences in the morphological aspects of the vasculature. While qualitative, this observation supports that differences in vessel architecture was not a confounding factor in the analysis of our data.
4.4. Limits of the OCT compliance estimator
The compliance estimator used in this work was based on the accurate measurement of blood flow, vessel diameter, blood speed change and vessel diameter change. Calculations of blood flow through a region of interest and of speed pulsatility in the cardiac cycle reconstruction were fairly robust operations yielding low sensitivity to measurement error while vessel diameter and area change were harder to estimate. In the case of blood flow estimations averaging multiple volume scans helped in increasing the quality of the measures. For blood speed variation, the comparison between slices taken in different orientations allowed for simple validation of the result and rejection of non conclusive cardiac profiles.
Amongst limitations of this work is the fact that vessels at the surface of the cortex have an elliptical cross section as opposed to a round one, estimation of the diameter was prone to error. When viewed from a top projection, the diameter measured is larger than when viewed from a side projection. The compliance evaluation model did not take into account the vessel’s irregular shape. However, the largest source of error in the compliance estimation was the accurate measurement of the change in vessel diameter. For a cross sectional image taken perpendicularly to the vessel direction, a change in vessel area over the cardiac cycle would be properly displayed in the cycle reconstruction. An acquisition made in the longitudinal axis of the vessel would only show an increase in it’s height over the cardiac cycle therefore underestimating the real area change. The use of a quadratic fitting procedure on the velocity profile was also investigated but results were not conclusive.
4.5. Interpretation of flow pulsatility modelling with regards to ex vivo results
The observed differential change between smaller and larger vessels when comparing ATX and WT mice could be simulated using three scenarios: decreasing smaller vessel compliance (Fig. 7C)), increasing larger vessel compliance (Fig. 7D) or increasing compliance of both smaller and larger vessels (Fig. 7E).
Application of the Ĉ estimator to vessels < 80 μm displays a trend towards an increase in compliance for the ATX mice compared to the WT mice leading to a reduced likelihood for the first scenario. Both subsequent scenarios involve an increase in the compliance of larger arteries. This hypothesis is corroborated by recent measurements performed on isolated resistance arteries [14]. Resistance arteries extracted from the base of the brain (which are directly connected to the circle of Willis) were subjected to pressure myography. These results indicated an increase compliance in the ATX model compared to WT. Resistance arteries have internal diameter in the 100–300 μm range at physiological internal pressure, thus the dimension of these vessels is comparable to that of the larger vessel group in the present study therefore suggesting a similar behaviour with regards to changes in compliance. In view of these results, a likely scenario is that compliance in both smaller and larger vessels increase but that our estimator Ĉ did not have high enough SNR to measure a statistical difference in larger vessels.
5. Conclusion
In this work we have demonstrated a new ECG gated reconstruction technique for evaluating flow pulsatility in CMV and vessel compliance. Comparison between an ATX and a WT group showed differences in flow pulsatility on different arterial segments. As it has been largely recognized, atherosclerotic lesions cause a hardening of the carotid arteries leading to a loss of compliance and higher blood pressure variations at the input to the circle of Willis. Recent evidence suggests that the resistance arteries at the base of the brain compensate this effect by increasing compliance. Our results showed increased flow pulsatility in small arterioles. This increase was modeled, amongst different scenarios, by an increase in compliance in both small and larger vessels corroborating ex vivo results. This supports that OCT can be used to study vascular function although modelling may be required to interpret its results.
Acknowledgments
E. Baraghis was supported by scholarships from the “Fonds de la recherche en santé du Québec” and the Natural Sciences and Engineering Research Council of Canada (NSERC). F. Lesage, C. Boudoux were supported NSERC Discovery grants. V. J. Srinivasan was supported by the National Institutes of Health ( K99NS067050) and the American Heart Association ( 11IRG5440002)
References and links
- 1.de la Torre J. C., “Is alzheimer’s disease a neurodegenerative or a vascular disorder? data, dogma, and dialectics,” Lancet Neurol. 3, 184–190 (2004). 10.1016/S1474-4422(04)00683-0 [DOI] [PubMed] [Google Scholar]
- 2.Hebert L., Scherr P., Bienias J., Bennett D., Evans D., “Alzheimer disease in the us population: prevalence estimates using the 2000 census,” Arch. Neurol. 60, 1119–1122 (2003). 10.1001/archneur.60.8.1119 [DOI] [PubMed] [Google Scholar]
- 3.Iadecola C., “Neurovascular regulation in the normal brain and in alzheimer’s disease,” Nat. Rev. Neurosci. 5, 347–360 (2004). 10.1038/nrn1387 [DOI] [PubMed] [Google Scholar]
- 4.Helzner E., Luchsinger J., Scarmeas N., Cosentino S., Brickman A., Glymour M., Stern Y., “Contribution of vascular risk factors to the progression in alzheimer disease,” Arch. Neurol. 66, 343 (2009). 10.1001/archneur.66.3.343 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fang Q., Sakadzic S., Ruvinskaya L., Devor A., Dale A. M., Boas D. A., “Oxygen advection and diffusion in a three-dimensional vascular anatomical network,” Opt. Express 16, 17530–17541 (2008). 10.1364/OE.16.017530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schaffer C., Friedman B., Nishimura N., Schroeder L., Tsai P., Ebner F., Lyden P., Kleinfeld D., “Two-photon imaging of cortical surface microvessels reveals a robust redistribution in blood flow after vascular occlusion,” PLoS Biol. 4, e22 (2006). 10.1371/journal.pbio.0040022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Murphy T., Li P., Betts K., Liu R., “Two-photon imaging of stroke onset in vivo reveals that nmda-receptor independent ischemic depolarization is the major cause of rapid reversible damage to dendrites and spines,” J. Neurosci. 28, 1756–1772 (2008). 10.1523/JNEUROSCI.5128-07.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang R. K., Jacques S. L., Ma Z., Hurst S., Hanson S. R., Gruber A., “Three dimensional optical angiography,” Opt. Express 15, 4083–4097 (2007). 10.1364/OE.15.004083 [DOI] [PubMed] [Google Scholar]
- 9.Vakoc B., Lanning R., Tyrrell J., Padera T., Bartlett L., Stylianopoulos T., Munn L., Tearney G., Fukumura D., Jain R.et al., “Three-dimensional microscopy of the tumor microenvironment in vivo using optical frequency domain imaging,” Nat. Med. 15, 1219–1223 (2009). 10.1038/nm.1971 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Srinivasan V. J., Jiang J. Y., Yaseen M. A., Radhakrishnan H., Wu W., Barry S., Cable A. E., Boas D. A., “Rapid volumetric angiography of cortical microvasculature with optical coherence tomography,” Opt. Lett. 35, 43–45 (2010). 10.1364/OL.35.000043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jia Y., An L., Wang R., “Label-free and highly sensitive optical imaging of detailed microcirculation within meninges and cortex in mice with the cranium left intact,” J. Biomed. Opt. 15, 030510 (2010). 10.1117/1.3432654 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Srinivasan V. J., Sakadžić S., Gorczynska I., Ruvinskaya S., Wu W., Fujimoto J. G., Boas D. A., “Quantitative cerebral blood flow with optical coherence tomography,” Opt. Express 18, 2477–2494 (2010). 10.1364/OE.18.002477 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.van Popele N., Grobbee D., Bots M., Asmar R., Topouchian J., Reneman R., Hoeks A., van der Kuip D., Hofman A., Witteman J., “Association between arterial stiffness and atherosclerosis: the rotterdam study,” Stroke 32, 454–460 (2001). 10.1161/01.STR.32.2.454 [DOI] [PubMed] [Google Scholar]
- 14.Bolduc V., Drouin A., Gillis M., Duquette N., Thorin-Trescases N., Frayne-Robillard I., Des Rosiers C., Tardif J., Thorin E., “Heart rate-associated mechanical stress impairs carotid but not cerebral artery compliance in dyslipidemic atherosclerotic mice,” Am. J. Physiol. Heart Circ. Physiol. 10.1152/ajpheart.00706.2011 (Sept. 2011). 10.1152/ajpheart.00706.2011 [DOI] [PMC free article] [PubMed]
- 15.Wojtkowski M., Srinivasan V., Ko T., Fujimoto J., Kowalczyk A., Duker J., “Ultrahigh-resolution, high-speed, fourier domain optical coherence tomography and methods for dispersion compensation,” Opt. Express 12, 2404–2422 (2004). 10.1364/OPEX.12.002404 [DOI] [PubMed] [Google Scholar]
- 16.Ren H., Sun T., MacDonald D., Cobb M., Li X., “Real-time in vivo blood-flow imaging by moving-scatterer-sensitive spectral-domain optical doppler tomography,” Opt. Lett. 31, 927–929 (2006). 10.1364/OL.31.000927 [DOI] [PubMed] [Google Scholar]
- 17.Kasai C., Namekawa K., Koyano A., Omoto R., “Real-time two-dimensional blood flow imaging using an autocorrelation technique,” IEEE Trans. Sonics Ultrason. 32, 458–464 (1985). [Google Scholar]
- 18.Boas D., Jones S., Devor A., Huppert T., Dale A., “A vascular anatomical network model of the spatio-temporal response to brain activation,” Neuroimage 40, 1116–1129 (2008). 10.1016/j.neuroimage.2007.12.061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pries A., Neuhaus D., Gaehtgens P., “Blood viscosity in tube flow: dependence on diameter and hematocrit,” Am. J. Physiol. Heart Circ. Physiol. 263, H1770–H1778 (1992). [DOI] [PubMed] [Google Scholar]
- 20.Drouin A., Bolduc V., Thorin-Trescases N., Bélanger É., Fernandes P., Baraghis E., Lesage F., Gillis M., Villeneuve L., Hamel E., Ferland G., Thorin E., “Catechin treatment improves cerebrovascular flow-mediated dilation and learning abilities in atherosclerotic mice,” Am. J. Physiol. Heart Circ. Physiol. 300, H1032–H1043 (2011). 10.1152/ajpheart.00410.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]