Abstract
The organization of computations in networks of spiking neurons in the brain is still largely unknown, in particular in view of the inherently stochastic features of their firing activity and the experimentally observed trial-to-trial variability of neural systems in the brain. In principle there exists a powerful computational framework for stochastic computations, probabilistic inference by sampling, which can explain a large number of macroscopic experimental data in neuroscience and cognitive science. But it has turned out to be surprisingly difficult to create a link between these abstract models for stochastic computations and more detailed models of the dynamics of networks of spiking neurons. Here we create such a link and show that under some conditions the stochastic firing activity of networks of spiking neurons can be interpreted as probabilistic inference via Markov chain Monte Carlo (MCMC) sampling. Since common methods for MCMC sampling in distributed systems, such as Gibbs sampling, are inconsistent with the dynamics of spiking neurons, we introduce a different approach based on non-reversible Markov chains that is able to reflect inherent temporal processes of spiking neuronal activity through a suitable choice of random variables. We propose a neural network model and show by a rigorous theoretical analysis that its neural activity implements MCMC sampling of a given distribution, both for the case of discrete and continuous time. This provides a step towards closing the gap between abstract functional models of cortical computation and more detailed models of networks of spiking neurons.
Author Summary
It is well-known that neurons communicate with short electric pulses, called action potentials or spikes. But how can spiking networks implement complex computations? Attempts to relate spiking network activity to results of deterministic computation steps, like the output bits of a processor in a digital computer, are conflicting with findings from cognitive science and neuroscience, the latter indicating the neural spike output in identical experiments changes from trial to trial, i.e., neurons are “unreliable”. Therefore, it has been recently proposed that neural activity should rather be regarded as samples from an underlying probability distribution over many variables which, e.g., represent a model of the external world incorporating prior knowledge, memories as well as sensory input. This hypothesis assumes that networks of stochastically spiking neurons are able to emulate powerful algorithms for reasoning in the face of uncertainty, i.e., to carry out probabilistic inference. In this work we propose a detailed neural network model that indeed fulfills these computational requirements and we relate the spiking dynamics of the network to concrete probabilistic computations. Our model suggests that neural systems are suitable to carry out probabilistic inference by using stochastic, rather than deterministic, computing elements.
Introduction
Attempts to understand the organization of computations in the brain from the perspective of traditional, mostly deterministic, models of computation, such as attractor neural networks or Turing machines, have run into problems: Experimental data suggests that neurons, synapses, and neural systems are inherently stochastic
[1], especially in vivo, and therefore seem less suitable for implementing deterministic computations. This holds for ion channels of neurons [2], synaptic release [3], neural response to stimuli (trial-to-trial variability) [4], [5], and perception [6]. In fact, several experimental studies arrive at the conclusion that external stimuli only modulate the highly stochastic spontaneous firing activity of cortical networks of neurons [7], [8]. Furthermore, traditional models for neural computation have been challenged by the fact that typical sensory data from the environment is often noisy and ambiguous, hence requiring neural systems to take uncertainty about external inputs into account. Therefore many researchers have suggested that information processing in the brain carries out probabilistic, rather than logical, inference for making decisions and choosing actions [9]–[22]. Probabilistic inference has emerged in the 1960’s [23], as a principled mathematical framework for reasoning in the face of uncertainty with regard to observations, knowledge, and causal relationships, which is characteristic for real-world inference tasks. This framework has become tremendously successful in real-world applications of artificial intelligence and machine learning. A typical computation that needs to be carried out for probabilistic inference on a high-dimensional joint distribution  is the evaluation of the conditional distribution
is the evaluation of the conditional distribution  (or marginals thereof) over some variables of interest, say
(or marginals thereof) over some variables of interest, say  , given variables
, given variables  . In the following, we will call the set of variables
. In the following, we will call the set of variables  , which we condition on, the observed variables and denote it by
, which we condition on, the observed variables and denote it by  .
.
Numerous studies in different areas of neuroscience and cognitive science have suggested that probabilistic inference could explain a variety of computational processes taking place in neural systems (see [10], [11]). In models of perception the observed variables  are interpreted as the sensory input to the central nervous system (or its early representation by the firing response of neurons, e.g., in the LGN in the case of vision), and the variables
are interpreted as the sensory input to the central nervous system (or its early representation by the firing response of neurons, e.g., in the LGN in the case of vision), and the variables  model the interpretation of the sensory input, e.g., the texture and position of objects in the case of vision, which might be encoded in the response of neurons in various higher cortical areas [15]. Furthermore, in models for motor control the observed variables
model the interpretation of the sensory input, e.g., the texture and position of objects in the case of vision, which might be encoded in the response of neurons in various higher cortical areas [15]. Furthermore, in models for motor control the observed variables  often consist not only of sensory and proprioceptive inputs to the brain, but also of specific goals and constraints for a planned movement [24]–[26], whereas inference is carried out over the variables
often consist not only of sensory and proprioceptive inputs to the brain, but also of specific goals and constraints for a planned movement [24]–[26], whereas inference is carried out over the variables  representing a motor plan or motor commands to muscles. Recent publications show that human reasoning and learning can also be cast into the form of probabilistic inference problems [27]–[29]. In these models learning of concepts, ranging from concrete to more abstract ones, is interpreted as inference in lower and successively higher levels of hierarchical probabilistic models, giving a consistent description of inductive learning within and across domains of knowledge.
representing a motor plan or motor commands to muscles. Recent publications show that human reasoning and learning can also be cast into the form of probabilistic inference problems [27]–[29]. In these models learning of concepts, ranging from concrete to more abstract ones, is interpreted as inference in lower and successively higher levels of hierarchical probabilistic models, giving a consistent description of inductive learning within and across domains of knowledge.
In spite of this active research on the functional level of neural processing, it turned out to be surprisingly hard to relate the computational machinery required for probabilistic inference to experimental data on neurons, synapses, and neural systems. There are mainly two different approaches for implementing the computational machinery for probabilistic inference in “neural hardware”. The first class of approaches builds on deterministic methods for evaluating exactly or approximately the desired conditional and/or marginal distributions, whereas the second class relies on sampling from the probability distributions in question. Multiple models in the class of deterministic approaches implement algorithms from machine learning called message passing or belief propagation [30]–[33]. By clever reordering of sum and product operators occurring in the evaluation of the desired probabilities, the total number of computation steps are drastically reduced. The results of subcomputations are propagated as "messages" or "beliefs" that are sent to other parts of the computational network. Other deterministic approaches for representing distributions and performing inference are probabilistic population code (PPC) models [34]. Although deterministic approaches provide a theoretically sound hypothesis about how complex computations can possibly be embedded in neural networks and explain aspects of experimental data, it seems difficult (though not impossible) to conciliate them with other aspects of experimental evidence, such as stochasticity of spiking neurons, spontaneous firing, trial-to-trial variability, and perceptual multistability.
Therefore other researchers (e.g., [16]–[18], [35]) have proposed to model computations in neural systems as probabilistic inference based on a different class of algorithms, which requires stochastic, rather than deterministic, computational units. This approach, commonly referred to as sampling, focuses on drawing samples, i.e., concrete values for the random variables that are distributed according to the desired probability distribution. Sampling can naturally capture the effect of apparent stochasticity in neural responses and seems to be furthermore consistent with multiple experimental effects reported in cognitive science literature [17], [18]. On the conceptual side, it has proved to be difficult to implement learning in message passing and PPC network models. In contrast, following the lines of [36], the sampling approach might be well suited to incorporate learning.
Previous network models that implement sampling in neural networks are mostly based on a special sampling algorithm called Gibbs (or general Metropolis-Hastings) sampling [9], [17], [18], [37]. The dynamics that arise from this approach, the so-called Glauber dynamics, however are only superficially similar to spiking neural dynamics observed in experiments, rendering these models rather abstract. Building on and extending previous models, we propose here a family of network models, that can be shown to exactly sample from any arbitrary member of a well-defined class of probability distributions via their inherent network dynamics. These dynamics incorporate refractory effects and finite durations of postsynaptic potentials (PSPs), and are therefore more biologically realistic than existing approaches. Formally speaking, our model implements Markov chain Monte Carlo (MCMC) sampling in a spiking neural network. In contrast to prior approaches however, our model incorporates irreversible dynamics (i.e., no detailed balance) allowing for finite time PSPs and refractory mechanisms. Furthermore, we also present a continuous time version of our network model. The resulting stochastic dynamical system can be shown to sample from the correct distribution. In general, continuous time models arguably provide a higher amount of biological realism compared to discrete time models.
The paper is structured in the following way. First we provide a brief introduction to MCMC sampling. We then define the neural network model whose neural activity samples from a given class of probability distributions. The model will be first presented in discrete time together with some illustrative simulations. An extension of the model to networks of more detailed spiking neuron models which feature a relative refractory mechanism is presented. Furthermore, it is shown how the neural network model can also be formulated in continuous time. Finally, as a concrete simulation example we present a simple network model for perceptual multistability.
Results
Recapitulation of MCMC sampling
In machine learning, sampling is often considered the “gold standard” of inference methods, since, assuming that we can sample from the distribution in question, and assuming enough computational resources, any inference task can be carried out with arbitrary precision (in contrast to some deterministic approximate inference methods such as variational inference). However sampling from an arbitrary distribution can be a difficult problem in itself, as, e.g., many distributions can only be evaluated modulo a global constant (the partition function). In order to circumvent these problems, elaborate MCMC sampling techniques have been developed in machine learning and statistics [38]. MCMC algorithms are based on the following idea: instead of producing an ad-hoc sample, a process that is heuristically comparable to a global search over the whole state space of the random variables, MCMC methods produce a new sample via a “local search” around a point in the state space that is already (approximately) a sample from the distribution.
More formally, a Markov chain 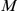 (in discrete time) is defined by a set
(in discrete time) is defined by a set  of states (we consider for discrete time only the case where
of states (we consider for discrete time only the case where  has a finite size, denoted by
has a finite size, denoted by  ) together with a transition operator
) together with a transition operator  . The operator
. The operator  is a conditional probability distribution
is a conditional probability distribution  over the next state
over the next state  given a preceding state
given a preceding state  . The Markov chain
. The Markov chain  is started in some initial state
is started in some initial state 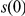 , and moves through a trajectory of states
, and moves through a trajectory of states  via iterated application of the stochastic transition operator
via iterated application of the stochastic transition operator  . More precisely, if
. More precisely, if  is the state at time
is the state at time  , then the next state
, then the next state  is drawn from the conditional probability distribution
is drawn from the conditional probability distribution  . An important theorem from probability theory (see, e.g., p. 232 in [39]) states that if
. An important theorem from probability theory (see, e.g., p. 232 in [39]) states that if  is irreducible (i.e., any state in
is irreducible (i.e., any state in  can be reached from any other state in
can be reached from any other state in  in finitely many steps with probability
in finitely many steps with probability  ) and aperiodic (i.e., its state transitions cannot be trapped in deterministic cycles), then the probability
) and aperiodic (i.e., its state transitions cannot be trapped in deterministic cycles), then the probability 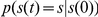 converges for
converges for  to a probability
to a probability  that does not depend on the initial state
that does not depend on the initial state  . This state distribution
. This state distribution  is called the invariant distribution of
is called the invariant distribution of  . The irreducibility of
. The irreducibility of  implies that it is the only distribution over the states
implies that it is the only distribution over the states  that is invariant under its transition operator
that is invariant under its transition operator  , i.e.
, i.e.
| (1) |
Thus, in order to carry out probabilistic inference for a given distribution  , it suffices to construct an irreducible and aperiodic Markov chain
, it suffices to construct an irreducible and aperiodic Markov chain  that leaves
that leaves  invariant, i.e., satisfies equation (1). Then one can answer numerous probabilistic inference questions regarding
invariant, i.e., satisfies equation (1). Then one can answer numerous probabilistic inference questions regarding  without any numerical computations of probabilities. Rather, one plugs in the observed values for some of the random variables (RVs) and simply collects samples from the conditional distribution over the other RVs of interest when the Markov chain approaches its invariant distribution.
without any numerical computations of probabilities. Rather, one plugs in the observed values for some of the random variables (RVs) and simply collects samples from the conditional distribution over the other RVs of interest when the Markov chain approaches its invariant distribution.
A convenient and popular method for the construction of an operator  for a given distribution
for a given distribution  is looking for operators
is looking for operators  that satisfy the following detailed balance condition,
that satisfy the following detailed balance condition,
| (2) |
for all  . A Markov chain that satisfies (2) is said to be reversible. In particular, the Gibbs and Metropolis-Hastings algorithms employ reversible Markov chains. A very useful property of (2) is that it implies the invariance property (1), and this is in fact the standard method for proving (1). However, as our approach makes use of irreversible Markov chains as explained below, we will have to prove (1) directly.
. A Markov chain that satisfies (2) is said to be reversible. In particular, the Gibbs and Metropolis-Hastings algorithms employ reversible Markov chains. A very useful property of (2) is that it implies the invariance property (1), and this is in fact the standard method for proving (1). However, as our approach makes use of irreversible Markov chains as explained below, we will have to prove (1) directly.
Neural sampling
Let  be some arbitrary joint distribution over
be some arbitrary joint distribution over  binary variables
binary variables  that only takes on values
that only takes on values  . We will show that under a certain computability assumption on
. We will show that under a certain computability assumption on  a network
a network  consisting of
consisting of  spiking neurons
spiking neurons  can sample from
can sample from  using its inherent stochastic dynamics. More precisely, we show that the stochastic firing activity of
using its inherent stochastic dynamics. More precisely, we show that the stochastic firing activity of  can be viewed as a non-reversible Markov chain that samples from the given probability distribution
can be viewed as a non-reversible Markov chain that samples from the given probability distribution  . If a subset
. If a subset  of the variables are observed, modelled as the corresponding neurons being “clamped” to the observed values, the remaining network samples from the conditional distribution of the remaining variables given the observables. Hence, this approach offers a quite natural implementation of probabilistic inference. It is similar to sampling approaches which have already been applied extensively, e.g., in Boltzmann machines, however our model is more biologically realistic as it incorporates aspects of the inherent temporal dynamics and spike-based communication of a network of spiking neurons. We call this approach neural sampling in the remainder of the paper.
of the variables are observed, modelled as the corresponding neurons being “clamped” to the observed values, the remaining network samples from the conditional distribution of the remaining variables given the observables. Hence, this approach offers a quite natural implementation of probabilistic inference. It is similar to sampling approaches which have already been applied extensively, e.g., in Boltzmann machines, however our model is more biologically realistic as it incorporates aspects of the inherent temporal dynamics and spike-based communication of a network of spiking neurons. We call this approach neural sampling in the remainder of the paper.
In order to enable a network  of spiking neurons to sample from a distribution
of spiking neurons to sample from a distribution  of binary variables
of binary variables  , one needs to specify how an assignment
, one needs to specify how an assignment 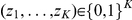 of values to these binary variables can be represented by the spiking activity of the network
of values to these binary variables can be represented by the spiking activity of the network  and vice versa. A spike, or action potential, of a biological neuron
and vice versa. A spike, or action potential, of a biological neuron  has a short duration of roughly
has a short duration of roughly  . But the effect of such spike, both on the neuron
. But the effect of such spike, both on the neuron  itself (in the form of refractory processes) and on the membrane potential of other neurons (in the form of postsynaptic potentials) lasts substantially longer, on the order of
itself (in the form of refractory processes) and on the membrane potential of other neurons (in the form of postsynaptic potentials) lasts substantially longer, on the order of  to
to 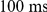 . In order to capture this temporally extended effect of each spike, we fix some parameter
. In order to capture this temporally extended effect of each spike, we fix some parameter  that models the average duration of these temporally extended processes caused by a spike. We say that a binary vector
that models the average duration of these temporally extended processes caused by a spike. We say that a binary vector  is represented by the firing activity of the network
is represented by the firing activity of the network  at time
at time  for
for  iff:
iff:
| (3) |
In other words, any spike of neuron  sets the value of the associated binary variable
sets the value of the associated binary variable  to 1 for a duration of length
to 1 for a duration of length  .
.
An obvious consequence of this definition is that the binary vector  that is defined by the activity of
that is defined by the activity of  at time
at time  does not fully capture the internal state of this stochastic system. Rather, one needs to take into account additional non-binary variables
does not fully capture the internal state of this stochastic system. Rather, one needs to take into account additional non-binary variables  , where the value of
, where the value of  at time
at time  specifies when within the time interval
specifies when within the time interval  the neuron
the neuron  has fired (if it has fired within this time interval, thereby causing
has fired (if it has fired within this time interval, thereby causing  at time
at time  ). The neural sampling process has the Markov property only with regard to these more informative auxiliary variables
). The neural sampling process has the Markov property only with regard to these more informative auxiliary variables  . Therefore our analysis of neural sampling will focus on the temporal evolution of these auxiliary variables. We adopt the convention that each spike of neuron
. Therefore our analysis of neural sampling will focus on the temporal evolution of these auxiliary variables. We adopt the convention that each spike of neuron  sets the value of
sets the value of  to its maximal value
to its maximal value  , from which it linearly decays back to
, from which it linearly decays back to  during the subsequent time interval of length
during the subsequent time interval of length  .
.
For the construction of the sampling network  , we assume that the membrane potential
, we assume that the membrane potential  of neuron
of neuron  at time
at time  equals the log-odds of the corresponding variable
equals the log-odds of the corresponding variable  to be active, and refer to this property as neural computability condition:
to be active, and refer to this property as neural computability condition:
| (4) |
where we write  for
for  and
and  for the current values
for the current values  of all other variables
of all other variables  with
with  . Under the assumption we make in equation (4), i.e., that the neural membrane potential reflects the log-odds of the corresponding variable
. Under the assumption we make in equation (4), i.e., that the neural membrane potential reflects the log-odds of the corresponding variable  , it is required that each single neuron in the network can actually compute the right-hand side of equation (4), i.e., that it fulfills the neural computability condition.
, it is required that each single neuron in the network can actually compute the right-hand side of equation (4), i.e., that it fulfills the neural computability condition.
A concrete class of probability distributions, that we will use as an example in the remainder, are Boltzmann distributions:
 |
(5) |
with arbitrary real valued parameters  which satisfy
which satisfy  and
and  (the constant
(the constant 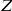 ensures the normalization of
ensures the normalization of  ). For the Boltzmann distribution, condition (4) is satisfied by neurons
). For the Boltzmann distribution, condition (4) is satisfied by neurons  with the standard membrane potential
with the standard membrane potential
| (6) |
where  is the bias of neuron
is the bias of neuron  (which regulates its excitability),
(which regulates its excitability),  is the strength of the synaptic connection from neuron
is the strength of the synaptic connection from neuron  to
to  , and
, and  approximates the time course of the postsynaptic potential in neuron
approximates the time course of the postsynaptic potential in neuron  caused by a firing of neuron
caused by a firing of neuron  with a constant signal of duration
with a constant signal of duration  (i.e., a square pulse). As we will describe below, spikes of neuron
(i.e., a square pulse). As we will describe below, spikes of neuron  are evoked stochastically depending on the current membrane potential
are evoked stochastically depending on the current membrane potential  and the auxiliary variable
and the auxiliary variable  .
.
The neural computability condition (4) links classes of probability distributions to neuron and synapse models in a network of spiking neurons. As shown above, Boltzmann distributions satisfy the condition if one considers point neuron models which compute a linear weighted sum of the presynaptic inputs. The class of distributions can be extended to include more complex distributions using a method proposed in [40] which is based on the following idea. Neuron  representing the variable
representing the variable  is not directly influenced by the activities
is not directly influenced by the activities  of the presynaptic neurons, but via intermediate nonlinear preprocessing elements. This preprocessing might be implemented by dendrites or other (inter-) neurons and is assumed to compute nonlinear combinations of the presynaptic activities
of the presynaptic neurons, but via intermediate nonlinear preprocessing elements. This preprocessing might be implemented by dendrites or other (inter-) neurons and is assumed to compute nonlinear combinations of the presynaptic activities 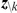 (similar to a kernel). This allows the membrane potential
(similar to a kernel). This allows the membrane potential  , and therefore the log-odds ratio on the right-hand side of (4), to represent a more complex function of the activities
, and therefore the log-odds ratio on the right-hand side of (4), to represent a more complex function of the activities  , giving rise to more complex joint distributions
, giving rise to more complex joint distributions  . The concrete implementation of non-trivial directed and undirected graphical models with the help of preprocessing elements in the neural sampling framework is subject of current research. For the examples given in this study, we focus on the standard form of the membrane potential (6) of point neurons. As shown below, these spiking network models can emulate any Boltzmann machine (BM) [36].
. The concrete implementation of non-trivial directed and undirected graphical models with the help of preprocessing elements in the neural sampling framework is subject of current research. For the examples given in this study, we focus on the standard form of the membrane potential (6) of point neurons. As shown below, these spiking network models can emulate any Boltzmann machine (BM) [36].
A substantial amount of preceding studies has demonstrated that BMs are very powerful, and that the application of suitable learning algorithms for setting the weights  makes it possible to learn and represent complex sensory processing tasks by such distributions [37], [41]. In applications in statistics and machine learning using such Boltzmann distributions, sampling is typically implemented by Gibbs sampling or more general reversible MCMC methods. However, it is difficult to model some neural processes, such as an absolute refractory period or a postsynaptic potential (PSP) of fixed duration, using a reversible Markov chain, but they are more conveniently modelled using an irreversible one. As we wish to keep the computational power of BMs and at the same time to augment the sampling procedure with aspects of neural dynamics (such as PSPs with fixed durations, refractory mechanisms) to increase biological realism, we focus in the following on irreversible MCMC methods (keeping in mind that this might not be the only possible way to achieve these goals).
makes it possible to learn and represent complex sensory processing tasks by such distributions [37], [41]. In applications in statistics and machine learning using such Boltzmann distributions, sampling is typically implemented by Gibbs sampling or more general reversible MCMC methods. However, it is difficult to model some neural processes, such as an absolute refractory period or a postsynaptic potential (PSP) of fixed duration, using a reversible Markov chain, but they are more conveniently modelled using an irreversible one. As we wish to keep the computational power of BMs and at the same time to augment the sampling procedure with aspects of neural dynamics (such as PSPs with fixed durations, refractory mechanisms) to increase biological realism, we focus in the following on irreversible MCMC methods (keeping in mind that this might not be the only possible way to achieve these goals).
Neural sampling in discrete time
Here we describe neural dynamics in discrete time with an absolute refractory period  . We interpret one step of the Markov chain as a time step
. We interpret one step of the Markov chain as a time step  in biological real time. The dynamics of the variable
in biological real time. The dynamics of the variable  , that describes the time course of the effect of a spike of neuron
, that describes the time course of the effect of a spike of neuron  , are defined in the following way.
, are defined in the following way.  is set to the value
is set to the value  when neuron
when neuron  fires, and decays by
fires, and decays by  at each subsequent discrete time step. The parameter
at each subsequent discrete time step. The parameter  is chosen to be some integer, so that
is chosen to be some integer, so that  decays back to
decays back to 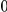 in exactly
in exactly  time steps. The neuron can only spike (with a probability that is a function of its current membrane potential
time steps. The neuron can only spike (with a probability that is a function of its current membrane potential  ) if its variable
) if its variable  . If however,
. If however,  , the neuron is considered refractory and it cannot spike, but its
, the neuron is considered refractory and it cannot spike, but its  is reduced by 1 per time step. To show that these simple dynamics do indeed sample from the given distribution
is reduced by 1 per time step. To show that these simple dynamics do indeed sample from the given distribution  , we proceed in the following way. We define a joint distribution
, we proceed in the following way. We define a joint distribution  which has the desired marginal distribution
which has the desired marginal distribution  . Further we formalize the dynamics informally described above as a transition operator
. Further we formalize the dynamics informally described above as a transition operator  operating on the state vector
operating on the state vector  . Finally, in the Methods section, we show that
. Finally, in the Methods section, we show that  is the unique invariant distribution of this operator
is the unique invariant distribution of this operator  , i.e., that the dynamics described by
, i.e., that the dynamics described by  produce samples
produce samples  from the desired distribution
from the desired distribution 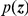 . We refer to sampling through networks with this stochastic spiking mechanism as neural sampling with absolute refractory period due to the persistent refractory process.
. We refer to sampling through networks with this stochastic spiking mechanism as neural sampling with absolute refractory period due to the persistent refractory process.
Given the distribution  that we want to sample from, we define the following joint distribution
that we want to sample from, we define the following joint distribution  over the neural variables:
over the neural variables:
 |
(7) |
This definition of  simply expresses that if
simply expresses that if 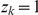 , then the auxiliary variable
, then the auxiliary variable  can assume any value in
can assume any value in  with equal probability. On the other hand
with equal probability. On the other hand  necessarily assumes the value
necessarily assumes the value  if
if  (i.e., when the neuron is in its resting state).
(i.e., when the neuron is in its resting state).
The state transition operator  can be defined in a transparent manner as a composition of
can be defined in a transparent manner as a composition of  transition operators,
transition operators,  , where
, where  only updates the variables
only updates the variables  and
and  of neuron
of neuron  , i.e., the neurons are updated sequentially in the same order (this severe restriction will become obsolete in the case of continuous time discussed below). We define the composition as
, i.e., the neurons are updated sequentially in the same order (this severe restriction will become obsolete in the case of continuous time discussed below). We define the composition as  , i.e.,
, i.e.,  is applied prior to
is applied prior to  . The new values of
. The new values of  and
and  only depend on the previous value
only depend on the previous value  and on the current membrane potential
and on the current membrane potential  . The interesting dynamics take place in the variable
. The interesting dynamics take place in the variable  . They are illustrated in Figure 1 where the arrows represent transition probabilities greater than 0.
. They are illustrated in Figure 1 where the arrows represent transition probabilities greater than 0.
Figure 1. Neuron model with absolute refractory mechanism.

The figure shows a schematic of the transition operator  for the internal state variable
for the internal state variable  of a spiking neuron
of a spiking neuron  with an absolute refractory period. The neuron can fire in the resting state
with an absolute refractory period. The neuron can fire in the resting state  and in the last refractory state
and in the last refractory state  .
.
If the neuron  is not refractory, i.e.,
is not refractory, i.e.,  , it can spike (i.e., a transition from
, it can spike (i.e., a transition from  to
to  ) with probability
) with probability
| (8) |
where  is the standard sigmoidal activation function and the
is the standard sigmoidal activation function and the  denotes the natural logarithm. The term
denotes the natural logarithm. The term  is the current membrane potential, which depends on the current values of the variables
is the current membrane potential, which depends on the current values of the variables  for
for  . The term
. The term  in (8) reflects the granularity of a chosen discrete time scale. If it is very fine (say one step equals one microsecond), then
in (8) reflects the granularity of a chosen discrete time scale. If it is very fine (say one step equals one microsecond), then  is large, and the firing probability at each specific discrete time step is therefore reduced. If the neuron in a state with
is large, and the firing probability at each specific discrete time step is therefore reduced. If the neuron in a state with  does not spike,
does not spike,  relaxes into the resting state
relaxes into the resting state  corresponding to a non-refractory neuron.
corresponding to a non-refractory neuron.
If the neuron is in a refractory state, i.e.,  , its new variable
, its new variable  assumes deterministically the next lower value
assumes deterministically the next lower value  , reflecting the inherent temporal process:
, reflecting the inherent temporal process:
| (9) |
After the transition of the auxiliary variable  , the binary variable
, the binary variable  is deterministically set to a consistent state, i.e.,
is deterministically set to a consistent state, i.e.,  if
if  and
and  if
if  .
.
It can be shown that each of these stochastic state transition operators 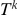 leaves the given distribution
leaves the given distribution  invariant, i.e., satisfies equation (1). This implies that any composition or mixture of these operators
invariant, i.e., satisfies equation (1). This implies that any composition or mixture of these operators 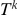 also leaves
also leaves  invariant, see, e.g., [38]. In particular, the composition
invariant, see, e.g., [38]. In particular, the composition  of these operators
of these operators  leaves
leaves  invariant, which has a quite natural interpretation as firing dynamics of the spiking neural network
invariant, which has a quite natural interpretation as firing dynamics of the spiking neural network  : At each discrete time step the variables
: At each discrete time step the variables  are updated for all neurons
are updated for all neurons  , where the update of
, where the update of 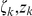 takes preceding updates for
takes preceding updates for  with
with  into account. Alternatively, one could also choose at each discrete time step a different order for updates according to [38]. The assumption of a well-regulated updating policy will be overcome in the continuous-time limit, i.e., in case where the neural dynamics are described as a Markov jump process. In the methods section we prove the following central theorem:
into account. Alternatively, one could also choose at each discrete time step a different order for updates according to [38]. The assumption of a well-regulated updating policy will be overcome in the continuous-time limit, i.e., in case where the neural dynamics are described as a Markov jump process. In the methods section we prove the following central theorem:
Theorem 1
 is the unique invariant distribution of operator
is the unique invariant distribution of operator
 , i.e.,
, i.e.,
 is aperiodic and irreducible and satisfies
is aperiodic and irreducible and satisfies
| (10) |
The proof of this Theorem is provided by Lemmata 1 – 3 in the Methods section. The statement that  (which is composed of the operators
(which is composed of the operators  ) is irreducible and aperiodic ensures that
) is irreducible and aperiodic ensures that  is the unique invariant distribution of the Markov chain defined by
is the unique invariant distribution of the Markov chain defined by  , i.e., that irrespective of the initial network state the successive application of
, i.e., that irrespective of the initial network state the successive application of  explores the whole state space in a non-periodic manner.
explores the whole state space in a non-periodic manner.
This theorem guarantees that after a sufficient “burn-in” time (more precisely in the limit of an infinite “burn-in” time), the dynamics of the network, which are given by the transition operator  , produce samples from the distribution
, produce samples from the distribution  . As by construction
. As by construction  , the Markov chain provides samples from the given distribution
, the Markov chain provides samples from the given distribution  . Furthermore, the network
. Furthermore, the network  can carry out probabilistic inference for this distribution. For example,
can carry out probabilistic inference for this distribution. For example,  can be used to sample from the posterior distribution
can be used to sample from the posterior distribution  over
over  given
given  . One just needs to clamp those neurons
. One just needs to clamp those neurons  to the corresponding observed values. This could be implemented by injecting a strong positive (negative) current into the units with
to the corresponding observed values. This could be implemented by injecting a strong positive (negative) current into the units with 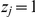 (
( ). Then, as soon as the stochastic dynamics of
). Then, as soon as the stochastic dynamics of  has converged to its invariant distribution, the averaged firing rate of neuron
has converged to its invariant distribution, the averaged firing rate of neuron  is proportional to the following desired marginal probability
is proportional to the following desired marginal probability
In a biological neural system this result of probabilistic inference could for example be read out by an integrator neuron that counts spikes from this neuron 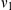 within a behaviorally relevant time window of a few hundred milliseconds, similarly as the experimentally reported integrator neurons in area LIP of monkey cortex [20], [21]. Another readout neuron that receives spike input from
within a behaviorally relevant time window of a few hundred milliseconds, similarly as the experimentally reported integrator neurons in area LIP of monkey cortex [20], [21]. Another readout neuron that receives spike input from  could at the same time estimate
could at the same time estimate  for another RV
for another RV  . But valuable information for probabilistic inference is not only provided by firing rates or spike counts, but also by spike correlations of the neurons
. But valuable information for probabilistic inference is not only provided by firing rates or spike counts, but also by spike correlations of the neurons  in
in  . For example, the probability
. For example, the probability  can be estimated by a readout neuron that responds to superpositions of EPSPs caused by near-coincident firing of neurons
can be estimated by a readout neuron that responds to superpositions of EPSPs caused by near-coincident firing of neurons 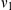 and
and  within a time interval of length
within a time interval of length  . Thus, a large number of different probabilistic inferences can be carried out efficiently in parallel by readout neurons that receive spike input from different subsets of neurons in the network
. Thus, a large number of different probabilistic inferences can be carried out efficiently in parallel by readout neurons that receive spike input from different subsets of neurons in the network  .
.
Variation of the discrete time model with a relative refractory mechanism
For the previously described simple neuron model, the refractory process was assumed to last for  time steps, exactly as long as the postsynaptic potentials caused by each spike. In this section we relax this assumption by introducing a more complex and biologically more realistic neuron model, where the duration of the refractory process is decoupled from the duration
time steps, exactly as long as the postsynaptic potentials caused by each spike. In this section we relax this assumption by introducing a more complex and biologically more realistic neuron model, where the duration of the refractory process is decoupled from the duration  of a postsynaptic potential. Thus, this model can for example also fire bursts of spikes with an interspike interval
of a postsynaptic potential. Thus, this model can for example also fire bursts of spikes with an interspike interval  . The introduction of this more complex neuron model comes at the price that one can no longer prove that a network of such neurons samples from the desired distribution
. The introduction of this more complex neuron model comes at the price that one can no longer prove that a network of such neurons samples from the desired distribution  . Nevertheless, if the sigmoidal activation function
. Nevertheless, if the sigmoidal activation function  is replaced by a different activation function
is replaced by a different activation function 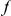 , one can still prove that the sampling is “locally correct”, as specified in equation (12) below. Furthermore, our computer simulations suggest that also globally the error introduced by the more complex neuron model is not functionally significant, i.e. that statistical dependencies between the RVs
, one can still prove that the sampling is “locally correct”, as specified in equation (12) below. Furthermore, our computer simulations suggest that also globally the error introduced by the more complex neuron model is not functionally significant, i.e. that statistical dependencies between the RVs  are still faithfully captured.
are still faithfully captured.
The neuron model with a relative refractory period is defined in the following way. Consider some arbitrary refractory function  with
with  , and
, and  for
for  . The idea is that
. The idea is that  models the readiness of the neuron to fire in its state
models the readiness of the neuron to fire in its state  . This readiness has value
. This readiness has value  when the neuron has fired at the preceding time step (i.e.,
when the neuron has fired at the preceding time step (i.e.,  ), and assumes the resting state
), and assumes the resting state  when
when  has dropped to
has dropped to  . In between, the readiness may take on any non-negative value according to the function
. In between, the readiness may take on any non-negative value according to the function  . The function
. The function  does not need to be monotonic, allowing for example that it increases to high values in between, yielding a preferred interspike interval of a oscillatory neuron. The firing probability of neuron
does not need to be monotonic, allowing for example that it increases to high values in between, yielding a preferred interspike interval of a oscillatory neuron. The firing probability of neuron  in state
in state  is given by
is given by  , where
, where  is an appropriate function of the membrane potential as described below. Thus this function
is an appropriate function of the membrane potential as described below. Thus this function  is closely related to the function
is closely related to the function  (called afterpotential) in the spike response model [5] as well as to the self-excitation kernel in Generalized Linear Models [42]. In general, different neurons in the network may have different refractory profiles, which can be modeled by a different refractory function for each neuron
(called afterpotential) in the spike response model [5] as well as to the self-excitation kernel in Generalized Linear Models [42]. In general, different neurons in the network may have different refractory profiles, which can be modeled by a different refractory function for each neuron  . However for the sake of notational simplicity we assume a single refractory function in the following.
. However for the sake of notational simplicity we assume a single refractory function in the following.
In the presence of this refractory function  one needs to replace the sigmoidal activation function
one needs to replace the sigmoidal activation function  by a suitable function
by a suitable function  that satisfies the condition
that satisfies the condition
| (11) |
for all real numbers  . This equation can be derived (see Methods section Lemma 0) if one requires each neuron
. This equation can be derived (see Methods section Lemma 0) if one requires each neuron 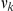 to represent the correct distribution
to represent the correct distribution  over
over  conditioned the variables
conditioned the variables  . One can show that, for any
. One can show that, for any  as above, there always exists a continuous, monotonic function
as above, there always exists a continuous, monotonic function 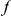 which satisfies this equation (see Lemma 0 in Methods). Unfortunately (11) cannot be solved analytically for
which satisfies this equation (see Lemma 0 in Methods). Unfortunately (11) cannot be solved analytically for  in general. Hence, for simulations we approximate the function
in general. Hence, for simulations we approximate the function 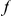 for a given
for a given  by numerically solving (11) on a grid and interpolating between the grid points with a constant function. Examples for several functions
by numerically solving (11) on a grid and interpolating between the grid points with a constant function. Examples for several functions  and the associated
and the associated  are shown in Figure 2B and Figure 2C respectively. Furthermore, spike trains emitted by single neurons with these refractory functions
are shown in Figure 2B and Figure 2C respectively. Furthermore, spike trains emitted by single neurons with these refractory functions  and the corresponding functions
and the corresponding functions 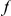 are shown in Figure 2D for the case of piecewise constant membrane potentials. This figure indicates, that functions
are shown in Figure 2D for the case of piecewise constant membrane potentials. This figure indicates, that functions  that define a shorter refractory effect lead to higher firing rates and more irregular firing. It is worth noticing that the standard activation function
that define a shorter refractory effect lead to higher firing rates and more irregular firing. It is worth noticing that the standard activation function  is the solution of equation (11) for the absolute refractory function, i.e., for
is the solution of equation (11) for the absolute refractory function, i.e., for  and
and  for
for  .
.
Figure 2. Neuron model with relative refractory mechanism.
The figure shows the transition operator  , refractory functions
, refractory functions  and activation functions
and activation functions 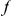 for the neuron model with relative refractory mechanism. (A) Transition probabilities of the internal variable
for the neuron model with relative refractory mechanism. (A) Transition probabilities of the internal variable  given by
given by  . (B) Three examples of possible refractory functions
. (B) Three examples of possible refractory functions  . They assume value
. They assume value  when the neuron cannot spike, and return to value
when the neuron cannot spike, and return to value  (full readiness to fire again) with different time courses. The value of
(full readiness to fire again) with different time courses. The value of  at intermediate time points regulates the current probability of firing of neuron
at intermediate time points regulates the current probability of firing of neuron  (see A). The x-axis is equivalent to the number of time steps since last spike (running from 0 to
(see A). The x-axis is equivalent to the number of time steps since last spike (running from 0 to  from left to right). (C) Associated activation functions
from left to right). (C) Associated activation functions 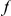 according to (11). (D) Spike trains produced by the resulting three different neuron models with (hypothetical) membrane potentials that jump at time
according to (11). (D) Spike trains produced by the resulting three different neuron models with (hypothetical) membrane potentials that jump at time  from a constant low value to a constant high value. Black horizontal bars indicate spikes, and the active states
from a constant low value to a constant high value. Black horizontal bars indicate spikes, and the active states  are indicated by gray shaded areas of duration
are indicated by gray shaded areas of duration  after each spike. It can be seen from this example that different refractory mechanisms give rise to different spiking dynamics.
after each spike. It can be seen from this example that different refractory mechanisms give rise to different spiking dynamics.
The transition operator  is defined for this model in a very similar way as before. However, for
is defined for this model in a very similar way as before. However, for  , when the variable
, when the variable  was deterministically reduced by
was deterministically reduced by  in the simpler model (yielding
in the simpler model (yielding  ), this reduction occurs now only with probability
), this reduction occurs now only with probability  . With probability
. With probability  the operator
the operator  sets
sets  , modeling the firing of another spike of neuron
, modeling the firing of another spike of neuron  at this time point. The neural computability condition (4) remains unchanged, e.g.,
at this time point. The neural computability condition (4) remains unchanged, e.g.,  for a Boltzmann distribution. A schema of the stochastic dynamics of this local state transition operator
for a Boltzmann distribution. A schema of the stochastic dynamics of this local state transition operator  is shown in Figure 2A.
is shown in Figure 2A.
This transition operator  has the following properties. In Lemma 0 in Methods it is proven that the unique invariant distribution of
has the following properties. In Lemma 0 in Methods it is proven that the unique invariant distribution of  , denoted as
, denoted as  , gives rise to the correct marginal distribution over
, gives rise to the correct marginal distribution over  , i.e.
, i.e.
This means that a neuron whose dynamics is described by  samples from the correct distribution
samples from the correct distribution  if it receives a static input from the other neurons in the network, i.e., as long as its membrane potential
if it receives a static input from the other neurons in the network, i.e., as long as its membrane potential  is constant. Hence the “local” computation performed by such neuron can be considered as correct. If however, several neurons in the network change their states in a short interval of time, the joint distribution over
is constant. Hence the “local” computation performed by such neuron can be considered as correct. If however, several neurons in the network change their states in a short interval of time, the joint distribution over  is in general not the desired one, i.e.,
is in general not the desired one, i.e.,  , where
, where  denotes the invariant distribution of
denotes the invariant distribution of  . In the Methods section, we present simulation results that indicate that the error of the approximation to the desired Boltzmann distributions introduced by neural sampling with relative refractory mechanism is rather minute. It is shown that the neural sampling approximation error is orders of magnitudes below the one introduced by a fully factorized distribution (which amounts to assuming correct marginal distributions
. In the Methods section, we present simulation results that indicate that the error of the approximation to the desired Boltzmann distributions introduced by neural sampling with relative refractory mechanism is rather minute. It is shown that the neural sampling approximation error is orders of magnitudes below the one introduced by a fully factorized distribution (which amounts to assuming correct marginal distributions  and independent neurons).
and independent neurons).
To illustrate the sampling process with the relative refractory mechanism, we examine a network of  neurons. We aim to sample from a Boltzmann distribution (5) with parameters
neurons. We aim to sample from a Boltzmann distribution (5) with parameters  ,
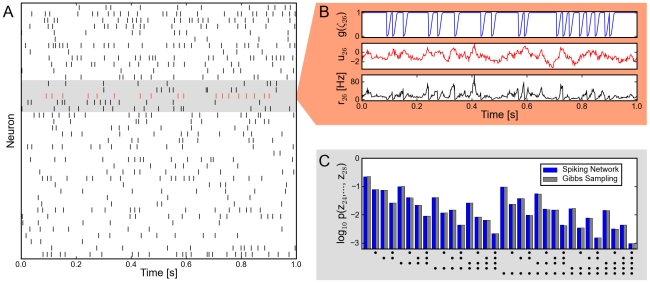
,  being randomly drawn from normal distributions. For the neuron model, we use the relative refractory mechanism shown in the mid row of Figure 2B. A detailed description of the simulation and the parameters used is given in the Methods section. A spike pattern of the resulting sampling network is shown in Figure 3A. The network features a sparse, irregular spike response with average firing rate of
being randomly drawn from normal distributions. For the neuron model, we use the relative refractory mechanism shown in the mid row of Figure 2B. A detailed description of the simulation and the parameters used is given in the Methods section. A spike pattern of the resulting sampling network is shown in Figure 3A. The network features a sparse, irregular spike response with average firing rate of  . For one neuron
. For one neuron 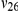 , indicated with orange spikes, the internal dynamics are shown in Figure 3B. After each action potential the neuron’s refractory function
, indicated with orange spikes, the internal dynamics are shown in Figure 3B. After each action potential the neuron’s refractory function  drops to zero and reduces the probability of spiking again in a short time interval. The influence of the remaining network
drops to zero and reduces the probability of spiking again in a short time interval. The influence of the remaining network  is transmitted to neuron
is transmitted to neuron  via PSPs of duration
via PSPs of duration  and sums up to the fluctuating membrane potential
and sums up to the fluctuating membrane potential  . As reflected in the highly variable membrane potential even this small network exhibits rich interactions. To represent the correct distribution
. As reflected in the highly variable membrane potential even this small network exhibits rich interactions. To represent the correct distribution  over
over  conditioned on
conditioned on  , the neuron
, the neuron 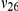 continuously adapts its instantaneous firing rate. To quantify the precision with which the spiking network draws samples from the target distribution (5), Figure 3C shows the joint distribution of
continuously adapts its instantaneous firing rate. To quantify the precision with which the spiking network draws samples from the target distribution (5), Figure 3C shows the joint distribution of  neurons. For comparison we accompany the distribution of sampled network states with the result obtained from the standard Gibbs sampling algorithm (considered as the ground truth). Since the number of possible states
neurons. For comparison we accompany the distribution of sampled network states with the result obtained from the standard Gibbs sampling algorithm (considered as the ground truth). Since the number of possible states  grows exponentially in the number of neurons, we restrict ourselves for visualization purposes to the distribution
grows exponentially in the number of neurons, we restrict ourselves for visualization purposes to the distribution  of the gray shaded units and marginalize over the remaining network. The probabilities are estimated from
of the gray shaded units and marginalize over the remaining network. The probabilities are estimated from  samples, i.e., from
samples, i.e., from  successive states
successive states  of the Markov chain. Stochastic deviations of the estimated probabilities due to the finite number of samples are quite small (typical errors
of the Markov chain. Stochastic deviations of the estimated probabilities due to the finite number of samples are quite small (typical errors  ) and are comparable to systematic deviations due to the only locally correct computation of neurons with relative refractory mechanism. In the Methods section, we present further simulation results showing that the proposed networks consisting of neurons with relative refractory mechanism approximate the desired target distributions faithfully over a large range of distribution parameters.
) and are comparable to systematic deviations due to the only locally correct computation of neurons with relative refractory mechanism. In the Methods section, we present further simulation results showing that the proposed networks consisting of neurons with relative refractory mechanism approximate the desired target distributions faithfully over a large range of distribution parameters.
Figure 3. Sampling from a Boltzmann distribution by spiking neurons with relative refractory mechanism.
(A) Spike raster of the network. (B) Traces of internal state variables of a neuron (# 26, indicated by orange spikes in A). The rich interaction of the network gives rise to rapidly changing membrane potentials and instantaneous firing rates. (C) Joint distribution of 5 neurons (gray shaded area in A) obtained by the spiking neural network and Gibbs sampling from the same distribution. Active states  are indicated by a black dot, using one row for each neuron
are indicated by a black dot, using one row for each neuron  , the columns list all
, the columns list all  possible states
possible states 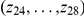 of these
of these  neurons. The tight match between both distributions suggests that the spiking network represents the target probability distribution
neurons. The tight match between both distributions suggests that the spiking network represents the target probability distribution  with high accuracy.
with high accuracy.
In order to illustrate that the proposed sampling networks feature biologically quite realistic spiking dynamics, we present in the Methods section several neural firing statistics (e.g., the inter-spike interval histogram) of the network model. In general, the statistics computed from the model match experimentally observed statistics well. The proposed network models are based on the assumption of rectangular-shaped, renewal PSPs. More precisely, we define renewal (or non-additive) PSPs in the following way. Renewal PSPs evoked by a single synapse do not add up but are merely prolonged in their duration (according to equation (6)); renewal PSPs elicited at different synapses nevertheless add up in the normal way. In Methods we investigate the impact of replacing the theoretically ideal rectangular-shaped, renewal PSPs with biologically more realistic alpha-shaped, additive PSPs. Simulation results suggest that the network model with alpha-shaped PSPs does not capture the target distribution as accurately as with the theoretically ideal PSP shapes, statistical dependencies between the RVs  are however still approximated reasonably well.
are however still approximated reasonably well.
Neural sampling in continuous time
The neural sampling model proposed above was formulated in discrete time of step size  , inspired by the discrete time nature of MCMC techniques in statistics and machine learning as well as to make simulations possible on digital computers. However, models in continuous time (e.g., ordinary differential equations) are arguably more natural and “realistic” descriptions of temporally varying biological processes. This gives rise to the question whether one can find a sensible limit of the discrete time model in the limit
, inspired by the discrete time nature of MCMC techniques in statistics and machine learning as well as to make simulations possible on digital computers. However, models in continuous time (e.g., ordinary differential equations) are arguably more natural and “realistic” descriptions of temporally varying biological processes. This gives rise to the question whether one can find a sensible limit of the discrete time model in the limit  , yielding a sampling network model in continuous time. Another motivation for considering continuous time models for neural sampling is the fact that many mathematical models for recurrent networks are formulated in continuous time [5], and a comparison to these existing models would be facilitated. Here we propose a stochastically spiking neural network model in continuous time, whose states still represent correct samples from the desired probability distribution
, yielding a sampling network model in continuous time. Another motivation for considering continuous time models for neural sampling is the fact that many mathematical models for recurrent networks are formulated in continuous time [5], and a comparison to these existing models would be facilitated. Here we propose a stochastically spiking neural network model in continuous time, whose states still represent correct samples from the desired probability distribution  at any time
at any time  . These types of models are usually referred to as Markov jump processes. It can be shown that discretizing this continuous time model yields the discrete time model defined earlier, which thus can be regarded as a version suitable for simulations on a digital computer.
. These types of models are usually referred to as Markov jump processes. It can be shown that discretizing this continuous time model yields the discrete time model defined earlier, which thus can be regarded as a version suitable for simulations on a digital computer.
We define the continuous time model in the following way. Let  , for
, for  , denote the firing times of neuron
, denote the firing times of neuron  . The refractory process of this neuron, in analogy to Figure 1 and equation (8)-(9) for the case of discrete time, is described by the following differential equation for the auxiliary variable
. The refractory process of this neuron, in analogy to Figure 1 and equation (8)-(9) for the case of discrete time, is described by the following differential equation for the auxiliary variable  , which may now assume any nonnegative real number
, which may now assume any nonnegative real number  :
:
 |
(12) |
Here  denotes Dirac’s Delta centered at the spike time
denotes Dirac’s Delta centered at the spike time  . This differential equation describes the following simple dynamics. The auxiliary variable
. This differential equation describes the following simple dynamics. The auxiliary variable  decays linearly with time constant
decays linearly with time constant  when the neuron is refractory, i.e.,
when the neuron is refractory, i.e.,  . Once
. Once  arrives at its resting state
arrives at its resting state  it remains there, corresponding to the neuron being ready to spike again (more precisely, in order to avoid point measures we set it to a random value in
it remains there, corresponding to the neuron being ready to spike again (more precisely, in order to avoid point measures we set it to a random value in  , see Methods). In the resting state, the neuron has the probability density
, see Methods). In the resting state, the neuron has the probability density  to fire at every time
to fire at every time  . If it fires at
. If it fires at 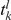 , this results in setting
, this results in setting  , which is formalized in equation (12) by the sum of Dirac Delta’s
, which is formalized in equation (12) by the sum of Dirac Delta’s  . Here the current membrane potential
. Here the current membrane potential  at time
at time  is defined as in the discrete time case, e.g., by
is defined as in the discrete time case, e.g., by  for the case of a Boltzmann distribution (5). The binary variable
for the case of a Boltzmann distribution (5). The binary variable  is defined to be 1 if
is defined to be 1 if  and 0 if the neuron is in the resting state
and 0 if the neuron is in the resting state  . Biologically, the term
. Biologically, the term  can again be interpreted as the value at time
can again be interpreted as the value at time  of a rectangular-shaped PSP (with a duration of
of a rectangular-shaped PSP (with a duration of  ) that neuron
) that neuron  evokes in neuron
evokes in neuron  . As the spikes are discrete events in continuous time, the probability of two or more neurons spiking at the same time is zero. This allows for updating all neurons in parallel using a differential equation.
. As the spikes are discrete events in continuous time, the probability of two or more neurons spiking at the same time is zero. This allows for updating all neurons in parallel using a differential equation.
In analogy to the discrete time case, the neural network in continuous time can be shown to sample from the desired distribution  , i.e.,
, i.e.,  is an invariant distribution of the network dynamics defined above. However, to establish this fact, one has to rely on a different mathematical framework. The probability distribution
is an invariant distribution of the network dynamics defined above. However, to establish this fact, one has to rely on a different mathematical framework. The probability distribution  of the auxiliary variables
of the auxiliary variables  as a function of time
as a function of time  , which describes the evolution of the network, obeys a partial differential equation, the so-called Differential-Chapman-Kolmogorov equation (see [43]):
, which describes the evolution of the network, obeys a partial differential equation, the so-called Differential-Chapman-Kolmogorov equation (see [43]):
| (13) |
where the operator  , which captures the dynamics of the network, is implicitly defined by the differential equations (12) and the spiking probabilities. This operator
, which captures the dynamics of the network, is implicitly defined by the differential equations (12) and the spiking probabilities. This operator  is the continuous time equivalent to the transition operator
is the continuous time equivalent to the transition operator  in the discrete time case. The operator
in the discrete time case. The operator  consists here of two components. The drift term captures the deterministic decay process of
consists here of two components. The drift term captures the deterministic decay process of  , stemming from the term
, stemming from the term  in equation (12). The jump term describes the non-continuous aspects of the path
in equation (12). The jump term describes the non-continuous aspects of the path  associated with “jumping” from
associated with “jumping” from  to
to  at the time
at the time  when the neuron fires.
when the neuron fires.
In the Methods section we prove that the resulting time invariant distribution, i.e., the distribution that solves  , now denoted
, now denoted  as it is not a function of time, gives rise to the desired marginal distribution
as it is not a function of time, gives rise to the desired marginal distribution  over
over  :
:
| (14) |
where  and
and  if
if  and
and  otherwise.
otherwise.  denotes Kronecker’s Delta with
denotes Kronecker’s Delta with  if
if  and
and  otherwise. Thus, the function
otherwise. Thus, the function  simply reflects the definition that
simply reflects the definition that  if
if  and 0 otherwise. For an explicit definition of
and 0 otherwise. For an explicit definition of  , a proof of the above statement, and some additional comments see the Methods section.
, a proof of the above statement, and some additional comments see the Methods section.
The neural samplers in discrete and continuous time are closely related. The model in discrete time provides an increasingly more precise description of the inherent spike dynamics when the duration  of the discrete time step is reduced, causing an increase of
of the discrete time step is reduced, causing an increase of  (such that
(such that  is constant) and therefore a reduced firing probability of each neuron at any discrete time step (see the term
is constant) and therefore a reduced firing probability of each neuron at any discrete time step (see the term  in equation (8)). In the limit of
in equation (8)). In the limit of  approaching
approaching  , the probability that two or more neurons will fire at the same time approaches
, the probability that two or more neurons will fire at the same time approaches  , and the discrete time sampler becomes equal to the continuous time system defined above, which updates all units in parallel.
, and the discrete time sampler becomes equal to the continuous time system defined above, which updates all units in parallel.
It is also possible to formulate a continuous time version of the neural sampler based on neuron models with relative refractory mechanisms. In the Methods section the resulting continuous time neuron model with a relative refractory mechanism is defined. Theoretical results similar to the discrete time case can be derived for this sampler (see Lemmata 9 and 10 in Methods): It is shown that each neuron “locally” performs the correct computation under the assumption of static input from the remaining neurons. However one can no longer prove in general that the global network samples from the target distribution  .
.
Demonstration of probabilistic inference with recurrent networks of spiking neurons in an application to perceptual multistability
In the following we present a network model for perceptual multistability based on the neural sampling framework introduced above. This simulation study is aimed at showing that the proposed network can indeed sample from a desired distribution and also perform inference, i.e., sample from the correct corresponding posterior distribution. It is not meant to be a highly realistic or exhaustive model of perceptual multistability nor of biologically plausible learning mechanisms. Such models would naturally require considerably more modelling work.
Perceptual multistability evoked by ambiguous sensory input, such as a 2D drawing (e.g., Necker cube) that allows for different consistent 3D interpretations, has become a frequently studied perceptual phenomenon. The most important finding is that the perceptual system of humans and nonhuman primates does not produce a superposition of different possible percepts of an ambiguous stimulus, but rather switches between different self-consistent global percepts in a spontaneous manner. Binocular rivalry, where different images are presented to the left and right eye, has become a standard experimental paradigm for studying this effect [44]–[47]. A typical pair of stimuli are the two images shown in Figure 4A. Here the percepts of humans and nonhuman primates switch (seemingly stochastically) between the two presented orientations. [16]–[18] propose that several aspects of experimental data on perceptual multistability can be explained if one assumes that percepts correspond to samples from the conditional distribution over interpretations (e.g., different 3D shapes) given the visual input (e.g., the 2D drawing). Furthermore, the experimentally observed fact that percepts tend to be stable on the time scale of seconds suggests that perception can be interpreted as probabilistic inference that is carried out by MCMC sampling which produces successively correlated samples. In [18] it is shown that this MCMC interpretation is also able to qualitatively reproduce the experimentally observed distribution of dominance durations, i.e., the distribution of time intervals between perceptual switches. However, in lack of an adequate model for sampling by a recurrent network of spiking neurons, theses studies could describe this approach only on a rather abstract level, and pointed out the open problem to relate this algorithmic approach to neural processes. We have demonstrated in a computer simulation that the previously described model for neural sampling could in principle fill this gap, providing a modelling framework that is on the one hand consistent with the dynamics of networks of spiking neurons, and which can on the other hand also be clearly understood from the perspective of probabilistic inference through MCMC sampling.
Figure 4. Modeling perceptual multistability as probabilistic inference with neural sampling.
(A) Typical visual stimuli for the left and right eye in binocular rivalry experiments. (B) Tuning curve of a neuron with preferred orientation  . (C) Distribution of dominance durations in the trained network under ambiguous input. The red curve shows the Gamma distribution with maximum likelihood on the data. (D) 2-dimensional projection (via population vector) of the distribution
. (C) Distribution of dominance durations in the trained network under ambiguous input. The red curve shows the Gamma distribution with maximum likelihood on the data. (D) 2-dimensional projection (via population vector) of the distribution  encoded in the spiking network showing that it strongly favors coherent global states of arbitrary orientation to incoherent ones (corresponding to population vectors of small magnitude). (E) 2-dimensional projection of the bimodal posterior distribution under an ambiguous input consisting of two different orientations reminiscent of the stimuli shown in A. The black trace shows the temporal evolution of the network state
encoded in the spiking network showing that it strongly favors coherent global states of arbitrary orientation to incoherent ones (corresponding to population vectors of small magnitude). (E) 2-dimensional projection of the bimodal posterior distribution under an ambiguous input consisting of two different orientations reminiscent of the stimuli shown in A. The black trace shows the temporal evolution of the network state  for 500 ms around a perceptual switch. (F) Network states at 3 time points
for 500 ms around a perceptual switch. (F) Network states at 3 time points  marked in E. Neurons that fired in the preceding 20 ms (see gray bar in G) are plotted in the color of their preferred orientation. Inactive neurons are shown in white. While states
marked in E. Neurons that fired in the preceding 20 ms (see gray bar in G) are plotted in the color of their preferred orientation. Inactive neurons are shown in white. While states  and
and  represent rather coherent orientations,
represent rather coherent orientations,  shows an incoherent state corresponding to a perceptual switch. Clamped neurons (which the posterior is condition on) are marked by a black dot. (G) Spike raster of the unclamped neurons during a 500 ms epoch marked by the black trace in E. Gray bars indicate the 20 ms time intervals that define the network states shown in F. Altogether this figure shows that a theoretically rigorous probabilistic inference process can be carried out by a network of spiking neurons with a spike raster that is similar to generic recorded data.
shows an incoherent state corresponding to a perceptual switch. Clamped neurons (which the posterior is condition on) are marked by a black dot. (G) Spike raster of the unclamped neurons during a 500 ms epoch marked by the black trace in E. Gray bars indicate the 20 ms time intervals that define the network states shown in F. Altogether this figure shows that a theoretically rigorous probabilistic inference process can be carried out by a network of spiking neurons with a spike raster that is similar to generic recorded data.
In the following we model some essential aspects of an experimental setup for binocular rivalry with grating stimuli (see Figure 4A) in a recurrent network of spiking neurons with the previously described relative refractory mechanism. We assigned to each of the 217 neurons in the network 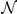 a tuning curve
a tuning curve  , centered around its preferred orientation
, centered around its preferred orientation 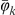 as shown in Figure 4B. The preferred orientations
as shown in Figure 4B. The preferred orientations  of the neurons were chosen to cover the entire interval
of the neurons were chosen to cover the entire interval  of possible orientations and were randomly assigned to the neurons. The neurons were arranged on a hexagonal grid as depicted in Figure 4F. Any two neurons with distance
of possible orientations and were randomly assigned to the neurons. The neurons were arranged on a hexagonal grid as depicted in Figure 4F. Any two neurons with distance  were synaptically connected (neighboring units had distance
were synaptically connected (neighboring units had distance  ). We assume that these neurons represent neurons in the visual system that have roughly the same or neighboring receptive field, and that each neuron receives visual input from either the left or the right eye. The network connections were chosen such that neurons that have similar (very different) preferred orientations are connected with positive (negative) weights (for details see Methods section).
). We assume that these neurons represent neurons in the visual system that have roughly the same or neighboring receptive field, and that each neuron receives visual input from either the left or the right eye. The network connections were chosen such that neurons that have similar (very different) preferred orientations are connected with positive (negative) weights (for details see Methods section).
We examined the resulting distribution 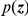 over the
over the  dimensional network states. To provide an intuitive visualization of these high dimensional network states
dimensional network states. To provide an intuitive visualization of these high dimensional network states  , we resort to a 2-dimensional projection, the population vector of a state
, we resort to a 2-dimensional projection, the population vector of a state  (see Methods for details of the applied population vector decoding scheme). Only the endpoints of the population vectors are drawn (as colored points) in Figure 4D,E. The orientation of the population vector is assumed to correspond to the dominant orientation of the percept, and its distance from the origin encodes the strength of this percept. We also, somewhat informally, call the strength of a percept its coherence and a network state which represents a coherent percept a coherent network state. A coherent network state hence results in a population vector of large magnitude. Each direction of a population vector is color coded in Figure 4D,E, using the color code for directions shown on the right hand side of Figure 4F. In Figure 4D the distribution
(see Methods for details of the applied population vector decoding scheme). Only the endpoints of the population vectors are drawn (as colored points) in Figure 4D,E. The orientation of the population vector is assumed to correspond to the dominant orientation of the percept, and its distance from the origin encodes the strength of this percept. We also, somewhat informally, call the strength of a percept its coherence and a network state which represents a coherent percept a coherent network state. A coherent network state hence results in a population vector of large magnitude. Each direction of a population vector is color coded in Figure 4D,E, using the color code for directions shown on the right hand side of Figure 4F. In Figure 4D the distribution  of the network is illustrated by sampling of the network for
of the network is illustrated by sampling of the network for  , with samples
, with samples  taken every millisecond. Each dot equals a sampled network state
taken every millisecond. Each dot equals a sampled network state  . In a biological interpretation the spike response of the freely evolving network reflects spontaneous activity, since no observations, i.e., no external input, was added to the system. Figure 4D shows that the spontaneous activity of this simple network of spiking neurons moves preferably through coherent network states for all possible orientations due to the chosen recurrent network connections (being positive for neurons with similar preferred orientation and negative otherwise). This can directly be seen from the rare occurrence of population vectors with small magnitude (vectors close to the “center”) in Figure 4D.
. In a biological interpretation the spike response of the freely evolving network reflects spontaneous activity, since no observations, i.e., no external input, was added to the system. Figure 4D shows that the spontaneous activity of this simple network of spiking neurons moves preferably through coherent network states for all possible orientations due to the chosen recurrent network connections (being positive for neurons with similar preferred orientation and negative otherwise). This can directly be seen from the rare occurrence of population vectors with small magnitude (vectors close to the “center”) in Figure 4D.
To study percepts elicited by ambiguous stimuli, where inputs like in Figure 4A are shown simultaneously to the left and right eye during a binocular rivalry experiment, we provided ambiguous input to the network. Two cells with preferred orientation  and two cells with
and two cells with  were clamped to
were clamped to  . Additionally four neurons with
. Additionally four neurons with  resp.
resp.  were muted by clamping to
were muted by clamping to  . This ambiguous input is incompatible with a coherent percept, as it corresponds to two orthogonal orientations presented at the same time. The resulting distribution over the state of the 209 remaining neurons is shown for a time span of
. This ambiguous input is incompatible with a coherent percept, as it corresponds to two orthogonal orientations presented at the same time. The resulting distribution over the state of the 209 remaining neurons is shown for a time span of 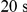 of simulated biological time (with samples taken every millisecond) in Figure 4E. One clearly sees that the network spends most of the time in network states that correspond to one of the two simultaneously presented input orientations (
of simulated biological time (with samples taken every millisecond) in Figure 4E. One clearly sees that the network spends most of the time in network states that correspond to one of the two simultaneously presented input orientations ( and
and 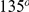 ), and virtually no time on orientations in between. This implements a sampling process from a bimodal conditional distribution. The black line marks a
), and virtually no time on orientations in between. This implements a sampling process from a bimodal conditional distribution. The black line marks a  trace of network states
trace of network states  around a perceptual switch: The network remained in one mode of high probability – corresponding to one percept – for some period of time, and then quickly traversed the state space to another mode – corresponding to a different percept.
around a perceptual switch: The network remained in one mode of high probability – corresponding to one percept – for some period of time, and then quickly traversed the state space to another mode – corresponding to a different percept.
Three of the states  around this perceptual switch (
around this perceptual switch ( ,
,  and
and  in Figure 4E) are explicitly shown in Figure 4F. Neurons
in Figure 4E) are explicitly shown in Figure 4F. Neurons  that fired during the preceding interval of
that fired during the preceding interval of  ms (marked in gray in Figure 4G) are drawn in the respective color of their preferred orientation. Inactive neurons are drawn in white, and clamped neurons are marked by a black dot (
ms (marked in gray in Figure 4G) are drawn in the respective color of their preferred orientation. Inactive neurons are drawn in white, and clamped neurons are marked by a black dot ( ).
).
Figure 4G shows the action potentials of the  non-clamped neurons during the same
non-clamped neurons during the same 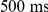 trace around the perceptual switch. One sees that the sampling process is expressed in this neural network model by a sparse, asynchronous and irregular spike response. It is worth mentioning that the average firing rate when sampling from the posterior distribution is only slightly higher than the average firing rate of spontaneous activity (
trace around the perceptual switch. One sees that the sampling process is expressed in this neural network model by a sparse, asynchronous and irregular spike response. It is worth mentioning that the average firing rate when sampling from the posterior distribution is only slightly higher than the average firing rate of spontaneous activity ( and
and  respectively), which is reminiscent of related experimental data [7]. Thus on the basis of the overall network activity it is indistinguishable whether the network carries out an inference task or freely samples from its prior distribution. It is furthermore notable, that a focus of the network activity on the two orientations that are given by the external input can be achieved in this model, in spite of the fact that only two of the
respectively), which is reminiscent of related experimental data [7]. Thus on the basis of the overall network activity it is indistinguishable whether the network carries out an inference task or freely samples from its prior distribution. It is furthermore notable, that a focus of the network activity on the two orientations that are given by the external input can be achieved in this model, in spite of the fact that only two of the  neurons were clamped for each of them. This numerical relationship is reminiscent of standard data on the weak input from LGN to V1 that is provided in the brain [48], [49], and raises the question whether the proposed neural sampling model could provide a possible mechanism (under the modelling assumptions made above) for cortical processing of such numerically weak external inputs.
neurons were clamped for each of them. This numerical relationship is reminiscent of standard data on the weak input from LGN to V1 that is provided in the brain [48], [49], and raises the question whether the proposed neural sampling model could provide a possible mechanism (under the modelling assumptions made above) for cortical processing of such numerically weak external inputs.
The distribution of the resulting dominance durations, i.e., the time between perceptual switches, for the previously described setup with ambiguous input is shown for a continuous run of  in Figure 4C (a similar method as in [18] was used to measure dominance durations, see Methods). This distribution can be approximated quite well by a Gamma distribution, which also provides a good fit to experimental data (see the discussion in [18]). We expect that also other features of the more abstract MCMC model for biological vision of [17], [18], such as contextual biases and traveling waves, will emerge in larger and more detailed implementations of the MCMC approach through the proposed neural sampling method in networks of spiking neurons.
in Figure 4C (a similar method as in [18] was used to measure dominance durations, see Methods). This distribution can be approximated quite well by a Gamma distribution, which also provides a good fit to experimental data (see the discussion in [18]). We expect that also other features of the more abstract MCMC model for biological vision of [17], [18], such as contextual biases and traveling waves, will emerge in larger and more detailed implementations of the MCMC approach through the proposed neural sampling method in networks of spiking neurons.
Discussion
We have presented a spiking neural network that samples from a given probability distribution via its inherent network dynamics. In particular the network is able to carry out probabilistic inference through sampling. The model, based on assumptions about the underlying probability distribution (formalized by the neural computability condition) as well as on certain assumptions regarding the underlying MCMC model, provides one possible neural implementation of the “inference-by-sampling paradigm” emerging in computational neuroscience.
During inference the observations (i.e., the variables which we wish to condition on) are modeled in this study by clamping the corresponding neurons by strong external input to the observed binary value. Units which receive no input or input with vanishing contrast (stimulus intensity) are treated as unobserved. Using this admittedly quite simplistic model of the input, we observed in simulations that our network model exhibits the following property: The onset of a sensory stimulus reduces the variability of the firing activity, which represents (after stimulus onset) a conditional distribution, rather than the prior distribution (see the difference between panels D and E of Figure 5. It is tempting to compare these results to the experimental finding of reduced firing rate variability after stimulus onset observed in several cortical areas [50]. We wish to point out however, that a consistent treatment of zero contrast stimuli requires more thorough modelling efforts (e.g., by explicitly adding a random variable for the stimulus intensity [35], [51]), which is not the focus of the presented work.
Figure 5. Firing statistics of neural sampling networks.
(A) Shown is the membrane potential histogram of a typical neuron during sampling. The data is that of neuron  from the simulation shown in Figure 3 (the membrane potential and spike trace of
from the simulation shown in Figure 3 (the membrane potential and spike trace of  are highlighted in Figure 3). (B) The plot shows the ISI distribution of a typical neuron (again
are highlighted in Figure 3). (B) The plot shows the ISI distribution of a typical neuron (again  from Figure 3) during sampling. The distribution is roughly gamma-shaped, reminiscent of experimentally observed ISI distributions. (C) A scatter plot of the coefficient of variation (CV) versus the average interspike interval (ISI) of each neuron taken from the simulation shown in Figure 3. The value of neuron
from Figure 3) during sampling. The distribution is roughly gamma-shaped, reminiscent of experimentally observed ISI distributions. (C) A scatter plot of the coefficient of variation (CV) versus the average interspike interval (ISI) of each neuron taken from the simulation shown in Figure 3. The value of neuron  from Figure 3 is marked by a cross. The simulated data is in accordance with experimentally observed data.
from Figure 3 is marked by a cross. The simulated data is in accordance with experimentally observed data.
Virtually all high-level computational tasks that a brain has to solve can be formalized as optimization problems, that take into account a (possibly large) number of soft or hard constraints. In typical applications of probabilistic inference in science and engineering (see e.g. [52], [53]) such constraints are encoded in e.g., conditional probability tables or factors. In a biological setup they could possibly be encoded through the synaptic weights of a recurrent network of spiking neurons. The solution of such optimizations problems in a probabilistic framework via sampling, as implemented in our model, provides an alternative to deterministic solutions, as traditionally implemented in neural networks (see, e.g., [54] for the case of constraint satisfaction problems). Whereas an attractor neural network converges to one (possibly approximate) solution of the problem, a stochastic network may alternate between different approximate solutions and stay the longest at those approximate solutions that provide the best fit. This might be advantageous, as given more time a stochastic network can explore more of the state space and avoid shallow local minima. Responses to ambiguous sensory stimuli [44]–[47] might be interpreted as an optimization with soft constraints. The interpretation of human thinking as sampling process solving an inference task, recently proposed in cognitive science [28], [55], [56], further emphasizes that considering neural activity as an inferential process via sampling promises to be a fruitful approach.
Our approach builds on, and extends, previous work where recurrent networks of non-spiking stochastic neurons (commonly considered in artificial neural networks) were shown to be able to carry out probabilistic inference through Gibbs sampling [36]. In [57] a first extension of this approach to a network of recurrently connected spiking neurons had been presented. The dynamics of the recurrently connected spiking neurons are described as stepwise sampling from the posterior of a temporal Restricted Boltzmann Machine (tRBM) by introducing a clever interpretation of the temporal spike code as time varying parameters of a multivariate Gaussian distribution. Drawing one sample from the posterior of a RBM is, by construction, a trivial one-step task. In contrast to our model, the model of [57] does not produce multiple samples from a fixed posterior distribution, given the fixed input, but produces exactly one sample consisting of the temporal sequence of the hidden nodes, given a temporal input sequence. Similar temporal models, sometimes called Bayesian filtering, also underlie the important contributions of [58] and [32]. In [32] every single neuron is described as hidden Markov Model (HMM) with two states. Instead of drawing samples from the instantaneous posterior distribution using stochastic spikes, [32] presents a deterministic spike generation with the intention to convey the analog probability value rather than discrete samples. The approach presented here can be interpreted as a biologically more realistic version of Gibbs sampling for a specific class of probability distributions by taking into account a spike-based communication, finite duration PSPs and refractory mechanisms. Other implementations based on different distributions (e.g., directed graphical models) and different sampling methods (e.g., reversible MCMC methods) are of course conceivable and worth exploring.
In a computer experiment (see Figure 4, we used our proposed network to model aspects of biological vision as probabilistic inference along the lines of argumentation put forward in [16]–[18]. Our model was chosen to be quite simplistic, just to demonstrate that a number of experimental data on the dynamics of spontaneous activity [51], [59], [60] and binocular rivalry [44]–[47] can in principle be captured by this approach. The main point of the modelling study is to show that rather realistic neural dynamics can support computational functions rigorously formalized as inference via sampling.
We have also presented a model of spiking dynamics in continuous time that performs sampling from a given probability distribution. Although computer simulations of biological networks of neurons often actually use discrete time, it is desirable to also have a sound approach for understanding and describing the network sampling dynamics in continuous time, as the latter is arguable a natural framework for describing temporal processes in biology. Furthermore comparison to many existing continuous time neuron and network models of neurons is facilitated.
We have made various simplifying assumption regarding neural processes, e.g., simple symbolic postsynaptic potentials in the form of step-functions (reminiscent of plateau potentials caused by dendritic NMDA spikes [61]). More accurate models for neurons have to integrate a multitude of time constants that represent different temporal processes on the physical, molecular, and genetic level. Hence the open problem arises, to which extent this multitude of time constants and other complex dynamics can be integrated into theoretical models of neural sampling. We have gone one first step in this direction by showing that in computer simulations the two temporal processes that we have considered (refractory processes and postsynaptic potentials) can approximately be decoupled. Furthermore, we have presented simulation results suggesting that more realistic alpha-shaped, additive EPSPs are compatible with the functionality of the proposed network model.
Finally, we want to point out that the prospect of using networks of spiking neurons for probabilistic inference via sampling suggests new applications for energy-efficient spike-based and massively parallel electronic hardware that is currently under development [62], [63].
Methods
We first provide details and proofs for the neural sampling models, followed by details for the computer simulations. Then we investigate typical firing statistics of individual neurons during neural sampling and examine the approximation quality of neural sampling with different neuron and synapse models.
Mathematical details
Notation
To keep the derivations in a compact form, we introduce the following notations. We define the function  of
of  to be
to be  if
if  and
and  otherwise. Analogously we define
otherwise. Analogously we define  . Let
. Let  denote Kronecker’s Delta, i.e.,
denote Kronecker’s Delta, i.e.,  if
if  and
and  whereas
whereas  denotes Dirac’s Delta, i.e.,
denotes Dirac’s Delta, i.e.,  . Furthermore
. Furthermore  is the indicator function of the set
is the indicator function of the set  , i.e.,
, i.e.,  if
if  and
and 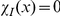 if
if  .
.
Details to neural sampling with absolute refractory period in discrete time
The following Lemmata 1 – 3 provide a proof of Theorem 1. For completeness we begin this paragraph with a recapitulation of the definitions stated in Results. We then identify some central properties of the joint probability distribution  and proof that the proposed network samples from the desired invariant distribution.
and proof that the proposed network samples from the desired invariant distribution.
For a given distribution  over the binary variables
over the binary variables 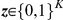 with
with  , the joint distribution over
, the joint distribution over 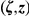 with
with  is defined in the following way (see equation 7):
is defined in the following way (see equation 7):
 |
The assumption  for all
for all  is required to show the irreducibility of the Markov chain, a prerequisite to ensure the uniqueness of the invariant distribution of the MCMC dynamics. Furthermore, for the given distribution
is required to show the irreducibility of the Markov chain, a prerequisite to ensure the uniqueness of the invariant distribution of the MCMC dynamics. Furthermore, for the given distribution  we define the functions
we define the functions  for
for  which map
which map  :
:
Instead of  we simply write
we simply write  in the following.
in the following.
Lemma 1. The distribution
 has conditional distributions of the following form:
has conditional distributions of the following form:
 |
These results can also be written more compactly in the following form:
 and
and  .
.
Proof. Here we use the fact that the logistic function  is the inverse of the logit function, i.e.,
is the inverse of the logit function, i.e.,  .
.
 |
This also shows that  is independent from
is independent from  given
given  , i.e.,
, i.e.,  . Now we show the second relation using Bayes’ rule:
. Now we show the second relation using Bayes’ rule:
 |
In order to facilitate the verification of the next two Lemmata, we first restate the definition of the operators  in a more concise way:
in a more concise way:
 |
where  .
.
Lemma 2. For all
 the operator
the operator
 leaves the conditional distribution
leaves the conditional distribution
 invariant.
invariant.
Proof. For sake of simplicity, denote  for
for  and
and  . We have to show
. We have to show  for
for  .
.
First we show  using
using  and
and  (which results from Lemma 1):
(which results from Lemma 1):
 |
Here we used the definition of the logistic function  and
and  .
.
Now we show  :
:
 |
Here we used  .
.
It is trivial to show  for
for  as
as  . Here we used the facts that
. Here we used the facts that  and
and  for
for  by definition.
by definition.
Lemma 3. For all
 the operator
the operator
 leaves the distribution
leaves the distribution
 invariant.
invariant.
Proof. We start from Lemma 2, which states that 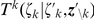 leaves the conditional distribution
leaves the conditional distribution  invariant:
invariant:
 |
Here we used the relations  and
and  as well as
as well as  which directly follow from the definitions of
which directly follow from the definitions of  and
and  .
.
Finally, we can verify that the composed operator  samples from the given distribution
samples from the given distribution  .
.
Theorem 1.
 is the unique invariant distribution of operator
is the unique invariant distribution of operator
 .
.
Proof. As all  leave
leave 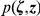 invariant, so does the concatenation
invariant, so does the concatenation  . To ensure that
. To ensure that  is the unique invariant distribution, we have to show that
is the unique invariant distribution, we have to show that  is irreducible and aperiodic.
is irreducible and aperiodic.  is aperiodic as the transition probabilities
is aperiodic as the transition probabilities  and
and  (this follows from the assumption
(this follows from the assumption  made above).
made above).
The operator  is also irreducible for the following reason. First we see that from any state
is also irreducible for the following reason. First we see that from any state  in at most
in at most  steps we can get to the zero-state
steps we can get to the zero-state  (and stay there) with non-zero probability, as
(and stay there) with non-zero probability, as  for
for  and
and  . Furthermore, it can be seen that any state
. Furthermore, it can be seen that any state  can be reached from the zero-state
can be reached from the zero-state  in at most
in at most  steps since
steps since 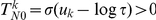 for any value of
for any value of  . Hence every final state
. Hence every final state  can be reached from every starting state
can be reached from every starting state  in at most
in at most  steps with non-vanishing probability.
steps with non-vanishing probability.
Details to neural sampling with a relative refractory period in discrete time
We augment the neuron model with a relative refractory period described by a function  . We first ensure existence of the corresponding function
. We first ensure existence of the corresponding function  . Based on these functions we then introduce the transition operator
. Based on these functions we then introduce the transition operator  of the Markov chain. This operator is shown to entail correct “local” computations.
of the Markov chain. This operator is shown to entail correct “local” computations.
Lemma 4. Let
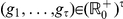 be a tuple of non-negative real numbers, with
be a tuple of non-negative real numbers, with
 and at least one element
and at least one element
 . This defines the refractory function via
. This defines the refractory function via
 . There exists a unique
. There exists a unique
 function
function
 with the following property
with the following property
 :
:
| (15) |
Furthermore, the function
 has the property:
has the property:
Proof. Let 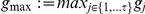 ; we know that
; we know that  . We define the function
. We define the function  :
:
 |
We can see that  is a positive
is a positive  function on
function on  . Furthermore,
. Furthermore,  is defined as a sum of functions of the form
is defined as a sum of functions of the form  . Each factor
. Each factor  is positive and strictly monotonous. Therefore,
is positive and strictly monotonous. Therefore,  is strictly monotonous on
is strictly monotonous on  with the limits:
with the limits:
 |
Hence the equation  has a unique solution for
has a unique solution for  called
called  for all
for all  . From applying the implicit function theorem to
. From applying the implicit function theorem to 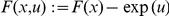 it follows that
it follows that 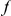 is
is  .
.
From here on, with the letter 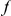 we will denote the function characterized by the above Lemma for the given tuple
we will denote the function characterized by the above Lemma for the given tuple  (which denotes the chosen refractory function).
(which denotes the chosen refractory function).
Definition 1. Define
 . The transition operator
. The transition operator
 is defined in the following way for all
is defined in the following way for all
 :
:
 |
with
 .
.
Lemma 5. For all
 the unique invariant distribution
the unique invariant distribution
 of the operator
of the operator
 fulfills
fulfills
 . This means, for a constant configuration
. This means, for a constant configuration
 , the operator
, the operator
 produces samples
produces samples
 from the correct conditional distribution
from the correct conditional distribution
 .
.
Proof. We define:
 |
where the function  is defined as:
is defined as:
 |
It is trivial to see that  has the correct marginal distribution over
has the correct marginal distribution over  :
:
 |
We now show that  is the unique invariant distribution of
is the unique invariant distribution of  . Because of the definition of
. Because of the definition of  , we only have to show that
, we only have to show that  is the unique invariant distribution of
is the unique invariant distribution of  . We denote
. We denote  and
and  , i.e., we have to show
, i.e., we have to show  .
.
It is trivial to show  for
for  , as there is only one non-vanishing element of transition operator, namely
, as there is only one non-vanishing element of transition operator, namely  :
:
 |
Here we used  for
for  and the definition of
and the definition of  .
.
Now we show  starting from equation (15) and additionally using the relations
starting from equation (15) and additionally using the relations  and
and  as well as the definition of
as well as the definition of  . We define for the sake of simplicity
. We define for the sake of simplicity  :
:
 |
We finally show  , using the definition of
, using the definition of  :
:
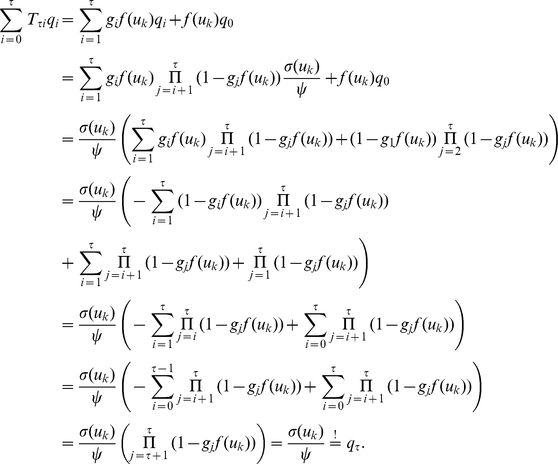 |
The argument that the transition operator  is aperiodic and irreducible is similar to the one presented in Lemma 1.
is aperiodic and irreducible is similar to the one presented in Lemma 1.
Details to neural sampling with an absolute refractory period in continuous time
In contrast to the discrete time model we define the state space of  to be
to be  for
for  , i.e., as the union of the positive real numbers and a small interval
, i.e., as the union of the positive real numbers and a small interval  . We will define the sampling operator in such a way that after neuron
. We will define the sampling operator in such a way that after neuron  was refractory for exactly its refractory period
was refractory for exactly its refractory period  , its refractory variable
, its refractory variable  is uniformly placed in the small interval
is uniformly placed in the small interval  , which represents now the resting state and replaces
, which represents now the resting state and replaces  . This avoids point measures (Dirac’s Delta) on the value
. This avoids point measures (Dirac’s Delta) on the value  . This system is still exactly equivalent to the system discussed in the main paper, as all spike-transition probabilities of
. This system is still exactly equivalent to the system discussed in the main paper, as all spike-transition probabilities of  for
for  are constant. Hence, it does not matter which values
are constant. Hence, it does not matter which values  assumes with respect to the spike mechanism during its non-refractory period as long as
assumes with respect to the spike mechanism during its non-refractory period as long as  .
.
Definition 2. For a given distribution  over the binary variables
over the binary variables  with
with  , we define a joint distribution over
, we define a joint distribution over  with
with  in the following way:
in the following way:
 |
where
 is the refractory resting state interval. In accordance with this definition we can also write
is the refractory resting state interval. In accordance with this definition we can also write
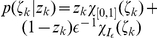 .
.
Lemma 6. The distribution
 has the following marginal distribution:
has the following marginal distribution:
 |
where  .
.
Definition 3. For
 and
and
 the operator
the operator
 is defined in the following way for a function
is defined in the following way for a function
 :
:
 |
where the functional
 is defined as the one-sided limit from above at 0:
is defined as the one-sided limit from above at 0:
The operator
 is defined in the following way for a probability distribution
is defined in the following way for a probability distribution
 on
on
 :
:
where
 denotes the function
denotes the function
 of
of
 where
where
 is held constant and
is held constant and
 .
.
The transition operator  defines the following Fokker-Planck equation for a time-dependent distribution
defines the following Fokker-Planck equation for a time-dependent distribution  :
:
The jump and drift functions  and
and  associated to the operator
associated to the operator  are given by:
are given by:
 |
Lemma 7. The operator
 leaves the conditional distribution
leaves the conditional distribution
 invariant with
invariant with
 , i.e.:
, i.e.:
Proof. This is easy to proof using calculus and the relations  and
and  .
.
Lemma 8.
 is an invariant distribution of
is an invariant distribution of
 , i.e., it is a solution to the invariant Fokker-Planck equation:
, i.e., it is a solution to the invariant Fokker-Planck equation:
Proof. We observe that  for a constant
for a constant  (which is not a function of
(which is not a function of  ). Hence:
). Hence:
 |
The Lemma follows then from the definition of  .
.
Details to neural sampling with a relative refractory period in continuous time
As already assumed in the case of the absolute refractory sampler in continuous time, we define the state space of  to be
to be  for
for  .
.
Lemma 9. Let
 be a continuous, non-negative function
be a continuous, non-negative function
 with
with
 for
for
 . There exists a unique
. There exists a unique
 function
function
 with the following property
with the following property
 :
:
| (16) |
Proof. We define the function  in the following way:
in the following way:
where  . From
. From  we can follow that
we can follow that  is non-negative.
is non-negative.  is differentiable with the derivative:
is differentiable with the derivative:
 |
Hence  is strictly monotonously increasing. Furthermore, the following relations hold:
is strictly monotonously increasing. Furthermore, the following relations hold:
Therefore the equation:
has exactly one solution  with
with  in
in  . From applying the implicit function theorem to
. From applying the implicit function theorem to  it follows that
it follows that 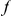 is
is  .
.
Definition 4. For all
 and
and
 the operator
the operator
 is defined in the following way for a function
is defined in the following way for a function
 :
:
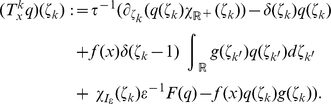 |
The transition operator  defines the following Fokker-Planck equation for a time-dependent distribution
defines the following Fokker-Planck equation for a time-dependent distribution  :
:
The jump and drift functions  and
and  associated to the operator
associated to the operator  are given by:
are given by:
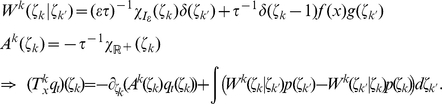 |
Lemma 10. For all
 the invariant distribution
the invariant distribution
 of the operator
of the operator
 fulfills
fulfills
 .
.
Proof. We define the distribution  as:
as:
where  . By applying the operator
. By applying the operator  to
to  one can verify that
one can verify that  holds using the definition of
holds using the definition of  given in (16). Furthermore we can compute the ratio:
given in (16). Furthermore we can compute the ratio:
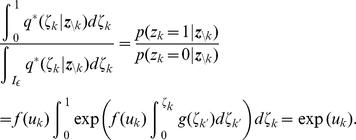 |
Details to the computer simulations
The simulation results shown in Figure 2, Figure 3 and Figure 4 used the biologically more realistic neuron model with the relative refractory mechanism. During all experiments the first second of simulated time was discarded as burn-in time. The full list of parameters defining the experimental setup is given in Table 1. All occurring joint probability distributions are Boltzmann distributions of the form given in equation (5). Example Python [64] scripts for neural sampling from Boltzmann distributions are available on request and will be provided on our webpage. The example code comprises networks with both absolute and relative refractory mechanism. It requires standard Python packages only and is readily executable.
Table 1. List of parameters of the computer simulations.
| Description | Variable | Value | Figure | Comment |
| Simulation Time | ||||
| Simulation step size |

|

|
2–7 | interpretation of an MCMC step |
| Burn-in time |

|
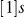
|
2–7 | before recording spikes |
| Simulation time |

|

|
2 | |

|
3,5–7 | |||

|
4 |
 for Figure 3C for Figure 3C
|
||
| Network | ||||
| Number of neurons |

|
3 | 2 | unconnected |
| 40 | 3,5,6 | randomly connected | ||
| 217 | 4 | |||

|
7 |
 networks networks |
||
| Connection radius |

|
2 | ||

|
3,5–7 | |||

|
4 | |||
| Recurrent weights |

|

|
3,5–7 | from Gaussian distribution |
| Falling edge |

|
[20] ms | 6,7 | for realistic PSP shapes |
| Rising edge |

|
[3] ms | 6,7 | |
| Scaling factor |

|
20/17 | 6,7 | |
| Neuron Model | ||||
| Number recovery steps |

|

|
2–7 | PSP duration 
|
| Refractory function |

|

|
2
|
normalized to  , , |

|
2–7 |

|
||

|
2 ,7 ,7 |
|||
| Excitability |

|
 or or 
|
2 | defines membrane potential 
|

|
3,5–7 | from Gaussian distribution | ||

|
4 | initial value | ||
| Tuning Function, Training and Inference ( Figure 4 ) | ||||
| Peakedness |

|

|
4 | measured: 
|
| Base sensitivity |

|

|
4 | measured: 
|
| Sensitivity contrast |

|

|
4 | measured: 
|
| Training samples |

|

|
4 | |
| Decorrelation steps |

|
4 | for contrastive divergence | |
| Learning rate |

|

|
4 | |
| Number of neurons clamped on/off |

|
4 | ||
Details to Figure 2: Neuron model with relative refractory mechanism
The three refractory functions  of panel (B) as well as all other simulation parameters are listed in Table 1. Panel (C) shows the corresponding functions
of panel (B) as well as all other simulation parameters are listed in Table 1. Panel (C) shows the corresponding functions  , which result from numerically solving equation (11). The spike patterns in panel (D) show the response of the neurons when the membrane potential is low (
, which result from numerically solving equation (11). The spike patterns in panel (D) show the response of the neurons when the membrane potential is low ( for
for  ) or high (
) or high ( for
for  ). These membrane potentials encode
). These membrane potentials encode  and
and  , respectively according to (3) and (4). The binary state
, respectively according to (3) and (4). The binary state  is indicated by gray shaded areas of duration
is indicated by gray shaded areas of duration  after each spike.
after each spike.
Details to Figure 3: Sampling from a Boltzmann distribution by spiking neurons with relative refractory mechanism
We examined the spike response of a network of  randomly connected neurons which sampled from a Boltzmann distribution. The excitabilities
randomly connected neurons which sampled from a Boltzmann distribution. The excitabilities  as well as the synaptic weights
as well as the synaptic weights  were drawn from Gaussian distributions (with diagonal elements
were drawn from Gaussian distributions (with diagonal elements  ). For the full list of parameters please refer to Table 1. One second of the arising spike pattern is shown in panel (A). The average firing rate of the network was
). For the full list of parameters please refer to Table 1. One second of the arising spike pattern is shown in panel (A). The average firing rate of the network was  . To highlight the internal dynamics of the neuron model, the values of the refractory function
. To highlight the internal dynamics of the neuron model, the values of the refractory function  , the membrane potential
, the membrane potential  and the instantaneous firing rate
and the instantaneous firing rate  of neuron
of neuron  (indicated with red spikes) are shown in panel (B). Here, the instantaneous firing rate
(indicated with red spikes) are shown in panel (B). Here, the instantaneous firing rate  is defined for the discrete time Markov chain as
is defined for the discrete time Markov chain as
| (17) |
As stated before, the neuron model with relative refractory mechanism  does not entail the correct overall invariant distribution
does not entail the correct overall invariant distribution  . To estimate the impact of this approximation on the joint network dynamics, we compared the distribution
. To estimate the impact of this approximation on the joint network dynamics, we compared the distribution  over five neurons (indicated by gray background in A) in the spiking network with the correct distribution obtained from Gibbs sampling. The probabilities were estimated from
over five neurons (indicated by gray background in A) in the spiking network with the correct distribution obtained from Gibbs sampling. The probabilities were estimated from  samples. A more quantitative analysis of the approximation quality of neural sampling with a relative refractory mechanism is provided below.
samples. A more quantitative analysis of the approximation quality of neural sampling with a relative refractory mechanism is provided below.
Details to Figure 4: Modeling perceptual multistability as probabilistic inference with neural sampling
We demonstrate probabilistic inference and learning in a network of orientation selective neurons. As a simple model we consider a network of  neurons on a hexagonal grid as shown in panel (F). Any two neurons with distance
neurons on a hexagonal grid as shown in panel (F). Any two neurons with distance  were synaptically connected (neighboring units had distance
were synaptically connected (neighboring units had distance  ). For the remaining parameters of the network and neuron model please refer to Table 1. Each neuron featured a
). For the remaining parameters of the network and neuron model please refer to Table 1. Each neuron featured a  -periodic tuning curve as depicted in panel (B):
-periodic tuning curve as depicted in panel (B):
| (18) |
with base sensitivity  , contrast
, contrast  , peakedness
, peakedness  and preferred orientation
and preferred orientation  . The preferred orientations
. The preferred orientations  of the neurons were chosen to cover the entire interval
of the neurons were chosen to cover the entire interval  of possible orientations with equal spacing and were randomly assigned to the neurons.
of possible orientations with equal spacing and were randomly assigned to the neurons.
For simplicity we did not incorporate the input dynamics in our probabilistic model, but rather trained the network directly like a fully visible Boltzmann machine. We used for this purpose a standard Boltzmann machine learning rule known as contrastive divergence [41], [65]. This learning rule requires posterior samples  , i.e., network states under the influence of the present input, and approximate prior samples
, i.e., network states under the influence of the present input, and approximate prior samples  , which reflect the probability distribution of the network in the absence of stimuli. The update rules for synaptic weights and neuronal excitabilities read:
, which reflect the probability distribution of the network in the absence of stimuli. The update rules for synaptic weights and neuronal excitabilities read:
 |
(19) |
While more elaborate policies can speed up convergence, we simply used a global learning rate  which was constant in time. The values of
which was constant in time. The values of  and
and  were initialized at
were initialized at 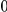 . We generated binary training patterns in the following way:
. We generated binary training patterns in the following way:
A global orientation
 was drawn uniformly from
was drawn uniformly from  ,
,each neuron was independently set to be active with probability
 ,
,the resulting network state
 was taken as posterior sample.
was taken as posterior sample.
To obtain an approximate prior sample  we let the network run for a short time freely starting from
we let the network run for a short time freely starting from  . The variables
. The variables  were also assumed to be observed with
were also assumed to be observed with  iid. uniformly in
iid. uniformly in  if
if  and
and  otherwise. After evolving freely for
otherwise. After evolving freely for  time steps, the resulting network state
time steps, the resulting network state  was taken as approximate prior sample and
was taken as approximate prior sample and  and
and  were updated according to (19). This process was repeated
were updated according to (19). This process was repeated  times. As a result, neurons with similar preferred orientations featured excitatory synaptic connections (
times. As a result, neurons with similar preferred orientations featured excitatory synaptic connections ( = mean
= mean  standard deviation of weight distribution), those with dissimilar orientations maintained inhibitory synapses (
standard deviation of weight distribution), those with dissimilar orientations maintained inhibitory synapses ( ). Here, preferred orientations
). Here, preferred orientations  and
and  are defined as similar if
are defined as similar if  , otherwise they are dissimilar. Neuronal biases converged to
, otherwise they are dissimilar. Neuronal biases converged to 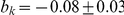 .
.
We illustrate the learned prior distribution  of the network through sampled states when the network evolved freely. As seen in panel (D), the population vector – a 2-dimensional projection of the high dimensional network state – typically reflected an arbitrary, yet coherent, orientation (for the definition of the population vector see below). Each dot represents a sampled network state
of the network through sampled states when the network evolved freely. As seen in panel (D), the population vector – a 2-dimensional projection of the high dimensional network state – typically reflected an arbitrary, yet coherent, orientation (for the definition of the population vector see below). Each dot represents a sampled network state  .
.
To apply an ambiguous cue, we clamped  out of
out of  neurons: Two units with
neurons: Two units with  and two with
and two with  were set active, two units with
were set active, two units with  and two with
and two with  were set inactive. This led to a bimodal posterior distribution as shown in panel (E). The sampling network represented this distribution by encoding either global perception separately: The trace of network states
were set inactive. This led to a bimodal posterior distribution as shown in panel (E). The sampling network represented this distribution by encoding either global perception separately: The trace of network states  roamed in one mode for multiple steps before quickly crossing the state space towards the opposite percept.
roamed in one mode for multiple steps before quickly crossing the state space towards the opposite percept.
We define the population vector  of a network state
of a network state  as a function of the preferred orientations of all active units:
as a function of the preferred orientations of all active units:
| (20) |
This definition of  is not based on the preferred orientations
is not based on the preferred orientations  which are used for generating external input to the network from a given stimulus with orientation
which are used for generating external input to the network from a given stimulus with orientation  . It is rather based on the preferred orientations
. It is rather based on the preferred orientations  measured from the network response. We used population vector decoding based on the measured values
measured from the network response. We used population vector decoding based on the measured values  , as they are conceptually closer to experimentally measurable preferred orientations, and this decoding hence does not require knowledge of the (unobservable)
, as they are conceptually closer to experimentally measurable preferred orientations, and this decoding hence does not require knowledge of the (unobservable)  . For every neuron
. For every neuron  the preferred orientation
the preferred orientation  was measured in the following way. We estimated a tuning curve
was measured in the following way. We estimated a tuning curve  by a van-Mises fit (of the form (18)) to data from stimulation trials in which neuron
by a van-Mises fit (of the form (18)) to data from stimulation trials in which neuron  was not clamped, i.e., where
was not clamped, i.e., where  was only stimulated by recurrent input (feedforward input was modeled by clamping 8 out of 217 neurons as a function of stimulus orientation
was only stimulated by recurrent input (feedforward input was modeled by clamping 8 out of 217 neurons as a function of stimulus orientation  as before). Due to the structured recurrent weights, the experimentally measured tuning curves
as before). Due to the structured recurrent weights, the experimentally measured tuning curves  were found to be reasonably close to the tuning curves
were found to be reasonably close to the tuning curves  used for external stimulation.
used for external stimulation.  was set to the preferred orientation of
was set to the preferred orientation of  (localization parameter of the van-Mises fit). The measured values
(localization parameter of the van-Mises fit). The measured values  turned out to be consistent with the preferred orientations
turned out to be consistent with the preferred orientations  (
( averaged over all
averaged over all  neurons). The mean and standard deviation of the remaining parameter values
neurons). The mean and standard deviation of the remaining parameter values  ,
,  and
and  of the fitted tuning curves
of the fitted tuning curves  are listed in Table 1 next to the ones used for stimulation.
are listed in Table 1 next to the ones used for stimulation.
The population vector  was defined in (20) with the argument
was defined in (20) with the argument  (instead of
(instead of  ) as orthogonal orientations should cancel each other and neighborhood relations should be respected. For example neurons with
) as orthogonal orientations should cancel each other and neighborhood relations should be respected. For example neurons with  and
and  contribute similarly to the population vector for small
contribute similarly to the population vector for small  . But counter to intuition the population vector of a state
. But counter to intuition the population vector of a state  with dominant orientation
with dominant orientation  will point into direction
will point into direction  . For visualization in panel (D) and (E) we therefore rescaled the population vector: If
. For visualization in panel (D) and (E) we therefore rescaled the population vector: If  in polar coordinates, then the dot is located at
in polar coordinates, then the dot is located at  in accord with intuition. The black semicircles equal
in accord with intuition. The black semicircles equal  .
.
The population vector 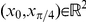 was also used for measuring the dominance durations shown in panel (C). To this
was also used for measuring the dominance durations shown in panel (C). To this  was divided into
was divided into  areas: (a)
areas: (a)  , (b)
, (b)  , (c)
, (c)  . We detected a perceptual switch when the network state entered area (a) or (c) while the previous perception was (c) or (a), respectively.
. We detected a perceptual switch when the network state entered area (a) or (c) while the previous perception was (c) or (a), respectively.
In panel (F) neurons  with
with  are plotted with their preferred orientation color code, inactive neurons are displayed in white. Cells marked by a dot (
are plotted with their preferred orientation color code, inactive neurons are displayed in white. Cells marked by a dot ( ) were part of the observed variables
) were part of the observed variables  . The three network states correspond to
. The three network states correspond to  with
with  ,
,  and
and  in the spike pattern in panel (G). The spike pattern shows the response of the freely evolving units around a perceptual switch during sampling from the posterior distribution. The corresponding trace of the population vector is drawn as black line in panel (E). The width of the light-gray shaded areas in the spike pattern equals the PSP duration
in the spike pattern in panel (G). The spike pattern shows the response of the freely evolving units around a perceptual switch during sampling from the posterior distribution. The corresponding trace of the population vector is drawn as black line in panel (E). The width of the light-gray shaded areas in the spike pattern equals the PSP duration 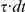 , i.e., neurons that spiked in these intervals were active in the corresponding state in (F).
, i.e., neurons that spiked in these intervals were active in the corresponding state in (F).
Firing statistics of neural sampling networks
In previous sections it was shown that a spiking neural network can draw samples from a given joint distribution which is in a well-defined class of probability distributions (see the neural computability condition (4)). Here, we examine some statistics of individual neurons in a sampling network which are commonly used to analyze experimental data from recordings. The spike trains and membrane potential data are taken from the simulation presented in Figure 3.
Figure 5A,B exemplarily show the distribution of the membrane potential  and the interspike interval (ISI) histogram of a single neuron, namely neuron
and the interspike interval (ISI) histogram of a single neuron, namely neuron  which was already considered in Figure 3B. The responses of other neurons yield qualitatively similar statistics. The bell-shaped distribution of the membrane potential is commonly observed in neurons embedded in an active network [66]. The ISI histogram reflects the reduced spiking probability immediately after an action potential due the refractory mechanism. Interspike intervals larger than the refractory time constant
which was already considered in Figure 3B. The responses of other neurons yield qualitatively similar statistics. The bell-shaped distribution of the membrane potential is commonly observed in neurons embedded in an active network [66]. The ISI histogram reflects the reduced spiking probability immediately after an action potential due the refractory mechanism. Interspike intervals larger than the refractory time constant  roughly follow an exponential distribution. Similar ISI distributions were observed during in-vivo recordings in awake, behaving monkeys [67].
roughly follow an exponential distribution. Similar ISI distributions were observed during in-vivo recordings in awake, behaving monkeys [67].
Figure 5C shows a scatterplot of the coefficient of variation (CV) of the ISIs versus the average ISI for each neuron in the network. The neurons exhibited a variety of average firing rates between  and
and  . Most of the neurons responded in a highly irregular manner with a CV
. Most of the neurons responded in a highly irregular manner with a CV  . Neurons with high firing rates had a slightly lower CV due to the increased influence of the refractory mechanism The dashed line marks the CV of a Poisson process, i.e., a memoryless spiking behavior. The CV of neuron
. Neurons with high firing rates had a slightly lower CV due to the increased influence of the refractory mechanism The dashed line marks the CV of a Poisson process, i.e., a memoryless spiking behavior. The CV of neuron  is marked by a cross. The structure of this plot resembles, e.g., data from recordings in behaving macaque monkeys [68] (but note the lower average firing rate).
is marked by a cross. The structure of this plot resembles, e.g., data from recordings in behaving macaque monkeys [68] (but note the lower average firing rate).
Approximation quality of neural sampling with different neuron and synapse models
The theory of the neuron model with absolute refractory mechanism guarantees sampling form the correct distribution. In contrast, the theory for the neuron model with a relative refractory mechanism only shows that the sampling process is “locally correct”, i.e., that it would yield correct conditional distributions 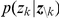 for each individual neuron if the state of the remaining network
for each individual neuron if the state of the remaining network  stayed constant. Therefore, the stationary distribution of the sampling process with relative refractory mechanism only provides an approximation to the target distribution. In the following we examine the approximation quality and robustness of sampling networks with different refractory mechanisms for target Boltzmann distributions with parameters randomly drawn from different distributions. Furthermore, we investigate the effect of additive PSP shapes with more realistic time courses.
stayed constant. Therefore, the stationary distribution of the sampling process with relative refractory mechanism only provides an approximation to the target distribution. In the following we examine the approximation quality and robustness of sampling networks with different refractory mechanisms for target Boltzmann distributions with parameters randomly drawn from different distributions. Furthermore, we investigate the effect of additive PSP shapes with more realistic time courses.
We generated target Boltzmann distributions with randomly drawn weights  and biases (excitabilities)
and biases (excitabilities)  and computed the similarity between these reference distributions and the corresponding neural sampling approximations. The setup of these simulations is the same as for the simulation presented in Figure 3. As we aimed to compare the distribution
and computed the similarity between these reference distributions and the corresponding neural sampling approximations. The setup of these simulations is the same as for the simulation presented in Figure 3. As we aimed to compare the distribution  sampled by the network with the exact Boltzmann distribution
sampled by the network with the exact Boltzmann distribution  , we reduced the number of neurons per network to
, we reduced the number of neurons per network to 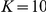 . This resulted in a state space of
. This resulted in a state space of  possible network states
possible network states  for which the normalization constant for the target Boltzmann distribution could be computed exactly. The weight matrix
for which the normalization constant for the target Boltzmann distribution could be computed exactly. The weight matrix  was constraint to be symmetric with vanishing diagonal. Off-diagonal elements were drawn from zero-mean normal distributions with three different standard deviations
was constraint to be symmetric with vanishing diagonal. Off-diagonal elements were drawn from zero-mean normal distributions with three different standard deviations  ,
,  and
and  , whereas the
, whereas the  were sampled from the same distribution as in Figure 3. For every value of the hyperparameter
were sampled from the same distribution as in Figure 3. For every value of the hyperparameter  we generated 100 random distributions. For Boltzmann distributions with small weights (
we generated 100 random distributions. For Boltzmann distributions with small weights ( ), the RVs are nearly independent, whereas distributions with intermediate weights (
), the RVs are nearly independent, whereas distributions with intermediate weights ( ) show substantial statistical dependencies between RVs. For very large weights (
) show substantial statistical dependencies between RVs. For very large weights ( ), the probability mass of the distributions is concentrated on very few states (usually 90% on less than 10 out of the
), the probability mass of the distributions is concentrated on very few states (usually 90% on less than 10 out of the  states). Hence, the range of the hyperparameter
states). Hence, the range of the hyperparameter 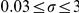 considered here covers a range a very different distributions.
considered here covers a range a very different distributions.
The approximation quality of the sampled distribution was measured in terms of the Kullback-Leibler divergence between the target distribution  and the neural approximation
and the neural approximation 
| (21) |
We estimated  from
from  samples for each simulation trial using a Laplace estimator, i.e., we added a priori
samples for each simulation trial using a Laplace estimator, i.e., we added a priori  to the number of occurrences of each state
to the number of occurrences of each state  .
.
Table 2 shows the means and the standard deviations of the Kullback-Leibler divergences between the target Boltzmann distributions and the estimated approximations stemming from neural sampling networks with three different neuron and synapse models: the exact model with absolute refractory mechanism and two models with different relative refractory mechanisms shown in the bottom and middle row in Figure 2B. Additionally, as a reference, we provide the (analytically calculated) Kullback-Leibler divergences for fully factorized distributions, i.e.,  with correct marginals
with correct marginals  but independent variables
but independent variables  for
for  .
.
Table 2. Approximation quality of networks with different refractory mechanisms.

|
Absolute refractory | Rel. late recovery | Rel. moderate recovery | Prod. of marginals |
| 0.03 |

|

|

|

|
| 0.3 |

|
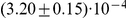
|

|

|
| 3.0 |

|

|

|

|
Mean and standard deviation of the Kullback-Leibler divergence  between reference Boltzmann distributions
between reference Boltzmann distributions  and neural sampling approximations
and neural sampling approximations 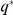 for three different neuron models (corresponding to columns) and three different values for the reference distribution hyperparameter
for three different neuron models (corresponding to columns) and three different values for the reference distribution hyperparameter  (corresponding to rows). The parameter
(corresponding to rows). The parameter  controls the standard deviation of the weights of the reference distributions
controls the standard deviation of the weights of the reference distributions  . In case of very strong synaptic interactions (leading to sharply peaked distributions,
. In case of very strong synaptic interactions (leading to sharply peaked distributions,  ) the approximation quality of the spiking network degrades, if the neurons feature a relative refractory mechanism. The data was computed from 100 randomly generated Boltzmann distributions and their neural approximations for each value of
) the approximation quality of the spiking network degrades, if the neurons feature a relative refractory mechanism. The data was computed from 100 randomly generated Boltzmann distributions and their neural approximations for each value of  .
.
The absolute refractory model provides the best results as we expected due to the theoretical guarantee to sample from the correct distribution (the non-zero Kullback-Leibler divergence is caused by the estimation from a finite number of samples). The models with relative refractory mechanism provide faithful approximations for all values of the hyperparameter  considered here. These relative refractory models are characterized by the theory to be “locally correct” and turn out to be much more accurate approximations than fully factorized distributions if substantial statistical dependencies between the RVs are present (i.e.,
considered here. These relative refractory models are characterized by the theory to be “locally correct” and turn out to be much more accurate approximations than fully factorized distributions if substantial statistical dependencies between the RVs are present (i.e.,  ,
,  ). As expected, a late recovery of the refractory function
). As expected, a late recovery of the refractory function  is beneficial for the approximation quality of the model as it is closer to an absolute refractory mechanism. Figure 6 shows the full histograms of the Kullback-Leibler divergences for the intermediate weights group (
is beneficial for the approximation quality of the model as it is closer to an absolute refractory mechanism. Figure 6 shows the full histograms of the Kullback-Leibler divergences for the intermediate weights group ( ). Systematic deviations due to the relative refractory mechanism are on the same order as the effect of estimating from finite samples (as can be seen, e.g., from a comparison with the absolute refractory model which has 0 systematic error). For completeness, we mention that the divergences of the fully factorized distributions of
). Systematic deviations due to the relative refractory mechanism are on the same order as the effect of estimating from finite samples (as can be seen, e.g., from a comparison with the absolute refractory model which has 0 systematic error). For completeness, we mention that the divergences of the fully factorized distributions of  out of the
out of the  networks with
networks with  are not shown in the plot.
are not shown in the plot.
Figure 6. Comparison of neural sampling with different neuron and synapse models.
The figure shows a histogram of the Kullback-Leibler divergence between  different Boltzmann distributions over K = 10 variables (with parameters randomly drawn, see setup of Figure 3) and approximations stemming from different neural sampling networks. Networks with absolute refractory mechanism provide the best approximation (as expected from theoretical guarantees). Networks consisting of neurons with relative refractory mechanisms, with only “locally” correct sampling, also provide a close fit to the true distribution (see inset) compared to a fully factorized approximation (assuming correct marginals and independent variables). Furthermore, it can be seen that sampling networks with more realistic, alpha-shaped, additive PSPs still fit the true distribution reasonably well.
different Boltzmann distributions over K = 10 variables (with parameters randomly drawn, see setup of Figure 3) and approximations stemming from different neural sampling networks. Networks with absolute refractory mechanism provide the best approximation (as expected from theoretical guarantees). Networks consisting of neurons with relative refractory mechanisms, with only “locally” correct sampling, also provide a close fit to the true distribution (see inset) compared to a fully factorized approximation (assuming correct marginals and independent variables). Furthermore, it can be seen that sampling networks with more realistic, alpha-shaped, additive PSPs still fit the true distribution reasonably well.
The theorems presented in this article assumed renewed (i.e., non-additive), rectangular PSPs. In the following we examine the effect of additive PSPs with more realistic time courses. We define additive, alpha-shaped PSPs in the following way. The influence  of each presynaptic neuron
of each presynaptic neuron  on the postsynaptic membrane potential
on the postsynaptic membrane potential  is modeled by convolving the input spikes with a kernel
is modeled by convolving the input spikes with a kernel  :
:
| (22) |
where  for
for  and
and  for
for 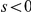 , and
, and  for
for  are the spike times of the presynaptic neuron
are the spike times of the presynaptic neuron 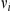 . The time constant governing the rising edge of the PSPs was set to
. The time constant governing the rising edge of the PSPs was set to  . The time constant controlling the falling edge was chosen equal to the duration of rectangular PSPs,
. The time constant controlling the falling edge was chosen equal to the duration of rectangular PSPs,  . The scaling parameter
. The scaling parameter  was set such that the time integral over a single PSP matches the time integral over the theoretically optimal rectangular PSP, i.e.,
was set such that the time integral over a single PSP matches the time integral over the theoretically optimal rectangular PSP, i.e.,  . These parameters display a simple and reasonable choice for the purpose of this study (an optimization of
. These parameters display a simple and reasonable choice for the purpose of this study (an optimization of  ,
,  and
and  is likely to yield an improved approximation quality). Figure 7A shows the resulting shape of the non-rectangular PSP. Furthermore the time course of the function
is likely to yield an improved approximation quality). Figure 7A shows the resulting shape of the non-rectangular PSP. Furthermore the time course of the function  caused by a single spike of neuron
caused by a single spike of neuron  is shown in order to illustrate that the time constants of
is shown in order to illustrate that the time constants of  and of a PSP are closely related due to the assumption
and of a PSP are closely related due to the assumption  made above. Preliminary and non-exhaustive simulations seem to suggest that the choice
made above. Preliminary and non-exhaustive simulations seem to suggest that the choice  yields better approximation quality than setting
yields better approximation quality than setting  or
or  ; however it is very well possible that a mismatch between
; however it is very well possible that a mismatch between  and
and  can be compensated for by adapting other parameters, e.g., the PSP magnitude or a specific choice of the refractory function
can be compensated for by adapting other parameters, e.g., the PSP magnitude or a specific choice of the refractory function  . Figure 7B shows the results of an experiment, similar to the one presented in Figure 3C , with additive, alpha-shaped PSPs and relative refractory mechanism. While differences to Gibbs sampling results are visible, the spiking network still captures dependencies between the binary random variables quite well.
. Figure 7B shows the results of an experiment, similar to the one presented in Figure 3C , with additive, alpha-shaped PSPs and relative refractory mechanism. While differences to Gibbs sampling results are visible, the spiking network still captures dependencies between the binary random variables quite well.
Figure 7. Sampling from a Boltzmann distribution with more realistic PSP shapes.
(A) The upper panel shows the shape of a single PSP elicited at time  . The lower panel shows the time course of the refractory function
. The lower panel shows the time course of the refractory function  caused by a single spike of neuron
caused by a single spike of neuron  at
at  . The grey-shaded area of length
. The grey-shaded area of length  indicates the interval of neuron
indicates the interval of neuron  being active (i.e.,
being active (i.e.,  ) due to a single spike of neuron
) due to a single spike of neuron  at time
at time  . (B) Shown is the probability distribution of 5 out of 40 neurons. The plot is similar to Figure 3C, however it is generated with a sampling network that features alpha-shaped, additive PSPs. It can be seen that the network still produces a reasonable approximation to the true Boltzmann distribution (determined by Gibbs sampling).
. (B) Shown is the probability distribution of 5 out of 40 neurons. The plot is similar to Figure 3C, however it is generated with a sampling network that features alpha-shaped, additive PSPs. It can be seen that the network still produces a reasonable approximation to the true Boltzmann distribution (determined by Gibbs sampling).
For a quantitative analysis of the approximation quality, we repeated the experiment of Figure 6 with additive, alpha-shaped PSPs (shown as green bars). The Kullback-Leibler divergence 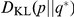 to the true distribution is clearly higher compared to the case of renewed, rectangular PSPs. Still networks with this more realistic synapse model account for dependencies between the random variables
to the true distribution is clearly higher compared to the case of renewed, rectangular PSPs. Still networks with this more realistic synapse model account for dependencies between the random variables  and yield a better approximation of
and yield a better approximation of 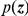 than fully factorized distributions.
than fully factorized distributions.
Acknowledgments
We would like to thank Mihai Petrovici, Robert Legenstein and Samuel Gershman for helpful discussions.
Footnotes
The authors have declared that no competing interests exist.
This paper was written under partial support by the European Union project #FP7-237955 (FACETS-ITN), project #FP7-269921 (BrainScaleS), project #FP7-216593 (SECO), project #FP7-506778 (PASCAL2) and project #FP7-243914 (BRAIN-I-NETS). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Rolls ET, Deco G. Oxford University Press; 2010. The Noisy Brain: Stochastic Dynamics as a Principle of Brain Function. [DOI] [PubMed] [Google Scholar]
- 2.Cannon R, O’Donnell C, Nolan M. Stochastic ion channel gating in dendritic neurons: morphology dependence and probabilistic synaptic activation of dendritic spikes. PLoS Comput Biol. 2010;6:e1000886. doi: 10.1371/journal.pcbi.1000886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Flight M. Synaptic transmission: On the probability of release. Nat Rev Neurosci. 2010;9:736–737. [Google Scholar]
- 4.Azouz R, Gray CM. Cellular mechanisms contributing to response variability of cortical neurons in vivo. J Neurosci. 1999;19:2209–2223. doi: 10.1523/JNEUROSCI.19-06-02209.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.GerstnerW, KistlerWM . Cambridge: Cambridge University Press; 2002. Spiking Neuron Models. [Google Scholar]
- 6.Brascamp JW, van Ee R, Noest AJ, Jacobs RHAH, van den Berg AV. The time course of binocular rivalry reveals a fundamental role of noise. J Vis. 2006;6:1244–1256. doi: 10.1167/6.11.8. [DOI] [PubMed] [Google Scholar]
- 7.Fiser J, Chiu C, Weliky M. Small modulation of ongoing cortical dynamics by sensory input during natural vision. Nature. 2004;431:573–583. doi: 10.1038/nature02907. [DOI] [PubMed] [Google Scholar]
- 8.Ringach DL. Spontaneous and driven cortical activity: implications for computation. Curr Opin Neurobiol. 2009;19:1–6. doi: 10.1016/j.conb.2009.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Geman S, Geman D. Stochastic relaxation, gibbs distributions, and the bayesian restoration of images. IEEE Trans Pattern Anal Mach Intell. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- 10.Rao RPN, Olshausen BA, Lewicki MS. MIT Press; 2002. Probabilistic Models of the Brain. [Google Scholar]
- 11.Doya K, Ishii S, Pouget A, Rao RPN. MIT-Press; 2007. Bayesian Brain: Probabilistic Approaches to Neural Coding. [Google Scholar]
- 12.Körding KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature. 2004;427:244–247. doi: 10.1038/nature02169. [DOI] [PubMed] [Google Scholar]
- 13.Kersten D, Mamassian P, Yuille A. Object perception as Bayesian inference. Annu Rev Psychol. 2004;55:271–304. doi: 10.1146/annurev.psych.55.090902.142005. [DOI] [PubMed] [Google Scholar]
- 14.Gopnik A, Tenenbaum JB. Bayesian special section: Introduction; Bayesian networks, Bayesian learning and cognitive development. Dev Sci. 2007;10:281–287. doi: 10.1111/j.1467-7687.2007.00584.x. [DOI] [PubMed] [Google Scholar]
- 15.Lee TS, Mumford D. Hierarchical Bayesian inference in the visual cortex. J Opt Soc Am A. 2003;20:1434–1448. doi: 10.1364/josaa.20.001434. [DOI] [PubMed] [Google Scholar]
- 16.Hoyer P, Hyvärinen A. Proceedings of the 16th Conference on Advances in Neural Information Processing Systems; December 2002. Vancouver, Canada: 2003. Interpreting neural response variability as Monte Carlo sampling of the posterior. NIPS 2002. [Google Scholar]
- 17.Sundareswara R, Schrater PR. Perceptual multistability predicted by search model for bayesian decisions. J Vis. 2008;8:1–19. doi: 10.1167/8.5.12. [DOI] [PubMed] [Google Scholar]
- 18.Gershman SJ, Vul E, Tenenbaum J. Proceedings of the 22nd Conference on Advances in Neural Information Processing Systems; December 2008. Vancouver, Canada: 2009. Perceptual multistability as Markov chain Monte Carlo inference. NIPS 2008. [Google Scholar]
- 19.Griffiths TL, Kemp C, Tenenbaum JB. Bayesian models of cognition. In: Sun R, editor. Handbook of Computational Cognitive Modeling. Cambridge University Press; 2008. pp. 59–100. [Google Scholar]
- 20.Yang T, Shadlen MN. Probabilistic reasoning by neurons. Nature. 2007;447:1075–1080. doi: 10.1038/nature05852. [DOI] [PubMed] [Google Scholar]
- 21.Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neurosci. 2007;30:535–574. doi: 10.1146/annurev.neuro.29.051605.113038. [DOI] [PubMed] [Google Scholar]
- 22.Sadaghiani S, Hesselmann G, Friston KJ, Kleinschmidt A. The relation of ongoing brain activity, evoked neural responses, and cognition. Front Syst Neurosci 4: Artikel. 2010;20 doi: 10.3389/fnsys.2010.00020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pearl J. Morgan Kaufmann; 1988. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. [Google Scholar]
- 24.Friston KJ, Daunizeau J, Kilner J, Kiebel SJ. Action and behavior: a free-energy formulation. Biol Cybern. 2010;102:227–260. doi: 10.1007/s00422-010-0364-z. [DOI] [PubMed] [Google Scholar]
- 25.Toussaint M. Probabilistic inference as a model of planned behavior. Künstliche Intelligenz. 2009;3:23–29. [Google Scholar]
- 26.Toussaint M, Goerick C. A Bayesian view on motor control and planning. In: Sigaud O, Peters J, editors. From motor to interaction learning in robots. Studies in Computational Intelligence. Springer; 2010. pp. 227–252. [Google Scholar]
- 27.Tenenbaum JB, Griffiths TL, Kemp C. Theory-based bayesian models of inductive learning and reasoning. Trends Cogn Sci. 2006;10:309–318. doi: 10.1016/j.tics.2006.05.009. [DOI] [PubMed] [Google Scholar]
- 28.Griffiths TL, Tenenbaum JB. Optimal predictions in everyday cognition. Psychol Sci. 2006;17:767–773. doi: 10.1111/j.1467-9280.2006.01780.x. [DOI] [PubMed] [Google Scholar]
- 29.Oaksford M, Chater N. Oxford University Press; 2007. Bayesian Rationality: The Probabilistic Approach to Human Reasoning. [DOI] [PubMed] [Google Scholar]
- 30.Rao RPN. Neural models of Bayesian belief propagation. In: Doya K, Ishii S, Pouget A, Rao RPN, editors. Bayesian Brain. Cambridge, MA: MIT-Press; 2007. pp. 239–267. [Google Scholar]
- 31.Steimer A, Maass W, Douglas R. Belief-propagation in networks of spiking neurons. Neural Comput. 2009;21:2502–2523. doi: 10.1162/neco.2009.08-08-837. [DOI] [PubMed] [Google Scholar]
- 32.Deneve S. Bayesian spiking neurons I: Inference. Neural Comput. 2008;20:91–117. doi: 10.1162/neco.2008.20.1.91. [DOI] [PubMed] [Google Scholar]
- 33.Litvak S, Ullman S. Cortical circuitry implementing graphical models. Neural Comput. 2009;21:1–47. doi: 10.1162/neco.2009.05-08-783. [DOI] [PubMed] [Google Scholar]
- 34.Sahani M, Dayan P. Doubly distributional population codes: Simultaneous representation of uncertainty and multiplicity. Neural Comput. 2003;15:2255–2279. doi: 10.1162/089976603322362356. [DOI] [PubMed] [Google Scholar]
- 35.Fiser J, Berkes P, Orbn G, Lengyel M. Statistically optimal perception and learning: from behavior to neural representations. Trends Cogn Sci. 2010;14:119–130. doi: 10.1016/j.tics.2010.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ackley DH, Hinton GE, Sejnowski TJ. A learning algorithm for boltzmann machines. Cogn Sci. 1985;9:147–169. [Google Scholar]
- 37.Hinton GE, Osindero S, Teh YW. A fast learning algorithm for deep belief nets. Neural Comput. 2006;18:1527–1554. doi: 10.1162/neco.2006.18.7.1527. [DOI] [PubMed] [Google Scholar]
- 38.Andrieu C, Freitas ND, Doucet A, Jordan MI. An introduction to MCMC for machine learning. Mach Learn. 2003;50:5–43. [Google Scholar]
- 39.Grimmett GR, Stirzaker DR. Oxford University Press, 3rd edition; 2001. Probability and Random Processes. [Google Scholar]
- 40.Nessler B, Pfeiffer M, MaassW . Proceedings of the 21th Conference on Advances in Neural Information Processing Systems; December 2008. Vancouver, Canada: 2009. Hebbian learning of Bayes optimal decisions. NIPS 2008. [Google Scholar]
- 41.Hinton GE. Learning to represent visual input. Philos Trans R Soc Lond B Biol Sci. 2010;365:177–184. doi: 10.1098/rstb.2009.0200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pillow JW, Shlens J, Paninski L, Sher A, Litke AM, et al. Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature. 2008;454:995–999. doi: 10.1038/nature07140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gardiner C. 3rd ed. Springer; 2004. Handbook of Stochastic Methods. [Google Scholar]
- 44.Leopold DA, Wilke M, Maier A, Logothetis NK. Stable perception of visually ambiguous patterns. Nat Neurosci. 2002;5:605–609. doi: 10.1038/nn0602-851. [DOI] [PubMed] [Google Scholar]
- 45.Blake R, Logothetis NK. Visual competition. Nat Rev Neurosci. 2002;3:13–21. doi: 10.1038/nrn701. [DOI] [PubMed] [Google Scholar]
- 46.Alais D, Blake R. MIT Press; 2005. Binocular Rivalry. [Google Scholar]
- 47.Bartels A, Logothetis NK. Binocular rivalry: a time dependence of eye and stimulus contributions. J Vis. 2010;10:3. doi: 10.1167/10.12.3. [DOI] [PubMed] [Google Scholar]
- 48.Binzegger T, Douglas RJ, Martin KA. A quantitative map of the circuit of cat primary visual cortex. J Neurosci. 2004;24:8441–8453. doi: 10.1523/JNEUROSCI.1400-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Binzegger T, Douglas R, Martin K. Topology and dynamics of the canonical circuit of cat V1. Neural Netw. 2009;22:1071–1078. doi: 10.1016/j.neunet.2009.07.011. [DOI] [PubMed] [Google Scholar]
- 50.Churchland MM, Yu BM, Cunningham JP, Sugrue LP, Cohen MR, et al. Stimulus onset quenches neural variability: a widespread cortical phenomenon. Nat Neurosci. 2010;13:369–378. doi: 10.1038/nn.2501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Berkes P, Orbán G, Lengyel M, Fiser J. Spontaneous cortical activity reveals hallmarks of an optimal internal model of the environment. Science. 2011;331:83. doi: 10.1126/science.1195870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bishop CM. New York: Springer; 2006. Pattern Recognition and Machine Learning. [Google Scholar]
- 53.Koller D, Friedman N. MIT Press; 2009. Probabilistic Graphical Models: Principles and Techniques. [Google Scholar]
- 54.Hopfield JJ, Tank DW. “Neural” computation of decisions in optimization problems. Biol Cybern. 1985;52:141–152. doi: 10.1007/BF00339943. [DOI] [PubMed] [Google Scholar]
- 55.Vul E, Pashler H. Measuring the crowd within: Probabilistic representations within individuals. Psychol Sci. 2008;19:645–647. doi: 10.1111/j.1467-9280.2008.02136.x. [DOI] [PubMed] [Google Scholar]
- 56.Denison S, Bonawitz E, Gopnik A, Griffiths T. Proceedings of the 32nd Annual Conference of the Cognitive Science Society; 29 July - 1 August 2009. Amsterdam, Netherlands: 2009. Preschoolers sample from probability distributions. CogSci 2009. [Google Scholar]
- 57.Hinton G, Brown A. Proceedings of the 13th Conference on Advances in Neural Information Processing Systems; December 1999. Vancouver, Canada: NIPS 1999; 2000. Spiking Boltzmann machines. [Google Scholar]
- 58.Zemel R, Huys QJM, Natarajan R, Dayan P. Proceedings of the 17th Conference on Advances in Neural Information Processing Systems; December 2004. Vancouver, Canada: NIPS 2004; 2005. Probabilistic computation in spiking populations. [Google Scholar]
- 59.Kenet T, Bibitchkov D, Tsodyks M, Grinvald A, Arieli A. Spontaneously emerging cortical representations of visual attributes. Nature. 2003;425:954–956. doi: 10.1038/nature02078. [DOI] [PubMed] [Google Scholar]
- 60.Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat Rev Neurosci. 2007;8:700–711. doi: 10.1038/nrn2201. [DOI] [PubMed] [Google Scholar]
- 61.Antic SD, ZhouWL, Moore AR, Short SM, Ikonomu KD. The decade of the dendritic NMDA spike. J Neurosci Res. 2010;88:2991–3001. doi: 10.1002/jnr.22444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Merolla P, Arthur J, Shi BE, Boahen K. Expandable networks for neuromorphic chips. IEEE Trans Circuits Syst I Regul Pap. 2007;54:301–311. [Google Scholar]
- 63.Bruederle D, Bill J, Kaplan B, Kremkow J, Meier K, et al. Proceedings of the IEEE International Symposium on Circuits and Systems; 30May - 2 June 2010. Paris, France: ISCAS 2010; 2010. Live demonstration: Simulatorlike exploration of cortical network architectures with a mixed-signal VLSI system. [Google Scholar]
- 64.Python 2011. The python language reference. Available: http://docs.python.org/reference/.
- 65.Hinton GE. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002;14:1771–1800. doi: 10.1162/089976602760128018. [DOI] [PubMed] [Google Scholar]
- 66.Pospischil M, Piwkowska Z, Bal T, Destexhe A. Characterizing neuronal activity by describing the membrane potential as a stochastic process. J Physiol Paris. 2009;103:98–106. doi: 10.1016/j.jphysparis.2009.05.010. [DOI] [PubMed] [Google Scholar]
- 67.Shinomoto S, Kim H, Shimokawa T, Matsuno N, Funahashi S, et al. Relating neuronal firing patterns to functional differentiation of cerebral cortex. PLoS Comput Biol. 2009;5:e1000433. doi: 10.1371/journal.pcbi.1000433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Softky W, Koch C. The highly irregular firing of cortical cells is inconsistent with temporal integration of random epsps. J Neurosci. 1993;13:334–350. doi: 10.1523/JNEUROSCI.13-01-00334.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]