Abstract
Perhaps the most consistent trend in the development of HPLC since its inception in the 1960’s has been the continuing reach for ever faster analyses. The pioneering work of Knox, Horvath, Halasz, and Guiochon set forth a theoretical framework that was used early on to improve the speed of HPLC, primarily through the commercialization of smaller and smaller particles. Over the past decade, approaches to improving the speed of HPLC have become more diverse, and now practitioners of HPLC are faced with the difficult task of deciding which of these approaches will lead them to the fastest analysis for their application. Digesting the rich literature on the optimization of HPLC is a difficult task in itself, which is further complicated by contradictory marketing messages from competing commercial outlets for HPLC technology. In this perspectives article we provide an overview of the theoretical and practical aspects of the principal modern approaches to improving the speed of HPLC. We present a straightforward theoretical basis, informed by decades of literature on the problem of optimization, that is useful for comparing different technologies for improving the speed of HPLC. Through mindful optimization of conditions high performance separations on the sub-minute timescale are now possible and becoming increasingly common under both isocratic and gradient elution conditions, and the continued development of ultrafast separations will play an important role in the development of two-dimensional HPLC separations. Despite the relatively long history of HPLC as an analytical technique, there is no sign of a slow-down in the development of novel HPLC technologies.
1. Introduction
The past few years have witnessed a series of explosive developments aimed at improving both efficiency (plate count) and speed (plates per unit time) in HPLC (see Table 1). In many ways the technology of HPLC was reborn a half decade ago. Specifically a number of approaches to speeding up HPLC including the introduction of smaller, i.e. sub-two micron, fully porous particles and smaller (sub-three micron) core-shell particles, improved monolithic columns, small non-porous particles, higher pressure and higher temperature operation of conventional columns have appeared. Many of these new column technologies have mandated extensive instrument modifications to fully exploit the benefits of the smaller particles e.g. significantly increased system pressures, drastic reductions in extra-column broadening, improved fittings, as well as faster and lower volume detectors. Interestingly these important developments, especially the use of smaller particles, shorter columns and higher pressures (up to 19,000 psi) precisely follow the historical trends in HPLC technology outlined by Snyder in his prescient article of 20001 although the “sub-two micron barrier” has now been breached. Indeed, many of these developments were anticipated in Giddings’s seminal work which compared the speed of separations in GC and LC2. He made clear that increasing the system pressure up to some critical pressure could increase the plate count at a given analysis time or decrease analysis time at a given plate count; furthermore Giddings pointed out that “…the comparative speed of separation (that is of LC vs. GC) depends, to a large extent, on the relative viscosity and diffusivity of liquids and gases.” Thus the beneficial impact of working at higher temperatures has been evident for a very long time and likely inspired Giddings’ work on supercritical fluid chromatography3. The observation of the strong dependence of the minimum analysis time on particle size and system pressure dates to the pioneering work of Knox4-7 and Purnell8. More recent work that has clarified how one can achieve maximum performance in HPLC includes that of Horvath9 and Guiochon 10 as well as Poppe11, Desmet12 and this laboratory13. Major stumbling blocks to understanding how one should optimize performance are the very different results obtained when performance is optimized with freely varying particle size (called three-parameter optimization)4, 6 and when only the column length and velocity are varied at fixed particle size (i.e. two-parameter optimization)11, 13. These differences will be a major theme of this report. Their consequences cannot be overestimated.
Table 1.
Comparison of the attributes of different approaches to fast HPLC
| Characteristics | Small Particles | High Pressure | Non-Porous Particles | Core-Shell Particles | High Temperature | Chemometric Curve Deconvolution |
|---|---|---|---|---|---|---|
| Overall Impact on Speed | ++ | ++ | + | ++ | +++ | ++ |
| Primary Effect on Speed | Lower plate heights, shorter column lengths, and higher optimum eluent velocities | Drives fluid faster. Used in conjunction with smaller particles and narrower columns (≤ 2.1 mm i.d.) | Improved interphase mass transfer and eddy dispersion | Lower reduced plate height through improved eddy dispersion, improved interphase mass transfer. | Reduces viscosity and thus pressure; allows fluid to move faster at same pressure. Improves interphase mass transfer. Can be combined with use of smaller particles | Decreases resolution needed for analytical purposes and thus can speed up analysis considerably |
| Requirements | Needs high pressure instrument; requires dramatic decrease in extra-column broadening | Needs high pressure instrument; requires dramatic decrease in extra-column broadening when used with small particles | Generally needs high pressure to drive liquid through particles around 1 micron; ultra low dispersion equipment | Requires low extra-column dispersion; almost as important as with sub-two micron porous particles | Does not require high pressure instruments but does require specialized solvent pre-heater and column temperature controller. Generally requires narrow column (≤ 2.1 mm) to minimize thermal mismatch. No PEEK in columns when used above 100 °C | No changes in hardware. But some approaches require extreme repeatability in peak shape and retention time. |
| Equipment Cost | High | High | High | Medium | Low | N/A |
| Primary Advantages | Can improve speed significantly. Has minimal effect on selectivity and thus simplifies method transfer from bigger particles of same manufacture. | Can improve speed significantly; The use of narrower columns can lower solvent consumption. | High efficiency for separations of large molecules, especially proteins. | Can be done with conventional HPLC equipment. | Can be done with conventional HPLC equipment. | No real change in instrument. |
| Primary Disadvantages | Requires mechanically very stable particles; frictional heating. | Generally requires narrow column (≤2.1 mm i.d.) to minimize frictional heating. | Very low sample load capacity and much less retention. Very small particles are hard to pack. | Slightly decreased sample load capacity and retention. | Requires thermally stable stationary phase and stable analytes. | Mathematically complex. Must have very precise retention if deconvolution methods are used. |
| Effect on relative retention | None provided the substrate and stationary phase chemistry are the same as for larger particles (excluding pressure effects, see right). | Small but real, and analyte dependent. | Minimal | Minimal under isocratic elution, larger under gradient elution. | Considerable | N/A |
| Sample Capacity | Good | Good | Much less | Somewhat less | Good | N/A |
| Available | Quite a few and | Quite a few and | Very limited | Few but growing. | Quite a few | N/A |
At this point we refer the reader to Table 1, which provides a concise overview of the various approaches to improving speed in HPLC. We comment on each of them briefly in the table, and refer the reader to the following sections for more detailed explanations of our perspective on each approach. Figure 1 shows a series of simulated separations of a hypothetical ten constituent mixture at constant plate count, retention factor, selectivity and thus resolution, where each chromatogram corresponds to a different set of operating conditions. Specifically, the impacts of increased column temperature and operating pressure are demonstrated here, showing the potential savings in analysis time when separations are properly optimized for high temperature and/or high pressure operation.
Figure 1.
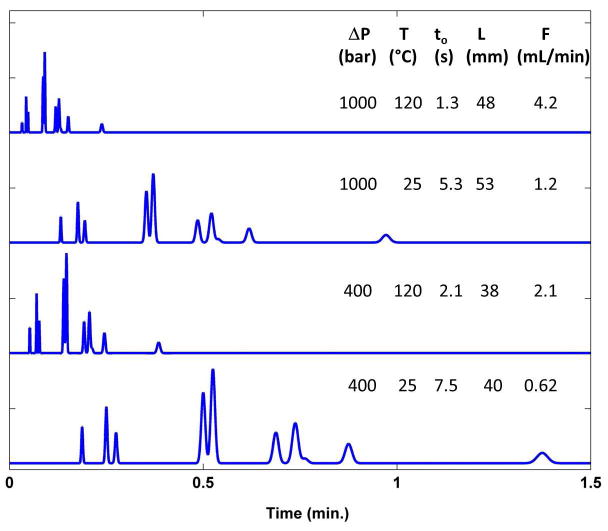
Simulated fast isocratic separations of a hypothetical ten constituent mixture at constant plate count, retention and selectivity. Optimum column lengths and flow rates (assuming 2.1 mm i.d. column) were calculated (see eqs 5-7 below) for different combinations of column temperature and maximum pressure drop using fully porous 1.8 μm particles to give the fastest separation yielding 10,000 plates. Effects of temperature and pressure on selectivity were neglected.
Smaller Particles and Pressure
A currently widely touted perception is that small particle size is synonymous with fast analysis in HPLC. Indeed, this is generally true in the sense that the particle size that produces a given number of plates in the least amount of time decreases as the target analysis time decreases. A different, yet useful view is that the speed of a particular analysis optimized for 5 μm particles, for example, can be improved substantially by re-optimizing the method for use of particles in the 2 μm range. A large fraction of the potential gain provided by the move to small particles often requires a concomitant increase in the available pump pressure; this has been a significant driving force for the recent dramatic increases in maximum pressure capabilities of commercial HPLC instrumentation. The pioneering work of Jorgenson and coworkers on ultra-high pressure HPLC14 was followed by the commercial introduction in 2004 of equipment capable of exceeding the long-standing 6000 psi pressure limit by Waters Corporation. Since then a number of manufacturers have developed ‘ultra high pressure’ equipment, along with a family of stationary phase chemistries on sub-two micron particles.
It is becoming increasingly clear that the theoretical advantages of small particles for fast separations cannot be realized without very high performance instrumentation with much smaller contributions to extra-column peak broadening than we have been accustomed to for many years. This is arguably the foremost barrier to wider use of sub-three micron particles, although certainly not the only barrier, in that a completely new instrument is required in addition to the new column technology.
Another major challenge of using smaller particles at ultra-high pressure is the loss of efficiency due to frictional heating. Halasz15 appears to have been the first to attempt to quantify the amount of frictional heating of a column and describe its impact on peak broadening. He attributed the ultimate limit of performance in HPLC in large part to this problem and indicated that particles smaller than 1 μm would probably not be useful except in very narrow capillaries. Clearly we are rapidly approaching this limit. Indeed, the Wirth group has leap-frogged past the sub-micron barrier to the use of monodisperse 300 and 500 nm particles packed in well ordered arrays in a very small capillary under flow conditions16-18. It is evident that column permeability varies greatly with particle diameter. At a fixed velocity each halving of the particle diameter quadruples the pressure drop. Under adiabatic conditions both the axial, but more importantly for peak broadening, the radial temperature gradient increases in proportion to this pressure drop. For an eluent with a heat capacity and density between that of water and methanol the adiabatic axial temperature change is between 0.02 and 0.05 °C/bar. Thus operating at a pressure of 400 bar can easily generate a differential temperature upwards of 10 °C across the length of the column. This axial differential per se is not a serious broadening problem although it does lead to variations in retention volume with flow rate. What is problematic is the concomitant radial gradient in temperature which causes a radial variation in axial solute zone velocity due to radial differences in the viscosity and worse in the retention factor19-23.
The best way to cope with the viscous heating problem is to use narrower columns. This is exactly what was done in electrophoresis by use of capillary tubes24. Thus columns packed with sub-two micron particles are frequently 2.1 mm or less in diameter and are typically short in length, and the peaks are very narrow (see Table 2). Keeping in mind that the extra-column broadening must be less than about 25% of the peak width so that N is not diminished by more than 10%, it is clear that extra-column effects must be held in check. This, in fact, is the major cause of the need to redesign the entire LC system including injection, tubing, fittings and detection. Clearly peak widths are very small in volume and commensurately in time units. Thus the extra-column contributions from the system become quite critical. Indeed, although use of core-shell particles greatly ameliorates the pressure and self-heating problems, they do require use of a system with very low dead volumes when a 2.1 mm i.d. column is used.
Table 2.
Effect of Column Length on Peak Half Width (μL)a
| Column Length (mm) | |||
|---|---|---|---|
| k’b | 30 | 50 | 100 |
| 0 | 2 | 3 | 4 |
| 1 | 4 | 5 | 7 |
| 2 | 6 | 8 | 11 |
| 5 | 12 | 16 | 22 |
| 10 | 22 | 29 | 41 |
Assumes column diameter of 2.1 mm, plate height of 1.8 μm.
Retention factor.
Temperature
In his historic paper comparing the speed of HPLC and GC2, Giddings pointed out that the chief reason that GC is generally faster than HPLC is that diffusion of analytes is faster in a gas than in a liquid. The fundamental virtue of high temperature conditions in the context of fast HPLC is that raising the temperature of the eluent decreases its viscosity, thereby decreasing pressure drop and increasing diffusivity in the eluent. In this way, high temperature HPLC is more GC-like and less HPLC-like in terms of speed. This improvement in the diffusivity of analytes plays a role in flattening the C-branch (high speed region) of the van Deemter curve, allowing one to operate a column at high eluent velocity without the loss of plates normally associated with such high velocities. In addition, the reduced eluent viscosity also allows one to use either longer columns or smaller particles at the same pressure, or to use the same column length and particle diameter operated at a higher flow rate, as compared to near-ambient temperature operation. As is the case with the use of small particles and ultra high pressures, high temperature conditions cannot always be used with existing column and instrument technology. Since the pioneering work of Horvath and coworkers25 on high temperature HPLC, the availability of thermally stable stationary phases has steadily improved. However, in contrast to the use of small particles and high pressures, high temperature HPLC can be carried out using conventional instrumentation augmented with an appropriately designed column heating system that minimizes the effects of thermal mismatch broadening that were studied over a decade ago22, 23, 26. In this context it is absolutely essential that the fluid entering the column be within a few degrees Centigrade (5 at most) of the column temperature.
Core-Shell
The idea of using core-shell particles to improve separation efficiency was pioneered by Horvath and Kirkland27, 28. The past three years have seen an intensely renewed interest in such particles, particularly after the introduction of sub-three micron core-shell particles (i.e., 2.7 μm Halo by AMT). With such materials, reduced plate heights on the order of 1.5 in 4.6 mm i.d. columns have been reported and this was a major advance in column technology since a well packed column with a traditional fully porous particle seldom gives a reduced plate height below 2.029. As a result, the sub-three micron core-shell particles can exhibit performance similar to sub-two micron fully porous particles but at lower operating pressures30-32. More core-shell particles have been introduced since then including Kinetex from Phenomenex33 and Poroshell 120 from Agilent. There are many hypotheses that have been put forth to explain the high performance of sub-three micron core-shell particles.
The particle size distribution of the core-shell particles is significantly narrower (< 5%) than that of the traditional fully porous particles. This tight distribution may reduce the radial and axial packed bed heterogeneity and thus reduce the van Deemter A-term34.
The lower internal porosity and the geometry of core-shell particles inhibits longitudinal diffusion of the analyte in the stationary phase and thus smaller B-terms are usually observed. This is a particularly advantageous feature that allows long coupled columns to be used at very low linear velocity, where the B term dominates the HETP, to achieve ultra-high efficiency for complex samples30, 35.
The premise which drove the development of core-shell particles is the reduced diffusion length for analytes inside core-shell particles compared to their fully porous counterparts. This could speed up the mass transfer process and reduce the internal van Deemter C-term. However, Gritti et al. showed that the C-terms were, at least for low molecular weight solutes, rather similar for these two particles of differing architecture. One explanation for such results is that external (film) not internal resistance to mass transfer is the main contributor to the C-term34. Indeed, Knox has argued very cogently the internal C-term is almost entirely negligible, typically less than 0.02 (in the dimensionless form of the van Deemter equation) for small molecules regardless of particle architecture36. An alternative explanation for the unexpectedly high C-terms is that the velocity dependence of eddy dispersion might inflate the C-term when an equation of the van Deemter form is used.
The thermal conductivity of core-shell particles is better than that of fully porous particles thereby lessening residual radial thermal effects under high velocity conditions37.
Molecules with high molecular weight and thus low diffusion coefficients such as peptides, proteins and nucleic acids will likely benefit from the improved internal kinetics of core-shell particles38, 39.
It should also be mentioned that high efficiencies of the core-shell particles with their low porosities and thus low dead volumes have put high demands on instrument performance. Minimizing the instrument extra-column broadening is critical to maximize the benefit of the columns, especially for fast separation applications where short columns are used.
Monoliths
About a decade ago there was a great deal of excitement around the introduction of both polymer- and silica-based monolithic materials for HPLC. The prevailing perception has been that monoliths are well-suited to fast analysis because of the open macropore structure which leads to high permeability and low backpressures. However, it has become evident that the price paid for this high permeability is a diminution of the mass transfer properties of the materials leading to lower than expected efficiencies on a plates per meter basis. Theoretical studies of this compromise by Desmet and coworkers40 have led them to the conclusion that monoliths are generally better suited to high efficiency separations involving long columns and high plate counts, rather than fast separations. Tanaka and coworkers also showed experimentally by using kinetic plots that the plate count threshold above which silica monoliths compare favorably to packed particle beds is about 30,00040. These conclusion were arrived at before the meteoric rise of small core-shell materials, and given their superior column dynamics the performance threshold for the superiority of monoliths is probably now shifted to even higher plate counts and longer analysis times41.
Colon and coworkers recently compared the performance of monoliths against core-shell and sub-two micron fully porous particles42. They found that the monolithic column gave a minimum plate height of about 8 μm, close to that of 3 μm fully porous particles. At very high linear velocities (ca. 9 mm/s), much better efficiencies can be obtained on core-shell and sub-two micron fully porous particles compared to monoliths. However, improvements are being made in monolith technology as shown by the superior performance of the recently introduced 2nd generation silica monolith compared to the 1st generation43.
Non-porous
Compared to core-shell particles, nonporous particles can totally eliminate intraparticle analyte diffusion and thus give faster mass transfer properties. Monodisperse nonporous silica particles can be easily made by the Stöber process in the sub-two micron range and have been shown to provide very high plate counts under ultra-high pressure conditions44-46. The main disadvantage of such particles is their much lower surface areas and thus lower sample loading capacities and lower retention compared to the core-shell or fully porous counterparts.
Wu et al. compared the mass transfer properties of nonporous and fully porous particles with similar sizes with small and large molecules. They observed similar efficiencies for small molecules while much higher plate counts were obtained for proteins on the nonporous particles at high linear velocities46. This result suggested that nonporous particles are most suitable for separations of high molecular weight compounds47.
Chemometrics
Chemometric data analysis is a frequently overlooked approach for improving sample throughput in LC. Although there are many different ways in which chemometric methods can be implemented e.g., by use of multivariate curve resolution, peak shape curve fitting, etc., the basic principle is to use chemometrics to significantly reduce the level of chromatographic resolution needed for accurate and precise analysis. The chromatographic resolution can be reduced to very low values even to the point where two peak maxima can no longer be seen (Rs < 0.5)48-51. Because chromatographic resolution is extremely expensive in terms of analysis time (see below) such a reduction in the required resolution has a profound effect on speed. A great deal of sophisticated software is commercially available for the implementation of chemometric analysis schemes. For some of the more common types of chemometric methods, e.g., PARAFAC and GRAM, one generally needs extreme precision in retention times, that is, repeatability better than only a few tenths of the peak half-width is essential. With other forms of chemometrics, e.g., when a hyphenated technique (e.g. LC-MS or LC-DAD) is used one must have spectra of the pure component or at least known mixtures containing all of the incompletely resolved species. Such methods do not require any knowledge of the peak shape nor do they require reproducible retention.
2. Theory
Two vs. Three Parameter Optimization of Column Performance
A real understanding of optimization in HPLC requires a clear appreciation of the difference between two very different ways to approach the optimization process:
A convenient particle size (e.g. 1.8, 3.0, 5.0 μm) is chosen and one asks -- how can performance at a fixed analysis time and operating pressure be optimized by varying only the column length and eluent velocity. We refer to this as two-parameter optimization.
One asks how performance can be optimized at fixed operating pressure and analysis time by searching for the best combination of particle size, column length and eluent velocity. We will call this three-parameter optimization.
The answer to the second question is that one should always work at the velocity corresponding to the minimum in the van Deemter curve, thus hmin will be given by eq 1, but one must then operate at values of the length, particle size and velocity given by eqs 2-4 6, 10, 52. Failure to recognize this requirement invalidates any subsequent analysis involving the value of h specified by eq 1. However, in practice most commonly one does two-parameter optimization as clearly recognized by Poppe11. Under these conditions the optimum performance is no longer obtained at the van Deemter optimum velocity but rather at the velocity given in eq 6 with a column whose length must be that given by eq 7. Once one pre-selects the particle size then optimization must be conducted according to the first scheme. In Horvath’s9 thorough paper on optimization a detailed reading clearly shows that he was conducting a three parameter optimization closely following the reasoning of Knox6. Similar three-parameter optimization was also conducted by Halasz almost three decades ago52. The lack of full understanding of these differences has led to much confusion in the recent literature.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Reorganization of eqs 2-4 yields eqs 8 and 9 which give the dependencies of analysis time (at constant plate count) and plate count (at constant analysis time) as a function of operational variables including the system pressure, column temperature (as it affects viscosity and diffusion), and the column dynamic properties as captured by the van Deemter coefficients A, B, and C (in dimensionless terms).
| (8) |
| (9) |
These are very powerful equations for the practitioner because they allow facile predictions of the potential impact of different approaches to high speed LC. For example, one can easily predict the effect of a factor of two increase in the system pressure or the column temperature, or a significant decrease in the van Deemter A-term as we have witnessed with the increasingly popular core-shell packing materials. Below we provide some example calculations using these equations; here we continue the discussion of theoretical considerations for organizational purposes.
With equations 1-9 in hand it is worthwhile pointing out a few relevant historical milestones. First, Guiochon10 pointed out that “The fastest possible analysis with any column design will be achieved with a column operated at the maximum possible pressure drop and having a length as to give the plate number necessary to perform the desired separation.” Very clear support for this conclusion is evident in eqs 8 and 9. Eq 8 gives the time required to generate a specified number of plates (N) as a function of a number of operational variables, including the system pressure. Clearly, as the pressure is increased this time decreases, and the shortest time will be achieved when the pressure is as high as practically possible. It is very important to note that if everything else is held constant eq 8 shows that doubling the pressure can only decrease analysis time two-fold. Similarly eq 9 clearly shows that at fixed dead time doubling the pressure will only improve the plate count by a factor of . Over the past few years claims have been made for very dramatic (ten-fold) improvements in the speed of HPLC by increasing system pressures from 400 bar to somewhat above 1000 bar; the claims being putatively supported by published work53, 54. Such statements are clearly at odds with the conclusions we draw from eqs 8 and 9. In general these claims are supported by comparing the performance of a conventional system (400 bar) operated at a low fraction (less than 50%) of the maximum pressure available pressure to that of a high pressure system (1200 bar) operated near its maximum13, 35.
It is vital to understand the role that chromatographic resolution (Rs) and selectivity (α) plays in establishing the analysis time. Given the Purnell relationship between Rs and N:
| (10) |
where k’ is the retention factor of the more retained member of the critical (least well separated) pair of peaks. We invert eq 10 to solve for N and insert in eq 8 to give:
| (11) |
We see that an increase in α can have an exceedingly beneficial effect on analysis time. For separations that will be done many, many times use of a thoroughly optimized method can save a tremendous amount of time in contrast to the brute force approach of throwing more plates at the problem. Conversely if an assay is not going to be repeated UHPLC techniques can save a lot of time in developing optimized assays. Another very important message of eq 11 is that if one can reduce the value of Rs needed for an acceptable assay, most likely by some form of chemometrics, one can greatly reduce the analysis time.
Careful reading of the seminal papers of Knox and Saleem6, Guiochon10, Halasz52, and Horvath9 on the optimization of speed in HPLC shows that the ideas communicated by eqs 2-5 and 8 and 9 have been known for some time. What has been less clear is that the derivation of eqs 8 and 9 are absolutely founded on the assumption that one will work at the van Deemter optimum velocity, and the optimum values of eluent velocity, column length, and particle size specified by eqs 2-4. Because of this strict requirement, some (including ourselves) have referred to the plate counts and analysis times given by eqs 8 and 9 as the ‘Knox-Saleem (K-S) Limit’. These values do truly represent a limit in that they represent the fastest way to generate a given number of plates, or the most plates that can be generated in a given time. Any deviation from the velocity, length, or particle size given by eqs 2-4 will result in poorer performance (slower speed or fewer plates) than is possible at the K-S Limit.
Over the past two decades two graphical approaches to understanding the speed/efficiency compromise have become popular55, namely the “Poppe plot” developed by Poppe in the late 1990’s11, and a family of ‘kinetic plots’ developed by Desmet and coworkers12. These approaches have dealt almost exclusively with the situation where a particle size other than that given by eq 4 is chosen, and a series of curves is developed that gives the combination of eluent velocity and column length (see eqs 6 and 7) that will give the best column efficiency at a particular analysis time. A set of four such curves is shown in Figure 2 below, for 1.8 μm particles and temperature (°C)/pressure (bar) combinations of 25/400, 120/400, 25/1000, and 120/1000. In this ‘Poppe plot’ each series of points on a solid curve represents the best plate counts that can be achieved as a function of analysis time under the stated conditions. The vertical axis is the separation speed (time required to generate units of efficiency), and the horizontal axis represents column efficiency. The plot shows that with 1.8 μm fully porous particles in a column operated at 25 °C and 400 bar, an efficiency of 10,000 plates is achievable on a column 40 mm long, at an eluent velocity that corresponds to a dead time of 7.5 s. The blue and red curves show the effects of increasing the system pressure or the column temperature to 1000 bar or 120 °C, respectively, while keeping the particle size constant at 1.8 μm. In this case we see that increasing the pressure reduces the analysis time by 29%, while increasing the temperature reduces the analysis time by 72%. If both the pressure and temperature are both increased, the analysis time is reduced by 83%.
Figure 2.
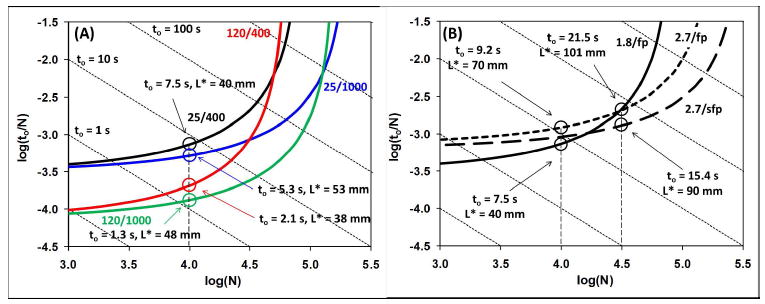
(A) Two-parameter curves for isocratic separations with fully porous particles of fixed size at 1.8 μm under different pressure/temperature (°C/bar) combinations: 25/400 (black), 25/1000 (blue), 120/400 (red), 120/1000 (green). Detailed equations for the calculation of points that contribute to each of the curves are given in ref. 13, but they are ultimately based on the fundamental eqs 5-7. van Deemter A, B, and C terms for fully porous materials were 1.0, 5.0, and 0.05, respectively; ϕ = 500; interstitial porosity (εe) = 0.38, intraparticle porosity (εi) = 0.30; diffusion coefficients were calculated at different temperatures assuming a value of 1.0 × 10-5 cm2/s at 40 °C; viscosities were calculated using the viscosity/temperature correlation described in ref. 26. (B) Two-parameter curves for isocratic separations comparing fully porous 1.8 or 2.7 μm particles to shell 2.7 μm particles at 25 °C and 400 bar. All calculations and values were the same as in (A) except that the van Deemter A, B, and C terms for the core-shell materials were 0.7, 3.0, and 0.05, respectively, and an intraparticle porosity of 0.20 was used.
The primary reason that increasing pressure is less beneficial than increasing temperature is that the 1.8 μm particle size is closer to the optimum particle size dictated by eq 4 for the high temperature case than in the high pressure case. An unfortunate consequence of eqs 2-4 is that the particle size ( ) that will deliver the performance at the K-S Limit is a function primarily of the system pressure, analysis time, and column temperature. The dependence of on analysis time is shown in Figure 3 for the same temperature/pressure combinations used in Figure 2.
Figure 3.
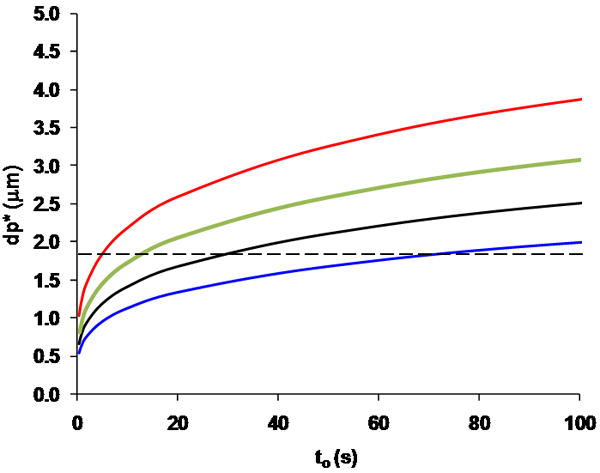
Particle diameters ( , calculated using eq 4) required to achieve the K-S Limit under isocratic conditions at different dead times under different operating conditions. The curves are coded the same as in Figure 2A. The dashed horizontal line represents the current practical limit of 1.8 μm.
In Figure 3 we see that at 25 °C and 400 bar, separations with dead times below about 20 s require particles smaller than 1.8 μm to reach the K-S Limit of performance. When the pressure is increased to 1000 bar, this time threshold actually moves out to around 50 s, whereas increasing the temperature effectively pushes the time threshold to shorter times such that the K-S limit can be reached with particles larger than 1.8 μm at dead times as short as 3.5 s. Equation 8 shows that increasing the system pressure to 1000 bar from 400 bar and the temperature to 120 °C from 25 °C should yield nearly the same reduction in analysis time for a specified number of plates. However, the current limit of around 1.8 μm for most commercially available particles greatly limits access to the gains in throughput that should be afforded by this pressure increase, and currently the use of high temperature conditions is a more efficient way to capitalize on the gains predicted by eq 8. Table 3 provides a quantitative assessment of the extent to which the potential gains in analysis time afforded by different approaches are not fully realized due to the limitations in the size of commercially available particles. For each of the temperature/pressure combinations discussed above and shown in Figure 2A, the best possible plate count for a dead time of 5 s is calculated using eq 9 and reported as the K-S Limit in Table 3. This value assumes that the particle size specified by eq 4 is available. Next, the best possible plate count achievable with 1.8 μm particles at a dead time of 5 s is calculated using the column length and eluent velocity specified by eqs 6 and 7; this is referred to as the 1.8 μm Limit. The difference between these values is presented as a percentage of the K-S Limit that is not gained due to the particle size constraint. We see that in both high temperature cases the difference is negligible because 1.8 μm is very close to the value given by eq 9 under these conditions. However, for the case where only the pressure is increased, the difference is nearly 30%, because in this case is about 1μm. Despite this limitation, though, increasing the pressure and/or the temperature invariably results in an improvement in analysis time compared to the standard condition (see the last column of Table 3). Interestingly, raising the temperature has the most dramatic effect on the 1000 bar case, where the improvement in the plate count over the 25/400 case changes from 29 to over 200%.
Table 3.
Comparison of plate numbers at the Knox-Saleem Limita and what is achievable with 1.8 μm particlesb for a dead time of 5 s.
| Condition | KS Limit (N) | dp*(μm)c | 1.8 μm Limit (N) | % Not Gainedd | % Over 25/400e |
|---|---|---|---|---|---|
| 25/400f | 8990 | 1.2 | 7920 | ||
| 25/1000 | 14200 | 0.95 | 10200 | 28 | 29 |
| 120/400 | 16200 | 1.8 | 16100 | 1 | 103 |
| 120/1000 | 25630 | 1.5 | 25000 | 2 | 216 |
Calculated using eq 9, using the values specified for fully porous materials specified in Figure 2A.
Calculated as described in Figure 2.
Calculated using eq 4.
Calculated as the fraction of the KS limiting plate count (with a particle size of ) that is not realized because of the 1.8 μm particle size limit.
Calculated as the improvement in the number of plates achieved relative to the performance obtained with 1.8 μm particles at 25 °C and 400 bar by increasing the pressure, temperature, or both.
Temperature (°C)/pressure (bar) combinations.
It is important to note that these comparisons are very sensitive to the magnitudes of the van Deemter coefficients used. We believe the values used here are quite reasonable and representative of good commercial materials; however, not all materials are created equal and some will exhibit much worse dynamic characteristics. These differences particularly impact the crossover points of the two-parameter curves, shifting the effective time ranges in which a material or condition exhibits superior performance. For fully porous materials, ‘good’ van Deemter terms are well established from years of experiment; core-shell materials (discussed below) are not nearly as well characterized, and quantitative comparisons of these materials should be used with great care.
The framework developed in eqs 1-9 can also be used to compare the performance of core-shell and fully porous packing materials. The use of core-shell particles warrants a discussion of their performance, as they are clearly becoming the material of choice for many users interested in fast separations. Part of the difficulty with comparing these materials is that the particle size options for core-shell particles are limited mostly to about 2.7 μm, although a 1.7 μm material was just introduced; this situation is certain to change shortly. Figure 2B shows a comparison of three curves: two curves for fully porous materials at 1.8 and 2.7 μm, and one curve for a core-shell material at 2.7 μm. The van Deemter coefficients chosen for the core-shell particles are based on reported values and result in a minimum reduced plate height (h) of 1.5, which is typical of what has been observed.
First, we see at the left vertical dashed line (N = 10,000) that the fully porous 1.8 μm material is superior, in that it yields 10,000 plates at a dead time of 7.5 s, whereas the core-shell material requires a dead time of 9.2 s to achieve the same plate count. While this difference is small, it does show that neither of these materials is universally superior for fast separations, as the core-shell material becomes superior to the 1.8 μm fully porous packing at a dead time of about 21 s and is superior at longer times. By comparing the three curves at the right vertical dashed line (N = 31,600), we see that the core-shell material is competitive with the 1.8 μm full porous material in spite of its larger particle size (2.7 μm). In other words, the difference between the 2.7 μm fully porous curve and the 2.7 μm core-shell curve in terms of the time required to generate 31,600 plates is all due to particle architecture. This type of comparison again demonstrates the utility of the framework described above and its superiority to van Deemter plots for assessing the benefits of a particular approach to fast HPLC.
3. Recent Developments
Fast gradient
With the help of small particles, ultra-high pressure and high temperature, ultra-fast isocratic elution separations can be achieved on the sub-minute scale32. These ultra-fast isocratic separations are critical to many applications, including high-throughput drug pharmacokinetic profiling56 and fast comprehensive online two-dimensional LC57, 58. However, achieving similarly fast gradient separations is more difficult than isocratic due to some major experimental challenges59, 60.
The first challenge is to reduce the system volumes, i.e. gradient delay and flush-out volumes of the LC instrument. The gradient delay volumes of new ultra-high pressure instruments have been substantially reduced by use of different fluid mixing designs from the order of 1 mL to less than 100 μL. One may also have the ability to delay injections with software to effectively “remove” the dwell volume, although this is not helpful in situations where several analyses are made back-to-back. These approaches make ultra-fast gradient elution possible. The flush-out volume is related to the gradient delay volume and is the volume that needs to be flushed out before the initial solvent of the next run reaches the column inlet. This volume can be as large as twice the delay volume and its reduction is important to reduce the re-equilibration time especially for narrow bore column as shown by Schellinger et al.59. Some examples of the speed that can be achieved with a very low gradient delay volume are shown in Figure 4.
Figure 4.
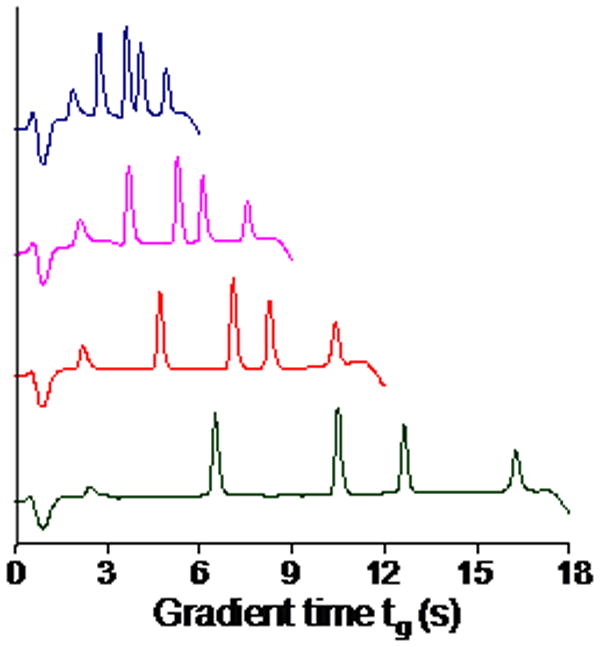
Ultra-fast gradient elution separations of a mixture of four peptides. Chromatographic conditions: Column, 30 mm × 2.1 mm i.d. Halo C18 (shell particles); flow rate, 3.0 mL/min; temperature, 100 °C; detection by UV absorption at 214 nm; gradient times were 6, 9, 12, and 18 s (top to bottom), and the system and column were reequilibrated for 3 s between injections; gradients were started at 5% acetonitrile and terminated at an acetonitrile level that positioned the last peak near the end of the gradient, and 0.1% trifluoroacetic acid in water was used as the aqueous component of the eluent (Dr. Xiaoping Li, unpublished work, University of Minnesota).
Another challenge is to reduce system extra-column band broadening. Under ultra-fast gradient conditions, peaks narrower than 1 s at the base can be generated with extremely small peak variances (see Fig. 4, and ref. 61). Excessive system volume will certainly compromise the performance of the columns. Under gradient conditions, the pre-column broadening is mostly eliminated by focusing on the head of column when an appropriate initial mobile phase condition and injection solvent can be chosen. However, the post-column tubing, connections, detector flow cell volume and detector time constant still contribute to the observed peak variance. Instrument manufacturers have been trying to reduce these contributions by introducing tubing with very narrow inner diameter (e.g., 62 μm i.d.), small volume flow cells (e.g. 500 nL), and fast scanning detectors (e.g. up to 160 Hz). However, even with these minimized volumes, significant loss of column efficiency (as much as > 50% for 2.1 mm i.d. column with low retention) can still happen due to system band broadening as shown by Gritti et al.62. System modification might become necessary to fully realize the benefits of highly efficient narrow bore modern columns. Additionally, the use of microbore columns (e.g., 1.0 mm column i.d.) still remains a big challenge with current instruments32, 63, 64.
The last major challenge is the optimization of ultra-fast gradient elution, where high peak capacity or peak capacity production rate is pursued. Although the optimization in isocratic elution is well developed and understood, optimizing particle size, column length and flow rate in gradient work is still by and large an experience-based process due to the large number of variables involved. Fortunately, isocratic theories are being extended to gradient elution and this allows for better translation of optimal isocratic conditions to optimal gradient conditions35, 65.
Fast 2DLC
Undoubtedly multidimensional separations have greatly benefited from the recent improvements in speed of HPLC. It has long been recognized66 that the speed of the second dimension separation is the dominant factor controlling the overall speed of comprehensive two-dimensional LC (2DLC) separations; the same is true for higher order separations67. This limitation has historically been a significant obstacle to widespread use of 2DLC, and motivated us to investigate the use of ultra-fast separations in the second dimension of a 2DLC system, particularly in the gradient elution mode. We now understand68 that both the raw speed (i.e., analysis time) and the productivity (i.e., peak capacity/time) of each second dimension separation are very important in optimizing the overall performance of a 2DLC separation. Specifically, we find that for low molecular weight, non-peptide compounds an optimum second dimension analysis time, including time for column and instrument re-equilibration, lies in the neighborhood of 15 to 20 s. This optimum time is heavily influenced by both instrument and column technology, and will likely change as significant advances in these areas are made. Figure 5 below shows a chromatogram obtained from a fast 2DLC separation of an extract of low molecular weight constituents of maize seed. The entire 2DLC analysis time is 30 min, with 85 consecutive 20-s gradient elution separations executed in the second dimension of the system during a single 2DLC analysis. This separation had a conventional peak capacity69 of 1020 and an effective peak capacity of 650. These rapid, high performance second dimension separations are possible through the use of short (30 mm) columns packed with small (3 μm) particles operated at high temperature (110 °C) and high mobile phase velocity. A body of recent work suggests that the effective peak capacity of 2DLC will exceed that of 1D gradient separations in times of only 10-15 minutes70.
Figure 5.
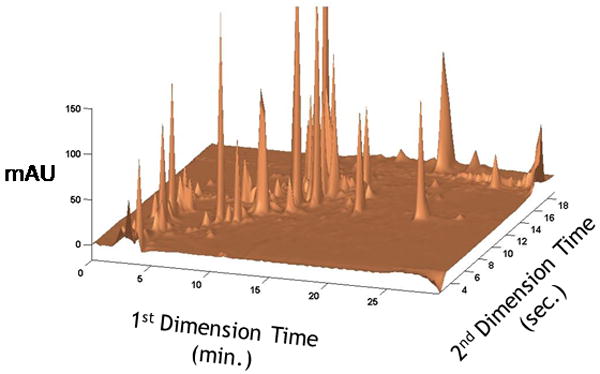
2DLC separation of low molecular weight constituents of an aqueous extract of maize seed powder. Several hundred peaks are observed in an analysis time of 30 min. Each second dimension gradient elution separation is 21-s, including time for column and instrument re-equilibration. Reprinted with permission from ref. 60.
4. Conclusions/Perspective
Ever since its introduction in the late ‘60s the trajectory of HPLC has been towards the use of smaller particles and higher pressure to achieve faster separations with the same or improved plate count. This trend has continued and indeed has greatly accelerated over the past half dozen years due to the introduction of sub-two micron particles, systems capable of pressures over 1000 bar, the use of higher temperatures (> 80 °C) and sub-three micron core-shell particles which offer higher speed with minor increases in operating pressures. Due to the need to minimize the deleterious consequences of viscous self-heating by use of narrower (2.1 mm) columns a significant decrease in solvent usage has been achieved. However, this is at the cost of the need for great decreases in instrument induced (extra-column) broadening. Thus, narrower tubing, and faster, smaller, and lower noise detectors are essential. Notwithstanding these issues sub-minute isocratic chromatography has become almost commonplace and gradient elution times have been reduced to several minutes. 2DLC has also benefited greatly from these trends; peak capacities of 1000 have been achieved in times of about 30 min using extremely fast (20 s) gradient elution in the second dimension. It is still nonetheless true that GC is faster than LC---due to its inherent advantages in terms of viscosity and diffusivity.
Acknowledgments
This work was supported in part by a grant from the National Institutes of Health (GM-54585-15) to the University of Minnesota. Dwight Stoll is the recipient of a Faculty Start-Up Award from the Camille and Henry Dreyfus Foundation.
Footnotes
The following statement is required by the administration of the University to be inserted in all publications where Professor Carr may have a conflict of interest: “Dr. Carr is a consultant for Agilent Technologies, a company that may commercially benefit from this research. This relationship has been reviewed and managed by the University of Minnesota in accordance with its conflict of interest policies.”
References
- 1.Snyder LR. Anal Chem. 2000;72:412 A–420 A. doi: 10.1021/ac002846r. [DOI] [PubMed] [Google Scholar]
- 2.Giddings JC. Anal Chem. 1965;37:60–63. [Google Scholar]
- 3.McLaren L, Myers MN, Giddings JC. 1968;159:197–199. doi: 10.1126/science.159.3811.197. [DOI] [PubMed] [Google Scholar]
- 4.Knox JH. Annu Rev Phys Chem. 1973;24:29–49. [Google Scholar]
- 5.Knox JH. 1961:433–441. [Google Scholar]
- 6.Knox J, Saleem M. J Chrom Sci. 1969;7:614–622. [Google Scholar]
- 7.Knox J. Gas Chromatography. John Wiley and Sons; New York: 1962. [Google Scholar]
- 8.Purnell H. Gas Chromatography. John Wiley and Sons; New York: 1962. [Google Scholar]
- 9.Chen H, Horvath C. J Chromatogr A. 1995;705:3–20. doi: 10.1016/0021-9673(94)01254-c. [DOI] [PubMed] [Google Scholar]
- 10.Guiochon G. In: Advances and Perspectives in Liquid Chromatography. Horvath C, editor. Academic Press; New York: 1980. pp. 1–56. [Google Scholar]
- 11.Poppe H. J Chromatogr A. 1997;778:3–21. [Google Scholar]
- 12.Desmet G, Clicq D, Gzil P. Anal Chem. 2005;77:4058–4070. doi: 10.1021/ac050160z. [DOI] [PubMed] [Google Scholar]
- 13.Carr PW, Wang X, Stoll DR. Anal Chem. 2009;81:5342–5353. doi: 10.1021/ac9001244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Macnair JE, Lewis KC, Jorgenson JW. Anal Chem. 1997;69:983–989. doi: 10.1021/ac961094r. [DOI] [PubMed] [Google Scholar]
- 15.Halász I, Endele R, Asshauer J. J Chromatogr A. 1975;112:37–60. [Google Scholar]
- 16.Malkin DS, Wei B, Fogiel AJ, Staats SL, Wirth MJ. Anal Chem. 2010;82:2175–2177. doi: 10.1021/ac100062t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wirth MJ, Wei B, Malkin DS. HPLC2010; L-02-20; Boston, MA. 2010. [Google Scholar]
- 18.Zheng S, Ross E, Legg MA, Wirth MJ. J Am Chem Soc. 2006;128:9016–9017. doi: 10.1021/ja062676l. [DOI] [PubMed] [Google Scholar]
- 19.Gritti F, Guiochon G. J Chromatogr A. 2007;1138:141–157. doi: 10.1016/j.chroma.2006.10.095. [DOI] [PubMed] [Google Scholar]
- 20.Gritti F, Guiochon G. Anal Chem. 2008;80:5009–5020. doi: 10.1021/ac800280c. [DOI] [PubMed] [Google Scholar]
- 21.Guiochon G. J Chromatogr A. 2006;1126:6–49. doi: 10.1016/j.chroma.2006.07.032. [DOI] [PubMed] [Google Scholar]
- 22.Poppe H, Kraak JC. J Chromatogr A. 1983;282:399–412. [Google Scholar]
- 23.Thompson JD, Brown JS, Carr PW. Anal Chem. 2001;73:3340–3347. doi: 10.1021/ac010091y. [DOI] [PubMed] [Google Scholar]
- 24.Jorgenson JW, Lukacs KD. Anal Chem. 1981;53:1298–1302. [Google Scholar]
- 25.Antia F, Horvath C. J Chromatogr A. 1988;435:1–15. [Google Scholar]
- 26.Thompson JD, Carr PW. Anal Chem. 2002;74:4150–4159. doi: 10.1021/ac0112622. [DOI] [PubMed] [Google Scholar]
- 27.Horvath CG, Lipsky SR. Anal Chem. 1969;41:1227–1234. doi: 10.1021/ac60279a024. [DOI] [PubMed] [Google Scholar]
- 28.Kirkland JJ. Anal Chem. 1969;41:218–220. [Google Scholar]
- 29.Gritti F, Cavazzini A, Marchetti N, Guiochon G. J Chromatogr A. 2007;1157:289–303. doi: 10.1016/j.chroma.2007.05.030. [DOI] [PubMed] [Google Scholar]
- 30.Cabooter D, Lestremau F, Lynen F, Sandra P, Desmet G. J Chromatogr A. 2008;1212:23–34. doi: 10.1016/j.chroma.2008.09.106. [DOI] [PubMed] [Google Scholar]
- 31.Cunliffe JM, Maloney TD. J Sep Sci. 2007;30:3104–3109. doi: 10.1002/jssc.200700260. [DOI] [PubMed] [Google Scholar]
- 32.Wang X, Mukherjee P, Petersson P. Pittsburgh Conference, 2160-5; Orlando, FL. 2010. [Google Scholar]
- 33.Gritti F, Leonardis I, Shock D, Stevenson P, Shalliker A, Guiochon G. J Chromatogr A. 2010;1217:1589–1603. doi: 10.1016/j.chroma.2009.12.079. [DOI] [PubMed] [Google Scholar]
- 34.Gritti F, Leonardis I, Abia J, Guiochon G. J Chromatogr A. 2010;1217:3819–3843. doi: 10.1016/j.chroma.2010.04.026. [DOI] [PubMed] [Google Scholar]
- 35.Zhang Y, Wang X, Mukherjee P, Petersson P. J Chromatogr A. 2009;1216:4597–4605. doi: 10.1016/j.chroma.2009.03.071. [DOI] [PubMed] [Google Scholar]
- 36.Knox J. J Chromatogr A. 2002;960:7–18. doi: 10.1016/s0021-9673(02)00240-6. [DOI] [PubMed] [Google Scholar]
- 37.Gritti F, Guiochon G. J Chromatogr A. 2010;1217:5069–5083. doi: 10.1016/j.chroma.2010.05.059. [DOI] [PubMed] [Google Scholar]
- 38.Guiochon G, Gritti F. HPLC2010; L-03-04; Boston, MA. 2010. [Google Scholar]
- 39.Schuster S, Kirkland JJ, Wagner B. HPLC2010, L-02-18; Boston, MA. 2010. [Google Scholar]
- 40.Gzil P, Vervoort N, Baron GV, Desmet G. Anal Chem. 2004;76:6707–6718. doi: 10.1021/ac049202u. [DOI] [PubMed] [Google Scholar]
- 41.Guiochon G. J Chromatogr A. 2007;1168:101–168. doi: 10.1016/j.chroma.2007.05.090. [DOI] [PubMed] [Google Scholar]
- 42.Brice RW, Zhang X, Colón La. J Sep Sci. 2009;32:2723–2731. doi: 10.1002/jssc.200900091. [DOI] [PubMed] [Google Scholar]
- 43.Cabrera K, Jung G, Piper A, Kowalczyk F, Kreher K, Knoell P, Machtejevas E. HPLC2010, P-1502-T; Boston, MA. 2010. [Google Scholar]
- 44.Patel KD, Jerkovich AD, Link JC, Jorgenson JW. Anal Chem. 2004;76:5777–5786. doi: 10.1021/ac049756x. [DOI] [PubMed] [Google Scholar]
- 45.Wu N, Lippert J, Lee M. J Chromatogr A. 2001;911:1–12. doi: 10.1016/s0021-9673(00)01188-2. [DOI] [PubMed] [Google Scholar]
- 46.Wu N, Liu Y, Lee ML. J Chromatogr A. 2006;1131:142–150. doi: 10.1016/j.chroma.2006.07.042. [DOI] [PubMed] [Google Scholar]
- 47.Barder TJ, Wohlman PJ, ThrallL C, Dubois PD. LC-GC North Am. 1997;15:918–926. [Google Scholar]
- 48.Bahowick TJ, Synovec RE. Anal Chem. 1995;67:631–640. [Google Scholar]
- 49.Bruckner Ca, Prazen BJ, Synovec RE. Anal Chem. 1998;70:2796–2804. [Google Scholar]
- 50.Excoffier J-L, Joseph M, Robinson JJ, Sheehan TL. J Chromatogr A. 1993;631:15–21. [Google Scholar]
- 51.Schure MR. J Chromatogr A. 1991;550:51–69. [Google Scholar]
- 52.Halász I, Görlitz G. Angew Chem Int Ed Engl. 1982;21:50–61. [Google Scholar]
- 53.Neue UD. In: Encyclopedia of Separation Science. Poole CF, Wilson ID, editors. Elsevier Science Ltd.; Oxford: 2007. [Google Scholar]
- 54.Wu NJ, Clausen AM. J Sep Sci. 2007;30:1167–1182. doi: 10.1002/jssc.200700026. [DOI] [PubMed] [Google Scholar]
- 55.Neue U. LC GC North Am. 2009;27:974, 976, 978, 980, 982–983. [Google Scholar]
- 56.De Nardi C, Bonelli F. Rapid Commun Mass Spectrom. 2006;20:2709–2716. doi: 10.1002/rcm.2649. [DOI] [PubMed] [Google Scholar]
- 57.Davis JM, Stoll DR, Carr PW. Anal Chem. 2007;80:461–473. doi: 10.1021/ac071504j. [DOI] [PubMed] [Google Scholar]
- 58.Schoenmakers PJ, Vivo-Truyols G, Decrop WMC. J Chromatogr A. 2006;1120:282–290. doi: 10.1016/j.chroma.2005.11.039. [DOI] [PubMed] [Google Scholar]
- 59.Schellinger A, Stoll D, Carr P. J Chromatogr A. 2005;1064:143–156. doi: 10.1016/j.chroma.2004.12.017. [DOI] [PubMed] [Google Scholar]
- 60.Stoll DR, Paek C, Carr PW. J Chromatogr A. 2006;1137:153–162. doi: 10.1016/j.chroma.2006.10.017. [DOI] [PubMed] [Google Scholar]
- 61.Stoll DR, Cohen JD, Carr PW. J Chromatogr A. 2006;1122:123–137. doi: 10.1016/j.chroma.2006.04.058. [DOI] [PubMed] [Google Scholar]
- 62.Gritti F, Sanchez CA, Farkas T, Guiochon G. J Chromatogr A. 2010;1217:3000–3012. doi: 10.1016/j.chroma.2010.02.044. [DOI] [PubMed] [Google Scholar]
- 63.Heinisch S, Desmet G, Clicq D, Rocca J-L. J Chromatogr A. 2008;1203:124–136. doi: 10.1016/j.chroma.2008.07.039. [DOI] [PubMed] [Google Scholar]
- 64.Lestremau F, Wu D, Szücs R. J Chromatogr A. 2010;1217:4925–4933. doi: 10.1016/j.chroma.2010.05.044. [DOI] [PubMed] [Google Scholar]
- 65.Broeckhoven K, Cabooter D, Lynen F, Sandra P, Desmet G. J Chromatogr A. 2010;1217:2787–2795. doi: 10.1016/j.chroma.2010.02.023. [DOI] [PubMed] [Google Scholar]
- 66.Bushey MM, Jorgenson JW. Anal Chem. 1990;62:161–167. doi: 10.1021/ac00201a015. [DOI] [PubMed] [Google Scholar]
- 67.Watson NE, Siegler WC, Hoggard JC, Synovec RE. Anal Chem. 2007;79:8270–8280. doi: 10.1021/ac070829x. [DOI] [PubMed] [Google Scholar]
- 68.Potts LW, Stoll DR, Li X, Carr PW. J Chromatogr A. 2010 doi: 10.1016/j.chroma.2010.07.009. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Giddings JC. Anal Chem. 1984;56:1258A–1260A. 1262A, 1264A. doi: 10.1021/ac00276a003. [DOI] [PubMed] [Google Scholar]
- 70.Stoll DR, Wang X, Carr PW. Anal Chem. 2007;80:268–278. doi: 10.1021/ac701676b. [DOI] [PubMed] [Google Scholar]


