From Statistical Associations to Causation: What Developmentalists Can Learn From Instrumental Variables Techniques Coupled With Experimental Data

Abstract

In this article, the authors aim to make accessible the careful application of a method called instrumental variables (IV). Under the right analytic conditions, IV is one promising strategy for answering questions about the causal nature of associations and, in so doing, can advance developmental theory. The authors build on prior work combining the analytic approach of IV with the strengths of random assignment design, whether the experiment is conducted in the lab setting or in the “real world.” The approach is detailed through an empirical example about the effects of maternal education on children's cognitive and school outcomes. With IV techniques, the authors address whether maternal education is causally related to children's cognitive development or whether the observed associations reflect some other characteristic related to parenting, income, or personality. The IV estimates show that maternal education has a positive effect on the cognitive test scores of children entering school. The authors conclude by discussing opportunities for applying these same techniques to address other questions of critical relevance to developmental science.

Understanding whether associations between children's micro- or macroenvironments and developmental outcomes are causal is critical to advancing developmental knowledge and theory. Indeed, identifying causal associations not only advances our understanding of development, but it also improves our ability to tailor interventions so that they successfully promote healthy development of children. Yet, traditional approaches to estimating associations between environments and children's developmental outcomes typically fall short of establishing causal relations.

Take the literature on the effects of parenting behavior on children's development as an example. On the one hand, parents may be viewed as agents of children's socialization (Bornstein, 2006; Collins, Maccoby, Steinberg, Hetherington, & Bornstein, 2000; Maccoby, 1992), with parents' behavior and sensitivity predicting their children's psychosocial and behavioral outcomes. On the other hand, children may influence their parents as well, such as when children with difficult temperaments or behavior regulation styles elicit differing parenting behaviors (Ge et al., 1996). A positive association between sensitive parenting and children's effective behavior regulation could be consistent with both of these theories, leaving researchers relatively uninformed about the direction of causality. Even further complicating matters, such a positive association might not be due to the processes described in either theory but rather might be attributed to an unobserved parental characteristic, such as personality, or an unobserved contextual characteristic, such as economic stress, that is associated with both parental sensitivity and children's behavior. As this discussion makes clear, developmental theory could be strengthened considerably by analytic tools that would allow us to identify the precise nature and direction of these associations. In the current example, if some third variable, such as economic stress, drives child behavioral problems and not parenting behavior, interventions targeting parenting behavior are likely to do little to change children's developmental trajectories.

In this article, we aim to make accessible the careful application of one particular type of method, called instrumental variables (IV). Under the right analytic and data conditions, which we describe in this article, IV methods can provide a way to approximate causal associations. Here, we combine the analytic approach of IV with the strengths of a random assignment design, whether the experiment is conducted in the lab setting or in the “real world” (see Angrist, Imbens, & Rubin, 1996, for a technical discussion, and Gennetian, Morris, Bos, & Bloom, 2005). IV methods can be used for two purposes. First, in combination with experimental data, IV methods may be able to identify the pathways by which intervention effects occur, unpacking what is commonly referred to as the “black box” of intervention effects. Second, this method can provide answers to basic developmental questions, such as whether parenting or mothers' education affects children's development. Our focus is to address this latter question by using IV methods in a nonexperimental extension of an experimental study.

A select set of prior developmental research has applied IV methods (e.g., see Foster & McLanahan, 1996), including the specific type of application we present here (Crosby, Dowsett, Gennetian, & Huston, 2006; Gennetian, Crosby, Dowsett, & Huston, 2006; Gibson-Davis, Magnuson, Gennetian, & Duncan, 2005; Morris, Duncan, & Rodrigues, 2006; Morris & Gennetian, 2003). We build on this prior work in two ways. First, we discuss the careful use of IV methods by documenting the theoretical underpinnings of this methodology, as well as its practical application (including the relative ease of statistical programming). We not only summarize the underlying assumptions for identifying IV models, but we also explicitly review the kinds of sensitivity analyses that should be performed when conducting an IV analysis. Second, we illustrate IV methods by examining the effects of maternal education on children's cognitive development, an area of substantial prior developmental research. Recognizing that not all researchers have access to the types of data we describe here, we also note, in the Discussion, opportunities for developmentalists to access instruments and estimate IV models relying on a variety of both experimental and nonexperimental data.

Developmentalists have long been interested in how parental characteristics, including socioeconomic status, affect children's development. Maternal education is among one of the strongest family predictors of children's later scholastic performance and cognitive development, and numerous theories describe the processes by which this effect might arise (Bornstein, Hahn, Suwalsky, & Haynes, 2003). For example, mothers with higher levels of education are more likely to expose their children to more varied and complex language and to provide more cognitively stimulating home environments (Davis-Kean, 2005). Yet, maternal education is also widely recognized to be a good proxy for a range of related parental characteristics, such as social class standing, intelligence, and motivation. Disentangling maternal education from these other characteristics that covary with maternal education is difficult and leaves a researcher in an unenviable position of having to decide between potentially overcontrolling or undercontrolling for confounding variables (Duncan, Magnuson, & Ludwig, 2003; Newcombe, 2003). This is why it is rare to attribute a causal interpretation to observed associations between maternal education and children's development (Sobel, 1998). We illustrate the use of IV to consider whether the association between maternal education and children's cognitive development is causal using data from a multisite, multiresearch random assignment study called the National Evaluation of Welfare-to-Work Strategies (NEWWS).

Establishing Causal Effects

Why is it critical to establish causal effects? Many interesting developmental questions are framed as testing unidirectional pathways. For example, what are the effects of parental responsiveness on the developmental trajectories of children? What are the effects of parental employment or family income on children's behavior? If the associations we observe are due entirely to children's influence on their parents, or the influence of some third variable (e.g., social networks) on both parents and children, then our models of developmental theory need to be revised to take into account these alternative pathways, and our intervention strategies would also need to be designed accordingly.

In seeking to establish causal associations, most empirical methods try to approximate what would be observed if we could assess the same individual in two different circumstances at the same point in time (Shadish, Cook, & Campbell, 2002). Random assignment experiments are often regarded as the “gold standard” of research designs, because they provide an approximation of this causal effect. The random assignment of individuals (or groups or places)¹ into control and treatment conditions results in groups (of individuals, groups, or places) that are comparable in all ways except for the treatment condition they experience. Consequently, if implemented correctly, with sufficiently large sample sizes and very little sample attrition over time, any subsequent differences across the groups are due to the treatment.

Because it is not possible or ethical to conduct experiments that answer all developmental questions, researchers must rely on a variety of nonexperimental methods, such as multivariate regression analyses and analyses of variance. As is well recognized, these approaches are often limited by their ability to support causal inferences. In particular, these nonexperimental approaches often fall short of ruling out the possible alternative explanations for observed associations. Concerns about alternative explanations loom large because the associations under study are often endogenous. That is, be it the influence of parenting on children or of peer relationships on social development, the key independent variables in analytic models are in part determined by the individuals or processes we seek to study, or in the case of children, by their parents. Thus, one important potential source of bias is third-variable or omitted-variable bias, which occurs when a third variable may explain the association between two variables being studied. Another is simultaneity bias, reverse causality of the estimated path (see Shadish et al., 2002, for a discussion of limitations of nonexperimental research). These biases are worrisome because they may incorrectly lead us to believe that an association is causal, when in fact it is at least in part spurious.

The Basic IV Model

IV estimation is designed to improve one's ability to draw causal inferences from nonexperimental data. IV estimation is built on the premise that most constructs are multidetermined, and therefore only part of the variation in a variable will introduce bias from unobserved characteristics or unobserved third variables. The basic idea is simple. If we isolate the portion of variation in our independent variables that is unrelated to unmeasured confound variables, then we greatly improve our ability to make causal inferences. Thus, IV methods seek to approximate experiments by focusing on exogenous variation that is due to some understood manipulation of the key independent variable and as a result is not associated with unmeasured or unobserved characteristics of the phenomena being studied.

Natural experiments, events or circumstances that are not manipulated by researchers but still result in the random distribution of the endogenous regressor, provide one type of exogenous variation (Angrist, 2002; Card & Krueger, 1994; Hotz, McElroy, & Sanders, 2005; Hoxby, 2001). In the case of maternal education, researchers have used historical changes in school-leaving laws as a source of variations in educational attainment (Oreopaulos, Page, & Stevens, 2006). Treatment status in an experimental study provides another type of exogenous variation. Random assignment to an intervention program that improves mothers' education, for example, would provide such variation. In both cases, the portion of variation that is exogenous is used to estimate the associations of interest.

To illustrate the basic intuition behind IV methods, we use the simple illustrative case of the association between mothers' years of completed education and children's achievement as an example. A basic nonexperimental regression estimating this association would take the following form:

$$Y_i={\alpha }_0+\beta X_i+{\varepsilon }_i$$ (1)

The intercept, α, represents the mean value of the outcome (children's achievement) for children, and ε is an error term. β, a regression coefficient, represents the increase in children's average achievement attributable to an additional year of maternal education. Because this analysis uses all of the naturally occurring variation in mothers' education, β represents a causal effect of the treatment (an additional year of maternal education) on the outcome (children's achievement), only under the assumption that levels of maternal educational attainment are randomly allocated across mothers, and consequently the error term, ε, is independent of (not associated with) the treatment, X. If ε is correlated with X—that is, if mothers with higher levels of education differ from those with lower levels of education in ways that also affect their children's outcomes—then ordinary least squares (OLS) will likely produce a biased estimate of β.

The IV approach to producing unbiased, causal estimates of β entails finding another variable, P, an instrument that is correlated with the treatment (mothers' educational attainment) but not otherwise associated with children's achievement (i.e., uncorrelated with ε).² One such possible (and hypothetical) example is an experimental educational intervention in which mothers are assigned to an educational intervention that increased mothers' educational attainment or to a control group. If all mothers who were assigned to the educational intervention completed an additional year of school, and those who were assigned to the control group did not have access to further education, then this provides a useful instrument, a source of exogenous variation in maternal education.

IV analyses typically proceed in two steps, although most statistical packages estimate both steps with just one command. In the first stage of the IV procedure, the key independent variable X (mothers' educational attainment) is predicted as a linear function of P (mothers' experimental status) using OLS regression:

$$X_i={\prod }_0+{\prod }_{1Pi}+{\mu }_i,$$ (2)

where μ is a random error term, ∏₀ is an intercept representing the average level of educational attainment in the control group, and ∏₁ is a regression coefficient representing the increase in educational attainment due to the educational intervention, in our example an additional year of school. The estimated first-stage model is used to compute a predicted value X̂_i for each sample member, which is then substituted for X_i in Equation 1, replacing the actual value of that variable. If the average educational attainment of the control group was a high school degree, and on average the intervention boosted mothers' education by 1 year, than the predicted values of X̂_i would be 12 and 13 for the control and experimental groups, respectively, and these values would be placed into the second-stage equation (Equation 1). Unlike mothers' actual levels of educational attainment, the predicted values of education (X̂_i) are not associated with other maternal or child characteristics. The values are only due to the random assignment status of mothers to the educational program, and as a consequence the resulting IV estimates of the effects of maternal education on children's achievement, β, are unbiased. Put another way, IV methods essentially throw away all naturally occurring variation in maternal education that is due to individual or other environmental factors and estimate the causal effects of maternal education on children's test scores using just the experimentally driven exogenous variation in maternal education.

In this simple hypothetical example, the resulting two-stage least squares IV estimate of the effects of maternal education on children's achievement is equivalent to the local average treatment effect, essentially a rescaling of the impact of the experimental intervention. In this case, the calculation of this local average treatment effect is the program impact on child outcomes divided by the program impact on mothers' education (for a more complete discussion, see Gennetian et al., 2005). This occurs because the difference in mean outcomes for children of mothers in the treatment group and for the control group, PY, equals the covariance between Y (children's achievement) and P (treatment status), and the difference in educational attainment of mothers in the treatment and control group, XP, equals the covariance between X (mothers' education) and P (treatment status). Hence, the IV estimator of β equals the ratio between the two covariances and thus the ratio between the two differences.

Finding Good Instruments

The exercise of searching for, and subsequently constructing, instruments is one that should be grounded in theory. Properly identifying an IV model further entails the satisfaction of key assumptions, some of which can be met more clearly and easily than others. Because a variable is only a “good” instrument if it is known a priori to be uncorrelated with any unmeasured explanatory variables, the best instruments are those whose values are assigned exogenously. That is why well-implemented randomized experiments, with program or treatment variables that have exogenously assigned values, offer a promising start as good instruments.

To obtain statistically sound IV estimates, an instrument P_i must also be highly correlated with the endogenous variable of interest, in our example with maternal education. When an instrument is not strongly associated with the endogenous variable, it is a weak instrument, and potential problems arise. First, there is the risk of having large standard errors on the IV estimates in the second stage of the procedure, which would make the estimates imprecise. Second, weak instruments can produce IV estimates that are vulnerable to bias due to chance correlations between the error terms in the different stages of the IV procedure. Strategies for assessing whether or not an instrument is weak are described, more explicitly, in our empirical example.

To complicate matters, one instrument may not be sufficient for addressing many of the questions of interest to developmental psychologists. Developmental processes are often characterized by equifinality, leading the researcher to consider the effects of multiple independent variables on a particular outcome of interest. In order to estimate the effects of multiple independent variables, there must be at least one instrument for each endogenous variable that is being used as a predictor in the second-stage equation.³

With multiple instruments, IV techniques can be used to estimate these multiple effects, but the model becomes more complicated. Obtaining reliable estimates in this case depends not only on having an exogenous source of variation for each of the independent variables, but also on having instruments that predict the two independent variables differently. That is, at least one of the instruments must provide unique predictive power for one of the independent variables.

Finally, how does the researcher find multiple instruments? Arguably, the best way is to take advantage of data from an experimental study with multiple research groups (see, for example, Gibson-Davis et al., 2005, and Morris & Gennetian, 2003). In such a design, participants are randomly assigned to one of several program groups or to a control group. The instrument set is constructed with separate indicators for each of the treatment streams representing assignment to each program group.

An alternative approach is to exploit the variability that occurs due to the implementation of comparable experiments across multiple sites (for example, see Ludwig & Kling, in press). It is possible to create more than one instrument by creating a set of indicators that are interactions between the random assignment variable and a set of site indicators. The result is an analysis in which variation in the implementation of the program is used to identify the multiple pathways.⁴ However, this strategy is only successful if the source of variation across sites is due to differences in program implementation, rather than differences in participant characteristics or social and economic context.

To empirically illustrate the use of IV, we build on the prior hypothetical example of estimating the association between maternal education and children's achievement. Whereas our previous example illustrated the simplest case of a single simple intervention, in our empirical example, we illustrate how IV methods can be applied to a more complicated experimental evaluation of an education and training program for low-income mothers.

Method

Data

Our data come from the NEWWS Child Outcomes Study (NEWWS-COS; McGroder, Zaslow, Moore, & LeMenestrel, 2000). The NEWWS was an experimental evaluation of the Job Opportunity and Basic Skills Training (JOBS) program, which was intended to move welfare recipients toward economic self-sufficiency by requiring that they participate in work and training activities in order to receive full cash benefits. Between 1991 and 1994, approximately 3,700 families in three cities (Atlanta, GA; Grand Rapids, MI; and Riverside, CA) were randomly selected to be enrolled in the NEWWS-COS. Once enrolled, mothers were randomly assigned to one of two JOBS program streams or to a control group (see Figure 1). In each COS site, one JOBS program emphasized Human Capital Development (HCD), by directing mothers to attend educational and job training programs, and another focused on Labor Force Attachment (LFA), by directing mothers to quickly transition into the labor market. The final sample for analyses of the 2-year COS consists of 3,108 (or 94%) of study participants and a focal child age of 3 to 5 years old. (See Table 1 for a summary of sample characteristics). The sample size for our study is reduced to about 2,858 because of missing data on the outcome variables, but the baseline characteristics of this analysis sample do not differ from those of the full sample.

Figure 1.

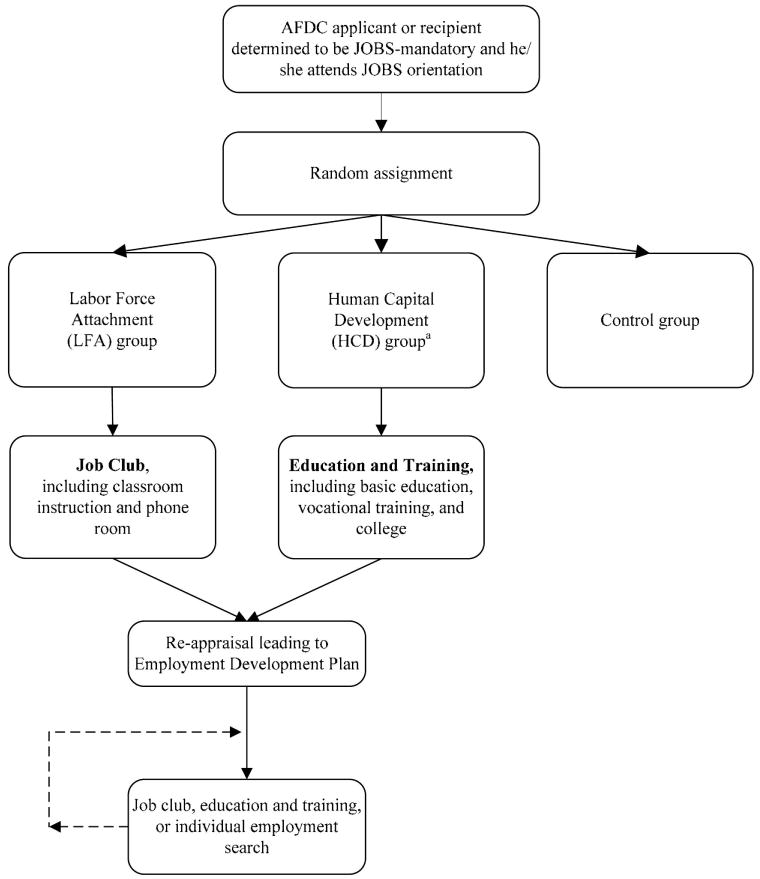
Steps leading to random assignment and intended sequence of activities in three National Evaluation of Welfare-to-Work Strategies sites. AFDC = Aid to Families With Dependent Children; JOBS = Job Opportunity and Basic Skills Training.

^aBy design, mothers who were not considered in need of basic education could not be randomly assigned to the Human Capital Development group in Riverside, CA.

Table 1. National Evaluation of Welfare-to-Work Strategies Child Outcomes Study Sample Characteristics at Baseline by Site and Experimental Status.

Baseline characteristic	Atlanta			Riverside			Grand Rapids
	Control	HCD	LFA	Control	HCDa	LFA	Control	HCD	LFA
Demographic information
Currently married (%)	1	1	1	2	3	2	2	3	2
Never married (%)	30	29	24*	56	51	60	56	51	60
Age	28.9	28.6	29.2	28.9	29.3	29.5	26.3	26.8	26.88
No. of children	2.2	2.3	2.3	2.1	2.3	2.3*	2.1	2.0	2.11
Black (%)	96	95	94	19	19	17	39	36	42
Hispanic (%)	0	0	1	32	43	32	6	6	6
Earnings in prior year	1,187	932	905*	1,445	1,113	1,663	2,087	2,179	1,772
No. of months receiving AFDC in prior year	10	10	10*	7	8	7	8	7	8.45
Average AFDC payment in prior year ($)	256	265	266*	489	535	485	360	330	354
Focal child age	3.93	3.98	3.93	3.66	3.63	3.6	2.97	3.01	2.98
Boy (%)	49	46	53	47	49	53	51	50	47
Educational attainment
No educational degree (%)	35	35	40	50	73	41*	42	36	37
Highest degree GED/HS diploma (%)	56	58	54	46	25	53*	53	59	60
Highest degree vocational or 2-year degree (%)	7	6	4	3	2	5	4	3	4
Sample size	506	520	396	486	256	208	216	205	225

Note. HCD = Human Capital Development; LFA = Labor Force Attachment; AFDC = Aid to Families With Dependent Children.

^aBy design, mothers who were not considered in need of basic education could not be randomly assigned to the HCD group in Riverside, and consequently the HCD members are compared only to members of the control group who were also found to be in need of basic education.

^*Statistically significant differences between treatment and control groups; p < .05.

Measures

Over the course of the evaluation, data on clients and their families were collected from several sources. Prior to random assignment, welfare intake staff collected baseline information, and participants completed a short survey about their attitudes toward work and welfare. These data were used to construct a series of covariates: high school degree completion, number of children in the household, prior marital experience, current educational activities, prior earnings, prior welfare receipt, access to social support, the number of barriers to work, the number of risk factors, and a measure of the mother's locus of control, as well as the child's age. In addition, respondents completed a literacy assessment, which was also included as a covariate.

Approximately 2 years after randomization, trained interviewers collected detailed information from participants about their education, employment, and job training experiences since baseline. These data provided information on the number of months that mothers attended educational programs. Administrative data on earnings were collected for the year prior to and the 2 years after random assignment, providing a measure of the number of quarters that mothers were employed and their total 2-year earnings.

Administered approximately 24 months after random assignment, the Bracken Basic Concept Scale/School Readiness Composite (BBCS/SRC; Bracken, 1984) directly assessed the focal child's academic cognitive performance or academic skills. On average, children answered about 47 out of 64 questions correctly, and the sample standard deviation was 11.7. During the survey, each mother was asked whether her child had received any special help in school for a learning problem and whether the child had repeated a grade since random assignment. A response of “yes” to either question was given a value of 1, and the answers to the two questions were summed to create an index of academic problems for the focal child. About 9% of the sample had one or more academic problems, and less than 1% had two problems.

Analytic Strategy

We estimated using both IV and OLS models the effects of maternal education and employment on children's school outcomes. The IV equations we used to estimate differed from Equations 1 and 2, presented earlier, in two important ways. First, rather than estimating the effects of mothers' educational attainment on children's achievement, we estimated the effects of the number of months that mothers participated in educational programs on children's achievement. Second, our models included covariates for individual characteristics. Covariates are often included in IV analyses to improve the precision of the estimates in the first and second stages.

We began by considering the case of a single instrument, HCD program treatment status, in a single site, Atlanta. As explained earlier, if the HCD program improved mothers' educational participation, then we might implement IV analyses to consider whether improvements in mothers' education benefitted their children—an analysis that is essentially similar to calculating the ratio of the experimental impact on children's achievement to the experimental impact on maternal education. Next, out of a concern that the experiment may have affected children through other pathways, and in the interest of increasing statistical power, we broadened the instrument set to include indicators for treatment status in two streams and across the three sites. This IV model can be estimated in SPSS, SAS, and STATA software, and we provide examples of syntax for each in the Appendix.

A graphical illustration of the multiple-variable IV model is provided in Figure 2. Although the HCD programs were designed to affect mothers' education, it was also the intent of these programs to increase mothers' employment—as their primary goal was to reduce the reliance on welfare and increase the employment of welfare recipients. The two treatment streams in each of the three sites did indeed predict maternal education as well as employment (even though it was our a priori expectation that some treatment streams would have stronger effects on maternal education and others would have stronger effects on employment).⁵ This suggests that the HCD and LFA programs may have affected children's achievement via these two possible pathways.

Figure 2.

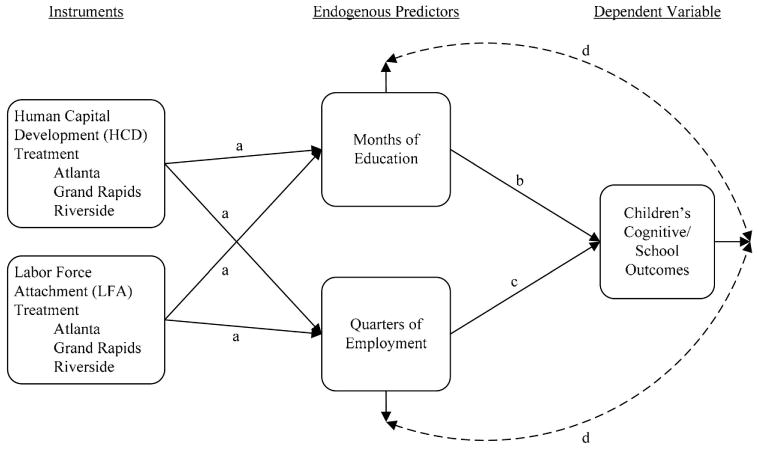
Graphical illustration of the structural model.

The first-stage IV model estimated these paths, which are denoted by “a” in Figure 2. Our interest is in using IV methods to estimate Path b, the effect of mothers' participation in education on children's cognitive development and school outcomes. Mediating processes (not shown) explain the associations between maternal education and children's outcomes and may include, for example, parent– child interactions involving literacy activities, a parent serving as a role model for the importance of learning and education, and increased language use in the home. Although these mediating processes are unmeasured, they do not bias the estimates of the effects of maternal education because they are encompassed in the total effect of education. Employment, on the other hand, may change alongside education as a result of the intervention, and therefore, as explained in more detail later, needs to be estimated in this model (Path c).

The second-stage IV model estimated Paths b and c. In the two-stage IV model, predicted values of months of education and quarters of employment make it such that Path d (the correlation between the error terms in the two equations) is zero. In a comparable structural equation model (SEM), Path d could be modeled as non-zero correlated error terms. Whereas SEM would model the pathways simultaneously as opposed to sequentially, the results of the estimated paths would be very similar to those estimated using the IV methods we describe here (see Schmitt & Bedeian, 1982, for an example). Note that without instruments, such a model could not be identified using SEM (or IV, for that matter).

The consistency of IV estimates is based on large-sample properties. Although it is not possible to determine what a sufficiently large sample size may be for an IV study, we caution researchers with particularly small samples that IV methods may fail. Irrespective of sample size, there are also key assumptions in IV methods that must be considered to assure that the application is appropriate. We apply a series of tests to see whether the instruments we have selected meet important assumptions (closely following the framework of Angrist, Imbens, & Rubin, 1996).

Checking the choice of instruments: Does the instrument predict the endogenous regressor?

When an instrument is not strongly associated with the endogenous variable, it is a weak instrument, and potential problems arise. First, there is the risk of having large errors on the IV estimates in the second stage of the procedure, which makes the estimates imprecise. Second, weak instruments can produce IV estimates that are vulnerable to bias due to chance correlations between the error terms in the different stages of the IV procedure. Thus, it is important to be certain that the instruments are strongly associated with the key endogenous regressors, in our example mothers' education and employment. If a program was not well designed or implemented, the experiences of mothers in the LFA and HCD groups may not have differed from the experiences of the control group. Consequently, a clear understanding of participants' experiences in the programs is necessary. In addition, the strength of the instruments can be assessed by the partial R-square and F statistics for the test of joint significance of the instruments in the first stage. These statistics provide a measure of how strongly correlated the instruments are with the endogenous regressors (Bound, Jaeger, & Baker, 1995). For mothers' education using multiple instruments or a single instrument (HCD in Atlanta), we find sufficiently large F statistics (see Tables 2 and 3).

Table 2. First- and Second-Stage Results for Single-Variable Instrumental Variables Model of Months in Adult Basic Education on Children's Cognitive and School Outcomes.

Independent variable	Atlanta HCD	OLS	IV
First stage
Months of education	2.32**
SE	0.34
95% CI	1.66, 2.99
F statistic for instruments	46.94**
Partial R2	.05
Sample size	977
Second stage
Model 1—BBCS/SRC scores
Months of education		0.06	0.35
SE		0.05	0.25
95% CI		−0.05, 0.17	−0.14, 0.84
Sample size		977	977
Model 2—Academic problems
Months of education		0.00	−0.01
SE		0.00	0.01
95% CI		0.00, 0.00	−0.03, 0.00
Sample size		974	974

Note. Covariates included are educational attainment and participation at baseline, race, child gender, maternal and child age, prior welfare receipt, maternal numeracy and literacy skills, marital status, number of children, prior earnings, access to social support, the number of barriers to employment, number of risk factors, and mothers' locus of control. HCD = Human Capital Development; OLS = ordinary least squares; IV = instrumental variables; CI = confidence interval; BBCS/SRC = Bracken Basic Concept Scale/School Readiness Composite (Bracken, 1984).

^**p < .01.

Table 3. First-Stage Instrumental Variables Coefficients, F Statistics, Partial R-Squares, and Confidence Intervals.

Measure and instrument	Coefficient	SE	95% CI	F statistic for instruments	Partial R2	Shea's partial R2	Full model R2	Sample size
Months of education				21.61**	.04	.04	.18	2,858
Atlanta HCD	2.43**	0.34	1.80, 3.06
Atlanta LFA	0.59†	0.34	−0.09, 1.27
Grand Rapids HCD	1.01*	0.50	0.04, 1.99
Grand Rapids LFA	−1.01*	0.49	− 1.97, −0.05
Riverside HCD	2.79**	0.42	1.97, 3.63
Riverside LFA	−0.37	0.44	− 1.25, 0.49
Quarters of employment				9.25**	.02	.02	.21	2,858
Atlanta HCD	0.14	0.16	−0.17, 0.47
Atlanta LFA	0.34†	0.18	−0.01, 0.68
Grand Rapids HCD	0.00	0.25	−0.50, 0.49
Grand Rapids LFA	0.95**	0.25	0.47, 1.44
Riverside HCD	0.76**	0.21	0.34, 1.18
Riverside LFA	1.17**	0.22	0.73, 1.61

Note. Covariates included are educational attainment and participation at baseline, race, marital status, child gender, maternal and child age, prior welfare receipt, maternal numeracy and literary skills, number of children, prior earnings, access to social support, number of barriers to employment, number of risk factors, and mother's locus of control. CI = confidence interval; HCD = Human Capital Development; LFA = Labor Force Attachment.

^†p < .10.

^*p < .05.

^**p < .01.

Because we wish to estimate both maternal education and employment in our IV estimation models, more than one instrument is necessary to identify the model. A set of highly collinear instruments, even if they are strongly predictive in the first stage, may result in inconsistent or imprecise IV estimates (Shea, 1997). In our case, there must be a distinct pattern of associations between program treatment streams in each site and employment versus education. We expect this to be the case because of the differing emphasis of the HCD and LFA programs, but this assumption can be formally tested. To assess instrument relevance with multiple regressors, Shea (1997) devised a partial R-square statistic that takes into account the correlation among the instruments. If a first-stage regression provides a large partial R-squared value but a small value for Shea's partial R-square, then it is likely that the instruments lack sufficient strength to explain the endogenous regressors, and the model may not be appropriately identified.⁶ We find that the partial R-square and Shea's partial R-square are similar in our analysis (Table 3). As such, we infer that our instruments predict sufficient variation in the maternal education and employment to proceed.

Checking the choice of instruments: Does the instrument capture exogenous variation?

The instruments also must be uncorrelated with observed and unobserved sample characteristics. This assumption hinges on two underlying ideas. First, the instrument must be as good as randomly assigned, and second, the assignment must have resulted in comparable comparison groups. With data from an experimental design, instruments should meet both of these criteria, in theory. Nevertheless, it is important to check for balance on key characteristics. If the groups created by the instruments have differing background characteristics, then the instrument is not valid. As illustrated in Table 1, control and experimental group members, for the most part, do not differ on key characteristics across sites, with one notable exception. The mothers who were assigned to the LFA program in Atlanta were more economically disadvantaged than mothers assigned to the control group.⁷ In addition, although the differences were less pronounced, the LFA group in Riverside appeared to have a higher level of education than the comparison group. Although we are able to control for these initial differences with covariates, these disparities raise the possibility that the comparison group may not be equivalent on unmeasured characteristics. Consequently, we should be cautious in using assignment to an LFA program in Atlanta as an instrument. We return to this in the Discussion.

Checking the choice of instruments: Is monotonicity violated?

A further assumption is that the program did not induce someone to get less education or employment than they would have if they had been assigned to the control group. Angrist et al. (1996) referred to this as the “monotonicity assumption” (p. 450) and to participants who do take up treatment when assigned to the control group but not when assigned to the treatment group as “defiers” (p. 450). That is, we must assume that mothers, if assigned to the HCD group, would not get less education than if assigned to the control group, and if assigned to the control group, would not get more education than if assigned to the HCD group.⁸ In our case, it was possible for the control group to seek out education or employment and for the experimental group to refuse to participate. If some of the control group decided to seek out education, this in and of itself would not be a problem. It simply would reduce the predictive strength of the instrument. However, if the education sought out by the control group had more or less of a benefit for children than for the HCD experimental group children, this might lead to bias in the IV estimates, as the outcomes of the control group would be altered in an unmeasurable way.⁹

The monotonicity assumption cannot be directly assessed, but it is possible to gauge potential violations of this assumption by examining the cumulative distribution of the HCD, LFA, and control groups' education (Figure 3) and employment (Figure 4). An illustrative set of graphs for the Atlanta groups suggests that at all points in the educational spectrum, the HCD group had higher levels of educational participation than did controls and LFA group members. At all points in the employment distribution, LFA group members had higher levels of employment. This indicates that mothers in the HCD group participated in at least as much education as did those in the control group, and likewise, mothers in the LFA group undertook at least as much employment as or more employment than did the mothers in the control group. Graphs for the other sites were similar.

Figure 3.

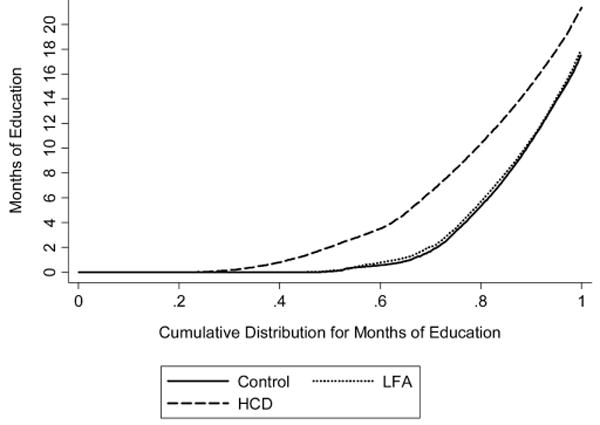
Cumulative distribution function for months of education in Atlanta GA. LFA = Labor Force Attachment; HCD = Human Capital Development.

Figure 4.

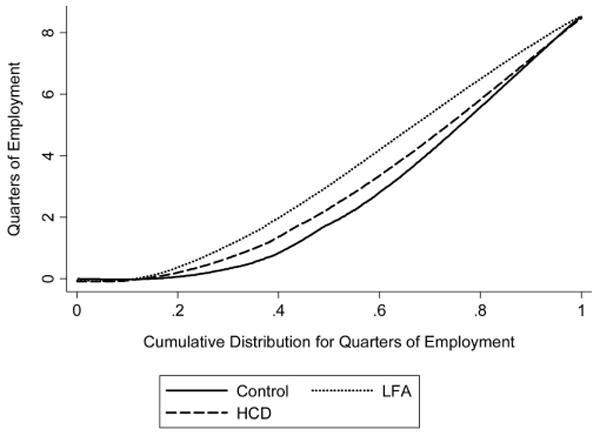
Cumulative distribution function for quarters of employment in Atlanta, GA. LFA = Labor Force Attachment; HCD = Human Capital Development.

These figures are also valuable for another reason. IV provides an estimate of the average effect of the portion of variation in the key independent variable predicted by the instrument. Whether the effect of the program was concentrated at a particular point in the distribution informs the interpretation of the estimates. For example, the HCD program may have induced mothers who otherwise would not have done so to attend school but may have done little to extend the schooling of those already attending school. If this was the case, we would likely see differences toward the lower end of the educational distribution rather than throughout the distribution. The figures make clear, however, that the HCD and LFA programs affected mothers at all points in the education and employment distributions.

Checking the choice of instruments: Meeting the exclusion restriction

One final key assumption is that the instruments only affect outcomes via the modeled pathways (i.e., endogenous regressors). Angrist et al. (1996) referred to this as the “exclusion assumption” (p. 447). The IV model assumes that the HCD and LFA programs only affected children's cognitive and school outcomes by increasing mothers' education or employment. If there are more instruments than endogenous regressors, then an overidentification test is useful.¹⁰ This test assumes that at least one instrument is exogenous, and thus the second-stage error term is correct. Under this assumption, correlating the remaining instruments with the second-stage error terms provides assurance that the other instruments yield consistent estimates. A common overidentification test for IV analysis is Sargan's statistic, which in our multiple-instrument example indicates that we should not reject the hypothesis that instruments are valid (4.6, p = .33).

Although passing the overidentification test is an important way to verify the validity of the instruments it is not foolproof as it assumes that at least one instrument is valid. Thus, it is also important to check the model for sensitivity to the inclusion of other potential pathways of influence (if a sufficient number of valid instruments allow). For this reason in the multiple-instrument example, we estimate the effect of three alternative pathways by which program participation may have affected children's outcomes.

Results

Suppose that as in the case of our earlier hypothetical example mothers were randomly assigned to just one education-related experimental condition, the HCD treatment, in just one site, Atlanta. If the HCD program improved mothers' educational participation, then we might implement IV analyses to consider whether improvements in mothers' education benefit their children. Figure 3 and Table 2 both demonstrate that indeed, the HCD program did increase mothers' educational participation. Limiting the analyses to the control and HCD group members (n = 976), the second stage of the IV results suggests that an additional month of education is associated with higher BBCS/SRC scores and lower levels of academic problems, but these estimates are quite imprecise, as shown by the confidence intervals in Table 2. The OLS estimates are in the same direction, but much smaller, and do not reach conventional levels of statistical significance.

The imprecision of the findings coupled with the knowledge that the HCD program also improved mothers' employment (see Figure 4) suggests that this simple case of a single instrument design limits our ability to draw any strong causal conclusions from the results. Capitalizing on three treatment streams across three treatment sites, we might increase our sample size and thus improve the power of our analyses (and the precision of the IV estimates). Using multiple instruments will also enable us to estimate more than one pathway by which the programs may have affected children.

The first panel of Table 4 presents the results for the OLS and IV estimations of the effect of mothers' educational activities on children's cognitive and school outcomes. The first column of the first row shows that, by OLS estimation, an additional month of mothers' education was significantly associated with a .089 higher score on children's BBCS/SRC scores (p < .05). The second column shows that, by IV estimation, an additional month of maternal education was associated with a .305 increase in a child's score (p < .10). The effect of maternal employment was positive in both the OLS and IV models but imprecisely estimated in the IV model.

Table 4. Instrumental Variables and Ordinary Least Squares Estimates of Months in Adult Basic Education on Children's Raw Bracken Basic Concept Scale/School Readiness Composite (BBCS/SRC; Bracken, 1984) Scores and Academic Problems.

Independent variable	Model 1		Model 2
	OLS	IV	OLS	IV
BBCS/SRC scores
Months in education	0.07*	0.31†	0.08**	0.31†
SE	0.03	0.17	0.04	0.17
95% CI	0.01, 0.14	−0.02, 0.63	0.01, 0.15	−0.02, 0.63
Quarters of employment			0.15*	0.49
SE			0.07	0.50
95% CI			0.01, 0.29	−0.50, 1.48
Sample size	2,858	2,858	2,858	2,858
Academic problems
Months in education	0.00	−0.01*	0.00	−0.01*
SE	0.00	0.01	0.00	0.01
95% CI	0.00, 0.00	−0.02, 0.00	0.00, 0.00	−0.02, 0.00
Quarters of employment			0.00	0.01
SE			0.00	0.02
95% CI			0.00, 0.01	−0.03, 0.04
Sample size	2,854	2,854	2,854	2,854

Note. Covariates included are educational attainment and participation at baseline, race, child gender, maternal and child age, prior welfare receipt, maternal numeracy and literary skills, marital status, number of children, prior earnings, access to social support, number of barriers to employment, number of risk factors, and mother's locus of control. OLS = ordinary least squares; IV = instrumental variables; CI = confidence interval.

^†p < .10.

^*p < .05.

^**p < .01.

The second panel of Table 4 presents the results of the OLS and IV estimates for the effect of months in educational activity on whether the focal child experienced any academic problems during the 2-year follow-up period. The OLS findings suggest that an additional month of maternal education did not predict children's academic problems. In contrast, the IV estimate suggests that an additional month of maternal education resulted in .012 fewer educational problems. Columns 3 and 4 show that estimating the effects of maternal employment as an independent variable did not change the size or significance of the IV or OLS coefficients and that maternal employment had no discernible effect on academic problems.

Why might the estimates of the IV analyses be larger than those from the OLS analyses? Although mothers were randomly assigned to a treatment stream, not all mothers complied with the treatment, and the length of their participation in educational activities was not randomly allocated across mothers. By program design, mothers with low basic skills were directed to educational activities and generally continued in these activities until their skills improved (Hamilton, Brock, Farrell, Friedlander, & Harknett, 1997). Therefore, mothers spent more time in educational activities if it took them longer to learn new skills, perhaps because they had lower levels of skills to begin with or were less motivated. Lower levels of initial skills or low motivation may be negatively associated with children's academic skills and positively associated with children's academic problems. Omitting these variables may lead OLS models to underestimate the effect of maternal schooling on children's school outcomes.

Choice of Functional Forms and Standard Error Corrections

Our analysis uses continuous measures of maternal education and employment, but an alternative is to focus on dichotomous ones (whether a mother was ever in school or ever employed). When the endogenous regressor is dichotomous, one must choose between using OLS methods in the first stage in an existing IV software procedure or manually estimating the two regressions (i.e., estimating the first stage, saving the predicted value as a variable, and using this predicted value as a covariate in the second-stage equation) and adjusting standard errors with matrix algebra (see Murphy & Topel, 1985). The first approach is recommended by Angrist and Krueger (2001) because OLS is often more stable than other functional forms, assuming that the predicted values from the first stage are plausible. In many applications a two-stage least square approach produces estimates similar to those from a more complicated nonlinear functional form.

To illustrate how sensitive our results are to the choice of functional form, we estimated an IV model with the treatment measured as whether the mother ever participated in an educational program. Using an existing IV procedure which implements OLS in the first stage, the resulting predicted values for whether a mother ever attended school ranged from −.13 to 1.31, with a mean of .34. In the second stage, the estimated effect of the mother's ever having attended school on the BBCS/SRC was 2.82, and the standard error was 1.48. Manual estimates with a probit model yielded predicted values that fell in a more appropriate range, between .02 and .99, with a mean of .34. Placing these predicted values in the second stage, the resulting association between the mother's ever having attended school and BBCS/SRC scores was about 2.90, with a standard error of 1.46. This confirmed that the estimates are not sensitive to the functional form of the first stage. Moreover, given that a month of education was associated with a .31 higher score on the BBCS/SRC, and the average mother who attended school in the HCD group did so for 8 months, these estimates provide a similar magnitude of total effects (.31 × 8.2 = 2.54). Manual calculations of the two stages resulted in a standard error that was smaller than the standard errors produced through a software routine, because there are no corrections for the artificially reduced variance in the predicted values.

When the outcome variable is dichotomous, researchers must also be concerned with the functional form of their models. For example, perhaps we had a measure of whether children had met a school readiness benchmark rather than a continuous measure. For cases in which the outcome but not the treatment is dichotomous, both linear two-stage least square models and nonlinear multivariate probit models, which are estimated with maximum likelihood functions, produce consistent estimates (Battacharya, Goldman, & McCaffrey, 2006). In cases in which both the treatment and the outcome are dichotomous or in cases in which the data deviate strongly from normality assumptions, multivariate probit models appear to perform better than two-stage least square models (Battacharya et al., 2006).¹¹

Further Checks on Violating IV Assumptions

We noted earlier that some baseline characteristics of the Atlanta LFA group differed from those of the Atlanta comparison group, raising questions about the validity of the Atlanta LFA instrument. We tested for the sensitivity of our results to the exclusion of the LFA instrument and participants, and in a second model also excluded the Riverside LFA instrument and participants. The resulting estimates for the effects of maternal education were slightly larger than those reported in Table 4 and more precisely estimated (for example, for the BBCS/SRC, these estimates were .34 [p < .10] and .38 [p < .05], respectively).

We might also worry that we have not modeled all of the key pathways by which assignment to the HCD and LFA program might have influenced children's academic skills. Mothers' earnings, welfare receipt, and sanctioning may have also been affected by the programs and perhaps affected children's achievement above and beyond the effect of months of maternal education and quarters of employment. One approach would be to model three pathways at once. Although F tests for the excluded instruments in the first stage were sufficiently large, discrepancies between the partial R-squares and Shea's partial R-squares suggest that there is not sufficient unique variation in our instruments to jointly estimate three endogenous regressors. Consequently, we estimated a series of models with just two instruments and substituted sanctioning, earnings, and welfare receipt for the number of quarters of employment. Resulting estimates were similar to those presented in Table 4.

Discussion

The IV technique is one promising strategy for answering questions about causality that can advance developmental theory and knowledge about the nature and magnitude of associations. We emphasize the careful examination of assumptions for estimating an IV model. The approach is detailed through an empirical example about the effects of maternal education that also substantively contributes to developmental research. We were able to assess whether maternal education causally improves children's academic skills or whether the observed associations reflect some other characteristic related to parenting, income, or personality. The IV estimates showed that additional maternal education among a welfare population has a positive effect on the academic skills of their young children.

That a broader variety of analytic approaches to identify causal paths has not entered a development psychologist's repertoire might strike some as surprising (Foster & McLanahan, 1996; National Institute of Child Health and Human Development Early Child Care Research Network & Duncan, 2002). In fact, IV in particular has been embraced by economists for some time (see reviews by Angrist & Krueger, 2001). We discuss two likely reasons why developmentalists have not used IV methodology.

First, instruments that satisfy the assumptions of IV may be hard to find. In this article, we focus on social policy experiments. In developmental psychology, there is a long tradition of lab-based experiments that could indeed be expanded to address questions about the magnitude of causal pathways. A body of research, for example, has examined how infants react to experimentally manipulated parent–child face-to-face interactions (Field, 1977; Murray & Trevarthen, 1985; Tronick, Als, Adamson, Wise, & Brazelton, 1978). These data could be leveraged to estimate the causal effect of controlling and responsive parenting on children's behavior.

IV models might also be used in the context of prevention/intervention research. Research conducted on the Fast Track Prevention Trial for Conduct Problems is a perfect case in point (Conduct Problems Prevention Research Group [CPPRG], 1999a, 1999b). The treatment targeted children's emotional awareness, affective–cognitive control, and social-cognitive understanding as a means to reduce aggressive behavior. Yet, the study has not yet been exploited for estimating the causal effects of these developmentally based competencies on children's peer relations.

The challenge, of course, is that interventions are multifaceted, and the primary target (e.g., childhood problem behaviors or achievement in school) might be influenced by a variety of paths. In this case, single instruments (treatment/control group status) will not be sufficient to capture these multiple pathways. One option is to exploit variation across multiple sites. In the case of Fast Track (CPPRG, 1999a 1999b), site variation in implementation, if it exists, can be used with IV estimation. This would be especially critical for the Fast Track high-risk sample, who received both the universal social skills training curriculum as well as specific parent-focused interventions; having multiple instruments is necessary to unpack the separate effects of these pathways.

It is also possible to pool or combine data from multiple interventions, if they had similar enough samples and intervention targets, and use the multiple treatment indicators as instruments to estimate multiple pathways (see, for example, Crosby et al., 2006; Gennetian et al., 2006; Morris et al., 2006). Interestingly, research by Beauchaine, Webster-Stratton, and Reid (2005) combined data across six randomized clinical trials to estimate mediational models of the effects of parenting on child conduct disorders. Their work, combining interventions that target parents' behavior, child social skills, and teachers' behavior, could clearly take advantage of the IV technique to identify the causal effects of each of these targets on child conduct disorders. Finally, experiments with multiple treatment arms can be designed a priori with IV applications in mind.

Experiments are promising but not always a feasible alternative for researchers. What other types of exogenous variation might be exploited? One traditional approach is to rely on naturally occurring variation in policies over time or across locations. Another is to take advantage of independent changes in one's environment: One recent example is the new availability of cable television in a community. Access to cable TV can serve as a proxy for exposure to different types of educational programming and possibly as a way to estimate effects of the quality of TV programming watched on children's development. We caution researchers that meeting the assumptions of IV are difficult when relying on naturally induced variation, and the opportunities to exploit circumstances such as the independent changes in the environment are rare.

The second reason that developmentalists may be reluctant to use IV is that many developmental questions are focused on testing structural models about phenomena rather than identifying a single pathway. And, admittedly, IV is best suited to address the latter. Two points are worth mentioning. First, as we illustrate, structural equation models can indeed be set up in such a way as to match the assumptions underlying the IV approach. Second, IV could be used to test causal assumptions about single pathways estimated in larger structural models. That is, IV may provide evidence as to the strength of particular causal pathways that are estimated in the context of larger structural models.

Researchers face a myriad of trade-offs in deciding the merits of appropriate methods. Our goal in this article is to illustrate and make accessible a compelling strategy for developmental research that will contribute to evidence about causation and, in so doing, to advance developmental science. It is our hope that this and other causal estimation techniques will be used with more frequency in developmental science and to answer a broader set of questions about how micro- and macroenvironments affect developmental outcomes for children.

Appendix: Examples of Syntax for Instrumental Variables Model

SPSS SYNTAX

*2-Stage Least Squares.

TSET NEWVAR = NONE.

WEIGHT BY fullwgt.

2SLS brackenscore WITH monthseducation covariates

/INSTRUMENTS athcd atlfa grhcd grlfa rivhcd rivlfa covariates

/CONSTANT.

SAS SYNTAX

proc syslin 2sls;

• weight fullwgt;

/* LIST MEDIATORS*/

• endogenous monthseducation;

• /*LIST INSTRUMENTS*/

  • instruments athcd atlfa grhcd grlfa rivhcd rivlfa;

/* MODEL THE ENDOGENOUS REGRESSOR AS FUNCTION OF INSTRUMENTS AND CONTROLS TO DISPLAY FIRST STAGE RESULTS*/

• model monthseducation = athcd atlfa grhcd grlfa rivhcd rivlfa covariates;

/* MODEL THE OUTCOME AS FUNCTION OF ENDOGENOUS REGRESSOR AND CONTROLS TO DISPLAY SECOND STAGE RESULTS*/

• model brackenscore = monthseducation covariates;

STATA SYNTAX

ivreg2 brackenscore (monthseducation = athcd atlfa grhcd grlfa rivhcd rivlfa) covariates, first; overid;