Abstract
Purpose: This work applies a cascaded systems model for cone-beam CT imaging performance to the design and optimization of a system for musculoskeletal extremity imaging. The model provides a quantitative guide to the selection of system geometry, source and detector components, acquisition techniques, and reconstruction parameters.
Methods: The model is based on cascaded systems analysis of the 3D noise-power spectrum (NPS) and noise-equivalent quanta (NEQ) combined with factors of system geometry (magnification, focal spot size, and scatter-to-primary ratio) and anatomical background clutter. The model was extended to task-based analysis of detectability index (d′) for tasks ranging in contrast and frequency content, and d′ was computed as a function of system magnification, detector pixel size, focal spot size, kVp, dose, electronic noise, voxel size, and reconstruction filter to examine trade-offs and optima among such factors in multivariate analysis. The model was tested quantitatively versus the measured NPS and qualitatively in cadaver images as a function of kVp, dose, pixel size, and reconstruction filter under conditions corresponding to the proposed scanner.
Results: The analysis quantified trade-offs among factors of spatial resolution, noise, and dose. System magnification (M) was a critical design parameter with strong effect on spatial resolution, dose, and x-ray scatter, and a fairly robust optimum was identified at M ∼ 1.3 for the imaging tasks considered. The results suggested kVp selection in the range of ∼65–90 kVp, the lower end (65 kVp) maximizing subject contrast and the upper end maximizing NEQ (90 kVp). The analysis quantified fairly intuitive results—e.g., ∼0.1–0.2 mm pixel size (and a sharp reconstruction filter) optimal for high-frequency tasks (bone detail) compared to ∼0.4 mm pixel size (and a smooth reconstruction filter) for low-frequency (soft-tissue) tasks. This result suggests a specific protocol for 1 × 1 (full-resolution) projection data acquisition followed by full-resolution reconstruction with a sharp filter for high-frequency tasks along with 2 × 2 binning reconstruction with a smooth filter for low-frequency tasks. The analysis guided selection of specific source and detector components implemented on the proposed scanner. The analysis also quantified the potential benefits and points of diminishing return in focal spot size, reduced electronic noise, finer detector pixels, and low-dose limits of detectability. Theoretical results agreed quantitatively with the measured NPS and qualitatively with evaluation of cadaver images by a musculoskeletal radiologist.
Conclusions: A fairly comprehensive model for 3D imaging performance in cone-beam CT combines factors of quantum noise, system geometry, anatomical background, and imaging task. The analysis provided a valuable, quantitative guide to design, optimization, and technique selection for a musculoskeletal extremities imaging system under development.
Keywords: musculoskeletal radiology, cone-beam computed tomography, cascaded systems analysis, flat-panel detector, imaging performance, noise-power spectrum, noise-equivalent quanta, anatomical clutter, system optimization, observer performance, detectability index
INTRODUCTION
Cone-beam computed tomography (CBCT) with flat-panel detectors (FPDs) has entered a host of applications in preclinical imaging (e.g., small animal scanners), diagnostic imaging (e.g., breast and maxillofacial scanners), and image-guided procedures (e.g., C-arms and medical linear accelerators). The technology provides volumetric imaging from a single rotation about the subject with submillimeter spatial resolution and soft-tissue visibility. As described previously,1, 2 a FPD-CBCT system is being developed for musculoskeletal extremities imaging. The system offers a compact embodiment for imaging the upper or lower extremities that complements CT and MR in the ability to image weight-bearing extremities and the capability for integrated radiography, motion/kinematic imaging, and volumetric imaging within the same platform.
Cascaded systems analysis has been shown to describe the imaging performance of CBCT in terms of Fourier domain metrics, including the fully 3D noise-power spectrum (NPS), modulation transfer function (MTF), and noise-equivalent quanta (NEQ).3, 4, 5, 6, 7, 8 Such analysis can be extended to simple models of observer performance in terms of task-based detectability index (d′),9 which has been shown to demonstrate reasonable correspondence with real observer performance for a variety of simple imaging tasks across a broad range of experimental conditions.10
A considerable body of previous work established the basis for modeling of CBCT imaging performance. For example, Siewerdsen and Jaffray11 showed a cascaded systems model for 3D NPS and NEQ in CBCT to agree with measurements and to reduce to the classic descriptions of voxel noise. They also exercised the model to examine trade-offs in spatial resolution and noise in the presence of x-ray scatter12 and the effect of direct- and indirect-detection FPD characteristics on CBCT image quality.13 Tward and Siewerdsen 5, 6 extended the model to task-based detectability index and described the effects of 3D noise aliasing. Such analysis applies to both limited-angle tomography (tomosynthesis)14, 15 and CBCT in that the extent of the source-detector orbit is a free parameter. Factors beyond quantum noise are known to have significant effect on CBCT image quality and can be similarly modeled—most notably, x-ray scatter, focal spot blur, and anatomical background clutter. X-ray scatter and focal spot blur depend strongly on system geometry and have been included in descriptions of the “system” NEQ.7, 16, 17, 18, 19 Jain et al.17 and Kyprianou et al.18 extended the analysis of MTF, NPS, and NEQ to include both scatter and focal spot blur, and Kyprianou et al.20 employed the model to investigate the performance of a neurovascular angiography system. The effect of anatomical background on detectability is a subject of considerable interest, commonly modeling the background as power-law noise κ∕fβ included as an additive noise term in the “generalized” NEQ. For example, in breast imaging, the power-law characteristic in 2D mammographic images was characterized by Bochud et al.,21 Burgess,22, 23 and others24 and extended to 3D breast imaging by Metheany et al.,25 Engstrom et al.,26 Glick et al.,27 Gong et al.,28 and Reiser and Nishikawa,29 showing β differs in 2D projections versus 3D tomosynthesis and CBCT reconstructions. In a fairly general context, Gang et al.30 showed power-law background noise to arise from superposition of self-similar (fractal) structures in 2D and 3D images, derived relations between β in projection, tomosynthesis, and CBCT, and incorporated the result in a generalized detectability index. Yoon et al.14 used such modeling to characterize the rejection of background clutter in tomosynthesis, and Siewerdsen et al.31 showed the dependence of CBCT detectability on the clutter factor (β) and the size of the stimulus (e.g., low- or high-frequency tasks).23, 32
The work below applies such approaches in a model that includes basic cascaded systems analysis parameters (quantum noise), system parameters (x-ray scatter and focal spot blur), and generalized parameters (anatomical background) toward the design and optimization of a CBCT system being developed for musculoskeletal extremities imaging. The research is distinct from previous work not only in the specific area of clinical application but also in the fairly comprehensive model that combines descriptions of quantum, system, and generalized noise factors. The sections below: (1) summarize the cascaded systems model; (2) extend to task-based detectability index; (3) compare to quantitative measurements of NPS and qualitative evaluation of cadaver images; and (4) evaluate the dependence of detectability on system geometry, acquisition techniques, and reconstruction techniques as a guide to design and optimization of an extremities CBCT scanner.
THEORETICAL METHODS
Cascaded systems analysis
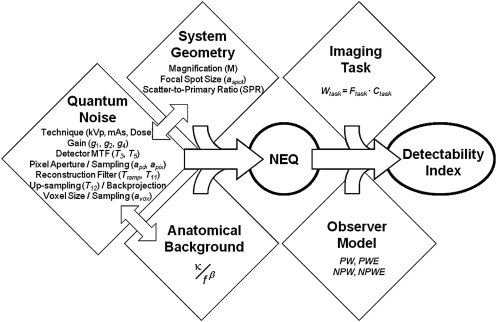
The fundamental aspects of cascaded systems analysis have been discussed in previous work3, 4, 33, 34 in modeling the imaging chain as a series of amplification, blur, and sampling stages, where output from one stage serves as the input for the next. Early work involved application of cascaded systems analysis in modeling of indirect and direct-detection FPDs,3, 4 extended to descriptions of mammography35 and angiography,7, 19 dual-energy imaging,36, 37 tomosynthesis,15 and CBCT.5, 30 Variations include incorporation of various system factors (viz., magnification, focal spot size, and x-ray scatter)16, 17, 18 and generalization to include noise factors other than quantum noise (viz., anatomical background clutter).30, 36 Such models have shown good agreement with measured MTF, NPS, detective quantum efficiency (DQE), and NEQ, and have been incorporated in task-based models of detectability index (d′) in a manner that yields reasonable correspondence with human observer performance for a variety of simple imaging tasks across a broad range of imaging conditions.10 A conceptual diagram combining factors of quantum noise, system parameters, background noise, and interdependencies in the NEQ is shown in Fig. 1.
Figure 1.
Flowchart illustration of the model for CBCT imaging performance combining factors of quantum noise, system parameters (focal spot blur, magnification, and x-ray scatter), and background anatomical noise.
The 3D NEQ
The NEQ is an important figure of merit describing the number of photons at each spatial frequency for which an ideal detector would produce the same NPS.38, 39 The following sections summarize three distinct forms of NEQ: (1) a form representing only the quantum noise (including factors of kVp, dose, scintillator, FPD design, readout electronics, etc.) propagated through the 2D image acquisition and 3D reconstruction process5; (2) an extension to include various system parameters (viz., magnification, focal spot size, and x-ray scatter)17, 18; and (3) an extension to include additional factors within the denominator of the NEQ (viz., anatomical background noise, originally termed a “generalized” NEQ by Barrett et al.40, 41).30 Finally, these forms are pulled together in a fairly comprehensive model of 3D NEQ as illustrated in Fig. 1, presenting a broad space of parameters and interdependencies to be considered in imaging system optimization. Details of the individual models and parameters are found in the references noted above and briefly summarized below.
“Quantum” NEQ
As described by Cunningham,38 there are several equivalent ways to define the NEQ (conceptual, descriptive, stochastic, and predictive). The “stochastic” form can be readily adapted to describe the 3D quantum noise in CBCT5
| (1) |
where fx, fy, fz are the 3D spatial-frequency coordinates, and represents the cylindrically symmetric radial frequency. and describe quantum noise and electronics noise associated with the total input quanta, , respectively (with the superscript tot distinguishing the total fluence from primary and scatter fluence terms, below). The Ti represent the transfer function (MTF) associated with different stages in the imaging chain—e.g., T3 (scintillator MTF), T5 (photodiode aperture MTF), T11 (apodization filter MTF), and T12 (interpolation filter MTF). Notation throughout is as consistent as possible with previous work5, 6 and summarized in Table TABLE I.. Note that the equation involves fully 3D MTF and NPS terms [the latter with units (μ2)(mm3), where μ is attenuation coefficient, e.g., (mm−1)], giving 3D NEQ with units [(mm−2), interpreted as (photons/mm2)].
Table 1.
Summary of terms used in cascaded systems analysis.
| Term | Definition | Nominal value |
|---|---|---|
| fu, fv | Spatial-frequency domain at the detector plane | — |
| fx, fy, fz | Spatial-frequency domain at the 3D object volume | — |
| gj | Gain at stage j | — |
| Tj | Transfer function at stage j | — |
| SQ | NPS due to quantum noise | — |
| SE | NPS due to additive electronics noise | — |
| κ | Anatomical clutter magnitude | 3.3 × 10−10 μ2 mm3 |
| β | Anatomical clutter power-law exponent | 3 |
| SB | Power spectrum due to anatomical background clutter | — |
| E | Eye-filter transfer function | — |
| Ni | NPS for observer internal noise | — |
| Mean fluence per projection incident on the detector after attenuation by object | 3.94 × 103 mm−2 | |
| X | Exposure per projection at the detector after object attenuation | 0.027 mR |
| apd | Photodiode width (square) | 0.16 mm |
| apix | Detector pixel aperture width (square) | 0.194 mm |
| avox | Voxel size (natural voxel size: avox = apix/M) | 0.15 mm |
| aspot | Focal spot size | 0.5 mm |
| SDD | Source-detector distance | 525 mm |
| SAD | Source-axis distance | 410 mm |
| M | System magnification, M = SDD/SAD | 1.28 |
| m | Number of projections | 480 |
| SPR | Scatter-to-primary ratio | ∼1.0 |
| σadd | Additive electronics noise | 2000 e/pixel |
| kVp | Beam energy (peak kilovoltage) | 90 kVp |
| D | Dose to water at isocenter (16 cm cylinder) | 5 mGy |
| hwin | (Cosine) reconstruction filter parameter | 0.5 (Hann) |
System NEQ
Factors of magnification, focal spot size, and x-ray scatter have been incorporated within the NEQ under the moniker of “system NEQ” (sometimes called “generalized NEQ,” but the former term is used here to avoid confusion with inclusion of anatomical background noise, below, with deference to Barrett’s original use of the term “generalized”40, 41). The x-ray focal spot is a source of blur16, 17, 18 for systems with geometric magnification, M, degrading the numerator of the NEQ (the system MTF) but not the stochastic quantum noise in the denominator, SQ. X-ray scatter from the object can be similarly included in the system NEQ,17, 18 and introduces blur, noise, and contrast degradation. The x-ray fluence at the detector includes both primary and scattered radiation ( and , respectively), giving for the system NEQ
| (2) |
where frequency notation on MTF and NPS terms is implicit but has been dropped for conciseness. Tspot is the focal spot MTF, Tscatter is the scatter MTF, is the total quantum noise due to primary and scattered fluence, and is the electronics noise (relative to the primary + scatter fluence as detailed in Appendix C). The superscript on NPS terms and is distinct from in that it allows for separate consideration of primary and scattered quanta in the 3D NPS (e.g., different x-ray spectra; see Appendix C). All of these terms carry implicit dependence on the system magnification, M. The focal spot was modeled as a uniform rect of width aspot. The scatter MTF was described by Seibert and Boone42 in the form of a “scatter psf,” modeled as the spatial domain product of Gaussian kernel and 1/r, where r is the radial distance from the origin. The corresponding Fourier domain scatter MTF is a product of a Gaussian and a zeroth-order modified Bessel function with a constant scale factor related to scatter fraction. Kyprianou et al.18 extended the analysis to a composite frequency distribution of blur given by addition of weighted MTF components of both primary and scattered radiations.
Generalized NEQ
The generalized NEQ includes any number of additional noise terms added to the denominator as suggested by Barrett.40, 41 Specifically, anatomical background clutter (i.e., anatomical structures present in the image but not associated with the signal to be detected) is included as an additional power spectrum, SB(f, fz). Extending the 3D quantum NEQ of Eq. 1 to include anatomical noise gives
| (3) |
where the various MTF terms are applied to SB to emphasize that SB is a property of the object being imaged, and that its presentation within the image is subject to blur by the imaging system. The power spectrum associated with anatomical clutter has been investigated in depth in the context of 2D projection imaging,21, 23, 36 and more recently in 3D imaging,25, 29, 43 with an empirical power-law (κ∕fβ) form being fairly ubiquitous and shown by Gang et al.30 to correspond to the projection (or 3D reconstruction) of a collection of randomly sized and oriented self-similar (fractal) objects. Details of the power-law form and dependencies on other system factors (e.g., beam energy) are discussed in Appendix D.
A comprehensive model
The quantum, system, and generalized forms of the NEQ summarized in Eqs. 1, 2, 3 can be brought together in a comprehensive form
| (4) |
where Eq. 2 was combined with Eq. 3 to yield a fairly comprehensive model for NEQ that accounts for all three factors: quantum noise, system factors (such as magnification, focal spot size, and x-ray scatter), and background anatomical noise. That is, the system NEQ of Eq. 2 ignores factors explicit in the generalized NEQ of Eq. 3—and vice versa; however, each can be combined in the fairly comprehensive form of Eq. 4, as each is grounded in the same underlying framework of linear systems analysis. While there is a temptation to continue applying a string of monikers and sub/superscripts (e.g., “generalized system NEQ”), we refer to it simply as the NEQ and refer instead to specific forms in Eqs. 1, 2, 3 by distinct labels of quantum, system, and generalized, respectively. For the sake of conciseness within the main text, details of individual terms in the NEQ are included in the Appendices. Appendix A describes the MTF terms. Appendix B describes the x-ray scatter model. Appendix C describes the NPS for quantum and electronics noise, Sq and SE, and Appendix D describes the power-law model of anatomical clutter.
Two simplifying assumptions are made regarding x-ray scatter. First, we assume that x-ray scatter imparts a reduction in contrast, an additive quantum noise source, but does not blur the image—i.e., is constant, independent of spatial-frequency, given by 1/(1 + SPR). Analysis without such assumption has been detailed by Kyprianou et al.18 We further assume the x-ray scatter spectrum has the same shape as the primary. The effects neglected in such analysis are believed to be small (e.g., maximum energy shift due to x-ray scatter <10 keV and scatter MTF dominated by focal spot and detector MTF). While neither is a necessary assumption, they allow simplification of the model to a relatively compact analytical form with respect to a system parameter space that is already quite broad. These simplifying assumptions yield a concise form for the NEQ including both system parameters of magnification, focal spot blur, and SPR as well as generalized parameters of anatomical background
| (5) |
The SPR term arises simply from the assumption of a constant Tscatter and reproduces the familiar factor (1/1 + SPR) as the (low-frequency) degradation due to a scatter. Neglecting the energy shifts in the scatter spectrum (as justified in Appendix C) reduces to . Note that the SB term [see Eq. D2 in Appendix D] also depends on SPR in such a way that scatter reduces the contrast of background clutter by a factor of 1/(1 + SPR), reducing the third term in the denominator in proportion to 1/(1 + SPR)2.
The 3D detectability index
Extension of the NEQ to task-based analysis of detectability index9 (d′) allows investigation of the broad space of system design parameters, acquisition techniques, and 3D reconstruction parameters in terms of a summary objective function (figure of merit) for multivariate optimization in the design of a CBCT scanner. The detectability index has been used as an objective function for system optimization in a variety of applications30, 37, 44 and Gang et al.10 have demonstrated reasonable correspondence with real observer performance for simple imaging tasks. The work of Gang et al.10 formed an important theoretical/experimental justification for the current work and provided confidence that the trends and optima computed in this paper will bear correspondence with real observer performance for simple imaging tasks. Basic observer models for d′ are as follows:
3D prewhitening (PW) model
The PW observer simply weights the NEQ by a template (a matched filter or “task function”) representing the spatial frequencies of interest in performing the task. It assumes an ideal observer capable of “whitening” (decorrelating) noise in the image9
| (6) |
where MTF represents the system MTF, MTF = T3T5T11T12TspotTscatter, and the integral is performed over the 3D Nyquist frequency region. Wtask is the frequency domain representation of the imaging task defined as the Fourier transform of binary hypotheses as detailed below.
3D nonprewhitening (NPW) model
The NPW observer45 does not decorrelate the image noise but instead applies a detection template in the form of the expected signal
| (7) |
The NPW model has been shown to describe human observers somewhat better than the PW model in cases of, for example, high-pass-filtered images, such as CT.10, 46
2D “slice” models including the eye filter and internal noise (PWEi and NPWEi)
The two models above can be extended to include an eye filter, E, and observer internal noise, Ni.47, 48 While the form of the eye-filter and internal noise models have been investigated for 2D image data, they have not been extended or validated with regard to 3D data (e.g., volumetric viewing, scrolling of slices) and fully 3D observer models are a subject of ongoing research within the perception community. The fully 3D forms for dPW' and dNPW' assume the observer is capable of perceiving the entirety of volumetric image information, which may or may not be the case for scrolling slices, etc. However, the fully 3D d′ can be reduced to a form describing detectability in a single (axial, coronal, or sagittal) slice extracted from a 3D volume as described by Gang et al.10 Since extraction of a slice in the spatial domain [e.g., in the axial (x,y) domain] corresponds to convolution with the Fourier profile of slice thickness in the orthogonal direction of the Fourier domain [e.g., in the fz direction], the slice detectability index can be written with an extra integral (convolution) over the orthogonal domain. For example, assuming an infinitesimally thin slice, the axial slice detectability index is given by convolution over fz (i.e., convolution with the Fourier transform of the delta function)
| (8) |
| (9) |
and similarly for the sagittal or coronal slice detectability with integrals over fx or fy, respectively. The detectability can now be written in a form including the 2D eye filter (E) and internal noise models (Ni). For the NPW model, for example, we have
| (10) |
where the eye filter was taken from Barten48
| (11) |
with c = 2.2 mm−1, and the internal noise was scaled as a function of viewing distance (e.g., D = 50 cm) and the zero-frequency component of the white noise-equivalent of total NPS49
| (12) |
where NPSeq is a white noise-power spectrum equivalent in total power to the total NPS (i.e., sum of SQ, Se, and SB), and the scale factor 0.001 as in Gang et al.10 The slice NPWEi model (i.e., the NPW model with eye filter and internal noise) has been shown to yield reasonable agreement with human observer response10 for simple tasks over a broad range of imaging conditions.
Imaging tasks
The task function explicit within the detectability index conveys the spatial frequencies of interest in performing the task, most simply defined in terms of binary hypothesis testing—e.g., a detection task with hypotheses of “signal present” versus “signal absent” or a discrimination task of hypotheses “stimulus A” versus “stimulus B.” Three imaging tasks were used in the work below, selected to represent a range in detail (i.e., low-, middle-, and high-frequency tasks) with general consideration of tissue contrasts relevant to extremity CT imaging (e.g., muscle, fat, and bone). The task function (WTask) may be written as a product of a spatial-frequency term (FTask) and a contrast term (CTask) representing the signal difference of the stimulus against background
| (13) |
| (14) |
| (15) |
where the contrast term CTask for CBCT images is fundamentally given by the difference in effective attenuation coefficients each computed by integrating the linear attenuation coefficients μ(E) over the x-ray spectrum and including two factors of contrast degradation: x-ray scatter [1/(1 + SPR)] and partial volume (Pvol) effect. The spectrum was modeled using the Spektr toolkit50 implementation of the TASMIP model.51 The attenuation coefficients were taken from NIST52 and ICRU Report 46.53 With regard to an extremity CT scanner, stimuli were assumed to be at the center of an object approximating a knee—i.e., a 16 cm water cylinder including an inner cylinder of 8 cm diameter bone (viz., 7.6 cm of trabecular bone and 0.4 cm of cortical bone).
The contrast term in each task function carries a dependence on kVp, SPR, system magnification, and a possible partial volume effect. The kVp dependence is implicit in the effective attenuation coefficients. The SPR dependence is manifest in the factor 1/(1 + SPR), which in turn depends on magnification as in Appendix B. The partial volume factor describes a loss in signal magnitude for stimuli smaller than the voxel size. An important caveat regarding partial volume effect must be noted: Pvol calculations assume that the 3D stimulus is located at the center of a single voxel, and that the signal is not spread across multiple voxels. This assumption violates the shift invariance assumption underlying cascaded systems analysis, invoking the “cyclostationary” condition suggested by Cunningham et al.54 and recognizing that the effects of such shift invariance is typically small.55 In this way, stimuli smaller than the voxel size (and assumed to reside entirely within a single voxel) present as a single enhanced voxel but with contrast reduced by the Pvol factor.
The frequency term was computed separately for three tasks emphasizing low, middle, and high frequencies. Task 1 was a low-contrast (“muscle stimulus vs water background”) task emphasizing low spatial frequencies in the detection of a Gaussian blob on a uniform background
| (16) |
with the size of the stimulus, atask, taken nominally as 1 mm. For task 1, was computed from the attenuation coefficient of muscle, and was computed from the attenuation coefficient of water.
Task 2 was a high-contrast (“bone vs fat”) task emphasizing middle frequencies corresponding to detection of a submillimeter cube (3D rect) against a uniform background
| (17) |
where the first conditional corresponds to a stimulus greater than the voxel size, and the second implies that the stimulus is smaller than the voxel size and is evident as an enhancement of the entire voxel (but at reduced contrast due to partial volume). The nominal stimulus size was atask = 0.3 mm, and the voxel size varied as (apix/M). For task 2, was computed from the attenuation coefficient of bone, and was computed from the attenuation coefficient of fat.
Task 3 was a low-contrast (“muscle vs water”) task emphasizing high spatial frequencies corresponding to discrimination of a Gaussian against statistically defined “white” noise background
| (18) |
where the size of the stimulus was atask = 0.65 mm. For task 3, and were the same as for task 1.
Optimization parameters
The optimization study was organized according to: (1) factors affecting spatial resolution; (2) factors affecting image noise and dose; and (3) multivariate combinations thereof. The range and nominal values for the most pertinent parameters are summarized as follows.
Factors of spatial resolution
Magnification
System magnification (M = SDD/SAD) varied from 1 to 2, keeping source-to-isocenter distance (SAD) fixed at 410 cm to fix the dose at isocenter irrespective of magnification. The nominal value was M = 1.28, corresponding to the value identified in preliminary work.1, 2 Variation in M affected a multitude of dependent parameters, including: focal spot and detector MTF (referenced to isocenter); fluence to the detector (inverse-square law); the “natural” voxel size (avox=apix∕M) and the SPR (via the scatter point source model in Appendix B).
Focal spot size
X-ray focal spot size varied from 0 to 1.5 mm, with a nominal value of aspot = 0.5 mm corresponding to a commercially available fixed-anode x-ray tube identified in preliminary work (Source-Ray XRS-125-7K-P, Source-Ray, Ronkonkoma, NY).
Pixel and voxel size
Pixel aperture ranged from 0.05 to 0.40 mm, typical of the range in FPDs. The nominal value was apix = 0.194 mm (corresponding to the PaxScan 3030+, Varian Imaging Products, Palo Alto, CA). For real FPDs, the fill factor depends on the pixel size due to finite feature size constraints in the fabrication process: for apix approaching 0.05 mm, the fill factor could be less than 50%, while for apix approaching 0.40 mm, the fill factor is ∼80%. For simplicity, we held the fill factor fixed at a nominal value of 0.68 in all cases. The voxel size was nominally calculated as the natural voxel size, avox = apix/M, giving nominal value of avox = 0.15 mm for apix = 0.194 mm and M = 1.28.
Reconstruction filter
The apodization cosine filter parameter hwin (Appendix A) varied from 0.5 to 1.0, corresponding to the range from Hann to ramp (Ram-Lak), respectively.
Factors of image noise and dose
kVp
Peak kilovoltage ranged from 60 to 140 kVp, with nominal value of 90 kVp identified in preliminary work.1, 2 Total filtration was fixed at 5.1 mm Al + 0.3 mm Cu. Filter thickness was based on the result in the companion paper (Ref. 2), which optimized 2D projection DQE as a function of kVp and added Cu filtration and determined a reasonable filter thickness of 0.3 mm, subject to x-ray tube operating power and heating constraints. Regarding the choice of material (e.g., Cu and Ag) sample calculations and previous experience suggest that filter material is not likely a parameter of first-order importance in single-energy CBCT. A body of previous work50, 56, 57 shows optimal filters that tend toward thick, high-Z materials, essentially monochromatizing the beam. Such optimal filters would carry high heat load requirements beyond the limits of the current system, as addressed partially in the companion paper (Ref. 2). Therefore, for the current work on single-energy CBCT modeling, added beam filtration was held fixed. In future work regarding dual-energy (DE) CBCT, the addition of differential filters in the high- and low-energy beams is recognized as important parameter58 that should be considered in system optimization.
Variation in kVp affected a multitude of dependent parameters, including patient dose, detector DQE (i.e., , etc.), fluence at the detector, anatomical background power spectrum (via the κ term in SB), and contrast [via attenuation coefficients μ(E)]. The range of deliverable kVp (and mA at a particular focal spot size) for a particular tube and generator depends on the available power (kW). Since the analysis below was intended to be fairly general, we allowed kVp to vary freely without constraining the power to that of a particular system, but the kW required to deliver a given kVp and mA (dose) was identified.
Dose
Absolute dose to the center of a 16 cm diameter water cylinder was varied from 0.1 to 10 mGy, with a nominal value of 5 mGy identified in preliminary work as appropriate to extremity CT.1 Dose was related to the exposure (X) at the detector after attenuation by the object as
| (19) |
where (SDD∕SDDSADSAD)2 corrects for inverse-square law, m is the total number of projections, R is the radius of the water cylinder (2R =16 cm), fwater is the f-factor for water ∼0.9 cGy/mR (from Hubbell and Seltzer52 averaged over the x-ray spectrum), and BSF ∼4.5 is the backscatter factor experimentally determined on an x-ray bench (described in Sec. 3A) for the proposed scanner geometry.
FPD electronics noise
The FPD readout electronics noise, σadd, ranged from 0 to 5000 e, with a nominal value of 2000 e corresponding to the PaxScan 3030+ FPD (Varian Imaging Products, Palo Alto, CA).
EXPERIMENTAL METHODS
Validation of measured and predicted noise-power spectrum
Such theoretical modeling has been widely employed in a variety of applications and was validated below for the nominal detector, system geometry, etc., associated with the extremity CBCT scanner. Previous work by Tward and Siewerdsen 5 demonstrated agreement of theoretical and measured 3D NPS in CBCT using the same underlying model, and similar validation is confirmed in the current work for a system differing significantly in the choice of system geometry, x-ray tube, and FPD. That is, the previous validation in the context of a system for CBCT-guided radiation therapy deserved re-examination in the context of a system for CBCT of MSK extremities. Given agreement between theory and measurement in the 3D NPS, Gang et al.10 extended the analysis to demonstrate reasonable correspondence between task-based detectability index (which is ultimately derived from the NPS) and the performance of human observers for a broad range of experimental conditions and simple imaging tasks. Thus, the work of Tward et al. in combination with that of Gang et al. supports a rationale in which validation of the 3D NPS model combined with simple task-based analysis of detectability index should yield results providing reasonable correspondence with real observer performance for simple imaging tasks. We therefore validated the cascaded systems model in terms of the 3D NPS but refrained from the (far more challenging) revalidation versus real observer performance. CBCT scans were acquired on an experimental imaging bench for tomosynthesis and CBCT having a fixed tube-detector and rotating object configuration on a system of translation and rotation stages. The operation of the bench is similar to that detailed in Tward and Siewerdsen .5 The system consisted of a PaxScan 4030CB panel (Varian Imaging Products, Palo Alto, CA) with 2048 × 1536 pixels at 0.194 mm pitch and a 250 mg/cm2 CsI:Tl converter. Model parameters for the 4030CB were equivalent to the 3030+ FPD, differing only in field of view (FOV). The x-ray tube was a DU694 in EA10 housing (Dunlee, Aurora, IL) with a 14° anode angle, focal spot size of 0.4 or 0.8 mm and peak tube voltage of 150 kVp. Motion control was provided by Compumotor 6k8 (Parker Hannifin, Cleveland, OH) and system geometry (magnification) was set to closely match the proposed scanner setup with focal spot size fixed at 0.5 mm.
CBCT images were acquired for measurement of the 3D NPS as a function of: kVp (70, 90, and 110 kVp), tube current (0.25, 0.5, and 0.8 mAs), and reconstruction filter window (Hann or ramp). Acquisition settings for a “nominal” CBCT scan were fixed at 90 kVp; 0.3 mm Cu + 4 mm Al added filtration; 0.25 mAs per projection; 360 projections across 360° circular orbit with uniform Parker weighting; SAD = 434 mm; SDD = 555 mm; with other parameters described in Table TABLE I.. CBCT images of air (no phantom) were acquired with 3 mm Cu filtration added to the beam to simulate x-ray attenuation similar to a 16 cm water cylinder. The absence of an object in the FOV avoided complications arising from nonuniform x-ray scatter, beam hardening, etc. Dark flood corrections were performed using 50 dark frames and 50 flood-field images acquired immediately before image acquisition with no object in the field of view.
The projections were reconstructed using the FDK algorithm.59 For each set of acquisition settings, two scans were repeated and the reconstructed volumes were subtracted. This operation removed spatial correlations (e.g., shading artifacts) between the two scans, and the resulting 3D difference image presented stochastic noise components (quantum and electronics noise), contributing independently between the scans. The NPS was measured from the ensemble average of the squared discrete Fourier transform (DFT) of volumes of interest (VOIs) in the difference image as follows5:
| (20) |
where Δi denotes voxel size (mm) in the i direction, Ni (= 71) is the number of voxels in each VOI in the i direction. VOIsub(x, y, z) is the mean-subtracted volume of interest in the difference image. The VOI in the difference image was found to have a very small, residual mean signal on the order of 10−7 cm−1 (units of attenuation coefficient). While this was likely an insignificant departure from a true zero-mean, we further performed mean subtraction on the VOI to obtain a signal as close to zero-mean as possible. VOIs (each 71 × 71 × 71 voxels) in the difference image were selected about two concentric circles (36 VOIs on each circle) at radii of 60 voxels and 80 voxels from the center of the volume. This avoided placing VOIs near the center (ring artifacts) or the edge (region outside circle of reconstruction) of the image volume. The factor of two in the denominator corrects for the subtraction of two statistically independent scans.
For display purposes, a radial average of the measured NPS about the fz axis was computed. The results show a 1D profile of the NPS taken slightly (one voxel) above the axial plane to avoid on-axis artifacts. Error bars were twice the standard deviation of samples in each frequency bin and normalized by the square root of the number of samples in each bin. Radial averaging reduced the statistical error in plots and condensed a large amount of 3D information to a form that was easily displayed. Since the NPS is not strictly radially symmetric, displaying the plots in this manner slightly distorts the underlying frequency dependence, but it still provides a fair comparison of theory with measurement (both slightly distorted by the radial average). The 3D NPS is reported with units of (μ2)(mm3), where μ refers to linear attenuation coefficient and carries units of mm−1.
Qualitative verification in phantom/cadaver studies
CBCT scans of a cadaver hand and knee were acquired on the imaging bench to provide a qualitative assessment of theoretical calculations. Three cases were investigated for qualitative comparison to the predicted dependence on: kVp (60 and 105 kVp, each with 5.1 mm Al + 0.3 mm Cu filtration, and mAs per projection adjusted to give 10 mGy for each scan (confirmed with a Farmer ionization in a 16 cm CTDI phantom and a Radcal dosimeter); pixel aperture [apix in full-resolution mode (0.194 mm) and half-resolution mode (0.388 mm)], and reconstruction filter window [hwin = 0.5 (Hann) and 1.0 (Ram-Lak)]. Nominal geometry and other settings were as described in Sec. 3A.
RESULTS
Results in the following sections include: (1) comparison of the theoretical model for 3D NPS to measurement under conditions corresponding to the proposed musculoskeletal scanner; (2) calculations of detectability index for various observer models; (3) analysis of the impact of background clutter; and (4) multivariate analysis of detectability as a function of factors affecting spatial resolution, noise, and dose.
Comparison of theory and measurement (NPS)
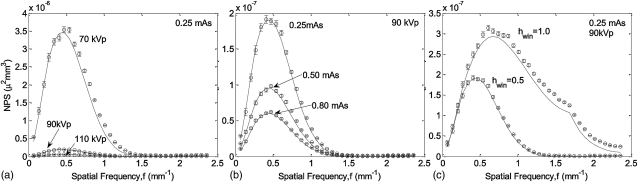
The theoretical and measured NPS are shown in Fig. 2. Figure 2a shows a strong decrease in NPS for higher kVp (at fixed mAs and, therefore, variable dose), attributed primarily to increased fluence at the detector. Figure 2b demonstrates the expected inverse relationship between NPS and mAs (at fixed kVp). Figure 2c shows the increase in NPS for sharper apodization filters (Hann versus Ram-Lak). Excellent agreement is demonstrated between theory and measurement overall, with a slight systematic underestimate in the case of the sharp (Ram-Lak) filter due to a numerical approximation of the 3D sampling process (stage 14, computed by summation of 26 nearest-neighbor replicants of the 3D NPS at multiples of the sampling frequency rather than a full 3D convolution). The underestimate is more evident for the Ram-Lak filter, since the sharper filter suffers a greater 3D noise aliasing effect. The results are consistent with the level of agreement demonstrated in previous work5, 6 and establishes a basic validation of the quantum noise model under conditions appropriate to the musculoskeletal scanner (i.e., system geometry, detector selection, etc.).
Figure 2.
Comparison of experimental and theoretical 3D NPS for various (a) kVp (70, 90, and 110 kVp at a fixed tube current of 0.25 mAs /projection), (b) mAs (0.25, 0.50, and 0.80 mAs per projection at a fixed tube voltage of 90 kVp), and (c) reconstruction filter (hwin = 0.5 Hann and hwin = l Ram-Lak). Each plot shows a radial average of the central axial slice of the fully 3D quantum NPS represented by Eqs. C3, C5.
Observer models
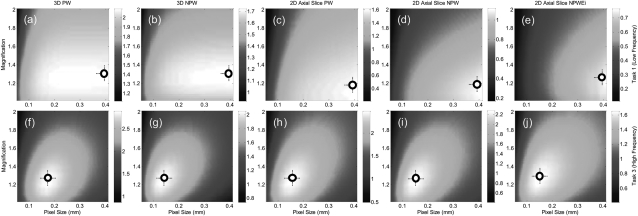
Figure 3 shows calculations of the detectability index for five observer models as described by Eqs. 6, 7, 8, 9, 10, 11, specifically 3D PW, 3D NPW, 2D PW axial, 2D NPW axial, and 2D NPWEi axial. In each case, calculations were performed for task 1 (low-frequency detection task) and task 3 (high-frequency discrimination task) as a function of geometric magnification and detector pixel size. The low-frequency task (top row) consistently suggests higher performance at lower magnification and larger pixel size—consistent with intuition for detection of a low-frequency Gaussian. The high-frequency task demonstrates an optimum in the range of M ∼ 1.2–1.3 and apix ∼ 0.1–0.2 mm. Although each of the five observer models suggests the same overall trend, there are appreciable differences. First, the magnitude of d′ is seen to decrease as expected from the ideal 3D PW observer to the various NPW, 2D slice, and eye-filter models. Moreover, the optima are a bit steeper for the latter models—e.g., the dependence on M for the low-frequency task—suggesting increased susceptibility to quantum noise.
Figure 3.
Detectability index computed for the five observer models in Eqs. 6, 7, 8, 9, 10 as a function of magnification and detector pixel size (apix). (Top row) d′(M, apix) for task 1 (low-frequency muscle vs water detection task). (Bottom row) d′(M, apix) for task 3 (high frequency muscle vs water discrimination task). The low-frequency task exhibits lower d′ overall due to background anatomical noise and is clutter-limited to a greater extent. The high-frequency task emphasizes detail and is less susceptible to clutter. Both tasks suggest highest performance at M ∼ 1.2–1.3. The low-frequency task favors large pixel size, as expected, whereas the high-frequency task demonstrates an optimum apix ∼ 0.1–0.2 mm.
For brevity, we limit the results displayed below to one observer model that conveyed the overall trends. Recent work10 examined the degree of correspondence between d′ and real observers and found the 2D NPWEi slice model to give reasonable agreement for a variety of simple tasks. The slice models, however, require selection of a given (axial, sagittal, or coronal) slice in Eqs. 8, 9, 10 (i.e., the integral over fz, fy, or fx, respectively), and we did not want to limit the results to a preferred plane of visualization. We, therefore, selected the 3D NPW model as the nominal choice in results summarized below, since: (a) it captured the fully 3D characteristics of the noise (as opposed to selecting a given slice), (b) it incorporated the nonprewhitening aspects that appear to be important in correspondence with real observers, and (c) it was consistent with the overall trends suggested by all models in Fig. 3 (i.e., it did not suggest optima that were significantly different from the others). The choice of 3D NPW in results summarized below is purely for brevity, and the analysis was performed (but not shown) for all five. While the d′ for the 3D NPW model is not expected to be absolutely predictive of real observer response (e.g., scrolling slices) in its magnitude, the trends and optima were consistent with those suggested by the other models and provided a concise, representative summary of results.
Background anatomical clutter
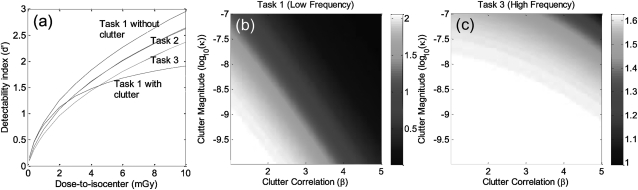
Figure 4 illustrates the impact of anatomical clutter on d′. Figure 4a plots d′ as a function of dose to isocenter for the three tasks with background clutter included (solid lines, κ = 3.3 × 10−10 μ2 mm3, β = 3, corresponding to muscle-water clutter, as derived in Appendix D) or excluded (dashed lines, κ = 0). The middle- and high-frequency tasks (task 2 and task 3) are seen to improve steeply with dose and are, therefore, governed primarily by quantum noise. By comparison, the low-frequency task (task 1) departs from this trend above ∼2 mGy, beyond which d′ increases slowly with dose, demonstrating that the task is largely “clutter-limited.” The result is consistent with the notion that background clutter presents a major impediment to low-frequency tasks (e.g., soft-tissue mass detection) and outweighs other noise sources (quantum and electronics). The medium (task 2) and high (task 3) frequency tasks place emphasis outside the low frequency clutter region and are impervious to background clutter. (The solid and dashed lines in Fig. 4 are nearly identical for tasks 2 and 3.).
Figure 4.
Effect of background anatomical clutter on detectability. (a) d′ computed as a function of dose for the three tasks with (solid lines) and without (dashed lines) background clutter in Eq. 7. For task 1 with clutter, the departure from quantum-limited performance (i.e., relative insensitivity to dose above ∼2 mGy) shows that the low-frequency task is clutter-limited. Tasks 2 and 3 are insensitive to clutter (solid and dashed lines overlapping). (b) d′(κ, β) for low-frequency task 1 exhibits a strong dependence on clutter, whereas (c) d′(κ, β) for high-frequency task 3 is relatively insensitive to clutter.
To illustrate the difference in dependence on anatomical clutter between low- and high-frequency tasks, d′ was computed as a function of clutter magnitude (κ) and correlation (β) in Figs. 4b, 4c. β varied from 1 to 5, whereas κ ranged in magnitude from 10−7(corresponding to measurements of clutter in a phantom consisting of acrylic-in-air30) to 10−10 (calculated for clutter consisting of muscle-in-water). The low-frequency task [Fig. 4b] exhibits a strong dependence on both κ and β, whereas the high-frequency task [Fig. 4c] is relatively insensitive to clutter (governed instead by quantum noise).
Factors of spatial resolution
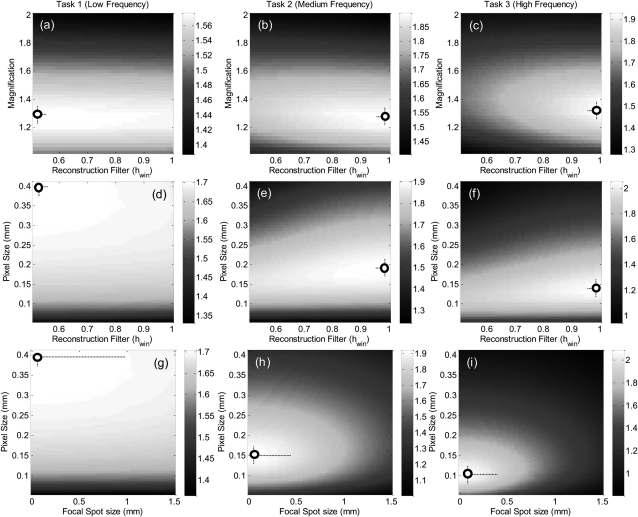
Among the parameters governing spatial resolution are the system geometry (M), focal spot size (aspot), pixel size (apix), voxel size (avox), and reconstruction filter window (hwin). As shown above [Fig. 3g], d′ (M, apix) exhibited an optimum at M ∼ 1.3 and apix ∼ 0.1–0.2 mm for the middle- and high-frequency tasks. The optimal magnification arises from the interplay between factors of focal spot size, detector exposure, pixel (voxel) size, and SPR—the first two favoring lower magnification, and the latter two favoring higher magnification. For the low-frequency task 1, a similar optimum M ∼ 1.3 was found, but there was no optimum in apix (favoring monotonically larger pixel size) over the range considered. With respect to magnification, the fact that a similar optimum was found for widely varying tasks is convenient from the perspective of system design—arguing that M ∼ 1.3 is optimal for both the geometric magnification required in high-frequency tasks as well as the SPR reduction required for low-frequency tasks. The lack of a single optimum in apix suggests a separate approach in image acquisition/reconstruction: for high-frequency tasks, projection data should be acquired near the optimum apix ∼ 0.1–0.2 mm; however, for low- frequency tasks, the same data should be binned to apix ∼ 0.4 mm and reconstructed separately.
Figure 5 illustrates the corresponding trends in d′ computed as a function of reconstruction filter (hwin) and focal spot size (aspot). Calculations of d′ (M, hwin) in Figs. 5a, 5b, 5c show a consistent optimum at M ∼ 1.3 for each task. The low-frequency task shows a weak dependence on reconstruction filter but favors the smoother filter (hwin ∼ 0.5), whereas the middle- and high-frequency tasks show a steeper dependence and favor the sharper filter (hwin ∼ 0.9–1.0). As shown in Figs. 5d, 5e, 5f, calculation of d′ (apix, hwin) for the low-frequency task again favors larger pixels and smoother filters, whereas the middle- and high-frequency tasks show an optimum apix ∼ 0.1–0.2 mm and favor sharp filters. The trends are consistent with intuition and suggest a separate reconstruction strategy for low versus middle/high-frequency tasks: binning and smooth filters for the former; full-resolution readout and sharp filters for the latter. While intuitive, the results confirm expected trends and quantify the trade-offs in detectability incurred by departures from the optima.
Figure 5.
Detectability computed as a function of factors intrinsic to spatial resolution in CBCT for three imaging tasks. (a–c) d′(M, hwin) demonstrates a consistent optimum at M ∼ 1.3, a slight preference for smoother filters for the low-frequency task, and steeper dependence toward sharper filters for high-frequency tasks. (d–f) d′(apix, hwin) reflects the task-dependent effects of pixel size as in Fig. 3 and a similar dependence on reconstruction filter. (g–i) d′(apix, aspot) shows monotonic improvement for smaller aspot, with arguably diminishing returns below aspot ∼ 0.4 mm.
Finally, Figs. 5g, 5h, 5i plot d′ as a function of apix and aspot, illustrating key factors of equipment selection—i.e., the FPD and x-ray tube. The familiar trends in apix are evident at all values of aspot considered (i.e., apix → 0.4 mm for the low-frequency task, while apix ∼ 0.1–0.2 mm optimizes the middle- and high-frequency tasks). For the low-frequency task, there is a very weak dependence on focal spot blur. For the middle- and high-frequency tasks, however, there is a fairly steep, monotonic trend toward finer focal spot. However, at optimal apix, one may argue that decrease in aspot below ∼0.4 mm provides diminishing return—an important consideration with respect to tube heat loading. At least as interesting, the plots allow a quantitative guide to system design questions—e.g., the conditions under which reducing pixel size or spot size in isolation improves performance (or has no effect at all) and the extent to which the best choice of these parameters depends strongly on one another and the imaging task.
Factors of image noise and dose
Among the factors governing image noise (aside from the spatial resolution factors above) are kVp, dose, and additive electronic noise (σadd). In the results below, d′ was analyzed as a function of each, recognizing that the contrast factor (CTask) in the task function tends to heavily weight the results toward lower kVp. An additional figure of merit was, therefore, computed—the integral of the NEQ [Eq. 5] over the 3D Nyquist region—equivalent to a delta-function detection task but without contrast dependence and conveying the trends associated solely with quantum noise, electronic noise, and anatomical clutter (but not the contrast of the stimulus).
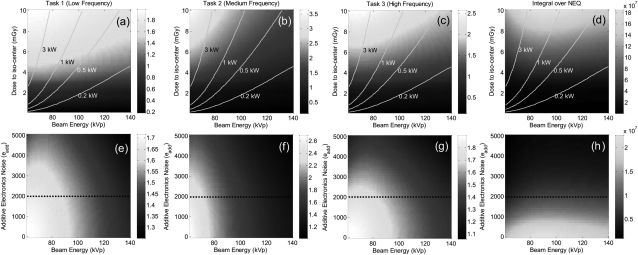
Figure 6 shows d′ computed as a function of kVp, dose, and σadd. While we do not expect an optimum in d′(dose, σadd), levels of diminishing return become evident—e.g., the dose beyond which d′ becomes entirely clutter-limited and does not increase appreciably with dose. Nominal operating points are, therefore, highlighted in each: dose ∼5 mGy and σadd ∼ 2000 e, as identified in previous analysis.1, 2 The trends suggest kVp in the range of 60–80 kVp for all three tasks, recognizing that d′ is strongly influenced by the CTask term (which improves monotonically with lower kVp). The isopower contour lines in Figs. 6a, 6b, 6c, 6d illustrate the need for careful selection of operating kVp: for a given dose, d′ analysis suggests lower kVp but at the cost of higher kW. The dependence of the underlying noise on kVp (independent of the stimulus contrast) is illustrated in the integral of NEQ in Figs. 6d, 6h, which suggests a fairly weak (slowly varying) optimum around ∼90 kVp (at 5 mGy). The NEQ analysis highlights the important trade-off between quantum noise (SQ) and anatomical clutter (SB) with kVp: quantum noise alone tends to favor low kVp (higher quantum detection efficiency, ), while higher kVp reduces κ and thus the clutter power spectrum. The same observation was made by Richard et al.36 in the context of chest radiography, providing an analytical basis for weighing the trade-offs between quantum noise and clutter “contrast.”
Figure 6.
Detectability as a function of factors contributing to image noise and dose for the three imaging tasks. The right column plots the integral over the 3D NEQ. The superimposed lines identify the generator power required for a given kVp and dose. While there is clearly no “optimum” in dose or σadd, reasonable operating points of D = 5 mGy and σadd = 2000 e are identified, and regions of diminishing return are evident.
The dependence on kVp and additive noise (σadd) is illustrated in Figs. 6e, 6f, 6g, 6h. Tasks 1 and 3 indicate an optimum ∼70–80 kVp at the nominal electronic noise level ∼2000 e, while task 2 (bone-fat contrast) suggests ∼60 kVp, owing to steep dependence of the CTask term on kVp. The integral of the 3D NEQ shows an optimum in the region of ∼90 kVp.
Multivariate optimization
Finally, the parameters governing spatial resolution and noise were considered together in Fig. 7. Calculations of d′(M, kVp) in the first row reflect the familiar optimum in the region M ∼ 1.3. For the high-frequency task at M = 1.3, an optimal kVp is evident at ∼70 kVp, while the integral of the 3D NEQ shows optima at M ∼ 1.2–1.3 and ∼90 kVp. Calculations of d′(apix, kVp) in the second row confirm the basic dependence on apix irrespective of kVp (i.e., apix → 0.4 mm for the low-frequency task, compared to apix ∼ 0.1–0.2 for the middle and high-frequency tasks). Calculations of d′(apix, aadd) in the third row demonstrate an interesting trade-off between pixel size and additive noise: for fixed electronic noise, reduction in pixel size increases quantum noise (i.e., electronics noise contribution grows by , Appendix C); hence, below a certain pixel size (apix ∼ 0.1 mm), the increase in quantum NPS outweighs the benefits of improved spatial resolution, and an “optimal” pixel size is suggested. The low-frequency task 1 is relatively insensitive to σadd and demonstrates diminishing returns [Fig. 7i] below σadd ∼ 2000 e at pixel size apix ∼ 0.4 mm—i.e., low-frequency detection tasks are dominated by clutter and not electronic noise. Finally, we see that the results provide a guide to another important system design question with respect to apix and σadd —namely, whether a reduction in pixel size alone will improve detectability, or whether a concomitant reduction in electronic noise is required. For example, considering the middle-frequency task 2 at σadd = 2000 e, one might wonder if a reduction in pixel size below 0.15 mm would improve performance; the answer [Fig. 7j] is that an improvement would only be gained if the electronic noise were also reduced.
Figure 7.
Detectability index and integral of the 3D NEQ computed for parameters governing both spatial resolution and noise. (a–d) Dependence on magnification and kVp. (e–h) Dependence on pixel size and kVp. (i–l) Dependence on pixel size and electronic noise (σadd).
DISCUSSION AND CONCLUSIONS
The cascaded systems model of 3D quantum noise in CBCT was extended to include system parameters (magnification, focal spot blur, and x-ray scatter) and background anatomical clutter. Of these three general groups of factors affecting NEQ (i.e., quantum, system, and generalized factors as in Fig. 1), previous work has tended to treat one or two—e.g., analysis of CBCT quantum noise by Tward and Siewerdsen ,5 inclusion of scatter by Siewerdsen and Jaffray,16 Jain et al.,17 and Kyprianou et al.,18 and incorporation of anatomical clutter as in Gang et al.30 The model presented above combines all three to examine trade-offs and interdependencies among factors of system design, image acquisition, and 3D reconstruction and applies the framework specifically to a CBCT system under development for MSK extremity imaging.
A fairly broad multivariate parameter space was investigated systematically in terms of factors affecting: (1) spatial resolution (magnification, focal spot blur, reconstruction filter, pixel size, and voxel size); (2) image noise (kVp, dose, x-ray scatter, and electronics noise); and (3) each of these factors in combination. Among the specific findings for the MSK extremity scanner are: (1) A fairly robust optimal geometry was identified at M = 1.3, weighing trade-offs among spatial resolution (i.e., pixel size and focal spot size) and x-ray scatter. (2) Intuitive trends were quantified regarding acquisition/ reconstruction techniques for low- and middle/high-frequency tasks—namely, 1 × 1 pixel readout (no binning; apix ∼ 0.15 mm) followed by 1 × 1 or 2 × 2 binning in reconstruction depending on the imaging task (i.e., 2 × 2 pixel binning and a smooth filter for low-frequency, soft-tissue tasks, and a sharp filter with no binning for high-frequency, bone detail tasks). (3) Detectability index favored lower kVp, driven primarily by the contrast term in the task function, whereas a contrast-independent figure of merit (integral over the NEQ) suggested ∼90 kVp as optimal and may better reflect the true performance limits associated with quantum noise for an intrinsically digital image (where display contrast may always be maximized via window/level). The 90 kVp setting is also better suited in terms of generator power requirement (<1 kW). (4) The generator power and focal spot size associated with these results are within practical considerations—e.g., a fixed-anode x-ray source identified in preliminary work (SourceRay XRS-125-7K-P, 0.875 kW, 0.5 mm spot). (5) The analysis guides selection of a nominal dose (∼5 mGy) above which performance is primarily limited by anatomical clutter and below which is limited by quantum noise—suggesting an operating point that is clinically reasonable (perhaps advantageous) in comparison to conventional CT,60 although direct comparison between absolute central dose (as in this paper) and CTDI (as in Biswas et al.60) can be problematic.
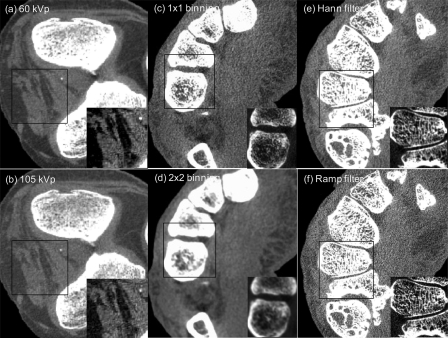
Having addressed such a broad parameter space from purely theoretical, quantitative terms, it is worthwhile to briefly consider the results in a complementary, qualitative sense. While a rigorous perception study is beyond the scope of the current work, an image can speak volumes, and it is useful to see the extent to which the calculations agree with the visual appearance of CBCT images. Figure 8 presents CBCT images of a cadaveric knee (a and b) and hand (c–f) acquired on the imaging bench under the nominal conditions summarized in Sec. 3A. Figures 8a, 8b show a central axial slice acquired at 60 and 105 kVp. Consistent with the d′ calculations (Figs. 67), low-frequency soft-tissue visibility (e.g., muscle-fat differentiation) is improved for the 60 kVp scan by virtue of improved soft-tissue contrast, and the zoomed insets similarly illustrate the improvement for ahigh-contrast detail (calcification). Consistent with the disparity between d′(which is maximized at 60 kVp) and integral of the NEQ (which is maximized at 90 kVp), the images also reflect a slight increase in quantum noise for the lower kVp, and it will fall to future work to assess via controlled reader studies, which image carries superior diagnostic performance.
Figure 8.
CBCT images of (a and b) a knee and (c–f) a hand qualitatively illustrating some of the trends in d′ theorized in Figs. 34567. To facilitate comparison, each image pair is displayed at equivalent grey-scale window width, with level equal to the average voxel value for muscle. Each image also contains a magnified inset at separate window/level to illustrate a given feature of interest. (a and b) Effect of kVp on image quality, illustrating improved soft-tissue contrast at 60 kVp but fairly complex trade-offs in the underlying quantum noise. (c and d) Effect of pixel aperture on image quality (1 × 1 binning = 0.194 mm pixels, while 2 × 2 binning = 0.388 mm). The former favors bone detail and the latter soft-tissue discrimination. (e and f) Effect of reconstruction filter on image quality. Soft-tissue detection favors the smooth filter and bone detail the sharp filter, but the effect appears to be weaker than pixel binning—consistent with the d′ calculations in Fig. 5.
Figures 8c, 8d qualitatively illustrate the effect of pixel aperture (binning) on visualization of soft-tissue and bone detail. The 1 × 1 binning image [Fig. 8c with zoom inset] shows a fine level of detail in trabecular structure but suffers by comparison to the 2 × 2 binning image [Fig. 8d] in terms of soft-tissue visibility. Conversely, the latter suffers a significant loss of detail. While intuitive, these observations are consistent with the quantitative results in Figs. 57 that suggested these task-specific acquisition/reconstruction techniques. Finally, Figs. 8e, 8f show the effect of the reconstruction filter on soft-tissue and detail, where the Hann filter is seen to improve soft-tissue visibility, while the Ram-Lak filter is suited for bony details. The basic result is consistent with that of Fig. 5 not only in the obvious conclusion (i.e., smoother filters for soft-tissue visualization) but also in the more subtle observation that the effect of the reconstruction filter on task performance is not nearly as strong as the effect of pixel binning [Figs. 8c, 8d]. As points of discussion, these images lend qualitative interpretation to the strength (i.e., the “steepness”) of the trends and optima identified in Figs. 34567 and qualitative support beyond the purely quantitative results. They also give some confidence that the calculations will bear correspondence with real observer performance.
A variety of limitations in the method and results are acknowledged. Fundamental to cascaded systems analysis, NPS, and NEQ are the assumptions of stationarity and shift invariance, which are known not to hold strictly for 3D filtered backprojection. As in previous work, the analysis should be interpreted as a “local” description of noise characteristics within a region (e.g., a region about the center of reconstruction) for which image statistics are locally invariant. Nonidealities in detector response—e.g., image lag—were ignored, although such effects can be expected to affect the noise in CBCT. While motion blur (i.e., motion during x-ray exposure) was neglected, the proposed scanner employs pulsed exposures, which largely eliminates motion blur over the duration of each pulse (<30 ms).2 As a simplifying assumption, we held the detector pixel fill factor fixed at 0.68 (corresponding to the fill factor on the FPD employed on the prototype) irrespective of the actual pixel size, which may not be a fair comparison considering the fact that smaller pixels tend to have smaller fill factors. Although the model accommodates MTF degradation due to scatter, the results involved the simplifying assumption that scatter only manifests as contrast degradation (1/1 + SPR) and a loss of primary quanta (an effective increase in noise). Finally, the results do not constitute a full multivariate analysis or true optimization within the rich multidimensional parameter space, presenting instead two-dimensional slices through the multivariate space of kVp, M, apix, hwin, etc., holding other parameters fixed at nominal values identified based on repeated calculations (not shown) and reasonable operating points. A multivariate optimization was not performed for the following reasons: (1) The vast number of possible permutations over the CBCT parameter space creates a computationally intense problem, the results of which can be difficult to interpret; (2) a global optimization is sure to yield different results depending on the imaging task, some of which may be intractable (e.g., separate optima in system magnification for separate tasks); and (3) with regard to parameters that impart a monotonic trend on d′ (e.g., focal spot size, dose, and additive electronics noise), an optimization is unnecessary—e.g., concluding simply that optimal aspot = 0 mm and optimal σadd = 0 e. The observer models invoked in the detectability index of Eqs. 6, 7, 8, 9, 10 are perhaps the simplest form of prewhitening, nonprewhitening, match-filter type of ideal observers one can envision in linking fundamental Fourier metrics (NEQ) to imaging task. Further, 2D slice detectability models assume the slice to be infinitesimally thin, which is an approximation of real tomography. For thick slices, the slice detectability can be modified to include a transfer function (sinc) corresponding to the thickness of the slice, as in the “slice extraction” analysis of Siewerdsen et al.61 Still, such metrics have shown reasonable correspondence with real observer performance,10 and the brief, qualitative assessment of cadaver images acquired under similar conditions lend confidence that the trends suggested by the d′ calculations are meaningful. This qualitative confirmation of trends in spatial resolution and contrast-to-noise ratio in cadaveric specimens falls short of a rigorous validation of the system optimization; however, a true optimization by physical experimentation is not only beyond the scope of the current manuscript (which aimed to provide a guide to system design) but also may be beyond the scope of practical measurement. Furthermore, analysis and optimization with respect to binary hypothesis-testing tasks does not pretend to convey the complexity of tasks performed by radiologists in reading diagnostic images, and the NPS, NEQ, and task-based detectability index should be considered as abstractions intended primarily as a guide to system design but not an absolute descriptor of diagnostic quality. Finally, the results considered three individual tasks with the potential for distinct optima. In cases where such optima concerned image processing or reconstruction parameters (e.g., the binning factor and choice of reconstruction filter), the results simply suggest parallel processing techniques. However, in cases, where such optima suggest distinct system design or image acquisition parameters (e.g., kVp or magnification), then a multitask optimization should be considered.
ACKNOWLEDGMENTS
The authors acknowledge countless valuable conversations with Dr. Ian Cunningham (Robarts Research Institute, London ON) regarding cascaded systems analysis, Dr. Angel Pineda (UC Fullerton, Fullerton CA) regarding noise stationarity and Fourier metrology, Dr. John Boone (UC Davis, Davis CA) on CBCT system design and the power-law nature of anatomical clutter, Dr. Norbert Pelc (Stanford University, Palo Alto CA) on NPS analysis and measurement, and Dr. Iacovos Kyprianou (FDA, Rockville MD) on NPS analysis and x-ray scatter. The work was supported by NIH 2R01-CA-112163 and academic-industry partnership with Carestream Health Inc. (Rochester NY).
APPENDIX A: MTF
The modulation transfer function (MTF) associated with different stages in the 3D cascaded systems model is summarized below. The MTF calculations account for detector cross-talk - e.g., spread of optical photons in the scintillator, integration over the pixel aperture, and any (believed to be small) charge sharing between photodiode elements. The MTF terms are defined in the 2D frequency domain (fu, fv) of the detector and related to the plane of the object (at isocenter) and the corresponding 3D frequency domain (fx, fy, fz) by demagnification: fu = f/M and fv = fz/M, where M is the magnification and f is the radial frequency, .
Focal spot MTF
The x-ray focal spot may be modeled as a uniform source distribution (e.g., rectangular aperture with characteristic width aspot) as in Johns and Cunnigham.62 The corresponding focal spot MTF in the detector plane depends on geometric magnification
| (A1) |
The focal spot MTF degrades as the detector moves farther from isocenter (i.e., M increases) and as focal spot size (aspot) increases.
Scintillator MTF
T3 describes the stochastic spread of optical photons in the CsI:Tl scintillator and was approximated by a Lorentzian fit to empirical data3
| (A2) |
In this work, the parameters were held fixed at a = 0.27, b = 0.91, and c = 1.66, corresponding to values measured for a 250 mg/cm2 CsI:Tl converter as on the proposed extremities CBCT scanner. The dependence of H on kVp, and effects of oblique incidence were assumed negligible in the current work.
Photodiode aperture MTF
T5 is the MTF associated with integration of quanta by the photodiode aperture
| (A3) |
We assume a square photodiode, apd, with the fraction of the total pixel size (apix) that is sensitive to light given by , where fpd is the pixel fill factor.
Apodization window
T11 represents the apodization (smoothing) window applied to the (ramp-filtered) projection data prior to backprojection—e.g., a cosine filter
| (A4) |
where hwin is an adjustable smoothing parameter varying from 0.5 (Hann filter) to 1.0 (all-pass apodization giving a pure ramp (Ram-Lak) filter).
Bilinear interpolation
T12 describes bilinear interpolation (up-sampling) performed on the filtered projection to approximate a continuous image prior to the backprojection step
| (A5) |
Other interpolation schemes, such as nearest-neighbor interpolation, may be used to up-sample the projection images, with MTF and potential aliasing effects described by Tward and Siewerdsen.5
APPENDIX B: X-RAY SCATTER
X-ray scatter is a significant source contrast degradation and artifacts in CBCT.16 Muntz et al.63 developed a scatter point-source model to describe the dependence of scatter-to-primary ratio (SPR) on system geometry. The model assumes scatter to originate from a virtual point source located at distance yscat from the object plane (isocenter), typically in the direction of the primary x-ray source. Neitzel64 employed the model and derived the selectivity of an air gap, Σ, leading to the following SPR formulation16 in the context of CBCT geometry:
| (B1) |
where F′ is the scatter fraction at the exit of the object and is dependent on object size and field of view. In the results reported here, F′ was held fixed at a value of 0.6, corresponding with low to moderate scatter conditions, as is the case for extremities.16 Object plane to detector gap is given by dgap = SDD − SAD and yscat is the effective scatter source location, taken to be fixed at 20 cm.65 The SPR is seen to depend strongly on magnification. We assumed SPR to be independent of kVp, a simplifying assumption supported by Monte Carlo simulations in CBCT that show SPR to be a weak function of kVp in the diagnostic energy range.66
APPENDIX C: QUANTUM AND ELECTRONICS NOISE
Quantum noise
The propagation of the NPS in FPDs was modeled as a serial and parallel cascade of stages,3, 37 and the resulting 2D projection NPS (without additive electronic noise) is given by
| (C1) |
where notation is consistent with previous work.5 is the total incident fluence at the detector, and are the mean gains associated with interaction of x rays in the scintillator and conversion to secondary quanta, respectively, T3 describes the spread of optical quanta, and PK is a composite term associated with the parallel cascade arising from K-fluorescence as described by Yao and Cunningham;34 describes the coupling of optical photons to the photodiode aperture (apd), T5 is the pixel aperture MTF, and III6 represents the sampling of the image at discrete pixel locations.
The 2D NPS formulation has been extended to the 3D reconstruction cascade,5, 6 including postacquisition binning (T8) and sampling (III8), the log normalization step, ramp and apodization filter (T11), interpolation (T12), filtered backprojection (1/f), 3D sampling (III14) stages and optional postreconstruction binning (T15) and sampling (III15). The resulting quantum noise-only 3D NPS is
| (C2) |
where the superscript on denotes quantum NPS due to primary and scattered components of total incident fluence . The total, primary, and scatter fluence are related as: and . The above NPS formulation requires separate computation of projection NPS and gain terms for primary (, etc.) and scattered (, etc.) quanta. The scatter dependence of quantum NPS has been shown to be small. Also, the maximum energy shift associated with incoherent scatter is small. (For example, for a monoenergetic x-ray E = 60 keV scattered at θ = 45°, the scattered x-ray has energy E'=E-[E2∕(mec2)](1-cosθ)=57.9 keV). We, therefore, make a simplifying assumption that the energy shift between primary and scattered spectra is negligible. In that case, the scatter NPS takes the same form as (except for the fluence term) and the 3D NPS reduces to
| (C3) |
Additive electronics noise
Sadd represents the additive electronic noise associated with dark noise from the a-Si:H pixel elements, uncorrected voltage fluctuations on the gate and bias lines, amplifier noise, and digitization noise in analog-to-digital converters.3 The term is approximated as: Sadd=(σadd.apix)2, where σadd is the pixel variance measured in “dark-only” images. The additive NPS after propagating through the 3D reconstruction cascade is
| (C4) |
where superscript on denotes dependence on primary and scattered components of incident fluence and remaining terms are as described above. We invoke the same assumption as above: the energy shift between primary and scattered spectra is small, giving , etc., and a simplified additive electronic NPS
| (C5) |
APPENDIX D: ANATOMICAL BACKGROUND NOISE
The anatomical background power spectrum describes the fluctuations intrinsic to the object (clutter) and is frequently characterized by a power-law relationship used to describe a wide variety of random and semirandom processes21, 22
| (D1) |
where κ describes the magnitude of fluctuation, β is the degree of correlation of the variations, and f3D is the 3D radial frequency, . For calculations pertaining to the musculoskeletal scanner described above, the numerator κ was computed for a muscle vs water contrast background scaled from the experimentally determined value (κacrylic) measured in an acrylic sphere “clutter phantom” as follows:30
| (D2) |
where κacrylic = 3.72 ×10−7 μ2 mm3. The exponent β = 3 was calculated based on fractal properties of self-similar objects (such as equal volumes of different sized spheres in the generic phantom above) and is similar to widely reported values.25, 26, 27, 43 The numerator κ carries a dependence on kVp because of the effective attenuation coefficients of object and background, and decreases with scatter as (1/1 + SPR)2. κ and hence, anatomical clutter, decrease as a function of increasing kVp (reduced relative contrast). For instance, reduction in overlying anatomical clutter is a principal motivation for the use of higher kVp techniques in projection chest radiography.36
References
- Zbijewski W., Jean P. D., Prakash P., Ding Y., Stayman J. W., Packard N., Senn R., Yang D., Yorkston J., Machado A., Carrino J. A., and Siewerdsen J. H., “Design and optimization of a dedicated cone-beam CT system for musculoskeletal extremities imaging,” Proc. SPIE, 7961, 796104 (2011). 10.1117/12.878077 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zbijewski W., Jean P. D., Prakash P., Ding Y., Stayman J. W., Packard N., Senn R., Yang D., Yorkston J., Machado A., Carrino J. A., and Siewerdsen J. H., “A dedicated cone-beam CT system for musculoskeletal extremities imaging: Design, optimization, and initial performance characterization,” Med. Phys. 38(8), 4700–4713 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siewerdsen J. H., Antonuk L. E., el-Mohri Y., Yorkston J., Huang W., Boudry J. M., and Cunningham I. A., “Empirical and theoretical investigation of the noise performance of indirect detection, active matrix flat-panel imagers (AMFPIs) for diagnostic radiology,” Med. Phys. 24, 71–89 (1997). 10.1118/1.597919 [DOI] [PubMed] [Google Scholar]
- Zhao W. and Rowlands J. A., “Digital radiology using active matrix readout of amorphous selenium: Theoretical analysis of detective quantum efficiency,” Med. Phys. 24, 1819–1833 (1997). 10.1118/1.598097 [DOI] [PubMed] [Google Scholar]
- Tward D. J. and Siewerdsen J. H., “Cascaded systems analysis of the 3D noise transfer characteristics of flat-panel cone-beam CT,” Med. Phys. 35, 5510–5529 (2008). 10.1118/1.3002414 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tward D. J. and Siewerdsen J. H., “Noise aliasing and the 3D NEQ of flat-panel cone-beam CT: Effect of 2D/3D apertures and sampling,” Med. Phys. 36, 3830–3843 (2009). 10.1118/1.3166933 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganguly A., Rudin S., Bednarek D. R., and Hoffmann K. R., “Micro-angiography for neuro-vascular imaging. II. Cascade model analysis,” Med, Phys, 30, 3029–3039 (2003). 10.1118/1.1617550 [DOI] [PubMed] [Google Scholar]
- Vedantham S., Karellas A., and Suryanarayanan S., “Solid-state fluoroscopic imager for high-resolution angiography: Parallel-cascaded linear systems analysis,” Med. Phys. 31, 1258–1268 (2004). 10.1118/1.1689014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Commission on Radiation Units and Measurements, “Medical imaging—the assessment of image quality,” ICRU Report No. 54, (International Commission on Radiation Units and Measurements, Bethesda, MD, 1996).
- Gang G. J., Lee J., Stayman J. W., Tward D. J., Zbijewski W., Prince J. L., and Siewerdsen J. H., “Analysis of Fourier-domain task-based detectability index in tomosynthesis and cone-beam CT in relation to human observer performance,” Med. Phys. 38, 1754–1768 (2011). 10.1118/1.3560428 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siewerdsen J. H. and Jaffray D. A., “Cone-beam CT with a flat-panel imager: Noise considerations for fully 3D computed tomography,” Proc. SPIE, 3977, 408–416 (2000). 10.1117/12.384515 [DOI] [Google Scholar]
- Siewerdsen J. H. and Jaffray D. A., “Cone-beam computed tomography with a flat-panel imager: Magnitude and effects of x-ray scatter,” Med. Phys. 28, 220–231 (2001). 10.1118/1.1339879 [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H. and Jaffray D. A., “Three-dimensional NEQ transfer characteristics of volume CT using direct- and indirect-detection flat-panel imagers,” Proc. SPIE, 5030, 92–102 (2003). 10.1117/12.479970 [DOI] [Google Scholar]
- Yoon S., Gang J. G., Tward D. J., Siewerdsen J. H., and Fahrig R., “Analysis of lung nodule detectability and anatomical clutter in tomosynthesis imaging of the chest,” Proc. SPIE, 7258, 72581M (2009). 10.1117/12.813836 [DOI] [Google Scholar]
- Zhao B., Zhou J., Hu Y.-H., Mertelmeier T., Ludwig J., and Zhao W., “Experimental validation of a three-dimensional linear system model for breast tomosynthesis,” Med. Phys. 36, 240–251 (2009). 10.1118/1.3040178 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siewerdsen J. H. and Jaffray D. A., “Optimization of x-ray imaging geometry (with specific application to flat-panel cone-beam computed tomography),” Med Phys 27, 1903–1914 (2000). 10.1118/1.1286590 [DOI] [PubMed] [Google Scholar]
- Jain A., Kuhls-Gilcrist A. T., Gupta S. K., Bednarek D. R., and Rudin S., “Generalized two-dimensional (2D) linear system analysis metrics (GMTF, GDQE) for digital radiography systems including the effect of focal spot, magnification, scatter, and detector characteristics,” Proc. Soc. Photo-Opt. Instrum. Eng. 7622 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kyprianou I. S., Rudin S., Bednarek D. R., and Hoffmann K. R., “Generalizing the MTF and DQE to include x-ray scatter and focal spot unsharpness: Application to a new microangiographic system,” Med. Phys. 32, 613–626 (2005). 10.1118/1.1844151 [DOI] [PubMed] [Google Scholar]
- Ganguly A., Rudin S., Bednarek D. R., Hoffmann K. R., and Kyprianou I. S., “Micro-angiography for neuro-vascular imaging. I. Experimental evaluation and feasibility,” Med. Phys. 30, 3018–3028 (2003). 10.1118/1.1617549 [DOI] [PubMed] [Google Scholar]
- Kyprianou I. S., Rudin S., Bednarek D. R., and Hoffmann K. R., “Study of the generalized MTF and DQE for a new microangiographic system,” Proc. SPIE 5368, 349–360 (2004). 10.1117/12.533512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bochud F. O., Abbey C. K., and Eckstein M. P., “Visual signal detection in structured backgrounds. III. Calculation of figures of merit for model observers in statistically nonstationary backgrounds,” J. Opt. Soc. Am. A Opt. Image Sci. Vis. 17, 193–205 (2000). 10.1364/JOSAA.17.000193 [DOI] [PubMed] [Google Scholar]
- Burgess A. E., “Mammographic structure: Data preparation and spatial statistics analysis,” Proc. SPIE, 3661, 642–653 (1999). 10.1117/12.348620 [DOI] [Google Scholar]
- Burgess A. E., Jacobson F. L., and Judy P. F., “Human observer detection experiments with mammograms and power-law noise,” Med. Phys. 28, 419–437 (2001). 10.1118/1.1355308 [DOI] [PubMed] [Google Scholar]
- Heine J. J., Deans S. R., Velthuizen R. P., and Clarke L. P., “On the statistical nature of mammograms,” Med. Phys. 26, 2254–2265 (1999). 10.1118/1.598739 [DOI] [PubMed] [Google Scholar]
- Metheany K. G., Abbey C. K., Packard N., and Boone J. M., “Characterizing anatomical variability in breast CT images,” Med. Phys. 35, 4685–4694 (2008). 10.1118/1.2977772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engstrom E., Reiser I., and Nishikawa R., “Comparison of power spectra for tomosynthesis projections and reconstructed images,” Med. Phys. 36, 1753–1758 (2009). 10.1118/1.3116774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glick S. J., Vedantham S., and Karellas A., “Investigation of optimal kVp settings for CT mammography using a flat-panel imager,” Proc. SPIE, 4682, 392–402 (2002). 10.1117/12.465581 [DOI] [Google Scholar]
- Gong X., Glick S. J., Liu B., Vedula A. A., and Thacker S., “A computer simulation study comparing lesion detection accuracy with digital mammography, breast tomosynthesis, and cone-beam CT breast imaging,” Med. Phys. 33, 1041–1052 (2006). 10.1118/1.2174127 [DOI] [PubMed] [Google Scholar]
- Reiser I. and Nishikawa R. M., “Task-based assessment of breast tomosynthesis: Effect of acquisition parameters and quantum noise,” Med. Phys. 37, 1591–1600 (2010). 10.1118/1.3357288 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gang G. J., Tward D. J., Lee J., and Siewerdsen J. H., “Anatomical background and generalized detectability in tomosynthesis and cone-beam CT,” Med. Phys. 37, 1948–1965 (2010). 10.1118/1.3352586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siewerdsen J. H., Moseley D. J., and Jaffray D. A., “Incorporation of task in 3D imaging performance evaluation: The impact of asymmetric NPS on detectability,” Proc. SPIE, 5368, 89–97 (2004). 10.1117/12.535744 [DOI] [Google Scholar]
- Samei E., Flynn M. J., and Eyler W. R., “Detection of subtle lung nodules: Relative influence of quantum and anatomic noise on chest radiographs,” Radiology 213, 727–734 (1999). [DOI] [PubMed] [Google Scholar]
- Cunningham I. A., Westmore M. S., and Fenster A., “A Spatial-frequency dependent quantum accounting diagram and detective quantum efficiency model of signal and noise-propagation in cascaded imaging-systems,” Med. Phys. 21, 417–427 (1994). 10.1118/1.597401 [DOI] [PubMed] [Google Scholar]
- Yao J. and Cunningham I. A., “Parallel cascades: New ways to describe noise transfer in medical imaging systems,” Med. Phys. 28, 2020–2038 (2001). 10.1118/1.1405842 [DOI] [PubMed] [Google Scholar]
- Vedantham S., Karellas A., Suryanarayanan S., Albagli D., Han S., Tkaczyk E. J., Landberg C. E., Opsahl-Ong B., Granfors P. R., Levis I., D’Orsi C. J., and Hendrick R. E., “Full breast digital mammography with an amorphous silicon-based flat panel detector: Physical characteristics of a clinical prototype,” Med. Phys. 27, 558–567 (2000). 10.1118/1.598895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richard S., Siewerdsen J. H., Jaffray D. A., Moseley D. J., and Bakhtiar B., “Generalized DQE analysis of radiographic and dual-energy imaging using flat-panel detectors,” Med. Phys. 32, 1397–1413 (2005). 10.1118/1.1901203 [DOI] [PubMed] [Google Scholar]
- Richard S. and Siewerdsen J. H., “Optimization of dual-energy imaging systems using generalized NEQ and imaging task,” Med. Phys. 34, 127–139 (2007). 10.1118/1.2400620 [DOI] [PubMed] [Google Scholar]
- Cunningham I. A., “Analyzing system performance,” The Expanding Role of Medical Physics in Diagnostic Imaging, edited by Frey G. D. and Sprawls P. (AAPM, Madison, WI, 1997), pp. 231–263. [Google Scholar]
- Cunningham I. A. and Shaw R., “Signal-to-noise optimization of medical imaging systems,” J. Opt. Soc. Am. A 16, 621–632 (1999). 10.1364/JOSAA.16.000621 [DOI] [Google Scholar]
- Barrett H. H., “Objective assessment of image quality: Effects of quantum noise and object variability,” J. Opt. Soc. Am. A 7, 1266–1278 (1990). 10.1364/JOSAA.7.001266 [DOI] [PubMed] [Google Scholar]
- Barrett H. H., Denny J. L., Gifford H. C., Abbey C. K., Wagner R. F., and Myers K. J., “Generalized NEQ: Fourier analysis where you would least expect to find it,” Proc. SPIE, 2708, 41–52 (1996). 10.1117/12.237805 [DOI] [Google Scholar]
- Seibert J. A. and Boone J. M., “X-ray scatter removal by deconvolution,” Med. Phys. 15, 567–575 (1988). 10.1118/1.596208 [DOI] [PubMed] [Google Scholar]
- Nishikawa R. M. and Yaffe M. J., “Signal-to-noise properties of mammographic film-screen systems,” Med. Phys. 12, 32–39 (1985). 10.1118/1.595781 [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H. and Antonuk L. E., “DQE and system optimization for indirect-detection flat-panel imagers in diagnostic radiology,” Proc. SPIE, 3336, 546–555 (1998). 10.1117/12.317057 [DOI] [PubMed] [Google Scholar]
- Wagner R. F., Brown D. G., and Pastel M. S., “Application of information theory to the assessment of computed tomography,” Med. Phys. 6, 83–94 (1979). 10.1118/1.594559 [DOI] [PubMed] [Google Scholar]
- Myers K. J., Barrett H. H., Borgstrom M. C., Patton D. D., and Seeley G. W., “Effect of noise correlation on detectability of disk signals in medical imaging,” J. Opt. Soc. Am. A 2, 1752–1759 (1985). 10.1364/JOSAA.2.001752 [DOI] [PubMed] [Google Scholar]
- Burgess A. E., Li X., and Abbey C. K., “Visual signal detectability with two noise components: Anomalous masking effects,” J. Opt. Soc. Am. A Opt. Image Sci. Vis. 14, 2420–2442 (1997). 10.1364/JOSAA.14.002420 [DOI] [PubMed] [Google Scholar]
- Barten P. G. J., Contrast Sensitivity of the Human Eye and Its Effects on Image Quality (SPIE, Bellingham, 1999). [Google Scholar]
- Richard S. and Siewerdsen J. H., “Comparison of model and human observer performance for detection and discrimination tasks using dual-energy x-ray images,” Med. Phys. 35, 5043–5053 (2008). 10.1118/1.2988161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siewerdsen J. H., Waese A. M., Moseley D. J., Richard S., and Jaffray D. A., “Spektr: A computational tool for x-ray spectral analysis and imaging system optimization,” Med. Phys. 31, 3057–3067 (2004). 10.1118/1.1758350 [DOI] [PubMed] [Google Scholar]
- Boone J. M. and Seibert J. A., “An accurate method for computer-generating tungsten anode x-ray spectra from 30 to 140 kV,” Med. Phys. 24, 1661–1670 (1997). 10.1118/1.597953 [DOI] [PubMed] [Google Scholar]
- Hubbell J. H. and Seltzer S. M., “Tables of x-ray mass attenuation coefficients and mass energy-absorption coefficients,” NIST Report No. 5632 (1995).
- International Commission on Radiation Units and Measurements, “Photon, electron, proton and neutron interaction data for body tissues,” ICRU Report No. 46 (International Commission on Radiation Units and Measurements, Bethesda, MD, 1992).
- Cunningham I. A., Sattarivand M., Hajdok G., and Yao J., “Can a Fourier-based cascaded-systems analysis describe noise in complex shift-variant spatially sampled detectors?,” Proc. SPIE, 5368, 79–88 (2004). 10.1117/12.534791 [DOI] [Google Scholar]
- Albert M. and Maidment A. D. A., “Linear response theory for detectors consisting of discrete arrays,” Med. Phys. 27, 2417–2434 (2000). 10.1118/1.1286592 [DOI] [PubMed] [Google Scholar]
- Samei E., J. T.Dobbins, III, Lo J. Y., and Tornai M. P., “A framework for optimising the radiographic technique in digital x-ray imaging,” Radiat. Prot. Dosim. 114, 220–229 (2005). 10.1093/rpd/nch562 [DOI] [PubMed] [Google Scholar]
- McKinley R. L., Samei E., Brzymialkiewicz C. N., Tornai M. P., and Carey J.Floyd E., Measurements of an Optimized Beam for X-Ray Computed Mammotomography (SPIE, n, 2004). [Google Scholar]
- Shkumat N. A., Siewerdsen J. H., Dhanantwari A. C., Williams D. B., Richard S., Paul N. S., Yorkston J., and Metter R., “Optimization of image acquisition techniques for dual-energy imaging of the chest,” Med. Phys. 34, 3904–3915 (2007). 10.1118/1.2777278 [DOI] [PubMed] [Google Scholar]
- Feldkamp L. A., Davis L. C., and Kress J. W., “Practical cone-beam algorithm,” J. Opt. Soc. Am. A 1, 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]
- Biswas D., Bible J. E., Bohan M., Simpson A. K., Whang P. G., and Grauer J. N., “Radiation exposure from musculoskeletal computerized tomographic scans,” J. Bone Jt. Surg., Am. 91, 1882–1889 (2009). 10.2106/JBJS.H.01199 [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H., Cunningham I. A., and Jaffray D. A., “A framework for noise-power spectrum analysis of multidimensional images,” Med. Phys. 29, 2655–2671 (2002). 10.1118/1.1513158 [DOI] [PubMed] [Google Scholar]
- Johns H. E. and Cunningham J. R., The Physics of Radiology, 4th ed. (Thomas, Springfield, IL, 1983). [Google Scholar]
- Muntz E. P., Jacobson G., Kaegi E. M., and Klein D. J., “Electronic grids for electrostatic imaging systems,” Radiology 121, 197–204 (1976). [DOI] [PubMed] [Google Scholar]
- Neitzel U., “Grids or air gaps for scatter reduction in digital radiography: A model calculation,” Med. Phys. 19, 475–481 (1992). 10.1118/1.596836 [DOI] [PubMed] [Google Scholar]
- Sorenson J. A. and Floch J., “Scatter rejection by air gaps: An empirical model,” Med. Phys. 12, 308–316 (1985). 10.1118/1.595690 [DOI] [PubMed] [Google Scholar]
- Kyriakou Y. and Kalender W. A., “X-ray scatter data for flat-panel detector CT,” Phys. Med. 23, 3–15 (2007). 10.1016/j.ejmp.2006.12.004 [DOI] [PubMed] [Google Scholar]