Abstract
Emotion (i.e., spontaneous motivation and subsequent implementation of a behavior) and cognition (i.e., problem solving by information processing) are essential to how we, as humans, respond to changes in our environment. Recent studies in cognitive science suggest that emotion and cognition are subserved by different, although heavily integrated, neural systems. Understanding the time-varying relationship of emotion and cognition is a challenging goal with important implications for neuroscience. We formulate here the dynamical model of emotion-cognition interaction that is based on the following principles: (1) the temporal evolution of cognitive and emotion modes are captured by the incoming stimuli and competition within and among themselves (competition principle); (2) metastable states exist in the unified emotion-cognition phase space; and (3) the brain processes information with robust and reproducible transients through the sequence of metastable states. Such a model can take advantage of the often ignored temporal structure of the emotion-cognition interaction to provide a robust and generalizable method for understanding the relationship between brain activation and complex human behavior. The mathematical image of the robust and reproducible transient dynamics is a Stable Heteroclinic Sequence (SHS), and the Stable Heteroclinic Channels (SHCs). These have been hypothesized to be possible mechanisms that lead to the sequential transient behavior observed in networks. We investigate the modularity of SHCs, i.e., given a SHS and a SHC that is supported in one part of a network, we study conditions under which the SHC pertaining to the cognition will continue to function in the presence of interfering activity with other parts of the network, i.e., emotion.
Keywords: Metastability, Transients
1 Introduction
The emotion-cognitive behavior has its basis in dynamical coordination of many brain centers, which often participate in both emotion and cognitive activity (Fales et al. 2008; Lewis 2005; Pessoa 2008). Due to this overlap, emotion and cognition are integrated in the sense of being partly separable (Gray et al. 2002). There are three main mechanisms of cognitive-emotional interaction: (i) involvement of multiple brain centers, like amygdala and prefrontal cortex, in both emotion and cognitive networks (Adolphs 2008; Phelps 2006); (ii) the high degree of connectivity between different brain areas (Bechara et al. 2000); and (iii) rhythmic brain activity (electric brain oscillations) at certain frequencies that supports coherent interactions between anatomically distinct regions of the brain during cognitive tasks, which require attention, working memory, or sensory processing (see, for example Kelso 1995; Buzsaki 2006; Buzsaki and Draguhn 2004). An intriguing aspect of emotion-cognition interaction is the cognitive control via emotions. On the neurobiological level, cognitive control may be attributed to prefrontal activity inhibiting relevant subcortical emotion processing regions.
Emotion and cognition are sequential dynamic processes resulting from interactions of different brain subsystems (circuits) and their coordination/synchronization in time (Scherer 1993). Such properties make the modeling of mental processes an intriguing problem from dynamical systems point of view. Several attempts have been taken recently in this direction and in modeling disorders (Huber et al. 2001, 2004; beim Graben and Potthast 2009).
Sequential steps of emotion-cognition interactions are directly relevant to action control, in terms of memory, decision-making, reasoning, attention, and emotion regulation (Reis et al. 2007). A predominant phenomenon governing the dynamics of the brain is that the nervous system is responsible for its internal regulation, i.e., the generation and distribution of the energy and memory resources between the emotions, thoughts, and actions. Thus, emotions and cognition are active processes that result in specific functional changing of the brain organization in time and the dynamical brain’s response to environmental information. These processes are determined by the functional (not necessary synaptic) connections between brain areas or neural circuits that participate in the execution of cognitive functions and generation of emotions. At different segments or steps of temporal emotional or cognitive process, the participating networks may vary, thus the temporal structure of the different emotions in the brain also is different. In terms of the collective network activity, emotion and cognition are not just spatial but spatio-temporal patterns, which are very sensitive to external or internal stimulus events. This is the way for brain to solve the fundamental conflict between the finite number of functionally-relevant centers in the representation and the continuous spectrum of different emotions and the huge variety of cognitive functions to be expressed. Such stimulus-dependent encoding is the origin of the enormous brain capacity. The understanding of the temporal structure of spatio-temporal patterns and experimentally verifiable models of the emotion-cognition sequential dynamics are the key steps to enlighten specific functional relationship within multiple neuro-anatomical structures, which are responsible for specific emotional and psychiatric disorders. The dynamical system theory is a natural domain for the analysis of such a complex network of neural clusters working coherently in time. Two key experimental observations guide us towards a dynamical model: (i) the existence of metastable cognitive states, and (ii) transitivity of reproducible cognitive processes (Rabinovich et al. 2008).
Despite the strong coupling between the cognition and emotions, their dependence on time can be quite different. The main difference is the following: the emotion may be quasi-static or recurrent in time, whereas a cognitive activity, by the nature of its task, must be transient in time until the termination of the executed cognitive function. It can then return back to a static or rhythmic regime. Nonlinear dynamics constitutes the only feasible medium that can accommodate such a behavior. The idea that emotion-cognitive activity can be understood using nonlinear dynamics has been intensively discussed at length for the last 15 years (Lewis et al. 2008; Friston 1997, 2000; Friston et al. 2003; Port and van Gelder 1995).
The main problem faced when using dynamical systems theory to describe transient neural activity is the fundamental contradiction between reproducibility and flexibility of transient behavior (Vogels et al. 2005; Abott 2008). A nonlinear dynamical behavior confined in a stable sequence of metastable states is the only feasible solution to this dilemma.
Metastability is a general nonlinear dynamics concept, which describes states of delicate equilibrium. A system is in a metastable state when it is in the vicinity of such an equilibrium, i.e., a state where the system spends an extended (but finite) period of time. Under the action of perturbations or interaction system is susceptible to fall into another state. Metastability in the brain is a phenomenon, which is being studied in neuroscience to elucidate how the human mind processes information and recognizes patterns. There are semitransient signals in the brain, which persist for a while and are different than the usual equilibrium state (Abeles et al. 1995; Werner 2007). Thus, metastability is a principle that describes the brain’s ability to make sense out of seemingly random environmental cues (Oullier and Kelso 2006). In the past 25 years, interest in metastability and the underlying framework of nonlinear dynamics has been fueled by advancements in the methods by which computers model brain activity. The metastability is supported by the flexibility of coupling among diverse brain centers or neuron groups (Friston 1997, 2000; Ito et al. 2007; Sasaki et al. 2007): that is, in the form of a continuum of dynamically shifting, discrete configurations of brain networks (for a review, see Fingelkurts and Fingelkurts 2006). The temporal order of the metastable states are determined by the functional connectivity of the underlying networks and their causality structure (Chen et al. 2009).The brain metastable states, in their turn, must appear in the EEG in the form of its piecewise stationary organization which can be studied by means of the change-point analysis (Kaplan and Shishkin 2000).
We develop here a theoretical description of the transient emotion-cognitive dynamics based on the interaction of functionally-dependent emotion-cognitive modes. The basis of this model has been recently discussed in Rabinovich et al. (2008) in the context of cognitive modes competition without taking into account an emotional influence. The core of this paradigm is a sequential Winnerless Competition (WLC) of different cortical subnetworks for the brain resources along the execution process. Such competition is reminiscent of the competition of different species for the environmental resources in ecology. WLC principle was formulated first for the sensory systems (Rabinovich et al. 2001; Levi et al. 2004) and was then applied for the description of some cognitive function like decision-making (Rabinovich et al. 2008). Recent experimental evidence pinpoints competition among metastable states in the rat gustatory cortex (Jones et al. 2007) also in olfactory system (Rabinovich et al. 2008). A competitive and concurrent activity of multiple brain areas (Fox et al. 2005, 2007) that collaborate in a large-scale cortical process is fundamentally important for thinking, in particular, for sentence comprehension (Just and Varma 2007). The physiological mechanism of such competition is inhibition (see for a review Aron 2007; Rabinovich et al. 2006).
The paper is organized as follows: The winnerless competition principle and a unified model of such joint activity among brain modes is introduced in the following section, which also presents a simulation that accounts for possible qualitative and quantitative aspects of their interaction. In Sects. 3 and 4, the mathematical frame-work of this interference is presented and rigorous conditions on the robustness of metastable behavior are derived.
2 Competition in the Brain
Neural activity demands certain physical (e.g., glucose, oxygen, etc.) and informational (e.g., sensory stimulation) resources. A predominant factor underlying the brain dynamics is the competition among brain centers and modes for these finite resources. The fundamental mechanism in carrying out this competition is inhibition, which is widespread in the cortex. Under mild constraints, the multi-agent competition induces a transient and predictable dynamics. The stable heteroclinic channel (SHC) is a solid embodiment of these vital features.
Thus, let us formulate the desired features of the basic dynamical model: (1) the model must be dissipative with an unstable trivial state (origin) in the phase space and corresponding linear increments must be stabilized by nonlinear decrements organized by self- and mutual-inhibition (modes competition); (2) the phase space of the system must include metastable states that represent the activity of an individual mode, when others modes are passive; and (3) these metastable states must be connected by separatrices in a specific order and build the sequence. Well-known rate models in neuroscience naturally satisfy these conditions in some regions of their control parameter spaces (Rabinovich et al. 2006).
2.1 Generalized Lotka–Volterra Equations
A widely-accepted rate model of competition among N agents is the Generalized Lotka–Volterra (GLV) system (Muezzinoglu et al. 2010; Murray 2002)
| (1) |
where xi ≥ 0 denotes the ith competitor, I summarizes all observable environmental factors that influence competition, σi ≥ 0 is the resources available for the competitor i to prosper, ρij is the competition matrix with nonnegative entries, and η is a noise process, capturing all unpredictable effects from the environment.
As introduced in Afraimovich et al. (2004), the following conditions ensure a periodic Stable Heteroclinic Sequence (SHS) (see Sect. 3.1) of N saddles:
| (2) |
| (3) |
| (4) |
The self-inhibition of each competitor is quantified by ρii = 1, and the noise magnitude |η| is assumed to be sufficiently small. Without loss of generality, these conditions place the N saddles on the N axes of the phase space with the ith one σi from the origin, and, order them along the SHC with respect to the index i (see Fig. 1).
Fig. 1.
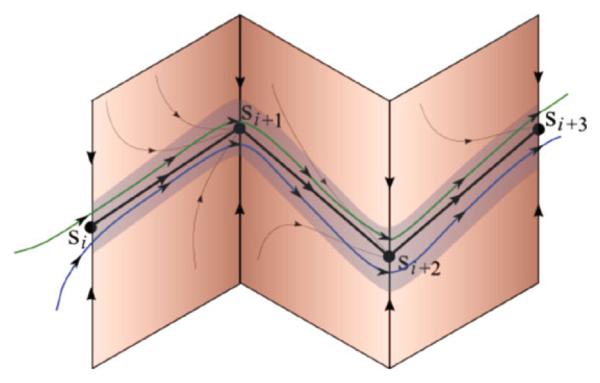
A structurally stable heteroclinic sequence of metastable states and the surrounding channel
2.2 Model of Weak Emotion–Cognition Interaction
We represent the cognitive modes participating in the modes interaction by Ai ≥ 0, i = 1, … , N. Following the competition principle discussed above, for a given cognitive load I, we adopt the GLV model (1) for the cognitive modes
| (5) |
where B = [B1 … BM] denotes the activity of emotional modes Bi ≥ 0, i = 1, … , M, and all other parameters are defined as in (1). We also assume that, in the absence of an emotional distractor (which may be a certain spatio-temporal pattern observed in B), the cognitive activity follows a sequence of metastable equilibria, i.e., the cognitive trajectory Ai(t), i = 1, … , N, is confined in an SHC. In particular, αi and ρij satisfy the conditions (2)-(4) and |ηA| is sufficiently small.
Generated by specific brain modes subject to competition, the emotional modes activity Bi is also considered to be varying according to GLV equations:
| (6) |
Here, S denotes the emotional stimuli (or stressor), and all other parameters are defined as above. In contrast to the cognitive process, we do not restrict the emotion model to a heteroclinic dynamics; it can also demonstrate periodic or chaotic oscillations.
Equations (5) and (6) describe the joint emotio-cognitive course-grain dynamics. In the sequel, we limit ourselves to the special case where the term αi(I, B) in (5) can be decomposed as σi(I) + ∊ · γi(B) and the competition matrix ρij is constant. With these assumptions, the joint dynamics also fall under the winnerless competition model introduced in (1).
2.3 Example
To illustrate the structural stability of sequential cognitive process, we simulated the interaction between cognitive and emotional activities in the framework of (5) and (6) with N = 5 cognitive and M = 5 emotional modes. The cognitive and emotional modes evolve in different manner: In particular, the former evolve in periodic way and the latter changing sequentially.
We simulated N = 5 cognitive and M = 5 emotional modes that evolve in periodic (closed) SHCs using the GLV equations (5) and (6). The simulation focused on the effect of emotional process on the cognitive process, thus we further simplified the emotion model by selecting ζi(S, A) = ζi(S) = S, and ξij as independent of A. The cognitive resource component σi(I) is selected as the unity.
The constant competition matrices ρij and ξij are set based on the conditions (2)-(4), with σi substituted by the unity in all inequalities. Specifically, we evaluated ρi−1,i and ρi+1,i at the mid-points of the intervals imposed in (2) and (3), and assigned ρji = ρi−1,i + 0.5 to satisfy (4). This establishes the periodic stable heteroclinic sequence e1 → e2 → … → e5 → e1, ei denoting the ith unit vector, in each of the cognitive and the emotive working (phase) spaces, when the resource terms αi and ζi equal 1 for all i.
Our setup assigns to certain emotional modes, namely B1 and B2, a distracting role on the sequential behavior on the A network, whereas B4 is a motivating emotional mode. We implement this through the coupling term γi(B) = [0.5 0.5 1.0 2.0 1.0]T · B for i = 1, ߪ , 5. With this interaction scheme, the distracting emotional modes slow-down the cognitive network’s switching pattern in time and reduce the cognitive modes magnitude. In the extreme distraction, the order of cognitive modes is disrupted.
We set the emotion process to evolve on a slower time scale, thus the noise terms ηA and ηB were selected as white noise processes with variances 10−8 and 0.005, respectively. The result is shown in Fig. 2.
Fig. 2.
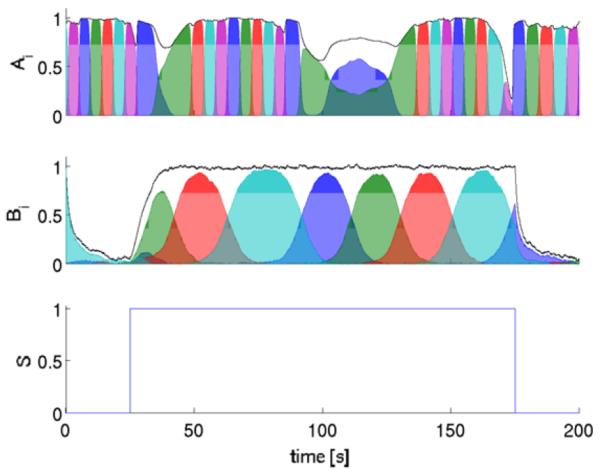
Simulation of the emotion-cognitive model with the parameters listed in the text. According to the selected interaction scheme γ(B), the emotion modes B1 and B2 (indicated by the blue and green curves in the second row) are capable of derailing the A network from the cognitive SHC. When the coupling ∊ is weak (as in the early and the late phases of the stressor cycle, the emotion modes B1 and B2 still inhibit (slow down) the cognitive process), but the cognitive network does not loose its prescribed track, i.e., emotion does not destroy cognition
3 General Mathematical Framework
3.1 Stable Heteroclinic Sequences and Channels
We will begin with the transient (cognitive) part of the dynamics, which we suppose is modeled by a Stable Heteroclinic Channel, a concept that we make precise now.
Definition 3.1 Consider a system of differential equations:
| (7) |
where . This system is said to possess a heteroclinic sequence if:
- It has a finite sequence {Q1, Q2, … , QN of equilibrium points and at Qi the eigenvalues of the linearization of (7) can be ordered as:
Thus, each Qi is a saddle with a 1 dimensional unstable manifold consisting of two components, and . For each 1 ≤ i ≤ N − 1, intersects the stable manifold of Qi+1.
Denote
The set Γ is commonly called a heteroclinic sequence. If in addition, QN is connected to Q1 by a heteroclinic orbit then the sequence is called periodic or a heteroclinic cycle.
Definition 3.2 The number
is called the saddle value for Qi. If νi > 1, then the saddle Qi is called dissipative. If all the saddles in a heteroclinic sequence are dissipative, then we call Γ a Stable Heteroclinic Sequence (SHS).
If a system has a Stable Heteroclinic Sequence, then it also has a Stable Heteroclinic Channel (SHC).
Theorem 3.3 (Afraimovich et al. 2004) In any neighborhood of a SHS there is a connected open set O called a Stable Heteroclinic Channel such that an orbit starting at any initial condition inside O will continue inside O until it emerges near QN. It is robust under an open set of small perturbations of f in the sense that given any neighborhood of Γ and ∊ sufficiently small, there is a set in the neighborhood that has the same properties as O for any perturbation of size ∊ in an open set of perturbations (in an appropriate Banach space of vector fields) and as ∊ → 0.
Remarks on the proof of this theorem The condition on each νi gives the existence of O. If we consider perturbations of size, ∊ because Qi is a saddle, is close to , and thus will approach a neighborhood, Vi+1 of Qi+1. The local piece of divides Vi+1 into two parts: the one containing will be denoted by . There are two possibilities: (1) enters , or (2) it enters . Each of these corresponds a different class of perturbations of f (x); call them S1 and S2. The main problem is to describe the conditions for the occurrence of the class S1 in a suitable form for i = 1, … , N − 1, since, if the situation S2 holds, then the x-coordinate of an orbit with an initial point close to can follow preventing the realization of the SHC. The important point is: of the conditions for the occurrence of S1, these conditions are “open”, i.e., they single out an open set in the Banach space of vector fields. For competition type equations, such as those considered in Sect. 2, case S2 is ruled out by the equations since no coordinate, Ai, can be negative. Under condition S1, the dissipativeness at each saddle was used in the proof of the theorem to show that O persists under small perturbations.
3.2 SHC in the Joint Emotion-Cognition Phase Space
In addition to the SHS in the components of the system represented by the x variables, we now suppose that the network has other components (emotive), represented by the vector variable . Later we will emphasize periodic and quasiperiodic behavior in the y variable, but first we formulate it generally, that is, the entire network (5), (6) satisfies equations of the form:
| (8) |
where for this f, (7) possesses a SHS. We will also consider the case as in the previous section where the equations for the x variables are of the competitive form:
| (9) |
We will denote by the solution flow on generated by (8) and we will use the notation ϕt to denote the flow on generated by the subsystem (7). When ∊ = 0 the x variable is uncoupled from the y variable and so the projection onto the x variables possess a SHS and SHC. We wish to study conditions for which some structure equivalent to the SHC persists for ∊ > 0 in the full equations. Thus, we will consider (8) with ∊ > 0 as a perturbation of ∊ = 0.
We will assume that h(x, y) in (8) is dissipative in y in the sense that for each x, the system:
| (10) |
contracts volume in phase space and has a ball of dissipation, i.e., a bounded ball such that any orbit in eventually enters B and no orbits in B escape from B in forward time. Under these conditions, (10) has a maximal compact attracting set Λx for each x. In particular, let Λi denote the maximal attracting set for x = Qi. This implies that for each Qi the system (8) with ∊ = 0 has a compact invariant set given by Qi × Λi.
We note here that each maximal attracting set Λi will contain one or more “attractors”. We say that a compact set A ∈ Λi is an attractor for a flow Ψt if (1) there is an open neighborhood U of A such that ⋂t>0 Ψt (U) = A and (2) A is the ω-limit set of at least one point in U.
If A ⊂ Λi is an attractor for (10), then Qi × A is an invariant set for (8) with ∊ = 0.
In the unperturbed equations (8) with ∊ = 0 even though the x variable contains a SHS, the full equations do not necessarily contain a SHS as defined above. There is an exception in a particular case that we describe next.
3.3 Exceptional Case: The Attractors Are Stable Equilibria
Suppose that each attractor A is a globally attracting fixed point. That is, for ∊ = 0, and each i, (10) has a globally attracting fixed point Pi. If this is the case, because Qi is a saddle point for φt, Qi × Pi is a saddle point for . It is a classical result that a saddle and its local stable and unstable manifolds are preserved for ∊ > 0.
Lemma 3.4 If for each i, Λi consists of a unique, globally attracting stable equilibrium, Pi, then for ∊ = 0 there is a heteroclinic connection between Qi × Pi and Qi+1 × Pi+1 for each 1 ≤ i < N − 1.
Proof By the assumptions, the unstable manifold of Qi × Pi is one-dimensional. Since Qi itself has a one-dimensional unstable manifold for (7), this manifold must be the projection onto x of the unstable manifold for Qi × Pi. If (x0, y0) is any point in this unstable manifold, since the x equation is uncoupled, it follows that φt(x0) limits onto Qi+1 in the forward direction. For ∊ = 0 this orbit must coincide with the x projection of . Now since Pi+1 is globally attracting for x = Qi+1, there is a globally attracting fixed point, near Pi+1 for (10) for x sufficiently close to Qi+1. Thus, once the x coordinate enters a sufficiently small neighborhood of Qi+1, the y coordinate will be attracted to a small neighborhood of Pi+1. We can take this later neighborhood arbitrarily small, and thus it follows that the y coordinate of the flow approaches Pi+1.
Thus, the set of equilibria along with the heteroclinic connections between them form a Heteroclinic Sequence (8) with ∊ = 0.
Since Pi is an attracting equilibrium for (10), the eigenvalues of the linearization of (10) at Pi must satisfy:
where m is the dimension of y. It follows that the eigenvalues of the linearization of (8) at Qi × Pi are simply: {λ1, … , λn, μ1, … , μm}. Thus, if in addition to the requirement that the heteroclinic sequence be dissipative for (7), we also have
then the equilibrium Qi × Pi is dissipative in the full equations (8) when ∊ = 0. If this is the case for each i, then the full system (8) has a SHS, and so by Theorem 3.3 it will have a Stable Heteroclinic Channel.
3.4 General Persistence of Solutions in the Channel
Since the x equations possess a SHC, O, the set is a weak generalization of the stable heteroclinic channel. Any orbit with an initial condition in it will remain in it and the x components of the orbit will obviously follow the heteroclinic sequence. The following is trivial.
Proposition 3.5 Suppose that x is in O and a small neighborhood of Q1. Then for any , the solution of (8) with ∊ = 0 and initial condition (x, y) will remain in until it emerges at QN.
We then easily have the following.
Proposition 3.6 Let γ (t), 0 ≤ t ≤ T be a solution segment of (8) for ∊ = 0 whose x coordinate is in O. Then for any δ > 0 sufficiently small there exists ∊ (δ) > 0 such that given any 0 < ∊ ≤ ∊ (δ), any orbit of starting with initial condition in a δ-ball centered at γ(0) will have x coordinate that remain in for 0 ≤ t ≤ T.
This follows simply because the time span considered is finite and a sufficiently small neighborhood of γ does not contain any singularity. Therefore, persistence follows from standard results on smooth dependence of solutions on initial conditions and parameters. This result is actually rather limited in scope. Given δ, there is not necessarily an ∊ sufficiently small so that the pertubed system has a SHC in a δ neighborhood of the heteroclinic cycle. In other words, the SHC does not persist in the sense of Theorem 3.3. To obtain that, we will consider the problem more deeply in the next section.
4 Preservation of the SHS
In this section, we consider stronger results in which invariant sets in the sequence and the SHC are preserved. This will be the case if the invariant sets happen to be hyperbolic, or more generally Normally Hyperbolic which we define in an Appendix for the convenience of the reader.
4.1 The Stable Heteroclinic Network
In general, not all of the attractors will be equilibria and a maximal attracting set Λi may contain more that one attractor. While each Λi may contain multiple attractors, not all of these attractors are relevant. Only those contained in a certain collection of attractors and heteroclinic connections plays a role in the preservation of a SHC. We define the Heteroclinic Network associated with the SHS, or simply the Net, inductively,
Any attractor A ⊂ Λ1 is in the Net.
An attractor C ⊂ Λi+1 is in the Net if there exists B ⊂ Λi such that there is a heteroclinic connection from Qi × B to Qi+1 × C. In this case C is a successor to B.
If attractor B is a successor to A, then we include all heteroclinic connections between Qi × A and Qi+1 × B in the Net.
This structure makes a partial ordering of the attractors in the Net in the obvious way. Consider the attractors as nodes, with directed vertexes connecting those nodes that have a heteroclinic connection, the Heteroclinic Network can be represented by a multipartite, acyclic directed graph.
We note that if Λi contains a (unique) global attractor, then that attractor is necessarily in the Heteroclinic Net.
Lemma 4.1 If Λi+1, 1 ≤ i ≤ N − 1, contains a global attractor B, then for any attractor A in Λi there is a heteroclinic connection between Qi × A and Qi+1 × B.
The proof is similar to that of Lemma 3.4.
Another simplification occurs if an attractor A in the Net is an equilibrium. In this case, the equilibrium has only a 1-dimensional unstable manifold, and thus there can only be one successor B to this attractor in the net. For any other type of attractor, the unstable manifold will have dimension greater than one. Since such a manifold contains an uncountable family of orbits, A may have any number of successors.
4.2 Normal Hyperbolicity at Attractors
Each Λi will contain at least one attractor, but maybe more, and each of these is necessarily invariant set of (8) for ∊ = 0. We saw in a previous section that if the attractor happens to be a stable equilibrium, Pi, then the point Qi × Pi will be a saddle in the full equations for ∊ = 0 with a 1-d unstable manifold. As it is hyperbolic, the saddle will persist under small perturbations, as will its local stable and unstable manifolds. A generalization of this situation is when an attractor happens to be a normally hyperbolic manifold (see the Appendix). Then it and its stable and unstable manifolds will be preserved for ∊ > 0.
There are two special cases of attractors A where normal hyperbolicity always occurs:
Periodic behavior in y Suppose that (10) has a periodic orbit in which we denote by γ. If γ is a stable attracting orbit for (10) then Mi = Qi × γ is automatically a hyperbolic periodic orbit for (8) with ∊ × 0. This is because each point in γ will have a one-dimensional unstable subspace, a one-dimensional center subspace T Γ along the direction of the flow and the rest of the directions will be strictly contracting. Thus Qi × γ and its local stable and unstable manifolds are preserved under small perturbations.
Quasi-Periodic behavior in y In this case A is an attracting torus with an irrational flow. If the flow on the torus is irrational then Qi × A will be normally hyperbolic since the directions T A (tangent space to A) will all be neutral. There will be one unstable direction at each point in A and all the other directions will be exponentially attracting.
It may happen that the maximal attracting set Λi contain more than one attractor. Each of these may be considered separately.
Note that each A is an attractor for (10). Thus if A is a manifold, the normal directions to the manifold must be stable. For Qi × A to be normally hyperbolic the only conditions are conditions on A with respect to y. Namely, if there is any contraction within A is must be weaker than the contraction due to the normal direction and if there is any expansion within A it must be weaker than the expansion in the one unstable x direction. If Ai is an attractor for (10) at Qi and is a normally hyperbolic manifold, then one may define an attraction rate for A as
.
By definition λs is negative. Parallel to Definition 3.2, we make the following definition.
Definition 4.2 Consider Qi × Ai. Let
where as before is the positive eigenvalue of the linearization of (7) at Qi. We call the saddle-value for Qi × Ai and say that Qi × Ai is dissipative if νs > 1.
We will now show that under certain conditions there will be an analogous structure to the SHC that will persist for ∊ > 0.
Theorem 4.3 Suppose that (7) has a SH and that for each i, Λi contains a global attractor Ai and Qi × Ai is a normally hyperbolic manifold for (8) with ∊ = 0. Suppose further that either
Then there exists an open set in the Banach space of vector fields (8) such that for ∊ > 0 sufficiently small the full system has a SHC and it persists for ∊ > 0. In this context, this means: Given any δ > 0, there exists ∊0 > 0 and an open set O in δ-neighborhood of the SHS such that any solution , with ∊ < ∊0 starting from an initial condition in O will remain in O until it leaves this set in a neighborhood of QN.
Outline of the Proof Because of the normal hyperbolicity assumption each Qi × Ai along with and its stable manifold will be preserved under small perturbations (A.1). Denote these structures by , and . Since the is close to locally, will enter a neighborhood, Vi+1 of Qi+1. The local piece of divides Vi+1 into two parts: the one containing will be denoted by . There are two possibilities: (1) enters , or (2) it enters . Each of these corresponds a different class of vector functions g(x, y), say, S1 and S2. In the case of S1, the x-coordinate of an orbit will follow . The conditions for the occurrence of S1 are “open”, i.e., they single out an open set in the Banach space of vector fields.
Now we consider case (1) Each Qi × Ai is dissipative. The proof is similar to that in Rabinovich et al. (2008). A piece of has an end point, say, with , Ki being a constant independent of ∊. Given an initial point (x0, y0) with , dist((x0, y0), (x, y)) < ∊, the corresponding solution (x(t), y(t)) of (8) at the instant of exit from satisfies the inequality
| (11) |
where is the saddle value of Qi × Ai. The validity of (11) can be shown by a local study of solutions of (8) in a neighborhood of a saddle invariant subset, similar to the considerations (Shilnikov et al. 1998, 2001). To proceed in the study from i to i + 1, one must be sure that
| (12) |
The condition (12) also singles out an open set in the Banach space of vector fields (8).
Next consider case (2); he x equation has the competitive form (9). Consider the linearization of (9) at Qi. Since the nature of the equations restricts Qi to lie on the xi axis, so that the xj coordinate is 0 for j ≠ i. (In effect the x-coordinates of are all restricted to be zero.) It is clear from that for ∊ small enough, the contraction rates for all x variables other than xi are only perturbed by the y term. The same is true for the expanding direction.
The only nontrivial direction is xi itself. The xi coordinate of Qi is σi. However, the equations do not restrict the xi coordinate of to be σi. Rather, the xi coordinate of will locally be a graph of a function ∊h(y,∊). Since is invariant, this graph will be invariant and if we make a local change of variables we again obtain a form where is the coordinate for and the linearization is again contractive. Since the perturbations are smooth, the contraction rate in the direction will be close to that of xi for ∊ = 0.
Now let us consider a passage through a neighborhood of . Fix δ > 0 (not necessarily small) and suppose ∊ > 0 is small. Denote by a neighborhood of whose x coordinates are no more than K ∊ from and whose y coordinates are within δ of . Note that g(y) can be uniformly bounded on a Kδ-neighborhood of . Suppose that solution enters . Note that since Ai is an attractor in the y direction, the y coordinates will remain within δ of . Further, from the previous analysis, we see that when the solution leaves its x coordinates will satisfy:
| (13) |
Since we may take , we see that this distance can be made less than ∊ for any ∊ sufficiently small.
Next, consider the passage from to . Since the x coordinate of the solution begins within distance ∊ of , and is close to , it follows that the x coordinate of the solution will come within K ∊ of in a finite time, while the y coordinate during the same time must come within Kδ of . However, since Ai is an attractor in the y direction, the y coordinate will also enter within a uniformly bounded time independent of ∊. Since we can make the time of passage close to arbitrarily long by making ∊ small, we see that the solution will in fact enter .
The proof in both cases is finished by induction.
Note that orbits described in the theorem when projected onto the x directions will come close to Q1, Q2, … , QN in order, thus executing the sequential pattern of activation associated with the original heteroclinic sequence in the isolated system.
Remark on Periodic and Quasi-periodic behavior in y Suppose that in the y variables the unperturbed system has an invariant globally attracting torus for each x in a neighborhood of the Stable Heteroclinic Sequence and this torus depends smoothly on x in this neighborhood. Further suppose that the flow is essentially quasi-periodic in the y variables for each x = Qi. By that we mean that the flow on the attractor is either irrational or periodic (a periodic attractor on the torus). In such a case, the attractor at each Qi is normally hyperbolic in the full unperturbed system.
In all such examples, the SHC is preserved by small perturbations. Thus, we see that a Stable Heteroclinic Channel is always compatible with weak coupling to a quasi-periodic or periodic action in other variables, i.e., transient functionalities encoded by a SHC can coexist with repetitive-type functionalities.
4.3 Return to the Winnerless Competition Model
In many applications, each xi represents the activation level of some neuron or cluster of neurons or mode oscillation, etc. and the phase space is a . In this situation, it is natural that each saddle Qi is on the boundary phase space and Γ− points outside. Thus, orbits entering a neighborhood of Qi cannot follow away from Qi, and so must follow Γ+, i.e., the case S1 occurs automatically.
In (5) and (6), let us emphasize that the dissipativeness of the system (6), for any fixed A and in the absence of noise follows directly from the assumption ξij(A) > 0.
In the absence of noise, the system (5) for ∊ = 0 has an equilibrium Qi : A(i) = (0 … σi 0 … 0) with characteristic exponents −σi and σj − ρji σi, j = 1, … , N, j ≠ i. Furthermore, for A = A(i), the system (6), in the absence of noise, has equilibria Pi,k : Bi,k = (0 … 0 ζk(S, A(i)) 0 … 0), with characteristic exponents −ζk,i := −ζk (S, A(i)) and ζk,i − ξk,mζm,i, m = 1, … , M, m ≠ k.
Next, consider the B equations in (6). We note that we have set the parameters for those equations such that the unperturbed system has a stable heteroclinic cycle. It was proved in Afraimovich et al. (2004) that for perturbations of this equation there is always born a stable limit cycle in the SHC. In the case of the simulations, we do not have precisely this situation because the perturbation is stochastic, but we do expect the behavior in the B variable to be close to being stably periodic. Thus in spirit, our main result Theorem 4.3 applies to the simulations.
5 Conclusions and Perspectives
We have presented a coupled emotion-cognitive model based on three principles governing the brain modes: competition, existence of metastable states, and robustness against noise together with sensitivity to incoming information. The model and rigorous mathematical results about the persistence of SHC are general enough and open new alleys in the quantitative theory of emotion-cognition interaction. We wish to formulate here a few of them:
It is clear from imaging experiments that emotion and cognition can be represented as the superposition of coarse-grain brain modes, whose activities are changing with time. According to our model, the cognitive and emotional modes may have distinct roles on different aspects of the mental activity. As our preliminary results show, the vibrating part of emotion acts as a multiplicative noise on the cognition vector field. This is consequential on the exit time from metastable states, i.e., the maximal time the system spends in the vicinity of saddles (see Kifer 1981; Stone and Holmes 1990 for a thorough treatment of this aspect). In fact, a local stability analysis in the vicinity of a saddle fixed point allows one to estimate this time in the light of the relation te = 1/l · ln 1/|g| where te is the mean exit time, |g| is the level emotion pulsation, and l is an eigenvalue corresponding to the unstable separatrix of the saddle. Thus, the vibrating part of emotion, unless it is too large in magnitude, just facilitates the execution of the cognitive problem as it accelerates the “stream of thought” along the SHC. Too strong emotion pulsation would move the cognitive system out of SHC. It is an important problem to estimate this critical value of emotional vibrations.
The slowly changing in time part of emotions (for example, chronic depression) is able to change the stability structure of the heteroclinic channel because it changes the effective increment σ. This part can generate saddles with multidimensional unstable manifolds. Although this scenario may seem inconsequential for the system performance (since the unstable direction with the maximum eigenvalue is likely to be followed on exit from the saddle), in reality, each exit direction would be assigned a certain probability for being followed by the system. We hope that it would be possible to formulate the relationship between this probability distribution and the eigenvalues.
In this article, we did not emphasize the fact that the B-system behaves also in a sequential manner and did not study the relation between the switching instants between metastable states in any of the systems. The coordination of multiple SHCs in coupled neural networks is an important problem that will have both theoretical and practical consequences.
It seems that the normal hyperbolicity approach works adequately in the considered situations. Conditions of normal hyperbolicity enlightens the boundaries of the instability in the emotion system to follow a prescribed cognitive function.
Acknowledgements
The authors would like to thank to the anonymous referees for their constructive comments. V.A. was partially supported by PROMEP grant UASLP-CA21. M.K. acknowledges the support from Jet Propulsion Laboratory grant 1396686. M.K. and M.I.R. acknowledge the support from ONR grant N00014-07-1-074. T.Y. was partially supported by NIH grant R01GM090207.
Appendix: Normal Hyperbolicity
We will use normal hyperbolicity as defined by Hirsh et al. (1977). An alternate definition was formulated earlier by Fenicchel (1971). Let ∥·∥ be the usual operator norm and let m(A) denote the minimum norm, i.e.,
for a linear transformation A. Suppose that is a differentiable flow and that M is a smooth (C∞) compact submanifold of that is invariant under Φt.
Definition A.1 (Hirsh et al. 1977) The flow Φt is r-normally hyperbolic at M for r ≥ 1 if Φt is Cr, and
- , the tangent bundle of over M, has a DΦt-invariant splitting
- There exists t0 ≥ 0 and a Riemann structure on such that for all p ∈ M, all t > t0:
- , and
The following is the Fundamental Theorem of Normally Hyperbolic Invariant Manifolds. A similar theorem was also proved by Fenicchel (1971).
Theorem A.2 (Hirsh et al. 1977) If Φt is r-normally hyperbolic at M, then through M pass stable and unstable invariant manifolds Ws(M) and Wu(M) respectively which are tangent at M to T M ⊕ Es and Eu ⊕ T M. They are of class Cr. The stable manifold is invariantly fibered by Cr sub-manifolds tangent at M to the subspaces Es (these are .) Similarly for the unstable manifold and Eu. These structures are unique and persistent under small perturbations of Φt.
One would wish to define normal hyperbolicity in terms of the vector field (differential equations) defining the flow, however, as pointed out in Hale (1969) and elsewhere, such conditions are subtle.
Footnotes
Open Access This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Contributor Information
Valentin Afraimovich, IICO-UASLP, A. Obregon 64, San Luis Potosi 78000, SLP, Mexico, valentin@cactus.iico.uaslp.mx.
Todd Young, Department of Mathematics, Ohio University, Athens, OH, USA, young@math.ohiou.edu.
Mehmet K. Muezzinoglu, BioCircuits Institute, University of California San Diego, La Jolla, CA, USA, mmuezzin@ucsd.edu
Mikhail I. Rabinovich, BioCircuits Institute, University of California San Diego, La Jolla, CA, USA
References
- Abeles M, Bergman H, Gat I, Meilijson I, Seidemann E, Tishby N, et al. Cortical activity flips among quasi-stationary states. Proc. Natl. Acad. Sci. 1995;92:8616–8620. doi: 10.1073/pnas.92.19.8616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abott LF. Theoretical neuroscience rising. Neuron. 2008;60:489–495. doi: 10.1016/j.neuron.2008.10.019. [DOI] [PubMed] [Google Scholar]
- Adolphs R. Fear, faces, and the human amygdala. Curr. Opin. Neurobiol. 2008;18:166–172. doi: 10.1016/j.conb.2008.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afraimovich VS, Rabinovich MI, Varona P. Heteroclinic contours in neural ensembles and the winnerless competition principle. Int. J. Bifurc. Chaos. 2004;14:1195–1208. [Google Scholar]
- Afraimovich VS, Zhigulin VP, Rabinovich MI. On the origin of reproducible sequential activity in neural circuits. Chaos. 2004;14:1123–1129. doi: 10.1063/1.1819625. [DOI] [PubMed] [Google Scholar]
- Aron AR. The neural basis of inhibition in cognitive control. Neuroscientist. 2007;13:214–228. doi: 10.1177/1073858407299288. [DOI] [PubMed] [Google Scholar]
- Bechara A, Damasio H, Damasio AR. Emotion, decision making and the orbitofrontal cortex. Cerebral Cortex. 2000;10:295–307. doi: 10.1093/cercor/10.3.295. [DOI] [PubMed] [Google Scholar]
- beim Graben P, Potthast R. Inverse problems in dynamic cognitive modeling. Chaos. 2009;19:015103. doi: 10.1063/1.3097067. [DOI] [PubMed] [Google Scholar]
- Buzsaki G. Rhythms of the brain. Oxford University Press; New York: 2006. [Google Scholar]
- Buzsaki G, Draguhn A. Neuronal oscillations in cortical networks. Science. 2004;304:1926–1929. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
- Chen Y, Bressler SL, Ding M. Dynamics on networks: assessing functional connectivity with Granger causality. Comput. Math. Organ. Theor. 2009;15:329–350. [Google Scholar]
- Fales CL, Barch DB, Rundle MM, Mintun MA, Snyder AZ, Cohen JD, et al. Altered emotional interference processing in affective and cognitive-control brain circuitry in major depression. Biol. Psychiatry. 2008;63:377–384. doi: 10.1016/j.biopsych.2007.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenicchel N. Persistence and smoothness of invariant manifolds for flows. Indiana Univ. Math J. 1971;21:193–226. [Google Scholar]
- Fingelkurts AA, Fingelkurts AA. Timing in cognition and EEG brain dynamics: discreteness versus continuity. Cogn. Process. 2006;7:135–162. doi: 10.1007/s10339-006-0035-0. [DOI] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, van Essen D, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl. Acad. Sci. USA. 2005;102:9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Raichle ME. Intrinsic fluctuations within cortical systems account for intertrial variability in human behavior. Neuron. 2007;56:171–184. doi: 10.1016/j.neuron.2007.08.023. [DOI] [PubMed] [Google Scholar]
- Friston KJ. Transients, metastability, and neuronal dynamics. NeuroImage. 1997;5:164–171. doi: 10.1006/nimg.1997.0259. [DOI] [PubMed] [Google Scholar]
- Friston KJ. The labile brain. I. Neuronal transients and nonlinear coupling. Philos. Trans. R. Soc. Lond. B, Biol. Sci. 2000;355:215–236. doi: 10.1098/rstb.2000.0560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Harrison L, Penny W. Dynamic causal modelling. NeuroImage. 2003;19:1273–1302. doi: 10.1016/s1053-8119(03)00202-7. [DOI] [PubMed] [Google Scholar]
- Gray JR, Braver TS, Raichle ME. Integration of emotion and cognition in the lateral prefrontal cortex. Proc. Natl. Acad. Sci. USA. 2002;99:4115–4120. doi: 10.1073/pnas.062381899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hale J. Ordinary differential equations. Interscience; New York: 1969. [Google Scholar]
- Hirsh MW, Pugh CC, Shub M. Lecture notes in math.: Vol. 583. Invariant manifolds. Springer; New York: 1977. [Google Scholar]
- Huber MT, Braun HA, Krieg J-C. On the impact of episode sensitization on the course of recurrent affective disorders. J. Pshychiatric Res. 2001;35:49–57. doi: 10.1016/s0022-3956(00)00044-3. [DOI] [PubMed] [Google Scholar]
- Huber MT, Braun HA, Krieg J-C. Recurrent affective disorders: nonlinear and stochastic models of disease dynamics. Int. J. Bifurc. Chaos. 2004;14:635–652. [Google Scholar]
- Ito J, Nikolaev AR, van Leeuwen C. Dynamics of spontaneous transitions between global brain states. Hum. Brain Mapp. 2007;28:904–913. doi: 10.1002/hbm.20316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones LM, Fonranini A, Sadacca BF, Miller P, Katz DB. Natural stimuli evoke dynamic sequences of states in sensory cortical ensembles. Proc. Natl. Acad. Sci. 2007;104:18772–18777. doi: 10.1073/pnas.0705546104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Just MA, Varma S. The organization of thinking: What functional brain imaging reveals about theneuroarchitecture of complex cognition. Cogn. Affect. Behav. Neurosci. 2007;7:153–191. doi: 10.3758/cabn.7.3.153. [DOI] [PubMed] [Google Scholar]
- Kaplan AY, Shishkin SL. Application of the change-point analysis to the investigation of the brain’s electrical activity. In: Brodsky BE, Darkhovsky BS, editors. Nonparametric statistical diagnosis: problems and methods. Kluwer Academic; Dordrecht: 2000. pp. 333–388. [Google Scholar]
- Kelso JAS. The self-organization of brain and behavior. MIT Press; Cambridge: 1995. [Google Scholar]
- Kifer Y. The exit problem for small random perturbations of dynamical systems with hyperbolic fixed point. Isr. J. Math. 1981;40:74–96. [Google Scholar]
- Levi R, Varona P, Arshavsky YI, Rabinovich MI, Selverston AI. Dual sensory-motor function for a molluskan statocyst network. J. Neurophysiol. 2004;91:336–345. doi: 10.1152/jn.00753.2003. [DOI] [PubMed] [Google Scholar]
- Lewis M, Haviland-Jones JM, Barrett LF. Handbook of emotions. 3rd ed. Guilford Press; New York: 2008. [Google Scholar]
- Lewis MD. Bridging emotion theory and neurobiology through dynamic systems modeling. Behav. Brain Sci. 2005;28:169–245. doi: 10.1017/s0140525x0500004x. [DOI] [PubMed] [Google Scholar]
- Muezzinoglu MK, Tristan I, Huerta R, Afraimovich V, Rabinovich MI. Transients versus attractors in complex networks. Int. J. Bifurc. Chaos. 2010;20:169–245. [Google Scholar]
- Murray JD. Mathematical biology: I. An introduction. 3rd ed. Springer; New York: 2002. [Google Scholar]
- Oullier O, Kelso JA. Neuroeconomics and the metastable brain. Trends Cogn. 2006;10:353–354. doi: 10.1016/j.tics.2006.06.009. [DOI] [PubMed] [Google Scholar]
- Pessoa L. On the relationship between emotion and cognition. Nature Rev. Neurosci. 2008;9:148–158. doi: 10.1038/nrn2317. [DOI] [PubMed] [Google Scholar]
- Phelps E. Emotion and cognition: Insights from studies of the human amygdala. Annu. Rev. Psychol. 2006;57:27–53. doi: 10.1146/annurev.psych.56.091103.070234. [DOI] [PubMed] [Google Scholar]
- Port RF, van Gelder T, editors. Mind as motion: explorations in the dynamics of cognition. MIT Press; Cambridge: 1995. [Google Scholar]
- Rabinovich MI, Huerta R, Laurent G. Transient dynamics for neural processing. Science. 2008;321:48–50. doi: 10.1126/science.1155564. [DOI] [PubMed] [Google Scholar]
- Rabinovich MI, Huerta R, Varona P, Afraimovich VS. Transient cognitive dynamics, metastability, and decision making. PLoS Computational Biology. 2008;4:e1000072. doi: 10.1371/journal.pcbi.1000072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabinovich MI, Varona P, Selverston AI, Abarbanel HDI. Dynamical principles in neuroscience. Rev. Modern Phys. 2006;78:1213. [Google Scholar]
- Rabinovich MI, Volkovskii A, Lecanda P, Huerta R, Abarbanel HDI, Laurent G. Dynamical encoding by networks of competing neuron groups: winnerless competition. Phys. Rev. Lett. 2001;87:068102. doi: 10.1103/PhysRevLett.87.068102. [DOI] [PubMed] [Google Scholar]
- Reis DL, Shamosh NA, Kiehl KA, Brackett M, Salovey P, Gray JR. Individual differences in emotional intelligence predict prefrontal cortical activity during social reasoning. NeuroImage. 2007;35:1385–1391. doi: 10.1016/j.neuroimage.2006.12.045. [DOI] [PubMed] [Google Scholar]
- Sasaki T, Matsuki N, Ikegaya Y. Metastability of active CA3 networks. J. Neurosci. 2007;27:517–528. doi: 10.1523/JNEUROSCI.4514-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scherer KR. Neuroscience projections to current debates in emotion psychology. Cognit. Emotion. 1993;7:1–41. [Google Scholar]
- Shilnikov LP, Shilnikov AL, Turaev DV, Chua LO. Methods of qualitative theory in nonlinear dynamics (Part 1) World Scientific; Singapore: 1998. [Google Scholar]
- Shilnikov LP, Shilnikov AL, Turaev DV, Chua LO. Methods of qualitative theory in nonlinear dynamics (Part 2) World Scientific; Singapore: 2001. [Google Scholar]
- Stone E, Holmes P. Random perturbations of heteroclinic attractors. SIAM J. Appl. Math. 1990;50:726–743. [Google Scholar]
- Vogels TP, Rajan K, Abott LF. Neural network dynamics. Annu. Rev. Neurosci. 2005;28:357–376. doi: 10.1146/annurev.neuro.28.061604.135637. [DOI] [PubMed] [Google Scholar]
- Werner G. Metastability, criticality and phase transitions in brain and its models. Biosystems. 2007;90:496–508. doi: 10.1016/j.biosystems.2006.12.001. [DOI] [PubMed] [Google Scholar]


