Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Nov 10.
Published in final edited form as: J Biomech. 2011 Sep 25;44(16):2747–2754. doi: 10.1016/j.jbiomech.2011.09.002

Shear strength and toughness of trabecular bone are more sensitive to density than damage

Jacqueline G Garrison 1, Joshua A Gargac 1, Glen L Niebur 1
PMCID: PMC3208752  NIHMSID: NIHMS326357  PMID: 21945570

Abstract

Microdamage occurs in trabecular bone under normal loading, which impairs the mechanical properties. Architectural degradation associated with osteoporosis increases damage susceptibility, resulting in a cumulative negative effect on the mechanical properties. Treatments for osteoporosis could be targeted toward increased bone mineral density, improved architecture, or repair and prevention of microdamage. Delineating the relative roles of damage and architectural degradation on trabecular bone strength will provide insight into the most beneficial targets. In this study, damage was induced in bovine trabecular bone samples by axial compression, and the effects on the mechanical properties in shear were assessed. The damaged shear modulus, shear yield stress, ultimate shear stress, and energy to failure all depended on induced damage and decreased as the architecture became more rod-like. The changes in ultimate shear strength and toughness were proportional to the decrease in shear modulus, consistent with an effective decrease in the cross-section of trabeculae based on cellular solid analysis. For typical ranges of bone volume fraction in human bone, the strength and toughness were much more sensitive to decreased volume fraction than to induced mechanical damage. While ultimately repairing or avoiding damage to the bone structure and increasing bone density both improve mechanical properties, increasing bone density is the more important contributor to bone strength.

Keywords: trabecular bone, shear toughness, microarchitecture, damage, bone quality

1. Introduction

Damage accumulation is detrimental to the mechanical competence of bone (Keaveny et al. 1999; Arthur Moore and Gibson 2002; Moore and Gibson 2003). In combination with the effects of damage in cortical bone (Fondrk et al. 1999; Reilly and Currey 2000; Jepsen et al. 2001), it may be an important factor in fracture susceptibility in whole bones (Hoshaw et al., 1997). Osteoporosis and aging decrease bone mineral density (BMD) and trabecular thickness, and increase structure model index. These factors are associated not only with lower strength and energy to failure (Garrison et al. 2009), but greater microdamage burden in trabecular bone as well (Wang and Niebur 2006; Arlot et al. 2008). As treatments for osteoporosis might have differing effects on bone mineral density, architecture, and damage repair, it is important to assess the relative effects of each of these in order to guide the development and evaluation of new treatments and diagnostic methods.

Bone strength, toughness, and modulus are modulated by bone mineral density, trabecular architecture, and damage level (Keaveny et al. 1994; Yeh and Keaveny 2001; Arthur Moore and Gibson 2002; Badiei et al. 2007). Many of the architectural quantities are highly correlated to volume fraction, especially for bone from a single anatomic site (Arlot et al. 2008). As such, subtle effects of architectural changes can be obscured when BMD or volume fraction are included as explanatory variables. Under compressive loading, the effects of architecture were more highly correlated to the toughness and strength of trabecular bone than volume fraction, even within a small range of physiological variation (Garrison et al. 2009). However, bone is also loaded multi-axially in vivo, particularly during falls, and compressive material properties may not be sufficient for assessing fracture risk.

Damage induced under a single loading condition has anisotropic effects on the residual mechanical properties in trabecular bone. If microdamage occurs predominantly in structures along one fabric direction (Shi et al. 2009), the effects of damage on the compressive and shear moduli may differ (Liu et al. 2003b). Experimentally, damage induced by on-axis compression of vertebral trabecular bone caused smaller reductions in modulus and strength in transverse than in on-axis loading (Badiei et al. 2007). However, shear loading may be a more sensitive loading mode to accumulated on-axis damage than transverse loading (Ford and Keaveny 1996; Liu et al. 2003a; Wang and Niebur 2006). In fabric tensor models of trabecular bone mechanics, the orthogonal compressive moduli depend on distinct eigen values of the fabric tensor, while shear moduli depend on the interaction between two eigen values (Zysset and Curnier 1995; Zysset and Curnier 1996). The shear modulus decreases following compressive overloads (Wang and Niebur 2006), and low shear strains cause propagation of microcracks induced by compression (Wang et al. 2005). As shear stresses are elevated in common fracture scenarios, such as a fall to the side (Lotz et al. 1995; Parkkari et al. 1999; Keyak 2001), the sensitivity of shear failure properties to damage might help to explain the variability in fracture risk estimated by BMD.

In this study, we assessed the effects of two levels of compressive mechanical damage on shear failure properties in trabecular bone. We hypothesized that the shear strength and energy to failure (toughness) in bone would be more sensitive to architectural and density variation than to damage induced by overloading. To address this hypothesis, we: 1) damaged bovine trabecular bone samples under uniaxial compressive loads along the principal mechanical axis; 2) tested the samples to failure in torsion to assess their strength and toughness; and 3) compared the mechanical properties to undamaged controls and assessed the relative sensitivity to damage, architecture, and bone volume fraction.

2. Methods

Fifty-five on-axis cylindrical specimens were prepared from the proximal metaphyses of fourteen bovine tibiae (Martin’s Meats, Wakarusa, IN). The principal material directions were aligned with the cylinder axis using μ-CT images in conjunction with finite element modeling (Wang et al. 2004). Briefly, parallelepipeds were cut from the tibiae and scanned at 74 μm resolution by μ-CT (μCT-80, Scanco Medical AG, Brüttisellen, Switzerland), and finite element models created from the images were used to determine the principal material axes relative to the parallelpiped (van Rietbergen et al. 1996). Using a custom jig, the samples were oriented with the principal axis aligned vertically, and cylindrical test specimens were prepared using a diamond coring drill (Starlite Industries, Bryn Mawr, PA) under constant irrigation. On average, the specimens were only 6.55 ± 3.04° from the principal fabric orientation. The mean diameter and overall length of the specimens were 8.19 ± 0.05 mm and 31.4 ± 2.7 mm, respectively.

2.1. Microstructural Characterization

The microarchitecture of the prepared cylindrical samples was quantified by μ-CT scanning at 20 μm isotropic resolution at 70 kVp with 500 projections for 210 ms per projection. The total scanning time was approximately 1 hour during which samples were kept hydrated with buffered saline. Architectural parameters were quantified by a model free method (IPL V4.3, Scanco Medical AG, Brüttisellen, Switzerland). The bone tissue and apparent bone mineral density (TMD and BMD, respectively) were measured using the scanner’s calibration phantom (Kazakia et al. 2008). A constant segmentation threshold of 200, corresponding to 407.3 (mg HA)/cc, was used for all samples.

2.2. Mechanical Testing

Specimens were assigned to control (CNT), low damage (LOW), or high damage (HIGH) groups for testing, all with similar BV/TV and architecture (Table 1). To minimize testing artifacts, the samples were embedded in brass endcaps that were subsequently gripped in the load frame for testing. The marrow was removed using a water jet while the sample was submerged to improve fixation in the endcaps. The absence of marrow should not affect the mechanical properties at the strain rates applied here (Carter and Hayes 1977; Pilcher et al. 2010). The effective gage length for compression was the exposed length of the sample plus one-half the embedded length (Keaveny et al. 1997). If damage were localized between the brass endcaps, this correction formula would overestimate the elastic modulus and underestimate modulus loss (Appendix A). The exposed length was used as the gage length for torsion experiments (Fenech and Keaveny 1999), and Nadai’s equation was used to account for the variation in the shear stress across the radius of the specimen (Nadai 1950; Ford and Keaveny 1996).

Table 1.

Architectural and structural measures for the samples (mean ± SD). The parameters were not significantly different between groups (p > 0.38). All measures are based on model free algorithms (Scanco IPL, version 5.11).

CNT LOW HIGH
N initial (final) 18 (15) 17 (14) 20 (13)
BMD (g-HA/cc) 0.210 ± 0.689 0.219 ± 0.633 0.200 ± 0.484
TMD (g-HA/cc) 0.827 ± 0.057 0.834 ± 0.044 0.807 ± 0.052
BV/TV 0.270 ± 0.066 0.273 ± 0.061 0.266 ± 0.049
DA 2.223 ± 0.289 2.201 ± 0.302 2.332 ± 0.361
Tb.N (mm−1) 1.532 ± 0.261 1.605 ± 0.215 1.458 ± 0.239
Tb.Th (mm) 0.187 ± 0.038 0.185 ± 0.030 0.199 ± 0.029
Tb.Sp (mm) 0.601 ± 0.140 0.566 ± 0.093 0.627 ± 0.111
Tb.Sp/Tb.Th 3.299 ± 0.891 3.082 ± 0.560 3.176 ± 0.547
SMI 0.441 ± 0.640 0.616 ± 0.570 0.596 ± 0.509
Open in a new tab

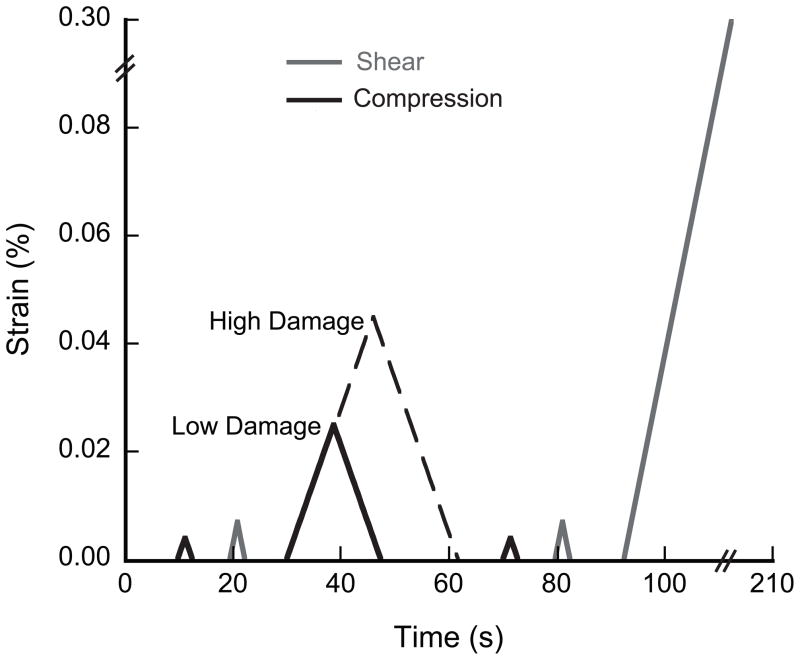
The shear and compressive moduli of each sample were first measured with two nondestructive loads to 0.7% apparent surface shear strain and 0.4% apparent compressive strain, respectively. The LOW and HIGH damage groups were then overloaded to 2.5% or 4.5% compressive strain, respectively, which was beyond the yield strain for all samples. Following the overload, the residual (damaged) moduli were measured up to strains of 0.7% torsion and 0.4% in compression. To avoid unintended damage, control specimens were not subjected to a sham overload or subsequent modulus measurement. Finally, the shear strength and toughness were measured in all three groups by loading in torsion to 30% shear strain at the outer radius (Fig. 1).

Figure 1.

Figure 1

Open in a new tab

The testing protocol for overloading specimens in uniaxial compression to low and high damage levels and then to failure in shear. To avoid unintentional damage, the control group was subjected to only the initial compressive and shear modulus measurements.

All tests were performed at room temperature using an Instron model 8821s biaxial servo-hydraulic load frame (Instron Corp., Canton, MA) at an apparent strain rate of 0.5% s−1. The modulus measurements and the compressive overload were measured using a biaxial extensometer (Epsilon, Jackson, WY). The final torsional load exceeded the strain limits of the extensometer, and was measured using the RVDT. The specimens were kept hydrated by wrapping in saline soaked gauze. Data were collected at 100 Hz and filtered with cross-validated splines (Woltring 1986) to remove high frequency noise.

The elastic and shear moduli were calculated from the derivative of a quadratic curve fit from 0.0% to 0.2% compressive strain (Morgan et al. 2001) or 0.0% to 0.4% shear strain (Ford and Keaveny 1996), respectively, and averaged over two trials. The compressive and shear yield strength and strain were determined using the 0.2% offset criterion. The elastic shear toughness (Uelastic) was defined as the area under the stress strain curve up to the yield point and the ultimate shear toughness (Uult) was calculated as the area up to the ultimate shear stress. The area was calculated using the trapezoid rule at intervals of 0.01% strain.

Thirteen specimens were lost during mechanical testing – three from the CNT, three from the LOW and seven from the HIGH damage groups, resulting in n=15, n=14, and n=13 for the CNT, LOW, and HIGH groups, respectively. The specimens were broken prematurely during overloading, or due to loss of machine control.

2.3. Statistics

Statistical analyses were performed using JMP 8.0 (SAS Institute Inc., Cary, NC). The mechanical properties were compared between groups using analysis of covariance (ANCOVA) to account for dependence on microarchitecture and BV/TV. The interaction term was included when using ANCOVA to determine if the slopes differed between groups. If the interaction term was not significant, the regression was repeated without the interaction term. Data was log transformed to obtain power-law regressions. Tukey’s HSD post-hoc test was used to identify differences between groups.

3. Results

The initial moduli of the three groups were similar. On average, the elastic and shear moduli were independent of group (p > 0.23, Table 2), but correlated to BV/TV using either linear or power-law relationships (p < 0.0001, ANCOVA, Table 3).

Table 2.

Mechanical properties from low damage (2.5% strain) and high damage (4.5% strain) compressive overload and shear failure. Mechanical properties include the mean ± SD of compressive: initial (Ei) and damaged (Ed) elastic moduli, modulus reduction, as well as the shear: initial (Gi) and damaged (Gd) moduli, yield strain (γyield), yield strength (τyield), yield toughness (Uelastic), ultimate strain (γult), ultimate strength (τult), and ultimate toughness (Uult). The regression slopes did not differ for any parameters. Parameters marked by the same letter were not significantly different between groups.

CNT LOW HIGH p
Compressive Ei (MPa) 2102 ± 711 2296 ± 701 2320 ± 676 0.23
Ed (MPa) 2102 ± 711A 1641 ± 630AB 1347 ± 934B 0.011
% Reduction -- 28.9 ± 15.8 44.6 ± 30.8 0.26†
Shear Gi (MPa) 288 ± 117 289 ± 117 280 ± 101 0.77
Gd (MPa) 288 ± 117 260 ± 109 225 ± 122 0.11
% Reduction -- 10.0 ± 11.0 23.7 ± 19.2 0.030*
γyield (%) 1.41 ± 0.28A 1.33 ± 0.13AB 1.13 ± 0.19B 0.004*
τyield (MPa) 3.31 ± 1.46A 2.70 ± 1.18AB 2.06 ± 1.41B 0.007
Uelastic (mJ/mm3) 0.025 ± 0.012A 0.018 ± 0.009AB 0.013 ± 0.011B 0.003
γult (%) 6.94 ± 2.17 6.26 ± 1.14 5.70 ± 1.91 0.20*
τult (MPa) 6.57 ± 2.46A 5.76 ± 2.49AB 4.38 ± 3.02B 0.008
Uult (mJ/mm3) 0.308 ± 0.127A 0.264 ± 0.157AB 0.197 ± 0.168B 0.033
Open in a new tab

p-values are based on ANCOVA between groups with BV/TV as covariate

†

ANCOVA with Tb.Sp as a covariate

*

p-value based on ANOVA between groups

Table 3.

Linear and power-law regression coefficients of mechanical properties with BV/TV: y=m•(BV/TV)+b or y=A•(BV/TV)B. Parameters marked with the same superscript letter are not significantly different between groups (p > 0.05, Tukey HSD). Regressions were performed assuming equal slopes (linear) or factors (power-law), as these did not differ between groups.

CNT LOW HIGH CNT LOW HIGH
y= m•(BV/TV)+b y=A•(BV/TV)B
m A
b B
R2 R2
Compressive Ei (MPa) 8323 * * 2.253 * *
20.2 1.400
0.54 0.73
Ed (MPa) −7.43A 7746 −710.8B 24753C 18676 CD 12992D
−385.1AB 1.09
0.49 0.64
Shear Gi (MPa) 1511 * * 2.092 * *
−115 1.898
0.70 0.84
Gd (MPa) 1506 * * 4081 C 3648 C 3108 D
−142 2.067
0.62 0.80
τyield (MPa) −1.07A 16.18 −2.24B 42.65 C 34.57CD 24.43D
−1.53AB 2.012
0.61 0.64
Uelastic (mJ/mm3) −0.0047A 0.108 −0.016B 0.283 C 0.210 C 0.122 D
−0.0099AB 1.949
0.53 0.52
τult (MPa) −2.50A 33.55 −4.54B 72.74 C 61.57 C 41.60 D
−3.02AB 1.864
0.66 0.64
Uult (mJ/mm3) −0.181A 1.896 −0.284B 8.099 C 7.006 CD 4.202 D
−0.209AB 2.594
0.59 0.56
Open in a new tab
*

Regressions had no significant differences between groups (p > 0.05, ANCOVA).

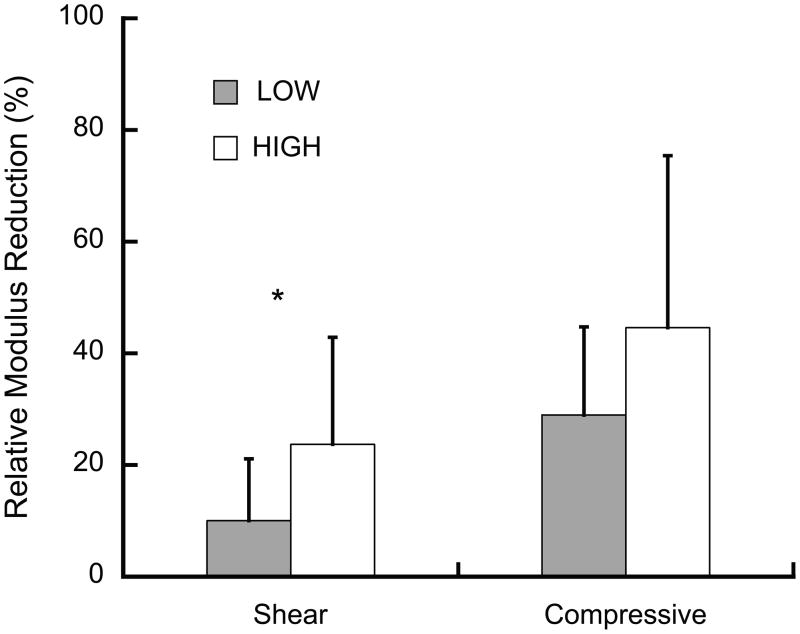
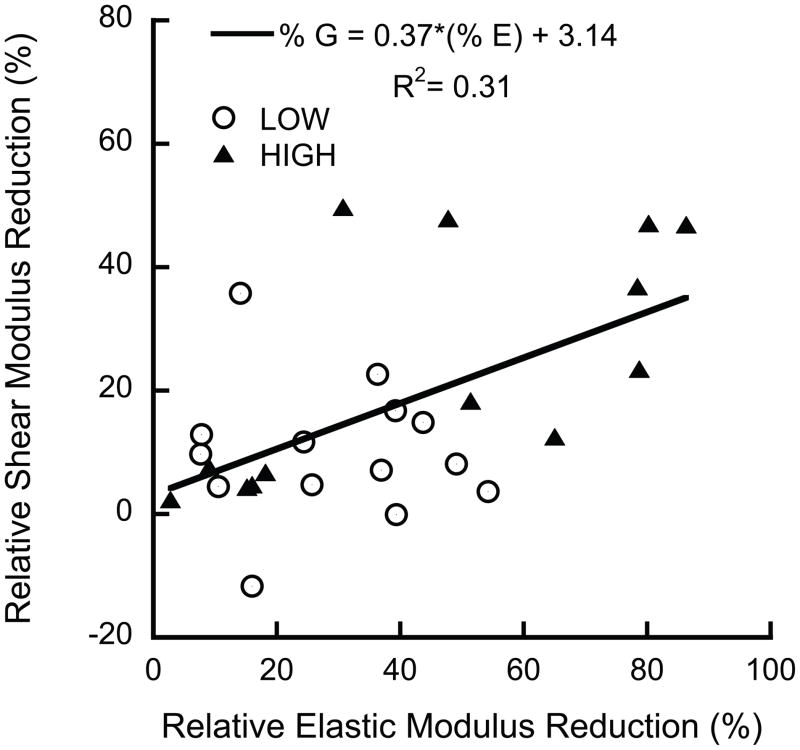
Overloading resulted in reductions in the elastic properties, indicative of mechanical damage. The elastic modulus reductions were positively correlated to Tb.Sp (p = 0.003, R2 = 0.30), but did not differ between groups (p = 0.26, ANCOVA). In contrast, the shear modulus reductions in the LOW and HIGH damage groups differed (Fig. 2). The shear modulus reductions were approximately 50% smaller than, but positively correlated to, the elastic modulus reductions (Fig. 3).

Figure 2.

Figure 2

Open in a new tab

The relative shear modulus reduction was greater in the HIGH than the LOW damage group (* p = 0.03, ANOVA) while compressive modulus reductions were independent of group (p = 0.26, ANCOVA). The compressive modulus reductions increased with increasing Tb.Sp. (p = 0.008, R2=0.30, data not shown), while shear modulus reductions were independent of architecture (p > 0.26). Error bars are one standard deviation.

Figure 3.

Figure 3

Open in a new tab

The shear modulus reductions were correlated to, but lower than the elastic modulus reductions (p = 0.003, ANCOVA). No difference was found between groups (p = 0.13, ANCOVA).

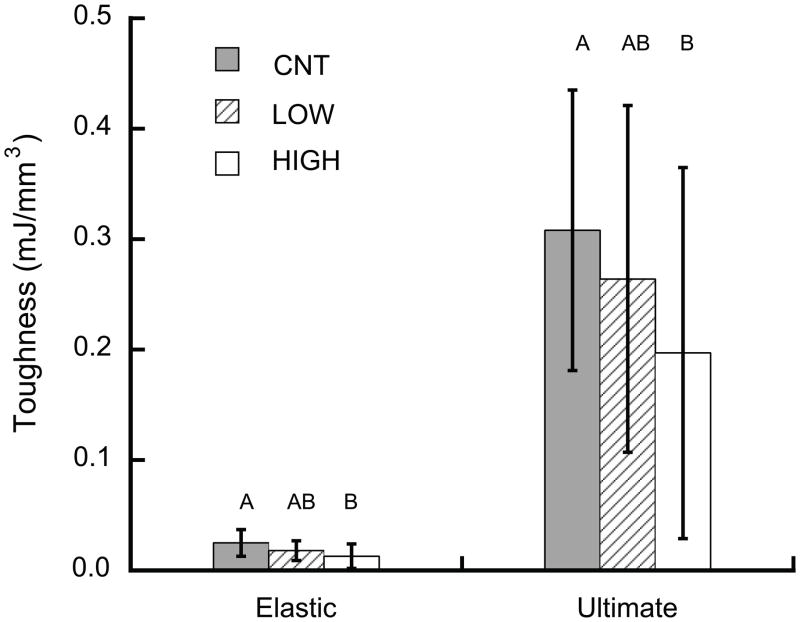
The HIGH overload group exhibited degraded shear failure properties compared to controls. Following damage, the shear yield toughness (Uelastic), ultimate shear toughness (Uult), shear yield strength (τyield), and ultimate shear strength (τult) were all lower in the HIGH overload group than in controls (p < 0.04, ANCOVA, Fig. 4), while the dependence on BV/TV was similar for all groups (p > 0.35). The shear yield strain (γyield) of the HIGH overload group was nearly 20% lower than in controls (p = 0.004), independent of architecture and density (p > 0.06).

Figure 4.

Figure 4

Open in a new tab

Shear toughness was lower in the HIGH overload group than controls (p < 0.033, ANCOVA with BV/TV as a covariate).

Based on power-law regressions, the post-damage properties were significantly lower in the HIGH damage group compared to the LOW damage group (Table 3). Although the exponent of the power law was similar between groups, the initial factor in the power-law was lower for the HIGH damage group compared to the CNT group for all parameters (p < 0.03).

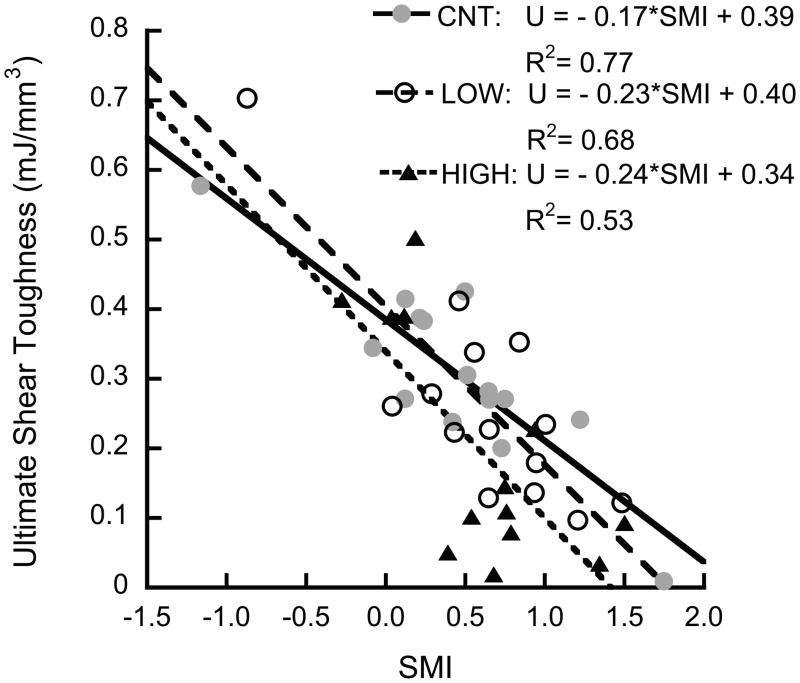
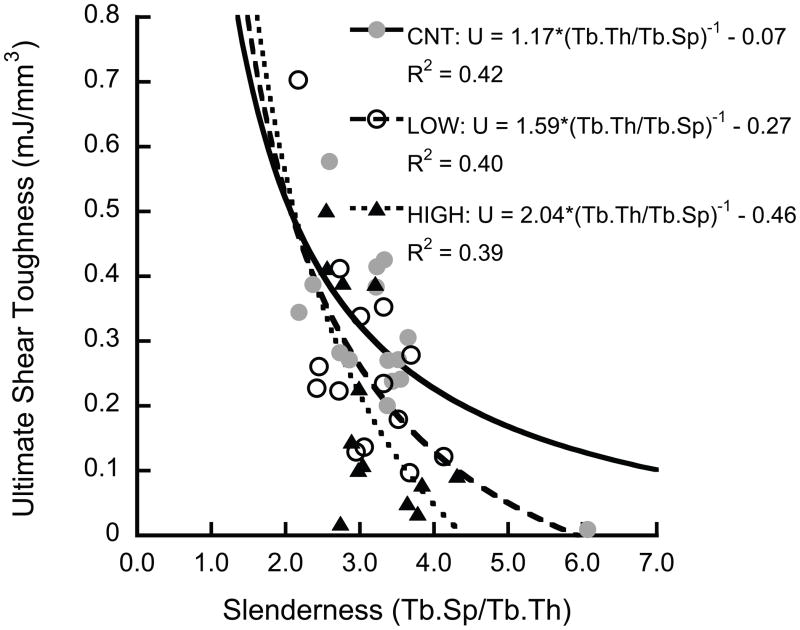
The shear properties decreased as the architecture became more rod-like. The ultimate shear toughness decreased with increasing SMI (p < 0.001, Fig. 5a), and was inversely correlated to slenderness ratio (Tb.Sp/Tb.Th) (p < 0.001, Fig. 5b).

Figure 5.

Figure 5

Figure 5

Open in a new tab

The ultimate shear toughness decreased with increasing SMI (p < 0.0001) (a), and was inversely correlated to slenderness ratio (p < 0.0003) (b). The HIGH overload group had lower toughness than the control group (p < 0.048, Tukey HSD, with slenderness ratio as covariate)

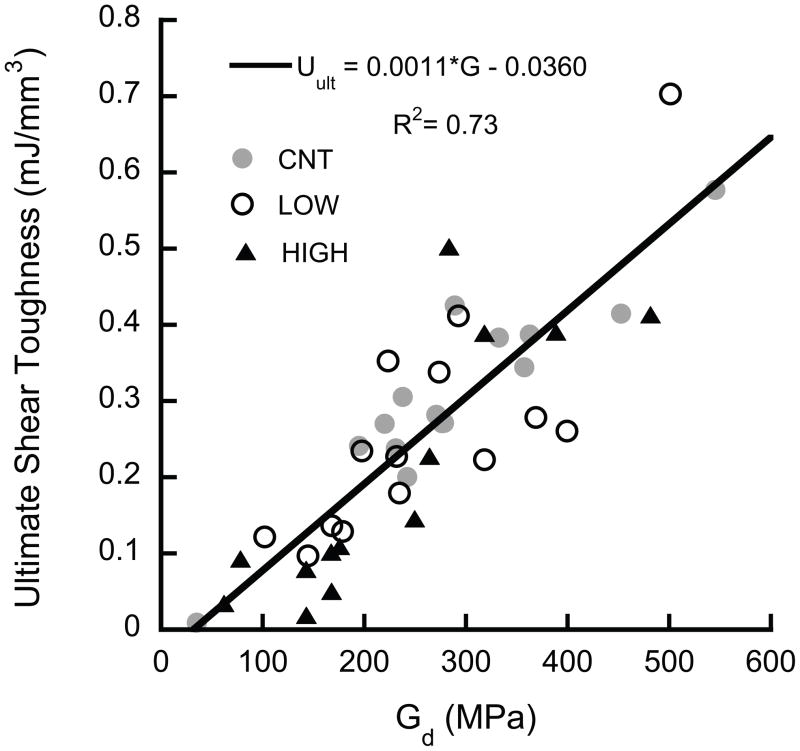
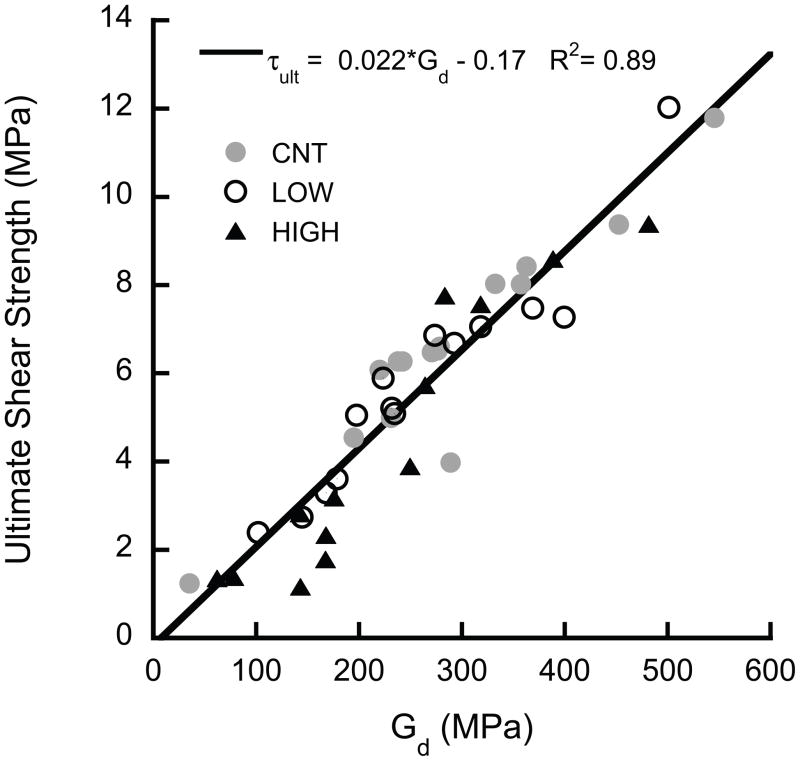
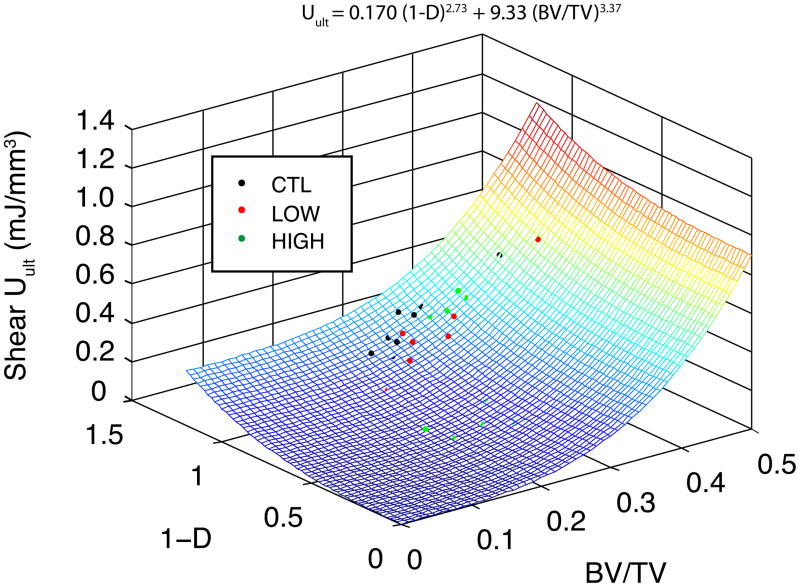
The ultimate shear properties (τult, Uult) were highly correlated to the shear modulus at the beginning of the overload (i.e. the damaged modulus for the LOW and HIGH groups and the initial for the CNT group), independent of group (p > 0.05, ANCOVA, Fig. 6). The yield properties (τyield, Uelastic) were lower, on average, in the HIGH overload group than CNT (p < 0.044, ANCOVA), but the dependence on modulus was similar for all three groups (p > 0.0001). In addition, u ltimate shear toughness was correlated to both damage (1−D), where D represents the fractional modulus reduction ((Eintial − Edamaged)/Einitial), and volume fraction (p < 0.01, multiple nonlinear regression, Fig. 7).

Figure 6.

Figure 6

Figure 6

Open in a new tab

The ultimate shear properties of (a) toughness and (b) strength were proportional to the shear modulus (p < 0.0001). No difference was detected between groups (p = 0.06). The intercept is not significantly different from zero (p = 0.63).

Figure 7.

Figure 7

Open in a new tab

Multiple nonlinear regression was used to predict the relative dependence of toughness on volume fraction and damage induction. The shear toughness was more sensitive to changes in volume fraction than to damage. Not all data points are visible, because some lie below the surface (R2=0.40).

4. Discussion

The potential detrimental role of accumulated damage due to aging and long-term administration of anti-resorptive drugs remains a clinical concern (Allen and Burr 2008). Quantification of the relative roles of damage, density, and architecture are needed to determine the balance between the positive effects of these treatments on density and architecture (Black et al. 1996; Fogelman et al. 2000; Reid et al. 2002; Dufresne et al. 2003; Recker et al. 2004) vs. the detrimental effects of accumulated microdamage (Mashiba et al. 2000; Mashiba et al. 2001b) and bone loss due to aging. In this study, bone was damaged to different levels by overloading in compression along the principal material axis in order to simulate superphysiological in vivo microdamage accumulation (Arthur Moore and Gibson 2002). The samples were subsequently tested to failure in shear, which is an important loading mode in falls (Lotz et al. 1995). The more highly damaged bone, as quantified by decreased elastic properties, had lower resistance to fracture under shear loads than similar undamaged bone. However, at low levels of damage, most mechanical properties were not statistically distinguishable from undamaged bone. As such, damage results in subtle losses of mechanical competence that can be obscured by the overall variability in the mechanical properties. Overall, the decline in shear strength was proportional to the decline in shear modulus, indicating that methods to determine the effects of damage on shear modulus could similarly identify the effects on strength.

The use of bovine bone in this study has both strengths and weaknesses. Bovine trabecular bone has almost no in vivo microdamage burden (Wang et al. 2005), which avoids the possibility of confounding effects of pre-existing damage and decreases the variability of mechanical properties in comparison to human bone. Unfortunately, the architectural variability of bovine bone is relatively small, thereby limiting the statistical power of regressions with architecture. In addition, the application of these results to human bone is limited because of the higher densities and superior microarchitecture compared to osteoporotic human bone.

Another limitation of this study is the quantification of damage by modulus reduction. Although modulus reductions are a standard method for quantifying damage in materials (Davy and Jepsen 2001; Jepsen et al. 2001), the relationship between modulus reductions and physically identifiable damage, such as microcracking, is not direct in heterogeneous materials like bone. Microdamage, in the form of microcracks and diffuse damage, increases exponentially with overloading (Arthur Moore and Gibson 2002), but correlations with modulus degradations are poor due to the high variability and the fact that many of the same architectural measures that affect modulus and modulus degradation also affect damage accumulation. For example, bone with higher SMI or greater trabecular spacing is more susceptible to microdamage accumulation (Wang and Niebur 2006; Arlot et al. 2008; Shi et al. 2010). Because the study design involved torsion to failure of the samples, it was impossible to directly measure the microdamage in these specimens.

The measures of damage differ in the literature in both cortical and trabecular bone. While measuring microdamage (Vashishth et al. 2000; Arthur Moore and Gibson 2002; Arlot et al. 2008) directly provides visual evidence of damage, secant modulus (Arthur Moore and Gibson 2002) and percent change in modulus (Davy and Jepsen 2001; Jepsen et al. 2001; Garrison et al. 2009) or strength (Keaveny et al. 1994; Garrison et al. 2009) can also provide insight into the mechanical integrity of the damaged material.

The effect of damage on the yield strain is notable. The yield and ultimate shear strains of trabecular bone within a single anatomic site are not statistically dependent on modulus (Turner 1989; Keaveny and Hayes 1993; Ford and Keaveny 1996; Morgan and Keaveny 2001). Our results for low damage levels and undamaged bone complement this result. However, the shear yield strain was lower in the HIGH overload group than controls. Computational models of bone failure may need to incorporate the effects of damaged bone tissue on shear properties when analyzing older individuals or those who have undergone long-term anti-resorptive therapy if damage accumulation is significant. Differences in the ultimate shear strains between damage levels were not detected, consistent with our previous findings for on-axis compressive failure (Garrison et al. 2009).

The reduction in shear modulus from compressive overloading was more than 5 times higher than in previous work done in our lab when samples were overloaded to 2% strain in compression (Wang et al. 2005). The progressively higher modulus reductions as a function of the compressive strain magnitude complement previous studies (Keaveny et al. 1999; Arthur Moore and Gibson 2002), although the modulus reductions we measured are lower, because we measured the reloading modulus rather than using the secant modulus to quantify damage.

The results of this study complement recent studies where overloads did not affect the compressive strength or toughness (Badiei et al. 2007; Garrison et al. 2009) of trabecular bone. Similarly, we found that bone with lower levels of damage did not differ from controls in any shear mechanical properties, including yield and ultimate toughness. This phenomenon is also seen in cortical bone, where damage resulting from fatigue did not affect the elastic modulus (Martin et al. 1997). However, increased overloading, and therefore damage, resulted in detectable differences in the mechanical properties. Damage primarily affected the initial nonlinear stress-strain behavior, which was reflected in a lower shear yield strain in highly damaged bone.

Anti-resorptive treatments are associated with simultaneous increases in both volume fraction (Borah et al. 2004) and microdamage accumulation (Mashiba et al. 2001a; Komatsubara et al. 2003; Allen et al. 2006). To assess the competing effects of damage (quantified by the fractional modulus reduction (D)) and volume fraction from these treatments, multiple nonlinear regression was used to determine the dependence of toughness on these two parameters (Fig. 7). The toughness was more sensitive to changes in volume fraction than to induced damage. As an illustrative example of the implication of this regression, we applied the regression to data from a study of risedronate treatment (Borah et al. 2004). In the three year study, the volume fraction of placebo patients decreased from 27.5% to 20.0%, on average. Assuming damage was constant during that period (1−D =1), the regression predicts a 27% decrease in toughness. In the treated group, the volume fraction increased by 3.5% (Borah et al. 2004), which would correspond to a 5.2% increase in toughness if damage were constant. Hence, treated individuals would have had to accumulate sufficient microdamage to cause a 32% decrease in modulus to attain the same total toughness loss as the placebo group. Alternatively, the treated group could sustain damage equivalent to a 26% loss in shear modulus while maintaining their baseline toughness. While any damage accumulation has negative effects on bone strength, treatments that maintain or improve bone density at the expense of minimal damage accumulation likely have a net positive effect, clinically. However, the goal should be development of treatments that maintain density without increasing damage burden.

Micromechanical models may provide insight into the mechanisms of the observed damage. Experimentally measured microcrack density correlated to the predicted yielded tissue in longitudinal rods from finite element models (Shi et al. 2010), suggesting that longitudinal rods are the most susceptible architectural feature for microdamage accumulation in compression. Removal of longitudinal rod elements, simulating highly damaged regions, resulted in on-axis elastic modulus reductions about twice as large as the reductions in the shear modulus (Liu et al. 2009). In addition, SMI and slenderness ratio were significant predictors of both compressive (Garrison et al. 2009) and shear toughness. Hence, although longitudinal rods represent a small fraction of the total trabeculae in bovine bone (Shi et al. 2010), they are susceptible to damage that can result in significant reductions in modulus, strength, and toughness. As such, formation of rod-like trabeculae by perforation of axial trabecular plates may be an important component of increased fracture risk (Akhter et al. 2007).

Our data complements a cellular solid model of trabecular bone damage. The initial factor – which is approximately the ratio of the apparent modulus to the tissue modulus in cellular solids (Gibson and Ashby 1999)– was lower in the HIGH damage than in the control group, consistent with a reduction in the effective stiffness of the individual trabeculae, potentially by a reduction in the effective cross section.

The correlation between residual moduli and strength or toughness is consistent with previous studies of pre-existing damage in both cortical and trabecular bone. The strength of cortical bone is similarly proportional to modulus (Currey 2004). In fatigue of whole bones and fracture toughness testing, the residual stiffness is correlated to reductions in strength or maximum load (Hoshaw et al. 1997; Yeni and Fyhrie 2002). Taken together, the proportional relationship between the stiffness and strength of bone is generally preserved across length scales in bone (Yeni et al. 2004).

Microdamage burden increases with age (Fazzalari et al. 1998; Arlot et al. 2008) and impaired architecture (Arlot et al. 2008). As such, adjusting the modulus–density and strength–density estimates used in biomechanical CT (Keaveny et al. 2010) and hip structural analysis (Melton et al. 2005; Kaptoge et al. 2008) to compensate for cases where microdamage is known to be high may further improve their ability to assess fracture risk. However, more complete characterization of the effect of microdamage on elastic modulus reductions in trabecular tissue may be needed to complete such a calibration.

Supplementary Material

01

Acknowledgments

United States National Institutes of Health AR52008 and AR52008S1.

Appendix A

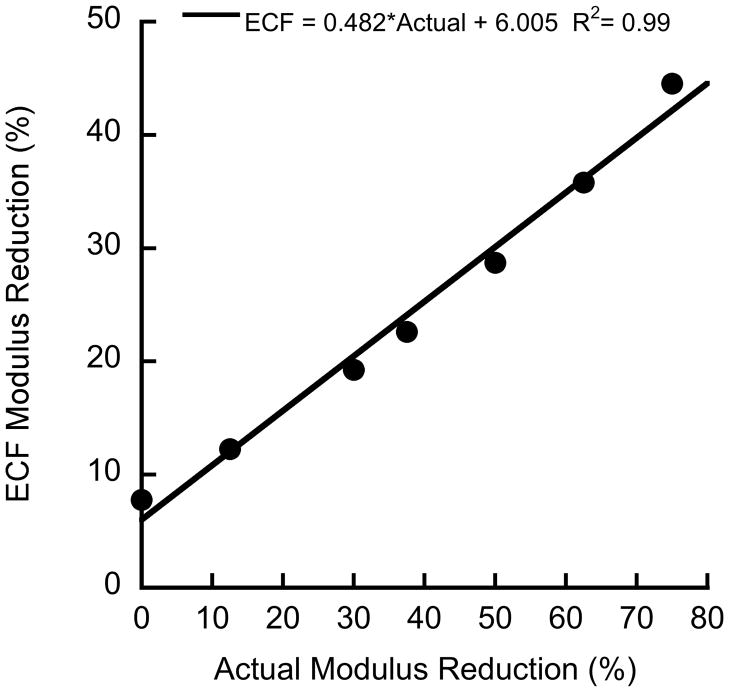
The effects of damaged bone on the endcap correction formula (ECF) for strain were investigated using an axisymmetric 2D finite element (FE) model replicating the original study (Keaveny et al. 1997). The model was created in a general-purpose finite element code (Adina 8.6, Watertown, MA) (Fig. A-1). The brass endcap was assigned a modulus of 110 GPa. The bone inside the endcap was assigned a modulus of 1 GPa, while the bone outside the endcap was assigned a series of moduli ranging from 250 MPa to 1 GPa to simulate damaged bone. A 0.2 mm region of bone along the outer radius of the bone was assigned a modulus of 100 MPa, representing the discontinuous trabecular elements that are fixed to the endcap (Keaveny et al. 1997). All regions had Poisson’s ratio of 0.3. Loads and boundary conditions were applied to simulate a displacement loading of the endcap. The stress in the bone sample was calculated from the reaction forces, and strain was calculated by dividing the applied displacement by the exposed plus half the embedded length of the bone. The ECF underpredicted the damaged modulus of the bone between the endcaps when the bone within the endcaps was assumed to remain undamaged (Fig. A-2). In the actual experiment, some of the bone within the endcap is likely to sustain damage, and the true modulus reduction is intermediate to that predicted by the ECF and the results of this model.

Figure A-1.

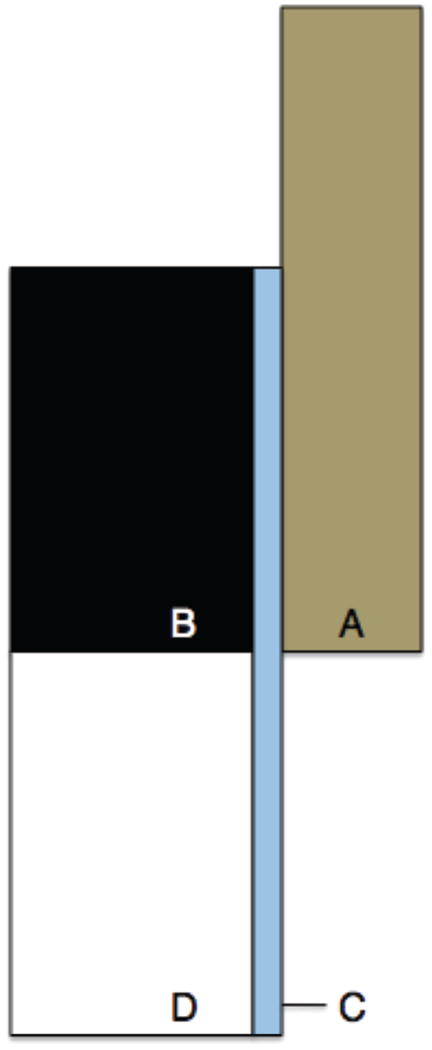
Figure A-1

Open in a new tab

Figure A1: 2D axisymmetric FE model of bone sample loading. Four distinct surfaces were defined, each with a different value of Young’s modulus to correspond with (A) the brass end caps (110 GPa), (B) undamaged bone in the end cap (1 GPa), (C) 0.2 mm thick area representing damage during sample processing (0.1 GPa), and (D) bone outside of the end cap (1 – 0.25 GPa).

Figure A-2.

Figure A-2

Open in a new tab

Change in endcap correction formula (ECF) modulus reduction versus actual modulus reduction. The ECF underpredicts the actual modulus reduction.

Footnotes

Conflict of Interest Statement

The authors have no conflicts of interest.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Akhter MP, Lappe JM, Davies KM, Recker RR. Transmenopausal changes in the trabecular bone structure. Bone. 2007;41:111–116. doi: 10.1016/j.bone.2007.03.019. [DOI] [PubMed] [Google Scholar]
  2. Allen M, Burr D. Skeletal microdamage: Less about biomechanics and more about remodeling. Clinical Reviews in Bone and Mineral Metabolism. 2008;6:24–30. [Google Scholar]
  3. Allen MR, Iwata K, Phipps R, Burr DB. Alterations in canine vertebral bone turnover, microdamage accumulation, and biomechanical properties following 1-year treatment with clinical treatment doses of risedronate or alendronate. Bone. 2006;39:872–879. doi: 10.1016/j.bone.2006.04.028. [DOI] [PubMed] [Google Scholar]
  4. Arlot ME, Burt-Pichat B, Roux JP, Vashishth D, Bouxsein ML, Delmas PD. Microarchitecture influences microdamage accumulation in human vertebral trabecular bone. Journal of Bone and Mineral Research. 2008;23:1613–1618. doi: 10.1359/jbmr.080517. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Arthur Moore TL, Gibson LJ. Microdamage accumulation in bovine trabecular bone in uniaxial compression. Journal of Biomechanical Engineering. 2002;124:63–71. doi: 10.1115/1.1428745. [DOI] [PubMed] [Google Scholar]
  6. Badiei A, Bottema MJ, Fazzalari NL. Influence of orthogonal overload on human vertebral trabecular bone mechanical properties. Journal of Bone and Mineral Research. 2007;22:1690–1699. doi: 10.1359/jbmr.070706. [DOI] [PubMed] [Google Scholar]
  7. Black DM, Cummings SR, Karpf DB, Cauley JA, Thompson DE, Nevitt MC, Bauer DC, Genant HK, Haskell WL, Marcus R, Ott SM, Torner JC, Quandt SA, Reiss TF, Ensrud KE. Randomised trial of effect of alendronate on risk of fracture in women with existing vertebral fractures. Fracture intervention trial research group. Lancet. 1996;348:1535–1541. doi: 10.1016/s0140-6736(96)07088-2. [DOI] [PubMed] [Google Scholar]
  8. Borah B, Dufresne TE, Chmielewski PA, Johnson TD, Chines A, Manhart MD. Risedronate preserves bone architecture in postmenopausal women with osteoporosis as measured by three-dimensional microcomputed tomography. Bone. 2004;34:736–746. doi: 10.1016/j.bone.2003.12.013. [DOI] [PubMed] [Google Scholar]
  9. Carter DR, Hayes WC. The compressive behavior of bone as a two-phase porous structure. J Bone Joint Surg Am. 1977;59:954–962. [PubMed] [Google Scholar]
  10. Currey JD. Tensile yield in compact bone is determined by strain, post-yield behaviour by mineral content. Journal of Biomechanics. 2004;37:549–556. doi: 10.1016/j.jbiomech.2003.08.008. [DOI] [PubMed] [Google Scholar]
  11. Davy D, Jepsen K. Bone damage mechanics. In: Cowin SC, editor. The bone mechanics handbook. CRC; New York: 2001. [Google Scholar]
  12. Dufresne TE, Chmielewski PA, Manhart MD, Johnson TD, Borah B. Risedronate preserves bone architecture in early postmenopausal women in 1 year as measured by three-dimensional microcomputed tomography. Calcified Tissue International. 2003;73:423–432. doi: 10.1007/s00223-002-2104-4. [DOI] [PubMed] [Google Scholar]
  13. Fazzalari NL, Forwood MR, Smith K, Manthey BA, Herreen P. Assessment of cancellous bone quality in severe osteoarthrosis: Bone mineral density, mechanics, and microdamage. Bone. 1998;22:381–388. doi: 10.1016/s8756-3282(97)00298-6. [DOI] [PubMed] [Google Scholar]
  14. Fenech CM, Keaveny TM. A cellular solid criterion for predicting the axial-shear failure properties of bovine trabecular bone. Journal of Biomechanical Engineering. 1999;121:414–422. doi: 10.1115/1.2798339. [DOI] [PubMed] [Google Scholar]
  15. Fogelman I, Ribot C, Smith R, Ethgen D, Sod E, Reginster JY. Risedronate reverses bone loss in postmenopausal women with low bone mass: Results from a multinational, double-blind, placebo-controlled trial. Bmd-mn study group. J Clin Endocrinol Metab. 2000;85:1895–1900. doi: 10.1210/jcem.85.5.6603. [DOI] [PubMed] [Google Scholar]
  16. Fondrk MT, Bahniuk EH, Davy DT. A damage model for nonlinear tensile behavior of cortical bone. Journal of Biomechanical Engineering. 1999;121:533–541. doi: 10.1115/1.2835084. [DOI] [PubMed] [Google Scholar]
  17. Ford CM, Keaveny TM. The dependence of shear failure properties of trabecular bone on apparent density and trabecular orientation. Journal of Biomechanics. 1996;29:1309–1317. doi: 10.1016/0021-9290(96)00062-0. [DOI] [PubMed] [Google Scholar]
  18. Garrison JG, Slaboch CL, Niebur GL. Density and architecture have greater effects on the toughness of trabecular bone than damage. Bone. 2009;44:924–929. doi: 10.1016/j.bone.2008.12.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gibson L, Ashby M. Cellular solids: Structure and properties. Cambridge University Press; 1999. [Google Scholar]
  20. Hoshaw SJ, Cody DD, Saad AM, Fyhrie DP. Decrease in canine proximal femoral ultimate strength and stiffness due to fatigue damage. Journal of Biomechanics. 1997;30:323–329. doi: 10.1016/s0021-9290(96)00159-5. [DOI] [PubMed] [Google Scholar]
  21. Jepsen K, Davy D, Akkus O. Observations of damage in bone. In: Cowin SC, editor. The bone mechanics handbook. CRC; New York: 2001. [Google Scholar]
  22. Kaptoge S, Beck TJ, Reeve J, Stone KL, Hillier TA, Cauley JA, Cummings SR. Prediction of incident hip fracture risk by femur geometry variables measured by hip structural analysis in the study of osteoporotic fractures. Journal of Bone and Mineral Research. 2008;23:1892–1904. doi: 10.1359/JBMR.080802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kazakia GJ, Burghardt AJ, Cheung S, Majumdar S. Assessment of bone tissue mineralization by conventional x-ray microcomputed tomography: Comparison with synchrotron radiation microcomputed tomography and ash measurements. Med Phys. 2008;35:3170–3179. doi: 10.1118/1.2924210. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Keaveny TM, Hayes WC. A 20-year perspective on the mechanical properties of trabecular bone. Journal of Biomechanical Engineering. 1993;115:534–542. doi: 10.1115/1.2895536. [DOI] [PubMed] [Google Scholar]
  25. Keaveny TM, Kopperdahl DL, Melton LJ, 3rd, Hoffmann PF, Amin S, Riggs BL, Khosla S. Age-dependence of femoral strength in white women and men. Journal of Bone and Mineral Research. 2010;25:994–1001. doi: 10.1359/jbmr.091033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Keaveny TM, Pinilla TP, Crawford RP, Kopperdahl DL, Lou A. Systematic and random errors in compression testing of trabecular bone. Journal of Orthopaedic Research. 1997;15:101–110. doi: 10.1002/jor.1100150115. [DOI] [PubMed] [Google Scholar]
  27. Keaveny TM, Wachtel EF, Guo XE, Hayes WC. Mechanical behavior of damaged trabecular bone. Journal of Biomechanics. 1994;27:1309–1318. doi: 10.1016/0021-9290(94)90040-x. [DOI] [PubMed] [Google Scholar]
  28. Keaveny TM, Wachtel EF, Kopperdahl DL. Mechanical behavior of human trabecular bone after overloading. Journal of Orthopaedic Research. 1999 doi: 10.1002/jor.1100170308. [DOI] [PubMed] [Google Scholar]
  29. Keyak JH. Improved prediction of proximal femoral fracture load using nonlinear finite element models. Medical Engineering and Physics. 2001;23:165–173. doi: 10.1016/s1350-4533(01)00045-5. [DOI] [PubMed] [Google Scholar]
  30. Komatsubara S, Mori S, Mashiba T, Ito M, Li J, Kaji Y, Akiyama T, Miyamoto K, Cao Y, Kawanishi J, Norimatsu H. Long-term treatment of incadronate disodium accumulates microdamage but improves the trabecular bone microarchitecture in dog vertebra. Journal of Bone and Mineral Research. 2003;18:512–520. doi: 10.1359/jbmr.2003.18.3.512. [DOI] [PubMed] [Google Scholar]
  31. Liu X, Wang X, Niebur G. Effects of damage on the orthotropic material symmetry of bovine tibial trabecular bone. Journal of Biomechanics. 2003a;36:1753–1759. doi: 10.1016/s0021-9290(03)00217-3. [DOI] [PubMed] [Google Scholar]
  32. Liu X, Wang X, Niebur GL. Effects of damage on the orthotropic material symmetry of bovine tibial trabecular bone. Journal of Biomechanics. 2003b;36:1753–1759. doi: 10.1016/s0021-9290(03)00217-3. [DOI] [PubMed] [Google Scholar]
  33. Liu XS, Zhang XH, Guo XE. Contributions of trabecular rods of various orientations in determining the elastic properties of human vertebral trabecular bone. Bone. 2009;45:158–163. doi: 10.1016/j.bone.2009.04.201. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lotz J, Cheal E, Hayes W. Stress distributions within the proximal femur during gait and falls: Implications for osteoporotic fracture. Osteoporosis International. 1995;5:252–261. doi: 10.1007/BF01774015. [DOI] [PubMed] [Google Scholar]
  35. Martin RB, V, Gibson A, Stover SM, Gibeling JC, Griffin LV. Residual strength of equine bone is not reduced by intense fatigue loading: Implications for stress fracture. Journal of Biomechanics. 1997;30:109–114. doi: 10.1016/s0021-9290(96)00113-3. [DOI] [PubMed] [Google Scholar]
  36. Mashiba T, Hirano T, Turner CH, Forwood MR, Johnston CC, Burr DB. Suppressed bone turnover by bisphosphonates increases microdamage accumulation and reduces some biomechanical properties in dog rib. Journal of Bone and Mineral Research. 2000;15:613–620. doi: 10.1359/jbmr.2000.15.4.613. [DOI] [PubMed] [Google Scholar]
  37. Mashiba T, Turner C, Hirano T, Forwood M, Johnston C, Burr D. Effects of suppressed bone turnover by bisphosphonates on microdamage accumulation and biomechanical properties in clinically relevant skeletal sites in beagles. Bone. 2001a;28:524–531. doi: 10.1016/s8756-3282(01)00414-8. [DOI] [PubMed] [Google Scholar]
  38. Mashiba T, Turner CH, Hirano T, Forwood MR, Jacob DS, Johnston CC, Burr DB. Effects of high-dose etidronate treatment on microdamage accumulation and biomechanical properties in beagle bone before occurrence of spontaneous fractures. Bone. 2001b;29:271–278. doi: 10.1016/s8756-3282(01)00575-0. [DOI] [PubMed] [Google Scholar]
  39. Melton LJ, 3rd, Beck TJ, Amin S, Khosla S, Achenbach SJ, Oberg AL, Riggs BL. Contributions of bone density and structure to fracture risk assessment in men and women. Osteoporosis International. 2005;16:460–467. doi: 10.1007/s00198-004-1820-1. [DOI] [PubMed] [Google Scholar]
  40. Moore TL, Gibson LJ. Fatigue microdamage in bovine trabecular bone. Journal of Biomechanical Engineering. 2003;125:769–776. doi: 10.1115/1.1631584. [DOI] [PubMed] [Google Scholar]
  41. Morgan EF, Keaveny TM. Dependence of yield strain of human trabecular bone on anatomic site. Journal of Biomechanics. 2001;34:569–577. doi: 10.1016/s0021-9290(01)00011-2. [DOI] [PubMed] [Google Scholar]
  42. Morgan EF, Yeh OC, Chang WC, Keaveny TM. Nonlinear behavior of trabecular bone at small strains. Journal of Biomechanical Engineering. 2001;123:1–9. doi: 10.1115/1.1338122. [DOI] [PubMed] [Google Scholar]
  43. Nadai A. The stress-strain curve in shear. McGraw-Hill; New York: 1950. Torsion of a round bar. [Google Scholar]
  44. Parkkari J, Kannus P, Palvanen M, Natri A. Majority of hip fractures occur as a result of a fall and impact on the greater trochanter of the femur: A prospective controlled hip fracture study with 206 consecutive patients. Calcified Tissue International. 1999;65:183–187. doi: 10.1007/s002239900679. [DOI] [PubMed] [Google Scholar]
  45. Pilcher Wang, Kaltz Garrison, Niebur Mason, Song Cheng, Chen High strain rate testing of bovine trabecular bone. Journal of Biomechanical Engineering. 2010;132:081012. doi: 10.1115/1.4000086. [DOI] [PubMed] [Google Scholar]
  46. Recker RR, Weinstein RS, Chesnut CH, 3rd, Schimmer RC, Mahoney P, Hughes C, Bonvoisin B, Meunier PJ. Histomorphometric evaluation of daily and intermittent oral ibandronate in women with postmenopausal osteoporosis: Results from the bone study. Osteoporosis International. 2004;15:231–237. doi: 10.1007/s00198-003-1530-0. [DOI] [PubMed] [Google Scholar]
  47. Reid IR, Brown JP, Burckhardt P, Horowitz Z, Richardson P, Trechsel U, Widmer A, Devogelaer JP, Kaufman JM, Jaeger P, Body JJ, Brandi ML, Broell J, Di Micco R, Genazzani AR, Felsenberg D, Happ J, Hooper MJ, Ittner J, Leb G, Mallmin H, Murray T, Ortolani S, Rubinacci A, Saaf M, Samsioe G, Verbruggen L, Meunier PJ. Intravenous zoledronic acid in postmenopausal women with low bone mineral density. New England Journal of Medicine. 2002;346:653–661. doi: 10.1056/NEJMoa011807. [DOI] [PubMed] [Google Scholar]
  48. Reilly GC, Currey JD. The effects of damage and microcracking on the impact strength of bone. Journal of Biomechanics. 2000;33:337–343. doi: 10.1016/s0021-9290(99)00167-0. [DOI] [PubMed] [Google Scholar]
  49. Shi X, Liu XS, Wang X, Guo XE, Niebur GL. Effects of trabecular type and orientation on microdamage susceptibility in trabecular bone. Bone. 2010;46:1260–1266. doi: 10.1016/j.bone.2010.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Shi X, Wang X, Niebur GL. Effects of loading orientation on the morphology of the predicted yielded regions in trabecular bone. Annals of Biomedical Engineering. 2009;37:354–362. doi: 10.1007/s10439-008-9619-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Turner CH. Yield behavior of bovine cancellous bone. Journal of Biomechanical Engineering. 1989;111:256–260. doi: 10.1115/1.3168375. [DOI] [PubMed] [Google Scholar]
  52. van Rietbergen B, Odgaard A, Kabel J, Huiskes R. Direct mechanics assessment of elastic symmetries and properties of trabecular bone architecture. Journal of Biomechanics. 1996;29:1653–1657. doi: 10.1016/0021-9290(96)00093-0. [DOI] [PubMed] [Google Scholar]
  53. Vashishth D, Koontz J, Qiu SJ, Lundin-Cannon D, Yeni YN, Schaffler MB, Fyhrie DP. In vivo diffuse damage in human vertebral trabecular bone. Bone. 2000;26:147–152. doi: 10.1016/s8756-3282(99)00253-7. [DOI] [PubMed] [Google Scholar]
  54. Wang X, Guyette J, Liu X, Roeder RK, Niebur GL. Axial-shear interaction effects on microdamage in bovine tibial trabecular bone. Eur J Morphol. 2005;42:61–70. doi: 10.1080/09243860500095570. [DOI] [PubMed] [Google Scholar]
  55. Wang X, Liu X, Niebur GL. Preparation of on-axis cylindrical trabecular bone specimens using micro-ct imaging. Journal of Biomechanical Engineering. 2004;126:122–125. doi: 10.1115/1.1645866. [DOI] [PubMed] [Google Scholar]
  56. Wang X, Niebur GL. Microdamage propagation in trabecular bone due to changes in loading mode. Journal of Biomechanics. 2006;39:781–790. doi: 10.1016/j.jbiomech.2005.02.007. [DOI] [PubMed] [Google Scholar]
  57. Woltring HJ. A fortran package for generalized, cross-validatory spline smoothing and differentiation. Advances in Engineering Software. 1986;8:104–113. [Google Scholar]
  58. Yeh OC, Keaveny TM. Relative roles of microdamage and microfracture in the mechanical behavior of trabecular bone. Journal of Orthopaedic Research. 2001;19:1001–1007. doi: 10.1016/S0736-0266(01)00053-5. [DOI] [PubMed] [Google Scholar]
  59. Yeni YN, Dong XN, Fyhrie DP, Les CM. The dependence between the strength and stiffness of cancellous and cortical bone tissue for tension and compression: Extension of a unifying principle. Biomed Mater Eng. 2004;14:303–310. [PubMed] [Google Scholar]
  60. Yeni YN, Fyhrie DP. Fatigue damage-fracture mechanics interaction in cortical bone. Bone. 2002;30:509–514. doi: 10.1016/s8756-3282(01)00696-2. [DOI] [PubMed] [Google Scholar]
  61. Zysset PK, Curnier A. An alternative model for anisotropic elasticity based on fabric tensors. Mechanics of Materials. 1995;21:243–250. [Google Scholar]
  62. Zysset PK, Curnier A. A 3d damage model for trabecular bone based on fabric tensors. Journal of Biomechanics. 1996;29:1549–1558. [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS326357-supplement-01.zip (90KB, zip)

RESOURCES