Abstract
WAXS, DSC and AFM methods were employed to compare phase structures of the coatings obtained from waterborne polyurethane cationomers which had been synthesised in the reaction of some diisocyanates (MDI, IPDI, TDI and HDI) with polyoxyethylene glycols (M = 600 and 2,000) and butane1,4-diol or N-methyl- or N-butyldiethanolamine and 2,2,3,3-tetrafluoro-1,4-butanediol. The structures were also analysed of the coatings derived from linear polyurethanes which had been synthesised on the basis of similar raw materials. Better rigidity was found for generally amorphous cationomer coats. Changes were discussed in the surface free energy (SFE) values and in their components, as calculated independently with the use of the van Oss–Good and Owens–Wendt methods. Polyurethane coats turned out more hydrophobic as compared to cationomer ones. In both coat types, fluorine incorporated into cationomers contributed to lower SFE values: from 50 down to about 30 mJ/m2.
Keywords: Polyurethane coatings, Phase structure, Physical interactions, WAXS, DSC, AFM, Surface free energy parameters by van Oss–Good and Owens–Wendt methods
Introduction
Polyurethane (PU) coatings make a group of materials which are widely used in various application domains, and in particular in the automotive industry, in building engineering and recently also in medical applications—as modern biomaterials [1–4]. The coats may be produced with the use of numerous techniques: as paint coats, powder coats and elastomer layers which are applied by means of special application units to steel or concrete surfaces to be protected [5–8]. The coats may also be obtained from organic solutions which are employed, e.g. to impregnate fabrics, or from aqueous dispersions, as the so-called waterborne polyurethane lacquers, which are used to protect wood, leather, ceramics and aluminium [9, 10]. For environmental reasons, waterborne polyurethanes have met with special approval in the markets recently. Of the greatest importance among them are the coatings which are based on polyurethane anionomers and contain ionic segments derived from dihydroxycarboxylic acids in their chains [11–14]. Cationomer coatings are also used, although they are less successful, while their polar groups make an additional contribution to improve mechanical properties. Those properties are much inferior in the case of anionomer coatings than for conventional elastomer coatings which are formed by application of organic solutions, while mechanical properties of cationomer coatings are equal to those of elastomer ones [15–17]. There is one additional characteristic feature of cationomers; it is the extensive potential for making structural modifications in their molecules, not only by changing the types of diisocyanate and polyol feeds but also by changing the ionic segments of cationomers which are derived from built-in tertiary amines and counterions specific for those amines that can produce additional hydrogen bonds and strong ionic effects which influence the interactions within scarcely miscible phases of (urethane and urea) rigid segments and (polyol) soft segments. As one of the important consequences of that, changes are observed in the surface free energy (SFE) of the coatings which are obtained from cationomers. That value is the determining factor for the polar performance of coats, and that in turn affects their chemical and biological resistance as well as their transfer properties with regard to gases and liquids, and also with regard to body fluids in case of biomaterials [18, 19]. For example, the relation was proven some time ago between the polar performance of the polyurethane material and its interactions with blood [20] and with microorganisms which can settle on the coat of the polyurethane elastomer [21].
Our earlier papers considered the surface properties of cationomer coats, with various structures of polyurethane chains which contained, e.g. additional fluorine compounds to strongly reduce the SFE value, or which contained the added nanoparticles of properly functionalised silsesquioxane [22, 23]. We put forward the preliminary hypothesis that the specific chemical and phase structures of a polyurethane cationomer, and in particular the presence of fluorine atoms in its rigid phase, affect the thermodynamic stability of that cationomer. Moreover, they considerably lower the SFE value of the coatings obtained with the use of that cationomer [22].
Going deeper into that question, this paper attempts to compare the properties of the coatings produced from organic solutions of linear polyurethanes and of those formed by waterborne polyurethane cationomers. The SFE values of PU coatings are principally affected by the chemical structures of polymer chains. Also, one may not neglect the effect of phase structure, and in particular the effect of arrangement within the phases which are made of rigid urethane and urea segments, where the interactions resulting from hydrogen bonds are strongest. In the case of cationomers, electrostatic interactions generate additional forces within those phases. Hence, adding to determinations of SFE, we found it advisable to study the nature of the phase arrangement in the produced polyurethanes and to verify whether the differences in the supermolecular structures, alike the differences in the chemical chain structures, are essential for the surface characteristic of the coats which had been obtained from linear polyurethanes (coats applied as organic solutions), and which had been obtained from polyurethane cationomers as environmentally friendly waterborne polyurethanes. The study involved inter alia the differential scanning calorimetry (DSC) method.
Experimental
Raw materials and reagents
The following reagents were used: 4,4′-methylenebis(phenyl isocyanate) (MDI), isophorone diisocyanate [5-isocyanato-1-(isocyanatomethyl)-1,3,3-trimethylcyclo-hexane] (IPDI), toluene-2,4-diisocyanate and toluene-2,6-diisocyanate (TDI) and 1,6-hexamethylene diisocyanate (HDI; all from Aldrich). The reagents were used as purchased. Polyoxyethylene glycols (POG; Aldrich), (M n ≈ 600 g/mol) and (M n = 2,000 g/mol), were dried under vacuum in nitrogen, at 120 °C, for 2 h). Polyoxypropylene glycol (PPG) (M n ≈ 450 g/mol; Rokopol 7P) was purchased from Chemical Factory “Rokita S.A.” in Brzeg Dolny (Poland) and was dried under vacuum in nitrogen, at 120 °C, for 2 h). N-Methyldiethanolamine (N-MDA), N-butyldiethanolamine (N-BDA), (N-phenyl-diethanolamine (N-PhDA), 2,2,3,3-tetrafluoro-1,4-butanediol (TFBD), 1,4-butanediol, 1,6-hexamethylenediamine (HMDA), 1-bromobutane and 1-bromodecane (all reagents from Aldrich) were used as purchased. In addition, the following were used: formic acid (HCOOH), 99%, analytically pure (POCh S.A., Gliwice, Poland); dibutyl tin dilaurate (DBTL) (from Huntsman Performance Chemicals); 14-dioxane, (Chempur, Poland); and chlorobenzene (POCh S.A., Gliwice, Poland). For the analytical reagents, diiodomethane, formamide, α-bromonaphthalene (from Aldrich) and redistilled water were used.
Method for the synthesis of linear polyurethane
Linear polyurethanes were synthesised in a two-stage polyaddition process with the use of appropriate diisocyanates and polyols at the molar ratio of 2:1. The process involved DBTL as a catalyst which was added at 0.1 wt.% on polyether POG 600 or POG 2000. The prepolymer was synthesised and then extended with a sui reactant (N-alkyldiethanolamine, BD or TFBD, respectively) in a solution, in 1,4-dioxane or chlorobenzene, at the concentration of about 40 wt.%, with the molar ratio of the –NCO and –OH functional groups maintained at 1:1. The chemical compositions of the produced polyurethanes were presented in Table 1 and as the Eq. 5. In order to obtain similar chain structures in polyurethanes and cationomers, the same N-alkyldiethanolamines were used as chain extenders for urethane prepolymers, both in the synthesis of selected linear polyurethanes and cationomers. It was thus possible to compare the impact of the structures of PU chains on the SFE values of the final coatings. The reference coats were prepared by coating poly(tetrafluoroethylene) (PTFE) plates with the solution of linear polyurethane (with conc. about 40 wt.%) and conservative evaporation of 1,4-dioxane or chlorobenzene in a vacuum drier, at 80 °C, over 6 h, followed by additional conditioning by exposure to ambient air for 10 days.
Table 1.
Chemical compositions of synthesised linear polyurethanes and results from WAXS analysis
| Sample no. | Type of diisocyanate | Type of polyol | Type of chain extender | Two theta angles, grad | Crystallisation degree, % | Two theta angle, grad | Crystallisation degree, % |
|---|---|---|---|---|---|---|---|
| Synthesis in dioxane | Synthesis in chlorobenzene | ||||||
| PU-1 | MDI | POG 2,000 | N-MDA | 19.48, 23.61 | 23.31 | 19.52, 23.64 | 25.80 |
| 26.81, 27.52 | 26.94, 29.83 | ||||||
| 29.76, 36.17 | 36.22, 43.59 | ||||||
| 21.02, 44.62 | 21.48, 44.65 | ||||||
| PU-2 | N-BDA | ||||||
| PU-3 | TFBD | 19.34,23.47 | 19.16 | ||||
| 26.72,36.03 | |||||||
| 61.61,20.89 | |||||||
| 44.28, | |||||||
| PU-4 | POG 600 | BD | 6.7, 29.17 | 4.92 | |||
| 29.49, 39.21 | |||||||
| 42.95, 47.32 | |||||||
| 48.32, 57.21 | |||||||
| 65.1, 20.79 | |||||||
| 44.32 | |||||||
| PU-5 | TFBD | ||||||
| PU-6 | IPDI | POG 2,000 | BD | 19.41, 23.54 | 34.06 | ||
| 26.79, 36.12 | |||||||
| 43.07, 49.53 | |||||||
| 20.43 | |||||||
| PU-7 | N-MDA | ||||||
| PU-8 | N-BDA | ||||||
| PU-9 | TDI | POG 2,000 | BD | 19.25, 23.37 | 31.82 | ||
| 26.55, 29.14 | |||||||
| 35.92, 39.15 | |||||||
| 42.9, 47.25 | |||||||
| 48.27, 50.23 | |||||||
| 57.16, 60.77 | |||||||
| 20.35 | |||||||
| PU-10 | HDI | POG 2,000 | BD | ||||
| PU-11 | N-MDA | ||||||
Method for the synthesis of urethane cationomers
Cationomers which were used in the research were synthesised using a four-stage polyaddition process. Fluorine was added to molecular chains of cationomers no. KPU-5–8 at stage 2 of the process, i.e. in the synthesis of prepolymer—in the reaction of isocyanate prepolymer (prepared from diisocyanate and polyol) and the mixture of N-MDA, N-BDA with 0, 5, 10 or 15 wt.% of TFBD, or N-PhDA, respectively. Alkylammonium cations were produced at stage 3 by alkylation of tertiary amine groups from N-BDA with C4H9Br (sample no. KPU-2) or C10H21Br (sample no. KPU-3) or by the reaction of tertiary amine groups from N-MDA, N-BDA or N-PhDA with HCOOH. Finally, aqueous dispersions were produced. That stage also involved the chain extension process: prepolymers with free –NCO groups were reacted with HMDA and water. The detailed description of the cationomer synthesis processes was provided in [22]. The polymer coatings for further tests were formed by applying the above-mentioned dispersions to a nonpolar surface of PTFE and evaporation of water by air drying at 20 °C. The coatings were then subjected to seasoning under such conditions over 10 days. Chemical compositions of cationomers can be found in Table 2 and in Scheme 1.
Table 2.
Chemical compositions of synthesised polyurethane cationomers
| Sample no. | Type of diisocyanate | Type of polyol | Type of tertiary amine | Type of quaternisation reagent |
|---|---|---|---|---|
| KPU-1 | MDI | PPG 450 | N-BDA | HCOOH |
| KPU-2 | C4H9Br | |||
| KPU-3 | C10H21Br | |||
| KPU-4 | POG 600 | N-MDA | HCOOH | |
| KPU-5 | N-MDA + 5% TFBD | |||
| KPU-6 | N-MDA + 10% TFBD | |||
| KPU-7 | N-MDA + 15% TFBD | |||
| KPU-8 | N-NDA + 15% TFBD | |||
| KPU-9 | IPDI | PPG 450 | N-MDA | |
| KPU-10 | POG 600 | |||
| KPU-11 | POG 600 | N-BDA | ||
| KPU12 | TDI | PPG 450 | N-MDA | |
| KPU-13 | N-PhDA | |||
| KPU-14 | HDI | PPG 450 | N-MDA | |
| KPU-15 | N-PhDA |
Scheme 1.
The polyurethane chain structure of the synthesised cationomers
WAXS analysis
The wide angle X-ray scattering (WAXS) investigations were performed at room temperature on a modified DRON-3-SEIFERT automated diffractometer. The radiation of CuKα and the nickel filter were employed. The operating conditions for the X-ray tube were as follows: 40 kV, 30 mA. X-ray diffraction patterns were taken within the range of 2θ from 1° to 60°, with a step scanning equal to 0.02° and at counting time of 10 s.
DSC method
The calorimeter used was a DSC823e from Mettler-Toledo. It was equipped with a sample robot and a Julabo FT400 intracooler, as well as with STARe software for the control of the experimental conditions and for data analysis. It was applicable in conventional DSC analyses and as a TOPEM instrument; the underlying heating rate was 5 K/min, samples of ca. 3.5 mg, under an argon atmosphere, and the intracooler was used for cooling.
Atomic force microscopy
The atomic force microscope (Nanoscope V firmware 8.10 from Veeco) was employed to study superficial structures of the coatings obtained from PU. The scans were taken at ambient temperature, in air, and at the moderate tapping mode (TM), R = 0.6 conditions, i.e. at direct contact between the sample surface and the tip. The pyramidal Si tip employed in the TM system had a spring constant of 22–100 N/m, f o = 300 kHz. Each scan was presented in the following data format: topographic image (height, amplitude and phase), two-dimensional or three-dimensional, 512 × 512 pixels.
Method for determination of components of surface free energy for solids
Physical parameters of surface energy of a solid γ S were found in the present study on the basis of the van Oss–Good and Owens–Wendt theory. The van Oss–Good model assumes that the surface free energy γ S,L may be presented as a sum of two components [24]:
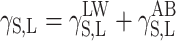 |
1 |
where:
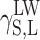
surface energy component connected with long-range interactions (dispersion, polar and induction interactions)
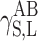
surface energy component connected with acid–base interactions, as results from the Lewis theory
(where: S is solid and L is liquid).
Equation 1 is generally applicable both to solids, and the subscript S is used then, and to wetting liquids (standard liquids or tested liquids), marked with the subscript L.
Let us use the symbol 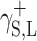 for the component of
for the component of 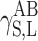 which is responsible for the surface free energy of the Lewis acid, and the symbol
which is responsible for the surface free energy of the Lewis acid, and the symbol 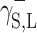 for the component representing the Lewis base.
for the component representing the Lewis base.
The surface free energy (SFE) parameters for solids (S) and for liquids (L) interacting with those solids should satisfy the equation of van Oss–Good:
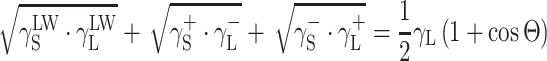 |
2 |
where Θ is the experimentally found wetting angle between a liquid drop and a solid surface under investigation. So, wetting angles Θ were first measured for the surfaces of cationomer coatings with the use of three model liquids (water, diiodomethane and formamide) with known parameters of γL,  ,
,  and
and 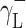 (Table 3), and then, the Eq. (2) was used to calculate the values of
(Table 3), and then, the Eq. (2) was used to calculate the values of 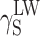 ,
, 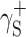 and
and 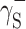 for the studied cationomers. The Owens–Wendt model assumes that the surface free energy γS,L may be presented as a sum of two components [25]:
for the studied cationomers. The Owens–Wendt model assumes that the surface free energy γS,L may be presented as a sum of two components [25]:
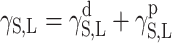 |
3 |
where:
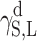
surface energy connected with dispersion interactions
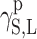
surface energy connected with polar interactions.
Table 3.
Surface properties of model measuring liquids [26]
| Model measuring liquid | Surface free energy parameters [mJ/m2] | ||||||
|---|---|---|---|---|---|---|---|
| γ L |
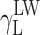
|
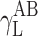
|
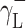
|
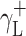
|
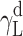
|
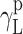
|
|
| Water | 72.8 | 21.8 | 51 | 25.5 | 25.5 | 21.8 | 51 |
| Formamide | 58.0 | 39.0 | 19.0 | 2.28 | 39.6 | – | – |
| Diiodomethane | 50.8 | 50.8 | 0 | 0 | 0 | 48.5 | 2.3 |
| α-Bromonaphthalene | 44.4 | 44.5 | 0 | 0 | 0 | – | – |
In order to find the SFE parameter according to that method, it is enough to measure the wetting angle value with the use of two model liquids with definitely different γL values, e.g. using formamide and diiodomethane or water and diiodomethane [26]. The components of SFE can be found in that case from a system of two algebraic equations:
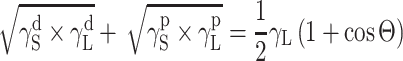 |
4 |
The contact angles Θ were measured with the use of the method suggested by Zisman [27], i.e. by means of an optical goniometer (Cobrabid Optica–Warsaw) with a digital camera installed in the axial extension of its lens. The liquid drops with a constant volume (about 3-5 μdm3) were applied to the surfaces of the studied samples with the use of a special micropipette. The samples were fixed on the stage of the goniometer. The measurements were taken at 21 ± 1 °C. The values of contact angles were found from the geometric analysis of the pictures taken for liquid drops, which involved the use of the original software developed by Kontrast (Pasłęk, Poland) for interpretation of the Young’s equation. The measuring errors for the angles Θ come from two sources. The first of them results from different shapes of liquid drops placed on the investigated coatings and from possible interactions between the standard liquid and that subgrade, as well as from different liquid vaporisation rates observed when the pictures were taken. Nine drops were analysed each time; they were placed on the surface simultaneously. Another source of potential errors is inaccuracy in graphical interpretation of the pictures with the use of the computer software. For each picture recorded (i.e. for each liquid drop), the geometrical shape analysis was repeated ten times: the extreme values were rejected, and the arithmetic mean value was calculated for the accepted findings.
Results and discussion
Structures of synthesised polyurethanes
The basic chain structure of the synthesised linear polyurethanes may be illustrated by the following formula:
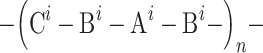 |
5 |
where:
i = 1,2
- A1 is the structure derived from POG (M n = 600 g/mol)
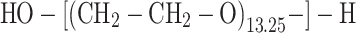
- A2 is the structure derived from POG (M n = 2,000 g/mol)

Bi is the structure derived from MDI, IPDI, TDI or HDI diisocyanate
C is the structure derived from chain extender: BD, TFBD, N-MDA or N-BDA.
The chain structures of the synthesised cationomers result from the molar ratios assumed for the reacting substances at successive stages of the polyaddition process, and they are more complex than above. They can be presented by the following molecular formula display in Scheme 1:
The chemical structures of the synthesised polyurethanes were confirmed by spectroscopic methods (an accurate structural analysis of cationomers at the similar structure by using 1H, 13C and 19F NMR spectrometry was presented into our earlier works [22, 28]).
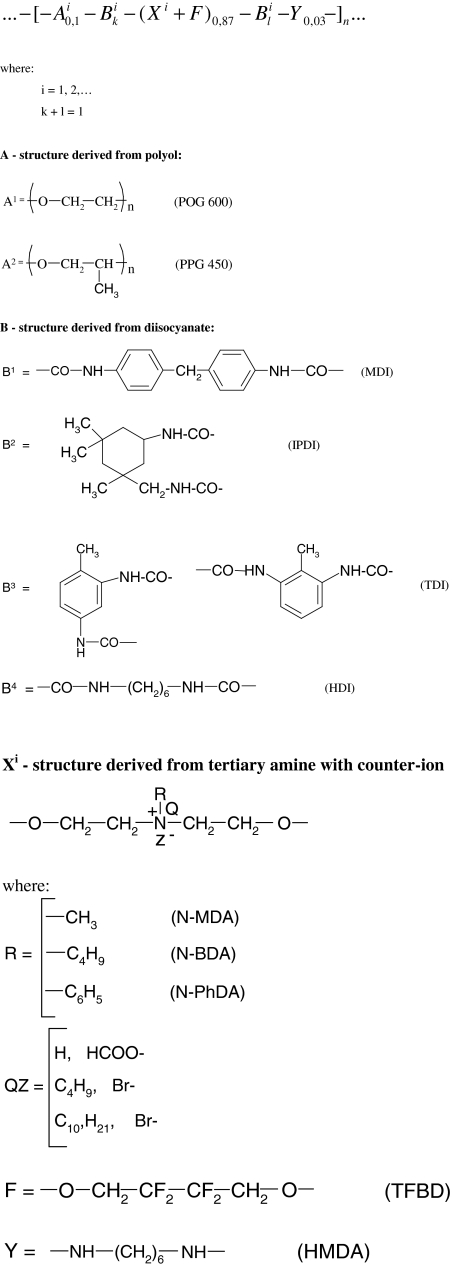
Table 1 provides same diffractive reflections which were noted for the analysed polyurethane coatings, and Fig. 1 shows an example of the WAXS diffraction pattern for linear polyurethane no. PU-6. The collected data indicate that polyurethanes PU-1, PU-2, PU-3, PU-6 and PU-9 exhibit a relatively high level of crystallinity, which relates to the coats obtained from the solutions both in 1,4-dioxane and in chlorobenzene. As opposed to that, the coats applied as aqueous dispersions of cationomers are generally amorphous. This is in line with the findings from our earlier research, as presented in [22]. That was also the case of cationomer coats KPU 5–8 which contained TFBD-derived fluorine segments. The amorphous phase makes the dominant phase in all those samples. The WAXS diffraction peak is composed of two sub-peaks: one of them is clearly amorphous, its full width at half maximum (FWHM) is higher than 10°, and the other is lower and narrower, which is a suggestion for some orderly arranged structures. There are also differences between samples within the size of their FWHM peaks. Those differences, however, are not sufficiently significant to support the conclusion that the presence of fluorine atoms controls the formation of crystalline phases in the synthesised cationomers.
Fig. 1.
WAXS diffraction pattern for linear polyurethane no. PU-6
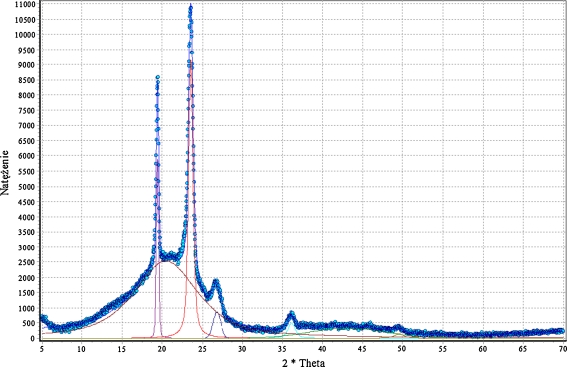
Phase structures
Since the changes in specific heat were small and there were relaxation effects observed, it was hard to obtain the value of T g directly from classic DSC curves—as was in the case of polyurethanes (Fig. 2a) and cationomers (Fig. 2b). The polyurethane coatings perform like elastomers, and they show two glass transition points: T g1 < 0 °C for soft segments and T g2 > 0 °C for hard segments. Hard segments are definitely superior in numbers in the studied polyurethanes, and they are formed by urethane groups (derived from a specific diisocyanate and BD, TFBD, N-MDA or N-MDA) and by urea groups which are present in relatively lower numbers (and which are derived from MDI and HMDA). Within the interactions between these segments, hydrogen bonds take the essential role in putting some order to the structure. Hence, the determined values of relaxation enthalpy may be incidental to a high degree. On the other hand, however, some clearly regular performance can be observed in the measured T g values which would represent the glass transition of soft segments (there is no T g1). That can be accounted for by a relatively low number of polyether-derived flexible segments in cationomers (the first equation on Scheme 1). Moreover, they must be separated from each other in fluorine-containing cationomers by rigid segments which are derived from MDI and TFBD.
Fig. 2.
DSC curves for a PU coatings and b PU cationomers
The thermograms as shown in Fig. 2b reveal some increase in T g2 for cationomers which contain 0% to 15% fluorine added with the polyether component. That increase speaks for some stiffening of the amorphous structure (Table 4). The stiffness can make it difficult to freely form the coatings from process solutions, which seems supported by the increased relaxation enthalpy value as observed for test samples KPU-5, 6 and 7.
Table 4.
Results of DSC analysis
| Sample no. | Type of polymer | Glass transition, °C | |
|---|---|---|---|
| Midpoint | ΔC p, J/g·deg | ||
| PU-4 | Linear PU | −23.1 | 0.349 |
| 45.6 | 0.166 | ||
| PU-5 | −3.1 | 0.308 | |
| KPU-4 | PU cationomer | 47.5 | 0.594 |
| KPU-5 | 31.1 | 0.430 | |
| KPU-6 | 42.8 | 0.532 | |
| KPU-7 | 46.1 | 0.655 | |
The phase structure was additionally analysed by the atomic force microscopy (AFM) method. Figure 3 presents various AFM images for PU-3 with about 20% of crystalline phase that results from WAXS analysis. The crystalline phase agglomerations can be clearly observed against the amorphous polymer matrix. As opposed to that, AFM analyses of cationomer coatings revealed generally the presence of inhomogeneous amorphous phase, which resulted from limited miscibility of hard and soft segments. However, “islands” of hard segments with dimensions 50–100 nm (Fig. 3b, c) with sharply outlined shapes were visible even in those samples against the background of the pretty homogeneous phase of soft segments.
Fig. 3.
Three-dimensional (a), phase (b) and amplitude (c) AFM images for PU-3 sample
The physical state of the analysed area with AFM method, especially coarseness, is very important for getting reliable results of contact angle measurements. AFM analyses (Fig. 3a) demonstrate that irregularities (hollows and tops) are in some places big, but do not exceed the ±20 nm value, which allows to perform solid SEP measurements.
The question remains open whether the differences in supermolecular structures of linear polyurethanes and cationomers as presented above affect the surface structures of coats, and if they do—whether those effects can be observed in their SFE values. That problem is complex since the superficial structure is usually different from the internal structure of the polymer material. In this specific case, the analysed coats had the thickness of about 50 μm. One may hence assume that the internal phase and the strictly superficial layer, which is available for the SFE measurements with the use of model liquid drops applied to the materials under investigation, interpenetrate each other to a certain degree. The phase structure of a coating, i.e. also its stiffness, should thus affect the values of SFE parameters to be determined. When analysing the phase structure, one should pay attention to the nature and values of chemical interactions (hydrogen bonds, ionic interactions) and to physical interactions: polar and dispersion effects. In order to give consideration to both those aspects, the SFE value was calculated with the use of two complementary methods: by van Oss–Good and by Owens–Wendt, which utilise the same measured values of the wetting angle Θ to calculate the values of various components of the parameter γ
S: 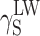 and
and 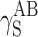 (van Oss–Good method) or
(van Oss–Good method) or 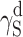 and
and 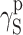 (Owens–Wendt method). In order to authenticate the findings, different sets of model liquids were used. The characters of interactions in polyurethanes and in cationomers could be compared in this way. That turned out possible since the values of γ
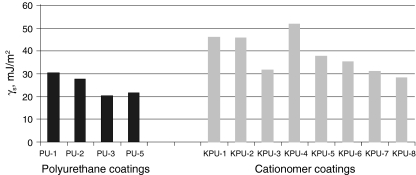
S, as found with those two methods, are much similar, which is confirmed by the data presented in Table 5 for same polyurethane coatings and in Table 6 for exemplary cationomer coatings. A higher number of measurements made it possible to eliminate errors which result inter alia from interactions between the drop of a polar liquid, e.g. water and a tested coat. The SFE results calculated in the Owens–Wendt method for the water–diiodomethane system turned out the least reliable. The measurement results were presented for interpretation in the form of diagrams in Figs. 4, 5, 6 and 7. The SFE of cationomers was clearly higher than the SFE of polyurethanes which had been synthesised with the use of the same diisocyanates; samples with similar chain structures were compared.1 As was shown in our earlier studies, the cationomer chain structure, which results from the employed components—diisocyanate, tertiary amines and compounds which add counterions, strongly affects the SFE parameters [28]. That was also confirmed by the results of our present research. The highest values of SFE (γ
S ≈ 50 mJ/m2) were noted for the cationomers which had been synthesised from MDI or IPDI, N-MDA and HCOOH. Much lower values were specific for the cationomers produced with the use of TDI and HDI (γ
S ≈ 40 mJ/m2), while the use of amines N-BDA and N-PhDA, and additional incorporation of counterions from C4H9Br or C10H21Br (γ
S ≈ 40 mJ/m2), yielded further decline of SFE (γ
S ≈ 34 mJ/m2; KPU-3). When fluorine is added, the SFE value may go as far down as to 30 mJ/m2 (KPU-7 and -8). The presence of even small amounts of TFBD-derived segments considerably lowers all long-range interactions
(Owens–Wendt method). In order to authenticate the findings, different sets of model liquids were used. The characters of interactions in polyurethanes and in cationomers could be compared in this way. That turned out possible since the values of γ
S, as found with those two methods, are much similar, which is confirmed by the data presented in Table 5 for same polyurethane coatings and in Table 6 for exemplary cationomer coatings. A higher number of measurements made it possible to eliminate errors which result inter alia from interactions between the drop of a polar liquid, e.g. water and a tested coat. The SFE results calculated in the Owens–Wendt method for the water–diiodomethane system turned out the least reliable. The measurement results were presented for interpretation in the form of diagrams in Figs. 4, 5, 6 and 7. The SFE of cationomers was clearly higher than the SFE of polyurethanes which had been synthesised with the use of the same diisocyanates; samples with similar chain structures were compared.1 As was shown in our earlier studies, the cationomer chain structure, which results from the employed components—diisocyanate, tertiary amines and compounds which add counterions, strongly affects the SFE parameters [28]. That was also confirmed by the results of our present research. The highest values of SFE (γ
S ≈ 50 mJ/m2) were noted for the cationomers which had been synthesised from MDI or IPDI, N-MDA and HCOOH. Much lower values were specific for the cationomers produced with the use of TDI and HDI (γ
S ≈ 40 mJ/m2), while the use of amines N-BDA and N-PhDA, and additional incorporation of counterions from C4H9Br or C10H21Br (γ
S ≈ 40 mJ/m2), yielded further decline of SFE (γ
S ≈ 34 mJ/m2; KPU-3). When fluorine is added, the SFE value may go as far down as to 30 mJ/m2 (KPU-7 and -8). The presence of even small amounts of TFBD-derived segments considerably lowers all long-range interactions 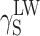 which is apparent in the case of cationomers KPU-4–7. When analysing the values of components γ
S, one may arrive at the conclusion that the highest contribution to SFE comes from
which is apparent in the case of cationomers KPU-4–7. When analysing the values of components γ
S, one may arrive at the conclusion that the highest contribution to SFE comes from 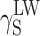 , where dispersion interactions
, where dispersion interactions 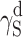 are prevailing both in polyurethanes and in cationomers. The share of polar interactions, which by their nature are more dependent on the structures of functional groups and which control inter alia the presence of hydrogen bonds, is clearly inferior both in polyurethanes and in cationomers. In the case of cationomers, on the other hand, because of the presence of ionic groups, acid–base interactions
are prevailing both in polyurethanes and in cationomers. The share of polar interactions, which by their nature are more dependent on the structures of functional groups and which control inter alia the presence of hydrogen bonds, is clearly inferior both in polyurethanes and in cationomers. In the case of cationomers, on the other hand, because of the presence of ionic groups, acid–base interactions 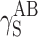 become apparent which can hardly be observed in nonionic polyurethanes. The effects as presented above, resulting from the nature of bonds and types of functional groups, must also be decisive for the phase structures of both types of polyurethane coatings. The presence of the crystalline phase in polyurethanes may thus be assumed to result from the improved structural arrangement and reduced extent of polar and dispersion interactions, which finally also gives lower SFE in polyurethane coats.
become apparent which can hardly be observed in nonionic polyurethanes. The effects as presented above, resulting from the nature of bonds and types of functional groups, must also be decisive for the phase structures of both types of polyurethane coatings. The presence of the crystalline phase in polyurethanes may thus be assumed to result from the improved structural arrangement and reduced extent of polar and dispersion interactions, which finally also gives lower SFE in polyurethane coats.
Table 5.
SFE components for linear polyurethane and coatings; estimation by Owens–Wendt and van Oss–Good methods
| Polyurethane sample no. by Table 1 | van Oss–Good method by formamide–iiodomethane–water, [mJ/m2] | Owens–Wendt method by formamide–diiodomethane, [mJ/m2] | Owens–Wendt method by water–diiodomethane, [mJ/m2] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| γ S |
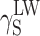
|
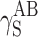
|
γ S |
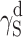
|
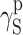
|
γ S |
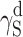
|
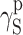
|
|
| PU-3 | 23.91 | 22.80 | 1.11 | 26.21 | 25.62 | 0.59 | 26.38 | 23.78 | 2.60 |
| PU-7 | 41.00 | 40.70 | 0.30 | 40.91 | 37.64 | 3.27 | – | – | – |
| PU-8 | 43.46 | 43.15 | 0.31 | 43.17 | 40.72 | 2.45 | – | – | – |
| PU-10 | 44.30 | 43.56 | 0.74 | 43.55 | 41.56 | 1.99 | – | – | |
| PU-9 | 40.54 | 38.59 | 1.95 | 44.49 | 43.78 | 0.71 | 44.17 | 42.49 | 1.68 |
Table 6.
SFE components for cationomer coatings; estimation by Owens–Wendt and van Oss–Good methods
| Cationomer sample no. by Table 2 | van Oss–Good method by formamide–diiodomethane–water, [mJ/m2] | van Oss–Good method by formamide-α–bromonaphtalene–water, [mJ/m2] | Owens–Wendt method by water–α-bromonaphtalene, [mJ/m2] | Owens–Wendt method by water–α-bromonaphtalene, [mJ/m2] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| γ S |
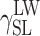
|
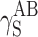
|
γ S |
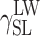
|
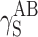
|
γ S |
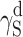
|
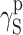
|
γ S |
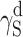
|
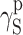
|
|
| KPU-4 | 51.83 | 43.00 | 8.83 | 50.77 | 42.09 | 8.68 | 50.92 | 35.76 | 15.16 | 49.33 | 36.29 | 13.04 |
| KPU-5 | 37.64 | 33.35 | 4.29 | 42.83 | 41.20 | 1.63 | 42.02 | 38.41 | 3.61 | 38.39 | 33.30 | 5.09 |
| KPU-6 | 35.21 | 29.92 | 5.29 | 38.36 | 35.92 | 2.44 | 35.97 | 35.81 | 0.16 | 35.13 | 28.71 | 6.42 |
| KPU-7 | 33.62 | 33.12 | 0.49 | 27.92 | 27.91 | 0.01 | 27.55 | 27.52 | 0.03 | 31.02 | 24.80 | 6.22 |
Fig. 4.
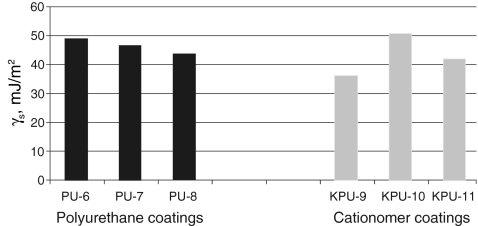
SFE graphical comparison of the coating preparation with linear PU and cationomer PU based on MDI diisocyanate
Fig. 5.
SFE graphical comparison for the coating preparation with linear PU and cationomer PU based on IPDI diisocyanate
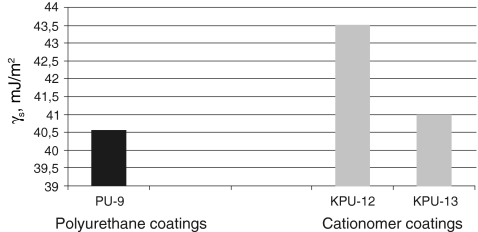
Fig. 6.
SFE graphical comparison for the coating preparation with linear PU and cationomer PU based on TDI diisocyanate
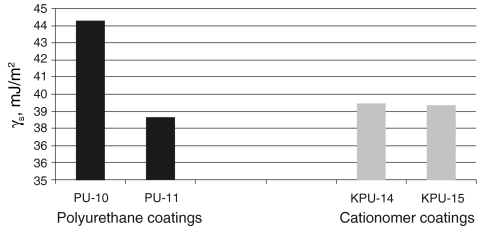
Fig.7.
SFE graphical comparison for the coating preparation with linear PU and cationomer PU based on HDI diisocyanate
Conclusions
The investigation with the use of WAXS and AFM methods revealed that polyurethane coatings perform like elastomers, and they contain up to 30% of crystalline phases which form clearly separated rigid domains against the background of the amorphous phase. The phase structure of cationomers, on the other hand, is completely amorphous, with the prevailing share of the dispersed rigid glassy phase, which may be responsible for the development of additional mechanical stresses at the moulding operations. Changes in the specific heat were analysed versus frequency of changes in temperature, with the TOPEM DSC method, and they demonstrated generally higher durability of the coatings obtained from linear polyurethanes.
The question of reducing polarity of polyurethanes, which is important from the viewpoint of a number of special applications of those materials, must hence be analysed with due consideration of the chemical structures of polymer chains, morphology of supermolecular structures and coat preparation methods. The detailed analysis, based on the Owens–Wendt and van Oss–Good methods and various combinations of model liquids for the measurements of the wetting angle values, revealed that the surface free energy of cationomer coatings was higher than that of linear polyurethanes with similar chemical compositions. It is possible in the case of cationomer coatings to reduce SFE of polyurethanes from 50 to 30 mJ/m2 by changing chemical structures of polymer chains and by adding segments which reduce polar interactions. In particular, diisocyanates may be changed, e.g. MDI may be replaced by less polar IPDI; more hydrophobic tertiary amines may be used which forms ammonium groups, e.g. N-butyldiethanolamine instead of N-methyldiethanolamine; and even small amounts of 2,2,3,3-tetrafluoro-1,4-butanediol may be added. The strongest effect on SFE in both polyurethane types comes from the component 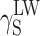 which represents long-range interactions, among which the dominant role is played by dispersion interactions which are described by means of the parameter
which represents long-range interactions, among which the dominant role is played by dispersion interactions which are described by means of the parameter 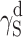 . Polar interactions
. Polar interactions 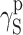 are much weaker, and ionic interactions
are much weaker, and ionic interactions 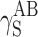 assume significant values for cationomers only.
assume significant values for cationomers only.
One may say in conclusion that the definitely more environmentally friendly coats, which are obtained from cationomer polyurethanes, make more polar materials than elastomer coats. However, the polar performance may be modified in ionic systems by changing their chemical compositions. Yet, structural durability of cationomers is much inferior, as it was shown by WAXS and DSC analyses. Those factors should be taken into consideration when replacing traditional polyurethane coats with the systems based on environmentally friendly waterborne polyurethanes.
Acknowledgement
This work has been supported by the Polish Ministry of Science and Higher Education under the contract no. N N507 329636. The authors would like to thank Mettler-Toledo for the possibility of using their TOPEM DSC.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Footnotes
Our next paper will provide attempts for mathematical generalisation of relations between polyurethane chemical structures and SFE values.
References
- 1.Król P. Linear polyurethanes. Leiden: Koninklijke Brill NV; 2008. [Google Scholar]
- 2.Deka H, Karak N. Progress Organic Coatings. 2009;66:192. doi: 10.1016/j.porgcoat.2009.07.005. [DOI] [Google Scholar]
- 3.Timothy D, Haugen HJ. J Mater Sci: Materials Med. 2008;19:2713. doi: 10.1007/s10856-008-3393-6. [DOI] [PubMed] [Google Scholar]
- 4.Ryszkowska JL, Auguścik M, Sheik A, Boccaccini AR. Composite Sci Technol. 2010;70:1894. doi: 10.1016/j.compscitech.2010.05.011. [DOI] [Google Scholar]
- 5.Król P. Progress Materials Sci. 2007;52:915. doi: 10.1016/j.pmatsci.2006.11.001. [DOI] [Google Scholar]
- 6.Markets, Farbe und Lack Focus Powder Coatings. 2010;2010:6. [Google Scholar]
- 7.Jie Z, Chun PH. Eur Polym J. 2008;44:3708. doi: 10.1016/j.eurpolymj.2008.08.019. [DOI] [Google Scholar]
- 8.Roland CM, Fragiadakis D, Gamache RM. Compos Struct. 2010;92:1059. doi: 10.1016/j.compstruct.2009.09.057. [DOI] [Google Scholar]
- 9.Garcia-Pacios V, Costa VV, Colera M, Martin-Martinez JJM. Internat J Adhesion Adhesives. 2010;30:456. doi: 10.1016/j.ijadhadh.2010.03.006. [DOI] [Google Scholar]
- 10.Bayer IS, Steele A, Martorana PJ, Loth E. Appl Surface Sci. 2010;257:823. doi: 10.1016/j.apsusc.2010.07.072. [DOI] [Google Scholar]
- 11.Athawale VD, Kularni MA. J Coating Technol Res. 2010;7:189. doi: 10.1007/s11998-009-9184-2. [DOI] [Google Scholar]
- 12.Delucchi M, Trombetta T, Ricatti R, Cerisola G, Turri S. J Appl Electroch. 2009;39:2107. doi: 10.1007/s10800-009-9872-8. [DOI] [Google Scholar]
- 13.Francolini I, D’Ilario L, Guaglianone E, Donelli G, Martinelli A. Acta Biomater. 2010;6:3482. doi: 10.1016/j.actbio.2010.03.042. [DOI] [PubMed] [Google Scholar]
- 14.Wenfeng Q, Handi Q, Zhifei C, Katian X. Biomaterials. 2011;32:3178. doi: 10.1016/j.biomaterials.2011.01.031. [DOI] [PubMed] [Google Scholar]
- 15.Arua P, Rao BS. Reactive Fuctional Polymers. 2009;69:20. doi: 10.1016/j.reactfunctpolym.2008.10.005. [DOI] [Google Scholar]
- 16.Shiram V, Radhakrishnan Polymer Bull. 2005;55:165. doi: 10.1007/s00289-005-0425-y. [DOI] [Google Scholar]
- 17.Zhu Y, Hu J, Yeung K. Acta Biomater. 2009;5:3346. doi: 10.1016/j.actbio.2009.05.014. [DOI] [PubMed] [Google Scholar]
- 18.Sundar S, Arua P, Venkateshwarlu U, Radhakrishnan G. Coll Polym Sci. 2004;283:209. doi: 10.1007/s00396-003-1012-0. [DOI] [Google Scholar]
- 19.Awkal M, Jonquires A, Clement R, Lochon P. Polymer. 2006;47:5724. doi: 10.1016/j.polymer.2006.05.058. [DOI] [Google Scholar]
- 20.Cao Q, Chuanbao ZH. J Materials Sci: Materials Med. 2004;15:607. doi: 10.1023/B:JMSM.0000026382.34900.b6. [DOI] [Google Scholar]
- 21.Flemming RG, Capelli CC, Cooper SL, Proctor RA. Biomaterials. 2000;21:273. doi: 10.1016/S0142-9612(99)00176-3. [DOI] [PubMed] [Google Scholar]
- 22.Król B, Król P, Pikus S, Chmielarz P, Skrzypiec K. Coll Polym Sci. 2010;288:1255. doi: 10.1007/s00396-010-2244-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Król P, Król B. Polimery. 2010;55:440. [Google Scholar]
- 24.Good JR. In: Fundamentals of adhesion. Lee LH, editor. New York: Dekker; 1991. p. 153. [Google Scholar]
- 25.Oss CJ. J Chem Res. 1988;88:927. [Google Scholar]
- 26.Żenkiewicz M (2006) Polimery, 51, 169 and 51, 584
- 27.Zisman WA. Ad in Chem Am Chem Soc. 1964;43:1. [Google Scholar]
- 28.Król P, Król B. Coll Polym Sci. 2009;287:189. doi: 10.1007/s00396-008-1966-z. [DOI] [Google Scholar]