Abstract
We propose a new coefficient, the adjusted Wallace coefficient (AW), and corresponding confidence intervals (CI) as quantitative measures of congruence between typing methods. The performance of the derived CI was evaluated using simulated data. Published microbial typing data were used to demonstrate the advantages of AW over the Wallace coefficient.
TEXT
Several molecular epidemiology studies of clinically relevant microorganisms provide a characterization of isolates based on different typing methods (3, 5, 7). The informed choice of which typing method is more appropriate in a given clinical or microbiological research setting lies in the ability of the method to identify isolates of interest, the execution time, the cost-effectiveness, and the ease of interpretation of the results (16). Nevertheless, to support the decision, a quantitative comparison of the results of the typing methods should also be performed (3).
Carriço et al. (3) proposed the use of the adjusted Rand coefficient (AR) and the Wallace coefficient (W) as measures to assess the congruence of typing methods. These have been applied in several studies comparing or proposing new typing methods (2, 3, 7, 9, 12, 17). AR provides a measure of the overall agreement between two typing methods and corrects the previously used coefficient of typing concordance (18) for chance agreement, avoiding the overestimation of concordance between typing methods (8). W provides information about the directional agreement between typing methods. WA→B is the probability that, for a given data set, two individuals are classified together using method B if they have been classified together using method A. In spite of its simple interpretation, one can obtain high values of W due to chance alone. For instance, if method A creates a high number of partitions (such as pulsed-field gel electrophoresis [PFGE] subtypes) and method B creates only two (such as the presence or absence of a given gene), WA→B will be high but may not be different from the value expected by chance alone.
The expected Wallace coefficient under independence (Wi) was previously proposed to evaluate whether the results of two typing methods could agree by chance alone (11). To assess whether the estimated W value is significantly different from the Wi value, one can use the proposed Wallace 95% confidence interval (CI) (11, 13). If the value of Wi is within the CI of W, the null hypothesis of independence between classifications cannot be rejected with the respective confidence level (11). One way to directly take into account Wi would be to calculate an adjusted version of W.
Albatineh et al. (1) had previously discussed the correction for chance agreement for several similarity indices, including W. Although this correction was never applied in the context of microbial typing studies, others have previously acknowledged the importance and usefulness of such a correction (15).
Derivation of AW.
The adjusted Wallace coefficient (AW) is derived by following an approach similar to that used for AR (8):
| (1) |
The following was demonstrated: Wi(A→B) = 1 − SIDB (11), where SIDB is Simpson's index of diversity of the B classification (14).
For a 95% CI, assuming a Gaussian distribution, the limits are given by
| (2) |
where Var(WA→B) is the variance of WA→B. A detailed description of AW and the 95% CI formula derivation and evaluation is given in the Appendix.
Evaluation of AW.
In order to illustrate the importance of the correction for chance agreement, we analyzed representative results from previously published data sets. The data sets used were results for 325 macrolide-resistant Streptococcus pyogenes isolates (group A streptococci [GAS]) (3) and 116 methicillin-resistant Staphylococcus aureus (MRSA) isolates (5) characterized by several typing methods. The data are summarized in Table 1.
Table 1.
Values of Wi, W, and AW and respective 95% confidence intervals for different typing methods used in previous studies
| Data set (reference) | Method A | Method B | Wi(A→B) | WA→B (95% CI) | AWA→B (95% CI) |
|---|---|---|---|---|---|
| Results for 325 macrolide-resistant GAS (3) | T typing | emm typing | 0.22 | 0.70 (0.62–0.77) | 0.61 (0.52–0.7) |
| T typing | Determination of MRPa | 0.49 | 0.72 (0.66–0.79) | 0.46 (0.33–0.58) | |
| Determination of MRP | T typing | 0.28 | 0.41 (0.36–0.45) | 0.18 (0.12–0.25) | |
| Determination of MRP | PFGE(SfiI68)b | 0.19 | 0.38 (0.34–0.43) | 0.24 (0.18–0.29) | |
| PFGE(SfiI68) | Determination of MRP | 0.49 | 0.97 (0.94–1) | 0.95 (0.88–1) | |
| Results for 116 MRSA isolates (5) | spa typing | eBURST analysisc | 0.29 | 0.96 (0.94–0.98) | 0.94 (0.91–0.97) |
| BURP analysisd | eBURST analysis | 0.29 | 0.76 (0.68–0.85) | 0.67 (0.54–0.79) | |
| eBURST analysis | BURP analysis | 0.21 | 0.56 (0.50–0.62) | 0.44 (0.37–0.51) | |
| eBURST analysis | SCCmec typinge | 0.17 | 0.20 (0.16–0.25) | 0.04 (0–0.09) | |
| SCCmec typing | eBURST analysis | 0.29 | 0.35 (0.28–0.43) | 0.09 (0–0.19) |
Three possible MRPs were considered: macrolide resistance without lincosamide resistance, constitutive macrolide-lincosamide-streptogramin B resistance, and inducible macrolide-lincosamide-streptogramin B resistance.
Clusters were defined as groups of isolates sharing at least 68% similarity in the UPGMA/Dice dendrogram of the PFGE profiles upon SfiI digestion.
Groups were defined as sets of isolates sharing at least 6 of the 7 alleles used in the multilocus typing scheme, corresponding to the commonly accepted definition of a clonal complex, by using eBURST (6).
Groups of isolates were defined by BURP (based upon repeated pattern) analysis of the spa types (10).
The staphylococcal cassette chromosome (SCC) type was defined as described previously (4).
For both data sets, only two of the calculated 95% CIs for W included the respective Wi. In all the other comparisons, the congruence between typing methods could not be attributed to chance alone. However, some higher values of Wi are observed for the methods with less discriminatory power (lower SIDB values), such as the macrolide resistance phenotype (MRP) method for the GAS data set. For high Wi values, a large part of the agreement that is being measured by W is due to chance. This could lead to more distinct differences between W and AW, as illustrated in the following examples. The value of AWT typing→MRP method of 0.46 (95% CI, 0.33–0.58) is considerably lower than the agreement measured by WT typing→MRP method of 0.72 (95% CI, 0.66-0.79) (Table 1). The reverse relationship, the ability of MRP to predict T types, was similarly affected: WMRP method→T typing is 0.41 and AWMRP method→T typing is 0.18 with CIs that do not overlap. A similar decrease was also observed in comparing the MRP method to PFGE(SfiI68), in which clusters were defined as groups of isolates sharing at least 68% similarity in the unweighted-pair group method using average linkages (UPGMA)/Dice dendrogram of PFGE profiles upon SfiI digestion. In the MRSA data set, even more distinct differences were observed for WeBURST→SCCmec typing. In the extreme case in which the 95% CI of W includes the Wi value (for instance, in the case of WSCCmec typing→eBURST), AW will be very close to zero, providing a clear indication that the agreement between typing methods is due to chance. However, such marked differences between W and AW are not universal. For several typing methods, only small decreases of AW relative to W were noted, for instance, in the case of WT typing→emm typing for GAS or WBURP→eBURST for MRSA isolates (Table 1). More predictably (see the Appendix), with W values close to 1, the AW value did not differ much from W. This can be observed for WPFGE(SfiI68)→MRP method in the GAS study and Wspa typing→eBURST in the MRSA study.
In order to facilitate the use of AW and respective CIs for the comparison of typing methodologies, these can be calculated with a freely accessible online tool at www.comparingpartitions.info. Bionumerics scripts for the calculation of AW and the respective CI are also available at this website.
Conclusion.
It is important to clarify the difference between the actual ability to predict the classification produced by a given typing method from the results obtained with another method and the fact that such congruence of classification could arise by chance. AW provides such correction to the now widely used W. A drawback of this approach is the loss of direct interpretation of the AW value as a probability compared to W, since the value of W is transformed by the correction for chance agreement. Nevertheless, we recommend the use of AW over W since it avoids the overestimation of unidirectional concordance between typing methods, similar to AR for bidirectional concordance. The use of these coefficients and respective CIs are tools for an effective comparison of the results of different molecular typing studies, providing a better evaluation of the strengths and weaknesses of each study and of each typing method.
Acknowledgments
This work was partially funded by the Fundacão para a Ciência e a Tecnologia (PTDC/SAU-ESA/71499/2006) and an unrestricted grant from GlaxoSmithKline.
We thank D. Ashley Robinson for insightful discussions about the need for an adjusted Wallace coefficient.
APPENDIX
Derivation of AW.
The derivation of AW is analogous to that of AR (8). The general form of an index corrected for chance agreement (8) is as follows:
| (3) |
where the expected index is the value expected in the case of independence between two typing methods. Assuming a maximum W of 1,
| (4) |
When W approaches 1, the correction for chance agreement, measured as the difference between W and AW, approaches 0. For smaller values of W, Wi may approach the value of W, resulting in stronger corrections and lower values of AW.
According to the expression
| (5) |
where SIDB is Simpson's index of diversity of the B classification (11), methods with lower diversity result in higher Wi values and, therefore, the difference between W and AW increases.
Considering the following properties for the variance of a variable X, where c is a constant,
| (a) |
| (b) |
an expression for the analytical confidence interval (CI) for AW can be deduced:
| (6) |
Assuming Wi(A→B)/(1 − Wi(A→B)) is constant, by property a,
| (7) |
Assuming Wi(A→B) is constant, by property b,
| (8) |
where Var(WA→B) is the variance of WA→B, calculated as described in reference 11.
For a 95% CI, assuming a Gaussian distribution, the limits are given by
| (9) |
The final expression for the CI is an approximation since it considers SIDB to be constant and assumes a Gaussian distribution for AW. Both assumptions were already used in the derivation of the Wallace CI (11), and their validity was assessed by simulation of the sampling process as described previously (13) (Fig. A1). Briefly, population frequency tables (PFTs) were generated according to the parameters R (representing the number of rows), C (representing the number of columns), alpha (determining the distribution of cluster sizes in the rows), and beta (determining the distribution of the elements in each row across columns). By following a multinomial distribution for the absolute frequencies of each PFT, 1,000 contingency tables representing samples of N elements from the infinite population were randomly generated.
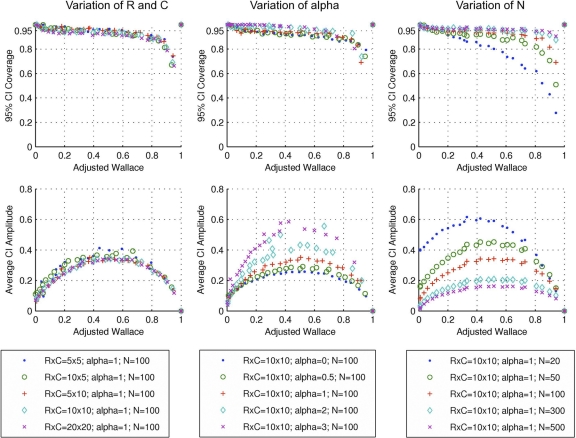
Fig. A1.
Coverage and average amplitude of 95% analytical confidence intervals for AW. Each dot represents a simulated population, with a particular set of parameters, and 1,000 samples taken from that population. Symbols and colors represent changes in the number of clusters (R × C) in each of the two classifications for the population (left panels), exponent alpha of a Zipfian distribution determining the distribution among clusters (middle panels), and sample size N (right panels).
The AW CI coverage is quite robust for changes in the number of clusters and the cluster size distribution (Fig. A1, first row). However, CI coverage is very sensitive to sample size (N), decreasing steeply for N of 20 and AW values higher than 0.2.
The amplitude of the CI also reflects the importance of the sample size for assessing the congruence between typing methods (Fig. A1, second row). As expected, smaller samples (N = 20) resulted in higher amplitudes and, therefore, greater uncertainty in the point estimate.
Footnotes
Published ahead of print on 14 September 2011.
REFERENCES
- 1. Albatineh A. N., Niewiadomska-Bugaj M., Mihalko D. 2006. On similarity indices and correction for chance agreement. J. Classif. 23:301–313 [Google Scholar]
- 2. Brolund A., et al. 2010. The DiversiLab system versus pulsed-field gel electrophoresis: characterisation of extended spectrum β-lactamase producing Escherichia coli and Klebsiella pneumoniae. J. Microbiol. Methods 83:224–230 [DOI] [PubMed] [Google Scholar]
- 3. Carriço J. A., et al. 2006. Illustration of a common framework for relating multiple typing methods by application to macrolide-resistant Streptococcus pyogenes. J. Clin. Microbiol. 44:2524–2532 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Chen L., et al. 2009. Multiplex real-time PCR for rapid staphylococcal cassette chromosome mec typing. J. Clin. Microbiol. 47:3692–3706 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Faria N. A., Carriço J. A., Oliveira D. C., Ramirez M., de Lencastre H. 2008. Analysis of typing methods for epidemiological surveillance of both methicillin-resistant and methicillin-susceptible Staphylococcus aureus strains. J. Clin. Microbiol. 46:136–144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Feil E. J., Li B. C., Aanensen D. M., Hanage W. P., Spratt B. G. 2004. eBURST: inferring patterns of evolutionary descent among clusters of related bacterial genotypes from multilocus sequence typing data. J. Bacteriol. 186:1518–1530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Friães A., Ramirez M., Melo-Cristino J. 2007. Nonoutbreak surveillance of group A streptococci causing invasive disease in Portugal identified internationally disseminated clones among members of a genetically heterogeneous population. J. Clin. Microbiol. 45:2044–2047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Hubert L., Arabie P. 1985. Comparing partitions. J. Classif. 2:193–218 [Google Scholar]
- 9. McLernon J., Costello E., Flynn O., Madigan G., Ryan F. 2010. Evaluation of mycobacterial interspersed repetitive-unit-variable-number tandem-repeat analysis and spoligotyping for genotyping of Mycobacterium bovis isolates and a comparison with restriction fragment length polymorphism typing. J. Clin. Microbiol. 48:4541–4545 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Mellmann A., et al. 2007. Based upon repeat pattern (BURP): an algorithm to characterize the long-term evolution of Staphylococcus aureus populations based on spa polymorphisms. BMC Microbiol. 7:98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Pinto F. R., Melo-Cristino J., Ramirez M. 2008. A confidence interval for the Wallace coefficient of concordance and its application to microbial typing methods. PLoS One 3:e3696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Rivero-Pérez B., Pérez-Roth E., Méndez-Alvarez S. 2010. Evaluation of multiple-locus variable-number tandem-repeat analysis for typing a polyclonal hospital-acquired methicillin-resistant Staphylococcus aureus population in an area where such infections are endemic. J. Clin. Microbiol. 48:2991–2994 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Severiano A., Carriço J. A., Robinson D. A., Ramirez M., Pinto F. R. 2011. Evaluation of jackknife and bootstrap for defining confidence intervals for pairwise agreement measures. PLoS One 6:e19539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Simpson E. H. 1949. Measurement of diversity. Nature 163:688 [Google Scholar]
- 15. Smyth D. S., Wong A., Robinson D. A. 2011. Cross-species spread of SCCmec IV subtypes in staphylococci. Infect. Genet. Evol. 11:446–453 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. van Belkum A., Struelens M., de Visser A., Verbrugh H., Tibayrenc M. 2001. Role of genomic typing in taxonomy, evolutionary genetics, and microbial epidemiology. Clin. Microbiol. Rev. 14:547–560 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. van Mansfeld R., et al. 2010. The population genetics of Pseudomonas aeruginosa isolates from different patient populations exhibits high-level host specificity. PLoS One 5:e13482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Versalovic J., et al. 1993. Penicillin-resistant Streptococcus pneumoniae strains recovered in Houston: identification and molecular characterization of multiple clones. J. Infect. Dis. 167:850–856 [DOI] [PubMed] [Google Scholar]