Support Vector Regression Scoring of Receptor-Ligand Complexes for Rank-Ordering and Virtual Screening of Chemical Libraries

Abstract

The Community Structure-Activity Resource (CSAR) datasets are used develop and test a Support Vector Machine-based scoring function in regression mode (SVR). Two scoring functions (SVR-KB and SVR-EP) are derived with the objective of reproducing the trend of the experimental binding affinities provided within the two CSAR datasets. The features used to train SVR-KB are knowledge-based pairwise potentials, while SVR-EP is based on physico-chemical properties. SVR-KB and SVR-EP were compared to seven other widely-used scoring functions, including Glide, X-score, GoldScore, ChemScore, Vina, Dock and PMF. Results showed that SVR-KB trained with features obtained from three-dimensional complexes of the PDBbind dataset outperformed all other scoring functions including best performing X-score, by nearly 0.1 using three correlation coefficients, namely Pearson, Spearman and Kendall. It was interesting that higher performance in rank-ordering did not translate into greater enrichment in virtual screening assessed using the 40 targets of the Directory of Useful Decoys (DUD). To remedy this situation, a variant of SVR-KB (SVR-KBD) was developed by following a target-specific tailoring strategy that we had previously employed to derive SVM-SP. SVR-KBD showed much higher enrichment outperforming all other scoring functions tested, and was comparable in performance to our previously-derived scoring function SVM-SP.

INTRODUCTION

A combination of faster computers, access to an ever increasing set of three-dimensional structures, and more robust computational methods has led to a constant stream of studies attempting to predict the affinity of ligands to their target. Today, it is established that one can reproduce experimental binding affinities with high fidelity, using methodologies such as free energy perturbation, thermodynamic integration, and other methods.^1–4 The implications of the accurate calculations of the free energy are profound in drug discovery, since the efficacy of a therapeutic is, after all, completely dictated by its binding profile in the human proteome. Unfortunately, the large computational resources required to accurately reproduce the free energy of binding has prevented the use of high-end methods in high-throughput screening efforts, where >10⁵ compounds are typically screened. To remedy this situation, investigators have resorted to approximations, known as scoring functions,^5,6 to rapidly estimate the binding affinity, or at least reproduce the trend of the binding affinity.

Early scoring functions were empirical in nature.⁷ In light of the approximations inherent to these models, their performance has been typically restricted to a subset of targets, often to those similar to members of the training set. However, given the large amount of binding affinity data that is currently available in various databases such as MOAD,⁸ PDBbind,⁹ BindingDB,¹⁰ PDBcal,¹¹ and others, it is now possible to create multiple distinct datasets to train and test the performance of scoring functions. Web portals, such as biodrugscreen (http://www.biodrugscreen.org), have also facilitated the process of deriving custom scoring functions using these databases. Performance of scoring functions is often measured using correlation metrics such as Pearson, but now more commonly Spearman and Kendall.¹² Over the years, correlations between measured and predicted scores have gradually ameliorated, but comparison among scoring functions has been challenging due to the lack of universal testing datasets. The (Community Structure-Activity Resources: http://www.csardock.org) CSAR effort seeks to remedy this situation, and we embrace this effort by employing the CSAR-SET1 and CSAR-SET2 sets to derive and test the performance of our support vector machine-based scoring functions.

While scoring functions that faithfully reproduce the experimental trend in the binding affinity are highly desirable, it remains unclear whether such functions will result in better enrichment in the virtual screening setting, given the inherent approximations involved in the process. Recently, we have developed a target-specific Support Vector Machine-based scoring method (SVM-SP) that consisted of training SVM models to distinguish between active and decoy molecules. It is worth mentioning that a number of studies had employed machine learning methods in virtual screening in the past.^13–15 But our scoring approach is a significant departure from these methods as the derivation of the scoring function is firmly rooted in three-dimensional structure of receptor-ligand complexes, in contrast to previous methods that used ligand-based features. More specifically, SVM-SP is trained on features that consisted of knowledge-based pair potentials obtained from high-resolution crystal structures for the positive set and a set decoy molecules bound to the target of interest for the negative set.¹⁶ In a comprehensive validation that included both computation and experiment, we found that SVM-SP exhibited significantly better enrichment when compared to other widely-used scoring functions, particularly among kinases.¹⁷ SVM-SP was put to the test by screening an in-house library of 1,200 compounds against kinase ATP-binding site. We were able to systematically identify inhibitors for three distinct kinases, namely the epidermal growth factor receptor (EGFR), calcium calmodulin-dependent protein kinase II (CaMKII), and more recently the (never in mitosis gene a)-related kinase 2 (NEK2).¹⁷

Here, since the primary objective is to reproduce a trend in the binding affinity, we follow a Support Vector Regression (SVR) approach, rather than a classifier route. As we have done previously, we train the Support Vector Machine algorithms using features from three-dimensional structures. We derive two different scoring functions. The first (SVR-KB) is trained on features consisting of pairwise potentials. The second scoring function (SVR-EP) is trained on physico-chemical properties computed from three-dimensional structures in the training set. Correlation of both scoring functions with experiment is assessed and compared with seven well-established scoring functions, among them X-score, Glide, and ChemScore. The correlation among scoring function is also evaluated to gain insight into the class of targets for which the scoring functions perform best. Finally, the scoring functions are tested in a virtual screening setting where their ability to enrich libraries—rather than show high correlation to experimental binding affinity—is assessed.

Materials and Methods

Datasets

The CSAR benchmark dataset (CSAR-SET1 and CSAR-SET2) consist of hundreds of protein-ligand crystal structures and binding affinities across multiple protein families (http://www.csardock.org/). Structures were curated to retain those with better than 2.5 Å resolution, and exhibit R_free and R_free − R values that are lower than 0.29 and 0.05, respectively. Structures with ligands covalently attached to proteins were not included by the creators of these datasets. In this release, a total of 343 structures were included (176 complexes for CSAR-SET1 and 167 complexes for CSAR-SET2). Structures in CSAR-SET1 were deposited to PDB between 2007 and 2008 while structures in CSAR-SET2 were deposited in 2006 or earlier according the CSAR Web site.

Knowledge-Based Potentials

The pairwise potentials were derived from crystal structures of protein-ligand complexes using Sybyl atom types. In this work, halogen atom types were only included for ligands and metals were only used for proteins. The complete list of atom types is provided in Table 1. The protein-ligand crystal structures were obtained from the latest version of sc-PDB database (release 2010),¹⁸ which contains 8,187 entries. The structures were filtered by resolution and R factor. Only those with resolution better than 2.5 Å and R factor less than 0.26 were retained. The structures were further clustered by protein sequence similarity and ligand structural similarity. A final set of 3,643 distinct and diverse crystal structures were used for pairwise potential derivation. The distance-dependent statistical potential μ̄(i,j,r) between atom types i and j is given by

$$\overline{\mu }(i,j,r)=\{\begin{array}{cc}\hfill -\mathit{\text{RT ln}}\frac{N_{\mathit{\text{obs}}}(i,j,r)}{N_{\mathit{\text{exp}}}(i,j,r)},& r<r_{\mathit{\text{cut}}}\\ \hfill 0,& r\ge r_{\mathit{\text{cut}}}\end{array}$$

where R is the ideal gas constant, T = 300 K, N_obs (i,j,r) is the number of (i, j) pairs within the distance shell r − Δr/2 to r + Δr/2 observed in the training dataset and N_exp (i,j,r) is the expected number of (i, j) pairs in the shell. r_cut = 12.0 Å was used in this study. The bin width Δr is 2.0 Å for r ≤ 2.0 Å, 0.5 for 2.0 < r ≤ 8.0, and 1 Å for r > 8.0 Å. A DFIRE reference state developed by Zhou and co-workers¹⁹ is used when calculating the number of N_exp (i,j,r). The atom type dependent potential P_i,j is given by

$$P_{\mathit{\text{ij}}}={\displaystyle \sum _r\overline{\mu }(i,j,r)}$$

In total, 146 pair potentials P_i,j were derived.

Table 1.

Atom Types Used to Derive Pair Potentials to train SVR-KB

Atom type	Location	Description	Atom type	Location	Description
C.3	P/L	C (sp3)	O.2	P/L	O (sp2) and S (sp2)
C.2	P/L	C (sp2)	O.co2	P/L	O (carboxylate & phosphate)
C.ar	P/L	C (aromatic)	P.3	P/L	P (sp3), S (sulfoxide & sulfone)
C.cat	P/L	C (guanidium)	S.3	P/L	S (sp3)
N.4	P/L	N (sp3)	Met	P	All metals
N.am	P/L	N (amide)	F	L	F
N.pl3	P/L	N (trigonal planar)	Cl	L	Cl
N.2	P/L	N (aromatic)	Br	L	Br and I
O.3	P/L	O (sp3)

In the SVR-KB model, only pair potentials P_i,j were used as the descriptors of a vector. When implementing this strategy, four scenarios were tested: 1-tier, 2-tier, 3-tier and short-range. In the case of short-range, only atom pairs less than 5 Å apart were considered. In the case of 1-tier, P_i,j was computed for atom types of (i, j) when r_ij ≤ r_cut = 12.0 Å. In the case of 2-tier, P_i,j was divided into $P_{i,j}^{\prime }\text{ and }{P}_{i,j}^{″}$, where $P_{i,j}^{\prime }\text{ and }{P}_{i,j}^{″}$ were the sum of potential for r_ij ≤ 5.0 and 5.0 < r_ij ≤ r_cut respectively. In the case of 3-tier, P_i,j was divided into $P_{i,j}^{\prime },P_{i,j}^{″}\text{ and }{P}_{i,j}^{‴}$, corresponding to the potential for r_ij ≤ 4.0, 4.0 < r_ij ≤ 7.0 and 7.0 < r_ij ≤ r_cut respectively. Following extensive testing we found that the 2-tier approach led to best performance, which was used to construct the SVR-KB models.

Descriptors

For descriptors other than knowledge-based potentials, we mainly used terms that were used for the derivation of the X-score scoring function (Table 2), namely: protein-ligand van der Waals interactions (VDW); hydrogen bonds (HB) formed between protein and ligand; hydrophobic effects; and ligand deformation upon binding. In addition, we added several other descriptors, such as ligand molecular weight, ratio of ligand buried solvent-accessible surface area (SASA) to unburied SASA, ratio of ligand buried polar SASA to ligand buried SASA (Table 2). The X-score program (version 1.2.1) was modified to obtain the descriptors.²⁰ Briefly, VDW was computed with Lennard-Jones 4–8 potentials and was equally weighted among all heavy atoms

$$\mathit{\text{VDW}}={\displaystyle \sum _{\mathit{\text{protein}}}{\displaystyle \sum _{\mathit{\text{ligand}}}{\left(\frac{r_m}{r_{ij}}\right)}^8-2{\left(\frac{r_m}{r_{ij}}\right)}^4}}$$

where r_m is the distance when the atomic potential reaches minimum and r_ij is the distance between two atom centers. The hydrogen atoms are not included in the calculation. Hydrogen bonds were calculated by taking into account both the distance and the relative orientation of the donor and the acceptor. The deformation effect is approximated with the number of rotatable bonds on the ligand. Hydrophobic effect represents tendency of non-polar atoms to segregate from water. The X-score program implements three algorithms to compute this effect: (i) Hydrophobic surface algorithm (HS), which corresponds to buried ligand hydrophobic solvent-accessible surface area; (ii) hydrophobic contact algorithm (HC), which is the sum of all hydrophobic atom pairs between protein and ligand; (iii) hydrophobic matching algorithm (HM), which takes into account the hydrophobicity of a micro environment surrounding each ligand atom. Solvent accessible surface area was calculated by summing the evenly-spaced mesh points on a surface using a probe radius of 1.5 Å.

Table 2.

Descriptors Used to Identify Components of SVR-EP

Descriptor	SVR Component	Description
1	Yes	Ligand molecular weight
2	Yes	van der Waals interaction energy
3	-	Hydrogen bond number between protein and ligand
4	-	Ligand rotatable bonds
5	-	Ligand unburied polar SASA in the complex
6	-	Ligand unburied nonpolar SASA in the complex
7	-	Total ligand SASA that is unburied in the complex
8	-	Ligand buried polar SASA in the complex
9	-	Ligand buried nonpolar SASA in the complex (hydrophobic effect computed with HP algorithm)
10	-	Total ligand SASA that is buried in the complex
11	-	Ratio of unburied SASA to buried SASA
12	Yes	Ratio of buried nonpolar SASA to buried SASA
13	Yes	Hydrophobic effect computed with HC algorithm
14	-	Hydrophobic effect computed with HM algorithm

Support Vector Regression (SVR)

Two SVR models were developed, SVR-KB and SVR-EP. SVR-KB model is derived using vectors consisting of knowledge-based pairwise potentials as we describe elsewhere.^16,17 To build SVR-EP model, a variable selection protocol was applied to the 14 empirical descriptors listed in Table 2. Simulated annealing showed that a subset of four descriptors that leads to best performance, namely ligand molecular weight (MW), van der Waals energy (VDW), hydrophobic effect computed with HC algorithm of X-score (HC), and ratio of ligand buried nonpolar SASA to buried SASA. Two of these descriptors, namely VDW and HC are also terms in the X-score scoring function. Target-specific SVR-KB models (termed as SVR-KBD) were built by adding into the training set the complexes of a specific target docked with some randomly picked lead-like compounds (decoys). The pKd values for those docked structures were set to zero. Preliminary test shows that including 500 decoys would yield good performance in virtual screening.

The PDBbind v2010 Refined Set and Core Set contain 2,061 and 231 entries respectively. The program of LIBSVM²¹ (version 3.0) was used for model training and prediction. The epsilon-SVR and radial basis function (RBF) kernel option has been used throughout this work. Grid search was conducted on some of the most important learning parameters, such as c (trade-off between training error and margin), g (γ, a parameter in kernel function) and p (ε, a parameter in loss function), to give the best performance in 5-fold cross validation. In each cross validation, 20 runs were performed on a random split basis and the quantity of average was recorded. The set of parameters (c = 5.0, g = 0.15, p = 0.3) for SVR-KB and (c = 5.0, g = 2.0, p = 0.3) for SVR-EP were used to train SVR models. To ensure that there is no overlap between PDBbind and the test sets CSAR-SET1 and CSAR-SET2, all overlapping structures (11 and 16 with CSAR-SET1 and CSAR, respectively) were removed from the training set.

Other Scoring Functions

The Glide score²² was computed with the Glide program in the Schrodinger Suite 2010. Complexes were allowed to relax using the Glide program and scored with SP option without docking. Vina scores²³ were computed with the program Autodock Vina (version 1.1.1). X-score was computed with the X-score program (version 1.2.1). We have used the consensus version of X-score, which is the arithmetic average of the three scoring functions implemented in X-score. ChemScore,^24,25 GoldScore,²⁶ Dock,²⁷ and PMF²⁸ were computed with the CScore module implemented in SYBYL-X (version 1.0).

Correlation and other Performance Metrics

In model parameterization and performance assessment, several metrics were used: Pearson’s correlation coefficient R_p, Spearman correlation coefficient ρ, Kendall tau τ, root mean squared error (RMSE) and residual standard error (RSE). Pearson correlation coefficient R_p is a measure of linear dependence between two variables. It was given by

$$R_p=\frac{{\displaystyle {\sum }_i(x_i-\overline{x})(y_i-\overline{y})}}{\sqrt{{\displaystyle {\sum }_i{(x_i-\overline{x})}^2·{\sum }_i{(y_i-\overline{y})}^2}}}$$

where x̄ and ȳ are the mean value for x_i and y_i respectively. The Spearman correlation coefficient ρ describes how well the association of two variables can be described by a monotonic function. It is given by

$$\rho =1-\frac{6{\displaystyle {\sum }_i{(x_i^{\prime }-y_i^{\prime })}^2}}{N(N^2-1)}$$

where $x_i^{\prime }\text{ and }{y}_i^{\prime }$ denote the ranks of x_i and y_i, N is the total number of x-y pairs. Kendall τ is a measure of rank correlations. It is given by

$$\tau =\frac{{\displaystyle {\sum }_{i<j}\mathit{\text{sign}}(x_j-x_i)·\mathit{\text{sign}}(y_j-y_i)}}{\frac{1}{2}N(N-1)}$$

when the values of x_i and y_i are unique. The median of unsigned error Emed is the median for a serial of absolute values for the error between predicted values and experimental values. The root mean squared error (RMSE) was used to assess the deviation of the predicted value from the experimental value

$$\mathit{\text{RMSE}}=\sqrt{\frac{1}{N}{\displaystyle \sum _i{(x_i-y_i)}^2}}$$

where x_i and y_i denote experimental value and predicted value respectively. However, RMSE cannot be used in our case since the scores generated are not binding affinities. In order to compare performance across different scoring functions and assess error between score and experimental value in a consistent manner, a linear model between experimental pK_d values and scores for each scoring function was constructed. The deviation of predicted values from pK_d were given by residual standard error computed by

$$\mathit{\text{RSE}}=\sqrt{\frac{1}{N-2}{\displaystyle \sum _i{(x_i-{\widehat{y}}_{\iota })}^2}}$$

where x_i is the experimental pK_d value and ŷ_ι is the fitted value from the linear model.

The 95% confidence interval was determined using bootstrap sampling. The bootstrap replicate was set to 5,000. The RMSE was computed by the LIBSVM program. All other analysis was done using packages in R (version 1.12.1).

Validation using DUD Dataset

The DUD dataset was used to assess the performance of SVM-SP in hybrid mode with SVR-KB and SVR-EP scoring functions. The complexes were obtained from our recently published study that described the SVM-SP scoring function in detail.¹⁷ ROC curves were constructed following the same procedures that were reported in the study.¹⁷

RESULTS AND DISCUSSION

SVR Methods in Rank-Ordering Complexes

We implement a Support Vector Machine in a regression mode (SVR) to derive scoring functions. The goal is to generate SVR models that will reproduce the trend observed in the experimental binding affinities. Two scoring functions emerged, namely SVR-KB and SVR-EP. The first was derived using knowledge-based pair potentials (SVR-KB) that were obtained as we have done previously.^16,17 The second scoring function (SVR-EP) consisted of physico-chemical descriptors as features that were used for the Support Vector regression analysis. Given the large number of possible descriptors that can be derived, simulated annealing was used to narrow the list of candidates to a smaller set of four terms (Table 2).

Performance of these scoring functions was evaluated using three correlation metrics, namely the square of Pearson’s correlation coefficient (R_p²), Spearman’s rho (ρ), and Kendall’s tau (τ). Pearson’s coefficient is the more traditional metric used to measure the correlation between observed and predicted affinities. Spearman’s rho is a non-parametric measure of the correlation between the ranked lists of the experimental binding affinities and the scores. It ranges between -1 and 1. A negative value corresponds to anti-correlation while a positive value suggests correlation between the variables. Kendall’s tau (τ) was also considered to assess rank-ordered correlation as suggested by Jain and Nicholls.¹² τ has the advantage of being more robust and can be more easily interpreted. It corresponds to the probability of having the same trend between two rank-ordered lists.

The PDBbind datasets (Refined and Core Sets), CSAR-SET1 and CSAR-SET2, were each used for training, while testing was done strictly on CSAR-SET1 and CSAR-SET2. We hasten to emphasize that training and testing were never performed on the same set. Regression statistics for each scoring function is provided in Table 3. Training on the smaller datasets (PDBbind Core Set, CSAR-SET1, and CSAR-SET2) produced the highest correlations especially for SVR-KB (R_p² = 0.96; ρ = 0.98; τ = 0.91) compared with SVR-EP (R_p² = 0.58; ρ = 0.78; τ = 0.59) when training was done on CSAR-SET1. For the substantially larger dataset PDBbind Refined Set, correlations remained high for SVR-KB (R_p² = 0.76; ρ = 0.88; τ = 0.72) and SVR-EP (R_p² = 0.37; ρ = 0.62; τ = 0.44).

Table 3.

Regression Statistics for SVR Scoring Functions

Model	Training set	$R_p^2$	ρ	τ	RMSE	Emed
SVR-KB	Refined Set	0.76	0.88	0.72	0.97	0.32
SVR-KB	Core Set	0.90	0.96	0.85	0.79	0.30
SVR-KB	CSAR-SET1	0.96	0.98	0.91	0.51	0.30
SVR-KB	CSAR-SET2	0.92	0.95	0.87	0.62	0.30
SVR-EP	Refined Set	0.37	0.62	0.44	1.56	1.03
SVR-EP	Core Set	0.44	0.65	0.47	1.69	1.14
SVR-EP	CSAR-SET1	0.58	0.78	0.59	1.49	0.86
SVR-EP	CSAR-SET2	0.58	0.76	0.57	1.42	0.89

The performance of the scoring functions was assessed by training and testing on different datasets. SVR-KB trained on PDBbind (Core and Refined Sets), CSAR-SET1 and CSAR-SET2 was tested on CSAR-SET1 and CSAR-SET2 (Table 4 and Fig. 1 and 2). Correlation with experimental binding affinities was highest when training was performed with PDBbind (Refined Set) and testing on CSAR-SET2 (R_p² = 0.67; ρ = 0.82; τ = 0.63). Training with the significantly smaller PDBbind (Core Set) resulted in a reduction of about 0.2 in all coefficients (R_p² = 0.48; ρ = 0.67; τ = 0.49) for CSAR-SET2. The reduction in performance was also see when SVR-KB was trained with CSAR-SET1 and tested on CSAR-SET2 (R_p² = 0.48; ρ = 0.69; τ = 0.51) and vice versa (R_p² = 0.42; ρ = 0.65; τ = 0.48). A similar trend is observed for SVR-EP, whereby training with PDBbind (Refined Set) resulted in highest predictive power (R_p² = 0.55; ρ = 0.76; τ = 0.57). Overall performance was lower when either scoring function is tested with CSAR-SET1.

Table 4.

Performance of SVR and other Scoring Functions

	Training	Test	Rp2	ρ	τ	RSE	Emed
SVR-KB	Refined set*	CSAR-SET2	0.67	0.82	0.63	1.25	0.83
SVR-KB	Refined set	CSAR-SET1	0.59	0.77	0.58	1.46	1.01
SVR-KB	Core set*	CSAR-SET2	0.48	0.67	0.49	1.57	1.05
SVR-KB	Core set	CSAR-SET1	0.44	0.65	0.46	1.71	1.19
SVR-KB	CSAR-SET1	CSAR-SET2	0.48	0.69	0.51	1.59	0.93
SVR-KB	CSAR-SET2	CSAR-SET1	0.42	0.65	0.48	1.74	1.15
SVR-EP	Refined set	CSAR-SET2	0.55	0.76	0.57	1.47	1.10
SVR-EP	Refined set	CSAR-SET1	0.50	0.72	0.53	1.62	1.10
SVR-EP	Core set	CSAR-SET2	0.48	0.69	0.50	1.57	1.09
SVR-EP	Core set	CSAR-SET1	0.42	0.65	0.47	1.74	1.16
SVR-EP	CSAR-SET1	CSAR-SET2	0.50	0.71	0.52	1.53	0.99
SVR-EP	CSAR-SET2	CSAR-SET1	0.50	0.73	0.53	1.61	1.12
X-score	-	CSAR-SET2	0.49	0.71	0.52	1.56	1.10
X-score	-	CSAR-SET1	0.38	0.64	0.46	1.79	1.14
Glide (SP)	-	CSAR-SET2	0.36	0.62	0.44	1.76	1.20
Glide (SP)	-	CSAR-SET1	0.31	0.54	0.39	1.90	1.43
Vina	-	CSAR-SET2	0.42	0.68	0.49	1.66	1.12
Vina	-	CSAR-SET1	0.35	0.59	0.42	1.86	1.25
ChemScore	-	CSAR-SET2	0.44	0.67	0.48	1.65	1.11
ChemScore	-	CSAR-SET1	0.38	0.63	0.45	1.79	1.23
GoldScore	-	CSAR-SET2	0.44	0.66	0.47	1.63	1.05
GoldScore	-	CSAR-SET1	0.24	0.49	0.34	1.99	1.45
Dock	-	CSAR-SET2	0.36	0.59	0.42	1.75	0.96
Dock	-	CSAR-SET1	0.14	0.36	0.25	2.13	1.59
PMF	-	CSAR-SET2	0.00	0.05	0.03	2.18	1.49
PMF	-	CSAR-SET1	0.00	0.01	0.00	2.29	1.55

^*PDBbind 2010

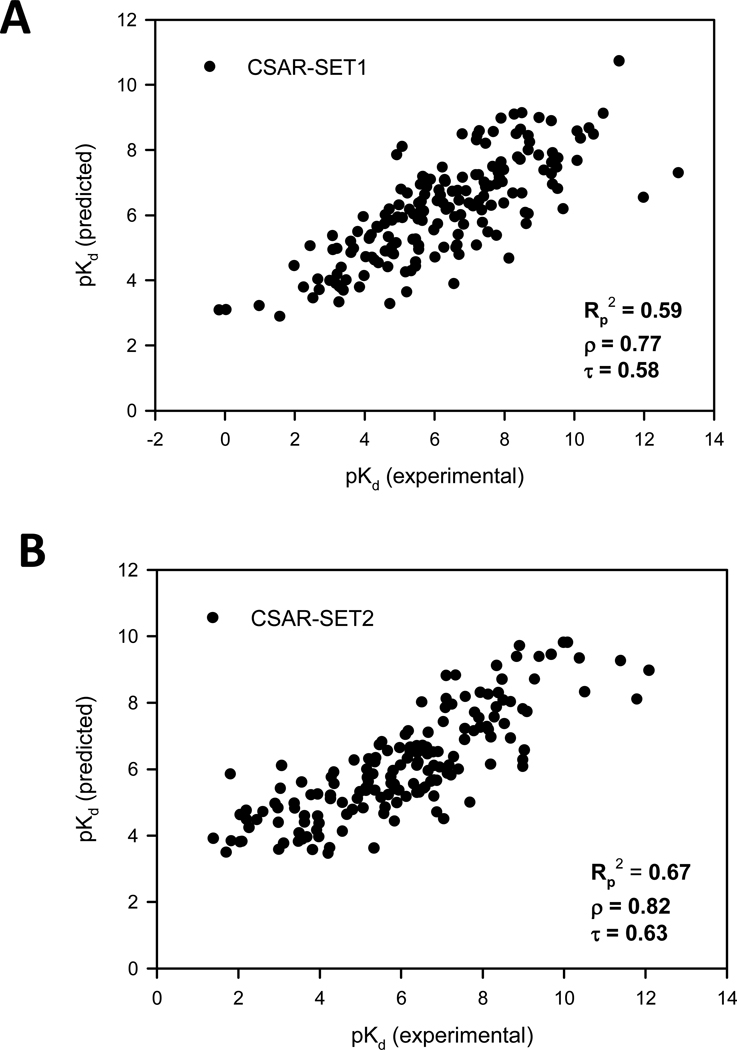
Figure 1.

The SVR-KB model prediction results when tested on (A) CSAR-SET1, and (B) CSAR-SET2.

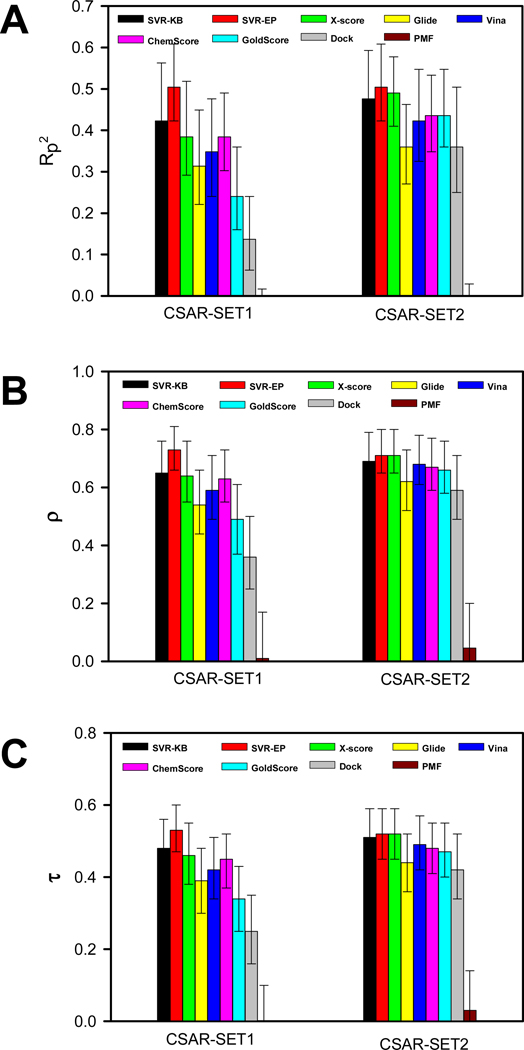
Figure 2.

Performance of scoring functions tested on CSAR-SET1 and CSAR-SET2 using (A) square of Pearson’s correlation coefficient; (B) Spearman’s ρ and; (C) Kendall’s τ correlation coefficients along with 95% confidence intervals for SVR and other scoring functions

Comparison of the SVR scoring functions to each other reveals that SVR-KB trained with PDBbind (Refined set) has the highest ability to reproduce the trend in the experimental binding affinities (Fig. 1). When testing on CSAR-SET1, SVR-KB outperforms SVR-EP by nearly 0.1 for R_p², and shows better correlation of the rank-ordered lists as evidenced by increases in both ρ and τ coefficients of nearly 0.05. Similar observations are made when SVR-KB and SVR-EP are tested on CSAR-SET2, with a larger difference for all coefficients at around 0.1. The differences between SVR-KB and SVR-EP are eliminated when the training is performed on a significantly smaller set, namely the PDBbind (Core set), CSAR-SET1, and CSAR-SET2. For example, SVR-KB trained on PDBbind (Core set) and tested on CSAR-SET2 led to correlation coefficients R_p² = 0.48, ρ = 0.67, τ = 0.49, and SVR-EP showed similar values R_p² = 0.48, ρ = 0.69, τ = 0.50.

The performance of SVR-KB and SVR-EP are compared to other widely-used scoring functions such as Glide, X-Score, Vina, ChemScore, GoldScore, PMF, and Dock (Table 4 and Fig. 1 and 2). Among the non-SVR scoring functions, rank-ordering was consistently higher when testing was done on CSAR-SET2 than CSAR-SET1. Among the SVR scoring functions, a similar trend was found. It is worth noting that while the magnitude of the individual correlations were different in CSAR-SET1 and CSAR-SET2, the relative performance of scoring functions, when compared to each other, was similar within these datasets.

Among the non-SVR scoring methods, X-score consistently showed the highest correlation with experimental binding affinities (R_p² = 0.49; ρ = 0.71; τ = 0.52) when the scoring function is tested with CSAR-SET2. The second best scoring function was ChemScore (R_p² = 0.44; ρ = 0.67; τ = 0.48), followed by GoldScore (R_p² = 0.44; ρ = 0.66; τ = 0.47), Vina (R_p² = 0.42; ρ = 0.68; τ = 0.49), Glide (R_p² = 0.36; ρ = 0.62; τ = 0.44), Dock (R_p² = 0.36; ρ = 0.59; τ = 0.42) and PMF (R_p² = 0; ρ = 0.05; τ = 0.03). PMF, the only knowledge-based potentials performed surprisingly poorly as evidenced by all three coefficients near 0. Another noteworthy observation was the performance of Glide, which was lower than X-score when using ρ and τ as measures.

We compared our SVR scoring functions to other scoring functions. The results show that SVR scoring outperforms all other scoring functions. SVR-KB trained with PDBbind (Refined Set) showed significantly better performance than all scoring functions (R_p² = 0.67; ρ = 0.82; τ = 0.63) when testing was done with CSAR-SET2. In fact, it outperformed the best non-SVR scoring functions, namely X-score, by nearly 0.2, 0.1, and 0.1 for R_p², ρ, and τ, respectively. This is highly encouraging as SVR-KB is a unique scoring function with components derived from knowledge-based pair potentials. SVR-EP, which is trained on physico-chemical descriptors, also results in good correlations, outperforming X-score but at a lower level than SVR-KB. Overall, the following trend in the performance is observed when testing with CSAR-SET2 and training with PDBbind Refined Set: SVR-KB > SVR-EP > X-Score > ChemScore ≥ GoldScore > Vina > Glide > Dock > PMF. For CSAR-SET1, the trend is the same despite the slightly lower correlation coefficients observed across all scoring functions. In sum, the data shows that SVR-KB has the highest performance among all scoring functions.

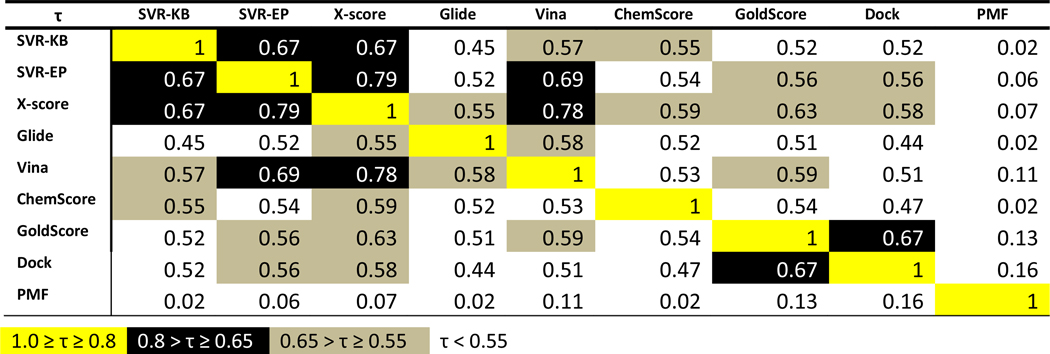
Probing Scoring Function Performance among Targets

While correlation coefficients provide insight into how faithfully the scoring functions reproduce the trends of the binding affinity, these numbers do not provide information about the individual targets or target class for which scoring functions perform best. To get insight into this, we compared the rankings of scoring functions to each other rather than to the experimental binding affinities. Kendall’s τ, which provides a probability that the scoring functions exhibit the same trends, was used for this purpose as reported in Fig. 3. The correlations coefficients are divided into four groups and color-coded according to these groups. Several scoring function exhibited strong correlations in their rankings as evidenced by a τ value greater than 0.65. For example, SVR-KB showed high correlation with SVR-EP (τ = 0.67), which was expected given that they are trained with the same set of structures, despite the completely different features that were used. SVR-KB and SVR-EP both shared a high correlation with X-score, but SVR-EP showed particularly high correlation to X-score, nearly 0.2 higher than SVR-KB (τ = 0.67). This can be attributed to the fact that SVR-EP is trained on X-score descriptors. SVR-EP also showed high correlation with Vina (τ = 0.69) in contrast to SVR-KB (τ = 0.57). X-score also showed remarkably high correlation with the Vina scoring function (τ = 0.78).

Figure 3.

Correlation between scores from scoring functions considered in this work using Kendal’s τ (testing was done with CSAR-SET2). Color-coding was used to highlight the level of correlation.

Performance of Scoring Function in Virtual Screening

Our SVR-based scoring functions have shown excellent performance in rank-ordering (Table 4 and Fig. 2). However, we wondered whether scoring functions that show excellent rank-ordering would result in better enrichment in virtual screening. To test this, we employ the Directory of Useful Decoys (DUD) validation set,²⁹ which provides actives and decoy molecules for nearly 40 targets. For every active, a total of 36 decoys are included. To assess the performance of a scoring function in enriching the DUD datasets, the receiver operating characteristic (ROC) plot is used.³⁰ These are constructed by ranking the docked complexes, and plotting the number of actives (true positives) versus the number of inactives (false positives). This process is repeated a number of times for a gradually increasing set of compounds selected from the ranked list. In an ROC plot, the farther away the curve is from the diagonal, the better the performance of the scoring function. The area under the ROC curve (ROC-AUC), can also be used as a representation of the performance of the scoring function. A perfect scoring function will result in an area under the curve of 1, while a random scoring function will have an ROC-AUC of 0.5.

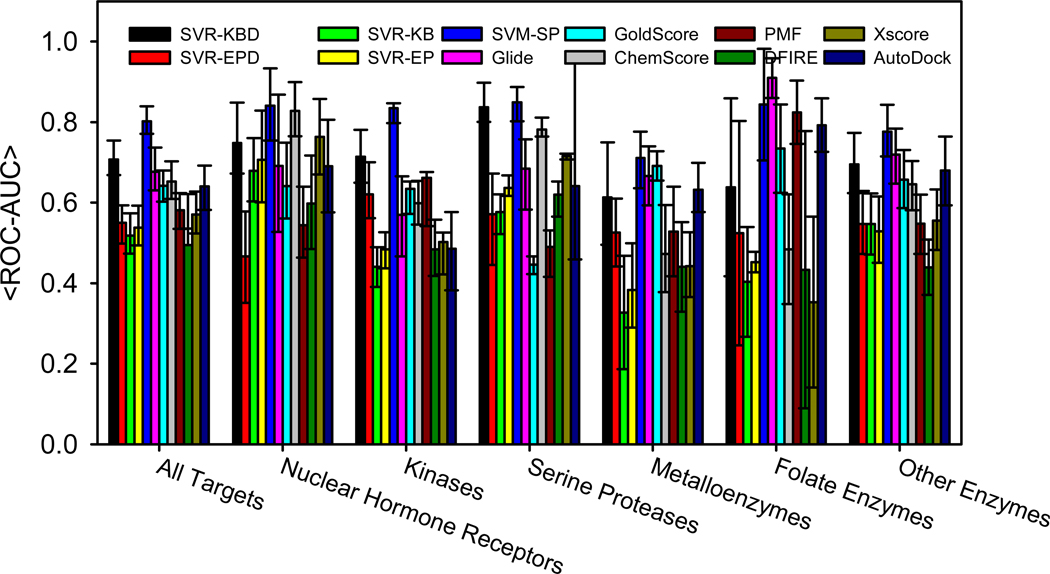
A plot of the mean ROC-AUCs (<ROC-AUCs>) over all 40 targets in DUD for all the scoring functions is shown in Fig. 4. We also include our previously derived SVM-SP scoring function as a reference. The data for the SVM-SP scoring function and all non-SVR scoring functions is obtained from a recent article, which also describes the SVM-SP scoring function in detail.¹⁷ When comparing SVR-EP and SVR-KB to other scoring functions, it was surprising that they showed lower performance despite their superior rank-ordering ability. In fact, Glide, which was ranked seventh among the ten scoring functions in rank-ordering, performed very well in virtual screening (Fig. 4). As observed previously, our SVM-SP remained by far the best performing scoring function, especially among kinases.

Figure 4.

Mean values for ROC-AUC scores from the 40 targets of the DUD validation set. Data for SVM-SP, ChemScore, GoldScore, Glide, PMF and DFIRE are taken from our recent published work.¹⁷

There are a number of reasons as to why SVR methods or X-score did not show high enrichment levels with the DUD datasets. One possibility is that the training of SVR was performed on high-quality crystal structures of receptor-ligand complexes while scoring in virtual screening is performed on docked structures that may or may not be the correct binding mode. To improve the performance of SVR-scoring methods in virtual screening, a similar strategy that was used to derive SVM-SP was followed. The success of SVM-SP was attributed to the fact that the scoring function was tailored to its target by including features obtained from complexes of decoy molecules docked to the target. Hence, the scoring function must be derived individually for each target. A similar strategy was used for SVR-KB. As shown in Table 5, the performance of the scoring function gradually improved with increasing number of decoys used in the training, eventually converging to <ROC-AUCs> = 0.71. We call this new scoring function SVR-KBD to reflect the inclusion of decoys in the training. While its performance did not exceed that of SVM-SP in virtual screening, SVR-KBD still showed higher enrichment than most scoring functions that were considered in this study.

Table 5.

ROC-AUC decoy size dependence for SVR-KB model tested on DUD targets in virtual screening

Number of Decoys	0	10	50	100	200	500	1000
SVR-KB	0.52	0.59	0.68	0.69	0.70	0.71	0.71