Correlation between P-wave Morphology and Origin of Atrial Focal Tachycardia – Insights from Realistic Models of the Human Atria and Torso

Abstract

Atrial arrhythmias resulting from abnormally rapid focal activity in the artia may be reflected in an altered P-wave morphology (PWM) in the ECG. Although clinically important, detailed relationships between PWM and origins of atrial focal excitations has not been established. To study such relationships, we developed computational models of the human atria and torso. The model simulation results were used to evaluate an extant clinical algorithm for locating the origin of atrial focal points from the ECG. The simulations showed that the algorithm was practical, and could predict the atrial focal locations with 85% accuracy. We proposed a further refinement of the algorithm to distinguish between focal locations within large atrial bundles.

I. INTRODUCTION

A trial arrhythmias, such as atrial fibrillation (AF), are characterized by rapid and irregular cardiac excitation waves, which is reflected in abnormal P-wave morphologies (PWM) in the electrocardiogram (ECG) [1]-[2]. Experimental evidence suggests that AF can result from reentrant excitation waves breaking up to form unsynchronized wavelets in the atria [2]. This may occur due to interactions of wavefronts originating from different regions within the atria. Thus, focal excitations originating from atrial regions other than the natural pacemaker site may predispose the development of AF. For successful treatment of AF by ablation procedures, it is crucial to locate the origins of atrial foci. However, due to the complexities of atrial anatomical structure and electrical heterogeneity, such focal origins are difficult to establish without using invasive diagnostic modalities.

The ECG is the most common non-invasive method for monitoring the activity of the heart by measuring the body surface potential (BSP) distribution. Correlations between the BSP and underlying electrical activity on the surface of the heart can be established by solving the inverse problem [3]. However, this method has some limitations, as it may not be able to locate the precise origins of atrial focal activity within the myocardium rather than on the heart surface. Besides, its implementation requires large multiple lead arrays (>200 leads) to map the BSP in detail not provided by the standard 12-lead ECG used in clinical studies.

Alternatively, computational models can be used to solve the forward problem in order to establish links between the origin of focal activity and the BSP. In this study, biophysically detailed computer models of the human atria and torso were developed to explore such links. The models were used to evaluate an existing clinical algorithm [1] for locating the origin of atrial excitation from the 12-lead ECG. A way of improving the algorithm was proposed in order to increase its predictive ability for focal origins within large atrial bundles.

II. METHODS

A. Heterogeneous 3D model of the human atria

The Courtemanche-Ramirez-Nattel (CRN) model [4] for the action potential (AP) of a human atrial myocyte was modified to incorporate electrical heterogeneity in the atria (Fig. 1A). Heterogeneity in the conductances of the transient outward current (I_to), L-type calcium current (I_CaL), and the rapidly activated potassium current (I_Kr) between cells of the crista terminalis (CT), atrial appendages (APG) and the atrio-ventricular ring (AVR) was based on experimental data from the canine right atrium (RA) [5]. Conductances of these ionic currents in the CRN model were respectively modified to produce AP morphologies for the CT, APG and AVR cells, as described previously [6], [7]. Briefly, in the standard CRN model [4], the conductances of I_to, I_CaL and I_Kr were 0.1652, 0.1294 and 0.0294 nS/pF, respectively. In the CT model, the conductance of I_to and I_CaL were set to 0.2115 and 0.2067 nS/pF. In the APG model, the conductance of I_to and I_CaL were set to 0.1123 and 0.1312 nS/pF. In the AVR model, the conductances of I_CaL and I_Kr were 0.0829 and 0.0449 nS/pF.

Fig. 1.

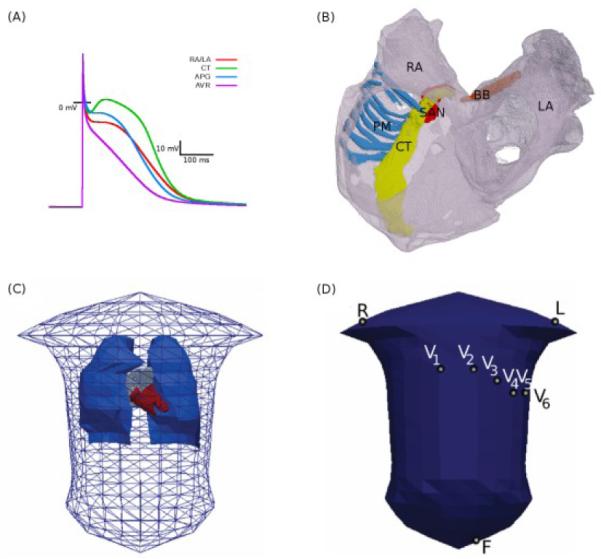
Model of the 3D human atria and torso. A: APs produced by the modified CRN equations for the atrial regions defined in the text. B: Atrial geometry extracted and segmented from the Visible Female dataset. Labeled are the RA and LA (grey), CT (yellow), PM (blue), BB (orange) and the assigned sinoatrial nodal region (SAN, red). C: Torso mesh with the lungs (blue) blood-masses of the atria (grey) and ventricles (red). D: elements selected as electrode placement locations for the derivation of P-waves in the 12-lead ECG. Some lead definitions: Lead II = F − R, Lead III = F − L, WCT = (R+L+F)/3, Lead V_1-6 = V_1-6 −WCT, Lead aVF = F − (R+L)/2.

The 3D anatomical structure of the human atria (Fig. 1B) was based on the Visible Female dataset with a spatial resolution of 0.33×0.33×0.33 mm³ [6]. The anatomical model was segmented into distinct regions of the RA, PM, CT, AVR, as well as the left atrium (LA) and Bachmann’s bundle (BB). A region at the superior CT was allocated as the sinoatrial node (SAN). Fibre orientation was manually introduced using the principal component analysis [6] for the major conduction pathways in the bundles of the CT, PM and BB.

The well-known monodomain partial differential equation equation [6]-[9] was used to describe the electrical excitation dynamics in the 3D tissue. It was solved using the finite difference approach based on the forward Euler method with a time step of 0.005 ms and a spatial step of 0.33 mm. The same time step was used to solve the respective ordinary differential equations describing the CRN single cell models.

B. Torso model and body surface potentials

The propagation of electrical activity from the myocardium of the atria to the surface of the body was simulated, and the forward problem was solved using the boundary element method (BEM), derived from Green’s theorem [8]-[10]. A previously created torso mesh model [11] with considerations of geometric representations for the lungs and the blood-masses of the atria and the ventricles (Fig. 1C) was used. The mesh consisted of 820 elements; note that increasing the mesh resolution to 13230 elements (~15-fold) resulted in a small convergence (~0.01%) of results simulated with the model. Conductivity in the torso was set to 0.2 S m⁻¹, whereas for the lungs and blood-masses it was 0.08 and 0.6 S m⁻¹ respectively [12]. The 3D atrial model was then positioned within the torso mesh using a recently published method [13]. First, the model was centered in the atrial co-ordinate system. Using the z-x-z co-ordinate convention for Euler angles acting on the heart the atrium was rotated by (315, 135, 310). Second, a translation of (−0.003, −0.075, −0.217) was applied to the atrium. Several triangular elements on the torso were selected as locations of the electrodes used in the standard 12-lead ECG (Fig. 1D), and P-waves were then derived from the BSP distributions.

C. Simulation of the P-wave morphology

An external current stimulus (2 nA during 2 ms to a region of ~5 mm³) was applied to the atrial model to initiate the AP excitation. To initiate sinus rhythm conduction, the stimulus was applied to the SAN region. To initiate ectopic foci, several well-known focal locations in the atria were selected as areas of interest: the superior and inferior CT (SCT and ICT), left and right pulmonary vein (LPV and RPV), left and right atrial appendage (LAA and RAA), and left septum (LS)/coronary sinus (CS). Various points within these locations, spread out around the vicinity of each location, were randomly selected as stimulation points to initiate excitation. Such selections enabled simulations of a variety of foci as seen clinically [1]. After the initiation, the APs were conducted through the whole atria. From the resultant excitation patterns, BSP distributions and P-waves were determined. The previously developed algorithm [1] was applied to predict the excitation origin from the P-waves, and the predicted origins were compared with the actual origins (tissue stimulation points). The algorithm was based on a simple decision tree illustrated in Fig. 2 along with the proposed improvement of the algorithm to resolve between excitations origins within the large RA bundle of the CT.

Fig. 2.

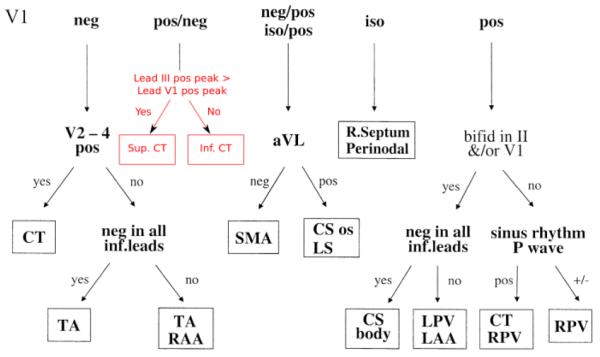
Illustration of the algorithm for locating the origin of focal atrial excitation from the 12-lead ECG [1]. The algorithm starts by considering the morphology of the P-wave in lead V₁ (positive, negative or isopotential), and then switching between other possible leads down the decision tree. After each switching to the next lead, P-wave morphology in this lead is considered and a new decision is made, such that the tree is continued until a focal location is defined. The block in red (which replaces a single location CT in the original figure) shows the proposed improvement to the algorithm in order to locate focal origins (superior or inferior) within the CT bundle.

In further test simulations, two areas of the atrium (the SAN and PV) were stimulated at various timings (simultaneously, and the PV stimulated 25, 50 and 75 ms before the SAN), and the resultant atrial activation patterns and BSP were studied.

III. RESULTS

A. Sinus rhythm conduction in the atria

Fig. 3A(i) shows the atrial activation pattern simulated by the 3D model under the sinus rhythm conditions. Excitation is initiated in the SAN region at the superior CT. It is then conducted rapidly down the CT and along the PM, through the fibres aligned along these bundles. The BB acts as the primary pathway for conduction between the two atria, with the first activation of the BB region at 26 ms. The total activation times for the RA and LA were 95 and 120 ms, respectively. These values were in good agreement with experimental data from human at body temperature [14], where the respective BB, RA and LA activation times were 31±13, 93±17 and 116±18 ms. Conduction velocities estimated from surface activation times were ~1.30 m s⁻¹ in the CT and 0.75 m s⁻¹ in the atrial wall, also in agreement with experimental data [15].

Fig. 3.

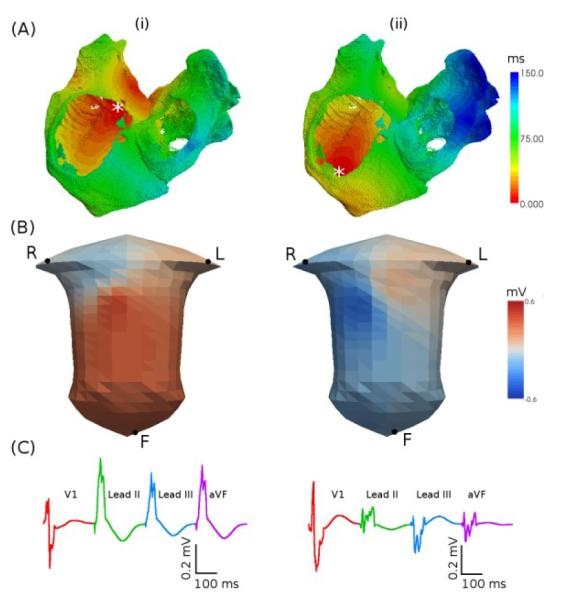
Activation patterns simulated with the human atrial and torso model. A: Activation times. B: BSP snapshots. C: P-waves. Two focal locations (indicated by an asterisk) are considered: superior (i) and inferior (ii) CT.

B. Simulated BSP and P-waves

Fig. 3B(i) shows a snapshot (50 ms after the initiation) of the BSP under the normal sinus rhythm conditions. The atrial conduction from the superior to inferior CT results in a BSP wave which propagates down towards the left leg, leaving a large positive region in the lower left torso and a negative region over the right shoulder. Such a BSP distribution is in agreement with experimental data [16]. Computed P-waves from some leads of the 12-lead ECG are shown in Fig. 3C (i). The P-wave is upright in the inferior limb leads (Leads II, III and aVF) due to the superior-inferior conduction in the atria.

C. Ectopic foci conduction

Study of the P-waves produced by excitation originating from different locations along the CT shows that PWM is dependent on the precise foci location within this long bundle. When excitation is initiated near the superior CT (Fig. 3A(i)), a positive P-wave is seen in leads II and III (Fig. 3C(i)) - but when excitation is initiated at the inferior CT (Fig. 3A(ii)), the P-wave in leads II and III is inverted (Fig. 3C(ii)). The latter is due to the effect of the inferior-superior atrial conduction on the BSP distribution (Fig. 3B(ii)). Such an inversion can be quantified by comparing the amplitude of the positive peak in lead V₁ with the peak amplitude in lead III. Thus, if peak in lead III is positive with the amplitude greater than that in V₁, excitation was initiated in the superior CT – the larger the difference, the more superior the excitation. If peak in lead III is negative, or has a smaller amplitude than the positive peak of V₁, then the excitation origin is in the inferior CT.

D. Focal origin prediction algorithm

As illustrated in Fig. 3, P-waves produced due to atrial excitations originating from different “ectopic foci” locations demonstrate markedly different PWM. Table 1 summarizes results of analyzing the P-waves due to various atrial focal excitations (section II-C) with the algorithm shown in Fig. 2. The algorithm correctly predicted the location of excitation origins in 59 of 77 simulations. Averaging the success ratio for each location gave the accuracy of the algorithm of 78%. One of the major inaccuracies of the algorithm was in determining the left and right PV. However, if these are considered simply as PV, the algorithm predicted the correct excitation origin in 68 out of 77 simulations, with an averaged accuracy of 85%.

Table 1.

Results of applying the clinical algorithm by Kistler et al. [1] to the simulated P-waves. N values refer to the number of simulations associated with each location. Numbers in brackets in the second column refer to the number of times the specified origin was predicted by the algorithm.

Location	Predicted Origins	Accuracy
LPV (N = 18)	LPV/LAA (15), RPV (2), CT (1)	83%
RPV (N = 16)	RPV (9), LPV/LAA (7)	56%
PV (N = 34)	RPV (11), LPV/LAA (22), CT (1)	97%
LAA (N = 13)	LPV/LAA (10), CS (3)	77%
RAA (N = 11)	RA/RAA (8), CT (3)	73%
CT (N = 9)	CT (9)	100%
LS/CS (N = 10)	CS/LS (8), SMA (2)	80%

Note that the original algorithm [1] considers the CT as a single location, which results in 100% accuracy in determining the focal origins in this long bundle (Table 1). The proposed improvement of the algorithm (Fig. 2 and section III-C) enabled determining various focal locations along the CT without affecting the overall accuracy of the algorithm.

IV. DISCUSSION

A. Model of the human atria

A realistic 3D model of the human atria which incorporates cell heterogeneity and fibre anisotropy has been developed.

Limitations of the model are either inherited from the single cell model used (previously discussed in [4]), or due to a lack of experimental data for human (cell heterogeneity and tissue anisotropy are based on animal data [6], [7]). However, the model reproduces conduction velocities and overall atrial activation patterns seen in experiments [14], as well as PWMs seen in clinical recordings [16]. Note that experimental data [14] were taken from patients with previous AF - however, the model was primarily designed for studies of arrhythmic atria.

Note also that we ran test simulations with resolution of the model increased to 0.25×0.25×0.25 mm³. These simulations produced activation patterns qualitatively similar to those obtained with the original resolution of 0.33×0.33×0.33 mm³, with a small convergence (~3%) in the conduction velocities.

B. Torso model and BSP

The 3D model of the atria was incorporated into a torso model to simulate the BSP. The BSP patterns and resultant PWMs were in agreement with experimental data [1], [16]. Note that the model is also capable of producing complex PWMs associated with AF [7] . Note also that computed P-waves in some leads had ‘notched’ morphologies, as opposed to smoother P-waves seen in clinical records. This may be due to the simplified torso geometry and omission of several inhomogeneities within the torso. Inclusion of such structures as the skeletal muscle (which is electrically excitable) may contribute to a smoothing of the P-waves produced. However, this would require the use of a finite element method (FEM), which is more computationally costly than BEM [3], [9], [12].

C. Multi-focal excitations

Simulations presented in this work consider only atrial electrical excitations from a single focus, whereas complex excitations during AF may originate from multiple foci [2]. Our test simulations showed that in the case of two foci in the SAN and PV, the resultant P-wave was clearly distinct from P-waves in either of the SAN or PV only cases when the PV was stimulated 50 ms before the SAN. With any other timing tested (0, 25 or 75 ms), the wavefront initiated in one of the regions overrides the wavefront initiated in the other. Primarily, the “overridden” wavefront may propagate for a short time, but this time is not sufficient for it to produce a significant effect on the BSP and the resultant P-wave. These simulations point out a limitation of using PWM for the monitoring of AF.

However, in the simulations of multi-focal excitation in both the SAN and PV, the algorithm [1] correctly identified the ectopic focal point in the PV – despite the obscuring presence of the normal excitation wave from the SAN. This gives validation of the algorithm itself, as well as the model.

D. Algorithm for locating focal origin

The accuracy of an existing algorithm for locating the origin of focal atrial excitation from the 12-lead ECG was evaluated. With the simulation results, an average of 85% of prediction accuracy was achieved, close to 93% reported previously [1]. Such a discrepancy may be due to either limitations of the model, or the algorithm. Notched P-waves seen in simulations and discussed above make some of the P-waves appear bifid even in the sinus rhythm conditions. In this case, the algorithm is less effective, as it can distinguish between focal origins in the left and right PV only based on bifidity in lead II or V₁.

The algorithm [1] has been improved to distinguish between various focal origins within the long bundle of the CT. This may have important implications, as clinically observed shifts of the leading pacemaker site along the CT have been linked to arrhythmic conditions [17]. The proposed improvement can help primarily to monitor such pacemaker shifts from ECG.