Opioid-Induced Quantal Slowing Reveals Dual Networks for Respiratory Rhythm Generation

Summary

Current consensus holds that a single medullary network generates respiratory rhythm in mammals. Pre-Bötzinger Complex inspiratory (I) neurons, isolated in transverse slices, and preinspiratory (pre-I) neurons, found only in more intact en bloc preparations and in vivo, are each proposed as necessary for rhythm generation. Opioids slow I, but not pre-I, neuronal burst periods. In slices, opioids gradually lengthened respiratory periods, whereas in more intact preparations, periods jumped nondeterministically to integer multiples of the control period (quantal slowing). These findings suggest that opioid-induced quantal slowing results from transmission failure of rhythmic drive from pre-I neurons to preBötC I networks, depressed below threshold for spontaneous rhythmic activity. Thus, both I (in the slice), and pre-I neurons are sufficient for respiratory rhythmogenesis.

Introduction

Two distinct neural networks in the ventrolateral medulla are separately proposed to be the essential substrate for respiratory rhythm generation (Onimaru et al., 1997; Rekling and Feldman, 1998): (i) I neurons in the pre-Bötzinger Complex (preBötC) (Gray et al., 2001; Smith et al., 1991) and (ii) pre-I neurons within and rostral to the preBötC (Onimaru et al., 1995). In neonatal rodent transverse medullary slices that isolate the preBötC and require elevated [K⁺]_o to generate a respiratory-related rhythm, neurons with pre-I firing pattern (Smith et al., 1991) have not been described, either because they are scarce, because their pattern of activity is transformed by removal of synaptic inputs, or because elevated [K⁺]_o disrupts their activity. The more inclusive en bloc brainstem-spinal cord preparation, which generates an essentially identical rhythm at normal (3 mM) [K⁺]_o (Smith and Feldman, 1987; Suzue, 1984), has both preBötC and pre-I networks. The connectivity and synaptic interactions between these populations have been inferred (Ballanyi et al., 1999; Mellen and Feldman, 2001), but the functional significance of their interactions has remained unresolved.

Opiates slow I neuron, but have no effect on pre-I neuron, burst period (Takeda et al., 2001). We exploited this differential sensitivity to test the roles of these populations in rhythm generation. If both the I and pre-I networks are rhythmogenic, then the effects of opioids on slowing respiratory period should differ between transverse slice and en bloc preparations. Inspiratory burst timing should be dominated by I neurons in transverse slices, whereas burst timing should depend on the interaction of I and pre-I neurons in en bloc preparations.

Results

Continuous Slowing in Slices

Consistent with earlier observations (Gray et al., 1999), in the transverse slice at 9 mM [K⁺]_o, respiratory period gradually slowed following bath application of the μ-opiate agonist DAMGO (200–300 nM; n = 5) (Figure 1A) and returned to control values following bath application of the μ-opiate antagonist naloxone (10 μM; data not shown). In normalized period histograms (Figure 1A, right), the graded nature of the opioid-induced slowing is apparent as a long tail to the right of the peak associated with control periods. Matching results were obtained in slices from P6 rats (n = 3, data not shown).

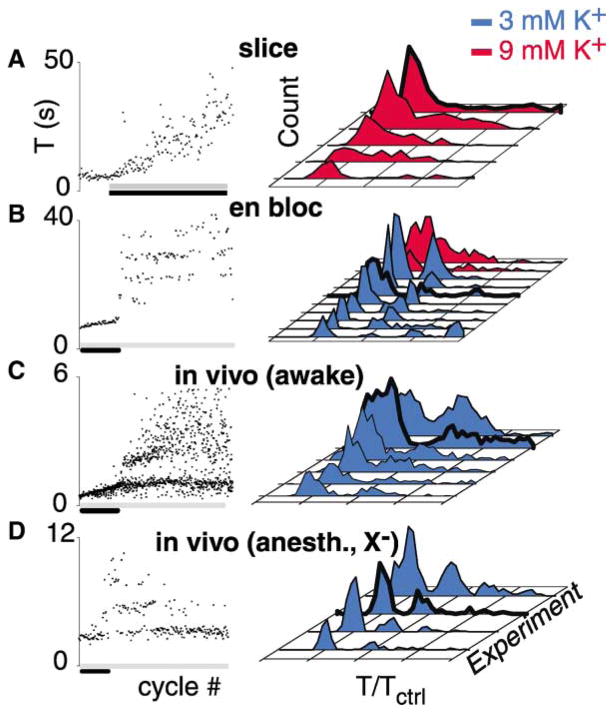
Figure 1. Opioid-Induced Quantal Slowing Is Seen En Bloc and In Vivo but Not in the Slice.

Bath application μ-opiate receptor agonists (gray bars, left) slows respiratory period (T) in the transverse slice, the en bloc preparation, the awake juvenile rat, and the anesthetized, vagotomized (anesth., X⁻) juvenile rat. Left: raster plot of respiratory periods.

(A) Continuous slowing (black bar) in transverse slice.

(B–D) After initial continuous slowing (black bars), quantal slowing is apparent in the en bloc preparation and in vivo (C and D). Number of cycles: (A), 180; (B), 200; (C), 900; (D), 250. Right: histograms of normalized periods from individual preparations (T/T_ctrl) show continuous slowing in slices (A) and quantal slowing in the en bloc preparation (B) and in awake intact (C) and anaesthetized vagotomized juvenile rats (D), apparent as peaks at integer multiples of the control period. At elevated [K⁺]_o (9 mM), opiate-induced slowing of respiratory period gives rise to continuously distributed periods en bloc ([B], red histograms). Heavy lines indicate histograms of experiments shown in left panels.

Quantal Slowing En Bloc and In Vivo

In the en bloc preparation (n = 8), bath-applied DAMGO (200–400 nM) initially caused a graded slowing of respiratory period over 20–40 cycles (Figure 1B, left, black bar). This abruptly gave way to quantal, i.e., step-like, slowing of respiratory period. In normalized period histograms, this quantal slowing is apparent as separate peaks at integer multiples of the control period (Figure 1B, right, blue histograms; Figure 3B). When this protocol was repeated with [K⁺]_o elevated to concentrations matching the transverse slice (9 mM), periods were distributed continuously (Figure 1B, right, red histograms), and respiratory rhythm persisted at DAMGO concentrations (>400 nM) that completely blocked respiratory rhythm at standard en bloc [K⁺]_o (3 mM).

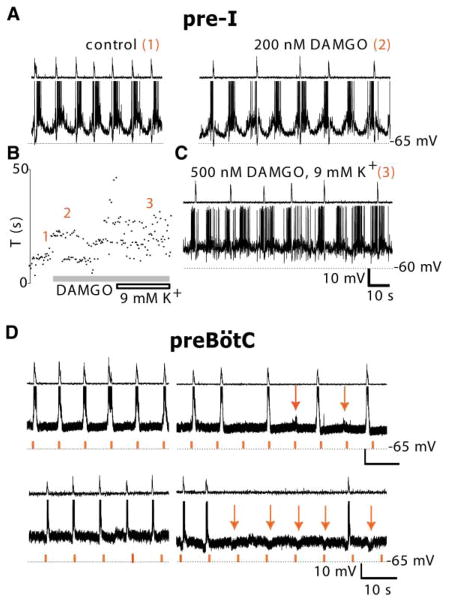
Figure 3. Opioids Modulate PreBötC, but Not Pre-I Neurons.

(A) Pre-I neurons were unaffected by DAMGO. Pre-I neuron (bottom trace) burst period and C3 ventral root activity (top trace) before ([A], left; epoch “1” in [B]) and during DAMGO-induced (200 nM; gray bar) quantal slowing ([A], right; epoch “2” in [B]) was unchanged.

(B) Raster plot of respiratory periods before (epoch 1) and after application of DAMGO (epochs 2 and 3).

(C) When [K⁺]_o was elevated to 9 mM, and DAMGO was increased to 500 nM (gray bar in [B]), pre-I period became irregular and motor output less tightly phase locked to pre-I firing (epoch “3” in [B]). (D) preBötC inspiratory neurons receive phasic drive during quantal slowing. Inspiratory neurons (middle trace) and C3 ventral root activity (top trace) before (left) and after DAMGO-induced quantal slowing (right) remained phase locked to motor output. During quantal slowing, phasic excitatory (top right) or inhibitory (bottom right) drive at control frequency (red tick marks in bottom trace) was apparent (red arrows); this phasic drive was never seen in the motor output.

If quantal slowing is an intrinsic property of the respiratory oscillator rather than an artifact of in vitro conditions, a similar response should be inducible in vivo. We tested this by systemic administration of the selective μ-opiate receptor agonist fentanyl citrate (Chen et al., 1996) to otherwise intact, unanesthetized juvenile rats (P5–P7). Low-order quantal slowing with a high variability of respiratory period was observed (Figure 1C, n = 6), with more pronounced initial continuous slowing compared to that seen in vitro. We speculated that this response was more dispersed than that seen en bloc due to both sensory feedback from the lungs (Bruce, 1996) and the effects of wakefulness. This was borne out by the more clearly observable opioid-induced quantal slowing obtained in anesthetized, vagotomized juvenile rats (P5–P7), (Figure 1D, n = 4).

Constraints on Quantal Slowing Mechanisms

Both the pre-I and preBötC networks are rhythmically active in the en bloc preparation; thus quantal slowing likely arises out of the mutual coupling of these two oscillatory networks. A common feature of multiperiodic dynamics of individual oscillatory networks (Del Negro et al., 2002; Hokkanen, 2000), or those arising out of interactions between mutually coupled oscillatory networks (Niizeki et al., 1993), is that transitions between periods are deterministic, i.e., the present period is determined by prior periods. If the strength of the bidirectional coupling varies stochastically, or if one of the networks merely follows the other, so that skips result from stochastic transmission failure, then the transitions between periods will appear random. Thus, in order to impose constraints on mechanisms for quantal slowing, we investigated whether transitions between long and short periods had temporal structure. We compared each period to preceding and subsequent periods (up to lag ± 7) to obtain the serial correlation coefficient (Perkel et al., 1967). The statistical significance of these coefficients was tested against surrogate serial correlation coefficients computed from shuffled periods (Figure 2, left). Statistically significant correlations during opioid-induced slowing of respiratory period were a consistent feature of awake in vivo preparations only (4/5; Figure 2D, left). None of the transverse slice or anaesthetized vagotomized preparations, and only 3/8 of the en bloc preparations, had statistically significant correlations. We also used Poincaré maps of successive periods, i.e., T_(n) versus T_(n+1) (Figure 2, right), to detect deterministic transitions between periods that would be missed by the serial correlation method, such as chaos (Garfinkel et al., 1992; Nayfeh and Balachandran, 1995). During continuous slowing in transverse slices, periods were distributed without pattern (Figure 2A, right), while during quantal slowing from en bloc and in vivo experiments, tight clustering of intervals at integer multiples of baseline period and with relatively even densities was apparent (Figures 2B–2D, right). Thus, by the methods used here, we failed to detect deterministic structure in the transitions between periods during quantal slowing in vitro or in anaesthetized deafferented rats. Two mechanisms are consistent with these findings: noisy mutual coupling between two oscillators (Schulte-Frohlinde et al., 2001), and random transmission failure of rhythmic drive arising from an oscillatory network unmodulated by opioids.

Figure 2. In Deafferented Preparations, Transitions between Slowed Cycles Are Nondeterministic.

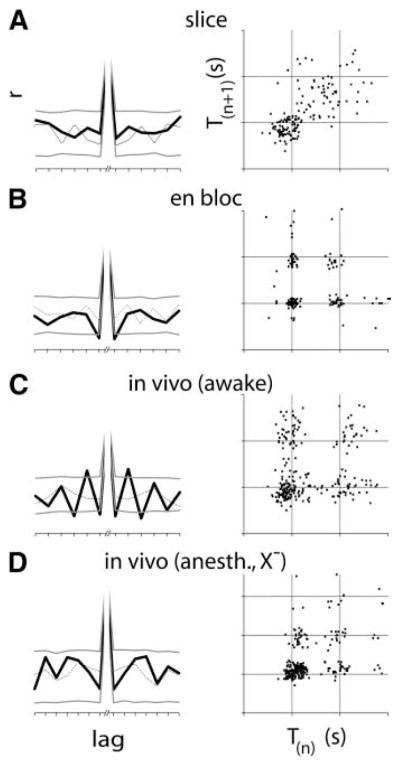
Left: during opioid-induced slowing, serial correlations of periods were consistently significant (4/5) in awake rats only (C). In the transverse slice (A) and the anesthetized vagotomized juvenile rat (D), no significant serial correlations were seen, while 3/8 en bloc preparations (B) produced significant serial correlations. Serial correlation coefficients of sequential periods (heavy black lines) are statistically significant when they fall above or below the 95th percentile of correlation coefficients obtained from shuffled periods (heavy gray lines). Correlation coefficients from one of the 1000 shuffled data sets are shown (fine line). Right: Poincaré maps of period (T_(n)) versus subsequent period (T_(n+1)) for transverse slices formed diffuse clouds away from the cluster at control period (A). In the en bloc preparation (B), in awake intact (C) and anaesthetized vagotomized (D) juveniles in vivo, periods were clustered at integer multiples of the control period with relatively even densities. Thus, while periods were tightly controlled during quantal slowing, transitions between periods were not.

PreBötC I Neurons Receive Subthreshold Drive during Skipped Cycles

To establish a cellular basis for quantal slowing, we recorded from pre-I (n = 4) and preBoötC inspiratory (n = 9), including type 1 (n = 2), neurons in en bloc preparations before and during quantal slowing. Pre-I neuronal firing, phase locked to firing motor output in control conditions (Figure 3A, left), remained phase locked during quantal slowing (Figure 3A, right). In addition, we tested whether at 9 mM [K⁺]_o pre-I activity was altered. During the transformation from quantal to continuous slowing following [K⁺]_o elevation from 3 to 9 mM (Figures 3B and 3C), pre-I rhythm became more variable and increasingly uncoupled from motor output (Figure 3C). The finding that pre-I neuron rhythm is stable and remains phase locked to motor output before and during quantal slowing, but not during continuous slowing, is consistent with the hypothesis that pre-I neuron activity determines inspiratory burst timing during quantal slowing. The finding that at 9 mM [K⁺]_o pre-I rhythm became irregular, and phase relations between pre-I bursts and motor output were disrupted, indicates that at [K⁺]_o standard in the transverse slice, if pre-I neurons are present, they are functionally uncoupled from preBötC I neuron networks.

If pre-I neurons determine inspiratory burst timing, then phasic drive to preBötC I neurons at control frequency should be observed during quantal slowing. In preBötC I neurons (n = 4/9), periodic subthreshold excitatory (Figure 3D, top) or inhibitory (Figure 3D, bottom) polarizations at close to control frequency were apparent during quantal slowing. This is consistent with the hypothesis that pre-I neurons provide phasic drive to preBötC I neurons.

Discussion

Over the past decade, a consensus has emerged that neurons responsible for respiratory rhythm generation are confined to the rostral ventrolateral medulla. Two mutually exclusive hypotheses regarding the essential constituents of these rhythmogenic networks have been proposed. We considered here the role of the two candidate populations: preBötC I neurons, sufficient to generate respiratory rhythm in the transverse slice, and more rostrally distributed pre-I neurons, each proposed as the essential substrate for respiratory rhythm generation (Gray et al., 1999; Koshiya and Smith, 1999; Onimaru et al., 1997; Rekling and Feldman, 1998; Smith et al., 1991). Opioids depress putative rhythmogenic subtypes of pre-BötC I neurons and slow the bursting frequency of all I neurons (Gray et al., 1999), but have no effect on pre-I rhythm (Takeda et al., 2001). If preBötC I neurons are both necessary and sufficient for respiratory rhythm generation, then the effect of opioids at concentrations sufficient to slow but not stop respiratory rhythm should be the same in preparations with or without pre-I neurons. Conversely, if pre-I neurons are sufficient for respiratory rhythm generation, then in networks retaining pre-I neurons, the effects of opiates on respiratory rhythm should follow pre-I rhythm. In the transverse slice, opioids lengthened respiratory periods continuously; in the en bloc preparation, in anesthetized, vagotomized juvenile rats, and to a lesser extent in intact, awake juvenile rats, respiratory periods were distributed at integer multiples of the control period.

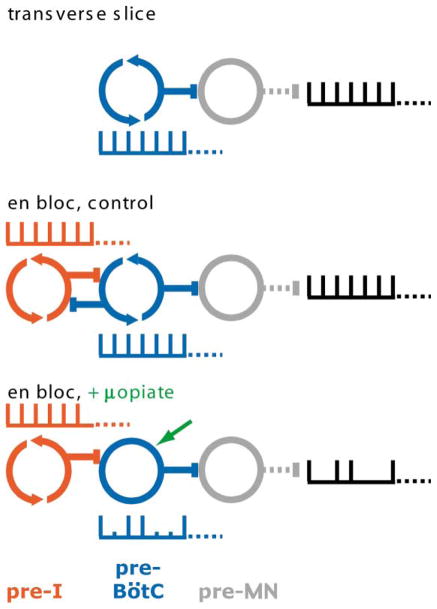
We propose that quantal slowing is due to differential effects of opioids on preBötC I neurons and pre-I neurons, which interact to generate respiratory rhythm (Figure 4). The preBötC I neuron network, with oligosynaptic projections to motoneurons, is sufficient to generate inspiratory-related motor output in the transverse slice (Figure 4, top) and includes rhythmogenic (Rekling et al., 1996), opiate-sensitive (Gray et al., 1999) type 1 neurons. In slices, opioids reduce their excitability, causing respiratory rhythm to gradually slow and at higher concentrations stop. The rhythmogenic (Onimaru et al., 1995), opiate-insensitive (Takeda et al., 2001), more rostrally located pre-I neurons are bidirectionally coupled to preBötC inspiratory neurons in the en bloc preparation (Ballanyi et al., 1999; Mellen and Feldman, 2001) and in vivo. The observation of subthreshold phasic drive to preBötC inspiratory neurons (Figure 3B), together with the clustering of periods at integer multiples of baseline period (Figures 1B–1D and 2, right) and the absence of determinism in transitions between long and short periods (Figure 2, left) suggest that opioid-induced quantal slowing results from transmission failure of periodic drive from unaffected pre-I neurons to depressed preBötC networks (Figure 4, bottom), in a manner analogous to type 2 atrioventricular block in the heart (Surawicz et al., 1978), although noisy mutual coupling between rhythmically active preBötC and pre-I networks cannot be ruled out.

Figure 4. A Dual Oscillator Model for Respiratory Rhythm Generation.

Top: in the transverse slice, rhythm is determined by opiate-sensitive rhythmogenic preBötC networks only (blue), which drive premotor neurons (gray). μ-opiate agonists hyperpolarize preBötC rhythmogenic neurons, decreasing their excitability and gradually slowing the rhythm. Middle: in the en bloc preparation, endogenously rhythmic preBötC and pre-I networks (red) interact. Differential distribution of modulatory inputs onto these distinct networks (Gray et al., 1999; Mellen and Feldman, 2000; Onimaru et al., 1998; Takeda et al., 2001) allows respiratory rhythm to be labile to modulatory inputs. Bottom: in vitro in 3 mM [K⁺]_o but not 9 mM [K⁺]_o or in vivo, μ-opiate agonists suppress the autorhythmicity and lower the excitability of preBötC networks but do not affect opiate-insensitive autorhythmic pre-I networks. Respiratory rhythm persists but with skipped beats because ongoing phasic excitatory drive from opiate-insensitive pre-I networks sometimes fails to cause the depressed preBötC neurons to fire as a population, i.e., transmission failure. This is apparent as the subthreshold, but not bursting, activity during skipped beats in these neurons (Figure 3D). Autorhythmic networks, circling arrows; driven networks, open circles.

Our findings indicate that two rhythmically active networks interact to generate respiratory rhythm and that under different conditions, each is sufficient to generate that rhythm. This finding has methodological consequences: a generally accepted heuristic used to distinguish between the kernel of neurons that generate the rhythm and relay neurons that have a matching pattern of activity is that neurons unaffected by experimental manipulations that change the rhythm are nonrhythmogenic. Here, however, opiate insensitive pre-I neurons appear to determine inspiratory burst timing during opiate-induced slowing of respiratory frequency en bloc and in vivo.

This organization differs from that of other multiple oscillator-mediated behaviors in vertebrates. In frog, respiration is also generated by two rhythmically active networks, each sufficient to maintain gas exchange, but each oscillator separately controls markedly different patterns of activity in distinct muscle groups for buccal (aquatic) and lung-driven (terrestrial) respiration (Gdovin et al., 1999; Wilson et al., 2002). Chains of bidirectionally coupled segmental oscillatory networks generate undulatory swimming in lamprey (Marder and Calabrese, 1996), but each segmental oscillator is similar in pharmacology, physiology, connectivity, and rhythmogenic mechanism. Multiple, pharmacologically separable networks may combine to generate locomotion in rodents (Cazalets and Bertrand, 2000).

PreBötC and pre-I networks respond differently to modulatory inputs other than opiates, including lung stretch receptor afferents (Mellen and Feldman, 2001) and serotonin (Onimaru et al., 1998). If each network is sufficient to generate respiratory rhythm, then this differential sensitivity extends the robustness of respiratory rhythm generation beyond that of either constituent oscillator, since modulators of one leave the other unaffected. Conversely, because the networks are coupled, differential sensitivity also assures responsiveness to appropriate inputs. A dual oscillator model of respiratory rhythm generation can account for how, during behaviors such as exercise, speech, and swallowing, respiratory rhythm rapidly departs from and returns to baseline. This organization thus offers one solution to a general problem faced by neural systems: how to combine robustness with responsiveness to appropriate inputs (Goldman et al., 2001).

Experimental Procedures

In Vitro Methods

In accordance with methods approved by the Institutional Animal Care and Use Committee, neonatal rats (P1–P3; n = 8) were anaesthetized by hypothermia, and following standard techniques (Smith and Feldman, 1987), the brainstem and spinal cord were quickly isolated. For en bloc in vitro preparations, the brainstem was transected at the level of vagal nerve roots; transverse slices (~600 μm thick), retaining hypoglossal rootlets, with the preBötC at the rostral surface of the slice, were cut according to standard techniques (Smith et al., 1991). Preparations were transferred to a bath continuously perfused (3 ml/min) with artificial cerebrospinal fluid (aCSF) containing 128.0 mM NaCl, 3.0 mM KCl, 1.5 mM CaCl₂, 1.0 mM MgSO₄, 21.0 mM NaHCO₃, 0.5 mM NaH₂PO₄, and 30.0 mM glucose, equilibrated with 95% O₂-5% CO₂, warmed to 27°C. In order to elicit stable activity from the transverse slice, [K⁺]_o was elevated to 9 mM. Inspiratory bursts were recorded from ventral roots C1-C3 (en bloc) or from hypoglossal rootlets (transverse slice), sampled at 20 kHz, saved to disk, and analyzed offline. At least 100 control cycles were recorded in standard aCSF at 27°C. We then added the μ-opiate agonist D-Ala, N-Me-Phe, Gly-ol-enkephalin (DAMGO; Sigma) to the perfusate for a final concentration sufficient to slow, but not stop, rhythmic motor output (200–400 nM), and at least 100 respiratory cycles were collected; after which, the μ-opiate antagonist naloxone (10 μM; Sigma) was applied to reverse DAMGO-mediated inhibition. Intracellular electrodes (~7 MΩ) filled with 140 mM K⁺-gluconate, 5 mM NaCl, 0.1 mM CaCl₂, 2 mM ATP (Mg²⁺), 1.1 mM EGTA, 10 mM HEPES, and 0.01 g/10 ml biocytin, and 0.003 g/10 ml Lucifer yellow, titrated to pH = 7.4 with KOH were used to obtain blind whole-cell patch-clamp recordings from preBötC inspiratory neurons (found just rostral to XII rootlets, at depths of 200–600 μm from the ventral surface) and from pre-I neurons (~600 μm rostral to XII rootlets, within 300 μm of the ventral surface). Junction potentials were not compensated.

In Vivo Methods

Awake Animals

Unanesthetized, intact juvenile rats (P5–P7; n = 6) were placed in a custom whole-body plethysmograph. Respiratory-related pressure changes within the chamber relative to the reference chamber were measured by a differential pressure transducer (DRAL501, Honeywell Data Instruments). Voltage proportional to differential pressure was acquired digitally at 200 Hz using Axoscope (Axon Instruments, Union City, CA), and analyzed offline. Because DAMGO does not cross the blood-brain barrier (Matsumura et al., 1992), following collection of control cycles, the blood-brain barrier crossing selective μ-receptor agonist fentanyl citrate (Abbott Laboratories, North Chicago, IL) was administered (subcutaneously, 0.035 mg/kg), and data was collected for 5–15 min postinjection. After recordings were completed, rats received naloxone hydrochloride (s.c., 0.4 ml of 5 μM solution in saline; Sigma Chemical Co., St. Louis, MO) and were returned to the nest. Their development was observed for 5 consecutive days and was normal. Vagotomized anaesthetized animals: juvenile rats (P5–P7; n = 4) were anesthetized with halothane (2.5% for induction, reduced to 1% thereafter). The animals were then bivagotomized and trachotomized and connected to a flow head. Respiratory activity before and during opiate agonist administration was recorded. Animals were then euthanized with pentobarbital (100 mg/kg, i.p.)

Data Analysis

Inspiratory burst times were obtained from the rectified, integrated (τ = 50 ms) population activity signal, recorded from cranial or ventral rootlets. Periods were obtained by subtracting inspiratory burst time from preceding inspiratory burst time. Control cycles obtained prior to DAMGO-induced slowing were used to obtain the value of T_ctrl. The raster plots of periods (Figure 1, left) truncate control cycles. To test for nonrandom transitions between periods, we calculated the serial correlation coefficient (Perkel et al., 1967) for lags (−7…7). To do this, we calculated the covariance C_j of periods of lag j:

$$C_j=\frac{{\displaystyle \sum _{i=1}^n}(T_i-\overline{T})(T_{i+j}-\overline{T})}{n}(\text{j}=-7,\dots ,-1,0,1,\dots ,7),$$

where T_i is the i^th period, and T is the sample mean, and n is the sample size. The serial correlation coefficient r of lag j is the ratio of the covariance, and the sample variance s²:

$$r_j=\frac{C_j}{s^2}.$$

The statistical significance of correlation coefficients was tested by comparing the actual correlation coefficients to the distribution of coefficients obtained over 1000 iterations using shuffled period data sets. A given r value was statistically significant if it exceeded the 95^th percentile of the corresponding r values obtained from shuffled data sets.