Osmotic Water Permeability of Isolated Protoplasts. Modifications during Development

Abstract

A transference chamber was developed to measure the osmotic water permeability coefficient (P_os) in protoplasts 40 to 120 μm in diameter. The protoplast was held by a micropipette and submitted to a steep osmotic gradient created in the transference chamber. P_os was derived from the changes in protoplast dimensions, as measured using a light microscope. Permeabilities were in the range 1 to 1000 μm s⁻¹ for the various types of protoplasts tested. The precision for P_os was ≤40%, and within this limit, no asymmetry in the water fluxes was observed. Measurements on protoplasts isolated from 2- to 5-d-old roots revealed a dramatic increase in P_os during root development. A shift in P_os from 10 to 500 μm s⁻¹ occurred within less than 48 h. This phenomenon was found in maize (Zea mays), wheat (Triticum aestivum), and rape (Brassica napus) roots. These results show that early developmental processes modify water-transport properties of the plasma membrane, and that the transference chamber is adapted to the study of water-transport mechanisms in native membranes.

The balance between water loss and water absorption in plants is one of the oldest physiological problems. It was realized early that osmotic and turgor pressures can determine the dynamics of water movement through the different compartments of the plant or tissue. The rate of water flow across membrane systems was modeled by Dainty (1963) using the nonequilibrium thermodynamic equations of Kedem and Katchalsky (1958). Each membrane can be characterized by a parameter, the hydraulic conductivity (L_p) or the related osmotic coefficient (P_os). In higher plants this parameter has been estimated mostly using the cell pressure-probe technique. In animal cells this parameter can be deduced from the kinetics of cellular volume change, as determined by light scattering or fluorescence quenching (for a general review, see Verkman et al., 1996); such measurements require a large population of cells and an elaborate mechanical and electronic apparatus. Recently, the P_os of single cells in epithelial sheets was measured by nonimaging interferometry (Farinas and Verkman, 1996). Light microscopy is the most straightforward method for determining individual cell membrane properties. It is based on the recording of time variations in the cell dimensions, induced by an osmoticum change in the external medium. Measurements of P_os by standard light microscopy have been performed on epidermal cells (Url, 1971; Stadelmann and Lee-Stadelmann, 1989) and more recently on mouse oocytes (Gao et al., 1994, 1996).

When individual cells cannot be easily observed in the tissue, it may be of interest to work on isolated protoplasts. In this paper we describe a new method for measuring P_os on protoplasts or vacuoles, 40 to 120 μm in diameter, isolated from higher-plant cells. The accuracy of the method was examined and the permeabilities obtained were compared with those from other techniques. Measurements were performed on root, hypocotyl, and leaf protoplasts from several plants. The values for P_os were strongly dependent on the tissue and the age of the plant used in the experiments. Water-channel proteins named aquaporins have been detected in various plant cell types (Maurel, 1997) and may provide mechanisms for the regulation of membrane water transport. The large P_os and variations observed in the present work suggested that aquaporin-mediated water transport was involved during developmental processes. This hypothesis was tested by comparing the variations of permeability with temperature on onion (Allium cepa), wheat (Triticum aestivum), and rape (Brassica napus) protoplasts. The effect of mercury ions on protoplasts and vacuoles is also discussed.

MATERIALS AND METHODS

Young seedlings from rape (Brassica napus), flax (Linum usitatissimum), and wheat (Triticum aestivum) were obtained from seeds soaked and germinated on well-watered filter paper in the dark for 3 to 5 d (the age of a plant mentioned in the experiments corresponds to the time elapsed since deposit of the seed on watered paper). Experiments were also performed on leaves from older plants. For these experiments, rape seeds were planted directly in a vegetable-mold-enriched soil and plants were collected after 3 to 4 weeks. Petunia (Petunia hybrida) was previously germinated and grown for 3 weeks in vermiculite moistened with nutrient solution (Morizet and Mingeon, 1976). The seedlings were then transferred into 100-mL containers filled with mold soils and collected after 5 to 8 weeks. All of the plants were grown in a climatic chamber at 23°C ± 1°C with a light/dark cycle of 16/8 h. The RH was kept between 65% and 85%. Fluorescent tubes (TLD 33 and chromasoleil TDL 83, Philips, Eindhoven, The Netherlands) were used to produce a PAR of 140 μmol m⁻² s⁻¹. Onion (Allium cepa) bulbs and beet (Beta vulgaris) roots were purchased at local stores.

Protoplasts were obtained from different tissues. Primary roots without tips and hypocotyls were taken from young seedlings (Ramahaleo, 1996). Pieces of leaves (5 × 10 mm) were taken from older plants. For petunia, it was possible to peel leaves from their lower epidermis before digestion.

Tissues were first digested for 60 to 90 min in a 30-mm-diameter Petri dish containing 2 mL of a digesting solution: 0.8% (w/v) cellulase RS (Yakult Honsha Co., Tokyo, Japan), 0.08% (w/v) Pectolyase Y-23 (Seishin Pharmaceutical Co., Tokyo, Japan), 0.5% (w/v) PVP (Sigma), 1 mm CaCl₂, 10 mm Mes/Tris, pH 5.5, and 0.4 to 0.8 mol kg⁻¹ sorbitol. The digestive solution was aspirated by mild suction before apparent disruption of the tissue occurred. Two milliliters of the same but enzyme-free medium (storing solution) was added to the Petri dish. Protoplasts were separated from the tissue by gentle shaking or by means of sharp needles (onion). Nearly all of the protoplasts from root and hypocotyl exhibited highly stranded vacuoles and cytoplasmic streaming. These criteria were used as a viability test on these materials.

All of the solutions used during measurements contained 100 mm KCl, 1 mm CaCl₂, 2 mm MgCl₂, 0.05% (w/v) BSA, and 10 mm Tris/Mes, pH 7.2, with a sorbitol concentration adjusted to give final osmolalities of up to 0.8 mol kg⁻¹ water. A vapor pressure osmometer (model 5500, Wescor, Logan, UT) was used to control the osmotic pressure.

Transference Chamber and Micropipette Technique

Basic Principle

The mathematical relationship between the protoplast volume V(t) and P_os is simple when the initial rate of the volume change, (dV/dt)₀, can be associated with a steep concentration change Δc₀ (referred to as the initial medium) in impermeant solute:

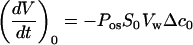1

where S₀ is the initial protoplast surface facing the external medium and V_w the partial molal volume of water (18 × 10⁻⁶ m³ mol⁻¹).

From the experimental point of view, using Equation 1 implies that a protoplast in osmotic equilibrium can be transferred instantaneously to the new medium and that the change Δc₀ takes effect immediately. The transfer can be considered as “instantaneous” only when the kinetics corresponding to the change in the solution (the “mixing time”) are much faster than the kinetics of water flow across the protoplast membrane (the “permeability time”).

Equation 1 indicates that the initial slope of V(t) plots depends on P_os, S₀, and Δc₀. To eliminate the effect of protoplast size and solute concentration, a new variable, z, has been used:

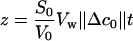2

where V₀ represents the initial value of protoplast volume. Equation 1 can be rewritten:

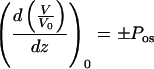3

Positive and negative signs in Equation 3 correspond to water influx (Δc₀ < 0) and outflux (Δc₀ > 0), respectively.

The Transference Chamber

For large cells such as the Xenopus oocyte, the permeability time is so long that the mixing time can usually be neglected. For smaller cells, permeability times of a few seconds can be expected and special care must be taken to reduce the mixing time. Low values for this parameter are obtained by fast washing of a microchamber in which the cell has been “fixed.” Several methods have been described to fix a cell. Animal cells normally adhere to a glass plate. Nonadherent cells can be maintained by aspiration through a porous membrane (Gao et al., 1996). Gao et al. (1994) also measured P_os by holding a cell (a mouse oocyte with a diameter of about 75 μm) through suction applied to a glass pipette during the change in extracellular osmotic solution. However, these authors restricted the pipette method to cell types with an outer “shell.” We have modified this method to measure the P_os of nonwalled cells that are 40 to 120 μm in diameter. The experiments were performed on protoplasts from root, hypocotyl, and leaf.

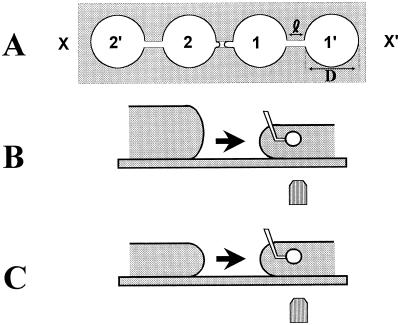
What we call the transference chamber is illustrated in Figures 1 and 2. It was designed to reduce diffusion/convection processes by joining four cylindrical compartments with a narrow slit or channel (Fig. 2A). The initial gradient (Δc₀) was created by filling compartments 1 and 1′ and 2 and 2′ with two solutions of different osmotic strengths. Capillary forces in the channel allow maintenance of an air gap between compartments 1 and 2 (Fig. 2, B and C) during filling operations. Communication between solutions was achieved by dragging solution 2 into solution 1 with a fine needle. To speed up replacement of the solution surrounding the protoplast, compartment 2 was filled at a level two times higher than that in compartment 1 (Fig. 2B). A flow of liquid was triggered by contact between solutions. This allowed measurement of the initial rate of volume change between solutions 1 and 2 in less than 1 s. The spreading of the mixing zone between solutions prevented symmetrical measurement of the rate of volume change between solutions 2 and 1 on the same protoplast. When reversibility of the volume changes between solutions had to be tested on the same protoplast, the mixing between solutions was reduced by keeping them at the same level between the different compartments (Fig. 2C).

Figure 1.

Temperature control of the transference chamber. Precooled or heated fluid (1:2, glycerol:water [v/v]) was pumped through a metallic tube (i.d., 2 mm) embedded in the stainless-steel chamber. The tube surrounded the compartments; the inlet and outlet are visible in the figure. The temperature in the solutions was measured with a thermocouple (±0.1°C). The variations in temperature remained within 1°C in the central part of the compartments. Dimensions of the metallic slide were 76 × 26 × 5 mm.

Figure 2.

Creation of a step osmotic change through use of the transference chamber. A, Top view of the chamber. Four holes were made in a 3- to 5-mm-thick plastic (nonthermostated chamber) or metallic (thermostated chamber) slide. Holes were connected by 400-μm-width slits. A cover slide was used to make the bottom of the chamber. The protoplast or vacuole was maintained with the pipette in compartment 1 near the slit. B, Solution 1 was rapidly replaced by solution 2 around the cell as follows: compartments 1 and 1′ were filled with 100 μL of solution, whereas compartments 2 and 2′ contained 200 μL each. A 1- to 2-mm air gap was maintained between solutions 1 and 2. A fine glass needle was used to establish contact between the solutions, then the stage was moved to the right so that the cell was transferred toward 2′. C, Reversibility of volume changes was tested by filling each compartment with 100 μL of solution. The equilibrium volume was first measured in isotonic compartment 1, then in hyperosmotic compartment 2, and finally back in compartment 1′.

Temperature Control of the Chamber

Unless stated otherwise, the experiments were performed at room temperature (20°C ± 2°C). A temperature-controlled chamber (±1°C) was used to measure the effect of temperature on P_os (Fig. 1).

Description of the Experiments

About 0.1 μL from the storing solution containing 10 to 20 protoplasts was sucked with a 120-μm-diameter pipette and added to compartment 1 of the transference chamber. The solution in compartment 1 had the same osmotic pressure as the storing solution.

The protoplast was held with the pipette by slight suction. The effects of this negative pressure were 2-fold. (a) The membrane was always under tension. It allowed measurements of P_os for both directions of the water flux, because V(t) always kept a cylindrical symmetry and could be determined from pipette and protoplast dimensions (Fig. 3) in the “equatorial plane.” (b) The protoplast was lifted up (usually about 10–30 μm) so that the stage and the attached chamber could be translated along the XX′ axis (Fig. 2A). Less than 2 s was necessary to shift compartment 2 at the initial location of compartment 1. All of the experiments were recorded on VHS videotape.

Figure 3.

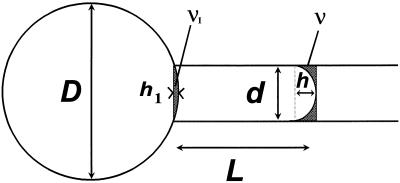
Measurement of volume and cell surface. V(t) was calculated from simple geometric considerations (see text) and microscope measurements for D, L, and d. d, i.d. of the transference pipette; D, protoplast diameter; L, length of the protoplast inside the pipette; v and v₁, volumes of the portions of spheres determined by h and h₁, respectively.

The Glass Pipettes

Pipettes were prepared with a microforge according to previously described techniques (de Fonbrune, 1949; Mitchison and Swann, 1954). The transference pipettes required a cylindrical part and a clean, straight end (Fig. 4). They were obtained from hard glass capillary tubes (model GC150–15, Clark Electromedical Instruments, Reading, UK). The inner pipette diameter was measured in the air, facing the end of the pipette to avoid distortion. The diameter of the pipette had to be wide enough so that the membrane could be visualized and the protoplast could enter the glass tube smoothly. The diameter of the pipettes was one-fourth to one-third of the protoplast diameter.

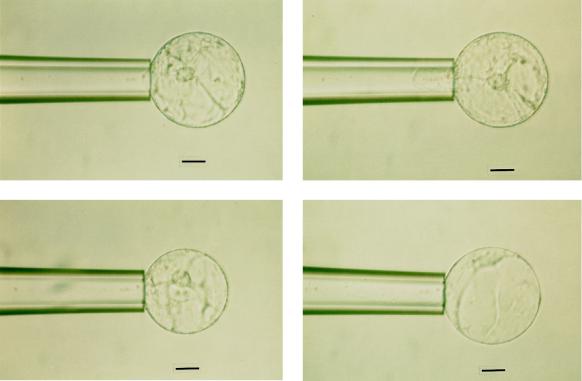
Figure 4.

Volume variation during transference of two rape root protoplasts from osmotic equilibrium (top and bottom left) into hyperosmotic (top right) or hypoosmotic (bottom right) solutions. The same pipette was used in both experiments. Scale bars = 25 μm.

Time Measurements

The recorder allowed a 40-ms resolution (25 frames/s) in the time scale. For the largest P_os values, a significant change in V(t) from its initial value (V₀) could be detected within two frames. The initial time (t₀) was attached to the last frame preceding any detectable change in protoplast dimensions. For the smallest permeability values, detectable changes in volume required several seconds, and t₀ was determined with an accuracy of 2 s, the maximum time necessary to displace the protoplast between compartments (see “The Transference Chamber” above).

Volume and Protoplast Surface Measurements

In our experiments the initial surface (S₀) used in Equation 1 corresponded to the initial protoplast surface minus the surface of the membrane area facing the pipette (the pipette being initially filled with isotonic solution, that part of the membrane was not submitted to the water flux at the initial time). S₀ was determined from D₀ and L₀ values in the initial frame. V(t) was measured by assuming a spherical shape with diameter D for the protoplast part outside the pipette. The inner part of its volume was expressed as a function of D and L at time t, and d (Fig. 3). According to the classic formula for the volume of the portion of a sphere:

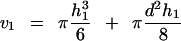4

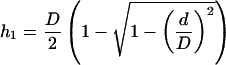5

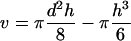6

V(t) was then expressed as:

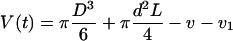7

During an experiment, h ≈ d/2 (Fig. 4). Its variations were smaller than 2 μm, and the resulting change in v with typical parameters (D = 60 μm; d = 20 μm) was less than 1% of V(t). These variations were neglected and V(t) was calculated assuming h = d/2 in v.

Control Experiments

The permeability measurements never lasted more than 2 min (usually less than 40 s). The true osmometer behavior of protoplasts was verified by measuring their volume at equilibrium in the same osmotic solution, before and after they were transferred to a medium with a ±0.2 mol sorbitol kg⁻¹ water difference in osmotic pressure. No significant change in volume was observed, indicating that solute fluxes can be neglected during experiments.

Accuracy of Measurements

Unless stated otherwise, each value for P_os was obtained from measurements on different protoplasts. The sd on P_os reflects both experimental errors and variability between protoplasts from the selected tissue. The smallest variations were obtained with rape root protoplasts from 3- to 5-d-old seedlings: P_os = 298 ± 114 (n = 31).

The reproducibility of measurements was tested on individual protoplasts. Two measurements of P_os (water outflux), separated by 10 min, were repeated on the same rape root protoplasts. For each protoplast, the ratio between the second and first measurements was 1.27 ± 0.45 (n = 5). The same experiments with petunia leaf protoplasts gave a ratio of 1.30 ± 0.66 (n = 5).

Histograms

Values of P_os from 1 to 1000 μm s⁻¹ were sometimes recorded from the same tissue sample, so a logarithmic scale was used in the histograms. The size of each class was chosen by taking, for the upper boundary, twice the value of the lower one. This corresponds to a 33% variation from the mean in each class.

Numerical Values

The values for P_os are given as means ± sd (where n indicates number of measurements). The sd values were also calculated for the activation energies (E_a) and the slope of linear regressions (see Fig. 9).

Figure 9.

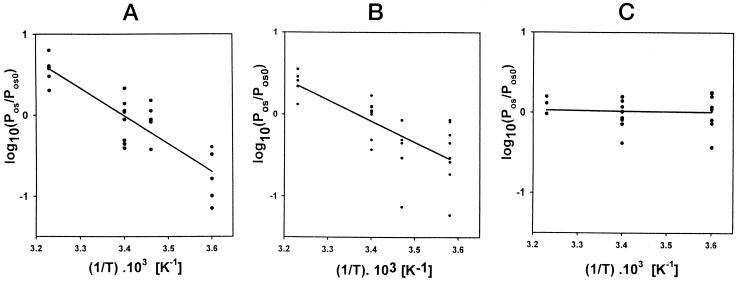
A, Measurements of permeability for different temperatures on protoplasts from epidermal cells of the onion bulb scale. At 5°C, 16°C, 21°C, and 37°C, P_os values were, respectively, 1.7 ± 1.1 μm s⁻¹ (n = 5); 7.2 ± 3 μm s⁻¹ (n = 6); 7.9 ± 4.7 μm s⁻¹ (n = 8); and 30.4 ± 11 μm s⁻¹ (n = 6). B, The same measurements on wheat root protoplasts. The roots were collected from 3-d-old plants. At 6°C, 15°C, 21°C, and 36°C, the P_os values were, respectively, 1.1 ± 0.8 μm s⁻¹ (n = 8); 1.16 ± 0.7 μm s⁻¹ (n = 5); 2.7 ± 1.1 μm s⁻¹ (n = 8); and 6.8 ± 2.2 μm s⁻¹ (n = 5). C, The same measurements on rape root protoplasts. The roots were collected from 3- to 5-d-old plants. At 5°C, 21°C, and 37°C, the P_os values were, respectively, 334 ± 133 μm s⁻¹ (n = 10); 292 ± 110 μm s⁻¹ (n = 8); and 373 ± 90 μm s⁻¹ (n = 3). P_os0, Mean value of the permeability at T₀ (294 K). The slope a of the lines fitted by linear regression were, respectively, a = −(3.42 ± 0.40) × 10³ K for onion; a = −(2.56 ± 0.50) × 10³ K for wheat; and a = −(0.067 ± 0.30) × 10³ K for rape.  

RESULTS

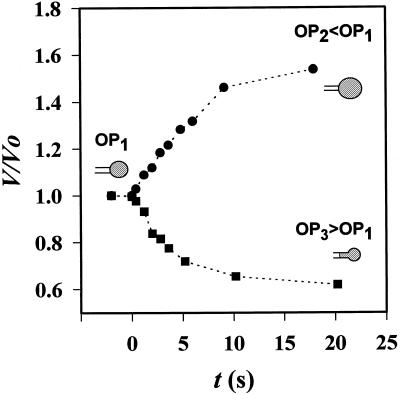
The experimental chamber was first used to record volume changes on rape root protoplasts. The initial volume was measured in compartment 1, in a solution isotonic with the storing solution. Two typical records, obtained from protoplasts with the same diameter (70 μm), each revealed that the rate of change in volume was initially constant for a sufficient period (Fig. 5) to allow proper determination of (dV/dt)₀.

Figure 5.

Variation of volume V for two protoplasts, after an osmotic change from isotonic OP₁ to hypoosmotic OP₂ or hyperosmotic OP₃ medium. Protoplasts were obtained from 3-d-old rape roots. V_0, Initial volume under isotonic conditions. OP₁ = 400 mosmol kg⁻¹; OP₂ = 200 mosmol kg⁻¹; and OP₃ = 600 mosmol kg⁻¹.

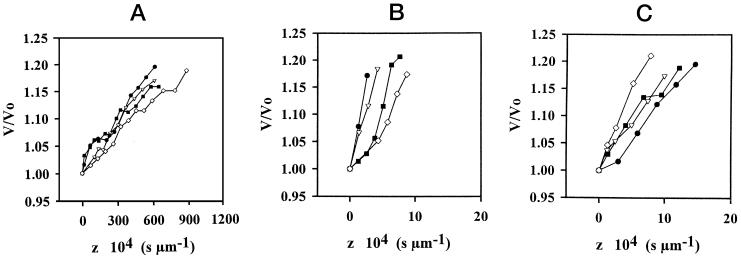
In the representation of the normalized volume V/V₀ along the z coordinate, the initial slope corresponded to P_os. It can be determined within the first 20% increase in volume, as shown in Figure 6. For wheat, rape, and flax protoplasts from 3-d-old roots, values for P_os(in) were: 2.5 ± 0.7 μm s⁻¹ (n = 13), 330 ± 140 μm s⁻¹ (n = 13), and 193 ± 43 μm s⁻¹ (n = 6), respectively.

Figure 6.

Initial swelling in the z coordinate of root protoplasts from 3-d-old wheat (A), 3- to 5-d-old rape (B), and 3-d-old flax (C). V₀, Initial volume of protoplasts in 400 or 600 mosmol kg⁻¹ solutions. The final osmolality in the medium was 275 mosmol kg⁻¹, and protoplast diameters ranged between 60 and 100 μm.

In the exosmotic experiments, the protoplast was aspirated into the pipette. The increase in L (Fig. 2B) prevented crumpling of the protoplast and allowed a regular decrease in volume without any significant change in surface area (data not shown; because the maximum volume enclosed by a given area S is spherical, a smaller sphere and a cylinder can have the same area). In the endosmotic experiments, modifications in protoplast surface area were greater and seemed to depend on the tissue itself (Table I). The root protoplasts did not burst.

Table I.

Maximal increase in surface area during measurements for hypocotyl and root protoplasts submitted to hyposmotic stress

Plant	(Smax − SI)/SI
	Hypocotyl (5 d)	Root (3–5 d)
Rape	0.14  ± 0.06 (5)	0.34  ± 0.06 (13)
Flax	0.15  ± 0.16 (9)	0.34  ± 0.03 (4)

The 60- to 100-μm-diameter spherical protoplasts were transferred from 450 to 250 mosmol kg⁻¹ solutions. S_max was measured after 2 min or immediately before bursting. Membrane disruption was observed for all but one hypocotyl protoplast. (S_max − S_I)/S_I (mean ± sd): relative change of the membrane surface, referred to initial value S_I of the protoplast. The number of experiments is given in parentheses.

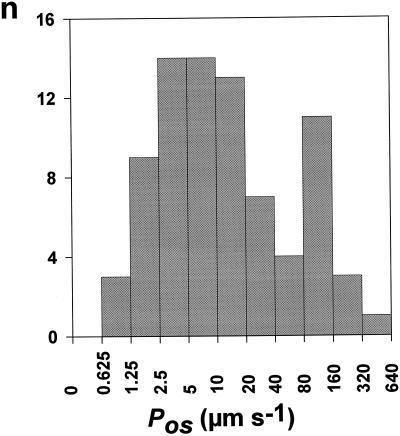
Table II summarizes our results for permeability measurements on protoplasts from various tissues. Values for P_os ranged between 8 ± 5 μm s⁻¹ (n = 8) and 400 ± 150 μm s⁻¹ (n = 5). For petunia and rape leaves, large variations in P_os were observed. The histogram in Figure 7 represents the distribution of P_os for petunia leaf protoplasts (a similar distribution was obtained with rape; data not shown). Large variations in P_os were also observed when the protoplasts were collected on a Ficoll gradient. We could not establish any correlation between the magnitude of the permeability and parameters such as the size of the protoplast or the time it spent in the storing solution before measurement.

Table II.

Endosmotic (In) and exosmotic (Out) permeability values (P_os ± sd) for protoplasts from various species and tissues: onion bulb scales, rape hypocotyl, and rape root

Flow	Onion Leaf	Rape Hypocotyl (5 d)	Rape Root (3–5 d)
	μm s−1
In	10  ± 7 (10)	400  ± 150 (5)	330  ± 140 (13)
Out	8  ± 5 (8)	340  ± 120 (7)	280  ± 90 (8)

The age of the plants and the number of experiments are given in parentheses.

Figure 7.

Histogram for P_os values from petunia leaf protoplasts. Mature leaves (about 30 mm in length) were collected from 5- to 8-week-old plants. P_os(in) and P_os(out) were measured on 29 and 50 (n = 79) protoplasts, respectively. The values ranged between 1 and 330 μm s⁻¹. n, Number of protoplasts in each class.

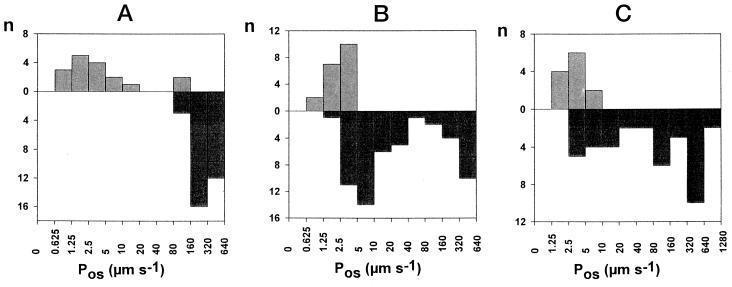
The situation was different with the root protoplasts from rape (Fig. 8A), wheat (Fig. 8B), and maize (Fig. 8C). The permeability was strongly dependent on the age of the roots used in the experiments. It was only 2 to 3 d after the first contact of the seed with water (see Methods) that P_os values larger than 100 μm s⁻¹ could be measured. Earlier in the development of these plants, nearly all of the P_os values were smaller than 10 μm s⁻¹.

Figure 8.

Histograms for P_os values from root protoplasts. A, Rape roots were collected from 2- (upper histogram) or 3- to 5-d-old (lower histogram) plants. B, Wheat roots were collected from 3- (upper histogram) or 5-d-old (lower histogram) plants. C, Maize roots were collected from 2- (upper histogram) or 3- to 5-d-old (lower histogram) plants. n, Number of protoplasts in each class.  

Mercury-sensitive water channels (aquaporins) have been described in a variety of animal and plant membranes. When fresh rape root protoplasts were incubated for 2 min with 100 μm to 1 mm HgCl₂, disruption of cytoplasmic strands occurred and cyclosis stopped. Protoplasts were then too fragile for further manipulation. Five millimolar 2-mercaptoethanol did not reverse the effects of the mercury. Mercury ion at concentrations less than 20 μm had no effect on cyclosis or permeability. Protoplasts kept overnight at room temperature were more resistant, and even with 200 μm mercury P_os could still be measured: 7 ± 4 μm s⁻¹ (n = 5). However, cyclosis disappeared almost immediately and the membrane usually ruptured within 10 min. When the sulfhydryl reagents p-chloromercuribenzoate and p-chloromercuribenzene sulfonate were used at 1 mm, cyclosis or P_os remained unchanged. No systematic study was performed on vacuoles, but assays with red-beet root vacuoles indicated that the dye leaked out rapidly, immediately after exposure to 1 mm HgCl₂. Bleaching or bursting usually occurred on 7 of 10 vacuoles tested.

The effect of temperature on membrane permeability to water has been used to detect membrane water channels. The E_a for the self-diffusion of water is less than 20 kJ mol⁻¹ (Sha'afi, 1981). Similar values for E_a of water diffusion through membranes are then considered indicative of a bulk flow of water through channels (Preston, 1992; Maurel, 1997). A high E_a value (about 60 kJ mol⁻¹) reflects strong interactions between membrane and water molecules (Sha'afi, 1981). It suggests a predominant diffusion of individual molecules through the pure lipid bilayer (Haines, 1994). The permeability of onion, wheat, and rape protoplasts was measured at different temperatures. For onion (Fig. 9A), the slope, a, of the fit corresponded to the Arrhenius energy, and E_a = 65.5 ± 7.7 kJ mol⁻¹. For wheat (Fig. 9B), E_a = 49 ± 9.6 kJ mol⁻¹. For rape (Fig. 9C), the decrease of P_os with temperature was small and E_a was more difficult to determine (E_a = 1.3 ± 5.7 kJ mol⁻¹).

DISCUSSION AND CONCLUSION

The measurement of water permeability by osmotic gradients requires the creation of a steep change in concentrations. This may be technically difficult for small, nonadherent cells. In addition, wall-less biological systems such as protoplasts or vacuoles are fragile and cannot withstand vigorous stirring. To circumvent these difficulties and calculate P_os from the time course of the cell volume (V(t)), a transference chamber was constructed to allow a fast concentration change in the extracellular solution. A micropipette was used to maintain a protoplast in position during hyperosmotic and hypoosmotic changes. The fast change in solution near the cell was achieved by creating a transient flow from compartment 2 to compartment 1.

We can only estimate the time (τ) that was necessary to replace the solution near a cell in the transference chamber (Fig. 2). If λ represents the mixing length between solutions and v represents the flow velocity, then τ = λ/v. The flow velocity v was given by the displacement rate of small particles after contact between solutions (v ≈ 10⁻² m s⁻¹, as measured on video recordings). The mixing length between solutions was limited by the narrow slit between compartments (Fig. 3) and was assumed to be shorter than its length. A value of 1 mm for λ would correspond to 100 ms for τ. This was probably the case, because fast protoplast swelling or shrinking could be completed in less than 1 s (data not shown).

Measurements of very small values of P_os on protoplasts (about 1 μm s⁻¹) implied constancy in Δc₀ during recordings lasting 60 to 100 s. This condition was realized by translating the protoplast into compartment 2′, far from the zone where mixing occurs.

Accuracy of P_os Measurements

Several errors, including both systematic and random types, were identified in the measurement of P_os with our technique (see Appendix).

The random error was mainly caused by the limited resolution in dimensions of the protoplast. Estimation of the propagated error on P_os (about 50%) could explain the sd of 30% to 40% found with hypocotyl and root protoplasts (Table II). This suggested that biological variations of P_os in the populations of hypocotyl and root protoplasts were much smaller than the sd. Consistent with this conclusion, sd was not reduced (35%) when control experiments were performed on the same protoplast. In the interpretation of the results, we considered that biological effects on protoplasts could be detected only when they induced at least a 50% change in P_os. In our experiments, values of P_os ranged from 1 to 1000 μm s⁻¹, and we selected a logarithmic scale to represent its variations (Figs. 7 and 8). In the histograms the size of each class was chosen by taking, for the upper bound, twice the value of the lower one, considering that biological variations within each class could be masked by experimental errors. Significant biological variations that were clearly detected on the protoplasts from petunia leaves (Fig. 7) will be discussed below.

The proposed method also may have introduced bias in the values of P_os. The permeability was measured on isolated protoplasts at zero turgor, a condition that was reported to produce an overestimation of P_os for some algae (Steudle and Zimmermann, 1974; Zimmermann and Steudle, 1974). The perturbation brought by the pipette, by creating a transcellular water flow between the pipette and the cell compartment, leads to an underestimation of P_os when calculated with Equation 1. However, the correcting factor, smaller than 1%, was not taken into account. The decrease in the driving force during measurements leads to an underestimation of P_os. An upper limit for this error was estimated as 32% (see Appendix). The use of Equation 1 to calculate P_os also implied neglecting the “unstirred layer effect.” This probably resulted in an underestimation for the larger protoplasts' permeabilities. For P_os ≈ 1000 μm s⁻¹, the time necessary for a perturbation to be damped inside of a cell becomes comparable with the time constant for the experiment. This suggests that resistances to water transport are evenly distributed between the membrane and the cell compartment, so that the membrane is no longer the only rate-limiting step to water transport.

Comparison between P_os(in) and P_os(out)

A polarity in water permeability has already been described, with P_os values for water inflow being larger than those for water outflow (Dainty and Ginzburg, 1964; Tazawa and Kamiya, 1966; Steudle and Zimmerman, 1974; Terwilliger and Solomon, 1981). In our experiments (Table II), the difference between P_os(in) and P_os(out) was comparable with sd for both permeabilities, and the method was not accurate enough to determine P_os(in)/P_os(out) individual ratios. We only calculated mean values of P_os(in) and P_os(out), which were similar within the group of either hypocotyl or root protoplasts (Table II).

The Effect of Membrane Expansion on P_os

Measurements of P_os(out) were obtained without modification of the cell surface, whereas measurements of P_os(in) revealed very different expansion capacities in protoplasts. The plasma membrane supported large deformations (Table I), especially in root cells (34% ± 6%; n = 13). Despite the differences in membrane expansion, no significant change was detected between P_os(in) and P_os(out). In our experiments the membrane tension and the factors that transduce them had no detectable influence in determining the permeability to water.

It must also be noted that elastic expansion of the cell membrane is considered to be less than 2% to 3%. The 34% change recorded in the protoplasts suggests the unfolding of invaginations in the membrane or transfer from an internal reservoir of membrane material (Wolfe and Steponkus, 1981).

Plasma Membrane Permeability

The different methods used to measure the water permeability of cellular membranes have been reviewed by Maurel (1997). Comparisons between data are not always straightforward, because the experimental conditions applied to the membrane under consideration depend on the method itself. Transcellular osmosis (Kamiya and Tazawa, 1956) allows measurements on intact cells under normal turgor, but it is restricted to giant cells. The pressure-probe technique has extended these in situ measurements to higher-plant cells and takes into account the contribution of plasmodesmata to the cell hydraulic conductivity. In the plasmometric method on entire cells, the turgor pressure is close to zero and contacts between the cell wall and the plasma membrane are nearly suppressed (Stadelmann and Lee-Stadelmann, 1989). Permeability to water was also deduced from the time course of shrinking of small (about 100-nm) vesicles purified from plasma membranes and endomembrane fractions (Niemietz and Tyerman, 1997). In our experiments we followed plasmolysis or deplasmolysis on the entire protoplasts. In the last two methods the cell wall was removed from the plasma membrane and was facing an artificial solution.

Plasmolysis of cells was first used by Pfeffer (1877) and de Vries (1884) to determine osmotic pressure in plants. Earlier measurements of the rate of water movement through isolated cells were reviewed by Crafts et al. (1949). Measurements by plasmolysis of cells in tissue strips or bulb-scale epidermis (onion) have been reported by Levitt and Gibbs (1936), Url (1971), and Lee-Stadelmann and Stadelmann (1989). Large P_os values for the tonoplast were obtained with the different techniques already used (Url, 1971; Kiyosawa and Tazawa, 1977; Maurel et al., 1997).

The situation is more contrasted with the plasma membrane. A wide range of values has been found with the pressure probe. Steudle (1989) cites values of P_os (given in hydraulic conductivity units) for individual root cells from different species in the range of 15 to 250 μm s⁻¹. In contrast, measurements on vesicles by both Maurel et al. (1997) and Niemietz and Tyerman (1997) point to low values (6–10 μm s⁻¹). We could measure both small and large P_os in the case of rape, wheat, and maize root protoplasts. It must be noted that if the contribution of plasmodesmata to water permeability could explain the high P_os obtained with the pressure probe, this was not the case in our experiments.

The Dependence of P_os on Development

Previous reports suggest that the water permeability of plant membranes could be modified during development. First, very accurate developmental regulations have been described for several plant aquaporin genes (Kaldenhoff et al., 1995). In addition, some aquaporins can be phosphorylated. Johnson and Chrispeels (1992) have reported that the level of αTIP phosphorylation was altered during the 3 d after germination in Phaseolus. This would also correspond to an increase in tonoplast water permeability, because phosphorylation regulates the water-channel activity of this aquaporin (Maurel et al., 1995).

In our experiments variations in P_os within protoplast samples depended on the origin of the samples. The smaller variations were obtained with root samples from 3-d-old plants (Fig. 8, B and C). The largest variations appeared with the older roots (Fig. 8, B and C) and with the petunia (Fig. 7) and rape (data not shown) leaves. Recently, Johansson et al. (1996) found that an aquaporin-like protein was preferentially expressed in cells associated with vascular tissue of spinach leaf. We suggest that the large variations found in P_os represent differences in aquaporin expression or activity.

We suspected that the heterogeneity observed on the leaves resulted from developmental processes, but their effect was easier to demonstrate on roots. Striking differences were detected between plants of different ages (Fig. 8). For all of the roots tested, the permeabilities measured during the earlier stages of development were usually smaller than 10 μm s⁻¹. All of the rape root cells experienced a large increase in P_os between the 2nd and 3rd d, without any change during the next 2 d. For maize and wheat, only a part of the cell population had high permeabilities after 5 d. The larger P_os suggests that aquaporins in an active form appear during development.

Criteria Used to Detect Aquaporins

Several criteria can be used to demonstrate that aquaporins predominate in a water exchange. The inhibition of water transport by mercury ions and its reversion by reducing agents have been reported by several authors, either on intact plant cells (Maggio and Joly, 1995; Carvajal et al., 1996), algae (Wayne and Tazawa, 1990; Henzler and Steudle, 1995; Steudle and Henzler, 1995; Tazawa et al., 1996), or vesicles (Maurel et al., 1997; Niemietz and Tyerman, 1997).

We could not reproduce these experiments because protoplasts were damaged by the treatment with mercury ions. The reduction in the rate of volume change detected in this case could be interpreted as a decrease in P_os or an induced leakage of the osmoticum across the membrane.

The heterogeneity in the values of P_os for the protoplast samples from younger or older roots (Fig. 8) prevented measurements of the Arrhenius E_a for the same protoplast at different ages. Measurements on onion and wheat protoplasts allowed an estimation of the Arrhenius E_a (Fig. 9, A and B), and the large value obtained, consistent with a low P_os, suggested that the major pathway for the water molecules was through the lipid part of the membranes. In contrast, the E_a in rape protoplast was difficult to determine because of its low value (Fig. 9C). Even if some ambiguity may exist in the interpretation of E_a (Finkelstein, 1987), this result suggests that water molecules were probably transported through an aqueous path in the rape membranes.

In conclusion, the technique developed in this paper allowed us to measure P_os on protoplasts from various cell types. The interpretation from variations in P_os is simpler on isolated protoplasts behaving as true osmometers than on cells in a tissue, where water and osmotica may be exchanged via plasmodesmata (Zhang and Tyerman, 1991). We detected a dramatic increase in P_os during the development of different plant roots, which may reflect the activation of aquaporins in the protoplasts. Our technique will be useful for further investigating the regulatory mechanisms that govern the water permeability of plant plasma membranes.

Abbreviations:

E_a

activation energy

P_os

osmotic permeability

APPENDIX: SOURCE OF ERRORS IN P_os MEASUREMENTS

The random errors in the measurement of P_os were estimated from Equation 1. The errors for each term were assumed to be uncorrelated, and the propagation theory (e.g. Meyer, 1975) was used to calculate sd values for P_os

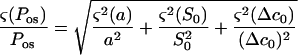A1

ς(x) is the sd value of x, and a represents the initial slope, estimated by

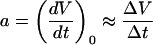A2

ΔV = V − V₀ corresponds to the volume change, assumed to be linear during the time interval Δt and

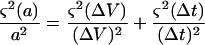A3

Because ΔV is small, the sd on ΔV is about twice the sd on V

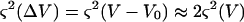A4

Using Equations A1, A3, and A4

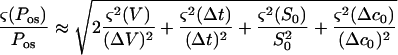A5

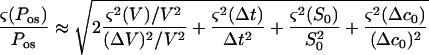A6

The errors in V and S₀ were attributable to limitations on optical measurements of the geometrical parameters D and L (Fig. 3). The boundary of the cell was resolved to within 0.5 μm. This corresponds to a 1-μm uncertainty in the diameter. For a 60-μm spherical protoplast, (ς(V)/V) = 3(ς(D)/D) ≈ 0.05 and (ς(S₀)/S₀) = 2(ς(D₀)/D₀) ≈ 0.033. For a typical value of 15% for ΔV/V, the first term on the right side of Equation A6 is approximately 0.22. The relative error on the time measurement is maximum for the smaller Δt observed, about 1 s. It originates from the uncertainty on the initial time t₀. With a 40-ms uncertainty on t₀, (ς(Δt)/Δt) ≤ 0.04. The relative error on concentration resulting from preparation of the solutions was estimated to be (ς(Δc₀)/Δc₀) ≤ 0.03. The last three terms in Equation A6 can then be neglected and

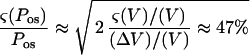A7

As already noted (Steudle, 1980), the total error on P_os measurements using light microscopy is mainly determined by the error in estimating the cell volume.

Several sources of systematic errors were also identified in the measurements:

1. The permeability of the plasma membrane measured on the protoplast could differ from its value in intact cells. In particular, the cell turgor was reduced to almost zero in the protoplast and possible interweaving between the cell wall and the plasma membrane in the intact cell was suppressed. For some algae, Nitella flexilis (Steudle and Zimmermann, 1974) and Valonia utricularis (Zimmermann and Steudle, 1974), it was found that the permeability was strongly increased by a reduction of turgor toward the plasmolytic point. Dainty (1976) drew attention to the possible bias introduced by permeability measurements on plasmolyzed protoplasts. The cell wall-digesting solutions used to prepare protoplasts could also alter the plasma membrane and modify P_os. Different cells may have different sensitivity to turgor and digesting solutions, so that the magnitude of the error on P_os may be dependent on the origin of the protoplast. However, although the absolute values might be different between a cell and its protoplast, it may be valid to make comparisons of P_os between protoplasts from cells that differ only by their age.

2. The tissue samples (root, hypocotyl, or leaf) used to prepare protoplasts contained various cell types that were not identified during the measurements. We can only establish comparisons with the results from the pressure probe at this tissue level. In the case of maize roots, Steudle (1989) gives values between 7 and 120 μm s⁻¹ (the relation P_os = (RT/V_w)L_p was used to convert the hydraulic conductivity (L_p) units). Our own measurements on 2-d-old maize root protoplasts were in the range 1 to 10 μm s⁻¹, but larger values (300–1000 μm s⁻¹) were found on protoplasts from the 3- to 5-d-old plants (Fig. 8).

3. The pipette used in our experimental system created the conditions of transcellular osmosis (Kamiya and Tazawa, 1956) by preventing part of the cell surface (S_p) from experiencing theosmotic change. For a cell under initial conditions (Fig. 4), rather than Equation 1 we can write:

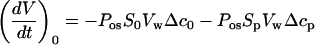A8

The first term on the right side of Equation A8 corresponds to the water flux across S₀, the cell surface outside of the pipette (other symbols from Eq. 1 have been used).

The solution inside of the pipette corresponds to the initial medium, but because of a water flux across the membrane outside of the pipette, a resulting change in intracellular concentration could create a water flow through the cell membrane inside of the pipette. The water flux through the area (S_p) of the membrane facing the pipette is attributable to the concentration gradient (Δc_p), which is built up during the measurements. Equation A8 can be rewritten as:

A9

It is possible to give an upper limit to the terms in brackets. As indicated below, about 15% volume variations were necessary to measure (dV/dt)₀. Because the protoplast behaves as a true osmometer, it would produce a final 15% change in concentration inside the cell. The maximum value for (Δc_p/Δc₀) is 0.15, and the ratio (S_p/S₀) can be approximated by:

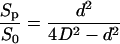A10

if we consider that S_p is close to the area of the circle defined by the pipette (Fig. 4), with (d/D) ≈ (1/3), then (S_p/S₀) ≈ (1/36). The correction factor in Equation A9, smaller than 1%, was then neglected and Equation 1 was used in the calculations for P_os.

4. Initial values of the parameters in Equation 1. The cell surface outside of the pipette and the concentration gradient were assumed to keep their initial values, S₀ and Δc₀, during the maximum 20% change in V, which was needed to measure (dV/dt)₀ in Equation 1. For a spherical protoplast that was swelling, this change in volume corresponded to a 13% increase in the membrane surface from its initial value S₀ and a 20% decrease in internal solute concentration. The driving force, which was initially Δc₀ = 200 mosmol kg⁻¹, was then reduced by 40% and the product S₀ Δc₀ was reduced by 32% (1 × 0.6 to 1.13 × 0.6) between the first and last measurements. This could lead to the same underestimation of P_os by Equation 1, if (dV/dt)₀ was determined only by the last point on the curves (Fig. 6). However, rather than the initial slope (dV/dt)₀, a mean value between the initial and final driving forces was estimated in the experiments and the systematic bias in P_os was probably smaller than 32%.

The error on Δc₀ also has its source in the presence of restrictions to diffusion in the solutions facing the membrane under study. Equation 1 was established by assuming that resistance experienced by water molecules in the solutions can be neglected compared with the membrane resistance. This approximation may not be valid when the membrane resistance is too small (corresponding to the larger P_os). Finding P_os in this case involves solving a complicated problem of diffusion under non-steady-state conditions (Steudle, 1989). The effect of the inner resistance can be estimated from previous calculations in non-steady-state diffusion problems (Crank, 1956). Let us consider a theoretical sphere that is bounded by a membrane with infinite permeability for a solute. When the sphere, initially equilibrated at a uniform concentration (c₁), has its outer surface concentration shifted to a different concentration (c₀), the inner concentration c₁ is modified and will eventually reach c₀. The difference between c₁ and c₀ is smaller than 10% in a time, τ, that is dependent on the diffusion coefficient (D_s) of the solute and on the radius, a, of the sphere:

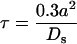A11

The fastest redistribution of osmoticum would be obtained with the more mobile ions. For K⁺ ions inside of a typical 60-μm-diameter cell, τ = 180 ms, assuming D_s ≈ 1.5 × 10⁻⁹ m² s⁻¹ (Bockris and Reddy, 1970). If the time interval, Δt, characterizing the water exchange during measurements is much longer than τ, the unstirred layer effect can be neglected. This is the case for P_os values less than 400 μm s⁻¹, for which Δt ≥ 4 s. For the larger P_os, Δt ≈ 1 s, and the water flux can decrease the concentration gradient applied to the membrane.

From the discussion by Steudle (1980), it seems possible to approximate the external unstirred layer around a spherical protoplast by a layer with thickness

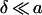A12

If we use the redistribution time τ_e

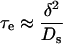A13

for a slab of thickness δ (Crank, 1956) to characterize this layer, Equation A12 indicates that τ_e < τ. The effect of the external unstirred layer is smaller than that of the internal layer.

Because of the lack of more precise calculations and knowledge of the osmoticum, we conclude that the smaller P_os values are not affected by the unstirred layers, whereas the larger P_os, obtained from Equation 1, could be underestimated.