The structure of networks that produce the transformation from grid cells to place cells

Abstract

Since grid cells were discovered in the medial entorhinal cortex, several models have been proposed for the transformation from periodic grids to the punctate place fields of hippocampal place cells. These prior studies have each focused primarily on a particular model structure. By contrast, the goal of this study is to understand the general nature of the solutions that generate the grids-to-places transformation, and to exploit this insight to solve problems that were previously unsolved. First, we derive a family of feedforward networks that generate the grids-to-places transformations. These networks have in common an inverse relationship between the synaptic weights and a grid property that we call the normalized offset. Second, we analyze the solutions of prior models in terms of this novel measure, and found to our surprise that almost all prior models yield solutions that can be described by this family of networks. The one exception is a model that is unrealistically sensitive to noise. Third, with this insight into the structure of the solutions, we then construct explicitly solutions for the grids-to-places transformation with multiple spatial maps, i.e., with place fields in arbitrary locations either within the same (multiple place fields) or in different (global remapping) enclosures. These multiple maps are possible because the weights are learned or assigned in such a way that a group of weights contributes to spatial specificity in one context but remains spatially unstructured in another context. Fourth, we find parameters such that global remapping solutions can be found by synaptic learning in spiking neurons, despite previous suggestions that this might not be possible. In conclusion, our results demonstrate the power of understanding the structure of the solutions and suggest that we may have identified the structure that is common to all robust solutions of the grids-to-places transformation.

Introduction

Four decades ago, O’Keefe and Dostrovsky discovered place cells, neurons in the hippocampus that are selectively active in one or more restricted regions of space, called place fields (O’Keefe and Dostrovsky; O’Keefe and Nadel, 1978). Since their discovery, many models have attempted to explain how this spatial selectivity arises within the hippocampus (Samsonovich and McNaughton, 1997; Kali and Dayan, 2000; Hartley et al., 2000; Barry and Burgess, 2007). With the discovery of grid cells in the medial entorhinal cortex (MEC), the input structure to the hippocampus (Hafting et al., 2005), the problem of explaining the neural representation of space has shifted to focus on two separate questions: First, how does the periodic firing of hexagonal grid cells in the MEC emerge (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Giocomo et al., 2007; Burgess et al., 2007; Burgess, 2008; Hasselmo and Brandon, 2008; Kropff and Treves, 2008; Burak and Fiete, 2009; Mhatre et al., 2010)? And second, how are the periodic grids in the MEC transformed into punctate place fields in the hippocampus (Fuhs and Touretzky, 2006; Solstad et al., 2006; Rolls et al., 2006; Franzius et al., 2007; Blair et al., 2007; Gorchetchnikov and Grossberg, 2007; Molter and Yamaguchi, 2008; Si and Treves, 2009; de Almeida et al., 2009; Savelli and Knierim, 2010)? In this paper, we focus on the latter question. We note, however, that there are alternatives to this simple view of how spatial representations arise in the hippocampus. We return to this issue in the Discussion.

The earliest model of the grids-to-places transformation viewed grid cells as the basis functions of a Fourier transformation and synaptic weights from MEC to hippocampus as the coefficients (Solstad et al., 2006). Other models are based on competition in the hippocampal layer: the summed input to a hippocampal cell from grid cells is only weakly spatially selective, but competition allows only the hippocampal cells with the strongest excitation at any given location to become active, thus increasing the spatial selectivity (Fuhs and Touretzky, 2006; Rolls et al., 2006; Gorchetchnikov and Grossberg, 2007; Molter and Yamaguchi, 2008; Si and Treves, 2009; de Almeida et al., 2009; Monaco and Abbott, 2011). Franzius et al. (2007) suggest that maximizing sparseness in periodic grid inputs leads to punctate place fields in the output of independent components analysis. Recently, Savelli and Knierim (2010) studied a Hebbian learning rule that could learn the weights in a feedforward network to generate the grids-to-places transformation. A few studies have also examined the network structure that produces the transformation (Solstad et al., 2006; Gorchetchnikov and Grossberg, 2007), but these solutions appear to be similar to each other and it is not clear how they are related to the solutions of other models.

Here we derive a solution for the grids-to-places transformation that was previously unknown, at least in its general and explicit form. We then study the solutions of other models in ways that the original authors of those models had not. We find that all examined models, but one (Blair et al., 2007), yield solutions with very similar structures despite their apparent differences. We then present solutions for multiple place fields in one environment and distinct place fields across different environments. (Muller and Kubie, 1987; Leutgeb et al., 2005; Fyhn et al., 2007). While other authors before us have hypothesized mechanisms to account for these two phenomena (Solstad et al., 2006; Rolls et al., 2006; Fyhn et al., 2007; de Almeida et al., 2009; Savelli and Knierim, 2010) no prior study has explicitly demonstrated a working solution where they could control the number and locations of place fields. We also find that multiple spatial maps can be learned by a local synaptic learning in a spiking network, something that Savelli and Knierim (2010) hypothesized to not be possible: “[a]ny feed-forward model that implicates plasticity in the formation of place fields from only grid-cell inputs […] is unlikely to account spontaneously for the memory of many place field maps […]”.

Materials and Methods

This paper focuses on understanding the structure of the solutions for the grids-to-places transformation and exploiting that insight to construct and learn specific solutions. A major goal of this paper is to study the solutions of prior models that are still not very well understood. In this section, we briefly describe these prior models as well as some of our novel analysis methods.

Grid cell firing maps

The rate map of grid cells over space (x⃗) can be described by a sum of three 2-d sinusoids (see Solstad et al., 2006; Blair et al., 2007):

$$g_j(\overrightarrow{x})=\frac{1}{4.5}\left(\sum _{\gamma =1}^{3}cos2\pi \overrightarrow{u_j^{\gamma }}·\frac{\overrightarrow{x}-\overrightarrow{{\xi }_j}}{a_j}+1.5\right)$$ (1)

where ξ_j is the spatial phase or offset, and a_j is the grid spacing. The $\overrightarrow{u_j^{\gamma }}$ are direction vectors that are orthogonal to the main axes of the grid:

$$\overrightarrow{u_j^1}=\frac{2}{\sqrt{3}}\left(\begin{array}{l}cos({\phi }_j+30°)\hfill \\ sin({\phi }_j+30°)\hfill \end{array}\right),\overrightarrow{u_j^2}=\frac{2}{\sqrt{3}}\left(\begin{array}{l}cos({\phi }_j+90°)\hfill \\ sin({\phi }_j+90°)\hfill \end{array}\right),\text{and}\overrightarrow{u_j^3}=\frac{2}{\sqrt{3}}\left(\begin{array}{l}cos({\phi }_j+150°)\hfill \\ sin({\phi }_j+150°)\hfill \end{array}\right),$$ (2)

where φ_j represents the orientation of the grid. An example of a grid cell firing map is shown in Figure 1A. Since the sum of cosines in Eq. 1 yields values between −3/2 and 3, the linear transformation ensures that the rates of grid cells are always positive. Using other gain functions does not seem to affect the grids-to-places transformation (Blair et al., 2007). We used different numbers of grid cells (N) as indicated throughout this paper. As observed experimentally (Hafting et al., 2005), co-localized cells in our simulations (n=10) share the same grid spacing a_j, and orientation φ_j, but each grid cell has its own independent spatial phase ξ_j. Grid spacings were drawn from a uniform distribution between 30cm and 70cm, orientations were uniformly distributed between 0° and 360°. Both grid spacings and orientations were independent between groups of grid cell with different spacings, except in one simulation, in which we studied the effect of aligning all grids at the same orientation as suggested by preliminary results (Stensland et al., 2010, Society for Neuroscience).

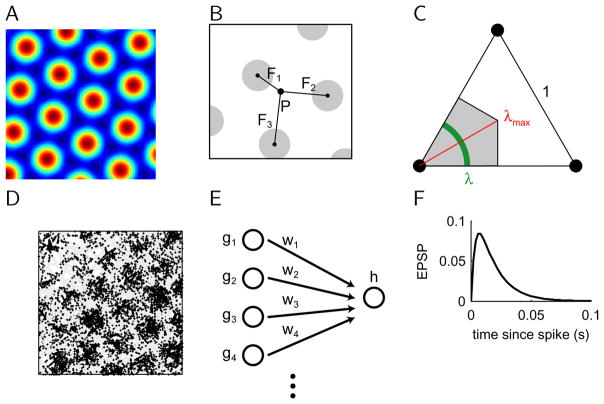
Figure 1. Definition of models and normalized offset.

A, Schematic of grid cell firing rate map. As in all firing rate and activation maps in this paper, red indicates maximum, while blue denotes zero. B, The normalized offset is defined as the shortest distance between the reference point P and the locations of the firing field peaks F_k, divided by the grid spacing. Grey disks mark regions of elevated firing rate. C, Schematic of key properties of normalized offset. For any point P within the equilateral triangle, those located within the grey-shaded area are closest to the vertex on the left. The normalized offsets with respect to all points in the green-shaded section are the same λ. The red line shows the maximum normalized offset that can occur in 2-d ${\lambda }_{max}=1/\sqrt{3}$. D, Example of grid cell spiking. Shown is a 10min session of random exploration. The simulated trajectory of the virtual animal is shown in grey. Each spike is marked by a black dot at the animal’s location when the spike occurred. E, Feedforward network architecture used in this study. The hippocampal cell receives the weighted sum of grid cell inputs. F, Time course of evoked post-synaptic potential.

To describe the spatial phase of a particular grid, we introduced a new measure that we call the normalized offset λ (Fig. 1B). It is the smallest distance between the reference point P and the centers of the firing fields F_β of the grid cell, normalized by the grid spacing:

$${\lambda }_j=\frac{\underset{\beta }{min}d(F_{\beta },P)}{a_j}.$$ (3)

Note that the normalized offset depends on the reference point P. We explore below how the normalized offsets relative to two different points are related. The range of normalized offsets is $0\le \lambda \le 1/\sqrt{3}\approx 0.577$ in 2-d (Fig. 1C), in 1-d it is 0 ≤λ≤ 0.5.

Analysis of firing rate maps

When constructing weights in the rate-based model, we needed to determine whether the network yields a valid solution for the given problem, i.e., a certain number of place fields in given locations. In the figures, we plot the full activation of the hippocampal neuron to show the background as well as the potential place fields. A threshold has to be applied to the activation to identify where the hippocampal cell will fire spikes. To determine the threshold, we proceeded as follows. The threshold was initially set slightly above the maximum activation, so that the cell was inactive across the entire environment. The cell was then allowed to spike in larger and larger parts of the environment by lowering the threshold successively. A place field was defined as a contiguous area of spiking that is wider than 10cm in 1-d, and larger than 50cm² in 2-d. If the desired number of place fields was found at the desired locations, the network was deemed a valid solution. Otherwise, the solution was not valid. We do not suggest that such a mechanism is operating in the biological network, nor is it necessary. In the spiking network model, which is more biologically plausible, the firing threshold is fixed; instead the weights are adjusted to generate place-specific firing.

Simulating spiking networks and synaptic plasticity

To study the grids-to-places transformation in a network of spiking neurons, we proceeded as follows. Given the rate map of the grid cells, we used the time-rescaling theorem (Brown et al., 2002) to generate spike trains for simulations of spiking neurons (Fig. 1D). The timesteps in our simulations were 2ms long. The grid cells send feed-forward projections to one hippocampal cell. The neuron was modelled as integrate-and-fire neuron, whose voltage potential is driven by spikes in the input neurons scaled by the corresponding synaptic weight w_j from grid cell j (Fig. 1E)

$$V(t)=\sum _j{w}_j\sum _{k}K(t-t_{jk}).$$ (4)

The shape and function of the evoked post-synaptic potential was described by the kernel

$$K(t-t_{jk})=V_0\left(e^{-(t-t_{jk})/\tau }-e^{-(t-t_{jk})/{\tau }_s}\right),$$ (5)

where t is the current time and t_jk is the time of the k-th spike fired by the j-th grid cell, and the constants are τ =15ms and τ_s = τ/4 (Fig. 1F). Since our goal was to study the principle of learning spatial representations in a spiking network, we simplified the network by including only one type of abstract current with an intermediate time course. Once the membrane potential crosses threshold, a spike is generated and the membrane potential is reset to the resting potential.

Previous papers have shown that the grids-to-places transformation can be learned by a synaptic learning rule (Gorchetchnikov and Grossberg, 2007; Savelli and Knierim, 2010). We extended these results by studying the solutions that are found and studying whether one network can learn multiple spatial maps. The synaptic learning we used is based on Hebbian plasticity and the amount of weight change at a time t is given by

$$\mathrm{\Delta }{w}_j(t)=\epsilon \left(\sum _{k}K(t-t_{jk})-q\right)y(t)$$ (6)

where ε is a learning rate, q is a plasticity threshold, and y(t) is the activity of the postsynaptic neuron. Synaptic strength can both increase and decrease depending on whether the summed synaptic activation is above or below q. In addition, divisive normalization is used to prevent weights from increasing without a bound and to introduce competition among grid inputs.

With associative Hebbian learning, the weights do not change if the output neuron never spikes. Several approaches are possible to ensure spiking in a novel environment, e.g., one can lower the firing threshold in novel environments, pick the initial weights carefully (Savelli and Knierim, 2010) or assume that plasticity in the hippocampus may occur without post-synaptic spiking (Golding et al., 2002; Frank et al., 2004). We chose to drive neurons with noisy spikes when the animal enters a novel environment for the first time. This mechanism is consistent with experimental observations that, in novel environments, place cells are more active (Karlsson and Frank, 2008) and spiking is less coordinated (Frank et al., 2004; Cheng and Frank, 2008). Additionally, we lowered the plasticity threshold and increased the learning rate for the brief initial period to allow for larger increases in synaptic weights, consistent with experimental reports of enhanced plasticity during novel exposures (Xu et al., 1998; Guzowski et al., 1999; Manahan-Vaughan and Braunewell, 1999; Straube et al., 2003; Li et al., 2003; Lisman and Grace, 2005). The specific parameters of the simulation have to be adjusted for the size of the network and are reported in the Results.

Simulating behavior

To simulate the behavior of a rat, we let a virtual animal randomly explore square enclosures of size 1×1m or 2×2m. We wanted the behaviour to be somewhat realistic, with some stretches of constant velocity and a fairly uniform coverage of the environment. The virtual rat runs with constant velocity between random switching times that are uniformly distributed between 0.4s and 1s. At each switching time, a new velocity is picked from a normal distribution with zero-mean and σ= 30cm/s. The mean speed of the simulated behavior is around 38cm/s. When the virtual rat hits a border, it is “reflected”, i.e., the component of its velocity in the direction of the hit wall is inverted. The results of this paper are not sensitive to the statistics of the behaviour since we obtained similar results with different parameters and with different statistics such as exploration in uniform zigzag lines or Lissajou patterns. Savelli and Knierim (2010) used a movement trajectory recorded from a rat; and their model successfully learned the grids-to-places transformation.

Competitive networks and learning algorithms

Several competitive learning schemes (Rolls et al., 2006; Molter and Yamaguchi, 2008; Si and Treves, 2009) rely on the mechanism first suggested in Rolls et. al. (2006). We therefore refer to these models collective as the “Rolls et al. model”. To understand the structure of these networks we simulated a network of 125 grid cells (g_j) and 100 hippocampal cells (h_i). The rate map was defined in a 1×1m square box divided into 5×5cm spatial bins for a total of 400 bins. In each bin, the activations of the hippocampal cells were given by

$$h_i(x)=\sum _j{w}_{ij}{g}_j(x)$$ (7)

Only the hippocampal cells with the highest activations produce spikes. In the model, the firing rate y_i at a location x is the activation squared for those cells that cross the threshold.

$$y_i(x)=\{\begin{array}{ll}{h_i}^2(\text{x}),\hfill & \text{if}{h}_i(x)>h_{\text{thres}}(x)\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (8)

The threshold h_thres is adjusted such that activity in the hippocampal layer is sparse, which means the activity level $\alpha =\frac{{\left({\sum }_i{y}_i/N_{\text{HPC}}\right)}^2}{{\sum }_i{y_i}^2/N_{\text{HPC}}}$, where N_HPC is the number of hippocampal cells, is around 0.02. In its simplest form, this algorithm requires some spatial anisotropy in the grid cell firing. We introduced anisotropy in our simulation by multiplying the firing rate map of grids cells (Eq. 1) with a random 20×20 matrix. The matrix entries were drawn from a uniform distribution between 0 and 1 and smoothed with a 2-d Gaussian with a standard deviation of a_j/4. Spatial selectivity in the Rolls et al. model is further improved by associative Hebbian learning. In each iteration, weights are adjusted as follows

$$\mathrm{\Delta }{w}_{ij}=\epsilon y_i{g}_j$$ (9)

and the weight vector is then normalized to unity length. We ran the learning algorithm for 100 iterations.

Recently, de Almeida et al. (2009) proposed a conceptually similar model, the E%-max winner-take-all network (“E%-max model”), that uses a different mechanism for competition in the hippocampal layer. The mechanism is tied to gamma oscillations in the hippocampus, which is hypothesized to have an inhibitory effect on the network. As cells are released from inhibition in an oscillation cycle, the neurons with the strongest activation become active first. These active neurons drive recurrent inhibition that prevents other neurons with weaker activations from becoming active.

$$y_i(x)=\{\begin{array}{ll}{h}_i(\text{x}),\hfill & \text{if}{h}_i(x)>(1-z)\underset{i}{max}{h}_i(x)\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (10)

where z = 0.08 is the fraction of cells that become active. In this model, the firing rate is linear in the activations. This model frequently yields place cell with multiple place fields, which are more characteristic of dentate granule cell (Jung and McNaughton, 1993; Leutgeb et al., 2007). A conceptually related mechanism based on release from periodic inhibition at theta frequencies was proposed by Gorchetchnikov and Grossberg (2007).

Maximizing sparseness – independent components analysis

Franzius et al. (2007) suggested that the transformation from grid cells to place cells is linear and set up to maximize sparseness. Under the assumption that distributions are Gaussian, maximizing sparseness is equivalent to independent components analysis (ICA). Here, we adopt the CuBICA algorithm like the original authors, although we note that the particular choice of the algorithm was shown to be inconsequential (Franzius et al., 2007). Since the algorithm operates in rate space, not in the physical space, the transformation from grid cells to place cells are given by:

$$y_i(t)=\sum _j{w}_{ij}{g}_j(t)+c_i$$ (11)

where g_j(t) and y_i(t) denote the rate of grid cells and place cells, respectively, as a function of time as the virtual rat traverses the square enclosure systematically, and the c_i ’s are constants. We performed ICA on 100 grid cells inputs at about 10⁴ time points and obtain the weight matrix w_ij that maximizes the independence among the 100 output cells. We note that this is essentially an unsupervised algorithm that takes grid cell inputs and generates punctate place-cell-like responses.

Tempotron

To explore whether there are other classes of solutions not represented in existing models, we used the Tempotron to learn the weights between the grid cell inputs and a hippocampal place cell. The Tempotron is a supervised learning algorithm that allows a single neuron to learn to classify complex spike-timing patterns in its inputs (Gutig and Sompolinsky, 2006). Here the goal is that the output neuron fires spikes only while the animal is located within a place field, a circle of 14cm diameter. Inputs were presented to the Tempotron in 200ms-long snippets. To generate the input patterns we turned spike trains from the simulated grid cells into digitized strings of 100 bits, where every bit represents the neural activity in a 2ms time window. A bit is set to 1 if at least one spike occurred within the time window and to 0 if no spike occurred. The dynamics of the Tempotron is the same as in Eqs. 4 and 5, except after the voltage crosses the threshold V_thres =1, the membrane potential is not reset and further inputs are shunted for the remainder of the 200ms window. If the animal is located within the place field, the output neuron should fire a spike at any time during the 200ms window. Otherwise, the output neuron should remain silent. If the neuron fired a spike incorrectly, then weights are decreased. If the neuron remained silent incorrectly, then weights are increased. The amount of weight change is given by

$$\mathrm{\Delta }{w}_j=\epsilon \sum _{t_{jk}<t_{max}}K(t_{max}-t_{jk})$$ (12)

where t_max is the time at which the membrane potential as the highest. We used a learning rate of ε = 0.3 and a momentum term (Gutig and Sompolinsky, 2006) to improve performance of the learning algorithm, i.e., Δw_j^current = Δw_j + μΔw_j^previous with μ = 0.8. We initialized the weights with uniform random numbers, and ran the algorithm for 50 iterations. The total length of the simulated session was 600s. Thus, 600s/200ms= 3000 patterns were presented to the Tempotron.

Comparing network solutions

An issue arises when comparing the results of network models that rely on competition, such as the Rolls et al. model, and single neuron models, such as the Tempotron. In single cell models, synaptic activations drive spiking of the downstream cell independently. In a network, however, the activations of the other cells in the layer can influence whether a given cell will spike. To make both types of models comparable, we computed the “effective synaptic weights” in network models as follows. Across the entire environment, we averaged the synaptic weights between grid cells with a given normalized offset and all the postsynaptic neurons that became active. This average can then be interpreted as the synaptic weight between one representative grid cell with that normalized offset and one representative hippocampal cell.

Results

Deriving a robust solution

We first derive a novel solution for the grids-to-places transformation. In the feedforward network, a number (N) of grid cells project with synaptic weight w_j to a single hippocampal neuron represented by h (Fig. 1E). In 1-d, grids are represented by periodic cosine functions

$$h(x)=\sum _{j=1}^N{w}_{j}cos2\pi \left(\frac{x-{\xi }_j}{a_j}\right).$$ (13)

If all basis functions had the same offset ξ_j = x₀ and the weights were a Gaussian function of the grid spacing, then this model would be a Fourier transformation as studied before in the context of the grids-to-places transformation (Solstad et al., 2006). As these assumptions are not likely to be realistic, we generalized this approach to include arbitrary offsets and different functions for the weights. If the offsets ξ_j are random, then the sum of cosines becomes homogenous and no spatial specificity arises (Solstad et al., 2006). This symmetry can be broken by assigning the weights based on the spatial offset of the grid. To see how this would help, we rewrote the cosines in Eq. 13 in terms of the normalized offset λ.

$$cos2\pi \left(\frac{x-{\xi }_j}{a_j}\right)=cos2\pi \left(\frac{x-x_0}{a_j}\pm {\lambda }_j\right).$$ (14)

Note that the normalized offset depends on the reference point x₀, the location where we want the place field to occur. If we assign the weights according to

$$w_j=mcos2\pi {\lambda }_j,$$ (15)

the sum over cosines breaks into two components

$$\begin{array}{l}h(x)=m\sum _{i=1}^{N}cos2\pi {\lambda }_{i}cos2\pi \left(\frac{x-x_0}{a_i}\pm {\lambda }_i\right)\\ =\frac{m}{2}\sum _{i=1}^{N}cos2\pi \left(\frac{x-x_0}{a_i}\right)+\frac{m}{2}\sum _{i=1}^{N}cos2\pi \left(\frac{x-x_0}{a_i}\pm 2{\lambda }_i\right).\end{array}$$ (16)

To get the second line, we used $cos\theta cos\phi =\frac{1}{2}(cos(\theta +\phi )+cos(\theta -\phi ))$. The first component gives rise to a peak at x₀, because the basis functions are aligned, while the second component has random phases and adds up to a noisy background (Fig. 2B,C). The derivation in 2-d are very similar and not repeated here.

Figure 2. The grids-to-places transformation is generated by a large class of networks.

When synaptic weights are assigned to periodic basis function (N= 100) with random spacings and spatial offsets according to Eq. 15 (A), place-specific activation emerges in both 1-d (B) and 2-d (C). Place fields can be identified by thresholding the activation of the hippocampal neuron shown here (see Methods). Place-specific activation also appear, if the relationship between weights and normalized offsets are a step function (D–F) or linear functions with added Gaussian noise (G–I). The derived solution is robust in that large deviations in the weights do not disrupt the transformation. J,K, Summary of robustness to Gaussian noise in the weights across 1000 simulations. The noise is quantified by the explained variance (R²). Shown is the fraction of simulations, in which a place field emerged in 1-d (J) and 2-d (K) for different network sizes N=10 (magenta), N=20 (cyan), N=50 (red), N=100 (green), and N=200 (blue). The dashed lines in K show results from simulations in which all grids shared the same orientation.

Feedforward networks with weights according to Eq. 15 are not the only solutions, in fact, we found that the functional shape is not essential. The important feature is that inputs from grids with small normalized offsets are favored over those with large offsets. For instance, the cosine can be replaced by a step function such that only closely aligned grids contribute, or by a linear function w_j = m(λ_j – λ₀), where λ₀<λ_max, and the activation of the hippocampal cell remains place-specific (Fig. 2).

To analyze the robustness to variations in the weights more systematically, we added varying amounts of Gaussian noise to the weights after they were set up as a linear function of the normalized offset. We quantified the noise by the explained variance (R²) in a linear regression between the weights and the normalized offsets. We performed 1000 simulations for different amounts of noise in the weights and network sizes (N=10, 20, 50, 100, 200). We then determined the fraction of simulations in which a single place field emerged at the desired location (see Methods). As expected, the lower the noise level, and thus more predictive the normalized offset was of the weights (e.g. the higher the explained variance), the more simulations produced a place field (Fig. 2J,K). Interestingly, very high robustness to noise in the weights was already achieved with relatively small networks of 50 grid cell inputs in both 1-d and 2-d (solid red lines in Fig. 2J,K). This solution is therefore robust for small networks, similarly to what previous studies found (e.g. Solstad et al., 2006). Note that the explained variance is a relative measure of variability. We found that the overall magnitude of the weights had little effect on robustness (data not shown).

Recent preliminary results suggest that the orientations of grid cells might be aligned, even for those with different grid spacings (Stensland et al., 2010, Society for Neuroscience). We therefore studied the robustness of the grids-to-places transformation in 2-d if all grids were aligned. The weighted summation of aligned grids yields a star shaped activation pattern, along the six cardinal directions (Solstad et al., 2006). Due to the alignment, we expect that the likelihood of spurious place fields increases. We found indeed that the grids-to-places transformation was less robust to noise when all grids were aligned (Fig. 2K, dashed lines). However, the reduction was somewhat small and the following results were obtained from networks with multiple grid orientations (see Methods).

In summary, we have found a novel family of solutions for the grids-to-places transformation. We showed that a noisy, inverse relationship between weights and normalized offset is sufficient to generate grids-to-places transformation in feedforward networks. In the following, we examine whether this condition is necessary to generate a solution. In other words, must valid solutions of the grids-to-places transformation have an inverse relationship between weights and normalized offset? As it is not clear whether a mathematical proof can be generated, we studied this question empirically by examining the solutions of various models.

The solution of robust models share a common structure

Little is known about the structure of the solutions that most prior models for the grids-to-places transformation generate. In our analysis, we were mainly interested in the relationship between the generated weights and the normalized offset. For the models that do not explicitly construct their solutions, we used the following method. We simulated the model to obtain a solution (Fig. 3A) and examined the relationship between the weights and normalized offset (Fig. 3B). The normalized offsets were determined posthoc with respect to the place field that emerged from the model. To compare weights between single-cell models and network models that rely on competition, we calculated an effective weight for the latter (see Methods). Each model was simulated 1000 times to generate a statistical distribution of solutions, each of which was quantified by the explained variance that was introduced in the previous section (Fig. 3C). To assess whether the distributions of explained variances are statistically significant, we compared the distributions to a shuffled distribution generated as follows. We randomly selected a solution of one of the models as a starting point, randomly shuffled the weights 1000 times and calculated the explained variance each time. The model distributions were then tested against the shuffled distribution using a two-sample Kolmogorov-Smirnov test.

Figure 3. The solutions of several other models share the same structure.

A, Sample place fields obtained from five different models named in each column (see Methods). B, (effective) weight vs. normalized offset for the sample shown in A. C, Distribution of explained variances over 1000 repetitions of the simulation. While there are clear differences between the models, their solutions all have a significant explained variance in the relationship between weights and normalized offset.

We used this method to study the solutions of three rate-based models: the competitive network and learning based on the Rolls et al. model (Rolls et al., 2006), the E%-max winner-take-all network (de Almeida et al., 2009), and an ICA-based model (Franzius et al., 2007). All three models generated place cells from grid inputs (Fig. 3A); and their solutions showed a strong inverse relationship between (effective) weight and normalized offset (Fig. 3B). The explained variance (Fig. 3C) was highly significant for the three models (p < 10⁻¹⁰).

We next studied the solutions of two models with spiking neurons and two different learning algorithms: one unsupervised and one supervised. The unsupervised learning rule is similar to the one proposed by Savelli and Knierim (2010) (see Methods). We used networks with N = 500 grid inputs. The initial period lasted 60s, during which noisy background spikes were generated at 1.5Hz subject to a maximum of 90 spikes, the learning rate was ε= 5 and the plasticity threshold q=0.012. Learning proceeded for a further 6 min with a learning rate of ε= 0.3 and plasticity threshold q=0.018. These parameters were chosen to generate place cell responses in many simulations (e.g. Fig. 3A, 4^th column). The solutions of this spiking network, too, show a strong correlation between weight and normalized offset (Fig. 3B, 4^th column). The explained variance is non-zero in almost all cases (Fig. 3C, 4^th column), consistent with our goal to select simulation parameters that generate place fields in many cases.

Figure 4. An example of a non-conforming, unstable solution.

A, rate map that results when grid cell inputs are multiplied with pseudoinverse solution (see Results). B, weight distribution of pseudoinverse solution. Linear regression is not significant (p=0.94) and the explained variance is negligible (R² = 1.3×10⁻⁵). C, Example of the extreme sensitivity to small deviations of the pseudoinverse solution. Each panel shows the output of the model if weights remain the same but the firing rate of one randomly chosen grid cell is increased by 1% (see Results).

Two studies constructed the solution explicitly. Gorchetchnikov and Grossberg (2007) suggested a solution in which a place cell receives uniform inputs from grid cells with firing fields aligned at the place field location, and no input from misaligned grids. In other words, the relationship between weights and normalized offset is a delta-function

$$w_j=\{\begin{array}{cc}1& \text{if}{\lambda }_j=0\\ 0& \text{otherwise}\end{array}$$

The authors also suggest a learning rule that is capable of learning this solution approximately. Solstad et al. (2006) studied a similar model with two important differences. First, the weights are not uniform, but chosen to generate a place field with a Gaussian shape. Second, the transformation was shown to be robust to jitter in the grid offsets of < 30% of the grid spacings. Put together, the solution looks like the delta function with variability in both the weights and the normalized offsets. Therefore, both explicitly constructed solutions show an inverse relationship between weights and normalized offset.

Since the models discussed so far were specifically introduced to explain the grids-to-places transformation, we next explored whether a general-purpose, supervised learning algorithm, such as the Tempotron (Gutig and Sompolinsky, 2006), would find solutions of a different kind. With grid cell spiking in the inputs, we required that the Tempotron spiked only when the animal was located within the place field (see Methods). The Tempotron learned the transformation (Fig. 3A, 5^th column). The weight distribution showed a strong linear relationship to the normalized offset in every case (Fig. 3B, C, 5^th column). The explained variance was highly significant for both spiking models (p < 10⁻¹⁰).

In summary, the results in this section show that several models yield solutions that share the same structure. While there are minor differences between the explained variance for the various models, which we will revisit in the Discussion, we find that a non-zero explained variance is a common property of the solutions of the several different models. This result suggests that the differences in the details of the examined models are not important for generating the grids-to-places transformation. However, there is a counterexample that we discuss now.

A non-robust solution yields a different solution

The analytical model proposed by Blair et al. (2007) generates place fields from grid cell inputs (Fig. 4A), however, we find that there is no discernable relationship between weights and normalized offset (Fig. 4B). A hint of an explanation for this discrepancy is already visible in the magnitude of the weights which span eight orders of magnitude (Fig. 4B). As we will show below, these unrealistic weights are related to the fact that the model’s solutions are unstable.

In the model, 2-d firing rate maps are binned and the rates stacked in each bin in vectors g⃗_j and h⃗, for grid and place cells, respectively. Then the relationship between the firing rate vector of grid and place cells is approximated with a linear relationship.

$$\overrightarrow{h}=[{\overrightarrow{g}}_1\cdots {\overrightarrow{g}}_N]\overrightarrow{w}$$ (17)

Generally, there is no solution to this equation since [g⃗₁…g⃗_N] is not necessarily a square matrix, but the Moore-Penrose pseudoinverse, denoted by ^†, can be used to get an approximate solution

$${\overrightarrow{w}}_{\text{PI}}={[{\overrightarrow{g}}_1\cdots {\overrightarrow{g}}_N]}^{†}\overrightarrow{h}.$$ (18)

This solution will minimize the Euclidean distance between the target h⃗ and the output of [g⃗₁…g⃗_N]w⃗_PI. The extreme values for the weights arise because the matrix [g⃗₁…g⃗_N] is ill-conditioned, with a condition number around 1.7 × 10¹⁷ in this particular example. Roughly speaking, a large condition number arises when the columns of the matrix g⃗₁, …, g⃗_N are too similar to each other. Generally, pseudoinverse solutions are unreliable, i.e., the solutions are highly sensitive to small deviations in the parameters, when the condition number is larger than 1. To demonstrate this sensitivity, we randomly chose one grid cell g⃗_j, increased its firing rate by only one percent ( g⃗′_j), and then computed h⃗′ = [g⃗₁…g⃗′_j…g⃗_N]w⃗_PI. The outcome of the model is very different from the original solution and essentially unpredictable in the eight different attempts (Fig. 4C).

By contrast, solutions with a linear relationship between weight and normalized offset are robust to noise as shown above. Robustness to noise is important for any model of a neural process because it makes the model more likely to be implementable in real neural networks. In conclusion, our empirical analysis indicates that an inverse relationship between weights and normalized offset might be a necessary condition for a robust solution to the grids-to-places transformation.

Generating solutions with multiple place fields

Next, we show that solutions for multiple place fields and global remapping can be generated with fields in arbitrary locations, which has not been demonstrated concretely before. The mechanisms that underlie the solutions are the robustness studied above and the specificity of the solutions. Having shown that the explained variance between the weights and normalized offsets λ_j(x₀) correlates with the emergence of place field at x₀ in all robust solutions, we examined how likely it is that a spurious place field emerges at another, random location x. In the examples in Fig. 2, strong spatial selectivity is only seen at the desired place field location, indicating that the solutions are specific in these cases. To assess specificity systematically, we set up a network with a place field at a reference point x₀ and analyzed the explained variance between the fixed weights and normalized offsets λ_j(x) for different locations x (Fig. 5). The advantage of this approach as compared to simply scanning the activation map for spurious place fields is this: We do not need a specification of what constitutes a place field, i.e., a threshold, a minimum size, etc., parameters which have to be set arbitrarily. A related advantage is that our approach naturally deals with above-threshold activation that does not meet the criteria for place fields. For small networks with N=10 grid cells, we found that there is a significant probability that place fields occur at multiple spurious locations as indicated by large values of the explained variance at many locations (Fig. 5A–C). However, with N as low as 100 it is highly unlikely that a place field emerges at an random location since the explained variances at locations away from x₀ are very small (Fig. 5D–F).

Figure 5. Solution is highly specific to the given reference location.

After assigning weights as linear function of normalized offset at the origin x₀=0, the explained variance between the fixed weights and the normalized offsets relative to other locations x are calculated in A,D, 1-d, and B,E, 2-d. C,F, same as in B, and E, but for a larger area (10×10m). For a small number of grid cell inputs (N= 10), high values of the explained variance occurs throughout the environment (AC). For larger networks (N= 100), high explained variance occurs only near the reference point, i.e., the solution is specific to the reference point (D–F).

The robustness to noise and specificity of the solution can be exploited to generate multiple fields in a single environment (Jung and McNaughton, 1993; Leutgeb et al., 2007; Fenton et al., 2008). For instance, to generate a place cell with three place fields in given locations (Fig. 6A), we divided the input weights from the grid cells into three sets. Each set of weights was set up to generate a place field in a different location (Fig. 6B). All synaptic connections are always active, but at any one place field location two sets of weights contribute a homogeneous background, which does not disturb the one place specific set since the solution is robust. Put simply, structure is hidden in the noise. In principle, this approach is similar to a previous hypothesis that a superposition of multiple solutions would yield a solution with multiple place fields (Solstad et al., 2006), however, we are the first to demonstrate a working example and to study its quantitative limitations. We found that this principle can account for a number of multiple place fields, so long as the network is large enough (Fig. 6C).

Figure 6. Accounting for multiple fields in single environment.

A, Example of firing rate map, in which the feedforward network was set up to generate place fields in the locations marked by three black dots. The activation map shown here was generated with hand-wired weights. B, The weights (N=600) are colored green, blue and magenta to separate them visually, but are indistinguishable in the simulations. Each set of weights were chosen so that they generate an activation peak in one of the desired locations. Relative to this location the other two sets of weight appear to be noise, thus contributing only a homogenous background to the activation. C, Summary for 2 (blue), 3 (green), 4 (red), 5 (cyan), and 6 (magenta) place field locations. Even small networks can support multiple place fields.

Global remapping and learning multiple simultaneous maps

We next turn our attention to global remapping, where place cells exhibit firing fields in unrelated locations in enclosures of the same shape placed in different spatial contexts (Muller and Kubie, 1987; Leutgeb et al., 2005; Fyhn et al., 2007). Global remapping is similar to a place cell having multiple place fields, except the fields are expressed in different spatial contexts (Fig. 7A). Recent simultaneous recordings from hippocampus and MEC have shown that grid cells in MEC shift and/or rotate their firing grid when global remapping occurs in place cells (Fyhn et al., 2007). Co-localized grid cells with the same grid spacing appear to shift their offsets by the same amount; and it has been suggested that grids with different spatial offsets shift and/or rotate independently (Fyhn et al., 2007), although the rotations might not be independent (Stensland et al., 2010, Society for Neuroscience). With this assumption we found that changes in the grids lead to a reshuffling of the normalized offsets, and, therefore, a solution in one environment is not necessarily valid in another (Fig. 7B). As a result, place fields can emerge in different locations in the different environments. Fine-tuning is not necessary to obtain global remapping. We ran 2000 simulations in which the desired place field locations in the different environments were drawn randomly from independent, uniform distribution. If the network is sufficiently large, place fields emerge in two environments in almost every simulation (Fig. 7C). Since the desired place cell locations in both boxes were drawn from independent distributions, the result shows that global remapping with independent place field locations is possible in a simple feedforward network.

Figure 7. Accounting for global remapping.

A, we constructed an example of global remapping, a place cell with place fields in different locations in two environments. B, Weights (N=400) are colored differently to separate them visually, however, they are indistinguishable in the simulations. The green weights were chosen so that they generate a place field in box 1. With respect to this location in box 1, the blue weights appear to be noise and do not drive spiking. By contrast, in box 2 with respect to another location, the blue weights form a valid solution and thus generate a place field in the other location, while the green weights appear to be noise. C, Shown are the fractions of 200 simulations in which the place field emerge at the specified location, and only there, in two (red) or three (cyan) environments.

We reasoned that a local unsupervised learning rule should be able to generate such a solution since multiple simultaneous spatial maps can be represented in a simple feedforward network. We used a network with N=1000 grid cells and a single hippocampal cell (see Methods), consistent with anatomical estimates that one hippocampal cell receives about a few thousand MEC inputs (Amaral et al., 1990). We used a similar learning rule as Savelli and Knierim (2010) and, like them, found that for many parameters learning in the second environment erased the spatial map in the first environment. We were, however, able to find parameters that balance the plasticity in the two environments. Some parameters influence the degree of synaptic plasticity directly. These are the learning rate and plasticity threshold in Eq. 6, as well as the amount of noise spiking during the initial exposure to a novel environment. However, other parameters can have an indirect effect on synaptic plasticity such as the size of the network or the strength of the evoked post-synaptic potential. In addition, we believe that the direct plasticity parameters change dynamically during learning. Due to the large number of parameters, and their nonlinear and dynamically-changing influence on the emergence of place fields, we know of no automated way to search this parameter space. We therefore performed a manual search, in which all network parameters were kept fixed and direct plasticity parameters were adjusted systematically until place fields emerged in both locations. In the following, we demonstrate Hebbian learning of multiple spatial maps for one particular set of parameters. Slightly different parameters can also generate multiple spatial maps, but with differing success rates in producing a place fields in only one or both environments.

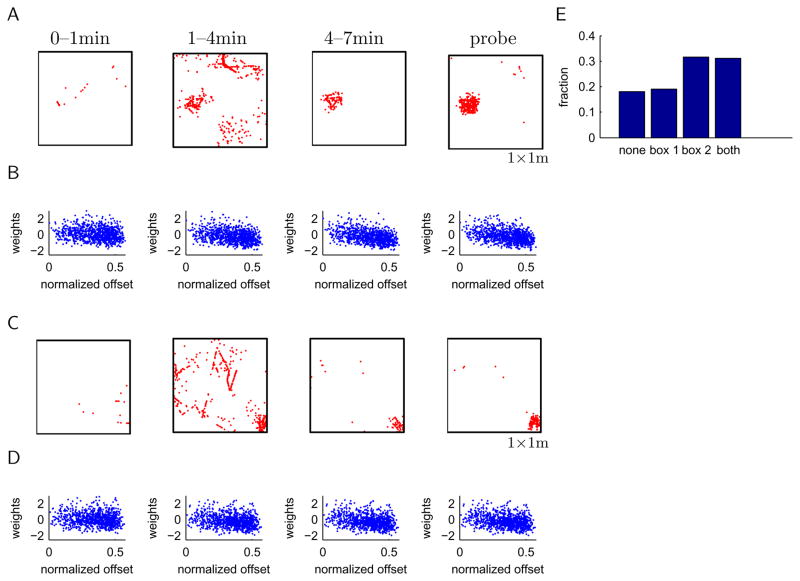
In the initial period of novel exposure, noisy background spiking was injected into the hippocampal cell for 60s at a mean rate of 1 Hz (max. 20 spikes), the learning rate was ε=1.2 and the plasticity threshold q=0. As a result, spiking during the initial exposure in a novel environment is fairly unstructured (Fig. 8A) and drives plasticity rapidly. After the initial period, learning continues for another 6 min with lower learning rates (ε= 0.1) and higher plasticity threshold (q = 0.02). We present the spiking maps separately for the first and second half of this learning period, i.e., from 1–4min and 4–7min, to show the development of the place specific firing (Fig. 8A). While spiking is relatively disperse at first, it becomes spatially selective similar to real place cells by the end of the learning period. Thus, place fields emerge on the time scale of minutes, consistent with experimental results (Frank et al., 2004). Further learning with plasticity engaged does not change the spike map or weight distribution significantly (data not shown). Plasticity is not required to maintain spatial selectivity since the place field remains stable when we switch off plasticity (Fig. 8A, “probe”). Note that we did not specify the location of the place field in the learning process, rather, the place field emerged spontaneously from the randomly assigned initial weights and noise spikes in the first minute of exposure. In other words, learning was unsupervised.

Figure 8. Unsupervised learning finds solution for global remapping.

A, Learning yields solution rapidly. Noisy spikes were added and plasticity turned up during the initial exposure, then lowered for the next 6min of learning. Spike maps show initially unstructured spikes and the rapid emergence of a clean place field. “Probe” refers to a simulation without plasticity after learning in both boxes was complete. B, Post-hoc analysis of weights plotted versus normalized offset, which were computed relative to the place field that emerged in the learning period. C,D, The network was then exposed to a second novel environment under the same conditions. In this example, a place field emerges in the second box in a different location. E, Summary of place field emergence in 200 repetitions of learning in both environments. Shown are the fraction of simulations in which the hippocampal cell expresses no place fields in either environment (“none”); in one, but not the other environment (“box1”, “box2”); or in both (“both”) environments.

After learning in the first box, the same learning procedure was applied in box 2. We note that after learning in box 2, the network is tested in both box 1 and 2 without any further plasticity (Fig. 8, “probe”). This is a hard test since the network does not have the opportunity to reshape the weights in box 1 after they were disturbed by learning in box 2. This protocol frequently generated place cells that exhibited global remapping (e.g., Fig. 8C,D). We repeated this procedure 200 times, generating new grids, initial weights, noise spikes and behavior for each run. The initial weights were generated as follows to make the starting conditions for learning in box 1 and box 2 as similar as possible. We took the weights from a previous simulation, permuted them randomly and performed the learning algorithm outlined above. The results of this “burn-in” run were discarded, only the weights were retained. We found that in more than 80% of the simulations a place field emerged in at least one box (Fig. 8E), evidence that the synaptic learning rule is quite robust in learning the appropriate weights for generating place fields (Savelli and Knierim, 2010). There is a bias towards establishing place fields in box 2. In about one third of the simulations, a single place field was found in box 2 only, compared to about one fifth in box 1 only. This bias is due to the fact that learning in box 2 can delete the place field in box 1, but not vice versa. Nonetheless, in contrast to previous reports (Hayman and Jeffery, 2008; Savelli and Knierim, 2010), we were able to generate place fields in both boxes in about one third of the simulations by balancing the plasticity induced in both environments. Our result thus demonstrates that a single feedforward network can learn multiple spatial maps through Hebbian plasticity.

Discussion

We derived a more general solution for the grids-to-places transformation than was previously known. This solution involves a simple inverse relationship between the synaptic weight of a grid cell input and the relative location of the grid cell peaks, as quantified by the normalized offset. We showed that this structure is common to all robust solutions generated by a number of disparate models. We used our insight into the structure of the solution to account for important properties of place cells such as multiple fields, and global remapping. The latter solution can be found by a local synaptic learning rule in a biologically-plausible network.

Comparison of different models

It is clear from our study that a network with a large explained variance in the relationship between (effective) weights and normalized offset is sufficient to generate the grids-to-places transformation. While the Blair et al. model shows that a nonzero explained variance is not necessary to obtain a solution, all robust solutions that we generated with different models of the grids-to-places transformation had significant explained variances. We therefore conjecture that a nonzero explained variance is necessary for a robust solution. We also used the general-purpose Tempotron to learn the transformation and every learned solution, without exception, had nonzero explained variance. Nonetheless, all this evidence still does not constitute a proof in the mathematical sense and it remains possible that robust solutions with zero explained variance exist. Future work might very well find that the class of robust solutions is larger than we suggest here, but until such time, we think that there is very convincing empirical evidence in favor of our conjecture.

While the explained variances are highly significantly different from zero for solutions of all models in Fig. 3C, the distributions are widely different from each other. This diversity is due to the various mechanisms in these algorithms. For instance, the Tempotron will stop changing the network weights as soon as the place cell does not fire spikes outside the imposed place field. Since the solution is robust to noise, solutions are possible with small values of the explained variance. The Tempotron’s solutions have therefore relatively low and narrowly distributed explained variances as compared to the other models. Furthermore, some models yield weights with zero explained variance in some simulations. These are generally cases where the algorithm failed to generate a place field in the output. The model by Rolls et al. yields a number of such cases, consistent with their intention to produce sparse activation of place cells, as observed in the dentate gyrus (Rolls et al., 2006). ICA also yields a large number of solutions with low explained variances, consistent with the fact that ICA generates a substantial fraction (~25%) of cells without clear place fields (Franzius et al., 2007).

Place field size

The place fields in our simulations are somewhat small for typical CA1 or CA3 cells, and are more consistent with those of DG cells. Like others before us (Solstad et al., 2006; Molter and Yamaguchi, 2008), we found that the size of the place fields are determined by the largest scale of the grid inputs. Thus, the place fields would be larger if grids of larger scale were included in the model. We could have included larger grid spacings than 70cm to obtain larger place fields. The largest grid spacings observed in MEC to date of around 5m (Brun et al., 2008) are sufficient to explain all but the largest place fields in the ventral part of the hippocampus (up to 10m) (Kjelstrup et al., 2008). However, the full extent of the MEC has not been recorded from, yet, and the scales might match when all grid cells are taken into account. Also, there is a recent suggestion that hippocampal place cells that receive direct inputs from MEC have tighter place fields than those that receive indirect projections (Colgin et al., 2009). Nevertheless, changing the spatial scale does not affect the principle of the grids-to-places transformation, which is the main focus of this study.

Emergence of place cells in unsupervised learning

In our simulations of Hebbian learning in a spiking network, a valid solution emerges in almost every run. One might ask then, why only about 30–50% of CA1 and CA3 cells (Wilson and McNaughton, 1993; Leutgeb et al., 2004; Karlsson and Frank, 2008) and far fewer DG cells (Jung and McNaughton, 1993; Chawla et al., 2005) are active in an environment. The answer here is that we chose simulation parameters, i.e. the rate and duration of spontaneous background spiking in a novel environment, the plasticity threshold and synaptic learning rate, to maximize the chance that a place field will emerge. In the real MEC-hippocampal system, these parameters might be optimized for some other purpose, for example, not all neurons might be driven equally by the spontaneous background spiking in a novel environment. Although one recent study reports that certain intrinsic cell properties predetermine which cells will develop place fields in a subsequent exposure to a novel environment (Epsztein et al., 2011), the parameters of the real system are largely unknown. The point of our study was to show that the solution can be learned robustly, not just in a few hand-picked instances.

Other concepts for global remapping

Our account of global remapping is essentially a linear superposition of multiple independent solutions. What we demonstrated is that, within certain limits, the multiple solutions do not interfere and place field locations can be chosen arbitrarily. Our approach contrasts with other mechanisms proposed to account for global remapping. Fyhn et al. (2007) suggested in the supplementary material two different ways to account for global remapping. One hypothesis is based on the assumption that subpopulations of grid cells (with the same grid spacing) realign independently, which we adopted here. Fyhn et al. hypothesized that place fields arise because firing fields of a number of grid cells overlap at the location of the place field and when the grids realign during global remapping the overlap occurs at a different location. While this idea appears conceptually similar to our approach, the authors suggest that the place field locations are fixed by where the grids happen to overlap, whereas in our approach we generate place fields in arbitrary, independent locations.

A possibility that cannot be excluded entirely based on experimental results is that grids remap coherently. If all grids shift coherently, then the place fields must shift by the same amount. Global remapping between two enclosures could then be easily explained (Fyhn et al., 2007). Grid cells and place cells shift coherently by some large amount when the animal is moved between the enclosures. As a result some place fields shift out of, some into the enclosure. Since measurements are obtained only within the enclosure, it will look like place fields are emerging or vanishing (e.g. Molter and Yamaguchi, 2008).

While not directly related to the grids-to-places transformation, we note that recurrent networks can also support multiple spatial maps simultaneously based on the internal dynamics (Samsonovich and McNaughton, 1997). In the multiple charts model, external inputs select different charts, i.e., spatial maps. The activity is maintained within a chart by the internal network dynamics.

The role of the network in generating place cells and global remapping

In this paper, we mainly focused on feedforward networks with grid cells in the input and a single hippocampal neuron in the output. In these networks, different hippocampal cells are independent of each other. Of course, this model is only a crude approximation of the much more complex hippocampal formation. However, this simplification is necessary to dissociate the contributions of the feedforward pathways from grid cells to place cells, the recurrent network dynamics, the correlations in input connections, and the contribution of inputs other than grid cells. That is why we studied what place cell properties could be accounted for by a minimalistic, feedforward model.

One advantage of having a network of hippocampal neurons might be a greater coding capacity. In terms of the number of different spatial maps, the coding capacity of a single neuron in our calculation is somewhat small (Fig. 7C). By combining many hippocampal neurons with independent spatial maps into a population code, we expect that the network could reach a much larger coding capacity than a single neuron.

We neglected the other major input to the hippocampus from the lateral entorhinal cortex (LEC) (Hjorth, 1972), where neurons exhibit spiking that is weakly modulated by the spatial location of the animal (Hargreaves et al., 2005). Since we did not include LEC input in our study to generate place-cell-like responses and global remapping, we conclude that LEC is not a prerequisite for these processes in contrast to what other authors hypothesized (Hayman and Jeffery, 2008; Si and Treves, 2009). Ultimately, the role of LEC in generating place cell responses and global remapping, if there is one, needs to be tested by experiments. Preliminary results suggest that LEC lesions might affect rate, but not global, remapping (Leutgeb et al., 2008 SfN abstract). This result would suggest that the LEC does not affect the spatial map itself, but facilitates the modulation of place cell firing by context (Renno-Costa et al., 2010).

Recent observations show that relatively normal place cells exist even when MEC neuron spiking does not show a clear grid pattern during early development (Langston et al., 2010; Wills et al., 2010) and when the medial septum is inactivated (Brandon et al., 2011; Koenig et al., 2011). These findings seem to suggest that grid-like inputs are not required to generate place cells in the hippocampus. Other inputs are available that could potentially drive place cell spiking, including weakly spatial inputs form LEC (Hargreaves et al., 2005) and spatially modulated, but nonperiodic, firing in superficial MEC – in fact even in MEC layer 2 only about half of the cells are significant grid cells (Boccara et al., 2010). However, it is also possible that weakly grid-like responses with a large amount of noise in MEC “grid cells” could drive place cell responses during early development and in the inactivation studies. Therefore, the simple grids-to-places transformation view cannot be rejected at this point.

Our results refute a claim by Hayman and Jeffery (2008) that summation of grids cells alone cannot account for three place field phenomena: First, place fields are punctate and nonrepeating; second, place cells are active in some, but not all environments; and third, global remapping. We have demonstrated in this paper that, if weights are chosen appropriately, a simple weighted summation of grids of different scales can exhibit the three place field phenomena referred to by Hayman and Jeffery.

In closing, we have demonstrated that neural network models that generate robust solutions for the grids-to-places transformation all yield solutions with the same structure and that understanding this structure facilitates the construction of solutions with arbitrary place field locations. These findings stress the importance of carefully studying the solutions of neural network models.

Highlights.

• We study theoretically how periodic grid cell spiking is transformed into punctate spiking of place cells.

• We derive a family of solutions that are robust to noise.

• We show that various other models also yield solutions with the same structure.

• This insight allows us to generate solutions with multiple spatial maps, which accounts for multiple place fields and global remapping.

• These multiple spatial maps can be learned by an unsupervised Hebbian learning rule.

Abbreviations

ICA

independent components analysis

MEC

medial entorhinal cortex

LEC

lateral entorhinal cortex