Variability in Proactive and Reactive Cognitive Control Processes Across the Adult Lifespan

Abstract

Task-switching paradigms produce a highly consistent age-related increase in mixing cost [longer response time (RT) on repeat trials in mixed-task than single-task blocks] but a less consistent age effect on switch cost (longer RT on switch than repeat trials in mixed-task blocks). We use two approaches to examine the adult lifespan trajectory of control processes contributing to mixing cost and switch cost: latent variables derived from an evidence accumulation model of choice, and event-related potentials (ERP) that temporally differentiate proactive (cue-driven) and reactive (target-driven) control processes. Under highly practiced and prepared task conditions, aging was associated with increasing RT mixing cost but reducing RT switch cost. Both effects were largely due to the same cause: an age effect for mixed-repeat trials. In terms of latent variables, increasing age was associated with slower non-decision processes, slower rate of evidence accumulation about the target, and higher response criterion. Age effects on mixing costs were evident only on response criterion, the amount of evidence required to trigger a decision, whereas age effects on switch cost were present for all three latent variables. ERPs showed age-related increases in preparation for mixed-repeat trials, anticipatory attention, and post-target interference. Cue-locked ERPs that are linked to proactive control were associated with early emergence of age differences in response criterion. These results are consistent with age effects on strategic processes controlling decision caution. Consistent with an age-related decline in cognitive flexibility, younger adults flexibly adjusted response criterion from trial-to-trial on mixed-task blocks, whereas older adults maintained a high criterion for all trials.

Introduction

Task-switching paradigms require alternation between two or more simple tasks, using internal or external cues (alternating runs vs. cued-trials paradigms; e.g., Rogers and Monsell, 1995; Meiran, 2000, respectively). Performance is poorer on task switch relative to task repeat trials in mixed-task blocks (switch cost) and on repeat trials in mixed-task than single-task blocks (mixing cost). Increasing the interval between the task cue and the target stimulus (cue-to-target interval, CTI) produces an overall reduction in response time (RT) as well as a reduction in switch cost. The interval effect is explained by advance preparation conceptualized as a set of proactive control processes (Braver et al., 2007) that bring the system to a state of readiness to perform the upcoming task (e.g., Rogers and Monsell, 1995; De Jong, 2000; Meiran, 2000; Rubinstein et al., 2001) and that can be flexibly applied to switch or repeat trials, depending on task context (for discussion see Karayanidis et al., 2010a; Ruge et al., in press).

However, a residual switch cost often remains even with long preparation intervals, suggesting that advance preparation is not always sufficient to equate switch and repeat trials (e.g., Allport et al., 1994; Rogers and Monsell, 1995). This residual switch cost arises from the time taken to complete reactive control processes (Braver et al., 2007) that deal with interference from the previously active task-set or difficulty activating the previously inhibited stimulus-set/response-set (e.g., Allport et al., 1994; Mayr and Keele, 2000). It can also result from failure of proactive control processes, that is, failure to complete preparation of the correct task-set on some proportion of trials (De Jong, 2000).

Mixing cost also reduces with increasing preparation interval (Rubin and Meiran, 2005; Jost et al., 2008), supporting the concept of proactive control as a multi-component process. Mixing cost has been attributed to a range of causes: greater working memory load arising from the need to select between and maintain multiple task-sets (Diamond, 2006), the need to apply top-down control to resolve task ambiguity when repeating a task in the context of a mixed-task block (Mayr, 2001; Rubin and Meiran, 2005), greater stimulus-driven ambiguity due to residual activation from the previous trial (Los, 1996), and incomplete disengagement of the alternative task-set on mixed-repeat trials (De Jong, 2001).

In present study, we examine the adult lifespan trajectory of control processes contributing to mixing cost and switch cost. We first apply an evidence accumulation model of choice to examine age effects on latent variables associated with decision processes. We then use the temporal information of event-related potentials (ERP) to examine age effects on proactive (cue-driven) and reactive (target-driven) control processes. Finally, we examine the associations between time-locked ERPs and latent model parameters to inform the processes that underlie age-related changes in task-switching performance.

ERP indices of proactive and reactive control in task-switching

Given their excellent temporal resolution of brain activity leading up to and following a behavioral response, ERPs provide a valuable measure of proactive and reactive control processes associated with switching tasks (for review see Karayanidis et al., 2010a).

In cued-trials switching paradigms, cue-locked ERPs show a larger centroparietal positivity for switch as compared to repeat trials peaking around 500 ms post-cue (e.g., Nicholson et al., 2005; Swainson et al., 2006; Jost et al., 2008). This differential switch cost positivity¹ is modulated by cue informativeness (Nicholson et al., 2006; Karayanidis et al., 2009; Jamadar et al., 2010) and is associated with the size of the RT switch cost (Lavric et al., 2008; Karayanidis et al., 2011). It is succeeded by a large frontocentral pre-target negativity that occurs for both switch and repeat trials and peaks at target onset. The cue-locked switch cost positivity has been associated with anticipatory reconfiguration, and the pre-target negativity with anticipatory attention (e.g., Brunia and van Boxtel, 2001) or response readiness processes common to both switch and repeat trials (e.g., Karayanidis et al., 2011).

In target-locked ERPs, compared to repeat trials, switch trials show a larger centrally maximal N2-type negativity followed by a reduced parietal P3b (e.g., Karayanidis et al., 2003; Nicholson et al., 2005; Jost et al., 2008). Target-locked switch-repeat difference waveforms show these effects as an extended switch-negativity over 200 ms to well beyond 600 ms post-target. There is still insufficient evidence as to whether this broad switch-negativity represents a single process or results from independent switch-related modulation of central N2 and parietal P3.

Event-related potentials also show differences between repeat trials performed in single-task vs. mixed-task blocks. In cue-locked ERPs, there is a smaller early cue-locked positivity for repeat trials when they are completed in a single-task block than when mixed with switch trials (e.g., Kray et al., 2005; Goffaux et al., 2008; Jost et al., 2008). This early differential mixing-cost positivity is consistent with less need for advance preparation on single-task blocks. Target-locked ERPs show a larger parietal P3 for repeats in single-task than in mixed-repeat blocks (e.g., Jost et al., 2008), consistent with less post-target interference on single-task blocks.

Evidence accumulation model parameters in task-switching

The Ratcliff diffusion model is an evidence accumulation model that provides a means of decomposing measures of overt behavior into latent variables characterizing cognitive processes (Ratcliff and McKoon, 2008). It assumes that, in a binary choice task, a decision is reached by accumulating (i.e., repeatedly sampling and combining) stimulus information until the evidence favoring one choice exceeds the evidence favoring the other choice by a criterion amount. The time to arrive at a decision is determined by the conservativeness of the criterion (response criterion, a) and the quality of information or rate of evidence accumulation (drift rate, v). Non-decision time (Ter) measures processes such as stimulus encoding and response activation/execution that occur before or after the decision process.

Recently, diffusion models have been applied to model performance in task-switching paradigms that involve alternating between two or more two-choice decision tasks. Madden et al. (2009) used the EZ diffusion model, a simplified version of the Ratcliff diffusion model that estimates the above latent variables from three observed variables: the mean and variance of RT for correct decisions and the error rate (Wagenmakers et al., 2007). As past diffusion applications assumed the response criterion does not differ between conditions that occur in an unpredictable order within blocks of trials, Madden et al. (2009) looked for switching effects on non-decision time and drift rate only. With a long (CTI, 1500 ms) that allowed advance preparation for the upcoming target, switch trials produced longer non-decision time and slower drift rate than repeat trials.

Karayanidis et al. (2009) applied the EZ2 diffusion model (Grasman et al., 2009), a generalization of the EZ model allowing response bias. They allowed all three parameters to vary with trial type, arguing that informative cues may allow criterion setting to be adjusted during the preparation interval. With a long CTI of 1000 ms, switch cost was due to a lower drift rate and a higher response criterion for switch than repeat trials, but no difference in non-decision time. The persistent residual switch cost due to slowing of the drift rate for switch trials is consistent with interference models of switch cost, whereas response criterion differences are consistent with control models that posit greater strategic adjustments on switch trials (see Kiesel et al., 2010 for review). Karayanidis et al.’s finding that response criterion can be flexibly adjusted on a trial-by-trial basis suggests that response criterion estimates provide a useful index of cognitive flexibility.

Karayanidis et al. (2009) also examined the relationship between diffusion parameters and cue-locked ERP measures. In young adults, criterion setting on switch trials was inversely correlated with the cue-locked positivity amplitude for switch trials, indicating that proactive control may lead to less conservative setting of response threshold on switch trials. In addition, a larger cue-locked positivity was related to reduced non-decision time and higher drift rate, consistent with the notion that ERP amplitude indexes the time to complete advance preparation which, in turn, leads to more efficient information.

Age-related changes in measures of task-switching

Increasing adult age is consistently associated with larger RT mixing cost (e.g., Kramer et al., 1999; Meiran et al., 2001; Kray, 2006). This has been attributed to greater difficulty in manipulating information in working memory or poorer resistance to interference between stimulus–response mappings. The latter interpretation is supported by findings that the age effect on mixing cost (1) is stronger when using bivalent than univalent task-sets that are highly prone to interference (Mayr, 2001), (2) can be eliminated when using univalent task-sets, that is, task-sets that do not involve overlapping stimuli or responses and therefore involve minimal interference between tasks (Eppinger et al., 2007; Buchler et al., 2008; West and Travers, 2008), and (3) reduce with task-switching practice (Buchler et al., 2008), that is, when stimulus–response mappings become more strongly established.

In contrast, there is little consistency regarding the effects of age on switch cost. Many studies report that RT switch cost does not vary with age (Salthouse et al., 1998; Kray and Lindenberger, 2000; Mayr and Liebscher, 2001). Other studies report an age-related increase (Meiran et al., 2001; Kray et al., 2002) and even in one case a decrease (Kray, 2006) in RT switch cost.

Although the basic morphology of the ERP waveform is maintained across the adult lifespan, age differences have been reported in the amplitude and distribution of ERP components associated with both preparatory and target-driven processes in task-switching. However, there is considerable variability in the pattern of age effects, possibly arising partly due to differences in paradigm, measures, and age demographics.

In cue-locked ERPs, both the cue-locked mixing cost positivity (Kray et al., 2005; Eppinger et al., 2007; West and Travers, 2008) and switch cost positivity (West and Moore, 2005; Eppinger et al., 2007; Friedman et al., 2007; but see Goffaux et al., 2008) emerge later and show a flatter fronto-parietal distribution in older adults. Goffaux et al. (2008) found that the pre-target negativity was more frontally distributed on mixed-task blocks, but only in older adults with poor working memory. In target-locked ERPs, differentiation between repeat trials in single-task and mixed-task blocks emerged later (West and Travers, 2008) and was smaller in old compared to young adults (Adrover-Roig and Barceló, 2010). Target-locked differentiation between switch and repeat trials also emerged later in older adults (West and Travers, 2008) but did not differ in amplitude (Eppinger et al., 2007).

The full Ratcliff diffusion model has been extensively used to investigate age effects on single-task performance. Older adults consistently have a higher response criterion and slower non-decision time than young adults, whereas a reduction in drift rate for older adults emerges less consistently (e.g., Ratcliff et al., 2005, 2006a,b). Ratcliff and colleagues argue that weak or absent drift rate effects are inconsistent with the generalized slowing hypotheses of aging (e.g., Brinley, 1965; Salthouse, 1996). Instead, they attribute aging effects to slowed peripheral processes (e.g., response production) and a strategic preference for accurate over speeded responding. However, recent evidence suggests that, in young adults, individual variability in response criterion is related to differences in structural connectivity within a fronto-striatal network associated with cognitive flexibility (Forstmann et al., 2010; Mansfield et al., 2011). By extension, this suggests that age differences in response criterion may be due to structural changes in brain connectivity rather than representing a preference for accurate performance.

Madden et al. (2009) is the only study to examine age-related changes in diffusion model parameters in a task-switching context. They found additive effects of task-switching and aging on both non-decision time and drift rate. So, switch trials and older adults produced longer non-decision times and a slower drift rate than repeat trials and younger adults, respectively. Older adults also had a higher response criterion than younger adults, but criterion differences between switch and repeat trials were not allowed in the diffusion model applied by Madden et al.

In summary, behavioral studies that use typical cued-trials switching paradigms show consistent evidence for a large and persistent increase in mixing cost with age. The evidence for changes in switch cost with aging is less consistent. Despite evidence for age differences in ERP components associated with proactive and reactive control in task-switching, there are still considerable gaps in our understanding of the processes that contribute to age variability. Diffusion model analyses show an age-related increase in response criterion and non-decision time, as well as slower rate of evidence accumulation in the task-switching context, indicative of age effects on both decision and non-decision processes. However, it remains unclear how these processes map onto the proactive and reactive control mechanisms that underlie the highly consistent effects of age on mixing cost but variable effects on switch cost.

A common cause?

The fact that task-switching studies consistently report an age-related increase in mixing cost but not switch cost needs to be interpreted with caution. Mixing cost and switch cost are not independent measures, as they rely on a common condition: the mixed-repeat trial. In particular, Whitson et al. (in press) provide behavioral evidence that an age effect on the processing of mixed-repeat trials may help explain both the consistent age-related increase in mixing cost and the variable effect of age on switch cost.

Whitson et al. (in press) examined adult lifespan changes in the effects of task practice on mixing cost and switch cost using a cued-trials paradigm. All age groups showed a significant reduction in mixing cost with increasing preparation interval. Although the size of the age effect on mixing cost reduced with task practice, a strong age effect on residual mixing cost persisted even after substantial practice. The effect of age on switch cost was much more variable. All groups showed a large RT switch cost across all practice sessions. However, the ability to use the preparation interval to reduce RT switch cost varied as a function of both age and practice. Young adults showed a significant reduction in RT switch cost with preparation by the second practice session, but this emerged only in the later session for older adults. The effect of age on residual RT switch cost also varied with practice; there was no age difference early in practice, a large age-related increase in residual switch cost in the second session and an age-related decline in residual switch cost thereafter.

Whitson et al. (in press) suggested that this complicated pattern of findings primarily has a single cause: an age effect on mixed-repeat trials². Specifically, the slope of the age effect on RT did not differ between all-repeat trials and switch trials, but was greater for mixed-repeat trials. Hence there is no need to invoke two distinct processes: one that increases mixing cost and another that reduces switch cost. Rather, both the increase in mixing cost and the reduction in switch cost occur because, even after extensive practice, older adults find mixed-repeat trials difficult and treat them like switch trials, resulting in a sustained mixing cost but an apparent reduction in switch cost.

In the current paper, we analyze data from Whitson et al. (in press) to identify the processes that underlie this age effect on mixed-repeat trials. In Section “Behavioral Results,” we apply the EZ2 model to identify age differences in latent parameters between all-repeat, mixed-repeat and switch trials. In Section “ERP Data,” we analyze cue-locked and target-locked ERP data to examine age effects on the time course of proactive and reactive control processes for all-repeat, mixed-repeat and switch trials. In Section “Relationships Between Behavioral and ERP Results,” we examine the relationship between diffusion and ERP measures. We only analyze age effects under prepared (long CTI) and practiced (test session) task conditions so as to minimize the influence of other sources of variability (e.g., task learning, temporal overlap of preparation, and task implementation processes).

Materials and Methods

Participants

Ninety-five participants who reported no current neurological disorder, recent head injury, or color blindness and had no prior experience with the task-switching experiment contributed to this study (18–80 years, mean age = 43 + /19.5 years, 32 male).

Most analyses involved a regression model with age as a covariate. However, for visual comparisons of age effects on ERP waveforms and for comparison of demographics, we defined four age groups based on breaks in mean RT across the age range (18–29 years: n = 25, 30–45 years: n = 20, 46–64 years: n = 20, 65–80 years: n = 30). Groups did not differ significantly in distribution of gender and handedness or in full scale IQ (WASI; Wechsler, 1999), forward or backward Digit Span (WAIS; Wechsler, 1997), or semantic fluency (COWAT: Spreen and Strauss, 1991). There was a small group effect on phonetic fluency [F(3,90) = 2.9, p = 0.038], but simple comparisons showed no significant differences between groups.

Stimuli and tasks

Each trial consisted of a cue–target sequence with a 150 or 1000-ms CTI and a 400-ms response–cue interval. Two hot and two cold cue colors were assigned to either the letter classification or the number classification task (Figure 1). Cue–task mapping was counterbalanced across participants. All targets consisted of a bivalent pair of stimuli (letter and number), with letter/number position varying randomly across trials (e.g., A4 vs. 4A). Responses were made using left and right index fingers, with hand-task mapping counterbalanced across participants. The letter and number forming the stimulus were incongruently mapped to response hand (i.e., if the letter was a vowel and was mapped to a left hand response, the number would be odd and mapped to a right hand response). Letter-digit pairs were randomly selected from the full set of incongruently paired exemplars, where identical stimulus repetition (e.g., A4–A4) and inverted stimulus repetition (e.g., A4–4A) did not occur on more than 0.5% of successive trials. This resulted in a total of 16 unique stimuli that could have been preceded by any of four cues, thereby forming 64 cue–target associations. Targets were presented for 5000 ms or until a response occurred. Cue–task and stimulus–response mappings remained constant across sessions for each participant.

Figure 1.

Cued-trials task-switching paradigm.

Single-task blocks included alternating cues corresponding to the same task (i.e., only hot or only cold cues). Mixed-task blocks included both hot and cold cues alternating in a pseudorandom order so that the overall switch probability was 50% and no more than four repeat or switch trials occurred in succession. Cue color was never repeated on successive trials in order to reduce the effects of repeating a physically identical cue.

Procedure

Participants attended two test sessions (delay 17 ± 1.7 days). The first session included neuropsychological testing and practice on the task-switching paradigm. The second session included further task practice and the EEG test session. Each practice session included task training (48 single-task trials per task; 64 mixed-task trials) followed by task practice. Task practice included two single-task blocks (48 trials per task at CTI = 1000 ms) and two mixed-task blocks (64 trials per CTI). The EEG testing session included four single-task blocks (i.e., 2 × 48 trials per task at CTI = 1000 ms) and six mixed-task blocks (6 × 64 trials per block) for each of the following CTI:RTI conditions: 150:1400, 1000:1400, and 150:750. Thus, for the test session, participants completed a total of 1344 test trials, including 192 all-repeat trials (at CTI = 1000 ms) as well as 192 mixed-repeat and 192 switch trials per CTI:RTI condition. Sets of blocks of the same condition were presented sequentially, but the order of conditions was counterbalanced across participants using a Latin square design with the restriction that single-task blocks were completed together.

Participants were instructed to respond as quickly and as accurately as possible. Each error was followed by immediate auditory feedback and the next trial was delayed by 1000 ms. Mean RT and error rate were displayed after each block and participants were encouraged to use this information to improve performance on the following block.

EEG recording

EEG was recorded from 18 scalp sites (Quikcap, Neuroscan; F7, T7, P7, F3, C3, P3, O1, Fz, Cz, Pz, OZ, F4, C4, P4, O2, F8, T8, P8) and two mastoids against a nose reference. Bipolar vertical electro-oculogram (EOG) was recorded from left supra- and infra-orbital regions and horizontal EOG from left and right outer canthi. EEG and EOG were continuously sampled at 500 Hz/channel on a Synamps II system (Neuroscan; bandpass 0.01–030 Hz, 50 Hz notch filter). EEG was re-referenced offline to average mastoid. Vertical eyeblink artifact was corrected in the continuous EEG files (Semlitsch et al., 1986) as implemented by Neuroscan software. Files were visually inspected and sections of EEG contaminated with channel saturation or noise were excluded from further analysis.

Data analysis

The first two trials of each run, trials associated with and immediately following an error, and trials associated with a response outside the pre-defined response window (200 ms – participant’s mean RT + 3SD) were excluded from all further analyses. This resulted in exclusion of an average of 3.35% of trials for error, post error and fast/slow responses. Mean RT and error rate are reported for repeat trials in the single-task blocks (all-repeat), repeat trials in a mixed-task block (mixed-repeat) and switch trials averaged over task. Mixing cost was calculated by subtracting performance on all-repeat from mixed-repeat trials. Switch cost was calculated by subtracting performance on mixed-repeat trials from switch trials.

ERP data

Cue- and target-locked averages were created by extracting 1400 ms epochs around the onset of the cue/target (−200 to 1200 ms) for each trial type. A −50 to 50 ms baseline was employed to account for the shifting pre-cue and pre-target baseline apparent in these waveforms (see also Karayanidis et al., 2003). Within each trial type, cue and target-locked ERP waveforms were averaged across task (number/letter). Mean amplitude windows were extracted using in-house software (EEG Display by W. R. Fulham).

Diffusion model parameters

The EZ2 diffusion model (Grasman et al., 2009) was used to estimate latent parameters for each trial type and task based on response accuracy, mean RT and variance of RT for correct decisions. The drift rate (v) and the response criterion (a) together determine mean decision time (DT), the time required to arrive at a decision in a two-choice response task. The remaining portion of mean RT is the non-decision time (Ter), which represents sensory and response processes unrelated to the decision. Within the context of the cued-trial switching paradigm with a long preparation interval, Ter also includes any task preparation not completed during the CTI. The EZ2 model estimates one drift rate and one non-decision time parameter for each response, criterion for one of the responses (the criterion for the other response is assumed to be zero without loss of generality) and the starting point for evidence accumulation (z). These six parameters are estimated based on six data points, accuracy, and the mean and variance of correct RT for each response. The number of parameters estimated equals the number of data points, but the equation relating the two cannot be solved to explicitly express model parameters in terms of data points. However, the EZ2 equation implicitly defines a unique solution from which least-squares parameter estimates can be easily obtained by standard optimization methods (see Grasman et al., 2009). We chose EZ2 because it requires fewer assumptions, is more robust and efficient than EZ estimation, and corresponds more directly to the model’s assumption that one evidence accumulation process is responsible for both choices.

We applied the diffusion analysis to data broken down by task and response as well as trial type. This resulted in small sample sizes for correct responses (less than 20) for some conditions in some subjects. In order to make mean and variance estimates robust, we based them on fits of the Ex-Gaussian distribution to correct RT deciles (Heathcote et al., 2002; see Wagenmakers et al., 2008, for a related approach to EZ estimation). We also based EZ2 estimates on the robust accuracy measure recommended by Snodgrass and Corwin (1988). In a few cases (<1%), Ter estimates were too small to be plausible (<100 ms). In such cases, we obtained parameter estimates by solving the EZ2 equations under the constraint that Ter > 100 ms. Note that, without constraint, EZ2 parameters produce a perfectly accurate description of accuracy and correct RT mean and variance. Although this is not necessarily the case when a constraint is imposed, the effect of the constraint used on our data was negligible, so that the account of these measures remained essentially perfect.

Behavioral Results³

Results

Young adults

Given that evidence accumulation models have not yet been widely implemented in task-switching paradigms, we first analyzed effects of trial type on behavioral mean (RT⁴, error rate) and diffusion model parameters (non-decision time: Ter, decision time: DT, response criterion: a, and drift rate: v) in young adults (18–29 years: n = 25) alone to allow comparison with Karayanidis et al. (2009). We used a Greenhouse–Geisser corrected three trial type (all-repeat, mixed-repeat, switch) repeated measures GLM with planned mixing cost (mixed-repeat – all-repeat) and switching cost (switch – mixed-repeat) comparisons. Family wise error rate correction was applied (α/2 < 0.025); however, marginal results (i.e., α < 0.05) are reported where necessary for comparability with previous research.

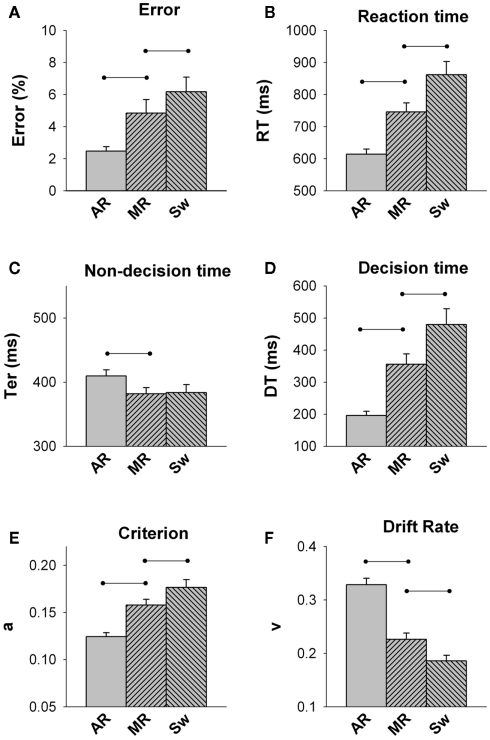
Figure 2 shows overt and latent performance measures for each trial type in young adults. The main effect of trial was significant for all measures [F(2,48) = 5.69–113.3, p = 0.01–0.001]. Young adults showed significant mixing cost and switch cost on both RT and error rate. Although non-decision time did not contribute to switch cost, it showed a small but significant negative Ter mixing cost [approximately 20 ms; F(1,24) = 5.68, p = 0.010]. In contrast, DT increased from all-repeat to mixed-repeat trials [approximately 170 ms DT mixing cost; F(1,24) = 44.25, p < 0.001] and from mixed-repeat to switch trials [approximately 120 ms DT switch cost; F(1,24) = 25.54, p < 0.001]. The slowing of decision processes was due to both a progressive increase in criterion and decline in drift rate across the three trial types [mixing cost: F(1,24) = 61.79, p < 0.001; F(1,24) = 92.31, p < 0.001, respectively; switch cost: F(1,24) = 13.62, p = 0.001; F(1,24) = 27.69, p = 0.001, respectively].

Figure 2.

Average error rate (A), reaction time (B), non-decision time (C), decision time (D), criterion (E) and drift rate (F) for each trial type in the Young group (18–29 y; AR = all-repeat, MR = mixed-repeat, S = switch). Lines represent significant contrasts.

In summary, under highly practiced and fully prepared conditions, young adults continued to show large mixing and switch costs on performance, arising from a higher response criterion and slower drift rate with increasing trial difficulty. The small reduction in non-decision time for mixed-task vs. single-task blocks indicates that young adults used the CTI to prepare for the upcoming trial in mixed-task blocks, and the fact that non-decision time did not differ between mixed-repeat and switch trials indicates that they were well prepared for both trial types. However, they still applied a more cautious decision strategy and showed slower rate of information on mixed-task vs. single-task blocks and on switch vs. repeat trials within the mixed-task block. So, it appears that neither practice nor preparation was able to remove post-target interference arising from the use of bivalent stimulus sets as well as bivalent and incongruently mapped responses. Importantly, response criterion setting differed between mixed-repeat and switch trials in the same block, indicating that younger adults can flexibly adjust response criterion on a trial-by-trial basis, so as to maximize performance. These findings are largely consistent with those reported earlier using a very different cued-trials switching paradigm (Karayanidis et al., 2009).

Adult lifespan effects

Age effects on behavioral and diffusion model parameters were analyzed using a three trial type (all-repeat, mixed-repeat, switch) repeated measures GLM with centered age (age) and centered age squared (age²) as covariates. Significant age effects were analyzed using mixing and switching comparisons to determine whether the slope of the age effect varied for each pair of variables. The age × mixing and age × switching interactions closely correspond to Pearson correlations between age and each cost measure.

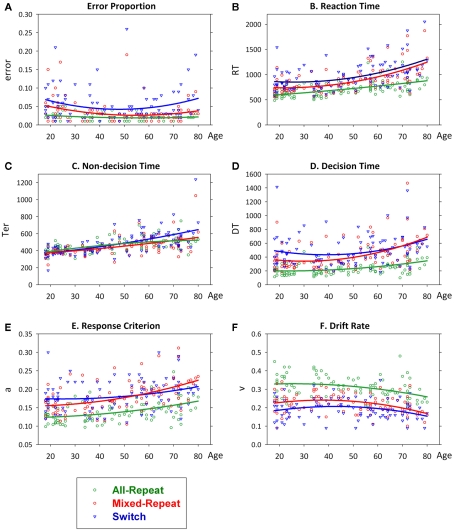
Variation in behavioral and diffusion parameters as a function of age is shown in Figure 3. Mixing cost and switch cost age functions for each measure are shown in Figure 4. There was a small quadratic effect of age on error rate, but no interactions with trial (Figure 3A). RT showed a largely linear increase with age [F(1,92) = 44.21, p < 0.001; Figure 3B] with strong linear and quadratic age effects on trial type [age × trial: F(2,184) = 7.24, p = 0.004; age² × trial: F(2,184) = 4.65, p = 0.023]. The relationship between age and RT varied between mixed-repeat and all-repeat trials [age × mixing cost: F(1,92) = 13.21, p = 0.001; age² × mixing: F(1,92) = 6.36, p = 0.013], but only marginally between switch and mixed-repeat trials [age × switching: F(1,92) = 4.31, p = 0.041].

Figure 3.

Scatterplots of error rate (A), reaction time (B), non-decision time (C), decision time (D), criterion (E) and drift rate (F) as a function of age superimposed for each trial type with quadratic lines of best fit. Effects remained highly significant when outliers for RT, Ter, and DT were removed.

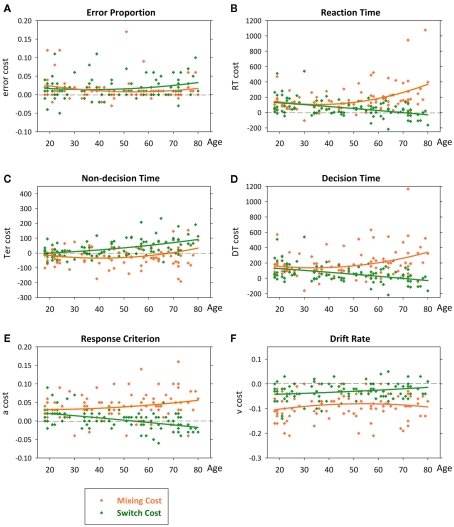
Figure 4.

Scatterplots of error rate (A), reaction time (B), non-decision time (C), decision time (D), criterion (E) and drift rate (F) as a function of age with quadratic lines of best fit. Effects remained highly significant when outlier for DT mixing cost was removed.

Thus, under practiced and prepared task conditions, there was no age effect on error rate, but increasing age was associated with a large quadratic increase in RT mixing cost (Figure 4B), resulting from a quadratic age trend for mixed-repeat trials on top of a linear effect on all-repeat trials. In contrast, increasing age was associated with a small though significant linear decrease in RT switch cost (Figure 4B). Pearson correlations testing the strength of linear relationship between age and both error and RT are shown in Table 1. To understand the processes that underlie this pattern of age effects on mixing cost and switch cost, we looked at age effects on diffusion parameters.

Table 1.

Pearson correlations between age and behavioral, latent and electrophysiological measures of mixing and switch costs, and for all-repeat, mixed-repeat and switch trials.

	Error	RT	Ter	a	v	Early cue positivity	Late cue positivity	Frontal N2	Early P3b	Late P3b
Mix cost		0.337#		0.218*			0.208*		−0.346∧	−0.319#
Switch cost		−0.212*	0.481∧	−0.463∧	0.248*		−0.231*	−0.318#		−0.246*
All-repeat	−0.218*	0.569∧	0.555∧	0.443∧	−0.326∧		−0.310**	0.452∧		0.357∧
Mixed-repeat		0.578∧	0.532∧	0.498∧	−0.267#		−0.202*	0.396∧
Switch		0.457∧	0.620∧	0.223*			−0.273#	0.299#	−0.204*

*p < 0.05, ^#p < 0.01, ^∧p < 0.001.

All diffusion parameters produced significant linear effects of age [F(1,92) > 14.32, p = 0.005–0.001], with DT and drift rate also showing small quadratic effects [F(1,92) = 4.32–4.83, p = 0.040–0.030]. So, with increasing age, there was a linear slowing of non-decision processes and a quadratic slowing of decision processes. The latter was attributed to a linear increase in response criterion and quadratic decline in drift rate with age. The linear relationship between age and each parameter differed across trial type [age × trial: F(2,184) = 3.99–12.01, p = 0.029–0.001]. As shown in Figures 3C,D, the slope of the age effect on mixed-repeat and switch trials was very different for non-decision time and DT parameters. The age effect on non-decision time was greater for switch than mixed-repeat trials (Figure 3C), resulting in an age-related increase in Ter switch cost [Figure 4C; age × switching: F(1,92) = 28.10, p < 0.001, r = 0.481; see Table 1], but there was no effect of age on Ter mixing cost. In contrast, the linear relationship between age and DT was significantly greater for mixed-repeat than either all-repeat or switch trials (Figure 3D), resulting in an age-related increase in DT mixing cost [age × mixing: F(1,92) = 7.26, p = 0.008, r = 0.263] but a significant decrease in DT switch cost [age × switching: F(1,92) = 21.13, p < 0.001, r = −0.432; Figure 4D].

The age effect on DT for mixed-repeat trials was mirrored in the response criterion (Figure 3E). Here, again, the linear relationship between age and response criterion was steeper for mixed-repeat than either of the other two trial types [age × mixing: F(1,92) = 4.67, p = 0.033; age × switching: F(1,93) = 25.30, p < 0.001], resulting in a significant increase in criterion mixing cost (r = 0.218) and reduction in criterion switch cost (r = −0.463; Figure 4E). Drift rate did not contribute to the age effect on mixing cost (Figure 3F), but the slope of the age effect on drift rate varied between mixed-repeat and switch trials [F(1,92) = 6.01, p = 0.016] resulting in a linear reduction in drift rate switch cost with age (r = 0.243; Figure 4F).

Together, these results show that the age-related increase in RT mixing cost was mediated by a differential increase in response criterion for mixed-repeat vs. all-repeat trials. In contrast, the age-related reduction in switch cost resulted from a combination of causes. The effect of age on both response criterion and drift rate was larger for mixed-repeat than switch trials, resulting in a reduction in DT switch cost. However, non-decision processes for switch trials were slowed with age, resulting in a higher Ter switch cost. The net effect was a small but significant decline in RT switch cost with age in the presence of a large increase in RT mixing cost.

Summary of behavioral findings

Diffusion parameters show that both non-decision and decision processes modulate performance on the task-switching paradigm and that the effect of these processes varies with age. For both single-task and mixed-task conditions, RT increased with age, and this effect was associated with an increase in both non-decision (100–200 ms) and decision processes (50–150 ms). DT was slowed by a combination of a more conservative response criterion and a slower rate of evidence accumulation. These findings are consistent with evidence for an age-related increase in non-decision time and response criterion across a wide range of two-choice tasks (e.g., Ratcliff et al., 2005). Consistent with Madden et al. (2009), we found an age-related slowing in drift rate in task-switching.

Importantly, we show that the size of the age effect on each model parameter differed according to trial type. Specifically, the age effect on non-decision time was largely identical for all-repeat and mixed-repeat trials (i.e., approximately 100 ms increase across the entire adult range), but was much steeper for switch trials. Although young adults showed a small decline in Ter from single-task to mixed-task blocks but no difference between mixed-repeat and switch trials, old adults’ non-decision time was much slower for switch trials, resulting in a large Ter switch cost (Figure 4C). The main effect of age on Ter may reflect a slowing of sensory processing and/or response execution processes. The specific age-related increase in Ter for switch trials is unlikely to result from inefficient preparation processes carrying over into the post-target interval and delaying the start of evidence accumulation, because at the test session, older adults showed a reduction in RT switch cost with increasing preparation interval that was equivalent to that of younger groups (Whitson et al., in press). Rather it is more likely to reflect either (1) less efficient or less consistent preparation for switch trials, or (2) greater post-target interference on switch than mixed-repeat trials, even under practiced and prepared task conditions. This interference may emerge at the level of sensory processing (i.e., less efficient suppression of irrelevant information) and/or at response selection/activation (i.e., partial activation of the incorrect response and/or slower execution of the correct response). These processes underlying the differential effects of age on switch trial Ter are not mutually exclusive and can be tested using ERP measures. Specifically, less efficient switch preparation would be evidenced by smaller cue-locked switch cost positivity, sensory interference from the irrelevant dimension would be found in early target-locked ERPs related to sensory processing, whereas response-level interference would affect the late part of the P3b.

The paradoxical age-related reduction in residual RT switch cost despite an increase in Ter switch cost can be reconciled when considering the complementary effects of age on decision processes. Young adults showed a gradual increase in DT from all-repeat to mixed-repeat to switch trials (Figure 3D), resulting in broadly equivalent mixing and switch costs (Figure 4D). Older adults showed a large increase in DT from single- to mixed-task blocks but no further differentiation between mixed-repeat and switch trials, resulting in a very large DT mixing cost but effectively no DT switch cost. This effect was primarily driven by an age-related increase in response criterion for mixed-repeat trials, resulting in largely equivalent response criterion for mixed-repeat and switch trials (Figure 3E). In turn, this resulted in a very large criterion mixing cost as well as a small negative criterion switch cost (Figure 4E).

This pattern of findings supports Whitson et al.’s (in press) conclusion that the consistent age-related increase in mixing cost as well as the variable age effect in switch cost arise because older adults are more likely to treat mixed-repeat trials like switch trials. Diffusion model analyses determined that this age effect is related to decision processes. Specifically, with increasing age, the response criterion became largely equivalent for mixed-repeat and switch trials and the decline in evidence rate was greater for mixed-repeat than switch trials, resulting in equivalent DT for both trials in the mixed-task block. The disproportionate slowing of decision processes for mixed-repeat trials, combined with a small delay in non-decision processes resulted in a smaller net RT switch cost in older as compared to younger participants.

So, both the large increase in RT mixing cost and the small but significant reduction in RT switch cost with increasing age can be accounted for by the disproportionate increase in response criterion to mixed-repeat trials. As noted earlier, there is ample evidence that older adults set a higher response criterion. What the current data offer beyond this consistent finding is that, under conditions that favor flexible adjustment of decision processes, young and old adults differ in their ability or desire to flexibly adjust their response criterion. Young adults vary criterion on a trial-by-trial basis so as to apply caution on switch trials but benefit from repetition of the same task rules on mixed-repeat trials (see also Karayanidis et al., 2009). Older adults set a high criterion for both trial types, suggesting that they either chose not to or cannot flexibly adjust response criterion on a trial-by-trial basis. The evidence that, in young adults, individual variability in response criterion is associated with strength of structural connectivity within a fronto-striatal network associated with cognitive flexibility (Forstmann et al., 2010; Mansfield et al., 2011) suggests that age-related structural brain changes may lead to less efficient cognitive flexibility.

The current data can explain both the highly consistent age effect on RT mixing cost and the variable and inconsistent age effect on RT switch cost. The large age effect on RT mixing cost was almost exclusively the result of older adults setting a very high response criterion on mixed-repeat trials. Neither non-decision time nor drift rate contributed to age differences in mixing cost. As only one process contributes to age variability in mixing cost, there is no possibility of trade-offs, resulting in a large and consistent age-related increase in RT mixing cost.

In contrast, both non-decision and decision processes contributed to age differences in switch cost. Moreover, they did so in opposite ways. With increasing age, switch trials has a slower non-decision time but a faster DT than mixed-repeat trials, resulting in greater Ter switch cost but less DT switch cost. In the current context, the net effect was a significant age-related reduction in RT switch cost. It is likely that changes in task parameters will independently affect the size of the age effect on non-decision and decision processes, thereby variably affecting the age effect on RT switch cost. For example, variations in CTI will affect preparation on switch trials. More opportunity for preparation should result in a smaller age effect on switch trial Ter, but little effect on drift rate, resulting in a net reduction of the age effect on RT switch cost. Conversely, univalent stimulus-sets or response-sets may reduce target-driven interference. This would reduce the age effect on DT for mixed-repeat trials (as a result of faster drift rate and/or lower criterion), and consequently allow the age-related increase in Ter switch cost to be brought out in RT switch cost. So, task parameters that differentially affect opportunity for advance preparation and magnitude of target-driven interference processes will differentially affect non-decision and decision parameters and can lead to variability in age effects in performance switch cost.

The fact that some of the age effects on diffusion parameters were not reflected in age differences in overt behavioral performance (e.g., age effect on Ter switch cost) highlights the fact that overt behavioral measures are the cumulative outcome of many, sometimes complementary, underlying processes and underscores the importance of integrative approaches that combine overt and latent behavioral variables as well as physiological variables (e.g., imaging, activation, psychophysiological measures; see Karayanidis et al., 2010a). In the next section, we examine cue-locked and target-locked ERP components in order to examine whether age effects on RT mixing and switch cost arise from proactive or reactive control processes.

ERP Data

For clarity of presentation, ERP waveforms are shown averaged across age groups as defined by Whitson et al.’s, in press; see also Materials and Methods). Statistical analyses retained age and age² as covariates. Cue-locked and target-locked waveforms were analyzed over the three midline sites where effects were largest.

Cue-locked ERPs Results

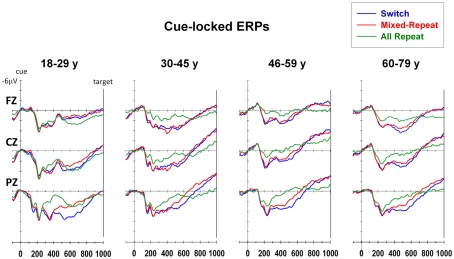
Young adults showed a larger parietal positivity for mixed-repeat than all-repeat trials (mixing cost positivity) over 300–550 ms and a partially overlapping later parietal positivity for switch than mixed-repeat trials (switch cost positivity) that spread over 450–850 ms (Figure 5). In young adults, these effects showed little spread anteriorly. Although the mixing cost positivity and switch cost positivity were evident within the same broad time windows in older age groups, both effects were more evenly distributed across the anterior–posterior plane. In addition, the three older age groups showed a much more pronounced pre-target negativity to both trial types in mixed-task blocks. The mixing cost positivity, switch cost positivity and pre-target negativity were measured using mean amplitude intervals over 300–500, 500–700, and 850–1000 ms, respectively.

Figure 5.

Cue-locked event-related potentials for each trial type at midline electrodes.

Initial analyses involved an [3 interval × 3 trial × 3 electrode (Fz, Cz, Pz)] ANCOVA with centered age and age² as covariates and Greenhouse–Geisser correction. This resulted in a significant main effect and interactions of interval (all p < 0.001). Age was a significant linear and quadratic covariate [F(1,92) = 4.05, p = 0.047; F(1,92) = 4.28, p = 0.041]. There were significant linear relationships between age and interval × trial, trial × electrode and interval × trial × electrode interactions [F(4,368) = 3.2–6.8, p = 0.047–0.001] and a quadratic relationship between age, trial, and electrode [F(4,368) = 6.12, p = 0.003]. Significant trial effects were examined using mixing and switching comparisons at each time interval.

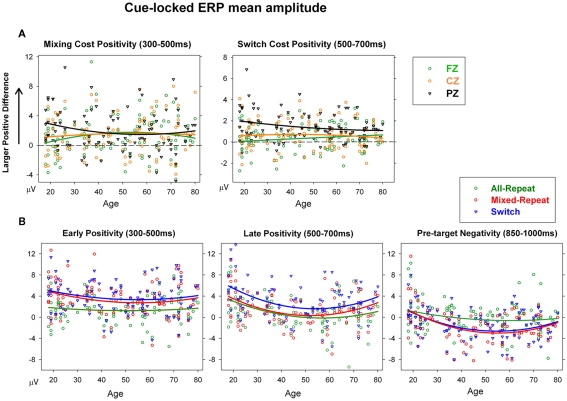
The mixing cost positivity was largest over 300–500 ms post-cue [F(1,92) = 15.36, p < 0.001] and showed strong quadratic changes with age that varied across the anterior–posterior plane [age × mixing × electrode: F(2,184) = 5.97, p = 0.007; age² × mixing × electrode: F(2,184) = 4.85, p = 0.017]. As shown in Figure 6A, the mixing cost positivity was larger parietally in young adults, but reduced parietally and was more evenly distributed across the scalp from around 40 years of age. This mixing cost positivity persisted in the 500–700-ms time window but only for older adults [age × mixing: F(1,92) = 3.14, p = 0.068; age² × mixing × electrode: F(2,184) = 4.27, p = 0.025]. Scatterplots of age against cue-locked mean amplitude at Pz (Figure 6B) show that, for the younger ages, the parietal mixing cost positivity (seen as the difference between all-repeat and mixed-repeat trials) was prominent over 300–500 ms (left panel) but largely dissipated by 500–700 ms (middle panel). In contrast, older adults showed a smaller early mixing cost positivity that persisted into the later time window.

Figure 6.

(A) Scatterplots of mean amplitude for cue-locked mixing cost positivity (mixed-repeat – all-repeat) and switch cost positivity (switch – mixed-repeat) at each midline electrode. (B) Scatterplots of age against mean amplitude for early positivity, late positivity, and pre-target negativity at Pz for each trial type in cue-locked ERPs.

The switch cost positivity emerged parietally over the 300–500-ms interval [Figure 5; switching × electrode: F(2,184) = 6.53, p < 0.002] but peaked over the 500–700-ms interval [switching: F(1,92) = 15.69, p < 0.001; switching × electrode: F(2,184) = 19.86, p < 0.001] which also produced a significant age × switching × electrode interaction [F(2,184) = 11.56, p < 0.001]. Although the switch cost positivity was parietally focused in younger adults (Figure 6A, right), it became smaller and more evenly distributed across the anterior–posterior plane with increasing age. At Pz, the switch cost positivity reduced linearly with age [age × switching: F(1,92) = 5.13, p = 0.026; Table 1].

The pre-target negativity (850–1000 ms) was significantly larger for mixed-repeat vs. all-repeat trials [F(1,92) = 13.04, p < 0.001], but did not differ between mixed-repeat and switch trials (F < 1; Figure 5). There was a strong quadratic relationship between age and pre-target negativity amplitude [Figure 6B, right; age² × trial × electrode: F(4,386) = 6.05, p = 0.002]. The pre-target negativity increased significantly with age for both mixed-task trials (but not single-task trials), with the effect stronger centroparietally [age: F(1,92) = 5.22, p = 0.025; age²: F(1,92) = 4.6, p = 0.035; Table 1]. This effect first emerged in the 30–45-years group (Figure 5) and showed a strong curvilinear pattern, peaking by 50 years and reversing gradually thereafter (Figure 6B, right).

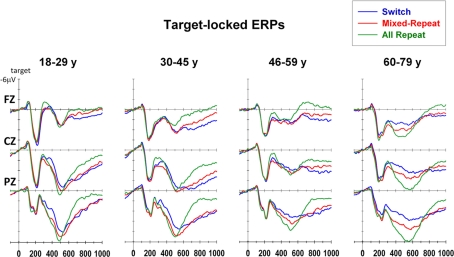
Target-locked ERPs

Target-locked ERP waveforms are presented in Figure 7. All trial types showed a small frontocentral N1 (100 ms) and large frontocentral P2 (200 ms). These were followed by a broad central N2 (250–400 ms) and a parietally maximal P3b that was maximal over 400–600 ms (early P3b) but extended beyond 650–800 ms (late P3b). Scatterplots of age against each of these three measures are shown in Figure 8. Both mixing cost and switch cost effects were evident as a reduction in positivity, resulting in a relative differential negativity, especially within the latency range of the P3b. Initial analyses using a 3 interval × 3 trial type × 3 electrode repeated measures ANCOVA with centered age and age² as covariates resulted in a significant interaction between interval and all other factors [F(8,736) = 14.20, p < 0.001]. Both covariates showed significant interactions with trial type [age: F(2,184) = 5.84, p = 0.002; age²: F(2,184) = 4.40, p = 0.025] and interval × trial type [age: F(4,368) = 6.07, p = 0.001; age²: F(4,368) = 3.71, p = 0.013], indicating both linear and non-linear age effects on stimulus-locked waveforms. Trials effects were examined using mixing and switching comparisons at each time interval.

Figure 7.

Target-locked event-related potentials for each trial type at midline electrodes.

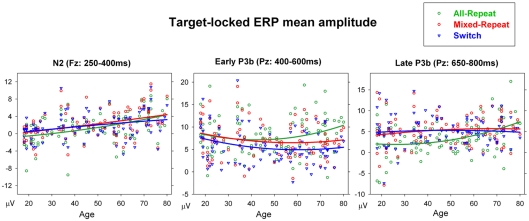
Figure 8.

Scatterplots of age against mean amplitude for frontal N2 at Fz, early and late P3b (at Pz) for each trial type in target-locked ERPs.

N2 was significantly smaller frontocentrally for mixed-repeat than all-repeat trials [mixing: F(1,92) = 5.55, p = 0.021; mixing × electrode: F(2,184) = 10.27, p < 0.001), and centroparietally for mixed-repeat than switch trials [switching: F(1,92) = 11.54, p = 0.001, switching × electrode: F(2,184) = 18.10, p < 0.001]. In younger adults, these effects appear to affect temporally distinct components of N2 (Figure 7) that cannot be differentiated in older participants. N2 amplitude reduced with age [F(1,92) = 7.51, p = 0.007], with significant negative correlations between frontal N2 amplitude and age for all trial types (Table 1). Age did not significantly moderate the size of the mixing cost effect on N2 amplitude but resulted in greater differentiation between mixed-repeat and switch trials on the frontal N2 [age × switching × electrode: F(2,184) = 11.06, p < 0.001; Table 1]. Note, however, that given the much broader anterior–posterior spread of the P3b and the reduction in N2 amplitude in older adults (Figure 7), it is difficult to determine whether this age effect is best described an increase in switch cost on N2 or earlier onset of switch cost effects on P3b.

The early P3b was parietally maximal [electrode: F(2,184) = 41.28, p < 0.001], but became more evenly distributed across the midline sites with increasing age [age × electrode: F(2,184) = 11.5, p < 0.001]. Early P3b was significantly larger for all-repeat than mixed-repeat trials [mixing × electrode: F(2,184) = 10.97, p < 0.001; Figure 7] and for mixed-repeat than switch trials [switching: F(1,92) = 12.61, p = 0.001; switching × electrode: F(2,184) = 21.36, p < 0.001]. As shown in Figure 7, both mixing and switch effects on the P3b were larger and more topographically widespread in the oldest age group. The effect of task mixing on early P3b (Figure 8, middle panel) increased with age [age × mixing: F(1,92) = 8.38, p = 0.005; age² × mixing: F(1,92) = 5.27, p = 0.024] and this was due to the combination of a linear age effect on mixed-repeat trials [Figure 7; age × electrode: F(,184) = 14.42, p < 0.001] and a quadratic age effect on all-repeat trials [age²: F(1,92) = 5.29, p = 0.024]. Note in Figure 8 (middle panel) that there was no differentiation between all-repeat and mixed-repeat trials on the left half of the age axis, but increasing differentiation across the right half. The effect of task-switching on the early P3b was centroparietally focused in younger adults, but showed a more even fronto-parietal distribution with increasing age [age × switching × electrode: F(2,184) = 5.37, p = 0.009].

The late P3b (650–800 ms) was less prominent for all-repeat trials but clearly evident for the other two trial types [Figure 7; mixing: F(1,92) = 29.22, p < 0.001]. The centroparietal P3b for all-repeat trials was prolonged in the older age range [Figure 8, right panel; age: F(1,92) = 5.75, p = 0.018; age × electrode: F(2,184) = 6.59, p = 0.003], resulting in significant age effects on mixing cost [mixing × age: F(1,92) = 7.07, p = 0.009; mixing × age²: F(1,92) = 8.20, p = 0.005]. There was a reversal of the switching effect frontocentrally, with a slow sustained positivity for switch trials [Figure 7; switching × electrode: F(2,184) = 5.92, p = 0.006] and this effect was delayed in the older age range [switching × age: F(1,92) = 4.84, p = 0.030].

Discussion of ERP findings

Consistent with previous studies (see Age-Related Changes in Measures of Task-Switching), cue-locked and target-locked ERP components associated with advance preparation and task implementation processes were clearly evident across the adult age range, but there were a number of age-related differences in the morphology of these components. Cue-locked ERPs produced an early mixing cost positivity and a later switch cost positivity that were larger parietally. Increasing age resulted in a more temporally prolonged mixing cost positivity and a smaller switch cost positivity, with both components being more evenly spread across the scalp. This pattern was due to a more sustained positivity for mixed-repeat trials (Figure 5), a finding reminiscent of the age effects on response criterion reported above. The pre-target negativity was larger for mixed-task than single-task trials and this effect was stronger centroparietally from 30 years onward (Figure 5).

Thus, the three main age-related changes in cue-locked ERPs that are temporally linked to proactive control were (1) a more sustained mixing cost positivity, suggestive of more effortful preparation of mixed-repeat trials (see also Kray et al., 2005; Eppinger et al., 2007; West and Travers, 2008), (2) a smaller switch cost positivity (see also West and Moore, 2005; Eppinger et al., 2007; Friedman et al., 2007), which together with the temporally overlapping increase in the duration of the mixing cost positivity, is consistent with the notion that older adults prepare for both mixed-repeat and switch trials, and (3) a larger centroparietal pre-target negativity for mixed-task blocks, suggestive of greater anticipatory attention (e.g., Brunia and van Boxtel, 2001) and/or task readiness (Karayanidis et al., 2010a).

In target-locked ERPs, increasing age resulted in a smaller frontal N2 and larger mixing and switching effects on the P3b. These findings differ from previous work showing that aging results in later (West and Travers, 2008) and smaller (Eppinger et al., 2007; Adrover-Roig and Barceló, 2010) P3b differentiation between trial types, possibly due to differences in task practice and post-target interference across paradigms. However, our ERP findings do corroborate the conclusions we drew from the diffusion variable analyses that, even under highly practiced and prepared task conditions, there continue to be age differences in the processing of switch and mixed-repeat trials.

Consistent with what has been previously labeled the switch-negativity (e.g., Karayanidis et al., 2003), switch trials produced a smaller P3b that spanned a latency range from 250 ms to beyond 600 ms. However, differential modulation of the early (i.e., overlapping the frontal N2) and late (i.e., overlapping the P3b) parts of this “switch-negativity” as a function of electrode and age strongly suggests that it is comprised of distinct temporally overlapping components. This conclusion is supported by the pattern of differences between repeat trials on the N2 and P3b: all-repeat trials had a larger early N2 as well as a larger parietal P3b than mixed-repeat trials.

Increasing age was associated with a linear reduction in frontocentral N2 for all trial types and quadratic effects on parietal P3b that varied with trial type. Overall, P3b showed a pattern of linear decline over 18–60 years followed by a reversal of this trend in older adults (Figure 7). The large quadratic age trend on P3b mixing cost was due to the large differentiation between all-repeat and mixed-repeat trials emerging very strongly after 60 years of age (Figure 8). This indicates a strong qualitative change in processing of both all-repeat trials (i.e., large increase in parietal P3b; Figure 7) and mixed-repeat trials (i.e., larger differentiation from all-repeat trials). The age-related increase in mixing effects on P3b, increase in switch effects on frontal N2b and parietal P3b and delay of P3b resolution suggest that many older adults (>60 years) show greater differential post-target processing switch and repeat trials than young adults, even after extensive task practice and a long preparation interval.

Relationships between Behavioral and ERP Results

Next, we examine the relationship between RT, diffusion parameters, and ERP components associated with proactive vs. reactive control. The rationale of this analysis is two-fold. We can use the timing information provided by ERPs to inform whether trial type differences in latent parameters are related to proactive vs. reactive control processes. Conversely, we can also use the diffusion model parameters to inform whether trial type differences in ERPs are associated with decision vs. non-decision processes. Together the associations between time-locked ERPs and latent model parameters can inform about the processes that underlie age-related changes in task-switching performance.

Given the pervasive age effects on RT, latent parameters and ERP measures (Table 1), we report correlations both before and after controlling for age using partial correlations. We reason that effects significant both before and after partialing age represent relationships between behavioral and ERP measures that exist independently of age. Significant relationships that are eliminated when controlling for age-related variance are likely to indicate that age mediates the relationship between behavioral and ERP measures. Relationships that only emerge when age is partialed out are likely to represent an association between behavioral and ERP measures that is obscured by age-related variance.

We focus on the three important age effects on latent measures: the increase in response criterion for mixed-repeat trials, the increase in non-decision time for switch trials and the reduction in drift rate for both mixed-task trials.

Cue-locked positivity and response criterion

Increasing age resulted in a disproportionate increase in response criterion for mixed-repeat trials, which led to both an increase in criterion mixing cost and a reduction in criterion switch cost (Figures 3E and 4E). Response criterion has previously been shown to be related to the amplitude of the cue-locked positivity (Karayanidis et al., 2009). We expect to replicate the relationship between criterion and cue-locked positivity in this lifespan sample. In addition, we expect this relationship to be moderated by age, suggesting a link between criterion adjustment and efficiency of preparation for trials in mixed-task blocks.

Increasing age was associated with both a higher criterion mixing cost and a more prolonged mixing cost positivity that extended into the 500–700-ms window (Table 1). The relationship between criterion mixing cost and mixing cost positivity was significant only when controlling for age [r = −0.19, p > 0.60; r_(age) = −0.246, p = 0.017]. These findings support the link between proactive control processes represented by cue-locked positivity and criterion adjustment for mixed-task blocks, and indicate that age moderates this relationship.

The link between cue-locked preparation processes and criterion setting was also supported in measures of switch cost. Increasing age was associated with a reduction in both criterion and RT switch cost, as well as a smaller switch cost positivity (Table 1). However, a larger switch cost positivity was associated with smaller RT switch cost (r = −0.205, p = 0.046). This relationship remained significant when controlling for age [r_(age) = −0.216, p = 0.036] but was eliminated when controlling for criterion switch cost (p > 0.14). Together with the large correlation between criterion and RT switch costs [r = 0.616, p < 0.001; r_(age) = 0.598, p < 0.001], these findings suggest that individuals with a high criterion switch cost tend to have a smaller switch cost positivity, leading to a higher RT switch cost.

The present pattern of findings supports earlier evidence for an association between cue-locked positivity and criterion setting (Karayanidis et al., 2009). Criterion adjustment appears to mediate the relationship between the cue-locked positivity and RT mixing/switching effects. This suggests that, independently of age, individual variability in cue-locked positivity and criterion settings affect behavioral mixing and switch cost measures. They also support the contention that age effects on RT mixing cost are mediated by greater activation of proactive control processes on mixed-repeat trials. Variation in these cue-locked ERP components was shown to affect the strength of the age effect on RT mixing cost and switch cost, through their relationship with criterion setting.

Age effects on switch trial non-decision time

In task-switching paradigms, when there is insufficient time to prepare for the upcoming target, the non-decision time parameter includes the time required to complete preparation processes in addition to sensory and response processes. With long preparation intervals, failure to efficiently prepare for the upcoming target or to complete preparation on some proportion of trials would also be expected to increase non-decision time. Karayanidis et al.’s (2009) finding of an inverse relationship between cue-locked positivity amplitude and non-decision time for switch trials in young adults supports this link between non-decision time and efficiency of preparation. In addition, an age-related increase in non-decision time has been consistently found in single-task paradigms (Ratcliff et al., 2005) and was recently reported for both switch and repeat trials under prepared task-switching conditions (Madden et al., 2009).

We expected to replicate the relationship between cue-locked positivity and non-decision time for switch trials and to show that this relationship may be modulated by age. In Section “Summary of Behavioral Findings,” we showed that aging produced a disproportionate increase in non-decision time for switch trials, which led to an age-related increase in Ter switch cost, despite an overall decline in RT switch cost. We argued that the Ter effect could be due to a number of processes, including less effective preparation for a switch trial and greater susceptibility to interference at the level of stimulus identification or response activation. ERPs produced evidence consistent with all three processes, showing that increasing age was associated with a smaller cue-locked switch cost positivity, a larger switch cost on the frontal N2 and a more prolonged switch cost effect on the late P3b (Table 1).

In order to identify the processes underlying age effects on Ter switch cost, we examined whether these age/ERP relationships remain significant after controlling switch cost variability in non-decision processes. We did this by including Ter switch cost as a control variable in the relationship between age and the switch cost effect on each ERP component. The relationship between age and the cue-locked switch cost positivity was eliminated (p > 0.10), whereas the correlation between age and switch cost on both frontal N2 and late P3b remained [r = −0.340, p < 0.001, r = −0.239, p = 0.020]. So, controlling for Ter switch cost reduced the relationship between switch cost positivity and aging but did not affect the age effect in target-locked ERPs. This suggests that the age-related increase in non-decision time for switch trials may be due to less efficient or less consistent use of the CTI to prepare for the upcoming switch trials. This, in turn, may lead to slower target encoding (frontal N2) and post-decision (late P3b) processes. The relationship between cue positivity and non-decision time may help explain the inconsistency of the age effect on residual switch cost. That is, older adults may be more sensitive to task conditions that reduce the likelihood of efficient preparation (e.g., fatigue, poorer attentional resources, weaker cue–task associations), resulting in a greater or more variable non-decision time contribution to switch trial performance.

Drift rate and cue-locked vs. target-locked ERPs

Conceptually, drift rate is associated with the quality of the information contributing to the decision process. Therefore, one would expect drift rate to be associated with target-locked ERP components associated with stimulus identification and response selection. However, Karayanidis et al. (2009) showed that drift rate was correlated with cue-locked positivity amplitude, suggesting that greater preparation may increase information accrual possibly by reducing interference from the alternative, irrelevant task set. Here we examine the relationship between drift rate and both cue-locked and target-locked ERP components and how this relationship is affected by criterion setting and age. We also examine whether the age-related reduction in drift rate in a task-switching context (Madden et al., 2009) is a consequence of less efficient preparation (cue-locked effect) or is associated with greater susceptibility to interference from the competing stimulus-set (and hence likely to affect early post-target processing reflected in the N2 and early P3b; see Verleger et al., 2005; Folstein and van Petten, 2008) or the competing response-set (and hence likely to affect response-related processes reflected in the late P3b).

When controlling for age, a larger mixing cost positivity was not only associated with smaller criterion mixing cost (see Cue-Locked Positivity and Response Criterion), but also with smaller mixing cost on both drift rate and RT [r_(age) = 0.215, p = 0.037; r_(age) = −0.210, p = 0.042, respectively]. Given that (1) preparation processes are conceptually linked to criterion adjustment during the CTI, whereas drift rate effects are linked to post-target decision processes and (2) criterion mixing cost was strongly correlated with mixing cost on both RT and drift rate (r = 0.744, p < 0.001, r = −0.587, p < 0.001, respectively) with effects remaining highly significant when controlling for age (p < 0.001), we reasoned that criterion-related variability may mediate the relationship between mixing cost positivity and mixing costs in RT and in drift rate. As predicted, including criterion mixing cost as a control variable eliminated the correlation between mixing cost positivity and both drift and RT mixing cost (p > 0.44), indicating that criterion mixing cost mediates these relationships. Thus, individuals who adopt a higher criterion for mixed-repeat relative to all-repeat trials tend to have a larger late mixing cost positivity as well as a lower drift rate and higher RT for mixed-repeat vs. all-repeat trials. For these mixed-repeat trials, a larger criterion is reflected in a larger cue-locked positivity and, along with a lower drift rate, results in higher RT mixing cost.

We expected drift rate to be susceptible to interference from the competing stimulus-set or response-set and hence to be related to target-locked N2 or P3 components. A larger (more negative) frontal N2 for mixed-repeat and switch trials was associated with slower drift rate for the corresponding trial type [r_(age) = 0.213, p = 0.039; r_(age) = 0.229, p = 0.026, respectively; all-repeat: p > 0.4] but only when controlling for age variability (without age covariate: p > 0.07), suggesting that stimulus level interference contributes to drift rate slowing. Increasing age was associated with smaller drift rate for mixed-repeat trials and smaller switch cost in drift rate (Table 1). Based on the association between N2 amplitude and drift rate, we expected that aging should also be associated with a larger N2, indicative of greater stimulus level interference. However, on the contrary, increasing age was correlated with a smaller (less negative) frontal N2 for both trial types and with greater N2 differentiation for switch vs. mixed-repeat trials (Table 1). The findings that a smaller N2 was associated with both increasing age and a smaller drift rate and that drift rate reduced with age suggest that age and drift rate independently affect frontal N2 amplitude. These findings can be reconciled if the age-related reduction on the frontal N2 for mixed-task trials represents the earlier onset of switch cost on the topographically widespread P3b rather than a direct age effect on N2 processes (see Target-Locked ERPs). By extension, this implies that age effects on drift rate are not related to stimulus level interference.

Within each trial type, larger P3b over 400–600 ms was positively associated with higher drift rate (r = 0.249, p < 0.015, r = 0.307, p = 0.002, r = 0.373, p = 0.001, for all-repeat, mixed-repeat and switch, respectively), but also negatively associated with faster non-decision time (r = −0.317, p < 0.002, r = −0.332, p = 0.001, r = −0.264, p < 0.001, respectively), lower criteria (r = −0.288, p = 0.005, r = −0.225, p < 0.028, r = −0.307, p = 0.002, respectively), and hence faster RT (r = −0.359, p < 0.001, r = −0.314, p = 0.002, r = −0.384, p = 0.001, respectively)⁵. Most of these effects remained highly significant when controlling for age. So, a larger P3b was associated with more efficient decision and non-decision processes.

We used partial correlations to examine whether the relationship between P3b and RT for each trial type was moderated by any of the latent variables for the corresponding trial type. Controlling for drift rate reduced the correlation between P3b and RT for mixed-repeat and switch trials (p > 0.19) but not all-repeat trials (p < 0.003). Controlling for non-decision time reduced the correlation for mixed-repeat trials only, whereas controlling for criterion had no effect on the relationship between P3b and RT. So, the relationship between P3b amplitude and RT was mediated by drift rate for both trials in mixed-task blocks, and by non-decision time only for mixed-repeat trials.

A large mixing effect on P3b, indicative of a greater reduction on P3b for mixed-repeat vs. all-repeat trials, was associated with a larger Ter mixing cost (r = −0.235, p = 0.022; r = −0.319, p = 0.002, respectively for early and late P3b). A larger switch cost on P3b amplitude, indicative of a greater reduction in P3b for switch vs. mixed-repeat trials, was associated with larger RT switch cost, (r = −0.295, p = 0.004, r = −0.267, p = 0.009, respectively for early and late P3b). Both effects were retained when partialing age. So, mixing effects on P3b are more specifically linked to non-decision processes, especially for mixed-repeat trials, whereas switch effects did not uniquely map onto any diffusion measure.

In summary, criterion mixing cost was related to cue-locked positivity mixing costs. In contrast, non-decision time and drift rate effects were related to target-locked ERP components. Frontal N2 was inversely related to drift rate, when controlling for age, but this did not explain effect of age on drift rate. The amplitude of the target-locked P3b correlated significantly with all latent parameters and RT. However, variance in the drift rate parameter moderated the P3b–RT relationship for both mixed-repeat and switch trials whereas non-decision time affected the P3b–RT relationship for mixed-repeat trials and moderated the mixing effect on the P3b.

General Discussion

Whitson et al. (in press) showed that, even under prepared and practiced conditions, increasing age is associated with an increasing mixing cost but a reducing switch cost. As this effect was due to steeper slope of the age effect on RT for mixed-repeat trials, Whitson et al. concluded that older adults process mixed-repeat trials as if they were switch trials⁶. In this paper, we set out to examine the underlying causes of this age effect on mixed-repeat trials using converging evidence from two levels of analysis: an evidence accumulation model, that estimates latent variables related to decision and non-decision processes, and ERP, that differentiate temporally between proactive (preparatory) and reactive (target-driven) control processes.

At both levels of analyses, we found that broad age effects on all trial types accompanied by more specific age effects on mixed-repeat trials within mixed-task blocks. The trajectories of age effects varied, with some having a clear linear progression (e.g., non-decision time increase; Figure 3C) and others a quadratic trend emerging early (e.g., pre-target negativity increase for mixed-task blocks; Figure 6B) or later (e.g., drift rate decline; Figure 3F). Below we first discuss the implications of the age-related changes in the processing of mixed-repeat trials. We then look at the broader set of age effects and discuss implications for current models of cognitive aging.

Age-related decline in flexible adjustment of response criterion

Both diffusion model parameters and ERP measures strongly support the conclusion that older adults treat mixed-repeat trials like switch trials (see Summary of Behavioral Findings and Discussion of ERP Findings). The age-related increase in RT mixing cost was associated with a disproportionate increase in response criterion for mixed-repeat trials, leading to higher criterion mixing cost and a smaller criterion switch cost with increasing age. Thus, older adults retained a high response criterion setting for both switch and mixed-repeat trials, whereas younger adults set a higher criterion for switch than mixed-repeat trials. This indicates that younger adults used the information provided by the task cue to flexibly adjust their criterion on a trial-by-trial basis, whereas older adults set a high criterion for all trials in the mixed-task block.

Variability in the criterion and in RT mixing cost was related to the amplitude of the cue-locked mixing cost positivity, and these relationships were moderated by age. Additionally, criterion mixing cost mediated the relationship between the cue-locked mixing cost positivity and RT mixing cost. These results provide strong evidence in favor of more conservative responding to mixed-repeat trials with increasing age (Ratcliff et al., 2005). However, they also indicate that a voluntary shift to a more conservative speed-accuracy trade-off by itself cannot account for the full set of cognitive control changes that evolve over the adult lifespan. A general preference for more careful performance (e.g., Starns and Ratcliff, 2010) predicts a similar or even greater increase in criterion for switch trials, especially since there is a tendency for an increase in errors on switch trials at both ends of the age range (Figure 3A). Yet criterion switch cost reduced with age. Hence, our findings are more consistent with a strategic choice or structural impediment that makes flexible adjustment of the criterion on a trial-by-trial basis less attractive or less viable with increasing age. According to this scenario, adoption of an accuracy-biased strategy by the aged is not because of a conscious preference for accuracy over speed. Rather it occurs because the neural networks that support speeded responding have flexibility in rapidly adjusting the response threshold to optimize performance under changing circumstances.

In addition to setting a higher response criterion on mixed-task trials, older adults had a more prolonged cue-locked mixing cost positivity, a larger drift rate mixing cost and a larger mixing effect on the target P3b. Moreover, differences between switch and mixed-repeat trials reduced with age, as indicated by the age-related reduction in RT, criterion and drift switch cost and a smaller cue-locked switch cost positivity. Together, these findings provide strong evidence that older adults process mixed-repeat trials more like switch trials, applying greater proactive control and benefiting less from repeated application of the same task-set on mixed-repeat trials. In the current paradigm, the net outcome was a reduction in RT switch cost, not because of more efficient processing of switch trials but because of less efficient processing of mixed-repeat trials.

Despite the net age-related reduction in RT switch cost, there was evidence that some switch-related processes are negatively affected by age. A greater non-decision time for switch trials was linked to less efficient preparation for switch trials and slower target encoding and post-decision processes. The finding that age effects on mixing cost were uniquely accounted for by increased criterion for mixed-repeat trials, whereas switch cost effects were influenced by variability in both decision and non-decision parameters, can explain fact that previous studies report a highly consistent age effect on RT mixing cost but inconsistent effects on RT switch cost. Although age effects on response criterion for mixed-repeat trials can explain the consistency with which mixing cost changes have been found with increasing age, the current data show that both proactive and reactive control processes associated with decision making contribute to the age-related changes in task-switching performance (see also Forstmann et al., in press).

Lifespan changes in task-switching performance

The lifespan analysis revealed both linear and quadratic trends for different variables across the adult lifespan. Non-decision processes showed a linear age effect that was steeper for switch trials, whereas decision processes had larger quadratic effects for mixed-repeat trials. Cue- and target-locked ERPs showed linear age effects on some components (e.g., N2 amplitude) but strong quadratic trends on others (e.g., mixing cost on P3b). These quadratic age effects emerged at different levels of the age scale. The pre-target negativity showed the earliest quadratic age effect with a large increase for both mixed-task trials first evident in mid-20 s, peaking in 50 s and reversing thereafter (Figures 5 and 6B). The shift in the cue-locked mixing cost positivity from a parietal effect to a smaller but broad anterior–posterior effect emerged in 30 s (Figures 5 and 6A). This cue-locked component was associated with response criterion, which showed a much steeper quadratic trend with age for mixed-repeat than either all-repeat or switch trials.

Other quadratic age effects emerged later. For example, both a) the age-related increase in non-decision processes for switch trials, reversal of criterion setting for mixed-repeat vs. switch trials, and steeper decline of drift rate for mixed-repeat trials, and b) the reversal of the age effect on the pre-target negativity for mixed-task trials and on the target-locked P3b for all-repeat trials, emerged in the older half of the age range. These effects are suggestive of a qualitative change in processing emerging at or around 60 years of age. So, although the age-related increase in mixing cost is closely linked to changes in criterion for mixed-repeat trials, evidence from latent variables and electrophysiological measures is suggestive of widespread aging-related changes in cognitive processing emerging at different time points in the adult lifespan that are not always directly evident as an overt performance change.

Support for goal maintenance account of aging (Braver and Barch, 2002)

The goal maintenance account of aging argues that age-related changes in cognitive control result from a specific decline in the ability to actively maintain goal representations so as to bias task-appropriate responding (Braver and Barch, 2002). Our task-switching paradigm satisfies conditions that predict a large impact of an age-related decline in goal maintenance (Braver and West, 2007). Specifically, in mixed-task blocks, two sets of goal representations need to be maintained in working memory and the appropriate representation needs to be activated by the task cue, which changes from trial-to-trial. The representation needs to be maintained over the preparation interval so as to bias task-appropriate responding in an environment of high goal equivocation caused by both stimulus and response bivalence. The top-down bias is required to suppress perceptual features and response tendencies arising from the alternative task-set.

In Whitson et al. (in press), we showed that age effects on mixing cost and switch cost varied dynamically as a function of task practice. Although mixing cost declined linearly with practice, it remained larger in older adults. The effects of both practice and aging on switch cost were more complex. Younger adults produced a large switch cost early in practice and a large reduction in switch cost with preparation interval only in the second practice session. Older adults required more task practice before showing the ability to reconfigure to the new task during the preparation interval. Together with recent findings by Paxton et al. (2008) using the AX-CPT paradigm, this indicates dynamic age changes in the implementation of proactive control processes relating to use of a predictive cue to optimize performance (Braver and West, 2007).

Our finding of a relatively brief mixing positivity and large switch positivity in younger adults suggests that they maintain activation of the previously relevant task representation and wait for the next cue to indicate whether a shift is necessary – only needing to load the alternative task representation if the cue indicates a change in task. This is consistent with evidence that young adults maintain a higher expectation for a repeat trial in cued-trials paradigms and show a greater preference for repeat trials in voluntary switching paradigms (see Vandierendonck et al., 2010, for a review).

If older adults have a specific difficulty in goal maintenance, they would be less likely to maintain activation of the previously relevant task representation. Instead, they would use the cue information to load the cued task on a trial-by-trial basis, resulting in cue-locked ERPs showing more similar positivity for mixed-repeat and switch trials. This can explain the larger RT mixing cost and lower RT switch cost in older adults. In addition, the large increase and prolongation of both mixing and switch effects on the P3b beyond 60 years of age (Figures 5 and 7) suggests that the strength of goal representations may weaken with age, leading to greater perceptual interference, evident in N2, and slower decision processes, evident in drift rate and P3b.

These findings are consistent with a recent fMRI study, which showed greater implementation of reactive control in older adults (Jimura and Braver, 2010). Jimura and Braver interpret their fMRI findings as an age-related shift from proactive to reactive control processes. However the ERP findings in the current study are more compatible with greater recruitment of both proactive and reactive control. Differences in the amount of task practice may partly account for this discrepancy. Whitson et al. (in press) showed that proactive control processes take longer to be instantiated in older adults. Jimura and Braver (2010) gave participants much less task practice than the present study.

Conclusion

An age-related decline in the ability to use task cues to flexibly adjust response criterion from trial-to-trial can account for our finding of a large age increase in mixing cost accompanied by a reduction in switch cost. This age-related decline in cognitive flexibility was accompanied by greater activation of proactive and reactive control processes for both trial types in mixed-task blocks and affecting both decision and non-decision processes. The age-related increase in RT mixing cost was exclusively mediated by a differential increase in response criterion for mixed-repeat vs. all-repeat trials. In contrast, the age-related reduction in switch cost resulted from effects on both decision and non-decision variables. This pattern of findings helps explain the consistent age-related increase in RT mixing cost but variable age effect on RT switch cost.

Age-related changes in latent parameters and ERP measures were not always evident in overt performance. Furthermore, both the pattern of the age trends and the onset of age changes varied considerably across variables, some emerging as early as 30 years of age. This pattern of age effects is consistent with cognitive aging models arguing that changes in cognitive processes with increasing age can be compensated for by alternative processing strategies, so there is little impact on overt performance until the compensatory strategies fail (e.g., Park and Reuter-Lorenz, 2009; Vallesi et al., 2011). Here we show that latent parameters and physiological measures can detect the early emergence of subtle age changes well before they affect overt behavior, suggesting they may aid in early detection of cognitive decline.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.