Predicting drug resistance of the HIV-1 protease using molecular interaction energy components

Abstract

Drug resistance significantly impairs the efficacy of AIDS therapy. Therefore, precise prediction of resistant viral mutants is particularly useful for developing effective drugs and designing therapeutic regimen. In this study, we applied a structure-based computational approach to predict mutants of the HIV-1 protease resistant to the seven FDA approved drugs. We analyzed the energetic pattern of the protease-drug interaction by calculating the molecular interaction energy components (MIECs) between the drug and the protease residues. Support vector machines (SVMs) were trained on MIECs to classify protease mutants into resistant and nonresistant categories. The high prediction accuracies for the test sets of cross-validations suggested that the MIECs successfully characterized the interaction interface between drugs and the HIV-1 protease. We conducted a proof-of-concept study on a newly approved drug, darunavir (TMC114), on which no drug resistance data were available in the public domain. Compared with amprenavir, our analysis suggested that darunavir might be more potent to combat drug resistance. To quantitatively estimate binding affinities of drugs and study the contributions of protease residues to causing resistance, linear regression models were trained on MIECs using partial least squares (PLS). The MIEC-PLS models also achieved satisfactory prediction accuracy. Analysis of the fitting coefficients of MIECs in the regression model revealed the important resistance mutations and shed light into understanding the mechanisms of these mutations to cause resistance. Our study demonstrated the advantages of characterizing the protease-drug interaction using MIECs. We believe that MIEC-SVM and MIEC-PLS can help design new agents or combination of therapeutic regimens to counter HIV-1 protease resistant strains.

INTRODUCTION

Inhibitors of human immunodeficiency virus type 1 (HIV-1) protease are widely used in the clinical treatment of acute immunodeficiency syndrome (AIDS). Currently, there are nine FDA-approved protease inhibitors (PIs), including atazanavir (ATV), darunavir (DRV), amprenavir (APV), indinavir (IDV), lopinavir (LPV), nelfinavir (NFV), ritonavir (RTV), saquinavir (SQV), and tipranavir (TPV). The effectiveness of these anti-HIV drugs is limited by the rapid dominance of drug-resistant variants in the viral population.¹ Genotypic and phenotypic resistance testing has become an important step in drug development and optimizing combination therapy for treating HIV infection: phenotypic assay measures viral replication rate in the presence of a drug with varying concentrations, and genotypic assay determines sequences of viral mutants. Because of the existence of many different mutations and mutation patterns related to drug resistance, it is not straightforward to correlate genotypic to phenotypic measurements.

Attempts have been made to develop computational methods for predicting HIV-1 protease drug resistance based on the genotypic data. One group of methods, usually referred as sequence-based approaches, applies statistical methods for analyzing the sequences of the resistant/nonresistant mutants,^2–10 and their prediction accuracies rely on the availability of a large and comprehensive training set. These methods are computationally efficient but they cannot predict resistant mutations for new inhibitors because no data are available to train the predictors. Another group of methods, often referred as structure-based approaches, utilizes the 3-D structural information to directly calculate the binding free energies between the protease mutants and the inhibitors under investigation.^11–19 These methods do not need a large set of training data and can make ab initio predictions, but noise/error in the free energy calculation often undermine their prediction performance.²⁰

We present here a method to combine the advantages of the above two groups of approaches to tackle this problem. We applied a structure-based strategy to predict the genotypic protease resistance by characterizing the energetic patterns of the protease-drug interaction. We calculated the molecular interaction energy components (MIECs) between each drug and protease residues using the molecular mechanics/generalized born (MM/GB) energy decomposition analysis.²¹ Different from the other structure-based methods that often rely on the precise calculation of the binding energy between the protease and drugs, MIECs can characterize the local environment of protease-drug interaction better and significantly reduce the noise caused by the inaccurate computation of energetic contributions from some residues. We have trained classification and regression models based on MIECs to predict the resistance of protease mutants to a given drug. These models can also provide structural insights of the molecular mechanism for resistance. More importantly, we applied our methods to predict mutant strains resistant to a newly approved drug, darunavir, before any clinical or experimental data are available. As far as we know, this is the first attempt along this line. Our study shows the possibility to use computational approaches for optimizing the known drugs and even for designing new inhibitors to combat resistance.

MATERIALS AND METHODS

The dataset

The genotypic resistance data for the seven FDA-approved protease drugs (ATV, APV, IDV, LPV, NFV, SQV, and ATV) used in this study were obtained from the Stanford HIV drug resistance database²² (Table I). Drug susceptibility is measured by the ratio of IC₅₀ (RI) between a mutant isolate and a standard wild-type control isolate.² Considering IC₅₀ values that roughly depend on the exponential of the binding free energy, we used log₁₀(ratio of IC₅₀)(pRI) in the regression analysis. In the classification analysis, based on the ratio of IC₅₀ values, the protease mutants were classified into either of the two categories: low (<10-folds) or high (≥10-folds) resistant strands¹⁵ or three categories: susceptible (<3 folds), low/intermediate resistance (between 3- and 20-folds), and high-level resistance (>20-folds).⁵

Table I.

Drug Susceptibility for Clinical Isolates

	Nisoa	Nstructb	Three classes			Two classes
			Susc (%)	Low/int (%)	High (%)	Low (%)	High (%)
Amprenavir (APV)	768	2327	68	21	11	83	17
Atazanavir (ATV)	329	796	35	29	36	55	45
Indinavir (IDV)	827	2444	54	31	15	68	32
Lopinavir (LPV)	517	1611	43	26	31	62	38
Nelfinavir (NFV)	844	2464	47	19	34	57	43
Ritonavir (RTV)	795	2407	51	17	32	65	35
Saquinavir (SQV)	826	2445	62	18	20	73	27

^aN_iso is the number of clinical isolates.

^bN_struct is the number of structures, which includes all possible combinations of mutations in each isolate.

Modeling mutant HIV-1 protease/drug complexes

The crystal structures of the HIV-1 protease complexed with eight drugs were used as templates to generate the mutant HIV-1 protease/drug complexes. The PDB entries are 1hxb (SQV),²³ 1hsg (IDV),²⁴ 1hxw (RTV),²⁵ 1ohr (NFV),²⁶ 1hpv (APV),²⁷ 1mui (LPV),²⁸ 2o4k (ATV),²⁹ and 1sg6 (DRV).³⁰ All missing hydrogen atoms of the proteins were added using the leap module in AMBER 9.0 software package.³¹ The protonated state of the ionizable residues, except for D25/D25′, was assigned based on the pKa values at pH = 7. For D25/D25′ of the protease, monoprotonated state was adopted as determined previously.¹⁸ In the monoprotonated state, the proton was placed at OD1 oxygen (the oxygen close to the drugs) of Asp25. Partial charges of the drug atoms were determined using the RESP fitting technique based on the electrostatic potentials, which was calculated using Hartree-Fock (HF)/6–31G* in Gaussian 98.³² The partial charges and the force-field parameters for the drugs were automatically generated using the Antechamber program in AMBER9.0.³³ AMBER03 (parm03),³⁴ and general AMBER force field (gaff)³⁵ were used for the protease and the drugs, respectively, in the simulation.

To model the mutated protease/drug complexes, we first mutated the wild-type protease using the scap program.³⁶ Individual mutations were introduced in both chains of the HIV-1 protease dimer. The conformations of the mutated residues were then optimized by allowing two-degree rotation on each rotatable bond to search for lower energy conformation. Next, energy minimization for the entire complex was carried out using the sander program in AMBER9.0. The solvent effect was considered by using the Hawkins et al. pair-wise generalized Born (GB) model³⁷ that was implemented in sander. The maximum number of minimization steps was set to 4000. The first 100 steps were performed using the steepest descent and the rest using the conjugate gradient. The convergence criterion for the root-mean-square (rms) of the Cartesian elements of the energy gradient was 0.1 kcal/(mol Å). The minimized structures for all protease/drug complexes were saved for further analysis.

The mutant protease/drug interaction energy components

The optimized complex structure was used in the following energy decomposition analysis. The interactions between each of the 99 protease residues and the drug were computed using the MM/GB protocol. Note that the residues on both protease chains were considered altogether for an individual mutation. The interaction for each residue–drug pair includes electrostatic (Coulombic) interaction (ΔE_ele), van der Waals interaction (ΔE_vdw), and polar contribution to desolvation free energy (ΔG_GB), which was calculated using the GB model. The cutoff for calculating ΔE_vdw and ΔE_ele was set to be 18.0 Å. The charges used in the GB calculations were taken from the AMBER03 force field. The values of interior and exterior dielectric constants were set to 1 and 80, respectively. The GB parameters developed by Tsui and Case were used.³⁸ The molecular interaction calculations, including read-in of the protease/drug complexes, definition of atom types in the GB calculation, and assignment of the force field parameters, were automatically carried out using the gleap program (which will be released in AMBER10 in early 2008).³⁹

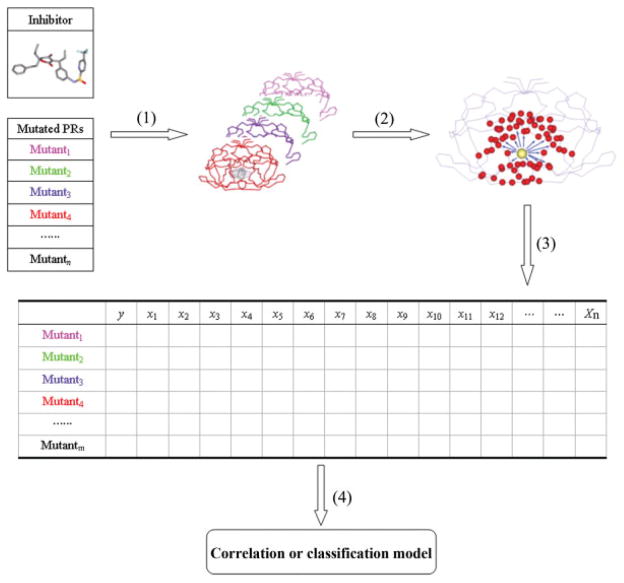
The ratio of IC₅₀ between a mutant isolate and a standard wild-type control isolate was converted to binding free energy difference as $\mathrm{\Delta }(\mathrm{\Delta }G)=\mathrm{\Delta }{G}_{\text{binding}}^{\text{wt}}-\mathrm{\Delta }{G}_{\text{binding}}^{\text{mut}}\approx \mathit{RT}ln({IC}_{50}^{\text{mut}}/{IC}_{50}^{\text{wt}})$. Because the resistant effect of a mutation to a drug depends on the binding free energy change between the wild type and the mutated proteases,^15,17 the difference between the interactions for each protease residue–drug pair in the mutated complex and those in the wild-type complex was used in the classification and regression analysis. For each drug, we obtained an m × n matrix from the molecular interaction energy component analysis, where m is the number of protease mutants and n is the number of MIECs (see Fig. 1).

Figure 1.

Scheme of the procedure to build the prediction models based on MIECs. (1) Model the protease/drug complexes based on Virtual Mutagenesis and GB-based molecular mechanics minimizations. (2) Determine the interactions between each drug and the protease residues using the MM/GB free energy decomposition analysis. The drug is shown as a yellow ball, and the protease residues are shown as red balls. (3) Generate the protease/drug MIECs. The columns of the table represent the drug-residue interaction pairs. (4) Apply statistical methods to analyze the MIEC matrix and build classification or regression models.

Classification models using support vector machine

Support vector machines (SVMs) were trained on the normalized MIECs of each drug to classify protease mutants into two or three resistance classes (as defined earlier). The LIBSVM program was used in this study.⁴⁰ A threefold cross validation was run for 500 times to evaluate the performance of the SVM. For the two-class (or binary) classification model TP (true positive), FP (false positive), TN (true negative), and FN (false negative) for the 500 test sets were counted. The predictive performance was evaluated by calculating the average values of the following: sensitivity (SE), TP/(TP + FN); specificity (SP), TN/(TN + FP), prediction accuracy for high-level resistant samples (Q+), TP/(TP + FP); prediction accuracy for low-level resistant samples (Q−), TN/(TN + FN); and Matthews correlation coefficient $C=\frac{\text{TP}\times \text{TN}-\text{FN}\times \text{FP}}{\sqrt{(\text{TP}+\text{FN})(\text{TP}+\text{FP})(\text{TN}+\text{FN})(\text{TN}+\text{FP})}}$. For the three-class (or ternary) classification model, the predictive performance was evaluated by calculating the average percentage of correctly predicted samples, defined as prediction accuracy, for each class in the test sets.

Regression models using partial least squares

To remove noninformative columns in the input MIEC matrix, the following filter was applied: if the difference between the maximum and the minimum values in a specific column is <0.05 kcal/mol, then that column was eliminated. Partial least squares (PLS) regression model was built for the predictor variable X (MIECs, its ith component x_i is the ith column in the matrix) and the response variable Y [log₁₀(ratio of IC₅₀)]. PLS regression searches for a set of principal components that performs a simultaneous decomposition of X and Y with a constraint that these components explain as much as possible of the covariance between X and Y. It is followed by a regression step where the decomposition of X is used to predict Y.⁴¹ Y and each x_i were normalized with a zero mean and unit standard deviation. To evaluate the performance of the model, threefold cross validations were conducted. A PLS model was built on the training data (2/3 of the total samples) using all x_i’s. The optimal number of the principal components of the model was chosen to achieve the squared leave-one-out (LOO) cross-validation regression coefficient (q²) for the training data. The prediction power of the model was then evaluated on the test set (1/3 of the total samples).

MM/GBSA calculations

Binding free energies between drugs and protease mutants were calculated using the MM/GBSA method^42,43:

$$\mathrm{\Delta }{G}_{\text{binding}}=G_{\text{complex}}-G_{\text{protein}}-G_{\text{ligand}}=\mathrm{\Delta }{E}_{\text{MM}}+\mathrm{\Delta }{G}_{\text{PB}}+\mathrm{\Delta }{G}_{\text{nonpolar}}-T\mathrm{\Delta }S$$ (1)

where ΔE_MM is the molecular mechanics energy calculated using sander in AMBER9.0 and it is the sum of van der Waals energy ΔE_vdw and electrostatic energy ΔE_ele; ΔG_GB is the polar component of the solvation energy computed using the GB model with the parameters developed by Tsui and Case (the values of interior and exterior dielectric constants were set to 1 and 80, respectively)³⁸; ΔG_nonpolar is the nonpolar component of solvation energy calculated based on solvent accessible surface area (SASA) as ΔG_nonpolar = 0.0072 × SASA; −TΔS is the conformational entropy change that was not included in this study because of the high computational cost.

RESULTS AND DISCUSSION

Predicting resistant mutants using classification models

We first examined whether the HIV-1 protease mutants resistant to a given drug can be successfully predicted using MIECs. This is indeed a classification problem, and we thus trained SVMs on MIECs to classify the protease sequences into low- and high-resistant categories. The number of sequences in different categories is shown in Table I. To choose the kernel function and MIECs that give the best classification results, we conducted a case study on amprenavir (APV). For each of the four commonly used kernel functions (linear, polynomial, RBF, and sigmoid), we trained SVMs on the following MIECs: van der Waals (ΔE_vdw) and electrostatic (ΔE_ele) (Model 1 in Table S1 in the supplementary materials), ΔE_vdw and polar (ΔG_polar, the sum of the electrostatic ΔE_ele and the polar desolvation energy ΔG_GB) (Model 2), and ΔE_vdw, ΔE_ele, and ΔG_GB (Model 3). The performance of each model was evaluated by the prediction accuracy on the test sets in the 500 runs of cross validations (Table S1 in the supplementary materials). Based on the Matthews correlation coefficients, a measure of the quality of a classifier, the linear kernel performs slightly better than the RBF kernel, and significantly better than the other two kernels in all three models. Comparison of linear and RBF kernels in predicting resistant mutants for the other six drugs further confirmed that the linear kernel achieved the best classification performance (Table II and Table S2 in the supplementary materials). For all drugs but SQV, the SVM trained on ΔE_vdw and ΔG_polar had the best performance.

Table II.

The Prediction Accuracies of the Best Binary SVMs for the Seven Drugs

Model	Drug	MIECs	Kernel	SEtest	SPtest	Q+	Q−	C
1	APV	ΔEvdw, ΔGpolar	Linear	87.2	93.8	73.6	97.4	0.758
2	ATV	ΔEvdw, ΔGpolar	Linear	91.2	92.8	91.3	92.8	0.841
3	IDV	ΔEvdw, ΔGpolar	Linear	92.0	93.7	87.3	96.2	0.846
4	LPV	ΔEvdw, ΔGpolar	Linear	93.1	95.0	92.1	95.7	0.879
5	NFV	ΔEvdw, ΔGpolar	Linear	94.3	94.7	93.1	95.6	0.888
6	RTV	ΔEvdw, ΔGpolar	Linear	95.8	96.1	95.6	99.0	0.952
7	SQV	ΔEvdw, ΔEele	Linear	92.1	95.2	87.5	97.1	0.859

The SVMs achieved high sensitivity, specificity, and prediction accuracies for all the drugs on the test sets in the 500 runs of cross validations (Table II). Matthews correlation coefficients for all drugs but APV are above 0.84. Even the lowest Matthews correlation coefficient of APV (0.758) is still satisfactory given the large unbalanced data set of positives and negatives. Overall, the SVMs trained on MIECs can accurately predict the drug susceptibility of protease mutations, which suggests that MIECs can characterize the energetic patterns of the interactions between the protease and the drugs.

Next, we addressed a more challenging question: despite the diverse chemical structures of the seven drugs, can we build a universal model to predict drug susceptibility for protease mutants? This is also a further test of whether MIECs provide a generic description of the protease-drug interactions. More importantly, it will allow prediction of protease mutants’ susceptibility to new inhibitors. The best universal SVM classifier trained on the combined MIECs of all the seven drugs using linear kernel and two MIECs, ΔE_vdw, and ΔG_polar, achieved an average Matthews correlation coefficient of 0.795 for all the drugs (Model 3 in Table III and Table S3 in the supplementary materials). The average sensitivity (92.3%), specificity (89.6%), positive prediction accuracy (81.0%), and negative prediction accuracy (96.0%) for the test sets are also satisfactory for the universal model.

Table III.

The Universal Binary Classification Model for the HIV-1 Protease Drugs

Model	MIECs	Kernel	SEtest	SPtest	Q+	Q−	C
1	ΔEele, ΔEvdw	Linear	91.5	88.7	79.5	95.6	0.776
2		RBF	81.9	91.0	81.3	91.3	0.728
3	ΔEvdw, ΔGpolar	Linear	92.3	89.6	81.0	96.0	0.795
4		RBF	86.2	90.0	80.6	93.1	0.750
5	ΔEele, ΔEvdw, ΔGGB	Linear	91.7	88.8	79.8	95.7	0.780
6		RBF	82.9	90.6	80.9	91.7	0.730

Comparison with the sequence-based models

To demonstrate the advantages of our method, we compared our predictions with the analysis by Rhee et al. on the same dataset using various statistical methods based on sequence.⁵ Rhee et al. divided the protease mutants into three categories: susceptible (<3-fold), low/intermediate resistance (between 3- and 20-fold), and high-level resistance (>20 folds). To have a direct comparison with Rhee’s results, we trained ternary classifiers and evaluated their classification performances on the test sets in the 500 runs of cross validations (Table S4 in the supplementary materials). Consistent with the observation for the two-class cases, SVMs using the linear kernel and MIECs of ΔE_vdw and ΔG_polar achieved the highest prediction accuracies, which were in the range of 86.4% (indinavir) and 92.5% (ritonavir). Overall, the performance of our ternary models is satisfactory.

When compared with the sequence-based methods in the study of Rhee et al., we found (1) our ternary models achieved better prediction accuracies for each individual drug: the average prediction accuracies of the best models in Rhee et al. study are 84% for APV, 77% for ATV, 79% for IDV, 81% for LPV, 82% for NFV, 89% for RTV, and 84% for SQV, respectively.⁵ The corresponding prediction accuracies of our models are 89%, 86%, 86%, 91%, 87%, 93%, and 89%, respectively (Table S4). (2) MIEC-SVM can naturally consider all positions in the model and does not impair prediction accuracy. Rhee et al. used three mutation sets in training models and predicting drug susceptibility of protease mutants: (a) a complete set of all mutations present in ≥2 sequences, (b) an expert panel mutation set, and (c) a set of nonpolymorphic treatment-selected mutations (TSMs). They found that the nonpolymorphic TSM set had the highest prediction accuracy. Using all mutations was not the best choice in sequence-based approach because some mutation positions introduced noise. TSMs did not include these positions and therefore noise introduced by these positions was removed from the prediction models. In our approach, the contribution of each protease residue to drug binding was naturally considered by the corresponding MIECs. Therefore, arbitrarily choosing mutation positions was avoided. (3) MIEC-SVM can but the sequence-based approaches cannot predict protease mutants resistant to new inhibitors that are not included in the training set. In the study of Rhee et al., no structure information was considered and the prediction power of their model completely relies on the availability of drug susceptibility data for an inhibitor. In contrast, the MIEC-SVM models were trained to characterize the energetic patterns of the interaction between protease and drugs and therefore the models can be applied to new inhibitors.

Predicting drug resistance for darunavir

In drug development, it is common that new inhibitors are often derivatives/variants of the existing ones. The last feature of our method discussed in the previous paragraph allows predicting drug resistance profiles in the early stage of drug development particularly during drug lead optimization. We showed the usefulness of our method on darunavir (TMC114), a recently approved HIV-1 protease drug. The chemical structures of darunavir and amprenavir only differ by a second tetrahydrofuran ring, part of which is referred as bis-THF moiety. Currently, no large-scale genotypic data are available for darunavir, which makes it impossible to train sequence-based models for predicting resistant mutations.

Given the highly similar chemical structures of darunavir and amprenavir, it is interesting to compare the binding profiles of these two drugs with the same set of protease mutants. To demonstrate the usefulness of our method on drug lead optimization, we chose to use the MIEC-SVM model trained on amprenaivir to predict the mutants resistant to darunavir (Model 1 in Table II): the percentages for the high- and low-resistant mutants were 10.5% (245/2327) and 89.5% (2082/2327), respectively. Obviously, the percentage of the high-resistant mutants for darunavir is much lower than that of amprenavir: 16.7% (388/2327) by experimental measurements or 20.1% (467/2327) by prediction. This observation is consistent with the in vitro mutation experiments that darunavir has a low liability for developing resistance compared with amprenavir and lopinavir.⁴⁴

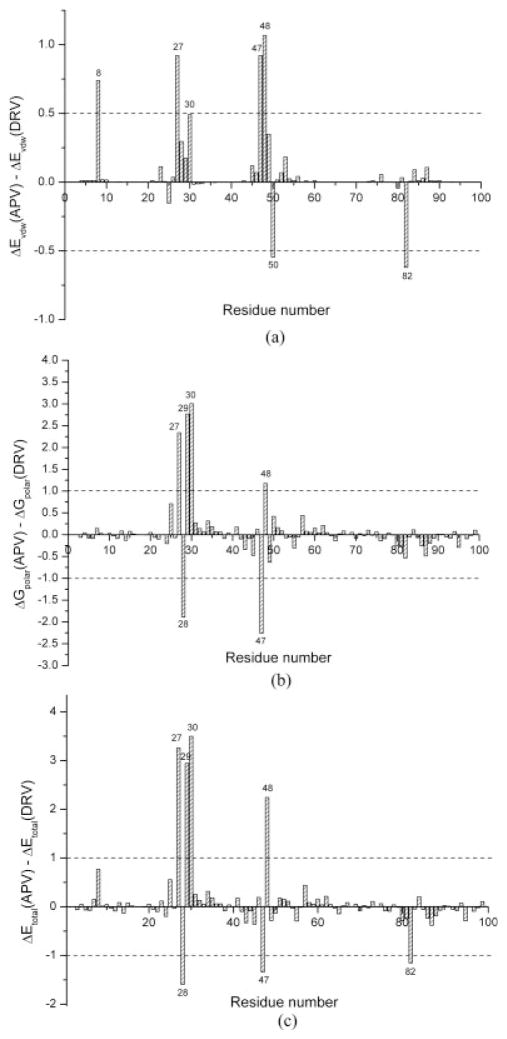
To examine the molecular basis of the difference between the potencies of amprenavir and darunavir, we compared the average contribution of each protease residue to binding with these two drugs in all the mutants (see Fig. 2). We found that Ala27, Asp29, Asp30, and Gly48 form more favorable interactions with darunavir through the bis-THF and the benzenesulfonamide moieties than with amprenavir [Fig. 2(c)]. In particular, two stable hydrogen bonds were observed between the bis-THF of darunavir and the backbone nitrogen atoms of Asp29 and Asp30. Three protease residues, Ala28, Ile47, and V82, form less favorable interactions with darunavir than with amprenavir. Further analyses showed that the major contribution to such differences was the polar contribution to binding, that is, the sum of Coulombic and polar contribution to desolvation energy [Fig. 2(a,b)].

Figure 2.

The difference of the molecular interactions between amprenavir (APV) and darunavir (DRV). (a) van der Waals, (b) polar (the sum of the electrostatic interaction and the polar contribution of solvation), and (c) total energy.

Because Ala27 and Asp29 are well conserved and presumably important for viral functions, stronger interaction with these residues should help combat resistance. Val82 and Ile47 are not conserved and potent drugs should have weaker interactions with these residues. Based on the above analyses, the modified chemical structure of darunavir may improve its potency by optimizing its interactions with these four residues to combat resistance. However, davunavir has more favorable interactions with Asp30 and Gly48 than amprenavir and does not reduce its interactions with resistant residues of Val32, Ile54, and Ile84. Therefore, further optimizing darunavir may be focused on improving the inhibitor’s interactions with these residues.

Regression models for genotypic resistance prediction

To quantitatively estimate the binding affinity for each drug and study the contribution of each protease residue to resistance, we fitted linear regression models to MIECs using partial least squares (PLS). It can be considered as an extension of the linear interaction energy method^45–47: the binding free energy is estimated from the residue–ligand interaction energy components rather than the total interaction energy components between the protein and the ligand.

Calculated binding affinities correlated well with the experimental values

For each drug, the regression models using different combinations of the three types of MIECs, that is, van der Waals, electrostatic, and polar contribution to desolvation energy, were trained and tested using threefold cross validations (see Methods). In the training, we selected the best models based on the squared fitting coefficients r² for the test sets (Table IV and Table S5 in the supplementary materials). For the seven drugs, values of q² for the test sets were in the range of 0.81 to 0.91, which suggested that the PLS models were fit well to the training data. A similar performance of the models on the test sets, r² ranging from 0.81 to 0.92 (Table IV, Table S5 and Fig. S1) demonstrated that the MIEC-PLS models achieved satisfactory performance of predicting drug susceptibility for the HIV protease mutants.

Table IV.

Performance of the Best PLS Models for the Seven Drugs

Model	Drug	Interaction fields	n1a	NPCb	Nc	r2 d	q2 e	RMSEf	XRMESg	n2h	$r_{\text{test}}^2$ i	RMSEtestj
1	APV	ΔEvdw, ΔGpolar	1551	50	118	0.852	0.814	0.573	0.645	776	0.810	0.636
2	ATV	ΔEvdw, ΔEele	531	110	125	0.898	0.805	0.514	0.719	265	0.828	0.669
3	IDV	ΔEvdw, ΔGpolar	1629	50	124	0.870	0.838	0.620	0.694	815	0.842	0.657
4	LPV	ΔEvdw, ΔEele, ΔGGB	1074	95	214	0.909	0.864	0.580	0.712	537	0.885	0.631
5	NFV	ΔEvdw, ΔEele, ΔGGB	1643	100	220	0.899	0.871	0.607	0.687	821	0.859	0.712
6	RTV	ΔEvdw, ΔEele, ΔGGB	1605	120	223	0.940	0.908	0.513	0.635	802	0.921	0.581
7	SQV	ΔEvdw, ΔEele, ΔGGB	1630	120	223	0.901	0.839	0.623	0.802	815	0.855	0.730

^an₁ is the number of samples in the training set.

^bN_PC is the number of principal components used in the model.

^cN is the number of MIECs terms.

^dr² is the squared regression coefficient for the training set.

^eq² is the squared leave-one-out cross-validation regression coefficient.

^fRMSE is the root mean square error for the training set.

^gXRMSE is the leave-one-out cross-validation root mean square error for the training set.

^hn₂ is the number of samples in the test set.

ⁱ $r_{\text{test}}^2$ is the squared regression coefficient for the test set.

^jRMSE_test is the root mean square error for the test set.

The contributions of the protease residues to drug resistance

The contributions of the HIV-1 protease residues to drug resistance were estimated by analyzing the fitting coefficients of the MIEC terms in the PLS models. The importance of MIECs was indicated by the values of the fitting coefficients for the van der Waals and the polar MIECs (Fig. S2). A positive fitting coefficient means the change of the residue’s contribution to the binding correlates with the change of the binding affinity between the drug and the protease mutants, that is, the residue contributes to resistance. A negative fitting coefficient means the residue helps reduce resistance. For example, several known major APV-resistant mutations including D30, I54, V82, I84, and L90 were recognized by their large positive fitting coefficients. Particularly, I54 and I84 had large positive fitting coefficients in the PLS models for seven and six drugs, respectively. This observation suggested that mutations at these two positions may cause strong cross-resistance to the seven drugs and thus leads to the failure of cocktail therapy. Because the major contributions are the van der Waals interactions, inhibitors with smaller molecular groups contacting these two positions may serve as complimentary drugs to the existing ones.

Some nonmutated residues that are neighbors to the above resistant positions also had positive fitting coefficients, such as A28 and G51 for APV. This is not totally unexpected because mutations on the resistant positions cause conformational change and thus affect the interactions between the neighboring residues and the drugs. Indeed, the change of the interaction between APV and G51 was anticorrelated with that between APV and I50 (r = (0.67). Therefore, the mutation on G48 and I50 caused conformational change that made the nonmutated neighboring residues to become “resistant” to drugs. Obviously, such mechanistic insights can only be obtained from computer modeling combined with statistical analysis but not from pure bioinformatics analysis based on sequences.

Comparison with the prediction based on the MM/GBSA technique

Free energy calculations have been widely applied to predicting resistance mutations of the HIV-1 protease.^11–16 The performances of these studies vary significantly depending on the size of the dataset and the approaches used to estimate the binding free energy. To our knowledge, there has been no study to calculate binding free energies for the drug susceptibility data we analyzed here. For the purpose of comparison, we conducted such calculations using MM/GBSA. The correlation coefficients between the calculated and the experimental binding affinities were not satisfactory (r² = 0.18–0.45) (Table S6 in the supplementary materials). We also investigated the correlation between each free energy component and the measured binding affinities. Compared with the van der Waals interactions (r² = 0.14–0.62), the electrostatic interactions (r² = 0.02–0.12), and polar contribution to desolvation (r² = 0.02–0.13) showed much worse correlations with the drug susceptibility data. This observation implied significant noise/error might be introduced in calculating the latter two components of the binding free energy.

To our knowledge, one of the possible reasons that the MIEC-PLS outperformed MM/GBSA is the following. The value of dielectric constant in the GB model depends on the local chemical environment. Therefore, a universal interior dielectric constant used by MM/GBSA for the entire complex could introduce noise to some residue/drug interactions. In contrast, MIEC-PLS weighted each interaction component between a protease residue and the drug, which is equivalent to calculate an effective dielectric constant determined by the local environments. In addition, the noisy residue–drug interactions should have small fitting coefficient in the regression model and thus their influence to the prediction accuracy would be reduced.

CONCLUSIONS

We present here a computational approach that combines computer modeling and statistical analysis to characterize the energetic patterns of the interactions between the HIV-1 protease and the inhibitors. We demonstrated that the MIEC-SVM models could successfully identify resistant mutants with high accuracy. In addition, we trained a unified MIEC-SVM model from the seven drugs with diverse chemical structures. The success of the unified model on predicting drug susceptibility of protease mutants supported that our method did capture the characteristics of the protein–ligand interactions. Previously, we have applied the MIEC-SVM and MIEC-PLS methods to study the interaction between the amphiphysin SH3 domain and 884 peptides. SH3 domain is about 60-amino acid long and its structure is completely different from the HIV-1 protease. The satisfactory performances of our approach on the two distinct systems suggested that MIEC coupled with statistical analysis may provide a generic means to decipher protein recognition code. Of course, further testing our approach on other molecules is needed to confirm the generality of our approach.

We showed that the MIEC-SVM models outperformed the sequence-based bioinformatics methods on classifying resistant/nonresistant protease mutants. More importantly, our method can predict resistant profiles for a new inhibitor but the sequence-based method cannot. This feature of our method makes it possible to optimize the potency of a drug lead at the early stages of drug development, which is no doubt critical in designing new anti-HIV inhibitors. We conducted a proof-of-concept study on predicting mutants resistant to a newly approved drug, darunavir, whereas no drug susceptibility data were available at the time. We predicted that darunavir had less percentage of high-resistant mutants than amprenavir. The comparison of the interaction profiles of the two drugs suggested that the higher potency of darunaivir might be a result of its weaker interactions with several drug-resistant residues, especially Ile47 and Val82, than amprenavir.

We also demonstrated that the MIEC-PLS models can quantitatively estimate the binding affinities between the drugs and the protease mutants. The calculation results correlate well with the experimental measures as show by high-correlation coefficients r² = 0.81–0.92. The prediction accuracies of the MIEC-PLS were much higher than those of the conventional MM/GBSA method even the modeling procedures of the two approaches were exactly same. We argue that MIECs coupled with statistical analysis can effectively filter out the noisy or error in the free energy calculation by, for example, adjusting the effective dielectric constant depending on the local chemical environment.

Compared with the sequence-based approaches, our method could provide structural insights into understanding the molecular mechanism causing resistance. For example, our analysis revealed the interdependence of protease residues’ contributions to drug resistance but sequence-based methods cannot provide such information. Although our approach is more computationally expensive than the sequence-based methods, we believe the MIEC-based methods will become more and more useful as more powerful computers are becoming available. Moreover, with the development of more accurate solvation models and force field parameters as well as more powerful conformational sampling techniques, we expect that the prediction accuracy of our approach can be further improved.