On the Interplay between the Evolvability and Network Robustness in an Evolutionary Biological Network: A Systems Biology Approach

Abstract

In the evolutionary process, the random transmission and mutation of genes provide biological diversities for natural selection. In order to preserve functional phenotypes between generations, gene networks need to evolve robustly under the influence of random perturbations. Therefore, the robustness of the phenotype, in the evolutionary process, exerts a selection force on gene networks to keep network functions. However, gene networks need to adjust, by variations in genetic content, to generate phenotypes for new challenges in the network’s evolution, ie, the evolvability. Hence, there should be some interplay between the evolvability and network robustness in evolutionary gene networks. In this study, the interplay between the evolvability and network robustness of a gene network and a biochemical network is discussed from a nonlinear stochastic system point of view. It was found that if the genetic robustness plus environmental robustness is less than the network robustness, the phenotype of the biological network is robust in evolution. The tradeoff between the genetic robustness and environmental robustness in evolution is discussed from the stochastic stability robustness and sensitivity of the nonlinear stochastic biological network, which may be relevant to the statistical tradeoff between bias and variance, the so-called bias/variance dilemma. Further, the tradeoff could be considered as an antagonistic pleiotropic action of a gene network and discussed from the systems biology perspective.

Background

For a long time, biologists have known that many biological functions and diseases cannot be explained by the function of an individual gene or protein. Instead, they are the result of an interactive network between a protein and another protein, or protein with other molecules.^1,2 It has also been found that some particular characteristics of biological systems evolve under robust regulation, despite large changes in the environment or alternations to the internal parameters of the system.^3,4 Robustness is a ubiquitously observed property of biological systems, at many levels, from biochemical to ecological systems.^5–9 For example, a genome may be robust, because it encodes proofreading and repairing systems that can reduce replication errors; a metabolic function may be robust, when it encounters stresses, like a temperature change, because some enzymes can maintain their shapes and specificity, or the interconnected network of their reactions can sustain the supply of product, even when they fail; an ecosystem might be robust, if it resists the extinction of some species because of the compensatory effect of other surviving species.¹⁰ In the genetic robustness, since the random variations, due to mutation, deletion, duplication, insertion, inversion, translation of a chromosome in germ cell or the random transmissions of genes from parent to offspring, arise constantly in the evolutionary process, it implies that evolution, as a genetic process, must allow for this randomness, because it provides the raw material for evolutionary adaptation. The mechanisms of genetic robustness, such as genetic redundancy, proofreading and repairing systems, are considered to be the fundamental features that balance the randomness of a complex evolvable gene network.¹⁰ However, too much robustness is not conductive to a biological system to adapt to environmental changes, which play an important role in the natural selection.

Robustness, undoubtedly, is the result of an organism’s ability to adapt to the environmental changes, through long-term evolution. In individual level, robustness has important implications for both disease and evolution, as it reduces the phenotypic expression of genetic changes. For evolutionary biologist, the concept of phenotype robustness (or phenotypic stability, sometimes referred to as ‘canalization’)¹¹ is viewed as genetic buffering that has evolved under natural selection in order to stabilize the phenotype.¹² Concerning the interplay between the evolvability and robustness, some important issues exist and claim that robustness can either increase or decrease the evolvability.^10,13 On one hand, high robustness implies low production of heritable phenotypic variation. On the other hand, both experimental and computational analyses of neutral networks indicate that robustness enhances evolvability. There should exist some delicate balance between the evolvability and network robustness, in an evolutionary biological network. The paradoxical tension between genetic robustness and evolvability has been confirmed by studying RNA genotypes and their secondary structure phenotypes.¹⁴ A high level of correlation between genetic robustness and environmental robustness was found from the biophysics of RNA folding that the genetic robustness observed in miRNA is considered as the byproduct of selection for environmental robustness.¹⁵ Based on the yeast gene deletion collection, the effects of mutations on environmental robustness,^16,17 genetic robustness^18,19 and phenotypic robustness^20,21 can be measured and compared on a genome-wide scale. Using global quantitative genetic datasets in yeast,²² the phenomenon, that the coupled genetic and environmental robustness are both also coupled to stochastic robustness, are found and largely consistent with Waddington’s intuition, ie, environmental change, phenotypic variation and genetic mutation have similar effects on an organism via the same underlying molecular processes. These brilliant research results provide the firm bases to make the global quantification of robustness become possible by recent genomic experiments. However, there still lack some appropriate mathematical methods to clarify the ambiguous relationship among these different types of robustness and the interplay between the evolvability and robustness.

It has been previously reported that robustness of biological systems may come from a precise network structure.⁵ To understand the interplay between the evolvability and network robustness of biological systems, in the evolutionary process, it is necessary to integrate the information of genome sequences, mRNA expression, proteomes and so on, from the system level point of view, and to analyze the composition of biological systems, at various levels- the interactions between modules, stochastic system dynamics, underlying stability robustness and sensitivity in control theory^23,24 and natural selection in evolution.^7,25 In the past, most molecular biologists and biochemists assumed that biological evolution occurs, due to random variations in genes and natural selection. However, the evolution of biological networks via natural selection is still in the conceptual phase, with no dynamic system rules.^8,9,25 The study of the evolvability and robustness of gene networks, or biochemical networks is still in its infancy. In fact, robustness allows changes in the structure and components of gene networks, due to intrinsic random fluctuations, while still allowing the specified network function to be maintained. Evolvability also allows some extrinsic random disturbances to influence gene networks, so that a new phenotype of the gene network may evolve by natural selection, to adapt to the new environment.⁹

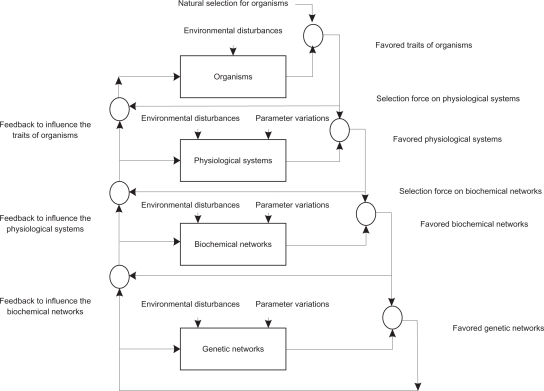
In this study, the interplay between the evolvability and robustness of a biological network in evolution, is considered from a systems perspective. According to the hierarchical network interplaying in Figure 1,⁸ the high-level selected network will specify a selection force on lower levels. The external environment molds the evolution of the local adaptation of organisms by natural selection. Once the favored organisms are selected, the low-level biological networks have to maintain the favored physiological systems of the selected organisms. Hence, these favored organisms become selection forces, able to select their favored physiological systems.^26–28 The favored physiological systems exert a selection force on the biochemical networks. The favored biochemical networks then become the selection forces for their regulatory gene networks. Finally, the low-level selected networks send feedback to influence the evolution of the high-level network. In this way, natural selection actually acts on the interplaying of multiple biological networks. The development of robust adaptive design rules, for the natural selection of biological networks, might allow more insight into the evolutionary mechanisms of biological networks, under the influence of random intrinsic noise and environmental disturbances.⁵

Figure 1.

The natural selection process on the interplaying of hierarchical biological networks. The high-level biological network selection will become the selection force on low-level biological network. The natural selection on organisms selects its favored organisms. Once the favored organisms are selected, the low-level biological networks have to maintain the favored physiological systems of the selected organisms. Hence, these favored organisms become the selection force to shape their favored physiological systems. The favored physiological systems will lead to the selection force on biochemical networks. The favored biochemical networks by natural selection will become the selection force on genetic networks. On the other hand, the lower-level selected networks will feedback to influence the higher-level networks in evolution. Therefore, the natural selection actually acts on the interplaying of the multiple bio-networks.⁸

One of the most important features of biology is that the organism’s phenotypes can be robust, against either heritable genetic variations or non-heritable environmental disturbances. In the evolutionary process, an evolving gene network can be represented by a nonlinear stochastic system that is subject to heritable random genetic variations and non-heritable random environmental disturbances. The phenotype of a gene network can be represented by the equilibrium point of a nonlinear stochastic system. There are many variations of phenotypes around this equilibrium point, due to intrinsic random genetic variations and extrinsic environmental disturbances.^8,9,29–32 When a variation of a phenotype is perturbed too much, from the domain of its equilibrium point into the domains of other equilibrium points, a new phenotype is generated and preserved, if it is suited to natural selection, otherwise the variation of the phenotype is terminated. A gene locus that does not help an organism to cope with the environmental stress, or to increase its fitness is neutral. These genetically varied phenotypes are heterogeneous and allow evolvability, to cope with environmental changes.⁹ In evolution, a robust gene network can harbor a large number of neutral genetic variations, before the phenotype transforms to another equilibrium point. The capacity to harbor these neutral genetic variations is called the genetic robustness of the phenotype in evolution. Therefore, the phenotype robustness of a stochastic gene network at the equilibrium point (phenotype), under the influence of parametric fluctuations, due to genetic variations, will be discussed from the point of view of stochastic Lyapunov stability.²⁹ Furthermore, the evolvability in response to environmental changes and the genetic variations of a stochastic gene network, in the evolutionary process, can be also discussed from the point of view of stochastic H∞ filtering.³³ In this study, both the evolvability and network robustness of a nonlinear stochastic gene network, in the evolutionary process, are discussed from a nonlinear stochastic system perspective. The tradeoff between the genetic robustness and environmental robustness is also investigated. It is found that, if a gene network has enough network robustness to cover both genetic robustness and environmental robustness, to buffer the effect of genetic variations and to resist environmental stimuli respectively, then the phenotype of the gene network is maintained, in the evolutionary process. However, the accumulation of these neutral genetic variations may destroy the network robustness and provide new material for evolution, so that a phenotype transition may eventually occur by a shift to another equilibrium point, with the help of environmental stimuli. However, any study of the interplay between the evolvability, to cope with environmental disturbances, and network robustness, to allow intrinsic genetic variations of the phenotype of the gene network, must deal with a very difficult Hamilton-Jacobi inequality (HJI). At present, there exists no method to efficiently solve the HJI analytically or numerically.

This study uses a global linearization method³⁴ to interpolate several linearized stochastic systems, at different operation points, to approximate the nonlinear stochastic gene network, so that the interplay between the evolvability and network robustness can be discussed from a systematic viewpoint, using a set of linear matrix inequalities (LMIs), instead of the HJI. Using this method, the evolvability and network robustness are related to the locations of the eigenvalues of the linearized stochastic systems of nonlinear stochastic gene networks. If the eigenvalues of these linearized stochastic systems of a nonlinear stochastic gene network are all located in the far left hand side of the s-complex domain, then the nonlinear stochastic gene network is more robustly stable but less adaptable, in the evolutionary process. On the other hand, if these eigenvalues are closer to the imaginary axis in the s-complex domain, and are more easily perturbed to the right hand side, then the nonlinear stochastic gene network is less robustly stable but more adaptable, in the evolutionary process. The quantitative measures of the evolvability and network robustness are also investigated, from this systematic perspective. If the capacity of the neutral genetic variations tolerated by a gene network is denoted as the genetic robustness, and the evolvability is considered as the inversion of the environmental robustness, then it is also found that the phenotype of the gene network is robust in evolution, if the genetic robustness plus the environmental robustness is less than the network robustness of a gene network under the influence of genetic variation and environmental disturbance, in the evolutionary process. The correlation between the genetic robustness and environmental robustness of a biological network in evolution,^15,35 can also be confirmed by the proposed network robustness, in the evolutionary process.

Since biochemical networks play the central role in cellular function, there is strong motivation to investigate the interplay between the evolvability and network robustness of evolutionary biochemical networks. As shown in Figure 1, the favored physiological systems exert a selective force on biochemical networks, in the evolutionary process. The varied phenotypes of the biochemical networks result from random changes in protein sequences, protein structure and promiscuous protein functions, due to the corresponding genetic variations, in the evolutionary process.⁹ Since several biochemical networks are the backbone of physiological systems, they should have enough network robustness to tolerate intrinsic parametric variation and less evolvability, in response to external stimuli,^36,37 which means that the steady state of the system variables (concentrations or rates) is invariant, under perturbations. In this study, based on the S-system model,³⁶ the evolvability and the network robustness of nonlinear stochastic biochemical networks are measured from the steady state perspective. A formula is also derived, to define their interplay, in order to discuss their relationship, in the evolutionary process. Finally, the interplay between the evolvability and network robustness of high-level biological networks, for example, physiological systems and bio-ecological systems, is also discussed in the same vein. The interplay between the evolvability and network robustness of a biological network in evolution is related to evolutionary antagonistic pleiotropy.³⁸ Based on the evolutionary theory of aging,³⁸ antagonistic pleiotropy holds that what is good for an organism when it is young can be bad for it when it is old. This study discusses some evolutionary antagonistic pleiotropic actions of a biological network, from the viewpoint of the tradeoff between the genetic robustness and environmental robustness in evolution. In this situation, the evolutionary antagonistic pleiotropic effect is extended, from the individual gene level to biological network level, for the evolutionary process. Furthermore, based on stability robustness,^23,39 noise filtering theory^33,40 and systems biology,^5,41 the interplay between the evolvability and network robustness in evolution, can be applied to a synthetic gene network to model its progress, using a fast evolutionary computation method (eg, genetic algorithm and evolution algorithm) to select adequate circuit components for a synthetic gene network, in order to achieve a desired behavior (ie, robustness and filtering ability).^42–49

In the following, the interplay between the evolvability and network robustness in a linear gene network is firstly discussed from the point of view of systems biology and then the results are extended to the evolutionary nonlinear gene network.

On the Interplay between the Evolvability and Network Robustness of Linear Stochastic Gene Regulatory Network

Network robustness of linear gene regulatory networks in evolution

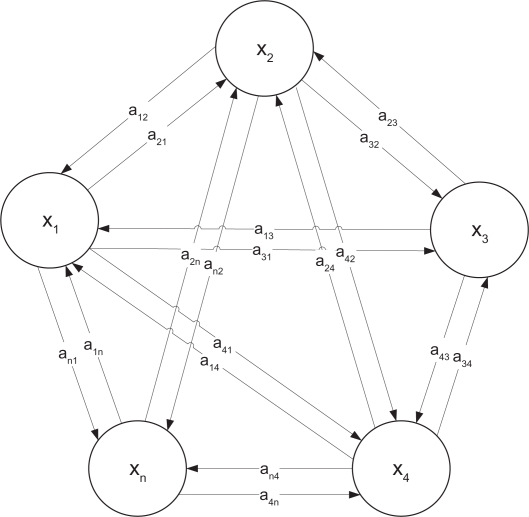
For initial simplicity of analysis, we consider a linear dynamic gene regulatory network as follows (see Fig. 2).

$$\dot{x}(t)=\mathit{Ax}(t)$$ (1)

where x(t) = [x₁(t) x₂(t) … x_n(t)]^T denotes the gene expressions of n genes in the network and

$$A=\left[\begin{array}{ccc}{a}_{11}& \dots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{n1}& \dots & a_{\mathit{nn}}\end{array}\right]$$

denotes the regulatory interaction matrix between these genes, for example a_ij denotes the regulatory interaction from gene j to gene i.

Figure 2.

A linear n-gene regulatory network. a_ij denotes the interaction from gene j to gene i and x_i(t) denotes the gene expression of gene i.

Remark 1: The linear gene regulatory system in (1) can be considered as a linearized system of a nonlinear gene network ẋ(t) = f (x(t)) at an equilibrium point (phenotype) x_e, ie, A = ∂f (x) / ∂x|_{x = xe}. Maintaining generality, the origin of the nonlinear gene network is always shifted to the equilibrium point (phenotype) x_e, ie, x_e = 0. The detail will be discussed in Section 3.

In the evolutionary process, the interaction a_ij may suffer from random parametric fluctuations, due to heritable DNA mutation, genetic variations and recombinations in the germ cell (see Fig. 2).

$$a_{\mathit{ij}}\to a_{\mathit{ij}}+\mathrm{\Delta }{a}_{\mathit{ij}}^l{n}_l(t),l=1,\dots ,L$$ (2)

where $\mathrm{\Delta }{a}_{\mathit{ij}}^l$ denotes the amplitude of random parametric fluctuation; n₁(t) is a white noise with zero mean and unit variance, ie, $\mathrm{\Delta }{a}_{\mathit{ij}}^l$ denotes the ranges of the corresponding parametric fluctuation and n₁(t) absorbs the stochastic properties of parametric fluctuation, due to the corresponding DNA mutations and genetic variations of the germ cell in evolution.⁹ Let us denote n₁(t), …, n_L(t) as L independent random parametric fluctuation sources, such as heritable DNA mutations, genetic variations and recombinations in evolution. Then their covariances are calculated as follows.^33,39

$$\mathit{Cov}[\mathrm{\Delta }{a}_{\mathit{ij}}^l{n}_l(t),\mathrm{\Delta }{a}_{\mathit{ij}}^l{n}_l(\tau )]={(\mathrm{\Delta }{a}_{\mathit{ij}}^l)}^2\delta (t,\tau )$$ (3)

In this equation, δ(t,τ) denotes the delta function, ie, δ(t,τ) = 1, if t = τ and δ(t,τ) = 0, if t ≠ τ. In other words, $\mathrm{\Delta }{a}_{\mathit{ij}}^l$ denotes the corresponding standard deviation of random fluctuation $\mathrm{\Delta }{a}_{\mathit{ij}}^l{n}_l(t)$ from the random source n_l(t). The reason why n_l(t) in (2) is assumed to be zero mean with unit variance is that the mean of n_l(t) can be merged in the nominal a_ij and the variance can be absorbed in $\mathrm{\Delta }{a}_{ij}^l$ in (2). Therefore, without loss of generality, n_l(t) is assumed as white noise with zero mean and unit variance.

Suppose the gene regulatory network in (1) suffers from the following genetic parameter fluctuations in evolution

$$\dot{x}(t)=\left(A+\sum _{l=1}^L{A}_l{n}_l(t)\right)x(t)$$ (4)

where

$$A_l=\left[\begin{array}{ccccc}\mathrm{\Delta }{a}_{11}^l& \dots & \dots & \dots & \mathrm{\Delta }{a}_{1n}^l\\ ⋮& \ddots & & & ⋮\\ ⋮& & \mathrm{\Delta }{a}_{\mathit{ij}}^l& & ⋮\\ ⋮& & & \ddots & ⋮\\ \mathrm{\Delta }{a}_{n1}^l& \dots & \dots & \dots & \mathrm{\Delta }{a}_{\mathit{nn}}^l\end{array}\right]$$

denotes the parametric fluctuations, due to the l-th random source of n_l(t). If $\mathrm{\Delta }{a}_{\mathit{ij}}^l$ in A_l is not affected by n_l(t), then let $\mathrm{\Delta }{a}_{\mathit{ij}}^l$ = 0. The term ${\sum }_{l=1}^L{A}_l{n}_l(t)$ denotes the accumulated kinetic parametric fluctuations, due to heritable genetic variations during the evolution of the gene network. The consequent kinetic parametric fluctuations, due to the heritable genetic variations in (4), will lead to permanent changes in the phenotypes.

The stochastic gene regulatory network in (4) is termed stochastically stable, if there exists a Lyapunov (power) function V (x) = x^T(t)Px(t) for a positive definite matrix P such that the expectation of the derivative E d/dt V (x) ≤ 0, ie, the average power of the gene network does not increase, with the parameteric fluctuations in evolution. For convenience, in the analysis of network robustness, the stochastic system in (4) can be written as the following Ito stochastic system.^33,39

$$\mathit{dx}(t)=\mathit{Ax}(t)\mathit{dt}+\sum _{l=1}^L{A}_{l}x(t){dw}_l(t)$$ (5)

where dw_l(t) = n_l(t)dt and w_l(t) denote the corresponding Wiener process or Brownian motion of random parametric fluctuations in evolution, ie, the stochastic system in (5) denotes the phenotypic heterogeneity in the gene network population, in evolution.

Proposition 1: The stochastic gene network in (5) is said to be robustly stable in evolution, with its phenotype x_e = 0, if the following phenotype robustness inequality holds.

$$P>0,PA+A^{T}P+\sum _{l=1}^L{A}_l^T{PA}_l\le 0$$ (6)

Proof: See Appendix A in Supplementary data.

Remark 2: In the case of the nominal gene regulatory network in (1), the robust stability condition is reduced to the following stability inequality with

$$P>0,PA+A^{T}P\le 0$$ (7)

ie, the stability condition for a gene network free of parametric fluctuations in (1). The stability inequality in (7) implies that all of the eigenvalues of A should be on the left hand side of the s-domain, ie, the real parts of all eigenvalues of A should be negative or zero.²³ However, for the stochastic gene regulatory network in (5), the eigenvalues of A should be more further to the left hand side of the s-domain, so that the phenotype robustness inequality in (6) can hold, ie, the eigenvalues of A should be more negative (robust), in order to tolerate the positive term ${\sum }_{l=1}^L{A}_l^T{PA}_l$, due to genetic parametric fluctuations, in the evolutionary process. Therefore, the smallest distance between the eigenvalues of A and the image axis in the s-domain can be considered as a measure of the network robustness of the linear gene regulatory network in (1). From (6), it is seen that the gene network with greater network robustness (ie, a more negative eigenvlaue) will tolerate more stochastic parametric fluctuations, due to the neutral genetic variations, in the evolutionary process, ie,

$$\sum _{l=1}^L{A}_l^T{PA}_l\le -(PA+A^{T}P)$$ (8)

Since the right hand side of (8) can be considered as an indication of the network robustness of the gene regulatory network, if the effects of these stochastic parametric fluctuations on the gene network, due to genetic variations, in evolution, can be overridden by the network robustness of the gene network, then they will be tolerated, without changing the pleiotropic phenotype of the gene network, in evolution. In this situation, the parametric fluctuations ${\sum }_{l=1}^L{A}_l{n}_l(t)$, due to genetic variations are neutral variations, which do not change the phenotype of the gene network, and the stochastic gene networks in (5) represent the neutral diversity of the gene network in (1). Therefore, a more robust gene network can harbor a large diversity of neutral gene networks in its population. These neutral gene networks may have the potential for evolutionary adaptation, if genetic variations are accumulated, such that the phenotype robustness in (6) or (8) is violated. In this situation, the evolutionary gene network in (5) becomes stochastically unstable and x(t) is hugely increased.

Evolvability of a linear gene regulatory network in evolution

Suppose the gene regulatory network in (1) only suffers from stochastic environmental stimuli as follows.^33,39

$$\dot{x}(t)=\mathit{Ax}(t)+\mathit{Bv}(t)$$ (9)

where v(t) = [v₁(t) v₂(t) … v_n(t)]^T denotes the external stimuli or molecular noises, due to environmental changes or stresses such as temperature or salinity, and B denotes the coupling matrix between external stimuli and the gene network. Environmental stimuli can perturb x(t) away from its phenotype x_e = 0. Let us denote the phenotype variation as x̃(t) = x(t) – x_e = x(t). Then the response r of the gene network to external stimuli from the environment, in the evolutionary process, is defined as

$$r=\frac{E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)\mathit{dt}}{E{\int }_0^{t_p}{v}^T(t)v(t)\mathit{dt}}$$ (10)

The numerator in (10) denotes the total average phenotype variations to present time t_p. The response r indicates the effect of environmental stimuli on the phenotype variations from a total energy point of view. The fitness function f for the phenotype x_e in evolution is inversely proportional to the response r of the gene regulatory network

$$f=\frac{1}{r}$$ (11)

ie, a gene network with less (more) response to environmental stimuli exhibits more (less) fitness to the phenotype x_e = 0. Therefore, the maximization of the fitness function for phenotype x_e = 0 in evolution is equivalent to the minimization of the response r in (10). We solve for the maximum fitness of phenotype x_e under the influence of environmental stimuli, using the following equivalent minimization problem for phenotype variation in response to environmental stimuli, in evolution

$$r_0=\text{min}\frac{E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)\mathit{dt}}{E{\int }_0^{t_p}{v}^T(t)v(t)\mathit{dt}}$$ (12)

We call r₀ the evolvability of the stochastic gene regulatory network in (9), in response to environmental stimuli, and the maximum fitness f₀ = 1/r₀ is an indicator of environmental robustness for phenotype x_e in the gene regulatory network. The minimization in (12) means that optimal tracking of the target phenotype x_e (ie, the minimization of $E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)\mathit{dt}$ is achieved and the effect of v(t) on x̃(t) is also minimized simultaneously. The choice of the fitness function in (11) is based on both the robust tracking of target phenotype x_e and the resistance against the environmental stimuli v(t) for the target phenotype tracking.

However, it is still very difficult to solve the minimization problem (12) for the evolvability r₀. A suboptimal method is employed to solve it, by minimizing its upper bound. Let us denote the upper bound of r in (10) as follows

$$\begin{array}{l}\frac{E{\int }_0^{t_P}{\tilde{x}}^T(t)\tilde{x}(t)\mathit{dt}}{E{\int }_0^{t_P}{v}^T(t)v(t)\mathit{dt}}\le \rho \hspace{1em}\text{or}\hspace{1em}E{\int }_0^{t_P}{\tilde{x}}^T(t)\tilde{x}(t)\mathit{dt}\\ \hspace{1em}\le E\rho {\int }_0^{t_P}{v}^T(t)v(t)\mathit{dt}\end{array}$$ (13)

where the evolution level ρ denotes the upper bound of the evolvability, ie, the upper bound of the influence of environmental stimuli, in the evolutionary process, on the phenotype variation of the gene regulatory network, from the average energy point of view. t_p denotes the present time. If ρ in (13) is large, then the influence of environmental stimuli (or disturbances) on the phenotype variation of the gene network is large, ie, the gene network is more evolvable to the environmental stimuli and vice versa. In the following, the upper bound ρ is minimized, until its minimum value approaches the evolvability r₀ in (12), ie, solving for r₀ in (12) by the so-called suboptimal method.³³ If the initial x̃(0) ≠ 0, its effect should be considered and (13) should be modified as follows.³⁹

$$E{\int }_0^{t_P}{\tilde{x}}^T(t)\tilde{x}(t)\mathit{dt}\le V(\tilde{x}(0))+E\rho {\int }_0^{t_P}{v}^T(t)v(t)\mathit{dt}$$ (14)

then we get the following result.

Proposition 2: For the gene regulatory network with environmental stimuli (or disturbances) in (9), in the evolutionary process, if the following inequality holds for P > 0.

$$A^{T}P+PA+I+\frac{1}{\rho }{\mathit{PBB}}^{T}P\le 0$$ (15)

then the evolutionary inequality in (13) or (14) holds, ie, the gene regulatory network in (9) has an evolution level ρ.

Proof: See Appendix B in Supplementary Data.

Since the evolution level ρ is the upper bound of the evolvability of the gene regulatory network, the evolvability r₀ of the gene regulatory network is obtained as follows

$$r_0=\underset{P>0}{\text{min}}\hspace{0.17em}\rho$$ (16)

subject to (15).

The constrained optimization problem for solving the evolvability r₀ for the linear gene regulatory network in (9) can be achieved by decreasing ρ until no solution P > 0 exists in (15). By Schur complement,³⁴ the quadratic inequality in (15) can be transformed into the following equivalent linear matrix inequality (LMI).

$$\left[\begin{array}{cc}{A}^{T}P+PA+I& \mathit{PB}\\ {(\mathit{PB})}^T& -\rho I\end{array}\right]\le 0$$ (17)

Therefore, the evolvability measure in (16) is equivalent to solving the following constrained optimization problem

$$r_0=\underset{P>0}{\text{min}}\hspace{0.17em}\rho$$ (18)

subject to (17).

The evolvability r₀ in (18) is measured by decreasing ρ until the LMI in (17) has no solution P > 0. The solution P > 0 of the LMI in (17) is easily obtained with the help of the LMI toolbox in Matlab.³⁴ After obtaining r₀ by solving the constrained optimization in (18), by the fact f₀ = 1/r₀, then the inequality in (15) can be modified as

$$I+\frac{1}{r_0}{\mathit{PBB}}^{T}P=I+f_0{\mathit{PBB}}^{T}P\le -(A^{T}P+PA)$$ (19)

From the above, it is seen that if the network robustness −(A^TP + PA) on the right hand side of (19) is larger (ie, with more negative eigenvalues of A), then the gene network has a small evolvability r₀ or large environmental robustness f₀ to resist external stimuli. In this situation, the gene network is less adaptive. Taken in a broad sense, f₀ is related to the environmental robustness or the buffering ability against environmental stimuli, in evolution, to resist these environmental stimuli,³⁵ ie, the evolvability r₀ is inversely proportional to the environmental robustness indicator f₀. Small r₀ indicates that the phenotype x_e has good environmental robustness and can resist environmental stimuli and large r₀ indicates that the phenotype x_e has less environmental robustness to environmental stimuli. If the network robustness of the gene network is large, or r₀ is small, evolutionary adaptation may be promoted, because of the increased likelihood of having a small subpopulation that can cope with the environmental stimuli. Conversely, if the network robustness of the gene regulatory network is small, the evolvability r₀ must be large enough to respond to environmental stimuli, in order to guarantee the evolution inequality in (19). In this case, the population becomes increasingly heterogeneous in evolution. It can be seen that the evolvability and network robustness are two antagonistic characteristics of the gene regulatory network, in the evolutionary process. If one is large, then the other must be small and vice versa.

Tradeoff between environmental robustness to respond to environmental stimuli and genetic robustness to tolerate parametric fluctuations in evolution

If the gene regulatory network in (1) suffers from simultaneous intrinsic parametric fluctuations and environmental stimuli in evolution, then we get

$$\dot{x}(t)=\mathit{Ax}(t)+\sum _{l=1}^L{A}_{l}x(t)n_l(t)+\mathit{Bv}(t)$$ (20)

Then we get the following result.

Proposition 3: If the following phenotype robustness criterion has a solution P > 0

$$A^{T}P+PA+\sum _{l=1}^L{A}_l^T{PA}_l+I+\frac{1}{\rho }{\mathit{PBB}}^{T}P\le 0$$ (21)

then the stochastic gene network in (20) has enough network robustness to tolerate genetic parametric fluctuations and an evolutionary level ρ that allows it to respond to environmental stimuli, in the evolutionary process.

Proof: See Appendix C in Supplementary data.

Then the evolvability of the stochastic gene network in (20) can be measured by solving the following constrained optimization problem.

$$r_0=\underset{P>0}{\text{min}}\hspace{0.17em}\rho$$ (22)

$$\text{subject}\hspace{0.17em}\text{to}\hspace{0.17em}\left[\begin{array}{cc}{A}^{T}P+PA+\sum _{l=1}^L{A}_l^T{PA}_l+I& \mathit{PB}\\ {(\mathit{PB})}^T& -\rho I\end{array}\right]\le 0$$

After solving r₀ from (22), the phenotype robustness criterion in (21) can be modified as

$$\begin{array}{l}\underset{\mathit{genetic}\hspace{0.17em}\mathit{robustness}}{\underbrace{\sum _{l=1}^L{A}_l^T{PA}_l}}+\underset{\mathit{environmental}\hspace{0.17em}\mathit{robustness}}{\underbrace{I+f_0{\mathit{PBB}}^{T}P}}=\sum _{l=1}^L{A}_l^T{PA}_l\\ \hspace{1em}+I+\frac{1}{r_0}{\mathit{PBB}}^{T}P\le \underset{\mathit{network}\hspace{0.17em}\mathit{robustness}}{\underbrace{-(A^{T}P+PA)}}\end{array}$$ (23)

From (23), it is seen that the phenotype of the gene network can be maintained, if the network robustness can take over the genetic robustness to tolerate parametric fluctuations, and the environmental robustness to resist environmental stimuli, in evolution. The interplay between the evolvability and network robustness of a gene regulatory network in evolution, is discussed in the following.

For the gene network with only environmental stimuli v(t) in (9) and with the network robustness in (19), if the eigenvalues of A are more negative, then the gene network is more robust and should be less evolvable (small evolvability r₀ or large environmental robustness indicator f₀) to resist the influence of environmental disturbance v(t). However, for the gene network in (20) with the same network robustness as in (23), ie, with the same network robustness −(A^TP + PA) as (19), the tradeoff between the evolvability and genetic robustness is discussed in the following. Since an extra genetic robustness ${\sum }_{l=1}^L{A}_l^T{PA}_l$ is needed to buffer genetic variations ${\sum }_{l=1}^L{A}_{l}x(t)n_l(t)$ in evolution, the evolvability r₀ must be decreased so that the environmental robustness f₀ is increased to provide greater resistance to environmental stimuli. If the stochastic gene network in (23) needs to maintain the same evolvability r₀ as the gene network in (9), more network robustness −(A^TP + PA) is needed, in order to cover the extra genetic robustness, ie, in order to maintain the phenotype in evolution, a more robust network is needed, in order to simultaneously tolerate intrinsic parametric variations and to resist the effect of environmental disturbance.^33,39,40 However, if the gene network is subject to both environmental disturbances and genetic parametric fluctuations in evolution, as shown in the stochastic system in (20), then from the criterion in (23), we get

$$\begin{array}{c}I+f_0{\mathit{PBB}}^{T}P=I+\frac{1}{r_0}{\mathit{PBB}}^{T}P\\ \hspace{0.17em}\hspace{0.17em}\le -(A^{T}P+PA)-\sum _{l=1}^L{A}_l^T{PA}_l\end{array}$$ (24)

Due to the destruction of network robustness by parametric fluctuations, the evolvability r₀ in (24) is increased, or the environmental robustness indicator f₀ is decreased, in order to guarantee the above inequality, because of the diminution of the network robustness, on the right hand side, ie, the effect of parametric fluctuations, due to genetic variations in evolution, may make the gene network more responsive (or evolvable) to environmental stimuli.⁵⁰ Similarly, the inequality can be changed to

$$\begin{array}{l}\sum _{l=1}^L{A}_l^T{PA}_l\le -(A^{T}P+PA)-(I+\frac{1}{r_0}{\mathit{PBB}}^{T}P)\\ \hspace{1em}=-(A^{T}P+PA)-(I+f_0{\mathit{PBB}}^{T}P)\end{array}$$ (25)

Due to the diminution of network robustness by the evolvability r₀ to the response to environmental stimuli in (25) or by environmental robustness, the tolerable amount of genetic parametric fluctuations ${\sum }_{l=1}^L{A}_l^T{PA}_l$ (genetic robustness) is diminished, for a gene regulatory network, in the evolutionary process. From (25), it is seen that a gene network cannot tolerate a large amount of genetic parametric variations and resist (respond less to) a large amount of environmental changes simultaneously in evolution. The results of this analysis show that the tradeoff between the genetic robustness to tolerate parametric fluctuations, due to genetic variations, and the environmental robustness to respond to the environmental stimuli, in the gene regulatory network in evolution, can be studied from the systematic perspective. Actually, the tradeoff between the genetic robustness and environmental robustness of a gene regulatory network in evolution, is equivalent to the tradeoff between stability robustness and sensitivity in linear system theory,²⁴ ie, “transfer function + sensitivity function = 1” in the frequency domain. The tradeoff between the genetic robustness and environmental robustness of a stochastic gene network is perhaps most relevant to the well-known statistical tradeoff between bias and variance.^24,51 Further discussion of this is undertaken, in the following sections.

Let us denote the tolerable value ${\sum }_{l=1}^L{A}_l^T{PA}_l$ in (23), due to genetic variations in (20), as the measure of genetic robustness,³⁵ the tolerable value I + 1/r₀ PBB^T P = I + f₀ PBB^T P in (23) as the measure of the environmental robustness of the stochastic gene network in (20) and −(A^TP + PA) as the measure of network robustness; then according to (23), the stochastic genetic network exhibits phenotype robustness under the influence of genetic variations and environmental disturbances in evolution, if the following phenotype robustness criterion holds

$$\begin{array}{l}\text{genetic}\hspace{0.17em}\text{robustness}+\text{environmental}\hspace{0.17em}\text{robustness}\\ \hspace{1em}\le \text{network}\hspace{0.17em}\text{robustness}\end{array}$$ (26)

ie, if the genetic robustness plus environmental robustness is less than the network robustness, in the evolutionary process, the phenotype of the stochastic gene network in (20) is robust in evolution.

In,³⁵ the evolutionary causes of genetic robustness were discussed, using different evolutionary scenarios. The correlation with environmental robustness is considered to be the most probable cause of genetic robustness in evolution. Based on the congruence scenario, the genetic robustness of a gene network in evolution is a by-product of the environmental robustness of a gene network to resist the environmental stimuli (or perturbations), because environmental stimuli (perturbations) are more frequent than the genetic perturbations in evolution, which have been confirmed in RNA folding and heat-shock proteins.^15,35 This correlation between the genetic robustness and environmental robustness is obvious in (23) and (26). In order to provide a buffer against environmental disturbances, the gene network may develop feedback, hub and redundant mechanisms, to improve its network robustness, resulting in a large −(A^TP + PA). This greater network robustness can also provide a buffer against large amounts of neutral genetic variations simultaneously in evolution. However, this large amount of genetic variations may provide raw material for new evolutionary possibilities. Therefore, the phenotype robustness criterion in (23), gives more insight into the interplay between the evolvability and network robustness.

On the Interplay between the Evolvability and Network Robustness of a Nonlinear Stochastic Gene Regulatory Network in Evolution

In real biological systems, the gene regulatory networks are always nonlinear. In the case of a nonlinear gene regulatory, the dynamic system in (1) is modified as

$$\dot{x}(t)=f(x)$$ (27)

where f(x) denotes the nonlinear interactive function vector among these regulatory genes in the gene network.

Network robustness of a nonlinear gene regulatory network in evolution

For a nonlinear stochastic gene regulatory network with stochastic parametric fluctuations in evolution, the stochastic system in (5) is modified as follows^29,42

$$\mathit{dx}(t)=f(x)\mathit{dt}+\sum _{l=1}^L{f}_l(x){dw}_l(t)$$ (28)

where f_l(x) denotes the nonlinear stochastic parametric fluctuation, due to the l-th random genetic fluctuation source w_l(t), in the evolutionary process. Sources of these random genetic fluctuations, in the evolutionary process, include DNA mutation, deletion, duplication, inversion and translocation of chromosome. The nonlinear stochastic system in (28) represents the phenotypic heterogeneity in a gene network population, due to random genetic variations in evolution.

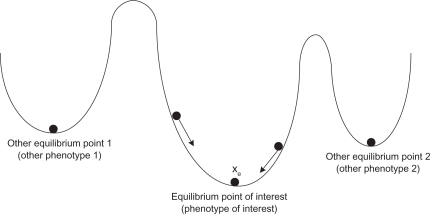
Consider the nonlinear system in (27) or (28). Many equilibrium points (phenotypes) exist (see Fig. 3). Suppose a phenotype near a stable equilibrium point x_e is of interest. For convenience in analysis, the origin of the nonlinear stochastic gene network in (28) is shifted to the equilibrium point (phenotype) x_e. In this case, if the shifted nonlinear stochastic system is robustly stable at the origin, then the equilibrium point (phenotype) of interest is also equally stable. Analysis of the procedure of the evolvability and network robustness of a nonlinear gene regulatory network in evolution, is thus simplified. Let us denote x̃(t) = x(t) – x_e, then the following shifted nonlinear stochastic gene network is obtained³⁴

$$d\tilde{x}(t)=f(\tilde{x}+x_e)dt+\sum _{l=1}^L{f}_l(\tilde{x}+x_e){dw}_l(t)$$ (29)

ie, the origin x̃(t) ≡ 0 of the nonlinear stochastic gene network in (29) is at the equilibrium point x_e of the original nonlinear stochastic gene network in (28).

Figure 3.

The stochastic nonlinear gene network has many local stable equilibrium points (phenotypes). The landscape of three stable equilibrium points is shown with vertical scale illustrating the relative network robustness of the equilibrium point (phenotype) of the nonlinear gene network. Suppose x_e is the equilibrium point (phenotype) of interest.

Then, let us consider the robust stabilization of the nonlinear stochastic gene network in (29) in evolution. Based on the stochastic Lyapunov stability,^33,39 the following result, for phenotype robustness, is obtained.

Proposition 4: The phenotype x_e of the stochastic nonlinear gene network in (29) exhibits phenotype robustness in evolution, if the following Hamilton Jacobi inequality (HJI) holds for some positive function V (x̃) > 0,

$$\begin{array}{l}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}f(\tilde{x}+x_e)+\frac{1}{2}\sum _{l=1}^L{f}_l^T(\tilde{x}+x_e)\\ \hspace{1em}\times \frac{{\partial }^{2}V(\tilde{x})}{{\partial }^2\tilde{x}}{f}_l(\tilde{x}+x_e)\le 0\end{array}$$ (30)

ie, the nonlinear fluctuating gene network in (28) or (29) is robustly stable, at the equilibrium point x_e, under the influence of random genetic fluctuations in evolution, if the above HJI holds for a positive function V (x̃) > 0.

Proof: See Appendix D in Supplementary data.

Remark 3: (i) If a nonlinear gene regulatory network is free of parametric fluctuations, then from (30), the stability of the nonlinear gene network in (27), at the equilibrium point (phenotype), is guaranteed by ∂V(x̃)/∂x̃ f (x̃ + x_e) ≤ 0. Therefore, if ∂V(x̃)/∂x̃ f(x̃ + x_e) is more negative, the nonlinear gene network in (29) is more robustly stable and more able to tolerate the term $1/2{\sum }_{l=1}^L{f}_l^T(\tilde{x}+x_e){\partial }^{2}V(\tilde{x})/{\partial }^2\tilde{x}\hspace{0.17em}{f}_l(\tilde{x}+x_e)$ in (30), by nonlinear parametric fluctuation, due to genetic variations in evolution. (ii) For the network robustness of nonlinear stochastic gene network in (29), the HJI in (30) replaces the quadratic inequality in (6), for the linear gene network in (5). If the network robustness is very great, ie, (∂V(x̃)/∂x̃)^T f(x̃ + x_e) is more negative and the basin of the phenotype is much deeper (see Fig. 3), the accumulated genetic variations ${\sum }_{l=1}^L{f}_l(\tilde{x}+x_e){dw}_l(t)$ in evolution cannot override the HJI inequality in (30), in order to escape from the basin of the phenotype. These genetic variations are termed phenotypically neutral genetic variations. If the stochastic phenotypically neutral genetic variations ${\sum }_{l=1}^L{f}_l(\tilde{x}+x_e){dw}_l(t)$ are accumulated in (29), so that the HJI inequality in (30) is violated in the evolution process, then they may cause a transition from one phenotype to another, for example, from the basin of x_e to another basin in Figure 3. The accumulation of neutral genetic variations is a common property of locally adapted gene regulatory networks.⁵⁰ (iii) In the evolutionary process, two strategies maintain the network robustness in (29). One strategy is to make the term (∂V (x̃)/∂x̃)^T f(x̃ + x_e) more negative (more robust), in order to tolerate more parametric fluctuations, due to genetic variations. Therefore, the negative feedback loops in the gene network are favored by natural selection. Another strategy is to attenuate the effect of the genetic variations, so that ${\sum }_{l=1}^L{f}_l(\tilde{x}+x_e){dw}_l(t)$ is small. In this case, some mechanisms, such as genetic redundancy, parallel components, proofreading and repairing mechanisms are also favored by natural selection, in the evolutionary process. (iv) Let us denote –(∂V (x̃)/∂x̃)^T f(x̃ + x_e) as a measure of the network robustness of the gene network in (27) or (28), and the tolerable value $1/2{\sum }_{l=1}^L{f}_l^T(\tilde{x}+x_e){\partial }^{2}V(\tilde{x})/{\partial }^2\tilde{x}{f}_l(\tilde{x}+x_e)$, due to genetic variations as a measure of the genetic robustness of the gene network, then the phenotype at x_e in (28) is robust in evolution, if the genetic robustness is less than the network robustness. If the genetic robustness is greater than the network robustness ie, the phenotype robustness criterion in (30) is violated, the phenotype at x_e may lose its robustness and the gene network may transit to another phenotype (another equilibrium point). At first sight, one might expect a large network robustness to slow or even stop the evolution of a phenotype in a gene network, but because the robust phenotype hides a large amount of neutral genetic variations, the robust phenotypes of gene networks might show increased rather than decreased evolutionary potential, in the long term. The reasons for increasing the evolvability of robust phenotypes include the accumulation of hidden neutral genetic variations that may be useful for later evolution, the buffering of the pleiotropic side effects of evolution and the increased potential for a neutral exploration of genotype space.³⁵ This is why network robustness is intrinsic to evolution and network robustness can improve evolutions.^5,35 This study extends these evolutionary results from the genetic level to a dynamic gene network level, using the systems biology perspective.

Evolvability of a nonlinear gene regulatory network in evolution

In the nonlinear gene regulatory network with only stochastic environmental stimuli, eq. (29) is modified as

$$d\tilde{x}(t)=f(\tilde{x}+x_e)dt+Bv(t)dt$$ (31)

Based on the nonlinear stochastic gene network in (31) and the evolution level ρ of the gene regulatory network defined in (13), the following result is obtained.

Proposition 5: For the nonlinear gene regulatory network with external stimuli in (31), if the following HJI holds for some positive function V(x̃) >0.

$$\begin{array}{l}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}f(\tilde{x}+x_e)+{\tilde{x}}^T(t)\tilde{x}(t)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{1}{4\rho }{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T{BB}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\le 0\end{array}$$ (32)

then the evolution level ρ in (13) holds for the gene regulatory network with a phenotype at the equilibrium point x_e.

Proof: See Appendix E in Supplementary data.

In this case, the evolvability measure of the gene regulatory network in (31) in evolution, can be obtained as follows

$$r_0=\underset{V(x)>0}{\text{min}}\rho$$ (33)

subject to (32).

Remark 4: (i) Comparing (33) with (16), it is seen that the evolvability inequality in (15), for the linear gene network, is replaced by the above HJI in (32), for the nonlinear gene network. (ii) If the nonlinear gene network is more robustly stable, ie, if (∂V (x̃)/∂x̃)^T f (x̃ + x_e) in (32) is more negative, then the evolvability r₀ is smaller, such that the nonlinear gene network has a greater ability to resist (or avoid) the environmental stimuli, ie, it is less responsive to environmental stimuli. In this case, the phenotype is constrained to the basin of a stable equilibrium point and finds it difficult to transit to another basin in Figure 3. (iii) If the nonlinear gene network is less robustly stable, ie, (∂V (x̃)/∂x̃)^T f (x̃ + x_e) is less negative, then the evolvability r₀ becomes larger and the gene network is more responsive to environmental stimuli. In this situation, the stress-induced genetic variation⁵⁰ becomes larger, so that the gene regulatory network may be pushed from the basin of one stable equilibrium point to another stable basin in Figure 3. (iv) The value 1/4 r₀ (∂V (x̃)/∂x̃)^T BB^T (∂V (x̃) ∂x̃) = 1/4 f₀ (∂V (x̃)/∂x̃)^T BB^T (∂V (x̃) ∂x̃) in (32) is related to the environmental robustness and −(∂V (x̃)/∂x̃)^T f (x̃ + x_e) is a measure of network robustness. Therefore, (32) shows that if the environmental robustness is still less than the network robustness, then the phenotype of the stochastic gene network in (31) is robust, under the influence of environmental stimuli, in the evolutionary process.

Based on evolutionary aging theory in,³⁸ if the gene network exhibits greater environmental robustness (ie, large f₀ or smaller r₀ in (32)) at an early stage, resulting in a diminution of the external stimuli and genetic variations, so that the phenotype always remains in the basin of an equilibrium point in Fig. 3, then the effects of pathogen infections and genetic variation can be easily attenuated by the gene network, and disease and cancer can be efficiently suppressed, at an early stage. However, at a more mature stage, the gene network is less robust to genetic variations, or more responsive to environmental changes, so that the phenotype will be easier to transit from one equilibrium to another and aging (senescence) of the gene network will occur. Therefore, the interplay between the evolvability and network robustness is inherent to the antagonistic pleiotropic effect of the gene network, in evolutionary process.

Tradeoff between the environmental robustness and genetic robustness of a gene regulatory network in the evolutionary process

If the nonlinear gene regulatory network (27) suffers from simultaneous parametric fluctuations and environmental stimuli in evolution, the result is the following nonlinear stochastic system

$$d\tilde{x}(t)=f(\tilde{x}+x_e)dt+\sum _{l=1}^L{f}_l(\tilde{x}+x_e){dw}_l(t)+Bv(t)dt$$ (34)

near the equilibrium point (phenotype) x_e.

Then we get the following result.

Proposition 6: If the following HJI has a positive solution V (x̃) > 0

$$\begin{array}{l}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}f(\tilde{x}+x_e)+\frac{1}{2}\sum _{l=1}^L{f}_l^T(\tilde{x}+x_e)\frac{{\partial }^{2}V(\tilde{x})}{{\partial }^2\tilde{x}}{f}_l(\tilde{x}+x_e)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\tilde{x}}^T(t)\tilde{x}(t)+\frac{1}{4\rho }{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T{BB}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\le 0\end{array}$$ (35)

then the nonlinear stochastic gene regulatory network in (34) has enough network robustness to tolerate genetic parameter fluctuations and a sufficient an evolution level ρ to respond to environmental stimuli, in the evolutionary process.

Proof: See Appendix F in Supplementary data.

Based on the HJI in (35), the evolvability of the nonlinear stochastic gene network, under the influence of both parameteric fluctuations and environmental stimuli, can be measured by solving the following constrained optimization

$$r_0=\underset{V(x)>0}{\text{min}}\rho$$ (36)

subject to (35).

If we substitute r₀ into (35), the following HJI is obtained, for phenotype robustness in evolution.

$$\begin{array}{l}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}f(\tilde{x}+x_e)+\frac{1}{2}\sum _{l=1}^L{f}_l^T(\tilde{x}+x_e)\frac{{\partial }^{2}V(\tilde{x})}{{\partial }^2\tilde{x}}{f}_l(\tilde{x}+x_e)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\tilde{x}}^T(t)\tilde{x}(t)+\frac{1}{4r_0}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T{BB}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\le 0\end{array}$$ (37)

Obviously, from (35), it is seen that a nonlinear gene network requires more network robustness in (37), than in (30) or (32), when it suffers from simultaneous genetic parametric fluctuations and environmental stimuli in evolution, ie, (∂V (x̃)/∂x̃)^T f (x̃ + x_e) must be more negative to enable the phenotype to tolerate the genetic parametric fluctuations and to resist environmental stimuli simultaneously, in the evolutionary process.

If a gene regulatory network selects a strategy with enough genetic variation tolerance and stimuli resistance,⁵⁰ the basin of the equilibrium x_e in Figure 3 must be deeper and wider, so that the genetic variations and environmental stimuli are inhibited and the phenotype can be securely retained within the basin. In this case, the term (∂V (x̃)/∂x̃)^T f (x̃ + x_e) in (37) must be more negative, in order to tolerate the term $1/2{\sum }_{l=1}^L{f}_l^T(\tilde{x}+x_e){\partial }^{2}V(\tilde{x})/{\partial }^2\tilde{x}\hspace{0.17em}{f}_l(\tilde{x}+x_e)$, due to genetic variations and to resist the term 1/4r₀ (∂V (x̃)/∂x̃)^T BB^T(∂V (x̃)/∂x̃) due to environmental stimuli. Let us denote –(∂V (x̃)/∂x̃)^T f (x̃ + x_e), $1/2{\sum }_{l=1}^L{f}_l^T(\tilde{x}+x_e){\partial }^{2}V(\tilde{x})/{\partial }^2\tilde{x}{f}_l(\tilde{x}+x_e)$ and 1/4r₀ (∂V (x̃)/∂x̃)^T BB^T(∂V (x̃)/∂x̃) = 1/4f₀(∂V (x̃)/∂x̃)^T BB^T(∂V (x̃)/∂x̃) in (37), respectively as the measures of the network robustness, genetic robustness and environmental robustness of a stochastic gene network (34). The phenotype robustness criterion in (37) can be denoted as “genetic robustness + environmental robustness ≤ network robustness”, ie, if the genetic robustness plus the environmental robustness is still less than the network robustness, then the phenotype of the gene network remains robust, under the influence of genetic variation and environmental disturbance, in the evolutionary process. The phenotype robustness in (37), shows that if greater network robustness is evolved, to allow a gene network to provide a buffer against the more common environmental disturbances in evolution, it can also provide a buffer against the genetic (heritable) variations. Obviously, the correlation between genetic robustness and environmental robustness affects the network robustness of a gene network, in the evolutionary process.

When the phenotype robustness inequality (37) holds, the accumulated genetic variations ${\sum }_{l=1}^L{f}_l(\tilde{x}+x_e){dw}_l(t)$ and the effect due to environmental stimuli cannot impel the gene network to move from one stable basin to another stable basin, to change the phenotype. In this case, the evolution is still in stasis state under the influence of environmental stimuli. However, if these random genetic mutations and stress-induced genetic variations persist and accumulate for a long time, so that the HJI inequality in (37) is violated, then a gene network transition, from the basin of one equilibrium point to another basin may occur, in order to change the phenotype. In general, the cost of the strategy of resistance to stimuli and tolerance of genetic variation is much higher.⁵⁰ In the case of the stress-avoidance strategy,⁵⁰ the basin of the equilibrium point in Figure 3, becomes shallow, ie, the term (∂V (x̃)/∂x̃)^T f(x̃ + x_e) in (37) is less negative. In this case, the evolvability r₀ must be large and environmental robustness must be small in evolution, so that the gene regulatory network is sufficiently flexible to respond to environmental stress under rapid evolutionary change.

In general, it is still very difficult to solve the HJI in (30) directly, in order to determine the extent to which stochastic parametric fluctuations can be tolerated by the gene network, or to solve the HJI-constrained optimization in (33) or (36), in order to measure the evolvability of the gene network, to gain a greater insight into the dynamic mechanism of a nonlinear stochastic gene network, in the evolutionary process. At present, there is no good method to solve the nonlinear partial differential HJI either analytically or numerically.^33,39,40 In this case, the global linearization technique^34,40 is used, to transform the nonlinear stochastic gene network (34) into an interpolation of a set of locally linearized gene networks, in order to simplify the analysis of the evolvability and network robustness of a stochastic gene network in evolution.

Using the global linearization method, if all the global linearizations are bounded by a polytope, consisting of M vertices, as^34,40

$$\left[\begin{array}{c}\frac{\partial f(\tilde{x}+x_e)}{\partial \tilde{x}}\\ \frac{\partial f_1(\tilde{x}+x_e)}{\partial \tilde{x}}\\ ⋮\\ \frac{\partial f_L(\tilde{x}+x_e)}{\partial \tilde{x}}\end{array}\right]\in \mathit{Co}\hspace{0.17em}\left[\left[\begin{array}{c}{A}_1\\ A_{11}\\ ⋮\\ A_{L1}\end{array}\right]\cdots \left[\begin{array}{c}{A}_i\\ A_{1i}\\ ⋮\\ A_{Li}\end{array}\right]\cdots \left[\begin{array}{c}{A}_M\\ A_{1M}\\ ⋮\\ A_{LM}\end{array}\right]\right],\forall \tilde{x}(t)$$ (38)

where Co denotes the convex hull of the polytope with M vertices, defined in (38), ie, if the linearized systems at all x̃(t) are inside the convex hull Co, then the state trajectories x̃(t) of the nonlinear shifted gene network in (34) will belong to the convex combination of the stable trajectories of the following M linearized gene networks, derived from the vertices of the polytope:³⁴

$$\begin{array}{l}d\tilde{x}(t)=\left(A_i\tilde{x}(t)+Bv(t)\right)dt\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\sum _{l=1}^L{A}_{li}\tilde{x}(t){dw}_l(t),i=1,\dots M\end{array}$$ (39)

Based on the global linearization theory,³⁴ if (38) holds, then every trajectory of the nonlinear stochastic gene network in (31) can be represented by a convex combination of the M linearized gene networks in (39). Therefore, if we can prove that the convex combination of the M linearized gene networks in (39) has the evolvability r₀ to respond to environmental stimuli and the network robustness to tolerate stochastic parametric fluctuations, due to genetic variations, then the original nonlinear stochastic gene network in (34) will also have the same evolvability and network robustness. The convex combination of the M linearized gene networks in (39) can be represented by^34,40

$$d\tilde{x}(t)=\sum _{i=1}^M{\alpha }_i(\tilde{x})\hspace{0.17em}\left[\left(A_i\tilde{x}(t)+Bv(t)\right)dt+\sum _{l=1}^L{A}_{li}\tilde{x}(t){dw}_l(t)\right]$$ (40)

where the interpolation function α_i(x̃) satisfies 0 ≤ α_i(x̃) ≤ 1 and ${\sum }_{i=1}^M{\alpha }_i(\tilde{x})=1$, ie, the trajectory of the nonlinear gene network in (34) can be represented by the interpolated gene network in (40), which is the convex combination of the M linearized gene networks in (39).

In the case of free of environmental stimuli, the global linearization approach in (40) is reduced to

$$d\tilde{x}(t)=\sum _{i=1}^M{\alpha }_i(\tilde{x})\hspace{0.17em}\left[A_i\tilde{x}(t)dt+\sum _{l=1}^L{A}_{li}\tilde{x}(t){dw}_l(t)\right]$$ (41)

which is the global linearization system for a nonlinear stochastic system (28). For the global linearization stochastic system in (41) with only stochastic parametric fluctuations, due to genetic variations in evolution, we get the following result.

Proposition 7: If the following linear matrix inequalities (LMIs) have a positive symmetrical solution P > 0.

$$A_i^{T}P+{PA}_i+\sum _{l=1}^L{A}_{li}^T{PA}_{li}\le 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots M$$ (42)

then the stochastic parametric fluctuations in (41) or (28) can be tolerated by the stochastic gene network in the evolution process, ie, the nonlinear stochastic gene network is robustly stable for the phenotype (ie, with phenotype robustness) at x_e (the equilibrium point of interest) under the influence of parametric fluctuations in evolution.

Proof: See Appendix G in Supplementary data.

Actually, the LMIs in (42) can be considered as a set of linearizations of the HJI in (30), ie, we could replace a nonlinear HJI by a set of LMIs, using the global linearization technique. If the stochastic gene network in (40) is free of genetic parametric fluctuations and is subject to only environmental stimuli in evolutionary process, then we get

$$d\tilde{x}(t)=\sum _{i=1}^M{\alpha }_i(\tilde{x})\left(A_i\tilde{x}(t)+Bv(t)\right)dt$$ (43)

which is the global linearization system of the nonlinear gene network in (31).

In this case, the evolutionary inequality in Proposition 2 can be extended to the case of a nonlinear gene network.

Proposition 8: If the following evolutionary inequality holds with P > 0 for a nonlinear gene network (31) or (43)

$$A_i^{T}P+{PA}_i+I+\frac{1}{\rho }{PBB}^T\hspace{0.17em}\hspace{0.17em}P\le 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots M$$ (44)

then the evolutionary inequality in (13) or (14) holds, ie, the nonlinear stochastic gene network in (31) or (43) has an evolution level ρ.

Proof: See Appendix H in Supplementary data.

Since ρ in (13) or (14) is the upper bound of the evolvability for the nonlinear gene network in (31) or (43), the evolvability of a nonlinear gene network is obtained as follows

$$r_0=\underset{P>0}{\text{min}}\hspace{0.17em}\rho$$ (45)

subject to (44).

The constrained optimization problem in (45), to solve the evolvability of nonlinear gene network in (31) or (43) can be achieved by decreasing ρ until no solution P > 0 exists for the quadratic inequalities in (44). By Schur complement,³⁴ the quadratic inequalities in (44) can be transformed to the following equivalent LMIs

$$\left[\begin{array}{cc}{A}_i^{T}P+{PA}_i+I& PB\\ {(PB)}^T& -\rho I\end{array}\right]\le 0,i=1,\dots M$$ (46)

Therefore, the evolvability measure in (45) is equivalent to solving the following constrained optimization problem

$$r_0=\underset{P>0}{\text{min}}\hspace{0.17em}\rho$$ (47)

subject to (46).

Remark 5: (i) The LMIs in (46) or the LMI-constrained optimization problem in (47) can be efficiently solved, using the LMI toolbox in Matlab. (ii) r₀ is obtained by decreasing ρ until no solution P > 0 exists for LMIs in (46) with the help of the LMI toolbox in Matlab. (iii) Based on the global linearization, the measure of the evolvability, from the HJI-constrained optimization in (33), can be replaced by the LMI-constrained optimization in (47).⁵² After solving the evolvability r₀ from (47), the inequalities in (44) can be modified as.

$$\begin{array}{l}I+\frac{1}{r_0}{PBB}^{T}P=I+f_0{PBB}^{T}P\le -(A_i^{T}P+{PA}_i),\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots M\end{array}$$ (48)

From (48), it is seen that if the eigenvlaues of A_i for all linearized gene networks are more negative (ie, more robust),²³ r₀ can be smaller to better resist the environmental stimuli, ie, there is a larger environmental robustness f₀. In this case, the gene network tends toward stasis, under the influence of extreme environments, a phenomenon that is observed in “living fossils”.⁵⁰ Conversely, if network robustness is smaller, the evolvability r₀ of a gene regulatory network must be larger, to ensure a response to environmental stimuli, in order to guarantee the inequality in (48), ie, there will be a smaller environmental robustness. This leads to the rapid evolutionary change of the gene regulatory network. Therefore, the interplay between the evolvability and network robustness of a nonlinear stochastic gene regulatory network in evolution, can be also investigated using the linear theory method. The phenotype robustness in (48) shows that if the network robustness of every local linearized gene network is larger than the environmental robustness, then the phenotype of a nonlinear gene network is robust, under the influence of environmental stimuli, in the evolutionary process.

If a nonlinear regulatory gene network is subject to genetic parametric fluctuations and environmental stimuli simultaneously, as in (34) or (40), then the following result. is obtained.

Proposition 9: If the following quadratic inequalities have a solution P > 0,

$$A_i^{T}P+{PA}_i+\sum _{l=1}^L{A}_{li}^T{PA}_{li}+I+\frac{1}{\rho }{PBB}^{T}P\le 0,i=1,\dots M$$ (49)

then the nonlinear stochastic gene network in (34) or (40) has sufficient network robustness to tolerate random genetic parametric fluctuations and with an evolution level ρ sufficient to respond to environmental stimuli in the evolutionary process.

Proof: See Appendix I in Supplementary data.

Based on Proposition 9, the evolvability of the stochastic gene network in (34) or (40) can be measured by solving the following LMI-constrained optimization problem

$$r_0=\underset{P>0}{\text{min}}\hspace{0.17em}\rho$$ (50)

subject to

$$\left[\begin{array}{cc}{A}_i^{T}P+{PA}_i+\sum _{l=1}^L{A}_{li}^T{PA}_{li}+I& PB\\ {(PB)}^T& -\rho I\end{array}\right]<0,i=1,\dots ,M$$

After solving the evolvability r₀ from (50), then the phenotype robustness inequality in (49) can be modified as.

$$A_i^{T}P+{PA}_i+\sum _{l=1}^L{A}_{li}^T{PA}_{li}+I+\frac{1}{r_0}{PBB}^{T}P\le 0,i=1,\dots ,M$$ (51)

In (51), $-\left(A_i^{T}P+{PA}_i\right)$, ${\sum }_{l=1}^L{A}_{li}^T{PA}_{li}$ and I + 1/r₀ PBB^T P = I + f₀PBB^TP represent the network robustness, genetic robustness and environmental robustness of the ith linearized gene network, respectively. This is the extended result of (21), from the linear gene network (20) to the nonlinear gene network (34). Therefore, if “genetic robustness + environmental robustness ≦ network robustness” for all linearized gene networks, then the phenotype x_e of the nonlinear stochastic system in (34) is robust, in the evolutionary process.

From (51), it can be seen that the tradeoff between the environmental robustness to resist the environmental stimuli, and genetic robustness to resist the stochastic parametric fluctuations in evolution. A more detailed discussion of the interplay between the evolvability and network robustness of the nonlinear stochastic gene network in (34) or (40) is undertaken in the following. Firstly, the phenotype robustness inequalities in (51) can be changed to the following equivalent inequalities.

$$\begin{array}{l}I+\frac{1}{r_0}{PBB}^{T}P=I+f_0{PBB}^{T}P\le -(A_i^{T}P+{PA}_i)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\sum _{l=1}^L{A}_{li}^T{PA}_{li},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,M\end{array}$$ (52)

Compared with (48), the term ${\sum }_{l=1}^L{A}_{li}^T{PA}_{li}$ in (52), which is due to accumulated random genetic parametric fluctuations, decreases the network robustness of each linearized gene network (ie, $-(A_i^{T}P+{PA}_i)$ becomes less positive by $-{\sum }_{l=1}^L{A}_{li}^T{PA}_{li}$ in (52), or the basin in Figure 3 becomes shallow) so that the right hand side of (52) becomes smaller and the evolvability r₀ becomes greater, ie, due to the shared ability of the environmental robustness f₀ to tolerate these accumulated genetic variations ${\sum }_{l=1}^L{A}_{li}^T{PA}_{li}$ in evolution, the network robustness of a gene network can not sufficiently attenuate more environmental disturbances simultaneously, so that it becomes more adaptive to them. Similarly, (49) is equivalent to.

$$\begin{array}{l}\sum _{l=1}^L{A}_{li}^T{PA}_{li}\le -(A_i^{T}P+{PA}_i)-(I+\frac{1}{r_0}{PBB}^{T}P)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=-(A_i^{T}P+{PA}_i)-(I+f_0{PBB}^{T}P),i=1,\dots ,M\end{array}$$ (53)

Due to adaptation to environmental stimuli, the network robustness of each linearized gene network is diminished, on the right hand side of (53), so that its tolerance of genetic parametric fluctuations is decreased, in the evolutionary process, ie, the tolerance to ${\sum }_{l=1}^L{A}_{li}^T{PA}_{li}$, due to genetic variations, or the genetic robustness, in the evolutionary process, becomes smaller when adaptation to environmental stimuli shallows the basin of the gene network at the equilibrium point x_e in Figure 3. Obviously, the tradeoff between the environmental robustness, which attenuates the environmental stimuli, and the genetic robustness, which tolerates parametric fluctuations due to genetic variations, of a nonlinear gene network in evolution can be discussed from the systematic perspective, using the global linearization technique. Greater network robustness facilitates the subsequent molecular evolution of local evolutionary mechanisms, by enabling a greater accumulation of genetic variations in the gene regulatory network. This increases genetic robustness and decreases the environmental robustness, so that the gene network is more evolvable to environmental stresses, in the evolutionary process.⁵⁰ According to (26), the phenotype robustness in (51) can be also interpreted as “genetic robustness + environmental robustness ≦ network robustness”, for each linearized gene network, ie, if the genetic robustness plus environmental robustness is less than the network robustness of every linearized gene network in (40), then the phenotype of the nonlinear stochastic gene network in (34) is still robust, under the influence of genetic variations and environmental stimuli in evolution. The correlated evolution of the genetic robustness and environmental robustness of the gene networks in (51) can be also discussed in terms of the phenotype robustness of the congruent mechanisms of gene networks. Because environmental perturbations often have a higher frequency and impact on fitness, they serve as the driving force for network robustness, whereas genetic robustness, to tolerate genetic variations, evolves as a by-product of environmental perturbation in the evolutionary process.

On the Interplay between the Evolvability and Robustness of Biochemical Networks in Evolution

Since the biochemical network plays the central role in cellular function, there is strong motivation to study for the underlying principles of the adaptive evolution of biochemical networks. As seen in Figure 1, the favored physiological systems will lead to the exertion of a selection force on biochemical networks, in the evolutionary process. Since the biochemical networks are the backbone of physiological systems, they have less evolvability to allow them to respond to external stimuli and enough network robustness to resist parametric fluctuations, so that the favored physiological functions can be preserved, in the evolutionary process.^36,37 In order to test whether a physiological function would prevails, in a new environment, the network robustness and the sensitivity measure the ability to tolerate the variations in the metabolite concentrations of a biochemical network, in the face of environmental changes.⁶ The mechanisms of the selection forces in biochemical networks, in the evolutionary process, were also discussed in.⁴⁹

In this study, the interplay between the evolvability and network robustness of a biochemical network will be discussed, based on the S-system model.³⁶ Actually, it can be extended to other dynamic models of biochemical networks. Using the S-system model, the dynamic system of a biochemical network, in the evolutionary process, can be represented by³⁶

$${\dot{x}}_i(t)={\alpha }_i\prod _{j=1}^{n+m}{x}_j^{g_{ij}}(t)-{\beta }_i\prod _{j=1}^{n+m}{x}_j^{h_{ij}}(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots n$$ (54)

where x₁(t), … x_n+m(t) are metabolites, such as substrates, enzymes, factors or products of a biochemical network in which x₁(t), … x_n(t) denote the n-dependent variables (intermediate metabolites and products), and x_n+1(t), … x_n+m(t) denote the m-independent variables (initial reactants and enzymes), α_i and β_i denote the rate constants, and g_ij and h_ij represent the kinetic parameters of the biochemical network. These parameters can be estimated using experimental data or microarray data.^53,54 Suppose that transient time is neglected, in the evolutionary process and, for simplicity, we focus on the evolvability and network robustness of a biochemical network in the steady state near the equilibrium point of interest (ie, the phenotype of the biochemical network). Consider the steady state of the biochemical network in (54), we get

$${\alpha }_i\prod _{j=1}^{n+m}{x}_j^{g_{ij}}(t)={\beta }_i\prod _{j=1}^{n+m}{x}_j^{h_{ij}}(t),i=1,\dots n$$ (55)

Taking the logarithm of both sides of (55), and introducing new variables y_j(t) = ln[x_j(t)], a_ij = g_ij – h_ij and b_i = ln(β_i/α_i), after some rearrangement, we get³⁶

$$\begin{array}{c}{a}_{11}{y}_1(t)+\cdots +a_{1n}{y}_n(t)=b_1-a_{1,n+1}{y}_{n+1}(t)-\dots -a_{1,n+m}{y}_{n+m}(t)\\ ⋮\\ a_{n1}{y}_1(t)+\cdots +a_{nn}{y}_n(t)=b_n-a_{n,n+1}{y}_{n+1}(t)-\dots -a_{n,n+m}{y}_{n+m}(t)\end{array}$$ (56)

The above equations can be represented by the following steady state equation,⁵⁵

$$A_D{Y}_D(t)=b-A_I{Y}_I(t)$$ (57)

where Y_D(t) = [y₁(t) … y_n(t)]^T, b = [b₁ … b_n]^T, Y_I(t) = [y_n+1(t) … y_m+1(t)]^T,

$$A_D=\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{n1}& \cdots & a_{nn}\end{array}\right],A_I=\left[\begin{array}{ccc}{a}_{1,n+1}& \cdots & a_{1,n+m}\\ ⋮& \ddots & ⋮\\ a_{n,n+1}& \cdots & a_{n,n+m}\end{array}\right]$$

In which A_D denotes the system matrix of the catalytic interactions between the dependent variables y₁(t) … y_n(t) in Y_D(t) and A_I indicates the catalytic interactions between dependent variables y₁(t) … y_n(t) in Y_D(t) and the independent variables Y_n+1(t) … Y_n+m(t) in Y_I(t) (ie, the environmental medium of the metabolic system). From the simple algebraic steady state equation in (57), obviously, the S-system in (54) is a useful model to describe the phenotype of the biochemical network.³⁶ If the inverse of A_D exists, the steady state (or phenotype) of the biochemical network is solved by.³⁶

$$Y_D(t)=A_D^{-1}\left(b-A_I{Y}_I(t)\right)$$ (58)

The steady state (phenotype) Y_D(t) in (58) is one of the equilibrium points of the nonlinear biochemical network in (54). Actually, there are many equilibrium points for (54), which represent different phenotypes. Only the equilibrium point (or phenotype) in (58) is favored by natural selection in evolution.

Suppose that there exist some random parametric variations Δα_i(t), Δβ_i(t), Δg_ij(t), Δh_ij(t), due to random genetic mutations in protein sequences, structure and function, and ΔY_I(t), due to environmental random disturbances, in the evolutionary process, ie,

$$\begin{array}{l}{\alpha }_i\to {\alpha }_i+\mathrm{\Delta }{\alpha }_i(t),{\beta }_i\to {\beta }_i+\mathrm{\Delta }{\beta }_i(t),g_{ij}\to g_{ij}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\mathrm{\Delta }{g}_{ij}(t),h_{ij}\to h_{ij}+\mathrm{\Delta }{h}_{ij}(t),Y_I(t)\to Y_I(t)+\mathrm{\Delta }{Y}_I(t)\end{array}$$ (59)

These random parametric variations, due to phenotypic noise and genetic variations, can be considered as the design parameters of the biochemical network, in the evolutionary process. Then the corresponding heterogeneous steady state (phenotypic heterogeneity) of the biochemical network in evolution is given by

$$\begin{array}{l}\left(A_D+\mathrm{\Delta }{A}_D(t)\right)\left(Y_D(t)+\mathrm{\Delta }{Y}_D(t)\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\left(b+\mathrm{\Delta }b(t)\right)-\left(A_I+\mathrm{\Delta }{A}_I(t)\right)\left(Y_I(t)+\mathrm{\Delta }{Y}_I(t)\right)\end{array}$$ (60)

Because biochemical networks are the backbone of the physiological systems of organisms, a biochemical network must be sufficiently robust to tolerate the random parametric variations and environmental changes, due to phenotypic variation and noise, in order to maintain its functional properties, in the evolutionary process (see Fig. 1). We can find the following phenotype robustness of biochemical network, in the evolutionary process.^6,56

Proposition 10: If the following phenotype robustness condition holds

$$E{\Vert A_D^{-1}\mathrm{\Delta }{A}_D(t)\Vert }_2<1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{or}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}E\left(\mathrm{\Delta }{A}_D(t)\mathrm{\Delta }{A}_D^T(t)\right)<A_D{A}_D^T$$ (61)

then the phenotype of a stochastically perturbed biochemical network exists, in the evolutionary process, as follows:

$$\begin{array}{l}\left(Y_D(t)+\mathrm{\Delta }{Y}_D(t)\right)={\left(A_D+\mathrm{\Delta }{A}_D(t)\right)}^{-1}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left[\left(b+\mathrm{\Delta }b(t)\right)-\left(A_I+\mathrm{\Delta }{A}_I(t)\right)\left(Y_I(t)+\mathrm{\Delta }{Y}_I(t)\right)\right]\end{array}$$ (62)

ie, if the covariance $E\left(\mathrm{\Delta }{A}_D(t)\mathrm{\Delta }{A}_D^T(t)\right)$ of random parametric fluctuation $\mathrm{\Delta }{A}_D(t)$, in the evolutionary process, is less than $A_D{A}_D^T$, which can be considered as a network robustness measure for the biochemical network in (54), then the random parametric fluctuations in evolution are tolerated and the phenotype of the biochemical network experiences only a small perturbation ΔY_D(t) as (62), in the evolutionary process.

Proof: Similar to ref. 6⁶ except the consideration of random variations.

If the phenotype robustness condition in (61) is violated, in the evolutionary process, the matrix inverse on the right hand side of (62) may cease to exist or move to another equilibrium point with a change of phenotype. The random variations, Δb(t) and ΔA_I(t), due to the mutations of protein sequences, and ΔY_I(t), due to the environmental change of the biochemical network, will influence the phenotypic variations ΔY_D(t) in (62), in the evolutionary process. Their effects on the phenotype can be measured from (62) by the following evolutionary analysis of the biochemical network.³⁶

$$\frac{\mathrm{\Delta }{Y}_D(t)}{\mathrm{\Delta }b(t)}=A_D^{-1},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\mathrm{\Delta }{Y}_D(t)}{\mathrm{\Delta }{A}_I(t)}=-A_D^{-1}{Y}_I(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\mathrm{\Delta }{Y}_D(t)}{\mathrm{\Delta }{Y}_I(t)}=-A_D^{-1}{A}_I,$$ (63)

In order to tolerate random variations, Δb(t), ΔY_I (t) and ΔA_I (t), in the evolutionary process, to preserve the phenotype of a biochemical network, the evolvabilities in (63) must remain below some values as follows

$$E{\Vert \frac{\mathrm{\Delta }{Y}_D(t)}{\mathrm{\Delta }b(t)}\Vert }_2\le a_1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}E{\Vert \frac{\mathrm{\Delta }{Y}_D(t)}{\mathrm{\Delta }{A}_I(t)}\Vert }_2\le a_2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}E{\Vert \frac{\mathrm{\Delta }{Y}_D(t)}{\mathrm{\Delta }{Y}_I(t)}\Vert }_2\le a_3$$ (64)

or equivalently, from (63) and (64), we get

$$\begin{array}{l}{\left(A_D{A}_D^T\right)}^{-1}\le a_1^{2}I,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(Y_I{Y}_I^T\right){\left(A_D{A}_D^T\right)}^{-1}\le a_2^{2}I,\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(A_I{A}_I^T\right){\left(A_D{A}_D^T\right)}^{-1}\le a_3^{2}I\end{array}$$ (65)

where a₁, a₂ and a₃ are some small evolvability values, such that the disturbed phenotype ΔY_D + ΔY_D(t) of the stochastic biochemical networks in (62) cannot change too much, in comparison with the nominal phenotype in (58), ie, ΔY_D(t) in (62) must still be in the basin of the phenotype in evolution. The evolvability criteria in (64) or (65) determine the ranges of the sensitivities of the phenotypic changes ΔY_D(t), due to random parametric and environmental fluctuations.

Based on the above analysis of the evolvability and network robustness of biochemical networks, the perturbed biochemical networks should satisfy the phenotype robustness criterion in (61), in order to prevent them being perturbed too far from their equilibrium points (phenotypes), in the evolutionary process. Because the violation of (61) generally implies a lethal phenotype mutation, the phenotype robustness criterion in (61) is the necessary condition for the survival of a phenotype of a biochemical networks, in the evolutionary process.⁴⁹ From the phenotype robustness criterion in (61), natural selection favors the perturbed biochemical networks with small-variance random phenotypic mutations, ie, with small $E\left[\mathrm{\Delta }{A}_D(t)\mathrm{\Delta }{A}_D^T(t)\right]$, so that the phenotype robustness criterion in (61) is not violated. A biochemical network with redundancy and self-regulation can attenuate random fluctuation ΔA_D(t), due to genetic and phenotypic mutations, in the evolutionary process. Furthermore, a biochemical network with adequate negative feedback loops can increase its network robustness $A_D{A}_D^T$ in (61), to tolerate large random parametric fluctuation, due to genetic and phenotypic mutations with large variance $E\left[\mathrm{\Delta }{A}_D(t)\mathrm{\Delta }{A}_D^T(t)\right]$, in the evolutionary process. These robust adaptive designs with adequate feedback loops are also favored by natural selection, in the evolutionary process of biochemical networks. This is why there are so many redundancies, hubs, modularities and self-regulation and feedback pathways in the biochemical networks of organisms.^34,57–59 A scale-free structure can also reduce the effect of $E\left[\mathrm{\Delta }{A}_D(t)\mathrm{\Delta }{A}_D^T(t)\right]$ on the phenotype robustness of biochemical networks and is also favored by natural selection in evolution.⁶⁰

On the other hand, the evolvability criteria in (64) or (65) determine the range of the adaptability of the phenotypic change ΔY_D(t) to random parametric variations, due to genetic and phenotypic mutations and random environmental changes, in the evolutionary process. For a functional biochemical network, the evolvability criteria should prevent the metabolic concentration from being changed, too much, by random genetic and phenotypic mutations and environmental changes. Hence, the steady state (phenotype) of a biochemical network can be preserved, while exposing the random genetic and phenotypic mutations and environmental changes to natural selection, in the evolutionary process.

When the network robustness in (61) is compared with the evolvability in (65), the interplay between evolvability and network robustness in biochemical networks is obvious in evolution. From (61), it is seen that a large $A_D{A}_D^T$ increases the network robustness, to allow tolerance of large parameter variations, due to genetic and phenotypic mutations, in the evolutionary process. However, the evolvability criteria in (65) shows that a large network robustness $A_D{A}_D^T$ decreases the evolvabilities a_i, i = 1, 2, 3, and vice versa. The interplay between the evolvability and network robustness in biochemical networks will be discussed in the following. The assumption that the three evolvability criteria in (64) or (65) all hold for natural selection is derived from the fact that biochemical networks are the backbone of physiological systems and can not be too evolvable to random genetic and phenotypic mutations and environmental changes. This is especially so, for some core (conserved) biochemical networks.^37,42 Actually, the evolvabilities, a_i in (64) or (65) are inversely dependent on the network robustness $A_D{A}_D^T$ of biochemical networks. If some evolvability criteria in (64) or (65) become larger, due to a smaller network robustness $A_D{A}_D^T$, ie, some of the inequalities in (64) or (65) have larger a_i, the biochemical network has more phenotypic heterogeneity, thanks to some random genetic and phenotypic mutations and environmental changes, and will provide more raw material for evolutionary novelty, in the evolutionary process. In this situation, the phenotypes of these biochemical networks are heavily influenced by random genetic and phenotypic mutations and environmental variations and can more easily move from their equilibrium points (phenotypes) toward other equilibrium points (other phenotypes), so that they may be more adaptive to environmental changes through random genetic and phenotypic mutations in the evolutionary process. In this case, new phenotypes are more easily generated, in order to be more adaptive to the natural selection force on biochemical networks under random genetic and phenotypic mutations and environmental variations in the evolutionary process.^9,25–28 The phenotype robustness criterion in (61) and the evolvability criteria in (64) or (65) consist of evolutionary rules for natural selection in biochemical networks via genetic and phenotypic mutations of the germ cell, in the evolutionary process. Most genetic and phenotypic mutations or perturbations of biochemical networks are harmful, because they violate the evolution rules of natural selection in (61) and (65), since biochemical networks are the backbone of the physiological systems of organisms and they should be robust enough, or less adaptive, to resist these effects of genetic and phenotypic variations. Evolution is possible only for very few genetic and phenotypic variations. If they are selected by natural selection, there will be some differences in phenotype among the selected biochemical networks with random genetic and phenotypic mutations. After several generations of the evolutionary process, due to the co-option of existing biochemical networks, diversities or heterogeneities will develop in biochemical networks with conserved physiological function but with different structure.^5,8 This is the origin of the diversity of biochemical networks within organisms in evolution. However, if the requirements of the phenotype robustness in (61) and the evolvability in (64) are stricter (or more conservative), ie, small a_i, only a very few solutions (or structures) can be selected by natural selection to meet these strict requirements. This is the reason why a conserved core biochemical network has less diversity.^36,37

On the Interplay between the Evolvability and Network Robustness of High-Level Biological Networks in Evolution

In this section, the interplay between the evolvability and network robustness of high-level bio-networks, such as physiological systems and ecological networks (see Fig. 1) will be discussed in a similar vein. In the evolutionary process, we assume a high-level biological network can be represented by the following nonlinear stochastic system

$$dx(t)=f(x)dt+\sum _{l=1}^L{f}_l(x){dw}_l(t)$$ (66)

where x(t) = [x₁(t), …, x_n(t)]^T denote n components of the high-level biological network such as organs or species, f(x) denotes the interactions between the components in the high-level biological network, the term ${\sum }_{l=1}^L{f}_l(x){dw}_l(t)$ denotes the accumulated intrinsic random fluctuations, in the evolutionary process, due to the random variations of low-level networks, ie, gene variations or phenotype variations. The nonlinear stochastic system in (66) shows that the behavioral heterogeneity of the biological network, in terms of population, differential survival rates and reproductive success from natural selection favors certain heritable variations and results in an increase in the number of those variants in the population.

Suppose we only discuss the biological phenomenon near an equilibrium point x_e, in which we are interested, ie, x(t) = x̃(t) +x_e. For the convenience, the origin of the high-level biological network in (66) is shifted to the equilibrium point, as follows

$$d\tilde{x}(t)=f(\tilde{x}+x_e)dt+\sum _{l=1}^L{f}_l(\tilde{x}+x_e){dw}_l(t)$$ (67)

Then we get the following result.

Proposition 11: For the high-level biological network with intrinsic random fluctuations in (66), if the following HJI has a positive solution V (x̃) > 0,

$$\begin{array}{l}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}f(\tilde{x}+x_e)+\frac{1}{2}\sum _{l=1}^L{f}_l^T(\tilde{x}+x_e)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \frac{{\partial }^{2}V(\tilde{x})}{{\partial }^2\tilde{x}}{f}_l(\tilde{x}+x_e)<0\end{array}$$ (68)

then the nonlinear stochastic biological network is robustly stable around the equilibrium point in evolution, ie, the system’s random fluctuation can be tolerated by the biological network, in the evolutionary process.

Proof: Similar to that for Proposition 4.

If the stochastic high-level biological network in (67) is also subject to environmental disturbance, in the evolutionary process, as follows

$$d\tilde{x}(t)=f(\tilde{x}+x_e)dt+Bv(t)+\sum _{l=1}^L{f}_l(\tilde{x}+x_e){dw}_l(t)$$ (69)

where v(t) denotes the environmental disturbances to the high-level biological network, such as impacts from environmental hormones or climatic anomalies, then we get the following result.

Proposition 12: For the nonlinear stochastic biological network in (69), under the influence of random parametric fluctuations and environmental disturbances in evolution, if the following HJI has a positive solution, V (x̃) > 0, and

$$\begin{array}{l}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}f(\tilde{x}+x_e)+{\tilde{x}}^T(t)\tilde{x}(t)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{1}{2}\sum _{l=1}^L{f}_l^T(\tilde{x}+x_e)\frac{{\partial }^{2}V(\tilde{x})}{{\partial }^2\tilde{x}}{f}_l(\tilde{x}+x_e)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{1}{4\rho }{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\le 0\end{array}$$ (70)

then the nonlinear stochastic biological network can tolerate the intrinsic random fluctuations and also has a sufficient evolution level ρ to respond to environmental disturbances, in the evolutionary process.

Proof: Similar to Proposition 6.

The evolvability of the nonlinear stochastic high-level biological network in (69) can also be measured, using the following constrained optimization method

$$r_0=\underset{V(\tilde{x})>0}{\text{min}}\rho$$ (71)

subject to HJI in (70).

Since it is very difficult to solve the HJI in (70), or to solve the HJI-constrained optimization in (71), for the evolvability and network robustness problem of the nonlinear stochastic high-level biological networks in (69), global linearization techniques can be also employed as with Proposition 7∼Proposition 9 in Section III. Therefore, they are neglected in this study. Similarly, the high-level biological network can also be modeled using the S-system model^36,37 of Section IV. Therefore, the interplay between the evolvability and network robustness of these high-level biological networks can be also discussed in a similar fashion to Proposition 10 and eq. (65), and are also neglected here too.

The interplay between the evolvability and network robustness of a biological network is related to the evolutionary antagonistic pleiotropy,³⁸ which can extend the antagonistic pleiotropy from the gene level to the biological network level, so that the antagonistic pleiotropy can be explained from a systematic perspective. For example, based on the evolutionary theory of aging,^35,38 a biological network can more robustly attenuate the effect of genetic variations and extrinsic pathogens to efficiently depress cancer, at an early stage, but the biological network must be less adaptive in its response to other environmental stresses, in old age, so that senescence occurs.³⁸

Discussion and Conclusion

In the evolutionary process of stochastic biological systems, phenotypic, environmental and genetic variations are systematically correlated, which accounts for their evolvability and network robustness. The robustness of phenotypes evolves in response to the need to cope with stochastic genetic and environmental variations. Native functions or phenotypes that play a permanent physiological role and have therefore been constantly under natural selection, must become more robust with respect to genetic, phenotypic and environmental variations. In contrast, latent, promiscuous, or coincidental phenotypes are easily perturbed by stochastic genetic, phenotypic and environmental variations, in evolution, and thereby provide the raw material for evolutionary novelty.⁶¹

Here, the living organism was considered as a robustness system under stochastic perturbations during the evolution. Therefore, the interplay of robustness and evolvability can be analyzed by using the well-developed system theories. From the system perspective, the phenotype robustness of the organism’s system in evolution can be seen as the network robustness needs to obey a phenotype robustness criterion (23) or (26), ie, “genetic robustness + environmental robustness ≤ network robustness”, which means the network robustness needs to be strong enough to tolerate either heritable perturbations (ie, intrinsic parameter fluctuations) or non-heritable perturbations (ie, external environmental disturbances) between generations so that phenotype of the network can be maintained in the evolutionary process. For the reason that the phenotype robustness of a stochastic gene regulatory network is completely consistent with the idea of Waddington.¹¹ Based on the criterion, the correlation among genetic robustness, environmental robustness and the phenotype robustness by recent genomic experiments in yeast, ie, genes confer similar robustness to genetic, environmental and phenotypic robustness,²² can be rationally explained. That is if the network robustness of a gene network is large enough then the genetic perturbations or environmental disturbances can be took over respectively or simultaneously to maintain the functional phenotype during the evolutionary process. The environmental robustness indicator f₀ reversely proportioned to the evolvability r₀ can also largely illustrate the antagonistic relationship between the robustness and evolvability found in the RNA secondary structure phenotypes.^10,14 Further, due to the hierarchical structure in biological networks, these results may not only suit for genetic network but also suit for high-level biological network in metabolic pathway or ecological system during evolution.^62–64

The dynamics of evolutionary change at molecular level, ie, the various molecular mechanisms in the long-term evolution of genomes, genes and their products, have been studied extensively.^61,65 In this study, based on the nonlinear stochastic model, the interplay between the evolvability and network robustness of biological networks is discussed from the perspective of system robustness and sensitivity theory. Using the global linearization technique, the evolvability and network robustness of biological network can be measured, from the locations of the eigenvalues of linearized systems and by solving a LMI-constrained optimization method.

Genetic, phenotypic and environmental random variations are inevitable in evolution, rather than desirable features of biological networks.^56,66 These random variations arise from the complexity and evolutionary history of biological systems. However, there is numerous evidence for the evolution of high fidelity and minimal noise, including the proof editing of DNA replication and protein translation. Enzymes have evolved toward high specificity. Gene expression is regulated by elaborate mechanisms, and stochastic variations seem to have been minimized, in the evolutionary process. For example, gene networks within bacterial operons may have evolved to minimize genetic and phenotypic noise and infidelity. However, chemophysical constraints regulate the specificity of biological networks and fidelity in biological networks is costly, so there is a tradeoff between the benefits of fidelity and its costs. Therefore, if biological networks want to retain enough network robustness and reduce their evolvability (small r₀) to genetic, phenotypic and environmental variations, in order to keep their functional accuracy (ie, phenotype robustness), much effort is needed and a high cost must be paid. In general, random genetic and phenotypic variation and heterogeneity are neither a desired nor a deliberate outcome of evolution.⁶⁶ Heterogeneity and diversity form the very basis of evolution, not only within genetically diverse populations but also within the same allele or genome.^55,65 Thus, random genetic, phenotypic and environmental fluctuations are inherent features of biological components and networks. Random perturbative biological networks may contain more widely connected and more interconnected components and may provide multifunctionality of the biological network. This multifunctionality results in an increased robustness and a capacity to cope with diverse challenges, including those that have never been encountered in evolution.^41,67 However, multi-functionality also increases the complexity and the variations in the biological network, which might increase adaptive potential. Thus, behind the façade of perfection and optimality, lies the messy biology that originates from evolution. The balance of the evolvability and network robustness, in stochastic biological networks, sheds light on the mechanisms that govern the exploitation and toleration of the messiness of the euolutionary process, from the systematic perspective. In the evolutionary scenario, network robustness is an intrinsic property of the evolvability and might in the long term, improve the evolution of all levels of biological networks.^5,35

In this study, a tradeoff between genetic robustness and environmental robustness in evolution is derived from the interplay between the evolvability and network robustness. Based on this tradeoff between the genetic robustness and environmental robustness of a biological network in evolution,³⁵ the evolutionary antagonistic pleiotropy is extended from gene level to biological level and can be discussed from the systematic perspective. In terms of gene networks, based on the evolutionary theory of aging^35,38 antagonistic pleiotropy holds that what is good for an organism when it is young can be bad for it when it is old.³⁸ Conventionally, this discussed from the point of view of individual genes. Based on the tradeoff between the genetic robustness and environmental robustness, the antagonistic pleiotropic actions of a gene network, in the evolutionary process, can be investigated from a nonlinear stochastic system perspective. Obviously, the tradeoff between the genetic robustness and environmental robustness in the evolutionary gene network is also inherent in an evolutionary antagonistic pleiotropy.

For different levels of biological networks, two favored strategies improve the phenotype robustness in evolution. One is to improve the network robustness, to resist the genetic variations and to filter the effect of environmental stimuli. Negative feedback is the mechanism that improves network robustness and is favored by natural selection at different levels of biological networks, in the evolutionary process. Another strategy is to reduce the effect of genetic variations and external stimuli on different biological networks. Redundancies and repairs are the mechanisms of this strategy and are favored by natural selection in evolution. This is the reason why there are so many different redundancies from duplicated genes in gene networks, redundant pathways in biochemical networks and species redundancy in ecological systems.³⁵

Recently, synthetic biology has spawned the engineering of artificial biological systems that fulfill a particular purpose, from off-the-shelf chemical ingredients, to allow a better understanding of biological design, using synthetic circuits.^41,67–73 High-throughput measurements are necessary, to determine what is evolved and how engineering genetic networks, in vivo, mimic the evolutionary process of genetic networks.^74–78 An approach involving directed evolution has been used to rationally design a synthetic network, in vivo.^61,66,79,80 Unfortunately, synthetic biologists are faced with the uncertainties of modeling and biochemical parametric variations, in vivo.^{55,65,71–73,81–85} To overcome this problem, the interplay between the evolvability and network robustness should be considered in the design procedure, so that the synthetic gene network can evolve to robustly track some desired behavior by evolution algorithm or genetic algorithm via the maximization fitness, at full speed to mimic the evolutionary process of a gene network, and then can function properly in the host cell, under the influence of parametric fluctuations and environmental disturbances.^{43,46,81,82,86–89} Here we provide some insights, from a stochastic system perspective, into how evolutionary biological networks sustain functions robustly, which might be useful in the design of in vivo gene networks.

In summary, this study proposes that: (i) The idea that genetic, phenotypic and environment variances pave the road for the evolvability of biological networks is an attractive one. However, their dynamic mechanisms are unclear. The proposed nonlinear stochastic systems can represent messy biological networks with intrinsic genetic and phenotypic mutations and environmental disturbances in evolution. (ii) Measures of the evolvability and the network robustness of a biological network in evolution can be obtained from the stochastical robustness theory and the H∞ filtering method. (iii) The interplay between the evolvability and network robustness of a biological network can also be discussed from a nonlinear stochastic system perspective.⁵² (iv) The criterion of phenotype robustness of a biological network in evolution is found as follows: The genetic robustness plus environmental robustness have to be covered by the network robustness in (26). This is also discussed for a stochastic biological network with genetic variations and environmental stimuli, in the evolutionary process. Based on the phenotype robustness of a gene network, the evolutionary cause of genetic robustness can also be discussed with reference to the congruent mechanism in.^15,35 (v) Based on the tradeoff between the genetic robustness and environmental robustness of evolutionary biological networks, the evolutionary antagonistic pleiotropy can be investigated, from the individual gene level^7,10 to biological network level, from the systems biology perspective. In order to avoid solving the nonlinear HJI for the evolvability and network robustness of biological networks in evolution, the global linearization technique is proposed to simplify the analysis, so that the measures of the evolvability and network robustness in a biological network only need to solve a set of LMIs and a LMI-constrained optimization, which can be easily achieved by the help of LMI toolbox in Matlab. Furthermore, the interplay between the evolvability and network robustness can be easily discussed with reference to the stability robustness and filtering ability of a biological network, from the linear system theory point of view.

The tradeoff between the genetic robustness and environmental robustness of a stochastic evolutionary biological network is most relevant to the well-known statistical tradeoff between bias and variance.^51,90 This bias/variance dilemma has been solved by some regularization method via selecting adequate regulation parameters.⁵¹ These regularization methods may provide other insights into the tradeoff between the genetic robustness and environmental robustness of a stochastic evolutionary biological network, which will be our future works.

Supplementary Data

Appendix: Equation section (next)

Before the proof of Propositions, the following lemma is useful for the proof of them.

Lemma 1: for any two vectors a ≠ 0 and b ≠ 0 and any scale ρ > 0.

$$2a^{T}b\le \frac{1}{\rho }{a}^{T}a+\rho b^{T}b$$

Appendix A: Proof of proposition 1

By choosing a Lyapunov function V (x) = x^T(t)Px(t) for the stochastic system in (4) or (5) and Ito formula,^33,39 we get the following

$$\begin{array}{ll}E\frac{dV(x)}{dt}\hfill & =E\left(\frac{\partial V(x)}{\partial x}\frac{dx(t)}{dt}+\frac{1}{2}\sum _{l=1}^L{x}^T(t)A_l^T\frac{{\partial }^{2}V(x)}{\partial x^2}{A}_{l}x(t)\right)\hfill \\ \hfill & =E\left(2x^T(t)P\left(Ax(t)+\sum _{l=1}^L{A}_{l}x(t)\frac{{dw}_l(t)}{dt}\right)+\frac{1}{2}\sum _{l=1}^L{x}^T(t)A_l^T\frac{{\partial }^{2}V(x)}{\partial x^2}{A}_{l}x(t)\right)\hfill \end{array}$$ (A1)

By the fact that E dw_l(t)/dt = En_l(t) = 0, x^TPAx = x^T A^T Px and ∂²V (x)/∂x² = 2P, we get

$$E\frac{dV(x)}{dt}=E\left(x^T(t)\left(A^{T}P+PA+\sum _{l=1}^L{A}_l^T{PA}_l\right)x(t)\right)$$ (A2)

If the inequality (6) holds, then E dV (x)/dt ≤0, ie, the stochastic gene network in (5) is stochastically stable.

Q.E.D.

Appendix B: Proof of proposition 2 equation section (next)

Consider the following equality.

$$E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt=EV(\tilde{x}(0))-EV(\tilde{x}(t_p))+E{\int }_0^{t_p}\left({\tilde{x}}^T(t)\tilde{x}(t)+\frac{dV(\tilde{x})}{dt}\right)dt$$

where V (x̃) = x̃^T (t)Px̃(t) is the Lyapunov function for stochastic gene regulatory network (9).

By the fact dV (x̃)/dt = (∂V(x̃)/∂x̃)^T dx̃(t)/dt = 2x̃^T (t) P(Ax̃(t) + Bv(t) (with $\dot{\tilde{x}}(t)=\dot{x}(t)=A\tilde{x}(t)+Bv(t)$) Then, we get

$$E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt\le EV(\tilde{x}(0))+E{\int }_0^{t_p}({\tilde{x}}^T(t)\tilde{x}(t)+2{\tilde{x}}^T(t)PA\tilde{x}(t)+2{\tilde{x}}^T(t)PBv(t))dt$$

By the fact 2x̃^T(t) PAx̃(t) = x̃^T (t) PAx̃(t) + x̃^T (t) A^T Px̃(t) and by Lemma 1 2x̃^T (t)PBv(t) ≤1/ρ x̃^T (t)PBB^T Px̃(t) ρv^T + (t)v(t).

Then, we get

$$E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt\le V\left(\tilde{x}(0)\right)+E{\int }_0^{t_p}{\tilde{x}}^T(t)\left(PA+A^{T}P+I+\frac{1}{\rho }{PBB}^{T}P\right)\tilde{x}(t)dt+\rho E{\int }_0^{t_p}{v}^T(t)v(t)dt$$

By the inequality (15), we get

$$E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt\le V\left(\tilde{x}(0)\right)+\rho E{\int }_0^{t_p}{v}^T(t)v(t)dt$$ (B1)

This is the inequality in (14). When x̃(0) = 0, V (x̃(0)) = 0. Then (B1) is reduced to the evolution level in (13).

Q.E.D.

Appendix C: Proof of proposition 3

For the stochastic gene regulatory network in (20), consider the following equality,

$$E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt=EV(\tilde{x}(0))-EV(\tilde{x}(t_p))+E{\int }_0^{t_p}\left({\tilde{x}}^T(t)\tilde{x}(t)+\frac{dV(\tilde{x}(t))}{dt}\right)dt$$

for Lyapunov function V (x̃) = x̃^T (t)Px̃(t) By Ito formula^33,39 and the fact EV (x̃ (t_p)) ≥ 0, we get

$$\begin{array}{l}E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt\le EV\left(\tilde{x}(0)\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+E{\int }_0^{t_p}\left({\tilde{x}}^T(t)\tilde{x}(t)+{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(A\tilde{x}(t)+\sum _{l=1}^L{A}_l\tilde{x}(t)\frac{{dw}_l(t)}{dt}+Bv(t)\right)+\frac{1}{2}\sum _{l=1}^L{\tilde{x}}^T(t)A_l^T\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{A}_l\tilde{x}(t)\right)dt\end{array}$$

By the fact E dw_l(t)/dt = En_l(t) =0, ∂V(x̃)/∂x̃ = 2Px̃(t), ∂²V(x̃)/∂x̃² = 2P, and by Lemma 1 2x̃^T(t)PBv(t) ≤1/ρx̃^T (t) PBB^T Px̃(t) + ρv^T (t)v(t), then we get

$$\begin{array}{l}E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt\le EV\left(\tilde{x}(0)\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+E{\int }_0^{t_p}\left({\tilde{x}}^T(t)\tilde{x}(t)+{\tilde{x}}^T(t)PA\tilde{x}(t)+{\tilde{x}}^T(t)A^{T}P\tilde{x}(t)+\sum _{l=1}^L{\tilde{x}}^T(t)A_l^T{PA}_l\tilde{x}(t)+\frac{1}{\rho }{\tilde{x}}^T{PBB}^{T}P\tilde{x}(t)+\rho v^T(t)v(t)\right)dt\end{array}$$

By the inequality in (21), we get

$$E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt\le EV\left(\tilde{x}(0)\right)+E\rho {\int }_0^{t_p}{v}^T(t)v(t)dt$$

which is the HJI in (14). If x̃(0) = 0, then V (x̃(0)) = 0 and the inequality (13) also holds.

Appendix D: Proof of proposition 4

For the nonlinear stochastic gene network in (29), let us choose the Lyapunov function V (x̃(t)) > 0 for all x̃(t) ≠ 0 and V(0) > 0. Then, by Ito formula and E dw_l (t)/dt = En_l (t) = 0, we get

$$\begin{array}{l}E\frac{dV(\tilde{x})}{dt}=E\left\{{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(f(\tilde{x}+x_e)+\sum _{l=1}^L{f}_l(\tilde{x}+x_e)\frac{{dw}_l(t)}{dt}\right)+\frac{1}{2}\sum _{l=1}^L{f}_l^T(\tilde{x}+x_e)\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_l(\tilde{x}+x_e)\right\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=E\left\{{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}f(\tilde{x}+x_e)+\frac{1}{2}\sum _{l=1}^L{f}_l^T(\tilde{x}+x_e)\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_l(\tilde{x}+x_e)\right\}\end{array}$$

(by the fact E dw_l(t)/dt = En_l (t) = 0).

By the inequality in (30), we get

$$E\frac{dV(\tilde{x})}{dt}\le 0$$

ie, the nonlinear stochastic system in (28) is stochastically stable.

Q.E.D.

Appendix E: Proof of proposition 5

For nonlinear gene network in (31), with Lyapunov function V (x̃(t)) > 0 for x̃(t) ≠ 0 and V(0) = 0, consider the following equality

$$\begin{array}{l}E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt=EV\left(\tilde{x}(0)\right)-EV(\tilde{x}(t_p))+E{\int }_0^{t_p}\left({\tilde{x}}^T(t)\tilde{x}(t)+\frac{dV(\tilde{x}(t))}{dt}\right)dt\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le EV(\tilde{x}(0))+E{\int }_0^{t_p}\left({\tilde{x}}^T(t)\tilde{x}(t)+{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(f(\tilde{x}+x_e)+Bv(t)\right)\right)dt\end{array}$$

By Lemma 1

$${\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}Bv(t)=2\frac{1}{2{\rho }^{1/2}}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{\rho }^{1/2}v(t)\le \frac{1}{4\rho }{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)+\rho v^T(t)v(t),$$

we get

$$E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt\le EV\left(\tilde{x}(0)\right)+E{\int }_0^{t_p}\left({\tilde{x}}^T(t)\tilde{x}(t)+{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}f\left(\tilde{x}+x_e\right)+\frac{1}{4\rho }{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)+\rho v^T(t)v(t)\right)dt$$

By the inequality in (32), we get

$$E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt\le EV\left(\tilde{x}(0)\right)+E\rho {\int }_0^{t_p}{v}^T(t)v(t)dt$$

This is the inequality in (14). If x̃(0) = 0 and V (x̃(0)) = 0, then we get the evolution level in (13).

Q.E.D.

Appendix F: Proof of proposition 6

For the nonlinear stochastic gene network in (34) with Lyapunov function V (x̃(t)) > 0 for x̃(t) ≠ 0 and V(0) = 0, we get the following inequality

$$E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt=EV(\tilde{x}(0))-EV(\tilde{x}(t_p))+E{\int }_0^{t_p}\left({\tilde{x}}^T(t)\tilde{x}(t)+\frac{dV(\tilde{x}(t))}{dt}\right)dt$$

By Ito formula,^33,39 and the fact E dw_l(t)/dt = En_l(t) = 0, we get

$$E\frac{dV(\tilde{x})}{dt}=E\left\{{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(f(\tilde{x}+x_e)+Bv(t)\right)+\frac{1}{2}\sum _{l=1}^L{f}_l^T(\tilde{x}+x_e)\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_l(\tilde{x}+x_e)\right\}$$

Then, by the fact V (x̃(t_p)) ≥ 0, we get

$$\begin{array}{l}E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt\le EV(\tilde{x}(0))\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+E{\int }_0^{t_p}\left({\tilde{x}}^T(t)\tilde{x}(t)+{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(f(\tilde{x}+x_e)+Bv(t)\right)+\frac{1}{2}\sum _{l=1}^L{f}_l^T(\tilde{x}+x_e)\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_l(\tilde{x}+x_e)\right)dt\end{array}$$

By Lemma 1, we get

$${\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}Bv(t)=2\frac{1}{2{\rho }^{1/2}}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{\rho }^{1/2}v(t)\le \frac{1}{4\rho }{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)+\rho v^T(t)v(t).$$

Then

$$\begin{array}{l}E{\int }_0^{t_p}{\tilde{x}}^T(t)\tilde{x}(t)dt\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le EV(\tilde{x}(0))+E{\int }_0^{t_p}\left(\begin{array}{l}{\tilde{x}}^T(t)\tilde{x}(t)+{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}f\left(\tilde{x}+x_e\right)+\frac{1}{2}\sum _{l=1}^L{f}_l^T\left(\tilde{x}+x_e\right)\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_l\left(\tilde{x}+x_e\right)\hfill \\ +\frac{1}{4\rho }{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)+\rho v^T(t)v(t)\hfill \end{array}\right)dt\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le EV\left(\tilde{x}(0)\right)+E\rho {\int }_0^{t_p}{v}^T(t)v(t)dt\end{array}$$

(by HJI in (35))

This is the inequality in (14). If x̃(0) = 0 and V (x̃ (0)) = 0, then we get the evolution level in (13).

Q.E.D.

Appendix G: Proof of proposition 7

Since we replace the nonlinear stochastic gene network in (28) by the interpolation of globally linearized system in (41), then the HJI of the stochastic stability condition (30) of nonlinear stochastic gene network can be replaced by

$${\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(\sum _{i=1}^M{\alpha }_i(\tilde{x})A_i\tilde{x}(t)\right)+\frac{1}{2}\sum _{l=1}^L\sum _{i=1}^M{\alpha }_i(\tilde{x}){\tilde{x}}^T(t)A_{li}^T\frac{\partial V(\tilde{x})}{\partial \tilde{x}}{A}_{li}\tilde{x}(t)\le 0$$

If we choose V (x̃) = x̃^T(t)Px̃(t), then we get

$$2{\tilde{x}}^T(t)P\left(\sum _{i=1}^M{\alpha }_i(\tilde{x})A_i\tilde{x}(t)\right)+\sum _{l=1}^L\sum _{i=1}^M{\alpha }_i(\tilde{x}){\tilde{x}}^T(t)A_{li}^T{PA}_{li}\tilde{x}(t)\le 0$$

or

$$\sum _{i=1}^M{\alpha }_i(\tilde{x}){\tilde{x}}^T(t)\left({PA}_i+A_i^{T}P+\sum _{l=1}^L{A}_{li}^T{PA}_{li}\right)\tilde{x}(t)\le 0$$

ie, if the LMIs in (42) hold, then the stochastic stability is guaranteed for the nonlinear stochastic gene network in (41).

Q.E.D.

Appendix H: Proof of proposition 8

Since we use the globally linearized system in (43) to replace the nonlinear gene network in (31), the HJI in (32) for solving the evolution level ρ could be replaced by the following inequality

$${\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(\sum _{i=1}^M{\alpha }_i(\tilde{x})A_i\tilde{x}(t)\right)+{\tilde{x}}^T(t)\tilde{x}(t)+\frac{1}{4\rho }{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\le 0$$

If we choose V (x̃) = x̃^T (t)Px̃(t), then we obtain

$$\sum _{i=1}^M{\alpha }_i(\tilde{x}){\tilde{x}}^T(t)\left({PA}_i+A_i^{T}P\right)\tilde{x}(t)+{\tilde{x}}^T(t)\tilde{x}(t)+\frac{1}{\rho }{\tilde{x}}^T(t){PBB}^{T}P\tilde{x}(t)\le 0$$

Because $\sum _{i=1}^M{\alpha }_i(\tilde{x})=1$, we get

The above inequality holds if the inequalities in (44) hold.

Q.E.D.

$$\sum _{i=1}^M{\alpha }_i(\tilde{x}){\tilde{x}}^T(t)\left({PA}_i+A_i^{T}P+I+\frac{1}{\rho }{PBB}^{T}P\right)\tilde{x}(t)\le 0$$

Appendix I: Proof of proposition 9

Since we use the globally linearized gene network in (40) to replace the nonlinear gene network in (34), the HJI in (35) for evolutionary evolution level ρ and network robustness in Proposition 6 could be replaced by

$${\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(\sum _{i=1}^M{\alpha }_i(\tilde{x})A_i\tilde{x}(t)\right)+\frac{1}{2}\sum _{l=1}^L\sum _{i=1}^M{\alpha }_i(\tilde{x}){\tilde{x}}^T(t)A_{li}^T\frac{\partial V(\tilde{x})}{\partial \tilde{x}}{A}_{li}\tilde{x}(t)+{\tilde{x}}^T(t)\tilde{x}(t)+\frac{1}{4\rho }{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\le 0$$

If we choose the Lyapunov function as V (x̃) = x̃^T (t)Px̃(t), then ∂V(x̃)/∂x̃ = 2Px̃ and ∂²V(x)/∂x² = 2P, then with $\sum _{i=1}^M{\alpha }_i(\tilde{x})=1$ we get

$$\sum _{i=1}^M{\alpha }_i(\tilde{x}){\tilde{x}}^T(t)\left({PA}_i+A_i^{T}P+\sum _{l=1}^L{A}_{li}^T{PA}_{li}+I+\frac{1}{\rho }{PBB}^{T}P\right)\tilde{x}(t)\le 0$$

Therefore, if the quadratic inequalities in (49) hold, then the evolution level ρ and network robustness hold for nonlinear stochastic gene network in (34) or (40).

Q.E.D.