Craniofacial form and function in Metriorhynchidae (Crocodylomorpha: Thalattosuchia): modelling phenotypic evolution with maximum-likelihood methods

Abstract

Metriorhynchid crocodylomorphs were the only group of archosaurs to fully adapt to a pelagic lifestyle. During the Jurassic and Early Cretaceous, this group diversified into a variety of ecological and morphological types, from large super-predators with a broad short snout and serrated teeth to specialized piscivores/teuthophages with an elongate tubular snout and uncarinated teeth. Here, we use an integrated repertoire of geometric morphometric (form), biomechanical finite-element analysis (FEA; function) and phylogenetic data to examine the nature of craniofacial evolution in this clade. FEA stress values significantly correlate with morphometric values representing skull length and breadth, indicating that form and function are associated. Maximum-likelihood methods, which assess which of several models of evolution best explain the distribution of form and function data on a phylogenetic tree, show that the two major metriorhynchid subclades underwent different evolutionary modes. In geosaurines, both form and function are best explained as evolving under ‘random’ Brownian motion, whereas in metriorhynchines, the form metrics are best explained as evolving under stasis and the function metric as undergoing a directional change (towards most efficient low-stress piscivory). This suggests that the two subclades were under different selection pressures, and that metriorhynchines with similar skull shape were driven to become functionally divergent.

1. Introduction

Metriorhynchid crocodylomorphs were an unusual group of tetrapods with no parallel in the living world. They are the only archosaurian reptile group to have evolved a fully pelagic lifestyle, and underwent a dramatic diversification between their Middle Jurassic origination from terrestrial ancestors until their sudden extinction during the Early Cretaceous [1]. The diversification of metriorhynchids during their short evolutionary history involved increasing morphological, functional and ecological diversity, including increasing variation in craniofacial form [1–3], dental morphology [4], body size [5] and cranial mechanical behaviour to applied loads [1,3]. Remarkably, several species of metriorhynchids often coexisted in the same marine ecosystems, and recent studies have suggested that niche partitioning, maintained via morphological and functional differentiation in the features described above, enabled high biodiversity [4,5].

Understanding the biology and evolutionary history of aberrant clades such as metriorhynchids is a fascinating, but difficult, research goal. How did metriorhynchids function as living animals? Were certain features of their skeletons associated with certain functional behaviours, which may have had ecological significance? What underpinned major patterns in their morphological evolution? Answering these questions depends on a firm understanding of the relationship between form and function, which requires an integrated toolkit of morphological, functional and phylogenetic data. This repertoire is rarely available for extinct vertebrate clades, but recent work on metriorhynchid cranial morphometrics [1,2], skull biomechanics [1,3], and phylogeny [5] provides an unprecedented reservoir of data for studying these unique crocodylomorphs.

Here, we assess the general relationship between morphological and functional evolution in metriorhynchids and determine which major models of evolution (random, stasis, directional, etc.) dominate. We find a general correlation between form and function across all metriorhynchid species, and most importantly, show that the group as a whole was undergoing directional functional evolution and that the two principal metriorhynchid subfamilies (the mostly megapredatory geosaurines and smaller, piscivorous metriorhynchines) underwent different evolutionary modes during the Mesozoic. Geosaurine form and functional evolution are best modelled as random, whereas metriorhynchines experienced static morphological evolution and directional functional evolution. Studies such as this should become increasingly possible, and more powerful, as palaeontologists compile morphological and functional data for extinct clades, and as analytical tools such as maximum-likelihood methods are progressively refined.

2. Material and methods

The ‘form’ of an organism is here considered a synonym of the structural and geometric morphology of its phenotype, which can be studied by quantitative techniques such as geometric morphometrics. Functional morphology (‘function’), on the other hand, can be investigated with explicit biomechanical methodologies such as finite-element analysis (FEA). Here we use two metrics derived from the same geometric morphometric analysis [1] to quantify craniofacial form in metriorhynchid species: the coordinate values from the first and second relative warp axes (RW1 and 2). The shape variation subsumed by these two axes explain 68.19 per cent of the variation around the mean shape (RW1 = 56.87%; RW2 = 11.32%). One function metric to describe each species was derived from an FEA [1]. This metric was calculated by taking the mean value of von Mises stress from 10 nodes along the midline of the mid-snout. All of these FE models had the same boundary conditions, loading regime (1000 N load to the anterior maxillary teeth) and material properties; the only variable was the skull (i.e. skull shape) [1]. Von Mises stress is a proxy for skull strength, as it can be used to indicate regions where plastic deformation is more probable under high applied loads [6].

To examine the general relationship between form and function across metriorhynchid species, we correlated both RW1 and RW2 against von Mises stress, using the Spearman rank correlation in the statistical language R [7]. All metrics were phylogenetically detrended using independent contrasts [8] prior to correlation, using branch lengths calculated using the first appearance datum of each species and the ‘equal’ method [9], in which zero-length branches gain lengths shared from preceding branches with a positive length. A similar correlation analysis was recently presented using a different metriorhynchid dataset and different protocols for measuring branch lengths [3].

Phenotypic evolution can be characterized in four general ways. The random walk, or unbiased random walk, describes evolution through Brownian motion and is equivalent to a zero mean step variance [10]. Directional change, or generalized random walk (GRW), occurs when the mean step variance favours either positive or negative changes (e.g. an ‘active’ mechanism [11]). Stasis describes a lack of net change, in which evolution fluctuates around a mean (and perhaps optimal) phenotype [12]. Finally, the Ornstein–Uhlenbeck (OU) model [13] describes evolution through Brownian motion towards an adaptive optimum [14].

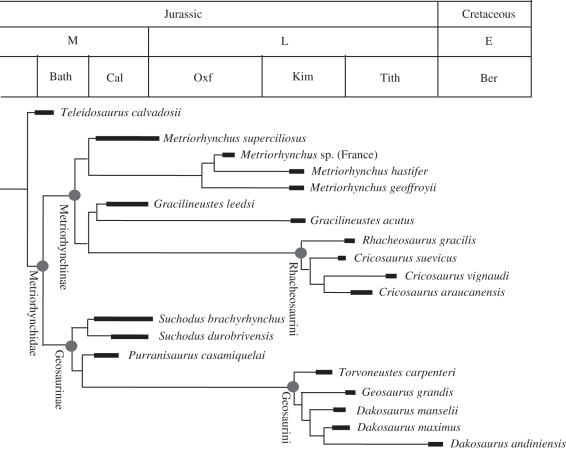
To examine major patterns in form and functional evolution in more detail, and in order to determine which of the preceding model(s) of phenotypic evolution best characterizes metriorhynchids, we conducted a novel maximum-likelihood analysis. Using the geiger package [15] for R [7], the four discussed models were used to fit the form and function measures (RW and von Mises stress) to a previously derived metriorhynchid phylogeny [5]. Branch lengths for the topology were calculated [9] and any taxon with missing data was subsequently pruned (figure 1). The fit of each model was assessed using the bias-corrected Akaike information criterion (AIC_c), which, when normalized to sum to 1, allows all models to be compared equally (the normalized score is the probability of support for the model) [16].

Figure 1.

Evolutionary relationships of metriorhynchid species used in the analyses herein. We erect Rhacheosaurini (tribe novum); phylogenetically defined as the most inclusive clade including Rhacheosaurus gracilis but not Metriorhynchus geoffroyii and Gracilineustes leedsi (see electronic supplementary material for diagnosis).

3. Results

Correlation using independent contrasts between RW1 and von Mises stress was statistically significant (R_s = 0.729, p = 0.011), but the correlation between RW2 and von Mises stress was not (R_s = 0.144, p = 0.672). Weighted AIC_c values for maximum-likelihood models (table 1) were in favour of Brownian motion for the evolution of both form metrics (RW1 and RW2 scores) in Metriorhynchidae. The same is true for the subfamily Geosaurinae, but for the subfamily Metriorhynchine, maximum-likelihood modelling of both form metrics was in favour of stasis (table 1). Most interestingly, there is strong support for a driven trend in cranial biomechanical performance in Metriorhynchidae, with GRW explaining most of the variance (table 1). The same is true for the metriorhynchine subfamily, but for the geosaurine subfamily, Brownian motion is favoured (table 1).

Table 1.

AICc weights for the four maximum-likelihood models of Metriorhynchidae and its two subfamilies, with the most likely model highlighted in bold.

taxon	metric	URM	GRW	OU	stasis
Metriorhynchidae	relative warp 1	0.672	0.171	0.157	<0.0001
	relative warp 2	0.450	0.181	0.189	0.179
	von Mises stress	0.305	0.644	0.049	0.002
Metriorhynchinae	relative warp 1	0.198	0.105	0.063	0.634
	relative warp 2	0.055	0.007	0.081	0.858
	von Mises stress	0.182	0.679	0.005	0.134
Geosaurinae	relative warp 1	0.800	<0.0001	0.024	0.176
	relative warp 2	0.780	0.041	0.024	0.156
	von Mises stress	0.824	<0.0001	<0.0001	0.176

4. Discussion

The significant correlation between the mean von Mises stress values (function) and the first relative warp axis (form) is intuitive. As the shape change across the first axis subsumes the change from a broad, short snout to an elongate, narrow snout [1], a strong correlation with the response to applied loads is understandable. The second relative warp axis, on the other hand, characterizes a more subtle shape change, involving the rostral development of the nasal bone and supratemporal fossae, and the posterodorsal retraction of the external nares. As such, the lack of a correlation between mean von Mises stress and this axis is not surprising. Indeed, similar results were recovered using a different dataset and slightly different methods by Pierce et al. [3], although their phylogenetically corrected analysis did recover a significant correlation between RW2 and von Mises stress.

The two most salient results of our study are that, based on the maximum-likelihood models of craniofacial form and functional evolution: (i) metriorhynchids as a whole were undergoing directional functional evolution, (ii) the two major metriorhynchid subfamilies were undergoing different modes of evolution, which perhaps is indicative of distinct selection pressures.

Within Geosaurinae, both the form and function metrics are best described as evolving under Brownian motion. This is interesting, as in Late Jurassic marine ecosystems geosaurines were either the apex predator or the second-tier super-predator [1,4] (specifically the subclade Geosaurini, figure 1). Although the cranial strength of the geosaurine Dakosaurus does increase through time, those of other geosaurines do not [1]. Coupled with the diversity of tooth crown and serration morphologies in geosaurines [4], it is hypothesized that contemporaneous geosaurines were limiting competition by stratifying available niches and ecological specialization. For example, Dakosaurus was adapted for delivering high bite forces and feeding on large-bodied, bony prey whereas Geosaurus was adapted for lower bite forces and gouging and slicing flesh off prey [1,4]. This great variety of cranial and dental form, however, seems to have evolved under something of a ‘random’ Brownian motion scenario.

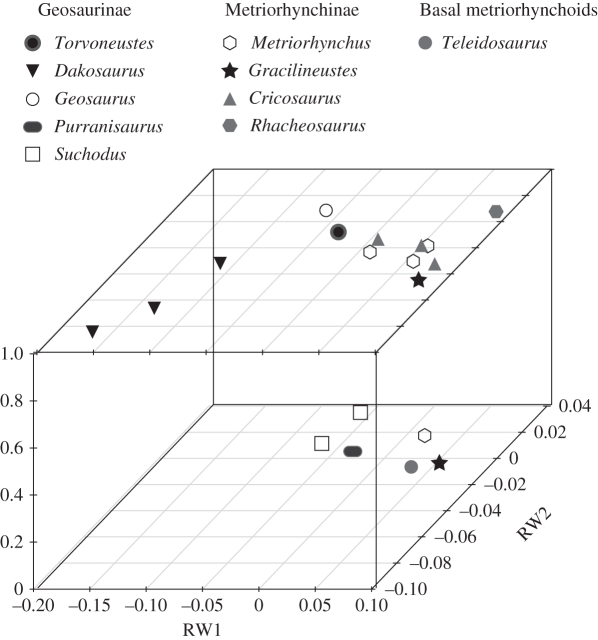
Metriorhynchines, however, were apparently experiencing a very different type of evolution. Both form metrics are best described by stasis (fluctuation around a mean morphology), but the function metric was changing in a directional manner. Young et al. ([1], p. 833) found that the basal (Metriorhynchus and Gracilineustes) and derived (Cricosaurus and Rhacheosaurus) metriorhynchine genera converged on the same region of cranial morphospace in the Late Jurassic, as Metriorhynchus and Cricosaurus occupied the meso-longirostrine morphospace region and Gracilineustes and Rhacheosaurus both occupied the longirostrine region (figure 2). Prior to the Kimmeridgian–Tithonian boundary, the basal genera were numerically dominant and had higher species diversity [1], but after the boundary, only the derived Rhacheosaurini (figure 1) are found. It was posited [1] that Rhacheosaurini acquired increasingly more sophisticated adaptations for piscivory/teuthophagy during the Mesozoic, which could explain why they replaced the basal genera. In particular, FE analysis [1] shows that the basal metriorhynchines became progressively less resistant to high applied loads, whereas the Rhacheosaurini were even less resistant (in other words, were progressively less suited for feeding on large prey, but better suited for feeding on smaller fish). The maximum-likelihood methods show these to have been driven trends. Perhaps competition between genera with similar cranial shapes drove significant changes in biomechanical skull function.

Figure 2.

Relative warps dorsal-aspect cranial morphospace, delimited by the first two axes divided into Late Jurassic (upper plot) and Middle Jurassic (lower plot). Note that the mean position for species with multiple specimens was taken.

In sum, our results show that the two metriorhynchid subfamilies underwent different modes of craniofacial form and functional evolution, suggesting that they experienced different selection pressures. Hypotheses of specific form–function relationships, non-random trends in evolution and ecological competition are notoriously difficult to assess with the fossil record. However, the steady compilation of large, integrated datasets, analysed using explicit phylogenetically based methods such as our maximum-likelihood tests, promise to unlock many secrets once deemed inaccessible to palaeontologists.