Explaining the heritability of an ecologically significant trait in terms of individual quantitative trait loci

Abstract

Most natural populations display substantial genetic variation in behaviour, morphology, physiology, life history and the susceptibility to disease. A major challenge is to determine the contributions of individual loci to variation in complex traits. Quantitative trait locus (QTL) mapping has identified genomic regions affecting ecologically significant traits of many species. In nearly all cases, however, the importance of these QTLs to population variation remains unclear. In this paper, we apply a novel experimental method to parse the genetic variance of floral traits of the annual plant Mimulus guttatus into contributions of individual QTLs. We first use QTL-mapping to identify nine loci and then conduct a population-based breeding experiment to estimate V_Q, the genetic variance attributable to each QTL. We find that three QTLs with moderate effects explain up to one-third of the genetic variance in the natural population. Variation at these loci is probably maintained by some form of balancing selection. Notably, the largest effect QTLs were relatively minor in their contribution to heritability.

1. Introduction

Is most complex trait variation caused by common alleles or is it largely owing to the aggregate contributions of many rare variants? How large are per-locus allelic effects? Is effect size correlated with allele frequency across quantitative trait loci (QTLs)? These are questions of import throughout biology. In human health, the ‘common disease/common variant hypothesis’ is a statement on these conditions [1,2] and its validity has clear clinical implications. A disease caused by a few intermediate frequency polymorphisms provides clear targets for diagnosis and perhaps drug development. The outlook is less promising if disease is caused by many rare variants. A classic population genetic question is how genetic variation is maintained by the balance of evolutionary forces [3]. Mutation–selection balance predicts that polymorphic loci will have rare alleles while balancing selection models typically predict intermediate allele frequencies [4,5]. The respective contributions of these evolutionary mechanisms determine the relevance of standing variation to adaptation and the extent to which trait evolution is limited by mutation as opposed to selection.

Flower size of Mimulus guttatus is a model for the study of complex trait variation in natural populations. This ecologically important trait has diversified extensively in Mimulus [6]. Flower size variation is highly polygenic and under strong natural selection within the well-studied Iron Mountain population [7–9]. Mutation–selection balance can explain only a fraction of the heritability in flower size [10,11], suggesting an important role for balancing selection. However, the genomic targets of this hypothesized selection remain obscure, despite the fact that many flower size QTLs have been mapped [8]. QTL mapping studies routinely report variance estimates, but these are specific to the mapping experiment and not the natural population from which genotypes were sampled. Rare alleles that contribute minimally to population variation could explain a large fraction of the variance in any particular mapping population.

Allelic effects and population allele frequencies jointly determine V_Q, the additive genetic variance generated by a QTL. This statistic is essential for evolutionary prediction and is a natural measure of the ecological or medical importance of a polymorphism. In this paper, we apply a two-phase approach to estimate V_Q. In the mapping phase, we identify a specific and limited set of loci affecting flower size. In the V_Q phase, we conduct a population-based breeding design to estimate how much each QTL contributes to variation in the natural population. Aggregating data across loci, we obtain a single overall test of whether mapped loci contribute to standing variation.

2. Material and methods

To identify loci affecting flower size, we mapped QTLs in two sets of nearly isogenic lines (NILs). All genetic variation in these NILs is derived from a single natural population located on Iron Mountain in Oregon, USA [8,12]. Five distinct QTLs (Q1, Q2, Q8a, Q8b and Q10b) were mapped in the IM62 genetic background and four more in the IM767 background (Q5a, Q5b, Q9 and Q10a), with the number following Q indicating the linkage group [13]. QTLs located on the same linkage group (e.g. Q5a and Q5b) have high recombination rates between them. IM62 and IM767 are homozygous lines extracted from Iron Mountain.

For the V_Q phase, we conducted a Replicated F2 breeding design. One hundred and thirty-eight inbred lines randomly extracted from Iron Mountain were each crossed to a single Reference line (IM767) to generate segregating F2 families [14]. Each of the 138 ‘Line Cross Families’ consists of replicate individuals of the parental Random line, F1s (between that Random line and the Reference) and F2s (from selfing the F1s). Plants were grown under common greenhouse conditions along with replicates of IM767 and measured for corolla width and pistil length (see [15] for a detailed description). Novel to this study, we genotyped a total of 37 markers in the genomic vicinities of flower size QTLs (see electronic supplementary material). The marker data determine whether the alleles of each F2 individual were descended from the random line or IM767. Combined with an interval mapping methodology, this allows us to estimate V_Q for each QTL without identifying causal alleles. The inference model applied to real data here is similar to that applied to simulated data in the study of Kelly [14], although because here we are not assuming two alleles per QTL, allele frequency cannot be estimated directly.

At each QTL, we test the null model (V_Q = 0) against the alternative model (V_Q > 0). V_Q = 0 if the QTL has no effect in any F2 family or if the population of random lines is fixed for a single alternative allele to the reference line allele (a uniform effect across line cross families). With V_Q > 0, random lines differ from each other in genotype at the QTL. As a consequence, the relationship between QTL genotype and phenotype will vary among line cross families. Inference is based on maximum-likelihood fits for each model to each QTL. Because V_Q is bounded to non-negative values, the null distribution for the likelihood-ratio test (LRT) is predicted to be an equal mixture of 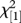and zero values. We have confirmed this with simulations (see electronic supplementary material).

3. Results

The variance among outbred plants was approximately 7.6 mm² for corolla width and 1.5 mm² for pistil length, with heritabilities (h²) of 0.41 and 0.42, respectively [15]. From the NIL mapping data, we compared alternative homozygotes at each QTL for the mean corolla width of the first two flowers on a plant. Estimates for 2a, the difference between homozygotes (QTL effect), are given in the left portion of table 1 (significance tests in electronic supplementary material). Pistil length was not measured in the NIL mapping.

Table 1.

The QTL effect (in millimetres) on corolla width as estimated in NILs is given in the second column. LRT statistics for V_Q > 0 are reported for both corolla width and pistil length. V_Q is reported in mm². h_Q²/h² is the proportion of the heritability explained by each QTL. Significance levels for QTL-specific LRT tests: *0.01 < p < 0.05, **0.001 < p < 0.01. Z = QTL-specific LRT values.

	NIL estimates		replicated F2 estimates
	corolla width		corolla width			pistil length
QTL	2a	SEM	LRT	VQ	hQ2/h2	LRT	VQ	hQ2/h2
Q1	3.599	0.568	0.05	0.044	0.014	1.48	0.053	0.084
Q2	0.857	0.271	6.75**	0.423	0.136	9.22**	0.158	0.251
Q5a	0.693	0.155	0.55	0.141	0.045	1.87	0.073	0.116
Q5b	1.181	0.114	3.56*	0.373	0.120	0.04	0.000	0.000
Q8a	2.011	0.475	0.00	0.000	0.000	0.03	0.005	0.008
Q8b	1.249	0.257	0.18	0.074	0.024	0.00	0.000	0.000
Q9	0.588	0.128	0.37	0.144	0.046	0.21	0.016	0.025
Q10a	0.324	0.099	0.94	0.149	0.048	1.42	0.059	0.094
Q10b	1.040	0.202	3.72*	0.342	0.110	9.40**	0.166	0.263
			combined LRT (Z)			combined LRT (Z)
			Z = 16.12, p = 0.007			Z = 23.67, p = 0.0003

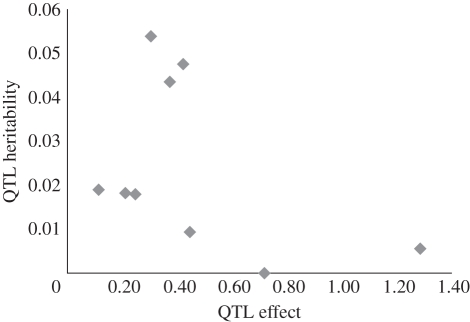
The right portion of table 1 summarizes hypothesis tests and V_Q estimates. The QTL heritability (h_Q²) is V_Q as a proportion of the phenotypic variance. For corolla width, we reject the null model for Q2, Q5b and Q10b. These QTLs each explain about 4–5% of the total phenotypic variance. In contrast, h_Q² for the QTL with the largest NIL effect (Q1) is only 0.006. The overall relationship between effect (in standard deviations) and h_Q² is depicted in figure 1 for corolla width. For pistil length, we reject the null model for Q2 and Q10b. Each of these loci explains about 10 per cent of the phenotypic variance and 25 per cent of the heritability in pistil length. An overall test for each trait is obtained by summing LRT values across QTLs. The null distribution for this sum can be calculated numerically (see electronic supplementary material) and p-values are reported in the last row of table 1.

Figure 1.

The relationship between estimated QTL effect (2a in units of phenotypic SD) and heritability for corolla width.

4. Discussion

Previous estimates for V_Q come from genome-wide association studies (GWAS), although with mixed success [16–20]. GWAS of human populations have detected many loci, but these loci typically explain little of the variation and most of the heritability remains unexplained. It is difficult to draw strong conclusions about particular polymorphisms in GWAS because the enormous number of tests leads to very stringent significance levels [20]. An advantage of our two-phase method is that the mapping phase limits the number of statistical tests performed in the V_Q phase. This is illustrated by our combined tests for flower size QTLs of Mimulus guttatus (bottom of table 1). The total sample size for our population experiment (n = 3118) is smaller than is typical of GWAS, yet the evidence that QTLs contribute to variation is compelling: p < 0.007 for corolla width and p < 0.0003 for pistil length. Admittedly, much of the genetic variance in both corolla width and pistil length remains unexplained. However, the nine loci considered here are a minor fraction of the floral QTLs that have been mapped within the Iron Mountain population [8].

The two-phase method also provides a means to contrast QTL effect in a homogeneous genetic background with V_Q. Intermediate effect QTLs had the largest estimated per-locus contribution to variation, while the largest effect QTLs (Q1, Q8a and Q8b) had the lowest V_Q estimates (figure 1). Allelic effect will be decoupled from variance if mutations with large effects routinely have negative consequences for fitness (detrimental pleiotropy) and thus exist at low frequency. For example, dwarfism mutations are large-effect QTLs for human height, but contribute minimally to V_Q [20]. Alternatively, V_Q can be large even when QTL effect is minimal if there is an allelic series at the QTL [21] and the two alleles compared in NILs are similar. Epistasis can also complicate the relationship between effect and variance. NILs provide statistically compelling estimates for QTL effect, but if effects are contingent on background, then the particular QTLs mapped in a NIL panel will depend on the specific identity of the isogenic background. Epistasis could reduce V_Q because population variation is based on QTL expression averaged across many genomic backgrounds. With either an allelic series or epistasis, the effect–variance relationship may be contingent on the method of QTL detection (selective genotyping of NILs in our case). Regardless of the cause, however, figure 1 is a notable result from the perspective of QTL mapping where the biological significance of a QTL is often equated to the magnitude of its effect.

Our previous quantitative genetic studies [10,11] indicate that mutation–selection balance can explain only a fraction of the heritability in flower size, suggesting an important role for balancing selection. Q2, Q5b and Q10b emerge as excellent candidates for balanced polymorphisms, because QTL heritabilities of ca 0.04 strongly suggest intermediate allele frequencies. Admittedly, the point estimates for these loci are close to our detection limit where rejecting the null model becomes more likely than not (see electronic supplementary material). In this situation, parameter estimates for significant loci will tend to be overestimated and those for non-significant loci underestimated [22]. That said, very large QTL effects would be required for rare alleles to generate the variance attributed to Q2, Q5b and Q10b, and these loci evidently have quite moderate effects (figure 1). Field studies are currently underway to measure the ecological and fitness consequences of these QTLs to determine the particular selective mechanisms that maintain alternative alleles.