Role of Solvation Effects in Protein Denaturation: From Thermodynamics to Single Molecules and Back

Abstract

Protein stability often is studied in vitro through the use of urea and guanidinium chloride, chemical cosolvents that disrupt protein native structure. Much controversy still surrounds the underlying mechanism by which these molecules denature proteins. Here we review current thinking on various aspects of chemical denaturation. We begin by discussing classic models of protein folding and how the effects of denaturants may fit into this picture through their modulation of the collapse, or coil-globule transition, which typically precedes folding. Subsequently, we examine recent molecular dynamics simulations that have shed new light on the possible microscopic origins of the solvation effects brought on by denaturants. It seems likely that both denaturants operate by facilitating solvation of hydrophobic regions of proteins. Finally, we present recent single-molecule fluorescence studies of denatured proteins, the analysis of which corroborates the role of denaturants in shifting the equilibrium of the coil-globule transition.

INTRODUCTION

Proteins are amino acid–based macromolecules that direct or participate in nearly every chemical reaction essential for life. Most proteins found in nature must adopt a specific conformation, called the folded or native state, to function properly in vivo. The hallmark of foldedness is the thermodynamic drive of proteins to explore an ensemble of highly structurally similar configurations that are all more or less equally competent to carry out some function by virtue of having the proper three-dimensional shape. Thus the protein folding problem—that is, the physicochemical question of how a given protein’s conformational preferences depend on its amino acid sequence and on characteristics of its surrounding environment—is of immense importance to our understanding of how biological systems operate at the molecular level (1–4).

For most proteins in solution, the choice between remaining natively folded or exploring a more structurally diverse ensemble of nonfunctioning unfolded or denatured conformations depends on the pH, ionic strength, and temperature of their aqueous surroundings (5), as well as on the presence or absence of other proteins [such as cofactors or chaperones (3, 6)]. Protein stability also may be modulated through the addition of various osmolytes and other cosolvents. Some of these, such as glycerol or trimethylamine N-oxide, stabilize the folded state (7), whereas others, such as guanidinium chloride (GdmCl) and urea (Figure 1), have a denaturing character (8). A vast literature has developed in particular around the use of chemical denaturants as probes of protein stability.

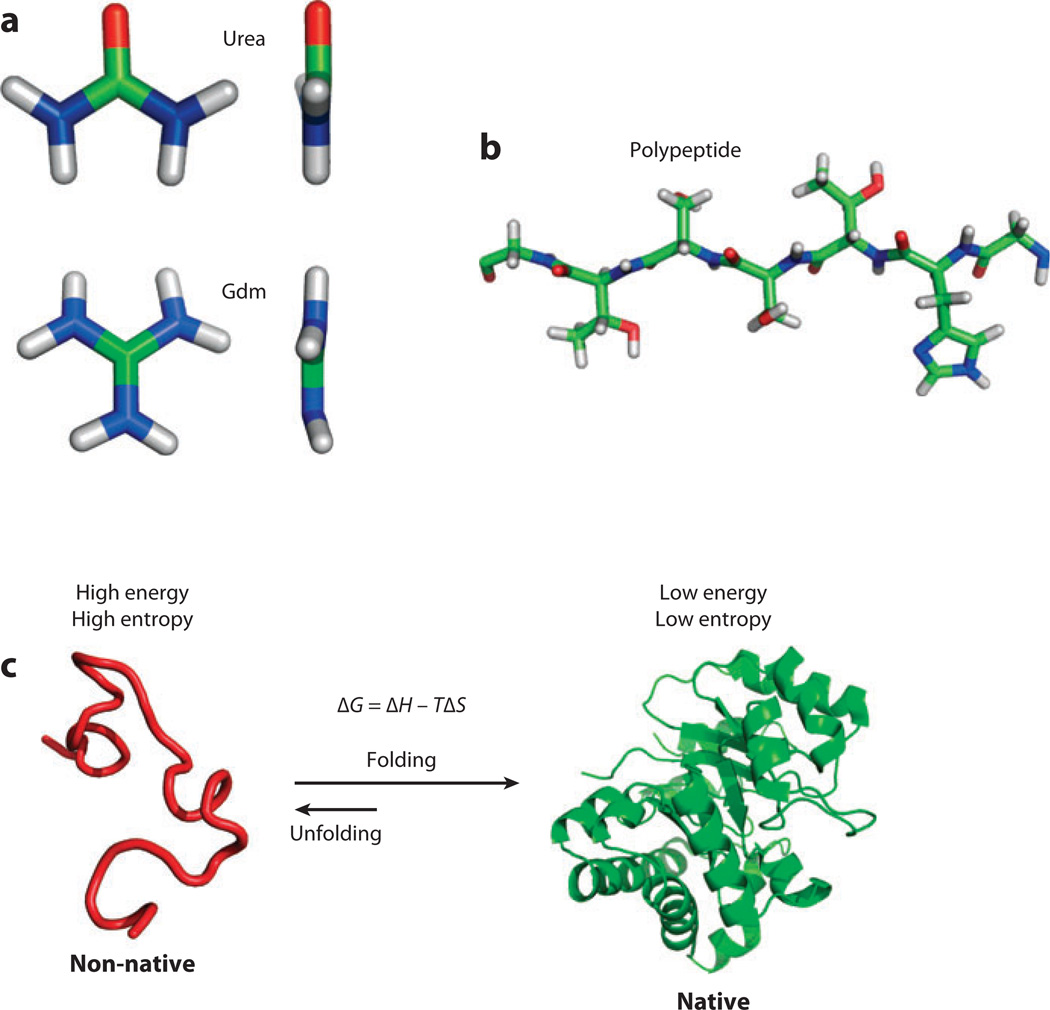
Figure 1.

Basic chemical ingredients. (a) Both the guanidinium ion and urea are roughly triangular, planar organic molecules with one central carbon (green). In urea, the oxygen (red) carries a partial negative charge, whereas the nitrogens (blue) carry a partial positive charge. In guanidinium (Gdm), the net positive charge of the molecule is distributed by resonance over the nitrogens attached to the carbon. (b) A polypeptide chain consisting of a backbone and side chains. The color scheme is the same as in panel a. (c) When a protein folds, it adopts a thermodynamically stable, low-entropy ensemble of conformations known as the native state. Native conformations are generally stabilized by their low energy relative to the typical energies experienced in the high-energy, high-entropy ensemble of non-native conformations.

Given the long-standing importance of GdmCl and urea to our empirical understanding of protein stability, it is remarkable that a mechanistic understanding of how they affect protein structure has remained elusive. The main difficulty arises from the fact that GdmCl and urea are weakly interacting molecules, and concentrations in the molar range usually are required to destabilize proteins (9). Controversy therefore still surrounds a variety of questions, such as whether the denaturant molecules modulate solution properties or interact with the protein directly. If the latter is correct, it is still not clear what type of interaction (be it polar, hydrophobic, or van der Waals) is the driving force for denaturation, and whether the effect of the cosolvent on the polypeptide backbone or on the amino acid side chains is more important (10). Moreover, it also may be the case that some of these questions ultimately will prove to have different answers for urea than for GdmCl.

In what follows, we review current thinking on possible mechanisms of protein denaturation. Incorporating findings from molecular dynamics (MD) simulation and experiment, we discuss the various debates that have raged over which driving forces are dominant in chemical denaturation. Focusing on several recent studies, we argue that a consensus finally has begun to emerge and suggest that past tension was, to some extent, illusory. The conclusions that microscopic studies of denaturant mechanism draw tend to depend most heavily on what questions are asked and which quantities subsequently are calculated from the simulation trajectories. Thus it is likely that the overall solvation properties of denaturants derive from the simultaneous action of a variety of microscopic phenomena that are now well established. In any case, the task of characterizing the conformational properties of denatured proteins remains, and recent progress on that front is quite promising. In particular, it has been suggested, based on recent experiments, that denaturants drive an expansion of denatured proteins that is similar to the coil-globule transition of polymers. This phenomenon, intimately related to the question of the mechanism of action of denaturants, has a profound influence on the thermodynamics of denaturation, as we argue in some detail below. We believe this discussion to be of interest not only from the point of view of protein biophysics, but also from the more general point of view of the physical chemistry of solutions and solvation, and we therefore attempt to cast our arguments in such terms.

FOLDING THERMODYNAMICS

In the classic view of two-state folding, a protein exists in dynamic equilibrium between (a) a compact, folded state of low energy and low entropy and (b) a high entropy, structurally disordered ensemble of higher-energy conformations called the unfolded state (11, 12). Experimentally, the degree of foldedness generally is measured by tracking some spectroscopic proxy, such as intrinsic fluorescence or ellipticity as measured by circular dichroism (13).

In examining the thermodynamics of folding in detail, it is useful to distinguish between two different stages (or steps) of energy-entropy trade-off in a typical globular protein (see Figure 2 for a qualitative phase diagram of proteins). The first of these is the coil-globule transition. Insofar as each protein is a polymeric chain with some average degree of solvophobicity determined by its amino acid composition, it is expected to recapitulate the classic results from the theoretical study of the physics of homopolymers, which describe a transition from a swollen coil to a collapsed globule as the interaction between the solvent and polymer is tuned from being more favorable to less favorable (14, 15). When the polymer-solvent interaction is highly favorable, there is no energetic cost to exploring a high-entropy swollen coil ensemble of states. As the interaction becomes less favorable, however, the chain decreases in entropy and collapses into a globule to minimize the surface area that it exposes to the solvent.

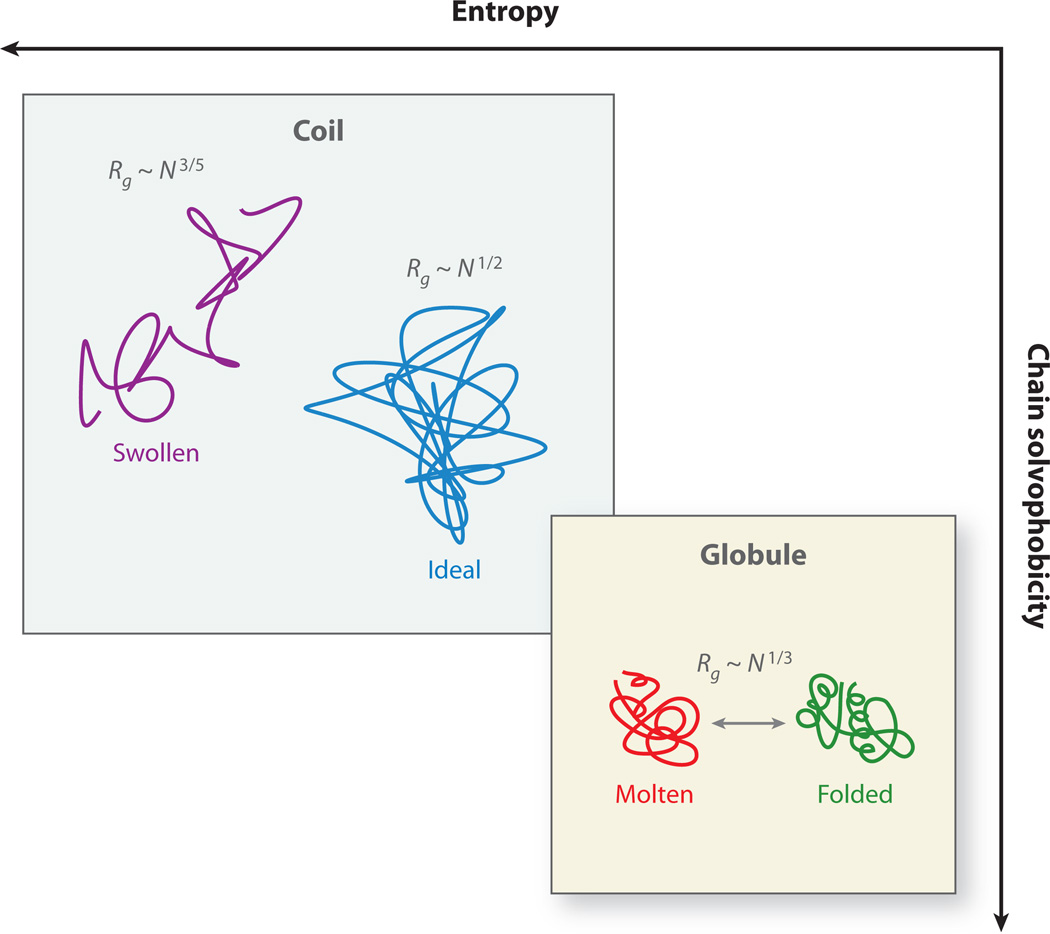
Figure 2.

A phase diagram for proteins. Many factors (such as net charge and average hydrophobicity) affect the degree to which a polymer chain is either attracted to or repelled by the surrounding solvent. The strength of this effective solvophobicity determines whether the polymer explores a globular or an expanded ensemble of conformations. Folded proteins tend to be more globular, whereas swollen coils cannot adopt unique native structures. As a polymer undergoes a coil-globule transition, the universal exponents that describe the relationship between the number of monomers N and the radius of gyration R_g change.

Even once a protein chain has collapsed into a globule, however, the process of folding still consists of an additional step. The folded state is a low-entropy subensemble of all possible collapsed globular conformations for the protein chain. In other words, there is a globular unfolded ensemble that has lower entropy than the swollen random coil, but this ensemble still has higher entropy than the folded state, and in order for folding to be favorable, the folded state must be sufficiently energetically favorable to overwhelm the higher entropy associated with structural disorder within the globular phase. It is the interaction of side chains in the folded state that provides the necessary enthalpic contribution for the transition from a disordered globular state to a folded state (16–19).

The above preliminaries are important to any discussion of denaturation because they illustrate that, for a given protein, it may be challenging to define both the folded and unfolded state. For example, the CFTR R domain is so hydrophilic in its amino acid composition that it is unable random coil state even as it carries out its biological function (20). More typically, proteins are competent to fold to a particular native state under the right conditions [it has been recognized recently that in some cases these conditions include binding to another protein (21)], but alteration of those conditions in general has the potential to affect both the energy and entropy of the folded and unfolded states of the protein. Thus it is crucial, when discussing the effects of chemical denaturation, to be precise about the meaning of phrases such as denatured state or unfolded state. For our purposes, in what follows, we use these phrases interchangeably, and take them to mean the ensemble of all conformations not belonging to the folded ensemble under a given set of conditions. Thus the unfolded state is a condition-dependent ensemble of conformations whose partition function is sensitive to factors such as the ambient temperature and concentration of chemical denaturants such as urea and GdmCl.

With this important semantic issue dealt with, we are now prepared to ask how it is that denaturants may affect the folding equilibrium of a typical protein. In the absence of denaturants, a protein below its melting temperature is driven at thermodynamic equilibrium toward the folded state, which compensates the loss of entropy associated with folding through a corresponding decrease in energy. With increasing concentration of denaturants such as urea and GdmCl, however, the free energy difference of unfolding ΔG_N→U becomes more negative until, at a critical concentration, a cooperative transition is observed and the equilibrium is driven to favor unfolding. The folded state is thought to be stable because of its high energetic favorability. Thus, to explain the action of denaturants, one first must understand how they affect the difference in energy between folded and unfolded conformations of a protein.

POSSIBLE MECHANISMS OF CHEMICAL DENATURATION

A protein’s energy derives principally from van der Waals, hydrogen bonding, and electrostatic interactions both within the polypeptide chain and between the chain and its surrounding aqueous solvent (22). One particularly important subset of these interactions is called the hydrophobic effect, which results from the propensity of water molecules to form many relatively strong hydrogen bonds with each other. The favorable self-interaction of water produces a strong tendency for a protein to bury those parts of its surface that are not sufficiently hydrophilic, i.e., that are not themselves polar enough to replace one of the waters in a water-water hydrogen bond. The collapse of the protein backbone into a dense globule and the burial of hydrophobic amino acid side chains in the protein’s core are both driven by the hydrophobic effect, and each phenomenon is crucial to the stability of a low-entropy folded state (1, 23).

The importance of solvation to protein structure has been identified as a possible explanation for the effects of denaturants. One of the most basic disagreements that has arisen over the denaturant mechanism turns on the question of whether urea and GdmCl interact directly with the proteins they denature, by binding to them at specific sites normally occupied by water molecules (24), or whether the denaturant cosolvents bring about amore global reorganization of the aqueous environment whose destabilizing effects result as much from the altered character of interactions between protein and water molecule as they do from direct contact between the polypeptide and the denaturant (25). This debate is difficult to adjudicate (and, perhaps, uninformative) because the molar concentrations at which chemical denaturants tend to operate make it certain that many cosolvent molecules will find themselves in close proximity to the protein chain. Thus, in the context in which chemical denaturation generally takes place, interaction between cosolvent and protein is a fact that must be contended with and accounted for in any discussion of the process of denaturation.

A related, but distinct dispute pertains to the impact of chemical denaturants on the strength of the hydrophobic effect. As folded proteins generally expose much less polypeptide backbone surface area and far fewer hydrophobic side chains to the surrounding solvent, it stands to reason that if denaturant cosolvents were to weaken the contribution of the hydrophobic effect to the energy change associated with unfolding, unfolded conformations would be stabilized relative to the native state. Alternatively, it may also be the case that favorable electrostatic interactions between cosolvent molecules and polar atoms in the protein that become exposed upon unfolding energetically stabilize non-native structures. In either of these pictures, there is also some disagreement about whether side-chain or backbone interactions are the cause of the effect (26, 27). It is possible that some property common to all protein backbones is important to stabilizing collapsed globular conformations like the native state, or it also could be that interactions between cosolvent molecules and particular types of amino acid side chains have the strongest destabilizing effect on protein structure.

Fortunately, advances in computer technology in recent years have opened the door to performing atomistic simulations of denaturant solutions to gain insight into the behavior of urea and guanidinium at the molecular level. Although all such computer-generated models carry with them their particular assumptions and correlative caveats, they nevertheless have begun to clarify the microscopic origins of the cosolvents’ properties. Thus a close-up portrait of each chemical denaturant has begun to emerge that can help to explain the destabilizing effects the cosolvents have on polypeptide chains.

SIMULATIONS SHED NEW LIGHT ON THE MICROSCOPIC MECHANISMS OF DENATURATION

To date, a variety of MD simulations of both urea and GdmCl solutions have been carried out, and researchers have made a diverse range of claims about their implications. These computations invariably involve assuming some force field for the interactions between different types of molecules and then solving Newtonian equations of motion using numerical tricks to fix thermodynamic quantities such as temperature and pressure (22). It is important to remember that, after carrying out any MD simulation, one always has an enormous quantity of raw data corresponding to the positions and velocities of the atoms in the simulation at each step in time. In principle, an endless variety of analyses of these data are possible, and researchers always must select a particular aspect of the trajectory in question to subject to scrutiny. The ever-present danger in this choice is that the way in which questions about the data are asked will influence strongly what kind of conclusions may be drawn. This danger is heightened particularly in circumstances in which a multiplicity of factors may give rise to the phenomenon of interest, as is the case for the process of chemical denaturation.

To start with, several studies have claimed that polar, electrostatic interactions between denaturants and polypeptide chains may be the determinative effect. For example, O’Brien et al. (28) simulated both urea and GdmCl solutions with a model peptide and focused on the relative frequency of direct contacts between cosolvent molecules and polar atoms on the protein. They observed strong, direct associations between the guanidinium cation and charged or polar groups in both protein side chains and backbone, but did not observe similar associations for urea, and thus argued that direct electrostatic interaction is a driving force for denaturation mediated by GdmCl more strongly than it is for urea. Mountain & Thirumalai (29), meanwhile, demonstrated that an alkyl chain collapsed in water was more susceptible to expansion by urea if the atom at one of its termini was charged and showed further that, upon swelling of the chain, the charged end was surrounded by a dense cloud of urea. In another paper from the same laboratory (30), it was shown that a valine dipeptide experienced conformational preferences in 8-M urea significantly urea at the amide backbone. On these bases, the authors have argued for a role for direct polar interactions between urea and the denatured protein. This thesis is in agreement with work from Bennion & Daggett (31), which showed in simulations of the protein CI2 that protein hydrogen bonds to solvent formed in the presence of urea at the expense of intraprotein hydrogen bonds that stabilize the native structure.

Against all these studies, the charge may be leveled that the co-occurrence of certain types of solvent-protein interactions with the action of denaturant does not establish whether they are a cause or merely a consequence that will be noticed if one elects to compute contact frequencies between cosolvent molecules and polar atoms. Taking the example of CI2 (31), the unfolding of the protein is bound to be accompanied by a loss of secondary structure, which virtually guarantees that more protein-solvent hydrogen bonds will be formed under denaturing conditions. Similarly, the charging of an alkyl chain’s tip by Mountain & Thirumalai (29) may simply tilt the balance in the favor of swelling driven by a denaturant-weakened hydrophobic effect. In other words, a cosolvent molecule’s direct interaction with a polar group may take place because the cosolvent molecule is already located nearby for reasons other than the energetic favorability of the interaction. This objection is especially significant both in light of a recent experimental hydrogen exchange study (32) casting doubt on the ability at least of guanidinium to hydrogen bond to the backbone and given evidence from simulation (discussed below) that additional factors affect the energy of the protein-denaturant interaction.

A similar story may be told for recent works that have pointed to the importance of dispersion forces in stabilizing the denatured state. Zangi et al. (33) simulated a hydrophobic chain in urea solution and showed that the main contribution to the enthalpic difference between collapsed and expanded conformations of the chain came from the dispersion attraction between urea and the chain, which was on average more favorable than the water-chain attraction. A similar work that focused on the denaturation of lysozyme showed again that the urea-protein dispersion interaction was most favorable (34).

Most recently, an equilibrated unfolding and refolding trajectory of a Trp-cage protein by García and colleagues (35) has provided a new demonstration that van der Waals interactions between urea and protein dominate the interaction energy. By using replica exchange methods to obtain thermodynamic information about the behavior of a 20-residue peptide in water and three different concentrations of urea, the authors were able to demonstrate systematically that, whereas both van der Waals and Coulombic interactions between the protein and solvent favored unfolding in the denaturant solution, the van der Waals portion of the energy was dominant. A similar study of a model hydrophobic chain in GdmCl conducted by Godawat et al. (36) points to the same conclusion: It is the coating of the polymer with the cosolvent, and the resulting favorable dispersion interactions, that energetically stabilizes the expanded coil state. Thus, although a direct interaction between denaturant and protein is increasingly plausible, it is dispersion attraction, rather than polar interactions, that is argued to be crucial.

Evidence for the importance of dispersion interactions, however, derives entirely from analyses of MD trajectories that ask and answer questions about the contribution of different parts of the force field to the total energy of the system. By asking a different type of question, an alternative line of argument has developed that describes the action of denaturants in other terms. The hydrophobic effect is well known to be an important driving force for protein folding (see the sidebar, The Hydrophobic Effect), and it has been suggested that both urea and GdmCl may play a role in modulating its strength. Initial attempts to examine this possibility in simulation were to some extent confounded by the length-scale dependency of hydrophobicity (28): The potential of mean force between two methane molecules does not necessarily provide an accurate reflection of how strong hydrophobic forces are when they act on surfaces of lower curvature and greater area, because solutes comparable in size to a single water molecule pack differently into the liquid than ones that are much larger (37). Careful studies of urea in simulations carried out by Stumpe & Grubmüller (38), however, have revealed that urea has a moderate tendency to aggregate, behaving like a marginally hydrophobic molecule with some inclination to phase separate from the more polar environment of water and thereby provide a locally more favorable solvent environment for other hydrophobic species. The authors also showed that when the enthalpic changes associated with breaking water-protein or water-water hydrogen bonds for the purpose of forming cosolvent hydrogen bonds are taken into account, it is difficult to argue that polar interaction drives denaturation (26). Instead, they computed the energetic change associated with substituting urea for water in the solvation shell of the protein backbone and side chains and found that urea interacts most favorably with hydrophobic side chains and the peptide backbone, which is consistent with its moderate tendency to separate from water. This result is supported further by a subsequent study in which they demonstrated that urea stabilizes partially unfolded proteins against hydrophobic collapse through the same types of solvation interactions (39), and by one in which urea is found to have a similar effect on a pure polyglycine chain, indicating that water is a poor solvent for the protein backbone itself (40).

A similar, although not identical, picture has come into view in the case of GdmCl. Although guanidinium ions do not aggregate in the same way that urea molecules do, they do appear, in both simulation (41) and experiment (42), to be dehydrated along their planar face and therefore participate in hydrophobicity-driven stacking interactions. As a result, guanidinium ions have a tendency to line up flat along a hydrophobic surface and coat it, thereby reducing the unfavorableness of its exposure to solvent (Figure 3). This effect was shown by England et al. (43) to weaken the hydrophobic effect in a study of hydrophobic dewetting between nonpolar plates in an MD simulation. Dewetting is the evacuation of the liquid phase between two hydrophobic surfaces that takes place when the interplate separation becomes small enough that the surface tension of the liquid next to the plates overwhelms the bulk pressure of the surrounding bath. The authors simulated water and 5-M aqueous solutions of denaturant between two purely hydrophobic surfaces. The advantage of a study of this kind is that, in the absence of any polar molecules in the system other than water and cosolvent, it is possible to pose and answer a simple question about the effect of chemical denaturants on the strength of the hydrophobic effect. The study found that both GdmCl and urea stabilize the liquid phase between the plates, and that guanidinium does so by flattening itself against the hydrophobic surfaces of the plates. Subsequently, Godawat et al. observed the same coating phenomenon in a simulation of the solvation of a hydrophobic polymer (36). Interestingly, although urea does not appear to undergo the stacking process observed for guanidinium (but rather seems to transiently aggregate near hydrophobic surfaces), both England et al. (43) and Zangi et al. (44) demonstrated that urea, like guanidinium, stabilizes a hydrophobically confined liquid phase against dewetting, and the latter group also showed that urea stabilizes a hydrophobic polymer against collapse (33). Taken together, all of these studies establish as emphatically as simulations can that both urea and GdmCl are capable of weakening the hydrophobic effect, which normally plays a decisive role in the structural stability of proteins.

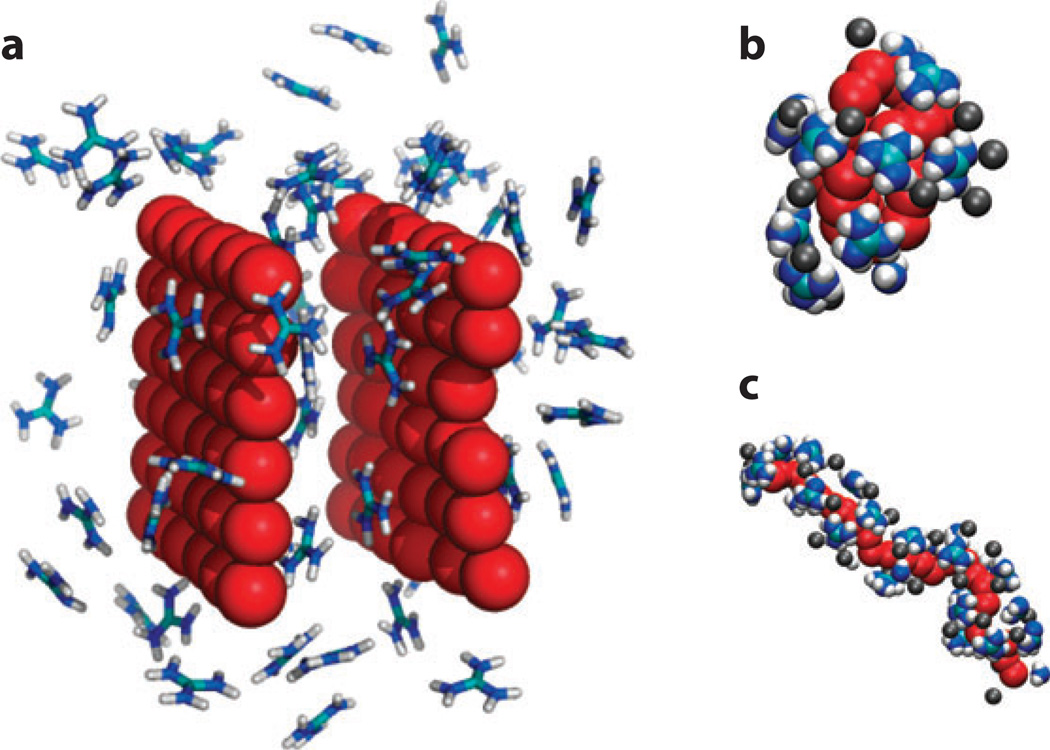
Figure 3.

Guanidinium ions exhibit a pronounced tendency in simulation to acquire a flattened conformation in proximity to hydrophobic surfaces. (a) Flat hydrophobic plates (43). (b,c) The folded and unfolded conformations of a model polymer (36). Here, nitrogens are colored in blue, chloride ions in gray, and carbon in teal. Both the plates and the polymer are built from idealized hydrophobic dummy atoms with no net charge and a weak van der Waals attraction to water. Molecular dynamics calculations in explicit solvent were carried out at 300 K and atmospheric pressure.

At this point, one may be inclined to ask what makes the real difference, dispersion interactions or modulation of the hydrophobic effect? It is arguable, however, that it is not meaningful or informative to try to distinguish between the two mechanisms, as they may be two different sides of the same coin that most of all reflects the type of analysis carried out in each study. In all cases in which stronger dispersion interactions between cosolvent and solute were observed, the interaction was averaged over the thermal ensemble of system configurations sampled during simulation. As a result, these interactions are computed for typical distributions of particles in space at thermodynamic equilibrium. If denaturant molecules can be said to be somewhat hydrophobic due to their moderate polarity, it is expected that at equilibrium they will prefer to be closer to a nonpolar surface than they would to water, or than water would to the surface. Because van der Waals interactions are attractive until hard-core repulsion takes over at extremely short ranges, the increased proximity associated with the hydrophobic effect should register as a more favorable interaction energy between denaturant and the nonpolar surface. Thus, in our view, there is no reason to try to distinguish one effect from the other; the important discovery, amply supported by the work of both camps, is that urea and GdmCl assist the aqueous solvation of nonpolar side-chain and backbone surface area exposed in unfolded conformations, thereby structurally destabilizing the native state.

What conclusions then may one draw from microscopic simulations of denaturant action? Perhaps the clearest is that the enthalpic contributions of polar interactions between cosolvent and protein do not seem strong enough to account, by themselves, for the potent effect of denaturants on protein stability. Moreover, multiple studies have demonstrated that both urea and GdmCl aid in the solvation of nonpolar surfaces, in facilitating the swelling even of polymer chains that contain no polar groups whatsoever, and in weakening dewetting phenomena that are hallmarks of the hydrophobic effect. Thus it seems plausible that the improved solvation of expanded conformations of the protein chain helps to unfold proteins in the presence of denaturants. It is less clear from simulations, however, whether the effects of urea and guanidinium on polypeptide backbone or amino acid side chains make a bigger difference to stability. In the final analysis, however, what is most important to our phenomenological understanding of the action of denaturants is that we recognize that the sum total of all their possible interactions with protein chains and water leads to an alteration of the solvation environment for both the backbone and side chain. In the following sections, we discuss how these issues can be approached from the point of view of thermodynamics and present a promising model for the impact of these altered solvation effects on folding.

TANFORD’S TRANSFER MODEL: AN EXPERIMENTAL WINDOW INTO THE CHEMICAL DENATURATION MECHANISM

Armed with an improved understanding of the impact of chemical denaturants at the microscopic level, we now are better prepared to examine the effects they have on whole proteins. Simulations indicate that both guanidinium and urea have the capacity to alter significantly the solvation physics of different parts of the protein they surround. Amino acid–transfer free energies and the so-called m-value analysis provide a well-established framework within which to examine the impact of denaturant-induced solvation effects on protein stability.

The thermodynamic description of chemical denaturation has been based traditionally on ideas that originated with the late, great protein chemist Charles Tanford. The well-known transfer model, suggested by Tanford (45, 46) almost 50 years ago, relates the free energy of unfolding at a denaturant concentration D, ΔG_N→U, to changes in solvation of amino acid residues when transferred from denaturant solution to water. The transfer model aims at quantitatively accounting for the empirical linear relation between the free energy of unfolding and D, $\mathrm{\Delta }{G}_{N\to U}\approx \mathrm{\Delta }{G}_{N\to U}^0-\mathit{\text{mD}}$. $\mathrm{\Delta }{G}_{N\to U}^0$ is the free energy of unfolding in the absence of denaturant. The slope in this relation, which is termed the m value in the folding literature, was written by Tanford in terms of δg_i, the transfer free energy of group i of the protein from water to a 1-M denaturant solution, and δα_i, the change in the (fractional) solvent-accessible surface area (SASA) of this group between the folded state and the unfolded state: m = ∑_i δα_i δg_i. The transfer model is rooted in the concept of two-state folding. The basic assumption behind it is that the folding process can be represented by two conformations, the folded conformation and the unfolded one, so that one needs to evaluate only two values for the SASA to compute ΔG_N→U. In other words, it is assumed that all δα_i values are constants, independent of denaturant concentration.

The transfer model can be used to provide an experimental route for assessing the contributions of various components of a protein to chemical denaturation. In other words, by enumerating the contribution of various amino acid side chains, as well as the protein backbone, to the overall free energy of folding in denaturant solutions, it should be possible to pinpoint the role of different types of interactions. To carry out such an exercise, one is required to have access to accurate δg_i values, i.e., transfer free energies of various protein groups. Nozaki & Tanford (47, 48) were the first to measure the δg_i’s of amino acids in urea and GdmCl solutions. More recently, Bolen and coworkers (49) remeasured δg_i values for transfer of various protein groups to urea, accompanying their measurements by a reassessment of the proper usage of activity coefficients to correct for concentration effects. A particularly meticulous work was made in the case of the backbone contribution (50), and several model compounds were used, in conjunction with careful consideration of necessary thermodynamic correction factors, to obtain an accurate estimate for the backbone transfer energy.

A second necessary ingredient for a transfer model calculation is the δα_i values for protein groups, i.e., changes in their SASA upon denaturation. But what is the conformation of the denatured state, and how does one compute SASA values of various protein groups in this conformation? Tanford originally obtained rough general estimates for exposure of different protein parts based on various experimental data, such as spectroscopic changes upon denaturation (45). Clearly, a model for the structure of the denatured state is necessary to obtain more accurate SASA values of various protein groups and use them in a realistic calculation of free energy of folding based on the transfer model. Rose and coworkers (51) developed two extreme models of the denatured state, which should provide bounds for the SASA. The upper bound was based on extended structures generated for a set of proteins, whereas the lower bound was based on chain segments excised from the same set of proteins. Schellman (52) proposed the use of an average of the two bounds as a basis for a calculation of protein stability in denaturant solutions, and that is indeed what Auton et al. (49) used in their m-value calculations. Interestingly, with these SASA values and their own δg_i values, they found that the backbone solvation by denaturants is by far the largest contributor to the m value. With this quantitative finding they were able to obtain estimates for m values of a series of proteins, which correlated rather well with the experimentally determined values (49).

The success in predicting m values seems to suggest that the Rose-Schellman model for SASA values is a reasonable description of the denatured state. In other words, it seems that denaturation of proteins can be described by assuming a single ensemble of denatured conformations, independent of the denaturant concentration. As shown below, this is unlikely to be a good representation of the denatured states of proteins. To understand why, we need to digress, and discuss first the structure of denatured proteins and their overall behavior in denaturant solutions.

THE DENATURED STATE AND THE COLLAPSE TRANSITION

Although it is now possible to determine the three-dimensional structure of a folded protein with relative ease, using either X-ray crystallography or nuclear magnetic resonance spectroscopy, there is no simple way to determine the structure of a denatured protein. The modern science of protein folding views the denatured state as an ensemble of microstates sampled rapidly by unfolded protein molecules. The denatured state of proteins has been conceived for many years as being similar to a random coil-like polymer (53), but it is now understood that unfolded protein molecules may not be entirely devoid of any internal structure. In fact, recent experiments suggest that under relatively mild denaturing conditions, proteins may possess some residual structure, including transiently formed secondary-structure elements (54). Nevertheless, the denatured state is perhaps more akin to a homopolymer than to a folded protein, both in its global properties, such as the radius of gyration (55–57), and in its dynamics (58). Thus concepts from polymer physics can be applied fruitfully to the description of many properties of denatured proteins.

As we mention above, a polymer in a good solvent (in which interactions between monomers and solvent molecules are more favorable than between monomers) adopts an expanded random coil conformation (15). The ideal, volume-free random coil obeys Gaussian statistics, which dictate that its end-to-end distance, as well as its radius of gyration, R_g, scales as N^1/2, where N is the number of monomers. However, a real polymer, whose chain segments cannot cross each other, behaves as a self-avoiding walk, with R_g ∝ N^ν, and ν = 3/5 in three-dimensional space. The N^3/5 scaling has been shown to hold for strongly denatured proteins (56).

In a poor solvent, in which monomer-monomer interactions are more favorable than those between monomers and the solvent, a polymer collapses to a compact globular structure, with R_g ∝ N^1/3. A protein is expected to fold to its native structure in a poor solvent (e.g., in water), but there is a range of solution conditions under which folded protein molecules should coexist with collapsed unfolded protein molecules (Figure 2). Methods for experimentally characterizing and measuring the equilibrium properties of the collapsed state, coexisting with the folded state, have appeared only in recent years (59–61).

In the context of this review we are interested in experiments that measure the overall size of denatured states of proteins as a function of denaturant concentration. Fluorescence resonance energy transfer (FRET) experiments, both on the ensemble level (62) and on the single-molecule level (see, e.g., 63–65; a more complete list of such experiments can be found in 61) identified denaturant-driven expansion of the denatured state under equilibrium conditions of coexistence with the native state. Such equilibrium expansion was also observed in small-angle X-ray scattering (SAXS) measurements (66, 67), and the inverse of this expansion, i.e., a collapse transition, was also found in numerous time-dependent SAXS experiments (see, e.g., 67, 68). [It should be noted that some SAXS experiments failed to observe a collapse transition, suggesting that it might not be an obligatory step in folding (69–71).] Below we focus on single-molecule fluorescence experiments, which are capable of separating the contributions of the folded and denatured states to the measured signals down to very low denaturant concentrations. In such experiments, a laser beam is focused within a dilute solution of protein molecules. Each molecule is labeled with two fluorescent probes, a donor and an acceptor. The passage of a molecule though the laser beam leads to excitation of the donor probe, which may then either emit a photon or transfer the energy to the acceptor (Figure 4a). This FRET process depends on the distance between the probes (72). Thus, by gauging the number of photons emitted from the donor and acceptor, one can infer the FRET efficiency, and from it the interprobe distance, for each protein molecule (73). Histograms then are constructed from the FRET efficiency values of hundreds or thousands of molecules (see an example in Figure 4b). For a folded protein there should be essentially a single FRET efficiency value, corresponding to the fixed interprobe distance, so only one peak appears in the FRET efficiency histogram. In a fully denatured protein, one expects a distribution of interprobe distances, which interconvert on a timescale faster than the molecular passage time. The FRET efficiency is therefore an average over the distance distribution and is still a single value, leading to a single peak in the histogram. At intermediate denaturant concentrations, under which folded and unfolded molecules coexist, two peaks show up in the FRET efficiency histogram. The surprise in virtually all single-molecule folding experiments was that the histogram peak corresponding to the denatured state not only changed its relative size with decreasing concentrations of a chemical denaturant, but also moved to higher FRET efficiency values (Figure 4b), indicating the collapse of the denatured protein molecules. Based on the continuous change of the signals, it was concluded that the collapse is a continuous, second-order transition in the thermodynamic sense, as opposed to folding, which is a two-state, first-order transition (78). Furthermore, the collapse transition seems to occur over a different range of denaturant concentrations than the folding reaction of the studied proteins. It is immediately reminiscent of the second-order coil-globule transition, already mentioned above (14, 74). This phase transition can be driven by any parameter that changes the solvent quality, including temperature (75). But is there a physical connection between collapse and folding? This is the subject of the next section.

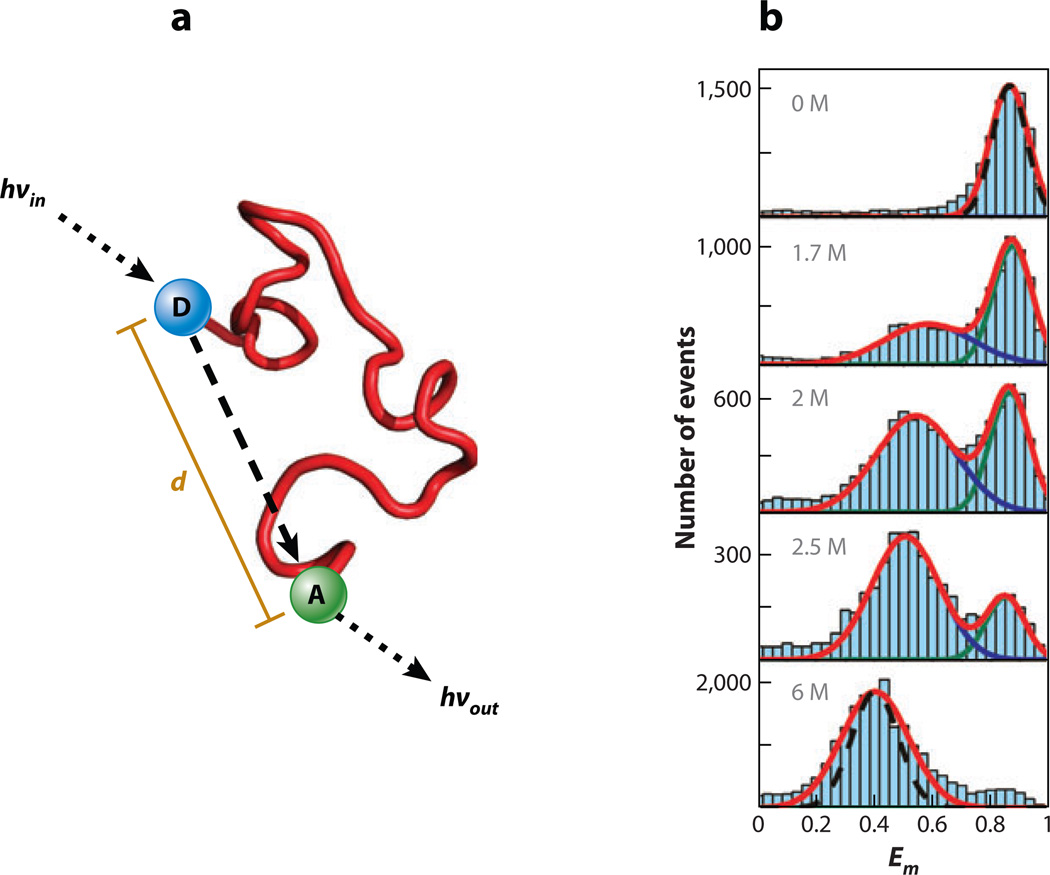
Figure 4.

(a)When two residues on a protein are fluorescently labeled, the distance d between them may be measured using fluorescence resonance energy transfer (FRET). An electronically excited donor fluorophore (D) may transfer energy to the acceptor fluorophore (A) in a process involving transition dipole–transition dipole interaction. The acceptor can then emit a photon in place of the donor. The efficiency of the process depends strongly on the interprobe distance. (b) FRET efficiency (E_m) histograms obtained from single-molecule measurements of double-labeled molecules of the cold shock protein. In the absence of denaturant, the fluorophores are close together in the folded state, but as the denaturant concentration increases, a new, lower-FRET-efficiency denatured ensemble emerges. This denatured ensemble expands as the denaturant concentration is increased, which decreases the FRET efficiency. Figure adapted with permission from Reference 80.

CALCULATING FOLDING FREE ENERGIES FROM SINGLE-MOLECULE COLLAPSE DATA

The theory of the coil-globule transition of polymers is well developed (14, 76, 77) and even has been applied to proteins in an attempt to generate a theory of the folding transition (8). It makes sense to use the coil-globule transition theory to fit single-molecule FRET data (78), and furthermore, it should be possible to use it to extract quantitative thermodynamic information from the experiments (61). A starting point for such an exercise is a model for the probability distribution function of R_g of denatured protein molecules. Following Sanchez (77), Ziv & Haran (79) used a probability distribution function that is weighted by the excess free energy per monomer with respect to the ideal chain, given by,

$$g(\varphi ,\epsilon )=-\frac{1}{2}\varphi \epsilon +k_{B}T\frac{1-\varphi }{\varphi }\text{ln}(1-\varphi ).$$ (1)

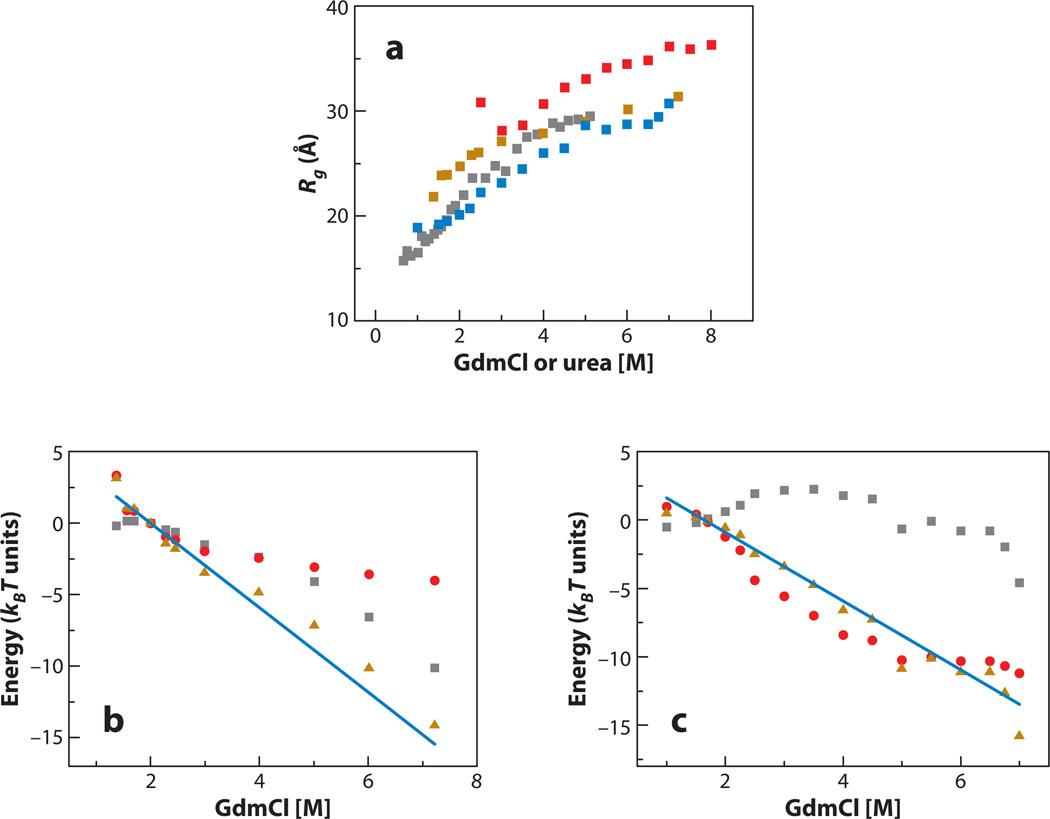
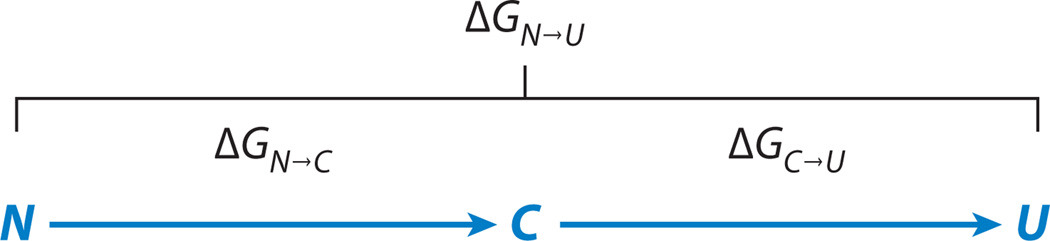
In this equation ϕ is the volume fraction occupied by the chain, which is related directly to R_g, ε is mean-field solvation energy of a monomer, T is the temperature, and k_B is Boltzmann’s constant. Inter-residue interactions can be of varied origins (e.g., hydrophobic, electrostatic, or backbone-mediated), and in principle ε includes all these in an average way. The first term in Equation 1 is the enthalpic contribution due to either attraction (ε > 0) or repulsion (ε < 0) between monomers, favoring chain collapse or expansion, respectively. The second term is the entropy arising from excluded volume interactions, which favors expansion. Using the weighted probability distribution function and experimental FRET efficiency values obtained over a range of denaturant concentrations, Ziv & Haran (79) evaluated ε from 12 data sets measured on five different proteins (64, 65, 78, 80–82). With values of ε in hand, they calculated different functions of the denatured state of each protein, including R_g and ΔG_C→U, which is the difference free energy for the transition from a putative maximally collapsed state, C (with a constant volume fraction of 1), to the unfolded state, U, as a function of denaturant concentration. Figure 5a shows the values of R_g for several proteins, indicating a clear expansion in all of them. The expansion difference free energy, ΔG_C→U, turned out to be essentially a linear function of denaturant concentrations for all proteins. Figure 5b,c shows two examples, including also decomposition of ΔG_C→U into enthalpic and entropic contributions. Importantly, the slope of the ΔG_C→U function for each protein was found to be essentially equal to the slope of the ΔG_N→U function, which is its m value (79). To understand the implication of this finding, it is useful to look at Scheme 1.

Figure 5.

Properties of denatured proteins as a function of denaturant concentration, calculated from the coil-globule transition theory (79). (a) The radius of gyration of the cold shock protein (gold, based on data from 80), protein L (blue, based on data from 78), immunity protein 9 (red, based on data from 65) and barstar (gray, based on data from 82). (b) Expansion difference free energy, ΔG_C→U, of denatured cold shock protein (gold triangles) compared with its m value (blue line). Also shown are the expansion enthalpy (gray squares) and conformational entropy (red circles). (c) Expansion difference free energy, ΔG_C→U, of denatured protein L (gold triangles) compared with its m value (blue line). Also shown are the expansion enthalpy (gray squares) and conformational entropy (red circles). Clearly, conformational entropy contributes significantly to the expansion free energy and hence also to the free energy of unfolding. GdmCl, guanidinium chloride.

Scheme 1.

In Scheme 1, the free energy of unfolding, ΔG_N→U, is decomposed into two parts, the first (ΔG_N→C) due to the transition from N to C and the second (ΔG_C→U) due to the expansion from C to U. The near-equality of the slopes of ΔG_N→U and ΔG_C→U as a function of denaturant concentration implies that the effect of denaturants on folding is mediated through the transition from coil to globule (C to U), and there is only a small effect, if any, on the transition from the folded state to the fully compact state (N to C). This finding establishes an intimate connection between denaturation and the coil-globule transition: As the protein chain expands, the denatured state is gradually stabilized, and therefore the propensity for unfolding in high denaturant concentration is increased. A corollary of this statement is that conformational entropy has a large contribution to the free energy of folding, as chain expansion by necessity involves a large entropic change (see Figure 5b,c).

Clearly, the classical transfer model cannot be correct in its standard implementation, which assumes a single configuration for the denatured state, independent of denaturant concentration, from which a single set of denatured-state SASA values is derived. Rather, the current picture suggests that the configuration of the denatured chain depends on denaturant concentration, and so do denatured-state SASA values! So how have Auton et al. (49) succeeded so well in predicting m values, as described above in the section Tanford’s Transfer Model? This is an interesting conundrum, for which, unfortunately, we cannot offer a solution here.

One way to rescue the transfer model, so that it correctly takes into account conformational propensities under different solution conditions, is by coupling it to MD simulations. O’Brien et al. (83) performed coarse-grained MD simulations of denatured proteins in the absence of denaturant and then used values of the free energy of transfer to denaturant solution, calculated separately for each conformation in the denatured-state ensemble, as weights to bias the conformational distribution. They found that this method allows for accurate simulation of the effects of denaturants and osmolytes on the free energy of folding. The next logical step is, obviously, to conduct full MD simulations in the presence of solvent and denaturant molecules, from which various components of the free energies of collapse and of folding are calculated. However, the need to obtain thermodynamically converged properties from such simulations limits them at this point in time to the smallest of proteins, such as the Trp-cage miniprotein studied by Canchi et al. (35). A computation of this type is in principle one way to make connections between the microscopic picture of denaturation discussed above and the more coarse-grained picture discussed in the current section, which emphasizes effects on overall chain dimensions, by comparing simulated and experimentally measured results. Another way to connect the two pictures would be to derive values for ε, the mean-field monomer solvation energy, from microscopic simulations and use these to fit experimental measurement of the coil-globule transition.

CONCLUSIONS

Chemical denaturants have served for many years as an effective means to disrupt protein structure to study subsequently the reverse process of folding. It is hardly surprising then that elucidation of the microscopic mechanisms of action of these molecules has been an aim of the protein folding community for many years. Yet, ironically, as work discussed in this review suggests, chemical denaturation is likely to involve a somewhat different set of interactions than those responsible for the formation of the folded states of proteins.

The stabilization of a particular folded state corresponding to a particular amino acid sequence is driven by specific interactions within the protein chain, which may depend on the detailed arrangement of hydrophobic side chains within the protein globule, as well as on the formation of hydrogen bonds, salt bridges, etc. In contrast, a largely nonspecific set of interactions appears to be responsible for the fact that, in aqueous solution, proteins collapse into the globular state that is so often a necessary precondition for folding. The collapse transition is driven not only by the hydrophobic side chains of the polypeptide, but also by the relatively nonpolar protein backbone. Indeed, this review demonstrates that both experimental and theoretical work points to the importance of the backbone in generating relatively compact conformational preferences for proteins in water.

The action of chemical denaturants is related to this nonspecific process. In fact, denaturants induce a dramatic transformation of the unfolded state, driving it from a globular to a coiled state. A more concentrated denaturant solution is a better solvent for expanded, coil-like conformations of the protein chain, and denaturants therefore act principally by making expanded, unfolded configurations more favorable than they are under native conditions.

Although it is possible that chemical denaturants, through their weakening of the hydrophobic effect, also could affect the interactions that contribute to the equilibrium between folded and unfolded conformations within the collapsed globular phase, they would still be powerful destabilizers of protein structure if they acted exclusively on the collapse transition, in which the lion’s share of their effect is felt. This realization still leaves room for many new and interesting lessons to be learned about folding from the point of view of the theory of solutions and solvation. Recent studies have started down this avenue of research, attempting to understand the microscopics of the effect induced by these weakly interacting molecules on solvent and solute alike (25, 84, 85). Many questions remain open. What makes urea and GdmCl different from other osmolytes that actually stabilize folded proteins? Do the latter work in a similar fashion, inducing the reverse of the coil-globule transition? These, and additional questions, are likely to be answered in coming years by computer simulations, which become ever more sophisticated, and by experimental work, using new methods, from single-molecule fluorescence to multidimensional femtosecond spectroscopy.

THE HYDROPHOBIC EFFECT.

The hydrophobic effect is an effective force that acts to minimize the amount of surface area that nonpolar molecules expose to their aqueous solvent. The effect derives from the strongly favorable hydrogen-bonding interactions between water molecules that are disrupted by the insertion of a nonpolar solute into the solution. The free energetic cost of solvating a nonpolar molecule is driven by the increased enthalpy associated with hydrogen-bond breakage or by the decreased entropy of the hydrogen-bond network as it cages around the offending solute. This free energy cost can be lessened by burial of nonpolar surface area. The drive to reduce exposed hydrophobic surface area is important both to the collapse of the polypeptide chain into a dense globule and to the selection of a particular tertiary structure that most effectively buries hydrophobic side chains in the globular core. The exact dependency of the free energy of solvation on exposed surface area, however, depends on the size of the solute. Small solutes can be accommodated without hydrogen-bond breakage through the ordering of the bond network in the surrounding water molecules. On this scale, the free energetic cost tends to scale with the volume of the solute. For larger solutes, however, the breakage of hydrogen bonds at the surface of the solute is unavoidable, the cost scales with the area exposed to the solvent, and the scaling parameter is known as the surface tension (37).

SUMMARY POINTS.

1. Many decades after the discovery that urea and GdmCl denature proteins, the microscopic mechanisms behind this denaturation reaction remain quite elusive.

2. Urea and GdmCl are weakly interacting molecules, and molar concentrations are required to induce denaturation. Classical models posit that chemical denaturants operate either by binding directly to the protein or by modifying the properties of the water solution.

3. Tanford’s transfer model attributes the linear free energy relation characterizing chemical denaturation to changes in the solvation of amino acid residues when transferred from denaturant solution to water. It has been suggested that the protein backbone is the main contributor to the transfer free energy.

4. MD simulations suggest that denaturants act mainly through dispersion interactions. Guanidinium in particular tends to interact with hydrophobic regions of a protein through its flat, nonpolar surface, while exposing its polar/charged edges to the solvent. Urea, in contrast, exhibits a moderate tendency to aggregate, which may help it to solvate exposed protein backbone.

5. Single-molecule fluorescence studies show that the denatured state of many proteins expands as the denaturant concentration is increased. Analysis of this coil-globule transition suggests that the accompanying thermodynamic stabilization of the denatured chain is the main cause of denaturation.

6. The picture arising from simulation and experiment alike is that chemical denaturation involves the stabilization of denatured, more expanded conformations of proteins by facilitation of solvation of their nonpolar surfaces, including the backbone.

FUTURE ISSUES.

1. Although the coil-globule transition now has been observed in many proteins, there are some examples, mainly from SAXS experiments, in which the protein seems to be expanded even at low denaturant concentrations. It remains to be found what causes such a difference in the behavior of these proteins.

2. Virtually nothing is known about the dynamics of the interaction of chemical denaturants with proteins. Novel spectroscopic methods, such as multidimensional infrared spectroscopy, might shed light on this issue. Such experiments might help validate the results from MD simulations.

3. There is also a need for experiments that will probe directly the kinetics of the collapse transition induced by the removal of denaturants. This transition occurs on timescales that are fast enough to elude current experiments.

Glossary

Osmolyte

small organic cosolvent molecule, such as urea, that can affect protein stability, when added to water

GdmCl

guanidinium chloride

MD

molecular dynamics

Coil-globule transition

the thermodynamic second-order phase transition of a polymer when transferred from a good to a poor solvent

Transfer model

a thermodynamic model due to Charles Tanford, which explains chemical denaturation through the free energy of transfer of amino acids from water to a denaturant solution, as well as the change in solvent-accessible surface area of each protein residue upon denaturation

SASA

solvent-accessible surface area

Fluorescence (or Förster) resonance energy transfer (FRET)

when a fluorophore is excited while in close physical proximity to another fluorophore of lower excitation frequency, the excitation can be transferred from the first (donor) fluorophore to the second (acceptor) fluorophore in a distance-dependent nonradiative fashion

Solvent quality

a quantity that describes the interaction of a solvent with the residues of a polymer; in a good solvent the interaction is attractive, and the polymer is a random coil; in a poor solvent the interaction is repulsive, and the polymer is collapsed and globular