Acoustic Analysis of Aperiodic Voice: Perturbation and Nonlinear Dynamic Properties in Esophageal Phonation

Abstract

Objectives/Hypothesis

Esophageal voice is a method of communication after total laryngectomy. Previous research suggests that perturbation analysis may inaccurately measure aperiodic voices and that nonlinear dynamic methods may be more appropriate for analyzing signals of this type. Therefore, we hypothesized that nonlinear dynamic analysis would be more capable than perturbation parameters for reliable measurement of the aperiodic esophageal voice.

Study Design

Acoustic comparison of esophageal and normal voice cohorts using nonlinear dynamic and perturbation measures.

Methods

Twenty subjects in two age-matched groups participated in the study. Jitter, shimmer, signal-to-noise ratio, correlation dimension, and second-order entropy were measured from audio recordings of subjects’ voices.

Results

Jitter and shimmer values were significantly higher for esophageal voices and signal-to-noise ratio values were significantly lower for esophageal voices than for normal voices. Error count values, which indicate perturbation analysis reliability, were 0 in normal voices and significantly higher in esophageal voices. Error was attributable to signal aperiodicity and demonstrated that perturbation analysis yielded questionable results for esophageal voice. However, nonlinear dynamics measures analyzed both cohorts reliably and indicated that esophageal voice was significantly more chaotic than normal voice.

Conclusions

The results demonstrated the capability of nonlinear dynamic methods to reliably quantify both aperiodic and periodic signals and to differentiate normal from esophageal voices. It is suggested that nonlinear dynamic analysis be used preferentially for acoustic characterization of aperiodic voices such as esophageal voice. Future research should focus on clarification of perturbation analysis reliability and further application of nonlinear dynamic measures to aperiodic voices.

INTRODUCTION

Total laryngectomy is the removal of the entire larynx, including the thyroid and cricoid cartilages, the upper tracheal rings, and the hyoid bone.¹ This total excision of laryngeal tissue drastically affects both respiration and phonation in the patient and typically requires rehabilitative training. One method of voice rehabilitation and production after total laryngectomy is the use of esophageal voice. Though usage of electrolarynx and other speech aids is dominant in the United States, esophageal voice remains a significant laryngectomee voice production method in some Asian countries, such as Japan and China. Esophageal voice is generated using the esophagus as an air supply and the pharyngoesophageal segment, located on the superior aspect of the esophagus, as a vibration source.² Air is deposited in the esophagus, and its controlled release leads to segment vibration and sound production.³ Speech is produced by moving the articulators to mouth words in the normal manner.⁴

The esophageal voice demonstrates perceptual qualities of harshness, hoarseness, gurgling, short phonation duration and low pitch and volume,³ all of which are indicators of aperiodicity in voice. Perturbation analysis of this perceptual abnormality has been accomplished, with results confirming the severe irregularity of esophageal voices. Signal-to-noise ratio, fundamental frequency, and intensity values were found to be lower and jitter and shimmer values were found to be higher in esophageal speech than in laryngeal speech.^2–3,5 However, recent research suggests that the validity of perturbation analysis is highly questionable when these measures are applied to aperiodic signals.^6–7

In contrast, nonlinear dynamic methods of acoustic analysis have shown potential to reliably quantify both periodic and aperiodic signals. The concept of human voice production as a chaotic system has been established in recent years through computer modeling, excised larynx experiments, and human voice analysis.^8–12 A chaotic voice often exhibits an irregular and aperiodic waveform, poor perceptual qualities, and extreme perturbation values. Because all human vocal folds exhibit some inherent chaotic properties, nonlinear dynamic methods are useful for quantifying the degree of aperiodicity and irregularity.

Previously, nonlinear dynamic analysis had not been applied to esophageal voices. Nor had the effectiveness of nonlinear dynamic analysis and perturbation analysis when quantifying the highly aperiodic esophageal voice been addressed. In this study, alaryngeal esophageal voice was compared to normal voice using perturbation and nonlinear dynamic analyses. It was hypothesized that nonlinear dynamic parameters would measure the highly aperiodic signals of esophageal voice more capably than perturbation measures, while still effectively distinguishing between esophageal and normal voice.

METHODS

Subjects

The Institutional Review Board at Shanghai EENT Hospital approved the protocol and consent procedure used in this study. Ten male speakers with esophageal voices participated in the study. All esophageal voice subjects were native speakers of Mandarin Chinese ranging in age from 50 to 65 years old (mean = 55.4). Esophageal speakers underwent total laryngectomy for cancer of the larynx and received esophageal voice training to improve post-surgical vocal quality. In addition to the esophageal speakers, ten age-matched male Mandarin Chinese speakers (age range = 42–60, mean age = 50.7) with normal voices were included for comparison. The normal voice subjects were healthy volunteers with no current or past evidence of voice disorders and normal larynges, as determined by clinical examination performed by an otolaryngologist.

Recording Procedure

Audio recordings of the ten laryngectomized patients’ voices were collected at an average of 5.78 months after commencement of esophageal voice training (st. dev. = 4.27). At each recording session, both normal and esophageal speakers were instructed to sustain phonations of /a/ at a comfortable pitch and volume for as long as possible. Recordings were made in a soundproof room with the recording microphone (AKG Acoustics, Vienna, Austria) positioned 10 cm from the subject’s mouth. Audio files were recorded at a sampling rate of f_s = 44.1 kHz using the Multi-Dimensional Voice Program, Model 3650 (Kay Elemetrics Corp., Lincoln Park, NJ). A middle stationary segment x(t_i), t_i = iΔt, Δt=1/f_s, i =1,2,· · ·, with a length of 1 second was selected for analysis from each subject’s recording. Voice onset and offset were excluded to avoid effects of speech intonation or interactions between the larynx and vocal tract on analyses. Perturbation and nonlinear dynamic measures were then applied to these normal and esophageal voices.

Perturbation Analysis

Perturbation analysis was conducted on the voice segments with CSpeech software, version 4.0 (Milenkovic and Read, Madison, WI). Two common measures of perturbation are jitter and shimmer. Jitter measures the cycle-to-cycle frequency variation of a voice signal, while shimmer measures the cycle-to-cycle amplitude variation. Signal-to-noise ratio (SNR), measured in decibels, reflects the dominance of the harmonic signal over aperiodic noise. Percent jitter, percent shimmer, and SNR values were obtained for each voice segment using CSpeech.

Reliability of perturbation measurements was determined by using error in perturbation measurement (err), a parameter calculated by the CSpeech program. Err counts “the number of times the analysis algorithm failed to compute a pitch period consistent with the peak of the autocorrelation function.”¹³ The autocorrelation function is used to calculate percent jitter, percent shimmer, and SNR values in CSpeech;¹⁴ therefore, err describes the validity of all three measures. Algorithm failure can be attributed to inaccurate pitch estimation or a failed attempt to analyze a highly aperiodic waveform.¹³ In comparing the error count of signals, Karnell et al. found that signals with err > 0 produced significantly higher perturbation values and were more aperiodic than signals with err = 0.¹⁵ An error count of 0 indicates that the analysis algorithm did not fail to compute pitch period intervals, meaning that error was sufficiently low and the signal was analyzed reliably via perturbation methods. Although minor algorithm failure corresponding to err = 0 is considered acceptable, err > 10 indicates loss of pitch track¹³ and indicates the unreliability of perturbation results.

Nonlinear Dynamic Analysis

Detailed descriptions of nonlinear dynamic analysis methods such as phase space reconstruction, correlation dimension, and second-order entropy to human voice production are widely found in the literature.^{8–12,19–22} These types of measures have complemented traditional perturbation measurements due to an ability to describe chaotic, aperiodic voices.^8–9,11

A reconstructed phase space can be created by plotting a voice signal against itself at some time delay. The reconstructed phase space qualitatively shows the dynamic behavior of a signal, as a periodic signal produces a closed trajectory while an aperiodic signal appears irregular.¹⁶ Correlation dimension D₂ specifies the number of degrees of freedom needed to describe a system; a more complex system has a higher dimension, which means that more degrees of freedom are needed to describe its dynamic state.¹⁷ The correlation dimension quantifies the irregularity of the reconstructed phase space: D₂ = 0 corresponds to a static state; D₂ = 1 corresponds to a periodic oscillation; D₂ = 2 describes a quasi-periodic tori (superposition of two or more oscillations with no rational fundamental frequencies or biphonation), and fractal D₂ describes an aperiodic or chaotic oscillation. Kolmogorov entropy quantifies the rate of loss of information about the state of a dynamic system as it evolves.¹⁸ Second-order entropy (K₂) indicates the rate of loss of information about the state of a dynamic system over time. For periodic behavior, this entropy is equal to zero. A chaotic system with a finite degree of freedom has a finite K₂ value, while the K₂ value of true random behavior approaches infinity.¹⁸

In this study, correlation dimension and second-order entropy calculations were performed using Nonlinear Dynamic Analysis software developed by the Laryngeal Physiology Laboratory at the University of Wisconsin. Calculations made by the software were based on the numerical algorithms described for studies analyzing excised larynx phonations⁸ and pathological human voices.^11,21–22 Briefly, an m-dimensional delay-coordinate phase space X_i = {x(t_i), x(t_i − τ), · · ·, x(t_i − (m − 1)τ)} was reconstructed using the time delay technique,¹⁶ where m is the embedding dimension and τ is the time delay. m was determined according to the embedding theorem²³: when m > 2D+1 (D is the Hausdorff dimension), the reconstructed phase space is topologically equivalent to the original phase space. The proper time delay τ was estimated using the mutual information method proposed by Fraser & Swinney.²⁴ The improved algorithm proposed by Theiler²⁵ was used to calculate the correlation integral C(r), where r is the radius around X_i. Correlation integral C(r) measures the number of distances between points in the reconstructed phase space that are smaller than the radius r. C(r) has a power law behavior C(r) ∞ r^D₂e^−mτK₂, which reveals the geometrical scaling property of the attractor.¹⁸ Based on C(r), D₂ and K₂ were estimated in the scaling region of the radius r with the increase of the embedding dimension m. For sufficiently large m, the correlation dimension and its standard deviation were derived using a curve fit to the curve of log₂ C(r) versus log₂ r in the scaling region.

The reliability of nonlinear dynamic analysis calculations was determined for each voice signal using the standard deviations of the estimated D₂ and K₂ values (hereafter referred to as SDD₂ and SDK₂, respectively). For reliable estimation of dimension and entropy in a particular signal, SDD₂ and SDK₂ values should be less than 5%. SDD₂ and SDK₂ values greater than 5% indicate that the nonlinear dynamic analysis program was unable to reliably calculate D₂ and K₂ values for a signal.

Statistical Analysis

SigmaPlot 8.0 and SigmaStat 3.0 software (Jandel Scientific, San Rafael, CA) were used to statistically analyze and graph acoustic analysis data of esophageal and normal voices. Nonparametric Mann-Whitney rank sum tests were employed to compare acoustic parameters of esophageal voice with acoustic parameters of normal voice. Statistical significance was set at the 0.05 level for all tests.

RESULTS

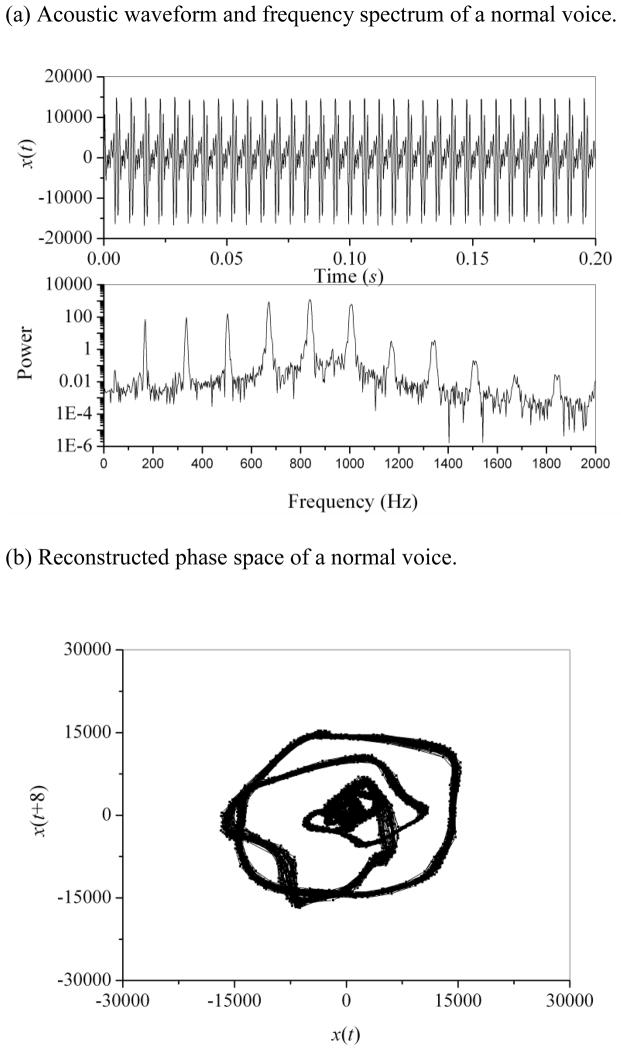
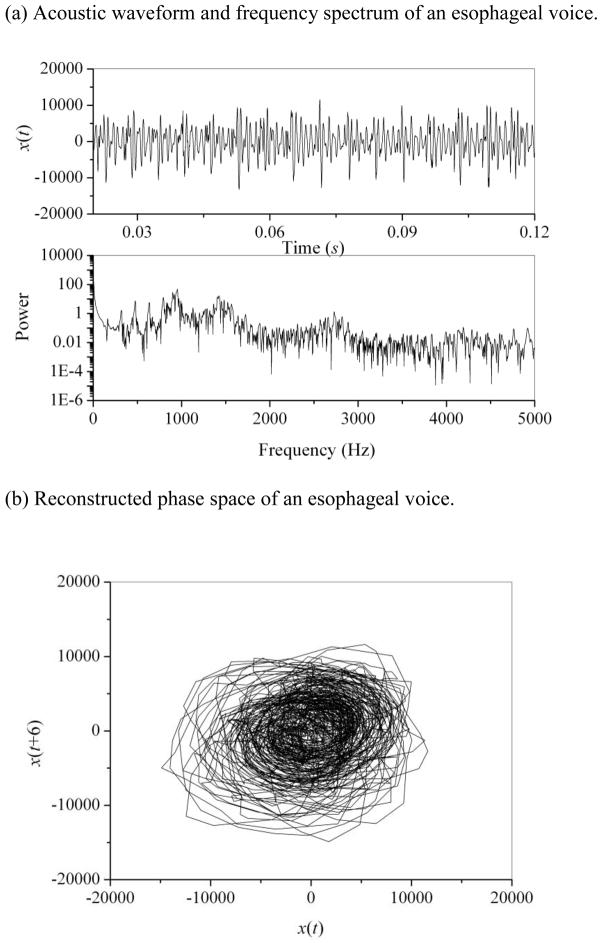
The typical results of acoustic analyses for a normal voice and an esophageal voice are given in Figs. 1 and 2, respectively. The normal voice produces a periodic waveform and a discrete frequency spectrum (Fig. 1(a)). Because err is zero, jitter (0.14%), shimmer (1.1%), and SNR (26.7 dB) can be reliably calculated for the normal voice. The reconstructed phase space in Fig. 1(b) shows a regular structure, where the proper time delay was estimated as 8Δt using the mutual information method. The correlation dimension and second-order entropy of the normal voice were calculated as 1.14 (SDD₂ = 1%) and 0.096 (SDK₂ = 0.1%), respectively. In comparison with the normal voice, the esophageal voice produces an aperiodic waveform and a broadband spectrum, as shown in Fig. 2(a). Pitch extraction is difficult for this aperiodic esophageal voice; therefore, the err parameter is 75 and the jitter (3.65%) and shimmer (47.26%) values are abnormally high, with SNR at 2.9 dB. Thus, for the aperiodic esophageal voice, jitter, shimmer, and SNR should be applied with caution, and nonlinear dynamic analysis should be complementarily applied. Irregular phase space of x(t) versus x(t+6) is shown in Fig. 2(b). The correlation dimension and second-order entropy of this esophageal voice were calculated as 4.41 (SDD₂ = 3%) and 0.403 (SDK₂ = 0.1%), respectively. It appears that the esophageal voice shows higher dimension and entropy values than the normal voice, with low SDD₂ and SDK₂ values indicating reliability of measurement. To confirm these findings, comparisons among all normal and esophageal voices were made.

Figure 1.

(a) Acoustic waveform and frequency spectrum of a normal voice.

(b) Reconstructed phase space of a normal voice.

Figure 2.

(a) Acoustic waveform and frequency spectrum of an esophageal voice.

(b) Reconstructed phase space of an esophageal voice.

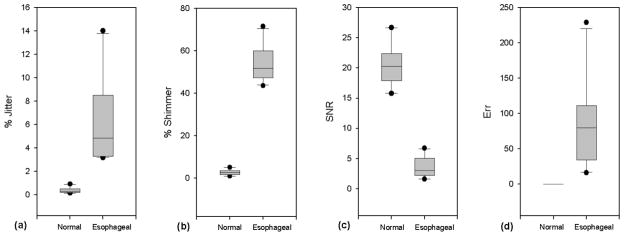
Results of perturbation analysis of normal and esophageal voices are summarized in Table 1. Mean jitter and shimmer values for esophageal voice were 6.374% and 53.61%, respectively, and mean SNR was low at 3.55 dB. Err values for esophageal voice were high and extremely variable (mean = 86.8, st. dev. = 62.939), as shown in Fig. 3(d), and all err values for esophageal voice were greater than the acceptable value of 10.¹³ Because err indicates reliability of results, values of jitter, shimmer, and SNR calculated for esophageal voices were considered to be highly questionable. In contrast, mean jitter and shimmer measures in normal voice were 0.447% and 3.075%, respectively, as shown in Figs. 3(a) and 3(b). Mean SNR was higher in normal voice (20.08 dB) than in esophageal voice, as shown in Fig. 3(c). Error count for perturbation analysis of all normal voices was 0 (Fig. 3(d)), indicating that perturbation measures were reliably calculated for these nearly periodic signals. Nonparametric Mann-Whitney rank sum tests on perturbation data indicated significant differences between normal and esophageal voice for all measures (p < 0.001). However, given the highly questionable reliability of these measures for analysis of the aperiodic esophageal voice, results could not be interpreted as accurate quantification of esophageal voices.

Table 1.

Perturbation analysis: jitter, shimmer, signal-to-noise ratio (SNR), error (Err), and Mann-Whitney rank sum test results

	Normal voice	Esophageal voice	Rank sum test results
% Jitter	M = 0.447 SD = 0.278	M = 6.374 SD = 3.83	T = 55 p < 0.001*
% Shimmer	M = 3.075 SD = 1.525	M = 53.61 SD = 8.32	T = 55 p < 0.001*
SNR (dB)	M = 20.08 SD = 3.939	M = 3.55 SD = 1.65	T = 155 p < 0.001*
Err	M = 0 SD = 0	M = 86.8 SD = 62.939	T = 55 p < 0.001*

M = mean, SD= standard deviation

^*Statistically significant at the p = 0.05 level

Figure 3.

Distributions of perturbation analysis in normal and esophageal voice signals. (a) Percent jitter; (b) Percent shimmer; (c) Signal-to-noise ratio (SNR); (d) Error count (err).

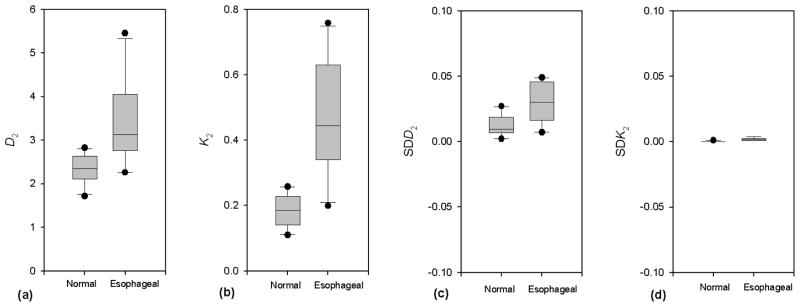
Table 2 summarizes results of nonlinear dynamic analysis. Mean correlation dimension was lower for normal voice (D₂ = 2.349) and higher for esophageal voice (D₂ = 3.401), as shown in Fig. 4(a). SDD₂, an indication of the stability and reliability of the calculated measure, was low for both esophageal and normal voices (mean values of 2.99% and 1.23%, respectively), as shown in Fig. 4(c). Mean second-order entropy was higher for esophageal voice (K₂ = 0.472) than for normal voice (K₂ = 0.185), as shown in Fig. 4(b). SDK₂ was low for esophageal and normal voices (mean values of 0.2% and 0.01%, respectively), indicating the reliability of second-order entropy calculations. Mann-Whitney rank sum tests proved the differences in D₂ and K₂ between voice types to be statistically significant (D₂: p = 0.003; K₂: p < 0.001), indicating that esophageal voices exhibited greater chaos than normal voices.

Table 2.

Nonlinear dynamic analysis: correlation dimension (D₂), second-order entropy (K₂), D₂ and K₂ standard deviation (SDD₂ and SDK₂), and Mann-Whitney rank sum test results

	Normal voice	Esophageal voice	Rank sum test results
D2	M = 2.349 SD = 0.343	M = 3.401 SD = 0.972	T = 65 p = 0.003*
K2	M = 0.185 SD = 0.047	M = 0.472 SD = 0.178	T = 58 p < 0.001*
SDD2	M = 0.0123*	M = 0.0299*
SDK2	M = 0.0001*	M = 0.002*

M = mean, SD = standard deviation

^*Statistically significant at the p = 0.05 level

Figure 4.

Distributions of perturbation analysis in normal and esophageal voice signals. (a) Correlation dimension (D₂); (b) Second-order entropy (K₂); (c) Standard deviation of D₂ (SDD₂) (d) Standard deviation of K₂ (SDK₂).

DISCUSSION

Upon viewing typical waveforms (Figs. 1(a) and 2(a)), it is qualitatively apparent that the esophageal voice signal is far more aperiodic than the normal voice signal. This difference is largely due to the physiological limits of esophageal voice production; the pharyngoesophageal segment, unlike the natural vocal folds, has a large mass and is not specialized for vibration. This results in imprecise and slow pharyngoesophageal segment movement² and causes significant acoustic differences from normal vocal fold vibration. The aperiodicity present in esophageal voice and other pathological voice has been measured via perturbation analysis methods. Using several parameters, studies have found esophageal voice to have characteristics indicative of significantly poorer quality than alternative forms of alaryngeal speech and normal speech.^2–3,5 However, studies using perturbation measures for analysis of extremely aperiodic voices such as esophageal voice seldom quantify the reliability of results.

It has been determined that values of percent jitter and shimmer are incapable of reliably evaluating aperiodic voice samples. As a practical guideline, it was established that signals demonstrating greater than 5% jitter or shimmer levels produce invalid perturbation values due to aperiodicity.^6,13 An additional measure of perturbation analysis reliability is the error count quantified by the CSpeech program, an indicator of either inaccurate pitch estimation or highly aperiodic signal waveform.¹³ All esophageal voice samples exhibited err values greater than 10, the set limit for acceptable error,¹³ as shown in Fig. 3(d). Conversely, all normal voice samples exhibited err values of 0, indicating low error in analysis. Therefore, CSpeech err measurements further support the assertion that perturbation analysis must be applied with caution to aperiodic signals such as esophageal voice. This comparison of normal to esophageal voice provides evidence that while normal voice can be reliably measured, traditional measures of jitter, shimmer, and SNR are insufficiently reliable to quantify the aperiodicity present in esophageal voice. Although perturbation measures were able to significantly differentiate between normal and esophageal voice, this finding is of questionable importance if it is determined that the aperiodic esophageal signal is unreliably calculated.

Although nonlinear dynamic parameters have been applied to distinguish normal voice from types of pathological voice,^11–12 the efficacy of nonlinear dynamic measures in measuring esophageal voice and distinguishing this aperiodic signal from normal voice has not been previously analyzed. Esophageal voice was significantly differentiated from normal voice in the present study using measures of correlation dimension and second-order entropy. These nonlinear dynamic measures defined esophageal voice as significantly more chaotic than normal laryngeal voice. The finite dimension values of esophageal voices in Fig. 4(a) suggest finite degrees of freedom might be needed to model the dynamics of esophageal voices. Importantly, significantly low SDD₂ and SDK₂ values indicate the reliability of nonlinear dynamic measures in quantifying both normal and aperiodic esophageal voices.

It is likely that nonlinear dynamic parameters such as correlation dimension and second-order entropy are more effective for analysis of aperiodic voice signals because these measurements are not dependent on the temporal domain. For perturbation measures, analysis programs must be able to define regular voice pitch periods in time in order to calculate cycle-to-cycle variations such as jitter and shimmer.¹¹ Since this is difficult or impossible for signals exhibiting extreme irregularity, such as esophageal voice, perturbation measures are unable to dependably characterize the entire signal. However, correlation dimension and second-order entropy do not require cycles to be marked; instead, the measures describe the geometric scaling property of a signal in phase space.¹¹ This makes it possible for nonlinear dynamic parameters such as these to quantify even severely aperiodic voice.

It is necessary to establish the capabilities of acoustic analysis methods in order to improve understanding of the qualities of pathological voice. This study has determined that the aperiodicity present in esophageal voice is considerable and produces highly questionable, possibly invalid perturbation analysis results. Conversely, the quantification of chaos in audio signals via correlation dimension and second-order entropy analysis provides a valuable measure of the irregularity of esophageal voice and should be applied clinically for reliable acoustic analysis of esophageal and other similar highly aperiodic vocal signals.

CONCLUSIONS

In this paper, we have applied acoustic measures of nonlinear dynamics and perturbation to the aperiodic esophageal signal and to normal voice. Although perturbation measures of jitter, shimmer, and SNR significantly differentiated between esophageal and normal voice, error count demonstrated the insufficient reliability of these measures in quantifying the aperiodic esophageal voice signal. Nonlinear dynamic measures of correlation dimension and second-order entropy also significantly differentiated between esophageal and normal voices. However, as evidenced by SDD₂ and SDK₂ results, these measures were able to reliably quantify the aperiodic esophageal signal. Future research should focus on additional clarification of the limits of commonly used perturbation analyses for measurement of aperiodic voice, taking into account internal reliability measures such as the err measurement of CSpeech. Furthermore, research should focus on clinical application of nonlinear dynamic analysis as a valuable, reliable tool for measurement of extremely aperiodic voice such as esophageal voice.