Biodiversity among Lactobacillus helveticus Strains Isolated from Different Natural Whey Starter Cultures as Revealed by Classification Trees

Abstract

Lactobacillus helveticus is a homofermentative thermophilic lactic acid bacterium used extensively for manufacturing Swiss type and aged Italian cheese. In this study, the phenotypic and genotypic diversity of strains isolated from different natural dairy starter cultures used for Grana Padano, Parmigiano Reggiano, and Provolone cheeses was investigated by a classification tree technique. A data set was used that consists of 119 L. helveticus strains, each of which was studied for its physiological characters, as well as surface protein profiles and hybridization with a species-specific DNA probe. The methodology employed in this work allowed the strains to be grouped into terminal nodes without difficult and subjective interpretation. In particular, good discrimination was obtained between L. helveticus strains isolated, respectively, from Grana Padano and from Provolone natural whey starter cultures. The method used in this work allowed identification of the main characteristics that permit discrimination of biotypes. In order to understand what kind of genes could code for phenotypes of technological relevance, evidence that specific DNA sequences are present only in particular biotypes may be of great interest.

Lactobacillus helveticus is a homofermentative thermophilic lactic acid bacterium largely present in the natural starters used in the production of aged Italian cheeses, such as Grana Padano, Parmigiano Reggiano, and Provolone, which are cheeses produced in geographically contiguous areas of Northern Italy. Parmigiano Reggiano and Grana Padano are aged cooked cheeses with similar organoleptic characteristics (1). They mainly differ in the scale of dairies and, consequently, in the standardization of the phases of cheesemaking. Provolone is an aged pasta filata cheese (11). All of these typical Italian cheeses are obtained by using natural whey starter cultures in which L. helveticus is the predominant species (21, 31). These particular mixed lactic acid bacteria cultures are produced by culturing the sweet whey resulting from everyday cheesemaking. Whey is fermented at a naturally decreasing temperature, decreasing in approximately 20 h from about 54°C to about 35°C, and a thermophilic selection is performed. Whey starter is added to the vat milk, and sweet whey is recovered after curd cooking at each cheese production. The dominant community of L. helveticus in natural whey starters is composed of different biotypes (3, 6-8, 14-16, 23, 24). Large differences in the expression of several technological characteristics were found among L. helveticus strains isolated from natural dairy starter cultures (3, 8, 25, 34).

Previous works have shown that these strains can be grouped in relation to their phenotypic (10, 18) and genotypic (12, 18) characteristics. The reasons of these differences have not been elucidated, even if the results obtained indicated that they may be related to the different technological cheesemaking parameters and whey fermentation which lead to the selection of dominant strain populations. The competitive fitness of some L. helveticus biotypes in the ecological niche of particular cheese types may be the consequence of a single trait or a combination of genotypic and phenotypic traits. A polyphasic strain characterization therefore provides a more solid basis to better understand the functional and ecological significance of the diversity of biotypes in natural dairy starter cultures.

In this context, the basic goal of this study was to understand what variables drive a specific phenomenon (the biodiversity within L. helveticus species) and to simplify the conditions that make an object (an L. helveticus strain) belong to one class (based on its origin) rather than another.

The reduction of the number of significative variables as well as the evaluation of their relative importance in the classification procedure can help to understand biological mechanisms on which the classification is based.

In food microbiology, classification studies often deal with homogeneous phenomena characterized by data sets in which all the variables are of the same type. When large data sets are available, food microbiologists have to face the problem of complexity, which can include high dimensionality of the data, mixtures of data types, nonstandard data structures, and nonhomogeneity, which means different relationships between variables in the different parts of measurement space.

Microbiologists have used some grouping techniques in order to classify microbial populations on the basis of genotypic and phenotypic measurements. Phenotypic characters have frequently been used for bacterial characterization and are the basis for numerical taxonomy (32). In the last several years, the introduction of specific molecular procedures, such as ribotyping, DNA-DNA hybridization, DNA homology, and restriction fragment length polymorphism (RFLP) analysis (13, 20, 22, 27), has lead to the general use of genotypic characters for taxonomic purposes.

A number of mostly nonhierarchical multivariate methods have been used for pattern matching to identify operational taxonomical units, which in turn can be circumscribed as a genus, a species, or a strain (4). Principal component analysis can furnish good dimensionality reduction and has found application in numerical taxonomy (19). Hierarchical cluster analysis is used to obtain dendrograms representing the similarity of operational taxonomic units in multidimensional spaces (32).

All of these techniques make use of an unsupervised approach to classification. In fact, groups of observations are identified by means of covariates, and their compliance with a known classification criterion is a posteriori verified. In this study, we use a supervised approach to classification. Trees made with the classification and regression tree (CART) system (2) have been used as a technique to exploit the polyphasic strain characterization of L. helveticus.

A collection of 119 L. helveticus strains isolated from Provolone, Grana Padano, and Parmigiano Reggiano whey natural cultures was used, each of which was studied for its physiological characters, as well as surface protein profiles and hybridization with a species-specific DNA probe. The total number of potential predictors, 71, is high, but few are informative. Thus, in the first instance, the aim of this work was to classify the strains of L. helveticus in relation to their origin. The innovation in this work consisted of the identification of the most important variables, among those considered, that group the strains on the basis of their isolation source through a robust classification procedure.

MATERIALS AND METHODS

Strains.

A total of 119 different L. helveticus strains, isolated from whey starter cultures and belonging to the collection of the Istituto Sperimentale Lattiero Caseario of Lodi, Lodi, Italy, were used. Forty-four strains were isolated from 19 Grana Padano natural whey starter cultures, 17 strains were isolated from 7 Parmigiano Reggiano natural whey starter cultures, and 58 strains were isolated from 14 Provolone natural whey starter cultures. The strains were identified with biochemical tests (17), surface proteins (9), and species-specific PCR (30). The strains were stored in MRS broth (Difco, Detroit, Mich.), with 15% glycerol added, at −80°C. Working cultures were prepared through two overnight transfers at 42°C in MRS medium.

Acidifying activity assay.

Acidifying activity was evaluated in sterilized skim milk (SSM) and SSM fortified with 0.6% (wt/vol) yeast extract (Difco) (YE) at 42°C as previously described (10). pH was measured after 3, 6, and 24 h. (pHmeter Metrhon 654; Metrhon, Ltd., Herisau, Switzerland), and values were expressed as pH decrease, calculated as the difference between the value immediately after inoculation and values at three successive times (3, 6, and 24 h) in SSM (SSM3, SSM6, and SSM24, respectively) and in SSM-YE at the same times (YE3, YE6, and YE24).

Peptidase activity assay.

Peptidase activity was evaluated as described in a previous work (10) with 0.656 mM solutions of phenylalanine-proline-βNa (Phe-Pro), arginine-βNa (Arg), and lysil-βNa (Lys) (Bachem Feinchemikalien AG, Bubendorf, Switzerland) substrates at pH 6.5 after 1 h of incubation at 37°C. Aminopeptidase activity was evaluated by measuring the optical density at 580 nm (OD₅₈₀) with a Diode Arrays Spectrophotometer (Hewlett Packard no. 84524; Cermusco su Naviglio, Italy).

Extraction and analysis of surface proteins.

Surface proteins were extracted from cells growing in the exponential growth phase, which were washed twice with sterile distilled water, resuspended in 5 ml of sterile distilled water to obtain an OD₆₀₀ of 2.0, and centrifuged (3,000 x g for 10 min at 4°C). Surface proteins were extracted from final pellets with 10 mM Tris-HCl, 10 mM EDTA, 10 mM NaCl, 2% sodium dodecyl sulfate (SDS [pH 8.0]) at 100°C for 5 min, and finally analyzed by SDS-polyacrylamide gel electrophoresis as described by Gatti et al. (9). They were defined according to their molecular mass (in kilodaltons). The presence or the absence of the resulting bands was evaluated by observation of electrophoretic gels. Using Coomassie blue staining, six different bands of about 35 (P35), 48 (P48), 50 (P50), 66 (P66), 110 (P110), and 120 (P120) kDa were detected.

Total DNA extraction.

Total DNA from the strains was extracted from 5-ml samples of fresh overnight MRS broth cultures by an alkaline lysis method according to the method of de los Reyes-Gavilàn et al. (5). The quantity and purity of DNA were assessed by A₂₆₀ and A₂₈₀ as described by Sambrook et al. (26).

DNA hybridization with the L. helveticus probe.

RFLP of L. helveticus isolates was performed by using a species-specific DNA probe in Southern blot (26) hybridization experiments as described in a previous work (12). Total DNA was cleaved by EcoRI (Life Technologies Italia, Milan, Italy). Restriction was carried out during 2 h at 37°C in 20-μl volumes of incubation buffer (Life Technologies) containing 10 U of EcoRI restriction enzyme and 0.25 μg of total DNA.

DNA restriction fragments were separated electrophoretically in agarose gels (1% [wt/vol]) and blotted on a Hybond N⁺ membrane (Amersham Pharmacia Biotech Italia, Milan, Italy) under alkaline conditions (0.4 N NaOH). DNA-DNA hybridization was subsequently performed with the enhanced chemiluminescence (ECL)-direct nucleic acid labeling and detection systems (Amersham Pharmacia Biotech Italia), according to the supplier's instructions. Overnight hybridization was carried out at 42°C by using an internal PCR-amplified 388-bp fragment of IS1201 as a DNA probe. IS1201 is a 1,387-bp insertion sequence isolated from L. helveticus (5, 28), which was kindly provided by P. Tailliez (Unité de Recherches Laitières et Genetique Appliquée, Jouy-en-Josas, France). IS1201 was obtained from a BssHII-digested pBluescript plasmid, which had been cloned in Escherichia coli CNRZ 1814 as described by Tailliez et al. (28). The 388-bp internal fragment was amplified from plasmid DNA of strain CNRZ 1814 by using the primers 5′ GCTGAGCGATAAGTTCTT 3′ and 5′ ATTGGCTTGCTGGTGAAT 3′. The two primers were designed to amplify the region 594 to 981 of the published IS1201 DNA sequence (24). After signal generation and detection, autoradiography films (Hyperfilm-ECL; Amersham Pharmacia Biotech Italia) were exposed to generate light according to the manufacturer's instructions. Approximate mole sizes (in base pairs) of the restriction fragments on the Southern blots were calculated by comparing migration distances with a HindIII-digested lambda DNA size marker (Life Technologies).

Analysis of the DNA-DNA hybridization fingerprints.

Exposed autoradiography films of Southern blot fingerprinting profiles from the RFLP experiment were scanned (Scanjet 6100 C/T; Hewlett Packard Italia, Milan, Italy), and the TIFF-formatted image was taken into the software package GelCompar, version 4.2. The bands were identified and sizes were determined for the statistical analysis according to the size (kilobases) calculated with respect to λ DNA/HindIII fragments. The bands were designated with a C followed by their size in kilobases.

The resulting densitometric traces of band profiles were analyzed by cluster analysis (GelCompar version 4.2). Calculation of similarity of the band profiles was based on the Pearson similarity coefficients. A dendrogram was deduced from the matrix of similarities by the unweighted pair group method using arithmetic average (UPGMA) clustering algorithm (33).

Classification trees.

In this section, we give a brief overview of binary classification trees methodology introduced by Breiman et al. (2).

Consider a population whose elements belong to C different classes, and let X be the sample space spanned by a set of p variables measured on the elements of the population. A classification rule is a function that assigns each x ∈ X to one of the C classes; the classification rule is usually defined on the basis of a training set: that is a sample for which class membership is known.

The idea underlying classification trees is very simple: we start considering the whole training set, then we search the best binary split: that is the split that divides the set in the two most homogeneous subsets. At the second step, we reapply the search of the best split to the two subsets previously created. In successive steps, partition continues recursively until some stopping rule (i.e., until a minimum size for the subsets is reached) is met. The subsets created by partitioning are called “nodes,” or “leaves” if they are terminal and if it is not possible, or reasonable, to split them further. Each of the leaves is assigned to a class minimizing the misclassification cost.

To complete the description, we point out how homogeneity is measured, how the best split is found, and how a stopping rule can be defined.

The homogeneity of a node is maximum when it contains only elements from a single class, while minimum homogeneity is reached when the units in the node are uniformly subdivided among the C classes. Intermediate situations are measured by impurity indexes, impurity being the dual of homogeneity. Formally, impurity indexes are concave, symmetric, and bounded real functions. The most common impurity indexes in the literature are the Gini index and the Shannon entropy measure (2).

For splitting a node, each of the p variables (called predictors) is considered separately, and provided it is orderable, a cutoff value is searched, for which the impurity of resulting nodes is minimum. Successively the p candidate splits are compared, and the best is selected. Note that this splitting criterion relies on the measure of impurity of the created nodes and can therefore be applied (with a tentative search of the cutoff) to categorical unordered variables.

The described recursive partitioning can be continued until we obtain leaves with only one element. Such a tree makes no classification errors, but is liable to the effect of random sample fluctuations and thus poor performance in the analysis of possible new data. A smaller tree (that is one with a smaller number of leaves) would probably be more stable, at the price of some misclassification.

More-severe stopping rules can be set: imposing, for instance, a minimum size for the leaves, but this would leave the question of what is the “right size” of the tree unanswered. The solution can be found by introducing a pruning rule: that is a criterion that selects the right-sized trees by pruning the more “unstable” branches of the tree. The established methodology is tree cost-complexity pruning, first introduced by Breiman et al. (2).

Let R(T) be the resubstitution estimate (i.e., the estimate carried out using the training sample) of the true overall misclassification cost R* (T). We can introduce the cost-complexity measure

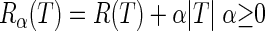where |T| is the number of leaves and α is a real number called the “complexity parameter.” For each value of α, it is then possible to find the tree T_α (subtree of T₀) such that

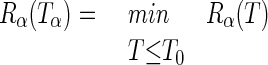(with T₀ being simply the largest possible tree). It can be shown that there exists a nested family {T₀, T₁,…, T_k,…T_root} of subtrees of T₀ such that each of the trees is optimal for a range of values of α: that is, we can find the optimal tree by a sequence of snip operations on the current tree (for a detailed description of the pruning computational algorithm see reference 2 by Breiman et al.).

Having obtained the sequence of pruned subtrees, the problem follows of which tree to select out of this sequence. A tree is selected in order to maximize the predictive power of the tree. To estimate this predictive power, the availability of an independent sample would in principle be the best option, but since it is advisable to use all data to “instruct” the tree in the best possible way, a cross-validation method is used (see reference 2 for details). Usually, the tree T_k0 with the minimum estimated prediction error is selected. A more severe pruning rule consists of selecting the smallest tree with an estimated prediction error not larger than the estimated prediction error of T_k0 plus its standard error (1-SE rule).

The above description is based on the notion of misclassification cost R(T), which can be defined as follows. We first impose the condition that 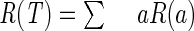, where a denotes the generic leaf of the tree. That is, we assume that the misclassification cost of a tree is obtained as the sum of that of all its leaves. The definition of R(a) can be written as

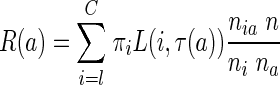where π_i is the a priori probability of class i, τ(a) the class to which the leaf a is assigned, L is a loss function such that 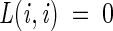and 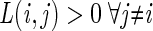, n_ia, and n_i are the numbers of members of class i in leaf a and the population.

We note that in the simplest setting, associated with simple random sampling from the population, prior probabilities estimated from the data (i.e., equal to the observed class frequencies in the training set) and 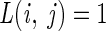for all i ≠ j, R(a) reduces to

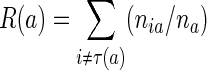which is minimized, assigning the leaf to the class to which the majority of its members belong.

In our application, we consider constant losses and prior probabilities, even though the proportions of the various classes in the sample are not constant. In fact, our aim is to equalize the misclassification rate (29). We also consider constant losses, because there is no reason to suppose that the different types of misclassification have different levels of relevance.

Statistical analysis.

For building classification trees, the S-Plus routine RPart was used. This routine is downloadable at StatLib (http:/lib.stat.cmu.edu) and implements many of the ideas found in the CART book (29).

RESULTS

Polyphasic strain characterization.

In this work, 119 strains of L. helveticus isolated from natural whey cultures (44 from Grana Padano, 17 from Parmigiano Reggiano, and 58 from Provolone) were studied for their physiological characteristics, surface proteins, and RFLP.

Table 1 summarizes the data relative to the strains isolated from natural whey starters of each cheeses relative to their technological characteristics (i.e., acidifying and peptidase activities). Almost all of the variables considered were characterized by different mean values in relation to their origin. In addition, the strains with the same origin showed marked differences in these activities, as indicated by the high variability coefficient values and the minimum-to-maximum ranges.

TABLE 1.

Peptidase and acidifying activities in L. helveticus strains in relation to their origin

Origin (n)a	Peptidase activity (OD580)						Acidifying potential (pH decrease)
	Phe-Pro		Avg		Lys		SSM3		SSM6		SSM24		YE3		YE6		YE24
	Mean (CV)b	Range	Mean (CV)	Range	Mean (CV)	Range	Mean (CV)	Range	Mean (CV)	Range	Mean (CV)	Range	Mean (CV)	Range	Mean (CV)	Range	Mean (CV)	Range
Grana Padano (44)	2.041 (3.99)	1.78-2.137	0.635 (116.10)	0.039-2.344	0.667 (48.82)	0.331-2.224	0.202 (45.82)	0.089-0.420	0.572 (57.20)	0.122-1.590	2.417 (42.79)	0.245-3.290	0.278 (44.95)	0.010-0.570	1.092 (54.07)	0.075-2.050	3.013 (16.83)	2.455-3.290
Parmigiano Reggiano (17)	1.899 (12.99)	1.263-2.114	1.337 (42.99)	0.333-2.172	0.919 (20.32)	0.539-1.287	0.120 (47.36)	0.008-0.292	0.195 (78.91)	0.539-1.287	0.888 (84.62)	0.184-2.584	0.136 (36.93)	0.095-0.307	0.243 (117.33)	0.088-1.248	2.452 (40.60)	0.135-3.374
Provolone (58)	1.519 (33.33)	0.754-2.568	1.209 (67.92)	0.210-2.761	1.043 (54.76)	0.210-2.761	0.114 (60.75)	0.010-0.310	0.327 (77.16)	0.040-1.180	1.883 (53.91)	0.430-3.211	0.321 (59.86)	0.050-0.770	1.317 (55.17)	0.088-2,430	2,989 (15.51)	0.853-3.427

^an, number of strains.

^bCV, relative variability coefficient.

Table 2 reports the distribution of surface proteins of the strain collection in relation to their molecular weight. In this case, the data are reported as the percentage of strains with detectable levels of each size class. The most interesting variables seem to be P66, characteristic for Grana Padano and Parmigiano Reggiano, and P110, which is present in 59% of strains from Parmigiano Reggiano and 5% of strains from the other cheeses. In addition, P50 was found in 2.3% of strains from Grana Padano, 17.7% of strains from Parmigiano Reggiano, and 81% of strains from Provolone.

TABLE 2.

Presence of surface proteins with different molecular masses in strains of L. helveticus

Proteina	% of proteinsb
	Grana Padano (n = 44)	Parmigiano Reggiano (n = 17)	Provolone (n = 58)	Total (n = 119)
P120	6.82	17.65	0.00	5.04
P110	4.55	58.82	5.17	12.61
P66	79.55	82.35	18.97	50.42
P50	2.27	17.65	81.03	42.86
P48	100.00	82.35	84.48	89.92
P35	18.18	0.00	1.72	7.56

^aThe number of each surface protein represents its molecular mass in kilodaltons.

^bn, number of strains.

The study of the profiles from RFLP analysis carried out on all the strains allowed the identification, on the basis of their size, of 56 bands. These bands are shown in Table 3, which also reports the percentage of their presence in the strains isolated from the different cheeses.

TABLE 3.

Presence of DNA fragments with different molecular sizes in L. helveticus

DNA fragmenta	% of fragmentsb
	Grana Padano (n = 44)	Parmigiano Reggiano (n = 17)	Provolone (n = 58)	Total (n = 119)
C16.7	11.36	52.94	12.07	17.65
C17.6	40.91	23.53	1.72	19.33
C18.4	34.09	0.00	6.90	15.97
C19.6	13.64	11.76	5.17	9.24
C20.4	34.09	5.88	6.90	16.81
C21.9	4.55	29.41	8.62	10.08
C23.5	2.27	5.88	15.52	9.24
C24.4	0.00	29.41	1.72	5.04
C25.9	59.09	41.18	17.24	36.13
C26.7	52.27	23.53	55.17	49.58
C27.7	27.27	35.29	13.79	21.85
C28.4	72.73	5.88	55.17	54.62
C29.5	54.55	11.76	20.69	31.93
C30	38.64	5.88	6.90	18.49
C31	4.55	29.41	89.66	49.58
C32.2	20.45	11.76	3.45	10.92
C33.1	54.55	0.00	8.62	24.37
C34.8	61.36	58.82	63.79	62.18
C36	22.73	29.41	15.52	20.17
C36.9	2.27	5.88	56.90	29.41
C37.6	20.45	5.88	5.17	10.92
C39.5	11.36	17.65	12.07	12.61
C40.4	70.45	47.06	72.41	68.07
C41.7	20.45	64.71	15.52	24.37
C42.8	9.09	17.65	62.07	36.13
C44	18.18	17.65	50.00	33.61
C44.7	65.91	23.53	41.38	47.90
C45.4	38.64	76.47	13.79	31.93
C46.8	88.64	52.94	46.55	63.03
C48	22.73	64.71	20.69	27.73
C48.7	75.00	47.06	44.83	56.30
C50.1	31.82	41.18	37.93	36.13
C51.7	15.91	64.71	1.72	15.97
C53	31.82	41.18	74.14	53.78
C53.7	0.00	35.29	8.62	9.24
C54.9	52.27	35.29	5.17	26.89
C56.5	90.91	64.71	32.76	58.82
C57.8	11.36	35.29	0.00	9.24
C59	100.00	70.59	43.10	68.07
C60.7	50.00	11.76	18.97	29.41
C61.9	47.73	17.65	31.03	35.29
C63.1	34.09	29.41	37.93	35.29
C64.1	15.91	11.76	8.62	11.76
C64.9	40.91	0.00	36.21	32.77
C65.9	50.00	0.00	5.17	21.01
C66.6	15.91	5.88	34.48	23.53
C67.6	45.45	23.53	25.86	32.77
C68.5	9.09	5.88	39.66	23.53
C69.1	13.64	11.76	13.79	13.45
C70.4	9.09	5.88	56.90	31.93
C71.4	13.64	17.65	18.97	16.81
C73	56.82	29.41	3.45	26.89
C74.5	11.36	0.00	55.17	31.09
C75.9	4.55	0.00	24.14	13.45
C77.2	9.09	23.53	3.45	8.40
C79.9	9.09	0.00	6.90	6.72

^aThe number of each DNA fragment represents its size in kilobases.

^bn, number of strains.

The comparison by means of cluster analysis among the RFLP patterns of L. helveticus strains isolated from Parmigiano Reggiano, Grana Padano, and Provolone whey starter cultures showed great biodiversity (Fig. 1). The value obtained for the cophenetic correlation value for the whole dendrogram (79%) indicated a not very good consistency of the dendrogram. As reported by Giraffa et al. (12), the clusters with similarity coefficients below 90% can be considered different. At such a similarity level, 91 clusters were found. Forty-four Grana Padano strains were split up among 23 clusters, and 58 Provolone strains were split up among 48 clusters. Parmigiano Reggiano strains, despite the low number of strains analyzed (17 strains), were split up among 17 different clusters. Only upon reducing the similarity level (40%) were L. helveticus biotypes clustered in 12 groups. In particular, 73% of Grana Padano strains were split up in one cluster, and the others are in other two clusters. Sixty-five percent of Provolone strains are in one cluster, and the others were split up in seven different clusters. Strains from Parmigiano Reggiano could be considered more biodiverse, because, despite the low number of strains analyzed, even at a low similarity level, they were split up among seven different clusters.

FIG.1.

Dendrogram based on the UPGMA clustering of the Pearson association coefficient of RFLP patterns obtained after hybridization of the internal PCR-amplified 388-bp fragment of IS1201 with total genomic DNA from all 119 L. helveticus strains following restriction with EcoRI. The scale at the top right shows the Pearson correlation from 0 to 100% (RFLP insertion sequence).

In some cases, the patterns obtained seem to be characteristic for some cheeses rather than others, but it is not possible to extrapolate a general and unequivocal rule able to distinguish the strains in relation to their origin.

The great variability in relation to the strain source of the variable considered has induced us to exploit all of these data with a supervised statistical procedure able to give clear responses about the factors that can differentiate the strains on the basis of their isolation. In a supervised approach to classification, the observed groups (Grana Padano, Parmigiano Reggiano, and Provolone) are used in order to identify a classification rule. Moreover, in the CART supervised approach, the classification rule splits the measurement space into homogeneous groups. In this way, a classification rule and a cluster of observation are jointly obtained. For this reason, attention has been focused on the classification tree methodology.

Classification of the strains.

The classification tree has been built by considering all 71 of the variables characterizing the 119 strains of L. helveticus previously described in relation to their origin.

In Table 4, the statistics relative to the sequence of trees obtained by the algorithm CART are reported. On the basis of the 1-SE rule (2) the tree with six terminal nodes has been chosen. The resubstitution and the cross-validated misclassification costs are reported in the same table as well as the relative costs compared to the tree with only one terminal node.

TABLE 4.

Tree sequence obtained using the S-Plus routine Rpart

Tree	No. of terminal nodes	Cross-validated relative cost (SE)	Resubstitution relative cost
1a	8	0.230 (0.053)	0.115
2b	6	0.246 (0.049)	0.148
3	5	0.328 (0.051)	0.180
4	4	0.344 (0.049)	0.230
5	3	0.393 (0.052)	0.311
6	2	0.410 (0.044)	0.410
7	1	1.000 (1.000)	1.000

^aTree with minimum cross-validated relative cost.

^bTree selected using the 1-SE rule.

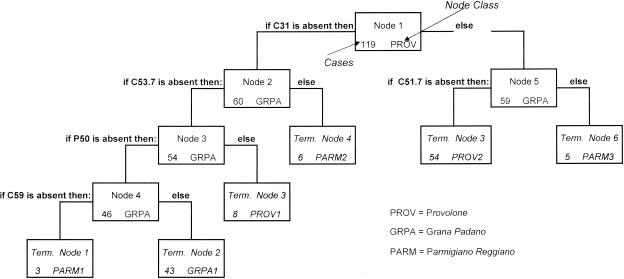
The results obtained are graphically shown in Fig. 2. The final tree used only five variables: four DNA fragments (C31, C51.7, C53.7, and C59) and one surface protein band (P50). This confirms that there are only a few informative characters in the analysis. The tree has six terminal nodes: three identified as Parmigiano Reggiano, PARM1, PARM2, and PARM3 (grouping 3, 6, and 5 strains, respectively); two identified as Provolone, PROV1 and PROV2 (8 and 54 strains, respectively); and one identified as Grana Padano, GRPA1 (43 strains).

FIG. 2.

Classification tree. Term., terminal.

The resubstitution classification table (Table 5) shows the actual versus predicted classes to which the strains are attributed in relation to their origin. Nine strains out of 119 were not correctly classified, with a misclassification rate of 7.6%. It is interesting to observe that five of the nine strains not correctly classified were isolated from Parmigiano Reggiano whey starter cultures, so that the specific misclassification rate relative to Provolone and Grana Padano isolates is considerably lower (3.9%).

TABLE 5.

Resubstitution classification table^a

Actual class	No. in predicted class
	Grana Padano	Provolone	Parmigiano Reggiano
Grana Padano	42	2	0
Provolone	0	56	2
Parmigiano Reggiano	1	4	12

^aShown is the class assigned by the tree (columns) versus the observed class (rows).

Table 6 reports the misclassified cases by node. Of the 5 strains out of 17 from Parmigiano Reggiano cheese not correctly assigned to the terminal nodes PARM1, PARM2, and PARM3, 1 strain was assigned to the Grana Padano terminal node (GRPA1) and 4 were assigned to Provolone nodes. In addition, two Grana Padano isolates were attributed to the Provolone node PROV2, while two Provolone isolates were misclassified in the Parmigiano Reggiano nodes PARM1 and PARM3.

TABLE 6.

Resubstitution misclassified cases by node^a

Terminal node	No. in actual class
	Grana Padano	Provolone	Parmigiano Reggiano
PARM1		1
GRPA1			1
PROV1			3
PARM2
PROV2	2		1
PARM3		1

^aThe labels of terminal nodes are those assigned by the tree.

In general, the strains isolated from Grana Padano and Provolone whey starters were mainly grouped in two bigger leaves (GRPA1 and PROV2, respectively). The PROV1 leaf (eight strains) grouped five Provolone and three Parmigiano Reggiano strains. The overall correct attributions of the strains in relation to the origin are 95.5% for Provolone, 96.6% for Grana Padano, and 70.6% for Parmigiano Reggiano.

When the predictive effectiveness of the model is evaluated by means of cross validation (Table 7), it is possible to note that, while the misclassifications of Provolone and Grana Padano isolates reflect the resubstitution results (5.2 and 4.5%, respectively), the number of errors for Parmigiano Reggiano isolates is somewhat higher. In fact, 10 out of 17 strains are misclassified (6 in the Grana Padano nodes and 4 in the Provolone nodes). Therefore, the model shows a weaker predictive power for Parmigiano Reggiano strains. In other words, leaves labeled as Parmigiano Reggiano seem to be quite unstable. However, it is important to stress that the cross validation estimates tend to be conservative in the direction of overestimating misclassification costs (29).

TABLE 7.

Cross-validation classification table^a

Actual class	No. in predicted class
	Grana Padano	Provolone	Parmigiano Reggiano
Grana Padano	42	2	0
Provolone	2	55	1
Parmigiano Reggiano	6	4	7

^aShown is the class predicted by the tree (columns) versus the observed class (rows).

DISCUSSION

The characterization of mixed microbial populations (in which isolates belonging to different genera, species, or strains of the same species can be found) is usually carried out by measuring phenotypic or genotypic features. The data acquired are commonly exploited with cluster statistical procedures by comparing the unknown isolates with reference microorganisms.

Statistical approaches such as cluster analysis allow the different sampling units to be grouped, and the taxonomical affiliation of an isolate can be obtained by judging its similarity to the reference microorganisms. Such a procedure does not consider the a priori knowledge relative to the observations (i.e., the isolates under examination), and, for example, environmental, technological, seasonal information is not considered. Moreover, clustering techniques give a visual representation of the groups obtained (based on similarity indices) without allowing a simple and immediate evaluation of the relative importance of the variables considered in the grouping procedure. Dalezios and Siebert (4) stressed the need for classification methods both tolerant of error and allowing imprecise matching, primarily in relation to intermediate responses to the test, which may not have a strictly binary choice.

The application of grouping techniques can be incorrect because they treat a supervised problem as an unsupervised one, and so a fundamental part of the information acquired is not considered.

Unlike clustering techniques, discriminant methods, like classification trees, base their classification potential on the consideration of the whole population as belonging to a number of different classes. Starting from such a priori knowledge, such methodologies try to identify classification rules that, on the basis of the variables considered, allow the different sampling units to be assigned to one of the classes identified. Within discriminant techniques, the classification trees can be particularly useful for the exploitation of microbiological data, because they are very simple to interpret and easily manage problems because of the high dimension of the space of predictors. Moreover they permit the treatment of different data types, providing a solution to problems due to the nonhomogeneity that arises when different relationships hold between variables in different parts of the space of predictors.

The most intriguing characteristic of classification trees is the possibility of easily recognizing what data are most important for discriminating objects. In this case, the results obtained demonstrated the importance of four different DNA fragments, whose physiological and/or metabolic significance is not currently known, and one surface protein.

The approach used in this study appears to be a promising tool for characterizing the presence of particular biotypes in different natural microbial ecosystems and to identify strains on the basis of their technological aptitudes. The method used highlights the main characteristics that permit discrimination of biotypes to be identified. In order to understand what kind of genes could code for phenotypes of technological relevance, the identification of specific DNA sequences present only in particular biotypes is of great interest.

The observed discrimination between L. helveticus strains isolated from Provolone and Grana Padano could be the result of the different temperatures of curd cooking (48 to 52°C for Provolone and 54 to 56°C for Grana Padano) that determine the subsequent evolution of whey temperature during its incubation. In addition, an initial temperature of whey lower than 50°C promotes the growth of Streptococcus thermophilus, a microorganism usually found in Provolone and less frequently found in Grana Padano and Parmigiano Reggiano whey starter cultures (11).

The Parmigiano Reggiano strains were more difficult to distinguish than strains of other sources. This could be due to the cheesemaking methods present in the Parmigiano Reggiano production area, which are the most artisan. Probably the smaller dimensions of Parmigiano Reggiano factories induce a range of specific traits in cheesemaking processes that are favorable to the selection in the natural whey culture of a wide variety of wild biotypes. Previous works using separate phenotypic or genotypic methods suggested that cheese technology parameters play a role in selecting dominant biotypes in natural starter cultures (10, 12, 18). The natural whey starter cultures consist of a never interrupted selection of microbial population by cheesemaking and whey fermentation parameters. A higher degree of standardization induces a more specific selection of wild biotypes present in whey starter. The higher the standardization process is, the lower the presence of different biotypes could be expected. The range of variability may be related to both the number of parameters involved in cheese production and the amplitude of the range of variability of each parameter.

It is interesting to observe that the factors able to discriminate the strains on the basis of their origin do not include the phenotypic characters considered in this work. The values observed for these variables in the strains isolated from different cheeses are characterized by high variability coefficients (Table 1). This confirms the presence in natural cultures of different biotypes of L. helveticus characterized by different levels of phenotypic expression. The strains are selected by the specific whey processing characteristics, which are not related to the phenotypic characteristics of technological concern. The fundamental role in strain grouping of particular DNA fragments and surface proteins leads to the hypothesis that the selection could be based first on the resistance to the extreme conditions found by bacteria and, in particular, resistance to thermal stress. In other words, the whey colonization by specific biotypes mainly depends on the ability of microorganisms to survive under prohibitive conditions, which characterize the successive colonization. Thus, several biotypes, with some common features, which enable them to survive in whey, collaborate and interact during the colonization of whey and cheesemaking. The typical contribution of the selected microflora to cheesemaking and ripening of each cheese relies on a precise equilibrium of several biotypes of the same species with different technological aptitudes and related by a few, but fundamental physiological abilities.

In conclusion, the ability to discriminate strains of ecological niches by studying simultaneously phenotypic characteristics such as acidifying and peptidase activities, surface proteins, and nonconserved DNA regions may be technologically and ecologically noteworthy. The methodology employed in this work demonstrates how the strains group into terminal nodes without difficult and subjective interpretation. In particular, good discrimination was obtained between L. helveticus strains isolated, respectively, from Grana Padano and Provolone natural whey starter cultures.

The modality of preparation of the whey starter cultures warrants the survival of different biotypes useful to the development of the ecosystem itself, and a mixture of strains of the same species is necessary to the natural starter evolution. A more specific selection of biotypes for the phenotypes of cheesemaking relevance could involve the presence of a lower number of biotypes and consequently a decrease of natural starter functionality.