Nonlinear Oscillations in Pain Prediction Accuracy: A Dynamical Systems Approach to Understanding Daily Pain Prediction

Abstract

Dynamical systems modeling was used to analyze fluctuations in the pain prediction process of people with rheumatoid arthritis. 170 people diagnosed with rheumatoid arthritis completed 29 consecutive days of diaries. Difference scores between pain predictions and next-day pain experience ratings provided a time series of pain prediction accuracy. Pain prediction accuracy oscillated over time. The oscillation amplitude was larger at the start of the diary than at the end, which indicates damping toward more accurate predictions. State-level psychological characteristics moderated the damping pattern such that the oscillations for patients with lower negative affect and higher pain control damped more quickly than the oscillations for their counterparts. Those findings suggest that low negative affect and high pain control generally contributed to a more accurate pain prediction process in the chronically ill. Positive affect did not differentiate the damping pattern but, within each oscillation cycle, patients with higher positive affect spent more time making inaccurate predictions than their counterparts. The current analyses highlight the need to account for change in data through dynamical modeling, which cannot be fully observed through traditional statistical techniques.

Cognition and affect play important roles in modulating the severity and duration of a variety of chronic pain disorders (Bair, Robinson, Katon, & Kroenke, 2003; Rainville, 2002). Among the cognitive processes that may contribute to the daily experience of chronic pain, the prediction of future pain stands out as a key variable that influences the perception of aversive pain. Overpredictions of pain can promote maladaptive, pain-avoidant behavior while underpredictions of pain can contribute to an increased perception of aversive pain (Rachman & Arntz, 1991). Pain prediction accuracy, then, is an adaptive skill in the negotiation of the physical (e.g., pain flares) and environmental (e.g., barriers for people with diminished mobility) threats that are encountered on a daily basis by people with chronic pain disorders. The patterns of pain prediction that give rise to accuracy over time are informative; state and trait variables of affective and cognitive style, for example, may be linked to general tendencies to overpredict, underpredict, or accurately predict pain. However, no study, to our knowledge, has examined meaningful day-to-day variations in pain predictions across repeated measurements—the dynamical structure. Through such an approach, the vicissitudes of daily life with chronic pain can be examined in a manner that accounts for the mutable influences of cognition and affect. In the current study, we explored the dynamical structure of oscillations in the relative accuracy of pain predictions over time among a sample of patients with rheumatoid arthritis (RA), a chronic autoimmune disease of the synovial joints characterized by disabling pain (Anderson, Bradley, Young, McDaniel, & Wise, 1985).

Pain prediction accuracy occurs when an individual’s level of pain experienced matches that which he or she predicted. Although people are largely accurate in predicting their pain, errors in pain prediction are common (Rachman & Arntz, 1991). Some studies have shown a tendency for people to underpredict future pain (Arntz & Peters, 1995; Finan, Zautra, & Tennen, 2008; McCracken, Gross, Sorg, & Edmands, 1993) and others have reported that overpredictions predominate (Arntz, van Eck, & Heijmans, 1990; Rachman & Lopatka, 1988). For example, people with chronic low back pain (Arntz & Peters, 1995) and those who are low in daily pessimism (Finan et al., 2008) tend to underpredict pain. On the other hand, when pain-related fear is high, avoidance behaviors drive people to overpredict their pain (Arntz et al., 1990). Thus, there are a variety of conditions that can create the context for a particular pattern of pain prediction to develop. A key departure in the current study is that we are not concerned with pain overprediction and underprediction per se. Rather, the expectation is that overpredictions and underpredictions occur systematically within patterns of change that move around a zero-point accuracy. To account for day-to-day fluctuations in pain prediction accuracy, a nonlinear dynamics approach is warranted.

Dynamical Systems and the Damped Oscillator Model

To date, fluctuations in pain predictions have been characterized as random, allowing tendencies in pain prediction accuracy to be accounted for by using means (Arntz et al., 1990; Finan et al., 2008; Rachman & Lopatka, 1988). The process of pain prediction, through the use of mean state analyses, has been treated as generally stable. Little is known about the underlying dynamical structure of repeated pain predictions in a naturalistic setting, where no single event would be expected to influence pain predictions over time. Fluctuations in a variable across time may not be random error and may instead be indicative of meaningful structure (Butner, Amazeen, & Mulvey, 2005; Chow, Ram, Boker, Fujita, & Clore, 2005; Vallacher, Nowak, & Kaufman, 1994). The temporal evolution of meaningful structure cannot be captured by mean state analyses alone, but rather, may be best analyzed with dynamical models that are specifically designed to analyze change. In the current study, fluctuations in pain prediction accuracy were assessed using a daily diary. Daily diary methodology lends itself well to dynamical modeling techniques, because information about particular variables is collected from participants across several days of measurement (Bolger, Davis, & Rafaeli, 2003).

An example of meaningful change in psychological processes is the cyclical or oscillatory motion in which fluctuations are periodic. Those fluctuations can be sustained (constant amplitude over time), amplified (increasing amplitude over time), or damped (decreasing amplitude over time). For example, fluctuations in the positive emotions of college students were sustained over time, repeatedly peaking during the weekend and dropping sharply on Mondays (Chow et al., 2005). Amplified oscillations have been observed in adolescent substance abuse (Boker & Graham, 1998). Small changes in cigarette or alcohol use were followed by amplified changes, resulting in increasingly unstable adolescent substance abuse. Damped oscillations have been observed in the emotional well-being of recently bereaved widows when they sought emotional support (Bisconti, Bergeman, & Boker, 2004). In that study, emotional well-being fluctuated with the loss of a spouse, while the amplitude of those fluctuations was reduced over time in the presence of a strong support structure.

The nonlinear damped oscillator model has been used previously to capture cyclical motion in a diverse set of phenomena from pendulum motion (Abraham & Shaw, 1992) to juggling (Beek & Beek, 1988) and other rhythmic movements (Beek, Schmidt, Morris, Sim, & Turvey, 1995; Butner et al., 2005). In the current study, the nonlinear damped oscillator model was used to examine the nature of fluctuations across time in pain prediction accuracy. A rather consistent finding in the pain prediction literature is that people become more accurate in predicting their pain as they gain experience doing so (Crombez, Vervaet, Baeyens, Lysens, & Eelen, 1996; Rachman & Arntz, 1991). Thus, we expected that damping in pain prediction accuracy would occur over time in our sample, such that individuals would initially experience rather large fluctuations in their ability to accurately predict their pain, but those fluctuations would decrease in amplitude with experience.

A visual representation of oscillations is the phase portrait in which a data point’s position and velocity (speed) are plotted against each other. For the current study, phase portraits represent pain prediction accuracy against the frequency at which pain prediction accuracy changes. Phase portraits are useful for the detection of influences on oscillations that change the amplitude of oscillations through insertion or deletion of energy. Energy typically enters the cycle at specific points through a mechanism known as an escapement (Abraham & Shaw, 1992; Butner et al., 2005), deforming the phase portrait. Changes in the speed of oscillations (e.g., number of cycles per unit time) are more subtle and might not be observed visually in the phase portrait, because similar positions are traversed from point to point within a cycle. They are important, though, as they may reflect occurrences like rapid progression through accurate pain predictions and slow progression through inaccurate pain predictions. Oscillation amplitude and oscillation frequency in psychological phenomena might therefore be self-adjusted through mechanisms related to goals, intentions and personal actions.

Given the influence of pain predictions on the way RA patients think, behave and experience pain, it is possible that pain predictions will vary based on individual differences in affect and perceptions of control. For chronic pain patients, high positive affect (PA) can serve as a resilience resource in the face of pain flares, and contribute to lower levels of pain over time (Zautra, Johnson, & Davis, 2005). Alternately, high negative affect (NA) can alter an individual’s perception of pain through a variety of endogenous pathways (Janssen, 2002) and, thus, potentially interfere with the ability to accurately predict future pain episodes. A high sense of control over pain is related to greater psychological well-being (Jensen & Karoly, 1991), while illness uncertainty is associated with higher stress and anxiety (Reich, Johnson, Zautra, & Davis, 2006). High PA, low NA, and high pain control may, thus, foster the acquisition of the adaptive skill of accurately predicting pain and provide a buffer against protracted periods of erroneous pain prediction.

Summary and Hypotheses

The current study included a daily diary containing 29 contiguous days of pain predictions matched with next-day pain experience ratings from a sample of patients with RA. By taking the difference between pain predictions and the next day’s experience ratings, a day-to-day index of pain prediction accuracy was obtained. The nonlinear damped oscillator model was used to characterize meaningful structure in patterns of pain prediction accuracy over time. Across participants and conditions, pain prediction accuracy was expected to damp over the course of the diary. We hypothesized that people high in PA, low in NA and high in pain control would evidence faster damping toward pain prediction accuracy and spend less time making erroneous pain predictions than people low in PA, high in NA and low in pain control. In dynamical terms, PA, NA and pain control can serve as escapements, changing the contour of the phase portrait of pain prediction accuracy and contributing to varying rates of progression through accurate versus inaccurate pain predictions.

METHOD

Participants

Participants were 170 people (45 men, 125 women; 21-86 years old (M = 55.2, SD = 13.3)) with a physician-confirmed diagnosis of RA. The sample was comprised primarily of Caucasians (92%). Approximately 42% of the participants reported that they had graduated from college, and 36% indicated that they were currently employed. Approximately 67% of the sample reported an annual income of greater than $30,000. Participants received $90 for their participation. Recruitment was conducted in the Phoenix, Arizona metropolitan area at local health fairs, physicians’ offices, the Phoenix Veterans Affairs Hospital and through the Arthritis Foundation. People were excluded from the study if they had Lupus, were taking estrogen-replacement drugs, or if they had significant cognitive impairment. Participants all provided informed consent, approved by the Institutional Review Board at the authors’ university, and were treated in accordance with the ethical principles of the American Psychological Association.

Procedure

The data presented in this report were extracted from a larger study that was aimed at investigating characteristics of RA patients through daily diary methodology. RA diagnosis was first confirmed with participants’ physicians. Participants were then sent a daily diary set with stamped envelopes addressed to the research team. A member of the research team contacted participants by phone and provided detailed instructions to aid in the completion and mailing of the diaries. They were instructed to complete one diary each night within 30 minutes of bedtime, and to mail the diary the next morning in a prepaid envelope.

Postmark verification was monitored for discrepancies between the postmark date and the date reported for the completed diary. If discrepancies were observed, then participants were contacted immediately and urged to comply with the time-sensitive demands of the study. After completing and mailing the diaries for three days, participants were contacted by phone, asked if they had any questions regarding the diaries and encouraged to continue completing the diaries every evening for the remainder of the study. Analyses revealed that 97.3% of the diaries included in the current study were received with a verified postmark. Of that number, 82.6% of diaries were postmarked on the morning after the diary was completed.

Measures

Pain Prediction Accuracy

At the beginning of each daily diary, participants were asked to estimate their “Average Level of Arthritis Pain Today.” At the end of each daily diary, participants were asked to estimate “How Much Pain Do You Expect Tomorrow?” Participants made their estimates on the 101-Point Numerical Rating Scale (NRS; Jensen, Karoly, & Braver, 1986). Estimates ranged from 0 (“No Pain”) to 100 (“Pain As Bad As It Can Be”). Numerical pain rating scales are equally effective as visual analog scales in detecting increases and decreases in pain ratings (Price, Bush, Long, & Harkins, 1994). Difference scores were then calculated between pain prediction estimates and corresponding next-day pain experience estimates. There were 28 corresponding pain prediction and pain experience estimates, which resulted in a time series of 28 daily diary scores showing the evolution of pain prediction accuracy.

Positive Affect (PA) and Negative Affect (NA)

PA and NA were measured in the daily diary using the Positive and Negative Affect Schedule (Watson, Clark, & Tellegen, 1988). Participants rated 10 standard mood adjectives each for PA and NA using a 5-point scale from 1 (“very slightly or not at all”) to 5 (“extremely”). Internal reliability was good, as Cronbach’s alpha was 0.96 for PA and 0.93 for NA, calculated from items aggregated across diary days.

Pain control

Participants rated the degree of their perceived control over pain each day using a 11-point scale from 0 (“no control at all”) to 10 (“complete control”) (Tennen, Affleck, & Zautra, 2006).

Data Analytic Strategy

Included were data for which observations were continuous throughout the 29 days of measurement. Participants who missed two or more consecutive pain prediction or pain experience values at any time in the 29 days of measurement were excluded from the sample. Single missing values were interpolated by taking a mean of the immediately preceding and immediately subsequent values. Participants missing a value on the final observation were excluded from the sample because there was no next-day observation with which to interpolate. In total, 57 participants were removed from the original sample of 227 to arrive at a final sample of 170 participants, a large N for dynamical systems analysis (Butner et al., 2005). The excluded participants did not differ from the sample participants in any major study variable, including PA (Sample: M = 2.72, SD = 0.68; Excluded: M = 2.61, SD = 0.83), F(1, 226) = 1.16, p = NS, NA (Sample: M = 1.32, SD = 0.35; Excluded: M = 1.34, SD = 0.35), F(1, 226) = 0.16, p = NS, pain control (Sample: M = 6.11, SD = 2.15; Excluded: M = 6.74, SD = 2.30), F(1, 226) = 3.43, p = NS, or average pain (Sample: M = 36.33, SD = 18.61; Excluded: M = 31.60, SD = 17.99), F(1, 226) = 2.73, p = NS, all aggregated across diary days.

Following earlier precedent (Butner et al., 2005), we used a multilevel modeling approach to the damped oscillator model. Multilevel modeling is useful when modeling repeated observations over time and increases the power to detect an effect relative to other regression-based approaches. For studies of dynamical systems models, multilevel modeling can capture a within-person oscillatory relationship when modeling time-varying covariates such as velocity and displacement. Fitting the damped oscillator model to the time series of pain prediction accuracy required centering and detrending pain prediction accuracy and calculating velocity, acceleration and nonlinear terms from pain prediction accuracy.

Centered and Detrended Pain Prediction Accuracy (x(t))

Pain prediction accuracy was first centered and then multiplied twice or thrice to create quadratic and cubic polynomials, respectively. A regression equation was then modeled in which the centered pain prediction accuracy variable and its polynomials served as independent variables and pain prediction accuracy served as the dependent variable. The residuals of this equation represented centered and detrended displacement, x(t), or the value of pain predition accuracy at time t. A score of zero identified an individual who was completely accurate on a given observation. Positive and negative displacements represented overprediction and underprediction, respectively.

Velocity (dx(t)/dt) and Acceleration (d²x(t)/dt²) of Pain Prediction Accuracy

Local linear approximation was used to estimate velocity and acceleration from the pain prediction accuracy time series. The local linear approximation method is a particularly good derivative estimation procedure in data with relatively few repeated measurements (for a review, see Boker & Nesselroade, 2002).¹ Velocity, dx(t)/dt, or the rate of change in pain prediction accuracy at time t, and acceleration, d²x(t)/dt², or the rate of change in the rate of change in pain prediction accuracy at time t, were the 1^st and 2^nd order derivatives of pain prediction accuracy, respectively. A one-step time delay was used to calculate the derivatives.

The Linear Damped Oscillator Model

Acceleration, velocity and displacement are used as the variables that comprise damped oscillator models. In the linear damped oscillator model,

$$\frac{d^{2}x\left(t\right)}{d{t}^2}=-\zeta \frac{dx\left(t\right)}{dt}-\eta x\left(t\right)$$ (1)

,zeta (ζ) is the linear damping coefficient, which represents linear changes in the amplitude of fluctuations through time, and eta (η) is the squared frequency of the oscillations. In the linear damped oscillator model, energy enters or exits the system at a constant rate. The result is a uniform damping effect on all data points, which results in a distinctly circular phase portrait. In reality, however, linear systems with completely circular phase portraits are unusual (Butner et al., 2005).

The Nonlinear Damped Oscillator Model

In contrast to the idealized linear influences, nonlinear influences result in elongation or compression of phase portraits (sometimes subtle) such that the phase portrait is no longer circular. In the nonlinear damped oscillator model for pain prediction accuracy,

$$\frac{d^{2}x\left(t\right)}{d{t}^2}=-\zeta \frac{dx\left(t\right)}{dt}-\eta x\left(t\right)-\rho {\left[\frac{dx\left(t\right)}{dt}\right]}^3-\nu \left[\frac{dx\left(t\right)}{dt}\right]x{\left(t\right)}^2-\delta {\left[x\left(t\right)\right]}^3-\mu {\left[\frac{dx\left(t\right)}{dt}\right]}^{2}x\left(t\right)$$ (2)

,all nonlinear terms are simply various products of velocity and/or displacement: Rayleigh (ρ), van der Pol (ν), Duffing (δ), and π-mix odd (μ). Rayleigh and van der Pol are nonconservative terms, characterizing changes in amplitude that are a function of velocity alone or both position and velocity, respectively. Duffing and π-mix odd are conservative terms, characterizing changes in frequency that are a function of position alone or both position and velocity, respectively. The variety of shapes a phase portrait can assume requires a coordinated analysis of these four characteristic nonlinearities (Beek et al., 1995). Note that if the estimates of all the nonlinear terms equals zero, then the nonlinear damped oscillator model in Eq. 2 reduces to the linear damped oscillator model in Eq. 1.

Multilevel Model

We applied a multilevel modeling approach to the nonlinear damped oscillator model. For studies of dynamical systems models, multilevel modeling can capture a within-person periodic relationship when modeling time-varying covariates such as velocity and displacement. The Level 1 multilevel model,

$$\begin{array}{cc}\hfill \text{Level}1:& {\text{acceleration}}_{tj}={\beta }_{1j}\left({\text{velocity}}_{tj}\right)+{\beta }_{2j}\left({\text{displacement}}_{tj}\right)+{\beta }_{3j}\left({\text{Rayleigh}}_{tj}\right)+\hfill \\ \hfill & {\beta }_{4j}\left({\text{vand er Pol}}_{tj}\right)+{\beta }_{5j}\left({\text{Duffing}}_{tj}\right)+{\beta }_{6j}\left(\pi {\text{-mix odd}}_{tj}\right)+r_{tj},\hfill \end{array}$$ (3)

, mirrors the nonlinear damped oscillator model in Eq. 2 with changes only to the mathematical syntax. Acceleration for an individual j at a given time point t was the dependent variable. The intercept was excluded from this analysis because we were not interested in average acceleration, but rather the relation of velocity and displacement to acceleration to characterize periodicity in pain prediction accuracy. Here, the linear terms (velocity and displacement) and the nonlinear terms (Rayleigh, van der Pol, Duffing, and π-mix odd) served as predictors. Zeta, eta and the nonlinear coefficients from Eq. 2 become the betas (β), or regression coefficients, in Eq. 3. β₁ was the damping coefficient and β₂ was the coefficient for squared frequency. β₃ through β₆ were the coefficients for the nonlinear terms. Additionally, a random error component (r) was included in the model.

When the values of the regression coefficients were estimated via our technique, their interpretation is opposite to the standard interpretation. The sign of the β₁ estimate indicates whether the process is damping (positive) or expanding (negative). Larger absolute magnitude estimates of β₁ are indicative of stronger damping or expansion. The square root of β₂ is the frequency of the oscillations (in radians). Larger estimates of β₂ are indicative of more rapid fluctuations. Negative estimates for nonconservative nonlinear terms (β₃, β₄) are indicative of nonlinear expansion, and positive estimates are indicative of nonlinear damping. Negative estimates for conservative nonlinear terms (β₅, β₆) are indicative of slower progression in the vicinity of an accurate prediction of pain. Importantly, positive estimates indicate that the individual is rapidly progressing through maximally accurate predictions. Behavior that can be described by positive nonconservative and negative conservative nonlinear terms may be adaptive in terms of pain prediction accuracy because those terms suggest an approach toward accuracy over the diary and spending more time day-to-day at accurate pain predictions.

Individual differences in average damping, squared frequency and each nonlinear term, and the variation in damping, squared frequency and each nonlinear term across individuals were assessed at Level 2. At Level 2 the regression coefficients for the Level 1 predictors became the dependent variables:

$$\text{Level}2:{\beta }_{1j}={\gamma }_{10}+{\omega }_{1j}$$ (4)

$$\text{Level}2:{\beta }_{2j}={\gamma }_{20}+{\omega }_{2j},$$ (5)

where the gammas (γ) were the average for each Level 1 coefficient (β) and the omegas (ω) were the interindividual variations in each coefficient across people. The Level 2 equations for each of the nonlinear terms were identical in form to the Level 2 equations for the linear terms only the dependent variables (β) changed.

All multilevel analyses were conducted using SAS PROC MIXED (Littell, 1996). Following the precedent of Singer (1998), the independent variables were also modeled as random effects and goodness-of-fit tests were used to determine if inclusion of any of the variables as random effects produced a model with a better fit of the variances and covariances than a model that excluded them. Only displacement improved the fit of the model. The final model, then, included displacement modeled as both a fixed and a random effect. Additionally, a first-order autoregressive variance-covariance matrix was chosen to model the within-subjects variance on the dependent variables.

Modulation in pain prediction accuracy via other psychological processes

Our final analytic goal was to determine if stable trait-like differences in NA, PA and pain control influenced the periodicity observed through either the linear or the nonlinear terms. To accomplish this, we separated out individuals in the top (high NA, PA and pain control) and bottom (low NA, PA and pain control) thirds (n = 56 in each third) for each variable based on their average scores aggregated across diary days. The model specified in Eq. 2 was then run separately for each group, which produced distinct, group-membership-dependent coefficient estimates.

RESULTS

Changes in Pain Prediction Accuracy Across the Daily Diary

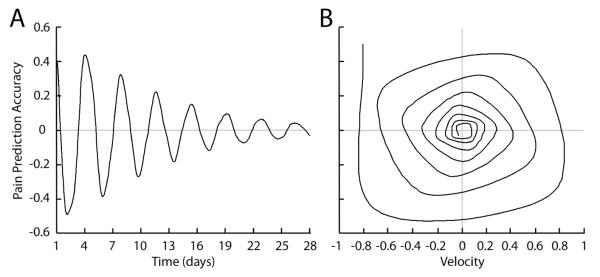
Fixed effects for the linear and nonlinear terms in Eq. 3 were estimated to determine whether pain prediction accuracy followed a damped oscillator pattern across participants. The chi square test of the model over and above a null model identified this as a good description of the temporal relationships, χ²(2) = 450.79, p < .001. Table 1 depicts all of the beta coefficients and corresponding significance levels that were yielded by the model. All beta estimates were entered into a 4^th order Runge-Kutta algorithm to simulate oscillatory patterns in the full model. Figure 1 depicts a simulated time series (Panel A) and phase portrait (Panel B) of pain prediction accuracy. Pain prediction accuracy oscillated between underprediction (below zero) and overprediction (above zero) throughout the time series. A damping trend was observed as the oscillation amplitude decreased over the time series (Panel A) and there was an inward spiral in the phase portrait (Panel B). The fact that the inward spiral was compressed, deformed and distinctly non-circular provided visual evidence for the presence of escapements in the full model.

Table 1.

Fixed Effects Estimates for Each of the Linear and Nonlinear Terms in the Multilevel Model of Pain Oscillations

	Model Category
Model Term	Full	Top 1/3	Bottom 1/3	Top 1/3	Bottom 1/3	Top 1/3	Bottom 1/3
	Model	NA	NA	PA	PA	Pain Control	Pain Control
Velocity (β1)	1.19 × 10−3	0.04	−0.07	−0.02	−0.02	2.28 × 10−3	7.38 × 10−3
Squared Frequency (β2)	−2.74***	−2.79***	−2.67	−2.76***	−2.788***	−2.74***	−2.75
Rayleigh (β3)	−1.20 × 10−4**	−1.50 × 10−4*	1.38 × 10−4	−1.20 × 10−4	−1.50 × 10−4	−2.50 × 10−4**	−1.00 × 10−4
van der Pol (β4)	6.50 × 10−5	3.20 × 10−5	−2.00 × 10−5	1.12 × 10−4	1.55 × 10−4	1.86 × 10−4**	3.30 × 10−5
Duffing (β5)	−3.00 × 10−5	−1.00 × 10−5	−7.00 × 10−5	−3.00 × 10−5	−5.00 × 10−5	−3.00 × 10−5	−1.00 × 10−5
π-mix Odd (β6)	−3.9 × 10−4***	−3.70 × 10−4**	−3.10 × 10−4	−3.00 × 10−4**	−5.30 × 10−4***	−5.70 × 10−4***	−3.50 × 10−4

^*Note. p < .05,

^**p < .01,

^***p < .001

Figure 1.

Time series (Panel A) and phase portrait (Panel B) of pain prediction accuracy simulated using a 4^th order Runge-Kutta algorithm. The diminished oscillation amplitude in the time series and inward spiral in the phase portrait are both indicative of nonlinear damping.

The shape of the oscillatory pattern presented in Figure 1 resulted from the contribution of nonlinear terms. Both Rayleigh, β = −1.2 × 10⁻⁴, t(4414) = −3.42, p < .001, and π-mix odd, β = −3.9 × 10⁻⁴, t(4414) = −5.78, p < .001, were significant predictors. Further, past research has indicated that these nonlinear terms are highly correlated, and so it is reasonable to assume that the overlap should generate slight multicollinearity under the regression-style model (Beek & Beek, 1988; Butner et al., 2005). Thus, even terms that did not meet the a priori p<.05 threshold may have contributed to the shape of the oscillatory pattern.

Upon inspection of either panel in Figure 1, one will notice a damping trend of seven cycles across the diary, with each new cycle starting at a position closer to complete pain prediction accuracy (i.e., the zero point) than the prior one. The frequency estimate allowed us to calculate how many diary days were required, on average, to complete one cycle of pain prediction, an example of which is underprediction through an accurate estimate to overprediction and back again. The estimate for frequency was significant, β = −2.74, t(4414) = −86.58, p < .001. Following the procedure outlined by Butner et al. (2005), we determined that the frequency per day was 0.26, indicating that approximately 25% of a pain prediction accuracy cycle was accounted for by one observation. Therefore, four days of making pain predictions constituted one full cycle.

Patterns in Pain Prediction Accuracy Vary as a Function of Individual Difference Variables

Variations in the oscillatory patterns of pain prediction accuracy as a function of NA, PA and pain control were also examined. All three variables were separately modeled as interaction terms with each of the linear and nonlinear terms in the original model. A significant NA x Rayleigh interaction emerged, β = −1.5 × 10⁻⁴, t(4321) = −2.69, p < .01, indicating that NA moderated the nonlinear damping pattern of pain prediction accuracy. NA did not significantly moderate any other terms of the model. In a separate model, there was a significant PA x Duffing interaction, β = −6.00 × 10⁻⁵, t(4328) = −2.92, p < .01, suggesting that PA moderated the nonlinear frequency of oscillations observed within people. There were no other significant PA interactions. Finally, pain control was examined as an interaction term, yielding significant pain control x van der Pol, β = 3.9 × 10⁻⁵, t(4318) = 2.47, p < .05, and pain control x Duffing, β = 1.30 × 10⁻⁵, t(4318) = 2.01, p < .05, interactions, suggesting that pain control moderated both nonlinear damping and the frequency of oscillations. No other significant pain control interactions emerged.

We took two approaches to measuring the amount of variance explained by the observed effects. First, we compared the within-person variance component of an unconditional (null) model with that of a model containing only the linear terms. This is accomplished by subtracting the conditional variance from the unconditional variance, and then dividing by the unconditional variance. The resulting pseudo-R² of the linear-only model explained 72% of the variance in acceleration, which was the dependent variable in all models. Together, the linear terms modeled simultaneously with individual difference variables, nonlinear terms, and their interactions explained 73% of the variance (pseudo-R²=.73) in acceleration, indicating a 1% increase in variance accounted for by the full model over and above a linear effects-only model.

We then focused on decomposing the variance explained by the individual difference variable x nonlinear term interactions compared with that explained by the individual difference variable main effects alone. In these analyses, we first fit models in which acceleration in pain prediction was predicted as a function of velocity, displacement, an individual difference variable (NA, PA, or Pain Control), and a nonlinear term (Rayleigh, van der Pol, or Duffing). We then calculated a pseudo-R² by entering an individual difference variable x nonlinear interaction term and compared within-person variance components. Those data, along with beta weights and associated p-values for the individual difference variable main effect and interaction terms are presented in Table 2. Due to concerns of multicollinearity resulting in inflated alpha values for interactions tested individually in this post-hoc procedure, we only included interactions that were statistically significant based on our a priori threshold in the original analyses from the full model.

Table 2.

Variance Explained (pseudo-R²) by Interactions Between Individual Difference Variables and Nonlinear Terms Over and Above Corresponding Main Effects-Only Models

Model Term	β	pseudo-R2
NA	−0.69*	-
NA X Rayleigh	−0.0001**	0.006
PA	0.24	-
PA X Duffing	−4.00 × 10−5*	0.004
Pain Control	0.23***	-
Pain Control X van der Pol	7.70 × 10−5***	0.010
Pain Control X Duffing	1.20 × 10−5**	0.001

^*Note. p < .05,

^**p < .01,

^***p < .001.

Results of this post hoc analysis indicated that much of the variance in pain prediction acceleration was explained by the main effects-only models, as indicated by the small pseudo-R² values. Although the variance in pain prediction acceleration associated with the interactions was small, those interactions result in meaningful differences in oscillatory patterns when considering extremes on the individual difference variables (NA, PA and pain control). Such differences can be observed in the top and bottom third simulations that follow.

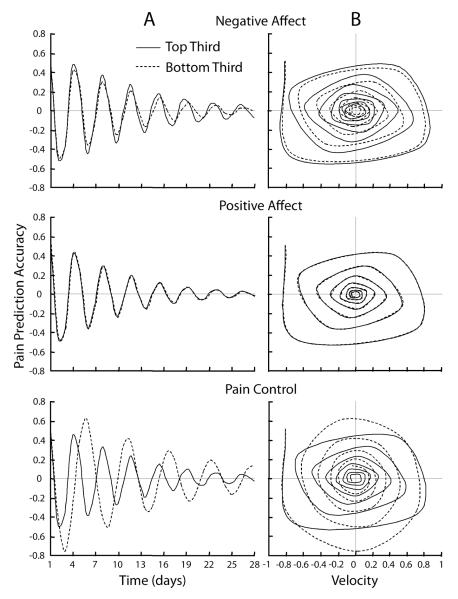
The significant interactions motivated subsequent exploration of differences in oscillatory patterns as a function of patient responding along the continuum of NA, PA and pain control. NA, PA, and pain control were aggregated for each participant across the diary. Fixed effects estimates were then estimated separately for participants in the top and bottom third on each variable. The middle third of responders on each variable were excluded from the analysis. Fixed effect estimates for high and low NA, PA and pain control models, respectively, are presented with the estimates for the full model in Table 1. The same procedure was followed as with the full model: fixed effects estimates were entered into a 4^th order Runge-Kutta algorithm to simulate oscillatory patterns for participants in each separate model. Figure 2 depicts simulated time series of pain prediction accuracy (Column A) and corresponding phase portraits (Column B) for participants that were either high (solid lines) or low (dashed lines) on NA (Top Panel), PA (Middle Panel) and pain control (Bottom Panel). Starting values for the Runge-Kutta algorithm were the same in each simulation in order to produce comparable simulation conditions.

Figure 2.

Time series (Column A) and phase portraits (Column B) of pain prediction accuracy simulated using a 4^th order Runge-Kutta algorithm for participants that were either in the top (solid lines) or bottom (dashed lines) thirds on negative affect (NA; Top Panel), positive affect (PA; Middle Panel) and pain control (Bottom Panel). The effect of individual difference variables on nonlinear damping are displayed through the differences between groups in oscillation amplitude in the time series and the shape of the spiral in the phase portrait.

Each simulation produced the observed damping trend: oscillations decreased in amplitude over the course of the time series and phase portraits displayed inward spirals. There were observable differences in damping between participants who were high (solid line) and low (dashed line) on NA and pain control, but not between participants who were high and low on PA. People with low NA (dashed line) damped faster than people with high NA (solid line) (Figure 2, Top Panel) and people with high pain control (solid line) damped faster than people with low pain control (dashed line) (Bottom Panel). The result was that participants with low NA and high pain control were more accurate than their counterparts in predicting pain by the end of the diary. In contrast, people with high (solid line) and low (dashed line) PA were nearly indistinguishable (Column B, Middle Panel) in their phase portraits, although the significant PA x Duffing interaction suggests that those groups traversed the phase portrait with different frequency characteristics.

Inspection of the time series and phase portraits provided visual evidence of nonlinearities in each model. Consistent with the full model, oscillations in each sub-model were generally compressed, deformed and distinctly non-circular. One exception comes from participants with low pain control (Figure 2, Column B, Bottom Panel, dashed line). When compared to each of the other sub-groups, participants with low pain control damped more slowly and in a more circular, less nonlinear, fashion.

DISCUSSION

In the current study, dynamical systems modeling was used to identify characteristics of the underlying oscillatory structure of the pain prediction process in a sample of people with a chronic pain condition. The hypothesis that oscillations in pain prediction accuracy would damp over time was supported, although that damping was partly a function of nonlinear influences. Examination of fluctuations in pain predictions revealed that meaning could be assigned to the patterns of pain predictions that were experienced by people with RA. In complement to earlier means-based studies, analyses in the current study, examined through the lens of dynamical systems, indicate that RA patients exhibit an oscillatory pattern of pain prediction and gradually become more accurate over time in their ability to predict next-day pain.

Evidence for Nonlinear Damping

The phase portrait of the full model, in which all terms were represented, contained evidence of nonlinear escapements in the form of distorted deviations from perfect circularity. Those distortions were accounted for by both a nonconservative Rayleigh term and a conservative π-mix odd term. The Rayleigh term indicates that energy in the pain prediction accuracy cycle increased only after passing through an overprediction or an underprediction. This pattern of results suggests that, overall, individuals reacted to maladaptive predictions rather than anticipating those maladaptive predictions. The π-mix odd term suggests that pain predictions slowly progressed near zero (accurate pain predictions) and rapidly progressed through large absolute values (maladaptive predictions). Considered together, the Rayleigh and π-mix odd terms indicate that acceleration in the pain prediction accuracy cycle varied depending on the value of the pain prediction.

If the Rayleigh and π-mix odd terms were solely responsible for the resulting oscillations, then damping would not be the predominant pattern. That is because the sign on the Rayleigh term in the full model suggests expansion rather than contraction and the π-mix odd term characterizes changes in frequency, not damping. Thus, the other terms in the model contributed to the damping pattern that emerged. The damping pattern observed in the full model is likely characterized by the linear damping and nonlinear van der Pol terms, which were both of proper sign to show damping. The entire context of terms should be considered in order to comprehend the overall oscillatory pattern. With that stated, both the significance of specific terms in the model and interactions between individual difference characteristics and the specific terms in the model are meaningful with respect to oscillatory patterns in pain prediction accuracy.

Contribution of Individual Differences

Achievement of pain prediction accuracy may be rooted in typical moderators of the pain prediction process: NA, PA and pain control. The observed interactions in the full model, NA x Rayleigh, PA x Duffing, pain control x Duffing and pain control x van der Pol, imply a matching of behavior at the high and low ranges of measurement to distinct patterns of oscillations. We observed many substantial visual differences in our simulations of behavior at those psychological extremes. Based on the classification of nonlinearities as either nonconservative or conservative, those interactions suggest that NA primarily affected damping, PA primarily affected the frequency of oscillation and pain control affected both damping and the frequency of oscillation.

The NA x Rayleigh interaction indicates that, while there were changes in the energy of the phase portrait for people with low NA and people with high NA, changes in energy were more robust for people with low NA than people with high NA. The result was a more rapid damping toward complete accuracy for the low NA group. Further examination of the phase portraits indicated that energy in the phase portrait increased following points of maximum inaccuracy, which resulted in rapid progression through maximum accuracy and slower progression through maximum inaccuracy within cycles. That effect was more enhanced for the low NA group than the high NA group. Although the low NA group damped more rapidly toward accuracy, a side effect of the position at which energy in the phase portrait changed was that they rapidly progressed through the most adaptive predictions and slowly progressed through the most maladaptive predictions.

The effect of the PA x Duffing interaction reflected a redistribution of energy or change in the frequency of oscillation within cycles, which is not easily observed upon visual inspection of the phase portraits. Interpretation of the Duffing term must be based on theory (Abraham & Shaw, 1992), which suggests that changes in the frequency of oscillation are dependent on position alone and that energy increases less robustly at maximum positions. Those individuals who scored high in PA progressed more slowly through inaccurate pain predictions within cycles than people with low PA and demonstrated a more circular damped oscillation. It should be noted that this finding is opposite to our initial prediction that adaptive individual characteristics, such as high PA, would produce adaptive oscillatory patterns in achieving pain prediction accuracy.

In contrast to the PA case, people higher in pain control had a larger Duffing term. For those with high pain control, increases in energy were less robust through points of maximal inaccuracy, such that they slowly progressed through accurate pain predictions within cycles. As evidenced by the pain control x van der Pol interaction, participants high in pain control damped toward accurate pain predictions more quickly than those with low pain control. Examination of the phase portraits for those two groups revealed that the high pain control group was always approximately one cycle ahead in pain prediction accuracy throughout the damping process.

It should be reiterated here that, although the nonlinear terms were important to the overall oscillatory trajectory, and especially to the explication of individual differences in that trajectory, the linear effects of velocity and displacement explained the majority of the variance in acceleration. In particular, the amount of acceleration and deceleration in pain prediction accuracy was largely determined by the displacement of the pain prediction (e.g., over, under, accurate). The strength of such linear effects is to be expected. The velocity term determines the general spiral shape in the phase portrait while the displacement term determines the frequency of movement through the phase portrait. Nonlinear terms determine subtle variations in that overall structure.

Implications and Future Directions

The influence of certain adaptive individual psychological characteristics on oscillatory patterns of pain prediction accuracy may have implications for the self-management of pain. RA patients with low levels of NA as well as those with a heightened sense of control over their daily pain may be better equipped than their counterparts to effectively manage their pain because they achieve greater pain prediction accuracy. Even more, we hypothesize that individual psychological characteristics that lead to increased time spent making accurate pain predictions within cycles is adaptive for pain management. The current findings warrant future efforts to explore the association of pain prediction accuracy and outcomes specific to coping efficacy, pain management and indicators of well-being.

In the current study, NA, PA and pain control were analyzed as trait-like variables. However, evidence of escapements in our model suggests that energy increases and diminishes at specific points in each pain prediction cycle. The implication is that those psychological escapements may also be oscillating processes rather than trait-like processes. Moreover, they may be coupled to pain prediction oscillations, allowing each psychological process to influence pain predictions in a periodic fashion. A logical future direction is to expand the current nonlinear damped oscillator model to a coupled oscillator model (Butner et al., 2005). Coupled oscillators can be modeled by allowing two damped oscillator models to interact via a spring term that allows each oscillator to push or pull the other (Butner et al., 2005).

The use of dynamical systems to model pain prediction accuracy has several implications for the field. Previous studies of pain prediction have used a repeated-measures format and have typically employed regression-based approaches (i.e., multiple regression, general linear models) to summarize the interdependency of pain predictions. Those approaches have led to a treatment of the pain prediction process as static, summarized generally as overprediction (Arntz et al., 1990; Rachman & Lopatka, 1988) or underprediction (Arntz & Peters, 1995; Finan et al., 2008; McCracken et al., 1993). Focusing attention on the pattern of change in the pain prediction process identifies a role for oscillations in pain predictions across repeated measures. Because overpredictions, underpredictions and accurate predictions of pain are interdependent and, to some extent, determinant of future accuracy levels, one should not be considered without the others. For example, in some samples, pain overpredictions have been shown to take on a unique characteristic of being resistant to disconfirmation if they are preceded by an underprediction (Rachman & Arntz, 1991). We argue, then, that a richer analysis of behavior can be achieved by modeling meaningful dynamical patterns in pain predictions over time.

Conclusion

For the broader psychological research field, the current study represents an early attempt to apply nonlinear damped oscillator models to questions of psychological interest. Psychological processes hypothesized to operate in cyclical patterns can now be explained through quantitative techniques. Research on chronic pain is particularly conducive to the development of dynamical models due to the tendency of many chronic pain disorders to cause pain flares spontaneously with varying levels of intensity and duration. As we have shown in the current study, variables that are theoretically linked to differences in the capacity to cope with chronic pain can be included in dynamical models to elucidate cognitive differences between people that would otherwise have been treated as random noise. It is our hope that new hypotheses will be tested and theory will continue to develop as these techniques become more accessible to the research community.