SIE calculations on molecular dynamics trajectories: Increasing the efficiency using systematic frame selection

Abstract

End-point methods such as Linear Interaction Energy (LIE) analysis, Molecular Mechanics Generalized Born Solvent Accessible Surface (MM/GBSA) and Solvent Interaction Energy (SIE) analysis have become popular techniques to calculate the free energy associated with protein-ligand binding. Such methods typically use molecular dynamics (MD) simulations to generate an ensemble of protein structures that encompasses the bound and unbound states. The energy evaluation method (LIE, MM/GBSA or SIE) is subsequently used to calculate the energy of each member of the ensemble, thus providing an estimate of the average free energy difference between the bound and unbound states. The workflow requiring both MD simulation and energy calculation for each frame and each trajectory proves to be computationally expensive. In an attempt to reduce the high computational cost associated with end-point methods, we study several methods by which frames may be intelligently selected from the MD simulation including clustering and address the question how the number of selected frames influences the accuracy of the SIE calculations.

Introduction

Docking is widely used in the drug discovery process for virtual screening, and to predict protein-ligand binding modes. In order to dock large ligand libraries used in virtual screening, a balance between accuracy and efficiency must be found when modeling the underlying physics of protein-ligand interactions. Consequently, the scoring functions used to quantify protein-ligand interactions in docking programs typically focus on an important, but relatively simple, subset of interaction elements, such as hydrogen bonds and hydrophobic contacts. This simplified representation of protein-ligand interactions significantly contributes to the failure of docking to accurately predict binding affinities.^1,2 Although recent docking methods have been refined to somewhat include protein flexibility known to be important for protein-ligand conformational adaptation, the docking predicted free energy of binding is still usually based on a single protein-ligand complex structure neglecting the fact that the protein-ligand complex samples local substates in the conformational vicinity of a given binding mode.

Post-processing methods provide a means to overcome the weaknesses of simple scoring functions used in docking by including the missing dynamic information in the energy estimate and utilizing a more sophisticated physical representation of protein-ligand interaction, thus more accurately estimating the free energy of binding.³ These techniques employ MD or MC simulations to provide a trajectory, and a free-energy estimation technique such as free-energy perturbation (FEP),⁴ thermodynamic integration (TI),⁵ molecular-mechanics Poisson-Boltzmann, generalized-Born surface-area (MMPBSA/GBSA),^6,7 or linear interaction energy analysis (LIE)⁸ is used to calculate the average energy over the trajectory. In docking applications that employ end-point methods (MMPBSA/GBSA, LIE, or SIE), either the top-scored binding pose or several favorably scored poses are used as input for the subsequent MD or MC simulations. Even if limited to a few ligands and a small number of binding poses, this post-processing step can significantly improve the successful identification of binding modes and prediction of binding affinities.³

MMGBSA and LIE have become popular post-processing methods due to their computational efficiency and applicability to diverse sets of ligands, drawbacks associated with the most accurate methods to predict relative free energies of binding, FEP and TI. LIE, however, requires a priori knowledge of a set of active ligands with experimentally known binding affinities in order to optimize the protein-dependent regression coefficients inherent to the LIE equations. In contrast, MMGBSA can be applied to any protein-ligand system without additional regression, but this method requires the calculation of an explicit entropy term that is prone to slow convergence⁹ and, for some systems, displays overly large contributions to the absolute free energy of binding.¹⁰ Other end-point methods used to quantify protein-ligand interactions include the mining minima approach,^11-14 linear response approximation (LRA) and the protein dipoles Langevin dipoles (PDLD/S-LRA) version thereof.^10,15,16

Solvated interaction energy (SIE)¹⁷ is a relatively new end-point method that shares elements from the LIE and MMPBSA/GBSA methods. Similar to MMPBSA/GBSA, SIE treats the protein-ligand system in atomistic detail and solvation effects implicitly. The free energy of binding between ligand and protein is computed by:

$$\Delta G_{\text{bind}}(\rho ,D_{\text{in}},\alpha ,\gamma ,C)=\alpha [\Delta E_{vdW}+\Delta E_{\mathit{Coul}}(D_{\text{in}})+\Delta G_{RF}(\rho ,D_{\text{in}})+\gamma \cdot \Delta SA(\rho \left)\right]+C,$$ (1)

where ΔE_vdW and ΔE_Coul are the intermolecular van der Waals and Coulomb interaction energy between protein and ligand, ΔG_RF (ρ, D_in) is the difference in the reaction-field energy between the bound and free state of the protein-ligand complex as calculated by solving the Poisson equation with BRI BEM,^18,19 and ΔSA(ρ) is the difference in molecular surface area between the bound and free state of the protein. The five parameters in equation (1) were fitted to the absolute free energy of binding of 99 protein-ligand complexes: The linear scaling factor ρ of the van der Waals radii of the AMBER99 force field, the dielectric constant inside the solute D_in, the coefficient γ for quantifying the free energy associated with the difference in surface area upon protein-ligand binding, and the prefactor α that implicitly quantifies the loss of entropy upon binding, also known as entropy-enthalpy compensation, and a constant C that includes protein-dependent contributions not explicitly modeled by the SIE methodology, e.g. the change in protein internal energy upon ligand binding. The default values of the parameters are: ρ = 1.1, D_in = 2.25, γ = 0.0129 kcal/(mol·A²), C = −2.89 kcal/mol, and α = 0.1048.

SIE has been utilized to estimate the binding free energy based on a MD trajectory of the protein-ligand complex.^20,21 In this process, individual SIE calculations on equally separated snapshots from the trajectory are averaged to provide an estimate of the free energy of binding. However, studies seldom address the question how many snapshots from the MD simulation are required to accurately predict the binding free energy. In this article we aim to address this question and focus on ways to reduce the computational time needed to accurately estimate binding energies using SIE. In particular, we address the following two questions: How does the number of snapshots used in the SIE calculation influence the accuracy of predicting the free energy of binding, and can we intelligently select frames from the MD simulation that represent structurally similar frames with similar contributions to the binding energy by clustering the full trajectory? This article can be related to other work studying the convergence of alternative endpoint methods such as MMPBSA and MMGBSA.^22-24

Materials and Methods

Protein Systems and Preparation

Our study was performed on three different protein systems, neuraminidase, avidin and thrombin. For neuraminidase, ten protein-ligand complexes were studied containing seven experimentally determined crystal structures (1bji, 1nnc, 1mwe, 2qwi, 2qwk, 1f8c, 1f8b) and three additional complexes by adding three ligands (Table 1, N8-N10) to the 1bji structure.²⁵ For these three complexes, the initial binding pose of the original 5-acetylamino-4-amino-6-(phenethyl-propyl-carbamoyl)-5,6-dihydro-4h-pyran-2-carboxylic acid ligand was used, but the propyl group was shortened to an ethyl group, a methyl group, or a hydrogen atom to generate the three additional pseudo X-ray structures (Table 1, N8-N10). For avidin, seven ligands were chosen that were previously used in MM/PBSA²⁶ and LIE²⁷ studies. Based on the biotin-avidin complex (1avd), six additional ligands (Table 1, A2-A7) were generated by manual mutation of the biotin ligand in the binding site of avidin. For thrombin, we used a dataset containing ten ligands from a single SAR study^28-32 and manually mutated the co-crystallized ligand from the 1mu6 crystal structure to generate the starting complex structures of thrombin with ligands T1-T10. All ligands and their associated binding affinities are displayed in Table 1.

Table 1.

Protein-ligand complexes used in our study: The ligand name (as used in this paper), the 2D representation of each structure, the PDB code of protein structure of each complex, and the binding affinity of each ligand is shown. Experimental affinities are taken from ^25-32.

Ligand name	Ligand structure	PDB of protein	Affinity in nM	Ligand name	Ligand structure	PDB of protein	Affinity in nM
Neuraminidase
N1		1bji	2	N2		1nnc	5
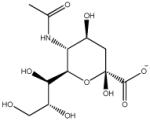
N3		1mwe	1·106	N4		2qwi	20
N5		2qwk	2	N6		1f8b	8600
N7		1f8c	320	N8		1bji	5
N9		1bji	320	N10		1bji	12000
Avidin
A1		1avd	1.4·10−6	A2		1avd	0.038
A3		1avd	0.063	A4		1avd	390
A5		1avd	1060	A6		1avd	2.3·105
A7		1avd	5.3·105
Thrombin
T1		1mu6	4.2	T2		1mu6	280
T3		1mu6	17000	T4		1mu6	0.042
T5		1mu6	44	T6		1mu6	0.5
T7		1mu6	12	T8		1mu6	0.36
T9		1mu6	2	T10		1mu6	3

The hydrogen-bond network of each crystal structure was optimized by rotating Asn, Gln, and His residues, and by assigning protonation states to His using the Reduce program.³³ The protein parameters used in the molecular mechanics minimizations and molecular dynamics (MD) simulations were assigned based on the Amber ff03³⁴ force field implemented in the Amber10 program suite.³⁵ The ligand force field parameters were assigned using the general Amber force field (gaff)³⁶ and partial charges were calculated using the AM1/BCC methodology.³⁷ Each protein-ligand system was placed in a rectangular box of TIP3P water with the minimum distance between any solute atom and the boundary of the box set to 10 Å. The system was neutralized by adding Cl⁻ or Na⁺ counter ions as needed. All protein-ligand systems were prepared using our in-house PyMOL³⁸ plugin that automatically calls the antechamber and tleap modules from the AmberTools 1.4 program suite.

MD simulation protocol

Periodic boundary conditions were applied to each protein-ligand system and the long range electrostatic interactions were calculated using the particle mesh Ewald (PME) method. After 500 steps of minimization, the water molecules were equilibrated for 250 ps restraining the position of any solute atom with an harmonic potential with a force constant of 5 kcal/(mol·Å²). Subsequently, the full system was equilibrated for 500 ps, and the final production MD simulation was run for 10 ns for each system. The time step was 2 fs, the temperature set to 310 K, and all bonds containing a hydrogen atom were constrained using the SHAKE algorithm.³⁹

All molecular mechanics minimizations and position restraint simulations were performed with the sander module of the Amber10 program suite and the equilibration and production runs used the pmemd module. 1000 equally spaced snapshots of the protein-ligand complex (every 10 ps) were generated from the production MD trajectory and all water molecules and counter-ions were removed before subsequent SIE analysis. This ensemble of 1000 snapshots is referred to as “full trajectory” throughout the article.

Free energy calculation using SIE

The free energy of ligand binding was determined by applying the sietraj¹⁷ software to the selected MD snapshots and averaging over the resulting free energies obtained from each snapshot. The correlation between the predicted and experimental free energy was determined using the default parameters in equation (1) as well as optimized parameters for α, γ and C. To obtain optimized parameters for each protein system, the parameters α and γ were systematically varied within physically meaningful ranges (α ∈ [0.05; 1.0], γ ∈ [0.005; 0.025] kcal/(mol·A²)) and C was optimized to minimize the sum of the absolute deviations between predicted and experimental affinity for all ligands in a protein dataset. The values for α need to be positive and smaller than one as they characterize the entropy-enthalpy compensation and γ should be in a range postulated by other studies^40,41 utilizing the difference in molecular surface area as contribution to the free energy of binding associated with non-polar desolvation.

Selection of snapshots

SIE calculations were performed using sietraj¹⁷ on the full MD trajectory, and on selected frames from the MD simulation. The following frame selection protocols were investigated: Equally spaced snapshots from each MD trajectory were selected using 1, 2, 3, 4, 5, 7, 10, 15, 20, 25, and 50 frames for separate analyses. Random selection of frames from the full trajectory was performed five times, yielding five different analyses for each number of frames (1, 2, 3, 4, 5, 7, 10, 15, 20, 25, 50) to be selected. As a last selection protocol, the MD trajectory was clustered based on pair-wise RMSD values between different snapshots from the MD trajectory. The RMSD values between different MD frames s and t were computed using only the heavy atoms of the protein:

$$\mathit{RMSD}(s,t)=\frac{\sum _{i\in \text{heavy atoms}}{w}_i\cdot \sqrt{{\mid r_i\left(s\right)-r_i\left(t\right)\mid }^2}}{\sum _{i\in \text{heavy atoms}}{w}_i}$$ (2)

and the weight w of each protein atom’s contribution to the RMSD was calculated using the formula:

$$w_i=\frac{1}{\exp (\lambda \cdot \left({\tilde{r}}_{iL}-\beta )\right)+1}$$ (3)

where ${\tilde{r}}_{iL}$ is the shortest distance between protein atom i and any heavy ligand atom in the initial frame of the MD simulation, and λ and β characterize the size and slope of the weight as a function of distance (see Figure 1). Thus, we weight protein atoms closer to the ligand more than atoms distant from it, in order to bias the calculation of RMSD toward the region surrounding the ligand. Different sets of values for parameters λ (0.1 Å⁻¹, 0.25 Å⁻¹, 0.5 Å⁻¹, 1.0 Å⁻¹, 5.0 Å⁻¹) and β (5 Å, 8 Å, 10 Å, 15 Å and 20 Å) were investigated (Figure 1). It should be noted that curves with λ = 5.0 Å⁻¹ approximate the standard RMSD calculations but include a cutoff defined by the parameter β (see Figure 1, left).

Figure 1.

Examples of weighting functions used to cluster the MD frames.

K-means clustering was performed using the RMSD values to generate 1, 2, 3, 4, 5, 7, 10, 15, 20, 25, and 50 clusters from the MD trajectory. The frame with the smallest sum of RMSD values to all members of the cluster is selected as the representative protein-ligand structure and subsequently used as the input for SIE calculations.

Measures of prediction accuracy

Two different criteria were selected to measure the influence of frame selection on the prediction quality of the free energies of binding. The first measure assumes that the SIE calculation on the full MD trajectory (containing 1000 frames) is the most precise estimation of the free energy of binding, referred to as “full” predicted free energy. The difference between the free energy computed using a reduced set of MD frames and the predicted free energy using the full MD trajectory serves as the criterion to define the accuracy of computing the free energy of binding. The second measure of accuracy is the difference between the Pearson regression coefficient (r) of the free energy of binding calculated when using the full trajectory and the reduced number of snapshots. A comparable analysis was performed using the Spearman’s rank correlation coefficient (r_s). The results for this analysis are shown in the Supporting Information S1.

Results and Discussion

Prediction accuracy of SIE using the full MD trajectory

To establish an “upper bound” for SIE’s ability to calculate binding free energies for the three selected protein systems, we computed the “full” predicted binding free energy based on all snapshots of the MD trajectories. Comparing the “full” SIE predicted free energies with experimental free energies (G_exp) revealed significant deviations (see Table 2) when using SIE’s default set of parameters (optimized on 99 PDB structures). In an attempt to improve the prediction of the absolute binding free energies, we optimized the SIE parameters α, γ and C. The predicted binding free energies using the optimized parameter set for each protein system reveals a significant reduction in the mean absolute deviation between the predicted and the experimental free energies of binding (Table 2). All three parameters (α, γ, and C) were significantly different than the default value, and different optimized parameter values were identified for each individual protein system. A twofold decrease (avidin) and increase (neuraminidase, thrombin) was observed for γ compared to the default value, and the parameter α increased by approximately a factor 2-5 in all protein systems. The largest deviation between default and fitted value was observed for the parameter C. Potential reasons for the need of refitting the three parameters for each system are inherent shortcomings of the molecular-mechanics force field (e.g. neglect of polarization, electron transfer or lone-pair directionality), the neglect of internal energy changes using a single trajectory approach (i.e. no individual protein or ligand simulation is performed) and explicit solvent effects. Furthermore, the ratio of entropy to enthalpy is not necessarily identical for each protein-ligand complex. Finally, it should also be noted that the experimental binding affinities themselves are not consistently measured for all three protein targets. A relative shift of binding free energies between the three protein systems is not unlikely.

Table 2.

Mean absolute deviation between the predicted and the experimental free energies when using the SIE (eq 1) default coefficients for α, γ and C and optimized parameters for each protein system. The default values are α = 0.1048, γ = 0.0129 kcal/(mol·A²), and C = −2.89 kcal/mol.

Protein system	Mean absolute deviation from Gexp (no parameter optimization) [kcal/mol]	Mean absolute deviation from Gexp (parameter optimization) [kcal/mol]	Optimized parameters
			α	γ [kcal/(mol·A2)]	C [kcal/mol]
Neuraminidase	2.26	1.39	0.22	0.023	2.5
Avidin	2.71	1.78	0.34	0.005	2.5
Thrombin	2.86	1.47	0.48	0.024	20.5

Representative plots displaying SIE energy versus time and all-heavy atoms RMSD (to the original protein-ligand complex structure) versus time for each protein system are displayed in Supporting Information S2 indicating how such terms fluctuate over the “full” trajectory for each protein system.

Using the optimized set of SIE parameters (Table 2), the Pearson correlation coefficients (r) between the experimental and SIE predicted free energy of binding were at least 0.7 for all three of the protein systems studied (shown in Table 3). To assess the generality of the regression model we performed leave-one-out (LOO) cross-validation. The difference between the LOO Pearson correlation coefficient (q) and r (see Table 3) suggests that the regression models for neuraminidase and avidin are relatively stable whereas a more significant difference between q and r was identified for thrombin. This is consistent with the largest deviation of the optimized parameters α, γ and C from the default values for thrombin compared to neuraminidase and avidin.

Table 3.

The accuracy of predicting binding free energies using SIE as measured by the Pearson correlation coefficient (r) between experimental and predicted binding free energies and the leave-one-out cross-validated Pearson coefficient (q). The r and q values are shown for three different protein systems using all 1000 snapshots from each MD simulation.

Protein system	Pearson correlation coefficient for full MD trajectory	Leave-one-out cross- validated Pearson coefficient for full MD trajectory
Neuraminidase	0.83	0.69
Avidin	0.89	0.77
Thrombin	0.71	0.41

Prediction accuracy based on a selection of snapshots

Next, we address the question how the number of frames selected from the MD simulation influences the accuracy of SIE calculated binding affinities. Using a selection of equally spaced frames from the MD trajectory, the absolute free energy difference between the SIE computed energy averaged over the selected MD snapshots and the mean energy using the full MD trajectory was computed. This deviation averaged over all complexes of each studied protein system quickly diminished to approximately 0.5 kcal/mol as the number of selected frames (Figure 2, green line) increased. Furthermore, only five snapshots from each protein system were needed to reach this level of accuracy. The maximum absolute deviation for any compound in each protein data set is below 1 kcal/mol if ten equally separated MD frames (Figure 2, green dashed line) were used.

Figure 2.

Absolute deviation of the free energy predicted from a set number of frames extracted from the MD trajectory compared to the free energy computed on the full MD trajectory. Displayed are the deviations as a function of number of selected frames (logarithmic scale) for the protein systems (a) neuraminidase, (b) avidin, and (c) thrombin. The results of using equally spaced frames (green line: absolute deviation averaged over all ligands; green dashed line: maximum absolute deviation of an individual ligand), snapshots chosen by random selection (red line: absolute deviation averaged over all ligands and all five different random selection runs; red dashed line: maximum absolute deviation of all ligands averaged over all five different random selection runs; red dotted line: overall maximum absolute deviation of an individual ligand among any of the five different random selection runs), and frames idenitified by k-means clustering using the pairwise RMSD values between MD frames as distance criterion (blue line: absolute deviation averaged over all ligands; blue dashed line: maximum absolute deviation of an individual ligand) are shown. For comparison the mean absolute deviation of the full trajectory from G_exp for neuraminidase, avidin and thrombin are 1.39 kcal/mol, 1.78 kcal/mol and 1.47 kcal/mol, respectively. Analysis of the individual contributions to the SIE energy (see Supporting Information S3) displays that the van der Waals (α·ΔE_vdW), electrostatic (α·ΔE_Coul(D_in)), and reaction field (α·ΔG_RF(ρ, D_in)) energy contributes about equally to the average deviation from the “full” free energy whereas the solvent accessible energy term (α·γ·ΔSA(ρ)) contributes less to the average deviation.

As an alternative to equally spaced frame selection, MD snapshots were randomly selected from the ensemble of 1000 frames from the full MD trajectory. For each amount of randomly selected frames (1, 2, 3, 4, 5, 7, 10, 15, 20, 25, 50) the random selection procedure was repeated five times. The mean (Figure 2, red line) and maximum (Figure 2, red dashed line) deviation between the predicted and the experimental binding free energy, averaged over the five different random selection procedures, was comparable in size to the deviations observed for equally spaced frame selection. Considering each individual random selection run separately (i.e. one of the five runs), however, produced less rapid approximations (compared to equal separation) of the free energy of binding when increasing the number of frames. This is evident from the dotted red line in Figure 2, showing the maximum deviation between randomly selected frames and using the full trajectory to predict the free energy of binding for an individual ligand. The reduction in predictive accuracy when randomly selecting frames compared to selecting equally separated frames is intuitive as fluctuations of the computed free energies over a 10ns MD trajectory may be partially smoothed out by selecting equally separated frames, whereas random selection can choose frames that are chronologically close on the timeline of the MD simulation. When this situation occurs in random selection, close snapshots can overweight the free energy contribution of frames that display large deviation from the average SIE energy of the MD trajectory.

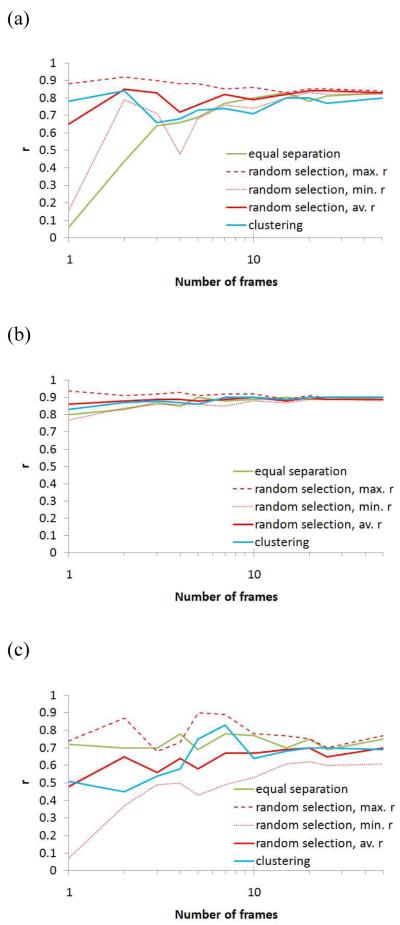
A similar relationship between the frame selection process and the prediction quality was observed when analyzing the variation of the Pearson correlation coefficient (r) as a function of the number of selected frames (Figure 3). Using a selection of five equally separated frames, r deviated by less than 0.1 from the full trajectory correlation coefficient in all three protein systems. On average, a random selection of five frames produced the same level of prediction quality when the same number of equally spaced frames was used. It should be noted that r did not significantly increase with number of selected frames (cf. Figure 3) in all protein systems.

Figure 3.

Pearson regression coefficient (r) of the predicted free energies based on a selected number of frames compared to the free energy computed using the full MD trajectory. Displayed are the r values as a function of number of selected frames (logarithmic scale) for the protein systems (a) neuraminidase, (b) avidin, and (c) thrombin. The results of using equally spaced frames (green line), snapshots chosen by random selection (red dashed line: maximum r among the five random selection runs; red dotted line: the minimum r among the five random selection runs; red line: r value averaged over the five random selection runs), and frames idenitified by k-means clustering using the pairwise RMSD values between the MD frames as distance criterion (blue line).

In an attempt to further improve the frame-selection process, snapshots were extracted from the full MD trajectory by clustering the trajectory using the pair-wise RMSD values between the snapshots. The RMSD values between different snapshots were calculated using eq 2 with different λ and β values. To identify the optimal combination of the λ and β value, the average and maximum deviation (over all complexes of a protein system) of the predicted free energy of binding using k number of extracted frames (= cluster centers) from the “full” predicted free energy was calculated for k = 1, 2, 3, 4, 5, 7, 10, 15, 20, 25, and 50. The best combination was then selected by a fitness function that averages over the deviations d_k of particular number k weighted by the number of clustered snapshots k:

$$f=\frac{\sum _{k}k\cdot d_k}{\sum _{k}k}\text{with}k\in \{1,2,3,4,5,7,10,15,20,25,50\}$$ (4)

The underlying idea of the fitness function is that predicted free energies based on a large number of frames are expected to have smaller deviations from the “full” free energy compared to energies that are based on a small number of frames. Consequently, large deviations using a large number of frames should be weighted more than similar sized deviations when using a smaller number of frames. The optimal values of λ and β are achieved when the fitness function is minimal.

Figure 4 displays the fitness function in form of a heat map for the average deviation over all compounds of a protein system (left column) and the maximum individual deviation of an individual ligand (right column) of the dataset when the value of λ and β are varied. Evident in Figure 4, different combinations of λ and β are optimal for each protein system, but a λ value of 0.1 Å⁻¹ consistently gives low fitness values for all three protein systems. Because no clear trend was identified when trying to determine the optimal value of β when λ = 0.1 Å⁻¹, we arbitrarily picked β = 8 Å for subsequent analysis and discussion.

Figure 4.

The fitness function f (eq 4) dependent on variables λ (vertical axis; units in Å⁻¹) and β (horizontal axis; units in Å) is shown for (a) neuraminidase, (b) avidin, and (c) thrombin. An “optimal combination of λ and β corresponds to the lowest fitness function value. The average deviations over all compounds of a protein system are displayed in the left column and the maximum individual deviation of an individual ligand in the right column.

The reasoning behind selecting frames by representative clusters of the MD trajectory is the assumption that similar protein-ligand structures results in similar protein-ligand interactions that are subsequently reflected in similar SIE energies. To test this hypothesis, we computed the RMSD values using eq. 2 between all 1000 snapshots of the MD trajectory for randomly selected ligands from our dataset and correlated the RMSD with the computed difference in SIE energies (Figure 5). The plots indeed support our hypothesis: low RMSD frame pairs tend to have small calculated energy differences, whereas frames with a large RMSD value between them frequently had large energy differences. However, the observed trend between RMSD and the energy difference between frame pairs is relatively weak and protein-system dependent. We note that for frame pairs with a low RMSD (< 1 Å), energy differences of up to 5 kcal/mol were observed. Due to this weak trend between structural and energetic similarity among the MD frames, the quality of the SIE predicted binding free energy did not significantly improve using our trajectory clustering scheme compared to using the equally spaced frame selection scheme (Figures 2 and 3).

Figure 5.

Difference in the predicted free energy (horizontal axis; units in kcal/mol) between two MD snapshots as a function of the RMSD between the snapshots (vertical axis; units in Å) for four selected protein-ligand complexes: (a) compound N1 binding to 1bji (neuraminidase), (b) compound A3 binding to 1avd (avidin), (c) compound T4 and (d) compound T8 binding to 1mu6 (thrombin). The RMSD values are distributed into bins with width of 0.1 Å and the differences in the SIE energy are distributed to bins with width of 0.5 kcal/mol. For each RMSD bin (row) the probability is normalized to one, and the color coding represents the probability of identifying a pair of MD frames with specified energy difference at given RMSD value. No pairs of frames with RMSD < 0.5 Å were sampled throughout the individual MD simulations and these lines are assigned a probability of zero. The same assignment is done for large RMSD bins that were not sampled by the MD simulation. The magnitude of the probability is color coded ranging from white (zero probability) over yellow and red to black (maximum probability).

Conclusions

Estimating free energies of binding using SIE is a potentially valuable addition to the tool set of end-point methods such as MM/GBSA and LIE. Studying three different protein systems, however, revealed that the default set of SIE parameters is not sufficient to accurately predict the absolute free energy of binding. Our studies suggest that retuning the parameter set, analogous to the standard tuning procedure used for LIE calculations, is necessary to achieve accurate calculations using SIE.

Remarkably, selecting 5-10 equally spaced snapshots displayed prediction accuracy comparable in quality to using the full MD trajectory. An analogy can be drawn to a study by Wang et al.⁴² on consensus scoring, if we assume that the energies associated with the different frames fluctuate around the mean following a normal distribution, and that the mean corresponds to the experimental free energy. Wang et al.⁴² showed that under this premise the mean of about five energy values from different scoring functions approach the true value, in their study the experimental binding affinity. Based on the idea that clustering of the MD trajectory would identify frames that cover the conformational space sampled by the protein-ligand complex, we utilized k-means clustering of the MD trajectory to select frames for SIE analysis. Due to the relatively minor trend between structural and energetic similarity between the MD frames when using SIE, the clustering scheme did not lead to an increase in prediction accuracy compared to using equally spaced frames from the trajectory

Based on the reported studies, SIE appears to have the potential to be a powerful post-processing tool that could be used to provide a better estimation of binding affinity for docking poses. It should, however, be noted that in this study we have used known binding poses and have not tested if SIE could differentiate native from decoy docking poses or can accurately predict binding affinities including structurally even more diverse families of ligands. In addition, only a small number of selected frames are needed to achieve the same level of accuracy when using the entire MD trajectory to estimate the free energy of binding.