Model for the fast estimation of basis set superposition error in biomolecular systems

Abstract

Basis set superposition error (BSSE) is a significant contributor to errors in quantum-based energy functions, especially for large chemical systems with many molecular contacts such as folded proteins and protein-ligand complexes. While the counterpoise method has become a standard procedure for correcting intermolecular BSSE, most current approaches to correcting intramolecular BSSE are simply fragment-based analogues of the counterpoise method which require many (two times the number of fragments) additional quantum calculations in their application. We propose that magnitudes of both forms of BSSE can be quickly estimated by dividing a system into interacting fragments, estimating each fragment's contribution to the overall BSSE with a simple statistical model, and then propagating these errors throughout the entire system. Such a method requires no additional quantum calculations, but rather only an analysis of the system's interacting fragments. The method is described herein and is applied to a protein-ligand system, a small helical protein, and a set of native and decoy protein folds.

INTRODUCTION

The application of quantum chemistry to large molecular systems is a challenging endeavor that is complicated by several factors. First, the high number of degrees of freedom makes orbital and conformational optimization very computationally demanding, which has led to novel linear scaling algorithms such as FMO,¹ MFCC,² and divide and conquer schemes.^{3, 4, 5} In addition, large molecular systems contain many different types of chemical interactions, all of which need to be accurately modeled by the energy function in order to reliably estimate the energy of the composite system.^{6, 7} Efforts have been made to estimate and correct for these fragment-based interaction energy errors as well.^{8, 9}

Compact molecular systems with many inter- and intramolecular contacts introduce yet another source of error in quantum chemical calculations on large systems: basis set superposition error (BSSE). BSSE is a consequence of using incomplete basis sets, and stems from the fact that fragment A of a system can use basis functions from a proximal nonbonded fragment B to variationally (and artificially) lower A's contribution to the electronic energy and, in the end, overestimate the strength of the nonbonded molecular interaction between fragments A and B. The counterpoise procedure has commonly been utilized to correct for BSSE in the intermolecular case.¹⁰ In the procedure, the energies of systems A and B are evaluated both with and without the basis functions of the partner system. The sum of energy differences between the calculations with (${\mathrm{E}}_{\mathrm{A}}^{\prime }$ and ${\mathrm{E}}_{\mathrm{B}}^{\prime }$) and without (E_A and E_B) the additional basis functions is the magnitude of artificial stabilization due to BSSE (ΔE_BSSE). ΔE_BSSE from Eq. 1 is always negative and should be subtracted from the calculated interaction energy between A and B:

$${\Delta \mathrm{E}}_{\mathrm{BSSE}}={\mathrm{E}}_{\mathrm{A}}^{\prime }-{\mathrm{E}}_{\mathrm{A}}+{\mathrm{E}}_{\mathrm{B}}^{\prime }-{\mathrm{E}}_{\mathrm{B}}.$$ (1)

Intramolecular BSSE (IBSSE) has been observed in molecules as small as benzene, for which a nonplanar optimum geometry is observed when using small Pople-style basis sets with MP2.^{11, 12} A main concern about IBSSE is that it affects the ability to compare different conformations of the overall system. Balabin's estimation of IBSSE in small peptides suggests that IBSSE can often be equal to or even greater in magnitude than the relative energies between small peptide conformations,¹³ which might prohibit quantum-based energy functions containing IBSSE from producing reliable results in any computational study requiring accurate potential energy surfaces such as free energy calculations, molecular dynamics simulations, or even simple geometry optimization. Most current methods of estimating IBSSE are intramolecular analogues of the counterpoise method for intermolecular systems. The overall system is broken down into molecular fragments (or in some cases individual atoms¹⁴) which are then analyzed with and without neighboring basis functions to estimate the energy differences due to IBSSE. These methods (with the exception of the atom-based method) require input from the user about how to fragment the overall system, which is non-unique. Furthermore, these methods require additional quantum calculations for each fragment, leading to a total of 2N + 1 calculations where N is the number of fragments (unless the isolated fragment or atomic energies are stored in a database, in which case there would be N + 1 calculations). The generated fragments may be left as radicals or saturated with hydrogen link atoms, either of which may alter the electronic environment of the fragment and yield uncertainties in the estimation of the fragment's contribution to IBSSE.

STATISTICAL MODEL OF FRAGMENT-BASED CONTRIBUTIONS TO BSSE

Recently we have introduced a method of estimating errors in energy functions for large molecules by estimating fragment-based errors and propagating these errors over the interacting fragments of the entire system.^{8, 9} The fragment-based error estimates are derived from a database of common interacting fragments found in proteins and protein-ligand complexes and the resulting error probability density functions constructed by comparing their calculated energies from a given method with accurate reference energies (e.g., CCSD(T)∕CBS). By assuming that the fragment-based interactions contain errors that are independent from one another (this seems to be an acceptable assumption for largely electron-localized systems such as proteins),¹⁵ each fragment's contribution to the overall error can be estimated with the appropriate probability density function and then be propagated throughout the overall system to yield an overall estimate of both systematic and random error.

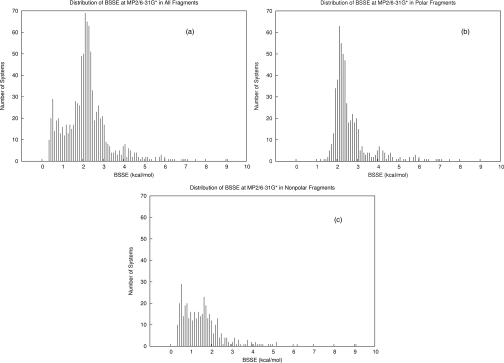
In order to apply these methods to the problem of BSSE, we have generated thousands of interacting molecular fragments from high resolution (<2.0 Å) crystal structures from the Protein Data Bank (PDB) with an in-house fragmentation program. Each PDB structure was first saturated with hydrogen atoms with the program REDUCE (Ref. ¹⁶) followed by an optimization of the hydrogen positions with ff99sb (Ref. ¹⁷) in AMBER (Ref. ¹⁸) before fragmentation. A description of the fragmentation algorithm is given in the supplementary material.²¹ A random sample of nearly 1000 interacting fragments was selected and categorized by the interaction types of backbone-backbone hydrogen bonds (312), charged (107), polar (224), and nonpolar (354) interactions. The interacting fragments were analyzed for gas-phase electronic interaction energy with MP2∕6-31G* (an arbitrary example energy model sure to yield significant BSSE) with and without the counterpoise correction in order to determine the BSSE magnitudes. The calculations were performed using the GAUSSIAN 09 program.¹⁹ The distributions of BSSE magnitudes (kcal∕mol) are plotted in Figure 1, which shows a clear distinction between the van der Waals∕nonpolar and hydrogen bonded∕polar fragment pairs.

Figure 1.

Distributions of BSSE magnitudes (at MP2∕6-31G*) of interactions in our protein fragment database. (a) Distribution of all types of interactions (N = 997). (b) Distribution of polar interactions including backbone-backbone hydrogen bonds and charged interactions (N = 643). (c) Distribution of nonpolar interactions (N = 354).

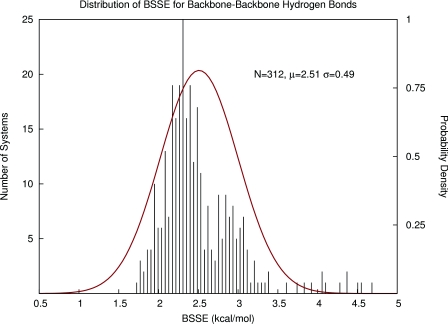
In our first attempt to estimate BSSE for large systems, we proposed to use the same strategy as described previously involving the construction of Gaussian probability density functions (pdf's) describing the likely magnitudes of BSSE between database fragments. An example pdf is given in Figure 2 for backbone-backbone hydrogen bonds. Simply using the mean and standard deviation of these functions to predict BSSE between fragment interactions may be a very fast method but it has some disadvantages. First, BSSE always increases the stability of dimers and thus will only lie on one size of zero on the real number line. Therefore, the BSSE values cannot be truly normally distributed. Second, for each interaction type, the approximate normal distributions are all very wide, which would yield imprecise BSSE estimates and large propagated random error bars. Finally, in each of the interaction type distributions, there were several outliers with extremely high values of BSSE which likely have arisen from poorly refined contacts (steric clashes) in the crystal structures. Either further optimization of the protein structures or some sort of database filtering criteria would be required to address this problem.

Figure 2.

Using Gaussian probability density functions to describe and predict BSSE in backbone-backbone hydrogen bonds in proteins.

Since BSSE has a strong dependence on the geometric orientation of two interacting fragments, we introduce a simple geometry-dependent model to estimate fragment contributions to BSSE rather than a Gaussian pdf. In order to build our model, we introduce a bimolecular proximity descriptor to quickly and roughly measure the proximity P of two fragments A and B:

$${\mathrm{P}}_{\mathrm{AB}}=\mathrm{a}+\mathrm{b}\sum _{\mathrm{i}}^{{\mathrm{N}}_{\mathrm{A}}}\sum _{\mathrm{j}}^{{\mathrm{N}}_{\mathrm{B}}}{\mathrm{e}}^{-{\mathrm{cr}}_{\mathrm{ij}}^2},$$ (2)

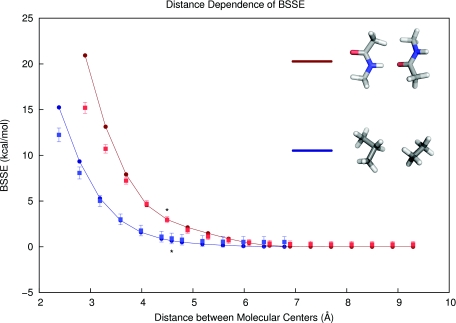
where N_A and N_B are the numbers of heavy (non-hydrogen) atoms in fragments A and B, a, b, and c are (positive and real) optimizable parameters, and r_ij is the distance between heavy atoms i and j. Thus, only the proximal non-hydrogen atoms on two different fragments significantly contribute to the overall proximity score. The score has a few desirable properties: it takes on only positive values, is small for non-interacting fragments, and it qualitatively models the exponential-like decay in actual distance dependence curves (see Figure 3). In addition, the BSSE estimator in Eq. 2 should be less sensitive to the molecular partitioning scheme than a counterpoise-based method for IBSSE, since the atomic contributions to BSSE fall off quickly with distance. In other words, including additional distant atoms in a fragment interaction will have little effect on the sum in Eq. 2. The parameters a, b, and c could be made to depend on the atoms i and j considered, since different fragment contributions to BSSE may have different distance dependencies (e.g., aliphatic vs. aromatic or ionic fragments), but in our initial investigations we used one parameter set for each type of interaction.

Figure 3.

Distance dependence of calculated and predicted basis set superposition error (at MP2∕6-31G*) in a pair of hydrogen-bonded backbone peptide fragments (red) and a nonpolar complex (blue) taken from our protein fragment database. The measured BSSE values are plotted as circles along lines, and the present model's predictions (Eq. 2) are shown as squares with their respective error bars. Asterisks mark the intermolecular distances found in the PDB structures. Since the model was parameterized with PDB geometries (i.e., near equilibrium), the BSSE model has more success with interactions at near-equilibrium distances than at very close intermolecular distances.

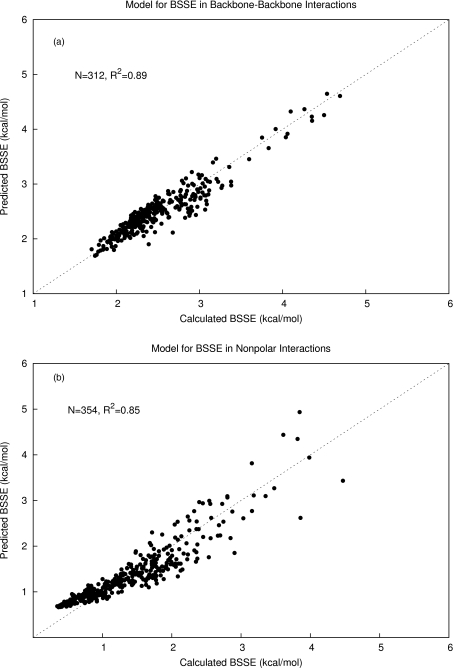
We trained Eq. 2 to fit the computed BSSE (at MP2∕6-31G*) of the 312 hydrogen-bonded backbone-backbone systems at their PDB geometries and found the best agreement with the calculated values when a = 0.254, b = 3.88, and c = 0.191. We investigated varying the power of r_ij in Eq. 2 and found no significant improvements from using r_ij rather than ${\mathrm{r}}_{\mathrm{ij}}^2$ in the backbone-backbone hydrogen bond complexes. Our best model had a coefficient of determination of R² = 0.89 (Figure 4a). The same function parameterized for the nonpolar (van der Waals) complexes yielded the optimal parameters a = 0.522, b = 9.11, and c = 0.285, and an R² of 0.85 (Figure 4b). The nonpolar complexes provided more of a challenge to fit than the backbone-backbone hydrogen bonds due to their higher chemical diversity. The charged systems were divided into positive and negatively charged interactions. The final parameter sets are shown in Table 1.

Figure 4.

(a) Model for predicting basis set superposition error trained with 312 protein backbone-backbone hydrogen bonding fragment interactions. The data were fit with a linear regression model using a bimolecular proximity descriptor as an independent variable and had an R² of 0.89. (b) The model for BSSE trained with 354 nonpolar complexes from the protein fragment database yielded an R² of 0.85.

Table 1.

Parameterization of Eq. 2 for four different interaction types.

Type	N	a	b	c	R2
Nonpolar	354	0.254	3.883	0.1907	0.85
Hydrogen bond	312	0.522	9.105	0.2847	0.89
Positively charged	44	0.983	29.35	0.4226	0.68
Negatively charged	63	1.57	29.28	0.3456	0.77

By using the fragment BSSE data as a reference set, we can now predict systematic and random errors due to BSSE in large biomolecular systems. After calculating a total energy for a system, it is fragmented according to the same rules used in designing the reference database. Each resulting fragment is then labeled according to interaction type. In the case of any fragment with multiple interaction types, a hierarchy was used which was determined by the relative contributions to BSSE from the four different interaction classes. Negatively charged moieties take the highest precedence due to being the highest BSSE-contributing interaction class. In the absence of negative charges, positive charges are sought, followed by hydrogen bonds. In the absence of all these features the interaction is considered nonpolar. The predicted “systematic error” (BSSE) then comes directly from evaluation of Eq. 2 (using the appropriate parameter set from Table 1) and the random error comes from the linear regression model as evaluated by Eq. 3 below, where t is the Student's t-value which depends on the population size N and the desired confidence limit, $\widehat{\mathrm{x}}$ is the newly estimated BSSE value, x_i and y_i are the database predicted and measured BSSE values, and $\overline{\mathrm{x}}$ is the mean predicted BSSE value in the reference set.

$${\mathrm{Error}}_{\mathrm{Random}}={\mathrm{tS}}^{1∕2}\sqrt{1+\frac{1}{\mathrm{N}}+\frac{{\left(\widehat{\mathrm{x}}-\overline{\mathrm{x}}\right)}^2}{{\sum }_{\mathrm{i}}^{\mathrm{N}}{({\mathrm{x}}_{\mathrm{i}}-\overline{\mathrm{x}})}^2}},$$ (3)

where

$$\mathrm{S}=\frac{{\sum }_{\mathrm{i}}^{\mathrm{N}}{\left[{\mathrm{y}}_{\mathrm{i}}-({\mathrm{bx}}_{\mathrm{i}}+\mathrm{a})\right]}^2}{\mathrm{N}-2}.$$ (4)

By assuming additivity of fragment contributions, the overall systematic error (total BSSE estimate) is then the arithmetic sum of the predicted fragment BSSE contributions and the overall random error (total error bar) is the Pythagorean sum of the random error estimates.

Applications

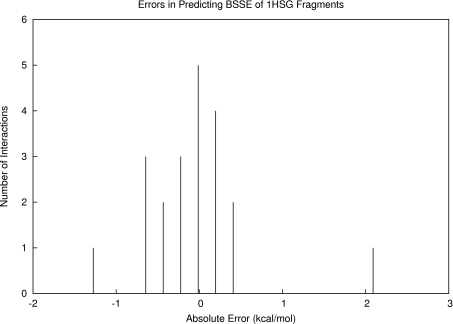
To demonstrate the use of these models, we first examined intermolecular BSSE in the case of protein-ligand binding by studying the HIV-2 protease∕indinavir complex (PDBID: 1HSG). The fragments studied were the same that were used in a previous study.⁸ The 21 fragments were evaluated for BSSE at MP2∕6-31G* and were classified according to interaction type. We predicted the fragment contributions to BSSE with Eq. 2 and Table 1 and compared our predictions with the measured BSSE values. The results are listed in Table 2. Over all 21 fragment interactions, we predicted the total BSSE to within an error of 1.02 kcal∕mol, which lay within our estimated error bar of 2.26 kcal∕mol (68% confidence). We observed that some of the individual fragment BSSE predictions were off by a significant amount (our model predicted fragment 4 to be 2.14 kcal∕mol too high in BSSE), but overall the population of individual errors seemed to cancel favorably toward zero (Figure 5).

Table 2.

Results from predicting the BSSE of 21 independent chemical fragments involved in the binding of indinavir to HIV-2 protease. The fragments are identified by system number and are labeled by interaction types: np: nonpolar, p: polar, pc: positively charged, and nc: negatively charged. The last two rows contain arithmetic and Pythagorean sums for the propagated systematic and random errors. Units are kcal∕mol.

Number	Type	Predicted BSSE	Measured BSSE	Predicted error	Measured error
1	np	1.49	2.05	0.30	−0.56
2	np	0.83	0.90	0.30	−0.07
3	pc	1.66	1.45	0.38	0.21
4	nc	10.40	8.27	1.01	2.14
5	nc	6.97	6.90	0.93	0.07
6	nc	2.10	3.47	0.93	−1.37
7	p	2.62	3.07	0.17	−0.44
8	np	1.45	2.13	0.30	−0.68
9	np	1.41	1.98	0.30	−0.56
10	np	2.08	1.90	0.30	0.19
11	np	1.26	1.33	0.30	−0.06
12	np	1.26	1.66	0.30	−0.40
13	np	1.43	1.72	0.30	−0.30
14	np	0.91	0.70	0.30	0.21
15	np	0.84	1.10	0.30	−0.26
16	np	0.73	0.63	0.30	0.11
17	np	1.51	1.15	0.30	0.36
18	np	1.33	1.28	0.30	0.05
19	np	0.88	1.05	0.30	−0.18
20	np	1.62	1.57	0.30	0.05
21	nc	3.26	2.77	0.92	0.49
Arithmetic sum		46.06	47.08	…	−1.02
Total error bar		…	…	2.26	…

Figure 5.

Distribution of errors in BSSE predictions for the fragments making up the HIV-2 protease∕indinavir complex. Although two of the individual errors were quite large, we observed favorable cancellation of these errors toward zero, which allowed for our close estimate of overall BSSE for the complex.

We then examined intramolecular BSSE in the case of a small, synthetic, helical protein with a known crystal structure (Figure 6, PDBID: 1AL1). The structure was saturated with hydrogen atoms, followed by an optimization of their positions with the ff99sb force field. The structure was then partitioned with our in-house fragmentation program into 10 backbone-backbone hydrogen bonded complexes and 3 nonpolar complexes from sidechain-sidechain interactions. By analyzing the intramolecular interactions making up the overall system and using the models built from Eq. 2 and propagating error estimates, we estimated the overall IBSSE at MP2∕6-31G* to be 30.94 ± 0.74 kcal∕mol (68% confidence). For comparison, we also separated the individual chemical fragments and measured the BSSE between them with the traditional intermolecular counterpoise method. The sum of fragment-based contributions was 31.60 kcal∕mol, which is close to the estimate from the statistical model and lies within the estimated error bar.

Figure 6.

Helical protein fragment structure (PDBID: 1AL1) used in the demonstration of the presented model for intramolecular basis set superposition error. The fragment-based model predicted 30.94 ± 0.74 kcal∕mol of overall IBSSE. The sum of calculated BSSE values for the interacting fragments was 31.60 kcal∕mol.

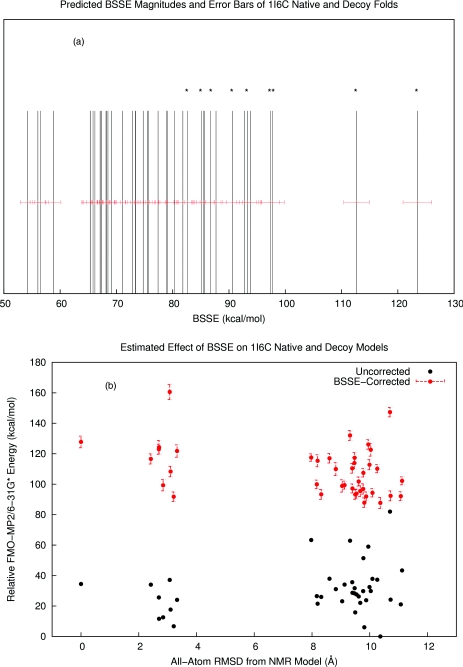
The last test of our method involved the investigation of a set of 9 native NMR and 33 decoy folds of the Pin1 WW domain (PDBID: 1I6C). A common way of testing score functions and methods of protein folding prediction is to compare native and decoy protein folds and attempt to energetically separate them. The free energy differences between native and non-native protein folds are typically on the order of 10–20 kcal∕mol, so accurate energy computation is very important for successful discrimination between native and decoy folds. FMO-MP2∕6-31G* + PCM energies of this particular set were evaluated previously²⁰ but were unable to discriminate between native and decoy folds. To examine the effect of IBSSE on this result, we estimated the magnitudes of IBSSE in each fold according to the presently described method. As a validation step, we computed the sum of measured fragment BSSE values for one of the native NMR models which was 97.7 kcal∕mol. Our estimated value using the statistical model was 93.28 ± 3.85 (95% confidence). Over the whole set of decoys, we observed that the native NMR models had tighter intramolecular packing and therefore yielded generally higher IBSSE estimates than the non-native folds. We also observed that the spread in IBSSE estimates was around 70 kcal∕mol, which was unexpectedly large. BSSE is usually thought of as a systematic error in that it always overestimates stability, and these errors are hoped to largely cancel when comparing different conformations of the same system. However, we observe in this set a very wide distribution of IBSSE values in the same protein system, implying that much of the error would not cancel when comparing conformational energies. This leads to a different ranking of folds by energy before and after IBSSE corrections (Figure 7).

Figure 7.

(a) The estimated intramolecular basis set superposition errors of a set of native and decoy folds of a small protein fragment, the Pin1 WW domain (PDBID 1I6C). The native NMR models are highlighted with asterisks. (b) The relative FMO-MP2∕6-31G* + PCM energies plotted against all-atom root mean square deviation from a reference NMR structure. Uncorrected energies are shown in black while BSSE-corrected energies are shown in red with their estimated error bars. All folds contained a significant amount of BSSE, but the variance in the BSSE magnitudes lead to a different ordering of folds by energy after BSSE corrections.

CONCLUSIONS

We have presented a simple parameterized model using a novel bimolecular proximity descriptor to quickly estimate the basis set superposition error of small molecular fragments constituting large biomolecules. These fragment-based BSSE estimations can be propagated over a large biomolecule or complex to estimate inter- or intramolecular BSSE. The method has the advantage of requiring no additional quantum calculations, but rather it requires an analysis of the comprising molecular interactions and relies on fitted statistical models that assume additivity of fragment contributions to overall IBSSE. Along with an estimate for overall BSSE, the method also can generate error bars, allowing the researcher to introduce confidence limits in their results when attempting to distinguish between protein folds or ligand poses. The method could easily be extended for use with other chemical systems, quantum methods, or basis sets by replacing the training set data.