SUMMARY
At the dawn of the era of personalized, systems-driven medicine, computational or in silico modeling and the simulation of disease processes is becoming increasingly important for hypothesis generation and data integration in both experiment and clinics alike. Arguably, this is nowhere more visible than in oncology. To illustrate the field’s vast potential as well as its current limitations we briefly review selected works on modeling malignant brain tumors. Implications for clinical practice, including trial design and outcome prediction are also discussed.
Keywords: brain tumor, computational biology, in silico cancer modeling, systems biology
INTRODUCTION
Biological sciences rely on modeling systems that help conceptualize, understand, test and predict the physiological and pathophysiological phenomena being studied. These modeling strategies are rich and diverse, and they include not only in vitro and in vivo but also theoretical or in silico approaches. Mathematical and computational cancer modeling have recently gained momentum. This is because of a combination of related factors, which include the advent of systems biology-driven concepts in biomedicine that draw from an ever increasing volume of molecular data,1–5 novel and cancer-focused interdisciplinary funding programs at the National Institutes of Health, such as the Integrative Cancer Biology Program or ICBP [http://icbp.nci.nih.gov/] and the availability of comparably inexpensive computational power necessary to run larger and clinically relevant simulations. In silico works such as the one by Anderson et al.,6 which presented a mathematical, continuum-discrete hybrid model on studying the microscopic interaction of a virtual tumor with its microenvironment, showcase this type of interdisciplinary approach to the broader biomedical community. Other prominent theory-inspired works on tumorigenesis include the application of game theory 7–9, scaling laws 10, 11, fractals 12–14 and graph theory 15, to name only a few. Using these and other methods and techniques, cancer-related topics of interest for applied mathematicians and biophysicists now go beyond the classic domains of studying volumetric tumor growth dynamics16, 17 and vascularization patterns.18–21 These techniques now extend to investigating, for instance, genetic instability22 and mutagenesis,23 as well as the complexity of tumor-immune system interaction.24, 25 A description of the entire field of in silico cancer research is beyond the scope of this review. We therefore have chosen to exemplify the development of modeling in clinical-cancer medicine by reviewing selected works on modeling progression and therapy of highly malignant brain tumors. We briefly discuss the current limitations as well as the potential of in silico cancer modeling for the near future.
IN SILICO MODELING OF BRAIN TUMORS
DEVELOPMENT OF INTEGRATED IN SILICO MODELS
Over the past decade, modeling of malignant brain tumors has become popular in the in silico research field. One reason is that despite all efforts, the outcome of patients suffering from high-grade astrocytomas or gliomas (most notably glioblastoma (multiforme; GBM) remains grim and, therefore, innovative approaches are desperately needed. Secondly, brain tumors grow within a biologically contained environment; that is, they tend not to metastasize outside the central nervous system, and thus seem to pose a more circumscribed and, from a mechanistic modeling perspective, bio-mechanically approachable problem. Thirdly, while countless experimental and clinical studies have undoubtedly advanced our understanding of the molecular and microscopic basis of this type of neoplasm, we are often left with too few clues as to how to connect the many data ‘dots’ across the scales of interest. Powerful integrative platforms are therefore required to capture the complex dynamics at all levels of organization (i.e. molecular, cellular, and organism)26. As such, the pathogenesis and pathophysiology of brain tumors provide an ideal target for applying computational and mathematical methods and techniques.
Starting in vitro
A significant body of in silico work has focused on developing a better understanding of glioma growth through the use of mathematical models that focus on data derived from in vitro growth studies. Some three decades ago, Greenspan27, 28 put forward two important, yet generic and rather simplified assumptions, that a micro-tumor’s geometry remains spherical at all time, and that the internal core of the tumor turns necrotic. Follow-up work by Chaplain and Sleeman29 introduced biomechanics, including elasticity, to describe the mechanical interactions between tissue and the expanding microscopic tumor. The authors modeled the material composition of a solid tumor using a strain energy function, attempting to deduce a basic mathematical description of the processes involved in cancer grading and staging from the in silico results of simulating solid tumor growth in conjunction with aspects of surface morphogenesis. Greenspan’s seminal work also provided the basis for a brain tumor model developed by Zheng et al.30 which presented a multi-scale hybrid (see Box 1) computer simulator to investigate the mechanisms of cancer infiltration based on in vitro data. More recently, Khain and Sander31 presented an invasive glioma model that used two coupled reaction-diffusion equations to study growth instabilities and the patterns emerging in vitro. Furthermore, Frieboes et al.32 studied the growth and shape of human gliomas in vitro and in silico as a function of oxygen, nutrient and growth factor concentrations and of cell adhesion forces. The authors built up a two-dimensional spatial tumor mass model that described growth dynamics and the change of morphology, using a finite element method to solve a set of nonlinear differential equations. Based on the results, the authors proposed that the instability of tumor morphologies, which lead to tumor invasion, is quantitatively related to spatial variations of molecular level diffusions. Since brain tissue can be described as a nonlinear viscoelastic solid 33, assuming displacement and strain to be small often turn out to be rather insufficient approximations of the actual tissue response, and so a finite element analysis is commonly employed to reduce the complicated mechanical problem to a more simplified matrix equation.34–36 Although these cancer models retain some level of validity for tumors cultured in vitro, in reality, tumors tend not to grow strictly spherical and the internal core of the tumor is not homogenously necrotic, rendering the initially stated assumptions somewhat unrealistic for describing the in vivo situation.
BOX 1. Terms and definitions used in in silico modeling.
Continuum models describe terms like the change in tumor cell density, chemoattractant diffusion and even kinetic molecular pathway networks with a set of differential equations.
A discrete model is commonly represented by a cellular automaton or CA. CA describes a spatial matrix in which the dynamics are defined by a set of local interaction rules among neighboring ‘nodes’ that can also decide the transition and communication among the grid points.
Hybrid approaches combine both continuum and discrete techniques in one form or another
ABM is a specialized CA technique that represents a complex system, regardless of its nature, as a collection of autonomous, decision-making entities called ‘agents’. Following a set of predetermined rules, each agent can individually execute a series of operations and make decisions. Note that such an agent can represent e.g. a cluster of cells, a single cell, protein(s), or gene(s) as an entity.
Adding the in vivo perspective
On the in vivo modeling side, Wasserman and Acharya 33 presented an integrated, universal framework to predict the direction and extent of spread of a primary brain tumor with respect to time. This tumor growth model is implemented using a nonlinear finite element method with several clinical applications in mind that ranged from prediction and tumor boundary delineation, to research on growth pattern, diagnostic decision support and radiotherapy planning. With these goals in mind, a number of mathematical continuum (Box 1) model have been developed,37–40 based largely on clinical imaging data such as serial CT scans, or more recently on nuclear magnetic resonance (NMR) images. These studies utilize, in one form or another, reaction-diffusion equations of the type detailed in Box 2. The results of these models support the notion put forward by Woodward et al.40 Firstly, that gliomas infiltrate so diffusely that they cannot be cured by surgery alone; secondly, that the more extensive the resection, the greater the life expectancy; and, thirdly, that measurements of the two rates, growth and diffusion, may be able to predict survival rates better than the current histology-based grading of gliomas.41–43 A considerable shortcoming of all these models is that, while they can grossly estimate the boundaries of the cortical and ventricular surfaces of the brain, they cannot account for the spatial heterogeneity of brain tissue with respect to grey and white matter. In an attempt to overcome this limitation, Swanson et al.44 presented a mathematical model of gliomas based on proliferation and diffusion rates that incorporated the effects of augmented cell motility on white matter compared with grey matter, which in turn allowed for asymmetric non-spherical tumour geometries to develop. The authors subsequently revised their model45 to quantify spatio-temporal growth and invasion of gliomas in three dimensions (3D) throughout a virtual human brain, in an effort to predict sites of potential tumor recurrence. The simulation results showed good agreement with clinically observed glioma progression patterns using CT scanning. Clatz et al.34 and follow-up work by this group35 also developed a set of 3D in vivo models based on clinical NMR images. Their models employed a finite element method to simulate the invasion of a GBM into the brain parenchyma and to simulate its mechanical interaction with the invaded structure. Clatz’s algorithm34 relies on diffusion tensor NMR imaging to account for anisotropic cell diffusion along white matter tracts; the algorithm couples the reaction-diffusion equation used to model tumor growth with the mechanical constitutive equation used to simulate its concomitant mass effect, i.e. the parenchyma’s mechanical reaction to the tumor’s expansion. The authors then compared their simulation results with glioma growth observed on two consecutive NMR imaging data sets from a patient with a brain tumor, and noted a good correlation between modeling results and imaging data.
BOX 2.
Here, c represents cell density, D· ∇2c stands for the diffusion of cells, r · c is growth, and m · c and K (t) · c describe cell loss due to mutation and treatment, respectively.40
Agent-based modeling, a hybrid approach
Despite their unquestionable merits, the above reviewed models describe glioma growth only as evolution of the local tumor cell density at a comparably macroscopic scale. Moreover, these models rely on reaction diffusion equations to account for tumor propagation and such a continuum approach inevitably fails to capture the discrete nature of an individual cell’s activity let alone a single sub-cellular protein. More generally, for the case of tumor angiogenesis, Orme and Chaplain46 already highlighted the shortcomings of employing a continuum framework. To address these limitations, Kansal et al.47, 48 introduced a discrete (Box 1) cellular automaton (CA)49 in an attempt to model Gompertzian GBM growth over nearly three orders of magnitude in tumor radius with only four microscopic parameters: the cell-doubling time, the nutritional needs of growth-arrested cells, the nutritional needs of proliferating cells, and the effects of mechanical confinement. Nonetheless, these CA models fell short of investigating relevant fluid physical aspects. Since neither a true continuum nor a discrete model can fully describe the cancer system under investigation, hybrid (Box 1) approaches including the so-called agent based modeling (ABM) technique, which encompasses both continuum and discrete modules, have gained popularity. In particular, the ability of the ABM technique to simulate tumor properties across multiple scales in space and time lends itself for studying highly malignant brain tumors.50 Mansury et al.51, 52 developed a set of two-dimensional brain cancer models, which simulated on the microscopic scale glioma cell proliferation, migration, quiescence and apoptosis using the aforementioned discrete module whereas the distribution and diffusion of chemo-attractants on the multicellular scale was modeled with a continuum module. Furthermore, Mansury and Deisboeck51 introduced a chemotactic ‘search precision’ (Box 3) to represent the impact of cell signal processing accuracy on the motility of glioma cells along the microenvironmental path of “least resistance, most permission and highest attraction”.50
BOX 3.
Here, Tj denotes the attractiveness of location j, Lj is the error-free evaluation of location j, and εj ~ N(μ, σ2) is an error term that is normally distributed with mean μ and variance σ. The parameter ψ takes on a positive value between zero and one and represents the extent of search precision.
Incorporating the molecular dimension
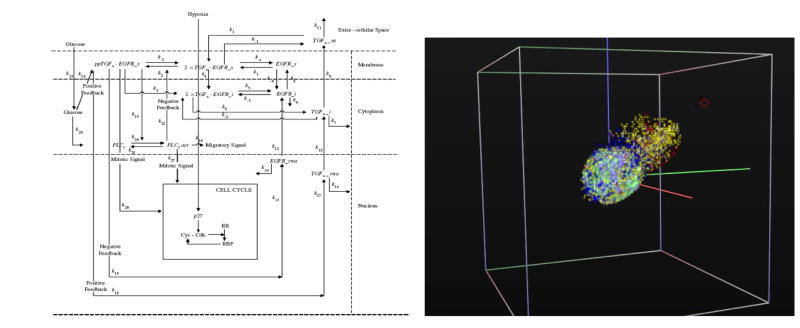
Athale et al.53, 54 expanded this ‘microscopic-macroscopic’ work by adding the all important molecular scale in form of a simplified representation of the EGFR pathway, which is crucially involved in glioma progression55 and could be of significance for therapeutic outcome.56 In this approach each EGFR pathway comprising molecule is represented by an equation of the kind described in Box 4. In this model, the EGFR-downstream protein phospholipase C-gamma (PLCγ) is employed to ‘decide’ the cell’s phenotype, in contrast to previous works that utilized a probability module to determine a cell’s phenotype. Using this novel design Athale et al. 53 described how the molecular profile of each individual glioma cell impacts the cell’s phenotypic switch, and how such single-cell decisions can potentially affect the dynamics of the entire tumor system. In a follow-up study,54 the authors then demonstrated that increasing the EGFR density per cell results in an acceleration of the entire tumor system’s spatiotemporal expansion dynamics. Zhang et al.57 extended this work by presenting a 3D multi-scale agent-based brain tumor model (Figure 1), which integrated an implicit mitogen-activated protein kinase (MAPK) module58 as well as a cell-cycle description, at the sub-cellular scale, which was modified from Alacon et al.59 This study also included a more complicated extracellular matrix representation at the microscopic scale and investigated how molecular perturbations percolate across scales in space and time. Together, this work has triggered specific experimental research at collaborating sites that may lead to the discovery of interesting therapeutic targets. This outcome illustrates how modeling can serve as a hypothesis-generating tool that can be explored in an experimental laboratory and eventually in clinics.
BOX 4.
Here, Xi is the mass of ith (i =1–14) molecules of the implemented EGFR signaling network and αi, βi (i =1–14) are the rate of synthesis and degradation rate of a given pathway molecule.
Figure 1.
The left schematic displays the simplified EGFR gene-protein interaction network, within a 3 compartment sub-cellular environment, implemented in each cancer cell (modified from Zhang et al.57). The simulation snapshot on the right depicts an advanced version of the model that implements a tumor progression path. As a result, various more aggressive tumor clones emerge that accelerate tumor expansion towards a chemotactic source (red circle, top right) [for more details, see http://arxiv.org/abs/q-bio.TO/0612037].
Conversely, models can confirm and expand clinical observations. For example, Frieboes et al.60 recently presented a novel predictive 3D algorithm, based on first-principle reaction diffusion equations. The model contains a variety of diffusive substrates and processes set within the context of micro-macro functional relationships. The work of these authors has allowed brain tumor morphology to be correlated to growth by quantifying the interdependence of tumor mass on both the microenvironment (including angiogenesis) and cell phenotypes.
PRACTICAL APPLICATIONS OF IN SILICO MODELING
Chemotherapy
From a clinical perspective, theoretical modeling has already found application particularly in simulating the impact of radiotherapy and chemotherapy on tumor growth. This is most relevant as both modalities are standard components of conventional, adjuvant treatment protocols following surgical resection of high-grade gliomas. Other than Woodward et al.40 who simulated brain tumor growth and infiltration following various extents of surgical resection, Tracqui et al.39 developed a basic mathematical algorithm that modeled the changes of glioma density, c(x,t), at location x and time t, to describe the tumor’s sensitivity to various chemotherapy regimens. As input data, the authors used eight serial CT scans from a patient with anaplastic astrocytoma, at the time of recurrence (i.e. 3 years after diagnosis and initial radiotherapy), taken over the course of 12 months. The patient’s treatment consisted of five cycles of six drugs (6-thioguanine, procarbazine, dibromodulcitol, CCNN, 5-fluorouracil, and hydroxyurea; given over 15 days, repeated every 6–8 weeks), and two cycles of cisplatin and neutron beam irradiation. An optimization algorithm that minimizes the error between simulated tumor area and glioma area on CT determined the best fit of the model’s six unknown parameters, which included proliferation rate and cell-diffusion coefficients. Overall, there was good agreement with the clinical data and the authors also showed that at a later stage during chemotherapy, the emergence of a chemo-resistant tumor sub-population was capable of causing treatment failure.39 Building on this work, Swanson et al.61 developed a similar continuum model but considered the impact that the brain’s known vascular heterogeneity may have on delivery and thus efficacy of chemotherapy. Considering that grey matter is more vascularized than white matter, and incorporating the notion that glioma cell motility is higher in white matter, cancer cells would spend more time in grey matter regions and thus be longer exposed to higher levels of chemotherapy. The authors implemented such underlying tissue heterogeneity in setting up a periodic region distribution and then simulated expansion, chemotherapy and recurrence of a high-grade glioma in the fronto-parietal region of the brain. Comparison with real NMR imaging patterns of a glioma patient treated with the receptor tyrosine kinase inhibitor imatinib mesylate suggested that indeed, the grey matter portion of the tumor may be more accessible to chemotherapy while tumor progression likely continues in the already infiltrated, adjacent white matter areas. Another mathematical approach has recently been reviewed by Sanga et al. 62, as an extension of the model presented by Frieboes et al.32 The authors applied the earlier concept using multicompartment pharmacokinetics modeling to examine the impact of chemotherapy (e.g., cisplatin and doxorubicin) on tumor response. Their simulation results confirmed that the overall growth of the tumor mass depends significantly on the diffusive distribution of nutrients, tissue pressure, and chemotherapeutic drugs.
Radiotherapy
In silico modeling has had an even longer standing track record in the area of radiotherapy. Kirby et al.63, 64 recently formulated a brain tumor growth model for predicting survival in a population of patients who underwent radiotherapy. More specifically, a stochastic modeling approach based on a Monte Carlo simulation was used to simulate a virtual population of 2,000 patients. These simulation data were then compared with clinical data (from 154 adult GBM patients who received 60 Gy radiotherapy without adjuvant chemotherapy), i.e. fitted to clinical survival data by minimizing the weighted sum of squares of errors between the simulated and real Kaplan-Meier survival curves. The results showed a close fit not only at early but also at later times when they were able to reproduce the rather dismal outcome with few long-term survivors. The authors go on to suggest that an escalation of the radiotherapy dose to 74 Gy would increase overall survival time as well as the portion of long-term survivors. This treatment ‘recommendation’ is in accordance with the one by Dionysiou et al.65 who presented a 3D spatio-temporal model to simulate tumor cell repopulation, expansion and shrinkage. Their work focused also on the cancer cell cycle in the presence of radiotherapy and a linear quadratic model described the number of cells killed. The results indicate that with regards to GBM control, a hyperfractionation scheme that delivers a total radiotherapy dose of 72 Gy in 6 weeks is superior compared with standard fractionation that delivers only 60 Gy over the same duration. This finding was supported by the clinical studies cited by the authors.66 Recently, the same group improved their model by incorporating tumor vasculature and oxygen supply based on imaging data.67 Comparing glioma eradication using hyperfractionation and accelerated hyperfractionation radiotherapy regimen, the model’s predictions, including improved tumor control through hyperfractionation irradiation, are semi-quantitatively in agreement with the clinical findings reported by the Radiation Therapy Oncology Group Study 83-02.
Future work on modeling treatment aspects will include adding an explicit molecular scale (incl. relevant cell signaling pathways), simulating therapeutic impact on the surrounding normal tissue, improvement of parameter values using patient-specific data, and systematic comparison of the modeling predictions with clinical data before, during, and after multimodality treatment.
FUTURE PERSPECTIVES
A review of selected neuro-oncology studies demonstrates that the field of in silico tumor modeling has indeed come a long way over the past decade. Is in silico tumor modeling ready for primetime? The answer to this question depends largely on the deliverables. While there certainly is much reason for optimism, realistically detailed and sufficiently accurate predictions that can reliably guide a patient’s treatment may still be years away. The in silico generation of experimentally testable hypotheses, however, is now a widely pursued interdisciplinary strategy in academic and in industrial labs around the globe, where computational modeling has also become an integral part of the elaborate drug discovery process.62, 68 Moreover, few would argue that the integration of ever increasing yet disparate data can be achieved with anything but cutting edge computational modeling. As such, in silico modeling already is a key force in cancer research, and it is likely to find applications in the clinic in the near future.
Multi-scale in silico modeling can yield valuable insights into the complex interactions of sub-cellular signaling networks and how molecular perturbations percolate throughout and across scales. The first and most critical step, however, is to decide on the scope of a model; this is an evolving target and always a compromise between model simplicity and thus tractability, and its accuracy or biological relevance. Ultimately, this decision will depend on the biomedical questions asked and hypothesis posed. The same considerations will determine the choice of the modeling technique and the approach taken, i.e. ‘top-down’ or ‘bottom-up’. In contrast to most wet-lab studies, in silico experiments can be done in a fast and relatively cost-efficient way because it is possible to vary multiple parameters reproducibly over a wide range. In silico predictions can readily assist scientists in focusing laboratory studies and eventually should aid clinicians in individualizing patient treatment plans. The goal of any such patient-specific, ‘systems medicine’ is to maximize effectiveness while minimizing negative side effects, with obvious benefits for the individual patient as well as for the public health-care system at large.
While potential applications for educational purposes in biomedical teaching and training are abundant, the real test of in silico oncology (i.e. its quantitative application to and reliability in the clinical setting69 ) is just at the beginning and several key obstacles will need to be tackled first to move the field to the next level. Firstly, in order to reduce the inaccuracy as a result of estimating yet unknown parameters, novel quantitative experimental techniques such as (phospho-proteomics and) molecular imaging70 need to make the transition into conventional clinics to allow for more-precise parameterization of the algorithms on the microscopic-molecular interface. Hence, this will increase the models’ predictive power and thus validity. Secondly, on the computational side, a considerable technical limitation is posed by the increasing size of the current algorithms. That is, generally, the higher a model’s spatial and temporal resolution, the higher is its compute power demand and thus the longer the run time of the code in a given information technology environment. For instance, while agent-based modeling has demonstrated significant potential, its main drawback is the relatively intense compute power that is currently required to describe a cancer system at the level of its many constituent units and at a clinically relevant scale. Given the enormous amount of data already collected and that we certainly will have to deal with in the near future, parallelization of the code for use in high-performance compute environments is likely only a temporary relief, and multi-scale, multi-resolution modeling seems a more promising route. Here, compute power would be allocated to areas of the tumor model, and at times, that likely have a more substantial impact on the predictive power, which will require a close evaluation with clinical data. Thirdly, another important aspect relates to improving the communication and interaction between in silico investigators and their experimental and clinical counterparts. In fact, access to raw data and exchange of expertise has been widely recognized as a critical obstacle that could hinder progress throughout the interdisciplinary Life Sciences field. It is here where new efforts such as the Center for the Development of a Virtual Tumor (CViT; https://www.cvit.org) will have a significant impact. Funded by the National Cancer Institute and charged with developing an online cancer modeling community and the innovative information technology infrastructure to support it, CViT is poised to develop a semantic digital model repository that is geared towards facilitating retrieval, exchange and usage of cancer modeling related tools and data.71
CONCLUSIONS
In summary, at the dawn of the era of cancer systems biology computational and mathematical (i.e., in silico) modeling is and will continue to be an integral part of oncology medicine. The in silico oncology field holds as much promise as it faces technical challenges, which it must resolve to reach its true potential – that is, facilitating and accelerating the paradigm-shifting transition from conventional population-based to patient-specific cancer medicine.
KEY POINTS.
In generating experimentally testable hypotheses and facilitating multi-modality data integration, in silico modeling is a driving force behind cancer systems biology.
As exemplified by reviewing selected works on malignant brain tumors, practical applications for computational and mathematical cancer modeling reach from simulating aspects of tumor initiation and progression to treatment impact modeling.
Such in silico modeling is an additional tool geared to aiding experimental researchers and physicians in investigating the ever increasing complexity of the processes involved in tumorigenesis, thus supporting innovative discovery research and accelerating the identification of promising targets.
While there is no single simulator platform that fits all needs, discrete-continuum (hybrid) modeling, and here especially agent-based approaches, are particularly promising in integrating molecular, microscopic and macroscopic oncology data and in analyzing processes across scales in space and time.
Acknowledgments
This work has been supported, in part, by the NIH grant CA 113004 (CViT; https://www.cvit.org) and by the Harvard-MIT (HST) Athinoula A Martinos Center for Biomedical Imaging and the Department of Radiology at Massachusetts General Hospital.
Biographies
Thomas S. Deisboeck, M.D. is currently Assistant Professor of Radiology at Massachusetts General Hospital (MGH) where he directs the Complex Biosystems Modeling Laboratory. He is affiliated with the Harvard-MIT Health Sciences and Technology Division (HST), the School of Engineering and Applied Sciences (SEAS) at Harvard University, and is a member of the Dana Farber/Harvard Cancer Center. Dr. Deisboeck graduated from Munich’s Technical University Medical School and did his internship in the Department of Neurosurgery at the Ludwig-Maximilians University of Munich, Germany. His laboratory’s focus at the MGH is on integrative multi-scale cancer modeling and simulation. Dr. Deisboeck serves also as Principal Investigator of the Center for the Development of a Virtual Tumor, CViT (https://www.cvit.org) one of NIH-NCI’s Integrative Cancer Biology Programs.
Le Zhang, Ph.D.: Postdoctoral Research Fellow
Jeongah Yoon, Ph.D.: Postdoctoral Research Fellow
Jose Costa, M.D.: Professor of Pathology and Medicine (Oncology)
References
- 1.Liu ET, et al. In the pursuit of complexity: systems medicine in cancer biology. Cancer Cell. 2006;9:245–247. doi: 10.1016/j.ccr.2006.03.026. [DOI] [PubMed] [Google Scholar]
- 2.Kitano H. Computational systems biology. Nature. 2002;420:206–210. doi: 10.1038/nature01254. [DOI] [PubMed] [Google Scholar]
- 3.Hornberg JJ, et al. Cancer: a Systems Biology disease. Biosystems. 2006;83:81–90. doi: 10.1016/j.biosystems.2005.05.014. [DOI] [PubMed] [Google Scholar]
- 4.Coffey DS. Self-organization, complexity and chaos: the new biology for medicine. Nat Med. 1998;4:882–885. doi: 10.1038/nm0898-882. [DOI] [PubMed] [Google Scholar]
- 5.Ahn AC, et al. The clinical applications of a systems approach. PLoS Med. 2006;3:e209. doi: 10.1371/journal.pmed.0030209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Anderson AR, et al. Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell. 2006;127:905–915. doi: 10.1016/j.cell.2006.09.042. [DOI] [PubMed] [Google Scholar]
- 7.Axelrod R, et al. Evolution of cooperation among tumor cells. Proc Natl Acad Sci USA. 2006;103:13474–13479. doi: 10.1073/pnas.0606053103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gatenby RA, Vincent TL. An evolutionary model of carcinogenesis. Cancer Res. 2003;63:6212–6220. [PubMed] [Google Scholar]
- 9.Mansury Y, et al. Evolutionary game theory in an agent-based brain tumor model: exploring the ‘Genotype-Phenotype’ link. J Theor Biol. 2006;238:146–156. doi: 10.1016/j.jtbi.2005.05.027. [DOI] [PubMed] [Google Scholar]
- 10.Guiot C, et al. Does tumor growth follow a “universal law”? J Theor Biol. 2003;225:147–151. doi: 10.1016/s0022-5193(03)00221-2. [DOI] [PubMed] [Google Scholar]
- 11.Guiot C, et al. The dynamic evolution of the power exponent in a universal growth model of tumors. J Theor Biol. 2006;240:459–463. doi: 10.1016/j.jtbi.2005.10.006. [DOI] [PubMed] [Google Scholar]
- 12.Baish JW, Jain RK. Fractals and cancer. Cancer Res. 2000;60:3683–3688. [PubMed] [Google Scholar]
- 13.Cross SS. Fractals in pathology. J Pathol. 1997;182:1–8. doi: 10.1002/(SICI)1096-9896(199705)182:1<1::AID-PATH808>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
- 14.Norton L. Conceptual and practical implications of breast tissue geometry: toward a more effective, less toxic therapy. Oncologist. 2005;10:370–381. doi: 10.1634/theoncologist.10-6-370. [DOI] [PubMed] [Google Scholar]
- 15.Goh KI, et al. The human disease network. Proc Natl Acad Sci U S A. 2007;104:8685–8690. doi: 10.1073/pnas.0701361104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Marusic M, et al. Analysis of growth of multicellular tumour spheroids by mathematical models. Cell Prolif. 1994;27:73–94. doi: 10.1111/j.1365-2184.1994.tb01407.x. [DOI] [PubMed] [Google Scholar]
- 17.Vaidya VG, Alexandro FJ., Jr Evaluation of some mathematical models for tumor growth. Int J Biomed Comput. 1982;13:19–36. doi: 10.1016/0020-7101(82)90048-4. [DOI] [PubMed] [Google Scholar]
- 18.Alarcon T, et al. A cellular automaton model for tumour growth in inhomogeneous environment. J Theor Biol. 2003;225:257–274. doi: 10.1016/s0022-5193(03)00244-3. [DOI] [PubMed] [Google Scholar]
- 19.Bauer AL, et al. A cell-based model exhibiting branching and anastomosis during tumor-induced angiogenesis. Biophys J. 2007;92:3105–3121. doi: 10.1529/biophysj.106.101501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.McDougall SR, et al. Mathematical modelling of dynamic adaptive tumour-induced angiogenesis: clinical implications and therapeutic targeting strategies. J Theor Biol. 2006;241:564–589. doi: 10.1016/j.jtbi.2005.12.022. [DOI] [PubMed] [Google Scholar]
- 21.Plank MJ, Sleeman BD. Lattice and non-lattice models of tumour angiogenesis. Bull Math Biol. 2004;66:1785–1819. doi: 10.1016/j.bulm.2004.04.001. [DOI] [PubMed] [Google Scholar]
- 22.Sole RV, Deisboeck TS. An error catastrophe in cancer? J Theor Biol. 2004;228:47–54. doi: 10.1016/j.jtbi.2003.08.018. [DOI] [PubMed] [Google Scholar]
- 23.Spencer SL, et al. Modeling somatic evolution in tumorigenesis. PLoS Comput Biol. 2006;2:e108. doi: 10.1371/journal.pcbi.0020108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Castiglione F, et al. Computational modeling of the immune response to tumor antigens. J Theor Biol. 2005;237:390–400. doi: 10.1016/j.jtbi.2005.04.024. [DOI] [PubMed] [Google Scholar]
- 25.Wu JT, et al. Analysis of a three-way race between tumor growth, a replication-competent virus and an immune response. Bull Math Biol. 2004;66:605–625. doi: 10.1016/j.bulm.2003.08.016. [DOI] [PubMed] [Google Scholar]
- 26.Sanga S, et al. Predictive oncology: a review of multidisciplinary, multiscale in silico modeling linking phenotype, morphology and growth. Neuroimage. 2007;37:S120–134. doi: 10.1016/j.neuroimage.2007.05.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Greenspan HP. Models for the growth of a solid tumor by diffusion. Stud Appl Math LI. 1972:317–340. [Google Scholar]
- 28.Greenspan HP. On the growth and stability of cell cultures and solid tumors. J Theor Biol. 1976;56:229–242. doi: 10.1016/s0022-5193(76)80054-9. [DOI] [PubMed] [Google Scholar]
- 29.Chaplain MA, Sleeman BD. Modelling the growth of solid tumours and incorporating a method for their classification using nonlinear elasticity theory. J Math Biol. 1993;31:431–473. doi: 10.1007/BF00173886. [DOI] [PubMed] [Google Scholar]
- 30.Zheng X, et al. Nonlinear simulation of tumor necrosis, neo-vascularization and tissue invasion via an adaptive finite-element/level-set method. Bull Math Biol. 2005;67:211–259. doi: 10.1016/j.bulm.2004.08.001. [DOI] [PubMed] [Google Scholar]
- 31.Khain E, Sander LM. Dynamics and pattern formation in invasive tumor growth. Phys Rev Lett. 2006;96:188103. doi: 10.1103/PhysRevLett.96.188103. [DOI] [PubMed] [Google Scholar]
- 32.Frieboes HB, et al. An integrated computational/experimental model of tumor invasion. Cancer Res. 2006;66:1597–1604. doi: 10.1158/0008-5472.CAN-05-3166. [DOI] [PubMed] [Google Scholar]
- 33.Wasserman R, Acharya R. A patient-specific in vivo tumor model. Math Biosci. 1996;136:111–140. doi: 10.1016/0025-5564(96)00045-4. [DOI] [PubMed] [Google Scholar]
- 34.Clatz O, et al. Realistic simulation of the 3-D growth of brain tumors in MR images coupling diffusion with biomechanical deformation. IEEE Trans Med Imaging. 2005;24:1334–1346. doi: 10.1109/TMI.2005.857217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Konukoglu E, et al. A recursive anisotropic fast marching approach to reaction diffusion equation: application to tumor growth modeling. Inf Process Med Imaging. 2007;20:687–699. doi: 10.1007/978-3-540-73273-0_57. [DOI] [PubMed] [Google Scholar]
- 36.Zienkiewicz OC. The Finite Element Method. 3. London: NCGraw-Hill; 1977. [Google Scholar]
- 37.Burgess PK, et al. The interaction of growth rates and diffusion coefficients in a three-dimensional mathematical model of gliomas. J Neuropathol Exp Neurol. 1997;56:704–713. [PubMed] [Google Scholar]
- 38.Cruywagen GC, et al. The modeling of diffusive tumors. J Biol System. 1995;3:937–945. [Google Scholar]
- 39.Tracqui P, et al. A mathematical model of glioma growth: the effect of chemotherapy on spatio-temporal growth. Cell Prolif. 1995;28:17–31. doi: 10.1111/j.1365-2184.1995.tb00036.x. [DOI] [PubMed] [Google Scholar]
- 40.Woodward DE, et al. A mathematical model of glioma growth: the effect of extent of surgical resection. Cell Prolif. 1996;29:269–288. doi: 10.1111/j.1365-2184.1996.tb01580.x. [DOI] [PubMed] [Google Scholar]
- 41.Burger PC, et al. Tumors of the Central Nervous Systems. 3. Washington DC: Armed Forces Institute Pathology; 1994. [Google Scholar]
- 42.Kleihues P, et al. The new WHO classification of brain tumours. Brain Pathol. 1993;3:255–268. doi: 10.1111/j.1750-3639.1993.tb00752.x. [DOI] [PubMed] [Google Scholar]
- 43.Kleihues P, et al. Histological Typing of Tumors of the Central Nervous System. 2. Berlin: Springer; 1993. [Google Scholar]
- 44.Swanson KR, et al. A quantitative model for differential motility of gliomas in grey and white matter. Cell Prolif. 2000;33:317–329. doi: 10.1046/j.1365-2184.2000.00177.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Swanson KR, et al. Virtual brain tumours (gliomas) enhance the reality of medical imaging and highlight inadequacies of current therapy. Br J Cancer. 2002;86:14–18. doi: 10.1038/sj.bjc.6600021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Orme ME, Chaplain MA. Two-dimensional models of tumour angiogenesis and anti-angiogenesis strategies. IMA J Math Appl Med Biol. 1997;14:189–205. [PubMed] [Google Scholar]
- 47.Kansal AR, et al. Simulated brain tumor growth dynamics using a three-dimensional cellular automaton. J Theor Biol. 2000;203:367–382. doi: 10.1006/jtbi.2000.2000. [DOI] [PubMed] [Google Scholar]
- 48.Kansal AR, et al. Cellular automaton of idealized brain tumor growth dynamics. Biosystems. 2000;55:119–127. doi: 10.1016/s0303-2647(99)00089-1. [DOI] [PubMed] [Google Scholar]
- 49.Wolfram S. Cellular Automata and Complexity: Collected Papers. MA: Addison-Wesley Reading; 1994. [Google Scholar]
- 50.Deisboeck TS, et al. Pattern of self-organization in tumour systems: complex growth dynamics in a novel brain tumour spheroid model. Cell Prolif. 2001;34:115–134. doi: 10.1046/j.1365-2184.2001.00202.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mansury Y, Deisboeck TS. The impact of “search precision” in an agent-based tumor model. J Theor Biol. 2003;224:325–337. doi: 10.1016/s0022-5193(03)00169-3. [DOI] [PubMed] [Google Scholar]
- 52.Mansury Y, et al. Emerging patterns in tumor systems: simulating the dynamics of multicellular clusters with an agent-based spatial agglomeration model. J Theor Biol. 2002;219:343–370. doi: 10.1006/jtbi.2002.3131. [DOI] [PubMed] [Google Scholar]
- 53.Athale C, et al. Simulating the impact of a molecular ‘decision-process’ on cellular phenotype and multicellular patterns in brain tumors. J Theor Biol. 2005;233:469–481. doi: 10.1016/j.jtbi.2004.10.019. [DOI] [PubMed] [Google Scholar]
- 54.Athale CA, Deisboeck TS. The effects of EGF-receptor density on multiscale tumor growth patterns. J Theor Biol. 2006;238:771–779. doi: 10.1016/j.jtbi.2005.06.029. [DOI] [PubMed] [Google Scholar]
- 55.Ohgaki H, Kleihues P. Genetic pathways to primary and secondary glioblastoma. Am J Pathol. 2007;170:1445–1453. doi: 10.2353/ajpath.2007.070011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Mellinghoff IK, et al. Molecular determinants of the response of glioblastomas to EGFR kinase inhibitors. N Engl J Med. 2005;353:2012–2024. doi: 10.1056/NEJMoa051918. [DOI] [PubMed] [Google Scholar]
- 57.Zhang L, et al. Development of a three-dimensional multiscale agent-based tumor model: simulating gene-protein interaction profiles, cell phenotypes and multicellular patterns in brain cancer. J Theor Biol. 2007;244:96–107. doi: 10.1016/j.jtbi.2006.06.034. [DOI] [PubMed] [Google Scholar]
- 58.Schoeberl B, et al. Computational modeling of the dynamics of the MAP kinase cascade activated by surface and internalized EGF receptors. Nat Biotechnol. 2002;20:370–375. doi: 10.1038/nbt0402-370. [DOI] [PubMed] [Google Scholar]
- 59.Alarcon T, et al. A mathematical model of the effects of hypoxia on the cell-cycle of normal and cancer cells. J Theor Biol. 2004;229:395–411. doi: 10.1016/j.jtbi.2004.04.016. [DOI] [PubMed] [Google Scholar]
- 60.Frieboes HB, et al. Computer simulation of glioma growth and morphology. Neuroimage. 2007;37 (Suppl 1):S59 – S70. doi: 10.1016/j.neuroimage.2007.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Swanson KR, et al. Quantifying efficacy of chemotherapy of brain tumors with homogeneous and heterogeneous drug delivery. Acta Biotheor. 2002;50:223–237. doi: 10.1023/a:1022644031905. [DOI] [PubMed] [Google Scholar]
- 62.Sanga S, et al. Mathematical modeling of cancer progression and response to chemotherapy. Expert Rev Anticancer Ther. 2006;6:1361–1376. doi: 10.1586/14737140.6.10.1361. [DOI] [PubMed] [Google Scholar]
- 63.Kirkby NF, et al. A mathematical model of the treatment and survival of patients with high-grade brain tumours. J Theor Biol. 2007a;245:112–124. doi: 10.1016/j.jtbi.2006.09.007. [DOI] [PubMed] [Google Scholar]
- 64.Kirkby NF, et al. Mathematical Modelling of Survival of Patients with Glioblastoma following Radical and Palliative Radiotherapy. Clin Oncol (R Coll Radiol) 2007b;19:S35–36. [Google Scholar]
- 65.Dionysiou DD, et al. A four-dimensional simulation model of tumour response to radiotherapy in vivo: parametric validation considering radiosensitivity, genetic profile and fractionation. J Theor Biol. 2004;230:1–20. doi: 10.1016/j.jtbi.2004.03.024. [DOI] [PubMed] [Google Scholar]
- 66.Fowler JF. The linear-quadratic formula and progress in fractionated radiotherapy. Br J Radiol. 1989;62:679–694. doi: 10.1259/0007-1285-62-740-679. [DOI] [PubMed] [Google Scholar]
- 67.Stamatakos GS, et al. A four-dimensional computer simulation model of the in vivo response to radiotherapy of glioblastoma multiforme: studies on the effect of clonogenic cell density. Br J Radiol. 2006;79:389–400. doi: 10.1259/bjr/30604050. [DOI] [PubMed] [Google Scholar]
- 68.Araujo RP, et al. A mathematical model of combination therapy using the EGFR signaling network. Biosystems. 2005;80:57–69. doi: 10.1016/j.biosystems.2004.10.002. [DOI] [PubMed] [Google Scholar]
- 69.Hu L, et al. Computational modeling to predict effect of treatment schedule on drug delivery to prostate in humans. Clin Cancer Res. 2007;13:1278–1287. doi: 10.1158/1078-0432.CCR-06-1610. [DOI] [PubMed] [Google Scholar]
- 70.Jaffer FA, Weissleder R. Molecular imaging in the clinical arena. Jama. 2005;293:855–862. doi: 10.1001/jama.293.7.855. [DOI] [PubMed] [Google Scholar]
- 71.Deisboeck TS, et al. Advancing cancer systems biology: Introducing the Center for the Development of a Virtual Tumor, CViT. Cancer Informatics. 2007:1–8. [PMC free article] [PubMed] [Google Scholar]