Abstract
Mediation is usually assessed by a regression-based or structural equation modeling (SEM) approach that we will refer to as the classical approach. This approach relies on the assumption that there are no confounders that influence both the mediator, M, and the outcome, Y. This assumption holds if individuals are randomly assigned to levels of M but generally random assignment is not possible. We propose the use of propensity scores to help remove the selection bias that may result when individuals are not randomly assigned to levels of M. The propensity score is the probability that an individual receives a particular level of M. Results from a simulation study are presented to demonstrate this approach, referred to as Classical + Propensity Model (C+PM), confirming that the population parameters are recovered and that selection bias is successfully dealt with. Comparisons are made to the classical approach that does not include propensity scores. Propensity scores were estimated by a logistic regression model. If all confounders are included in the propensity model, then the C+PM is unbiased. If some, but not all, of the confounders are included in the propensity model, then the C+PM estimates are biased although not as severely as the classical approach (i.e. no propensity model is included).
Mediation occurs as part of a hypothesized causal chain of events: The independent variable (e.g. a life skills training intervention) has an effect on the mediator (e.g. participation in leisure activities), which then affects the outcome variable (e.g. substance use). Mediators are measured after an intervention or treatment has occurred, but usually prior to the primary outcome of interest. For example, knowledge of health consequences, attitudes, social norms, availability, and refusal skills have been documented to mediate the effect of prevention interventions on adolescent smoking (MacKinnon, Taborga, & Morgan-Lopez, 2002).
Classical Approach for Assessing Mediation
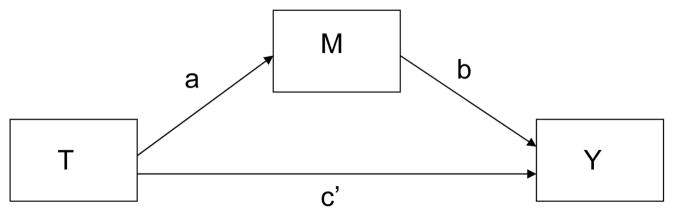
Mediation is often tested using a regression analysis procedure (Baron & Kenny, 1986; MacKinnon, Fairchild, & Fritz, 2007). The first step is to determine whether there is a relationship between the treatment or hypothesized cause, T, and the outcome variable, Y. This relationship is often called the total effect (typically denoted by c). Many researchers (e.g. Cole & Maxwell, 2003; Collins, Graham, & Flaherty, 1998; MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002; Shrout & Bolger, 2002) have argued that this step is unnecessary and we do not consider it here. The second step is to determine whether there is a relationship between T and the mediator, M (path a in Figure 1). The third step is to regress Y on both T and M. Figure 1 is a path diagram that illustrates the second and third steps. The effect of M on Y holding T constant is denoted b (see Figure 1). The estimated mediating (or indirect) effect, ab, is the estimated regression coefficient for path a multiplied by the estimated regression coefficient for path b. The direct effect is the effect of T on Y when controlling for M and the estimate is denoted by c′ to distinguish it from c, the effect of T on Y when M is not in the model. According to this approach, the effects are additive such that the direct effect plus the indirect effect equals the total effect. This additivity assumption further implies that there are no interactions between T and M (this assumption is sometimes referred to as the no interaction assumption). A single mediator model is shown in Figure 1. The second and third steps are usually fit simultaneously using SEM software rather than as two separate regressions. We will refer to this method as the classical approach to assessing mediation. In summary, the classical approach estimates the effect of the intervention on the mediator, of the mediator on the outcome, and of the intervention on the outcome when controlling for the mediator.
Figure 1.
Single mediator model.
Throughout this article, randomization to an intervention or treatment is assumed. Randomized treatments allow for causal inference regarding the effect of the treatment on the mediator because randomization ensures that there are no confounders of T and M. However, as several authors (Robins & Greenland, 1992; Rosenbaum, 1984; Rubin, 2004) have pointed out, the classical approach to mediation analysis relies on the assumption that individuals are also randomly assigned to levels of the mediator if causal inferences are to be made about the relationship between the mediator and the outcome. Randomization to levels of the mediator guarantees that there are no confounders (i.e. third variables) that influence both the mediator and the outcome. This assumption is also known as sequential ignorability. If all confounders of M and Y are measured and adjusted for, then causal inferences can be made about the M to Y relationship. One method of adjusting for confounders is an analysis of covariance (ANCOVA) or regression adjustment approach in which the confounders are included in the regression models for mediation. Another method is to use propensity score models.
Propensity score methods have advantages over ANCOVA/ regression adjustment methods that have been detailed elsewhere in the non-mediation context (see for example, Schafer & Kang, 2008 and VanderWeele, 2006). Briefly, propensity score methods allow the inclusion of a large number of potential confounders. Even when the number of confounders is not large, propensity score methods have advantages over regression adjustment methods in that regression adjustment methods extrapolate to regions of the covariate space in which there may not be individuals in the sample to support causal inference. Propensity score methods and the diagnostics that are used to assess balance and overlap bring these issues to the attention of the researcher.
The purpose of the present manuscript is to call researchers’ attention to the problem of confounding of the M and Y relationship and to propose that researchers use propensity score methods to adjust for this confounding. The paper is organized as follows. First, the potential outcomes framework for causal inference (Holland, 1986; Rubin, 1974), on which propensity score methods are based, is introduced. Second, we introduce propensity scores. Third, we present a simulation study and results from that simulation study to show that inclusion of propensity scores in a mediation context provide unbiased estimates of mediated effects and that not adjusting for confounders of the M to Y relationship results in biased estimates of the mediated effect. Finally, we discuss limitations, future directions, and suggestions for applied researchers.
The Potential Outcomes Framework
Non-Mediation Context
Here we introduce the potential outcomes framework for the simplest case, that is for estimating the causal effect of T on Y. In the next section, we introduce a mediating variable. In the potential outcomes framework, each individual has a potential outcome for each possible treatment condition. When there is a treatment group and a control group, there are two potential outcomes for each participant: the outcome that would be obtained under the treatment condition and the outcome that would be obtained under the control condition. Let Ti denote the treatment received by participant i, i = 1, . . . , N. Those with Ti = 1 are said to be treated, and those with Ti = 0 are said to be untreated. Let Yi(0) be the outcome if Ti = 0, and Yi(1) be the outcome if Ti = 1. The individual causal effect is the difference between these two potential outcomes for participant i, Yi(1) – Yi(0). Because each participant can be observed in only one of these conditions, in every case one of the potential outcomes is missing and therefore, the individual causal effect can not be computed directly. However, various strategies have been proposed to estimate the average causal effect (ACE) defined as E(Yi(1) – Yi(0)), the causal effect averaged over participants in the study.
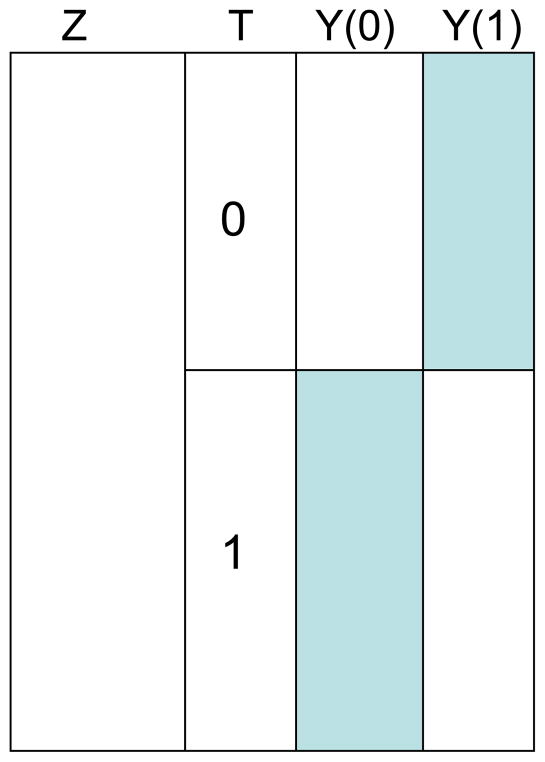
A graphical depiction of a data set for a sample of N individuals is shown in Figure 2. For those individuals who do not receive the treatment (Ti = 0) the potential outcomes under the treatment (Yi(1)) are missing as denoted by shading. Likewise, for those individuals who receive the treatment (Ti = 1), the potential outcomes, Yi(0), are missing as denoted by the shading. Finally, let Zi denote a vector of additional pre-treatment confounders which may influence the probabilities of Ti = 1 and Ti = 0 in any setting other than a completely randomized experiment. These confounders are variables that take on their values before the intervention and, thus, cannot be affected by it.
Figure 2.
Hypothetical data set with potential outcomes. Shading indicates missing data. Y(0) represents the value of the outcome under the control condition and Y(1) represents the value of the outcome under the treatment condition. Z represents pre-treatment confounders.
Mediation Context
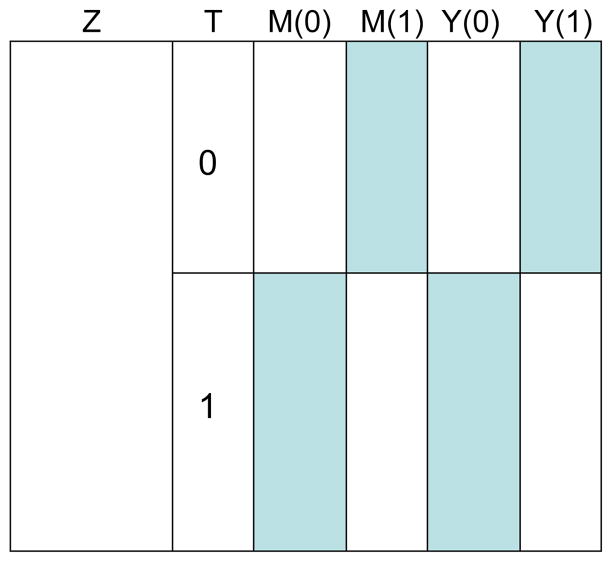
When a mediator is involved, the situation becomes more complicated because there are now potential outcomes for both the mediator and the outcome. Figure 3 shows that for individuals who do not receive the treatment, the potential outcomes for the mediator, Mi(1), and the outcome, Yi(1), under treatment are missing as indicated by the shading. Likewise, for individuals who receive the treatment, the potential outcomes for the mediator, Mi(0), and the outcome, Yi(0), are missing as indicated by the shading. Hence, there are many missing values because the mediator is re-expressed as a set of potential outcomes Mi(1), Mi(0) corresponding to the possible values of Ti = 1, Ti = 0. The outcome then becomes a function of both the treatment received and the mediator. Although much has been written about the potential outcomes framework in general (Little & Rubin, 2000; Rubin, 2005; Winship & Morgan, 1999) and in the context of mediation specifically (Gallop et al., 2009; Jo, 2008; Lynch, Kerry, Gallop, & Ten Have, 2008; Sobel, 2008; Ten Have et al., 2007), to our knowledge the use of propensity score methods for adjustment of confounders of the M to Y relationship has not yet been proposed.
Figure 3.
Hypothetical data set with potential outcomes for both the mediator and outcome. Shading indicates missing data. M(0) represents the value of the mediator under the control condition and M(1) represents the value of the mediator under the treatment condition.
Propensity Scores
We introduce propensity scores for estimating the causal effect of a non-randomized T on Y, which is the simplest case. We will then introduce propensity scores in the context of mediation. Rosenbaum and Rubin (1983b) defined the propensity score as the probability that an individual receives the treatment, πi = Pr(Ti = 1 | Zi) given measured confounders, Zi. Propensity scores balance covariates in the following sense: In a subset of the population with equal πi’s, treated and untreated participants have identical distributions for Zi. The balancing property of the propensity score has led to many propensity-based techniques for estimating ACE’s, including matching (Rosenbaum & Rubin, 1985), subclassification (Rosenbaum & Rubin, 1984) and inverse-propensity weighting (Robins, Rotnitzky, & Zhao, 1995). The πi’s are commonly obtained by logistic regression of Ti on Zi, but more flexible alternatives, including generalized boosted regression (McCaffrey, Ridgeway, & Morral, 2004), classification trees (Luellen, Shadish, & Clark, 2005) and robit regression (Liu, 2004; Kang & Schafer, 2007) have also been applied.
An advantage of propensity scores is that they reduce the large number of potential confounders into a single numerical summary. More importantly, a comparison of individuals in the control group with individuals in the intervention group who have the same (or nearly the same) propensity score is the same as a comparison of intervention conditions which were randomly assigned (Rosenbaum, 2002; Rosenbaum & Rubin, 1983b). In other words, they create a random assignment environment even in non-randomized experiments (assuming that the propensity model includes all confounders).
Recall that the primary criticism of the commonly applied classical approach for assessing mediation is that individuals are not randomly assigned to levels of the mediator and therefore, we cannot assume that there are no confounders which influence both the mediator and the outcome. We propose an approach, which we will refer to as Classical+Propensity Model (C+PM) in which the mediator is treated as any other non-randomly assigned treatment variable and propensity scores are used to help remove the selection bias that may result when individuals are not randomly assigned to levels of the mediator. The use of propensity scores assumes that all confounders are measured and included in the propensity model for predicting selection into the levels of the mediator. This assumption is untestable; however, sensitivity analysis (Rosenbaum & Rubin, 1983a) may be done to determine the degree to which results may be biased. The C+PM approach estimates the same effects (i.e. a, b, and c′) as the classical approach but adjusts for confounding by using propensity score methods. The rationale underlying the C+PM approach is that if we could incorporate a model for selection on the mediator, then we could obtain an unbiased estimate of the effect of M on Y (i.e. path b), which we could then multiply by the estimate from a regression of M on T (i.e. path a; recall T is randomized and so path a may be given a causal interpretation).
The fundamental problem in assessing mediation using the classical approach is that individuals are not randomly assigned to levels of the mediator and, therefore, the effect of the mediator on the outcome will be biased unless this selection is taken into account. The research questions we wish to address are 1) whether incorporating the propensities in the classical mediation model (i.e. C+PM) recovers unbiased estimates of the effect of the mediator on the outcome and therefore, unbiased estimates of the indirect effect of the treatment on the outcome, 2) whether 95% confidence intervals (CI) for the indirect effect perform well, and 3) whether including a subset of the confounders in the propensity model reduces bias and improves CI coverage compared to not including a propensity model (i.e. the classical approach). Next, we present a Monte Carlo simulation study to address these questions.
Method
The population model for the simulation study was one in which values of the treatment indicator, T, were generated from a random binomial distribution with p = .5. The mediator also had only two levels (M = 1, M = 0). The outcome was continuous. Receiving the treatment increased the odds of M = 1 by 2.72 (i.e. the logistic regression coefficient was equal to 1.0). The standardized regression coefficient of the effect of the mediator on the outcome (i.e. path b) was .7, .5, or .3. Therefore, the indirect effect was ab = .7, .5 or .3. The standardized regression coefficient for the direct effect (i.e. path c′) was .2. Four confounders, z1, z2, z3, and z4 were specified to have increased the odds of M = 1 by 1.35, 1.65, 2.01, and 2.46 (i.e. logistic regression coefficients of .3, .5, .7, and .9), respectively. These four confounders had regression coefficients for the effect on the outcome all equal to .4. The confounders were randomly generated from a multivariate normal distribution and were allowed to covary, as it is likely that in practice confounders are correlated. The correlations among all confounders were all equal to .3. The four confounders had varying influences on the mediator. For example, z1 has much less influence on M than z4, which has a larger influence that may occur if z4 was a measure of M at a previous time point. Values for M were generated from a random binomial distribution with p = 1/[1 + exp−(T +.3z1+.5z2+.7z3+.9z4)]. The outcome variable was generated with an error term randomly drawn from a normal distribution. Three outcome variables were generated corresponding to the three different values of path b as described above.
The simulation study included four sample size conditions (N = 100, 250, 500, and 1000) and three conditions for inclusion of confounders in the propensity model (no confounders, two confounders (z3 and z4), all four confounders). The model with only two confounders included the two with the largest influences on M. We used these two because we are assuming that an investigator would most certainly be aware of confounders in their substantive area that have influences as strong as these. For example, most investigators would include a measure of M from a previous time point as a confounder. For each condition, 1000 replications were obtained and the bias, relative bias, and MSE were computed. The Sobel standard errors (Sobel, 1982) for the indirect effect were computed. The propensity score model was estimated using logistic regression and the logit propensity score was then included as a covariate in the mediation analysis. There are numerous methods for incorporating the propensity scores in the mediation model (e.g. matching; Rosenbaum & Rubin, 1985) but this simulation study will focus on incorporating the logit propensity score as a covariate. Comprehensive simulation studies comparing different methods of estimating propensity scores have been presented elsewhere (Lee, Lessler, & Stuart, 2010). This is not the goal of this study. Instead, the goal is to demonstrate that propensity score methods can be used to adjust for confounding in the mediation context. In the simulation study, M is binary but it is not necessary that M be binary. Propensity score methods for continuous treatments have been developed (Hirano & Imbens, 2004; Imai & van Dyk, 2004) and would apply to a continuous M as well. Whether M is binary or continuous will not change the conclusions of the simulation study.
Results
Results are presented in Table 1 for path a, Table 2 for path b, Table 3 for path c, and Table 4 for the indirect effect, ab. Confidence interval coverage proportions for the indirect effect, ab, are presented in Table 5. As may be expected, variability of the estimates and mean squared error decreases as sample size increases. Thus, conclusions summarized below apply to all sample size conditions and sample size will not be discussed further.
Table 1.
Simulation results for path a, the effect of treatment on the mediator (population value = 1.0).
| All confounders | Half of confounders | No confounders | |
|---|---|---|---|
|
N = 100
| |||
| Mean | 1.068 | 0.997 | 0.709 |
| Bias | 0.068 | −0.003 | −0.291 |
| Rel. Bias | 0.068 | −0.003 | −0.291 |
| SD | 0.560 | 0.537 | 0.423 |
| MSE | 0.318 | 0.289 | 0.264 |
|
| |||
|
N = 250
| |||
| Mean | 1.035 | 0.976 | 0.689 |
| Bias | 0.035 | −0.024 | −0.311 |
| Rel. Bias | 0.035 | −0.024 | −0.311 |
| SD | 0.329 | 0.321 | 0.255 |
| MSE | 0.110 | 0.104 | 0.162 |
|
| |||
|
N = 500
| |||
| Mean | 0.998 | 0.939 | 0.664 |
| Bias | −0.002 | −0.061 | −0.336 |
| Rel. Bias | −0.002 | −0.061 | −0.336 |
| SD | 0.228 | 0.217 | 0.178 |
| MSE | 0.052 | 0.051 | 0.144 |
|
| |||
|
N = 1000
| |||
| Mean | 1.002 | 0.942 | 0.666 |
| Bias | 0.002 | −0.058 | −0.334 |
| Rel. Bias | 0.002 | −0.058 | −0.334 |
| SD | 0.172 | 0.166 | 0.137 |
| MSE | 0.029 | 0.031 | 0.130 |
Table 2.
Simulation results for path b, effect of the mediator on outcome (population values are .7. .5, and .3).
| All confounders | Half of confounders | No confounders | |||||||
|---|---|---|---|---|---|---|---|---|---|
| b = .7 | b = .5 | b = .3 | b = .7 | b = .5 | b = .3 | b = .7 | b = .5 | b = .3 | |
|
N = 100
| |||||||||
| Mean | 0.707 | 0.506 | 0.316 | 1.001 | 0.799 | 0.608 | 1.932 | 1.725 | 1.532 |
| Bias | 0.007 | 0.006 | 0.016 | 0.301 | 0.299 | 0.308 | 1.232 | 1.225 | 1.232 |
| Rel. Bias | 0.010 | 0.013 | 0.053 | 0.431 | 0.597 | 1.027 | 1.760 | 2.449 | 4.106 |
| SD | 0.264 | 0.256 | 0.260 | 0.285 | 0.282 | 0.289 | 0.275 | 0.271 | 0.280 |
| MSE | 0.070 | 0.066 | 0.068 | 0.172 | 0.169 | 0.178 | 1.594 | 1.573 | 1.596 |
|
| |||||||||
|
N = 250
| |||||||||
| Mean | 0.703 | 0.499 | 0.300 | 1.000 | 0.796 | 0.596 | 1.921 | 1.721 | 1.520 |
| Bias | 0.003 | −0.001 | 0.000 | 0.300 | 0.296 | 0.296 | 1.221 | 1.221 | 1.220 |
| Rel. Bias | 0.005 | −0.003 | 0.000 | 0.429 | 0.592 | 0.986 | 1.744 | 2.443 | 4.066 |
| SD | 0.156 | 0.157 | 0.156 | 0.177 | 0.170 | 0.176 | 0.181 | 0.171 | 0.170 |
| MSE | 0.024 | 0.025 | 0.024 | 0.121 | 0.117 | 0.118 | 1.523 | 1.521 | 1.516 |
|
| |||||||||
|
N = 500
| |||||||||
| Mean | 0.702 | 0.501 | 0.297 | 1.001 | 0.798 | 0.596 | 1.921 | 1.724 | 1.518 |
| Bias | 0.002 | 0.001 | −0.003 | 0.301 | 0.298 | 0.296 | 1.221 | 1.224 | 1.218 |
| Rel. Bias | 0.003 | 0.001 | −0.012 | 0.431 | 0.597 | 0.986 | 1.745 | 2.447 | 4.061 |
| SD | 0.111 | 0.110 | 0.119 | 0.123 | 0.122 | 0.128 | 0.126 | 0.126 | 0.128 |
| MSE | 0.012 | 0.012 | 0.014 | 0.106 | 0.104 | 0.104 | 1.507 | 1.513 | 1.501 |
|
| |||||||||
|
N = 1000
| |||||||||
| Mean | 0.700 | 0.503 | 0.306 | 1.001 | 0.802 | 0.606 | 1.926 | 1.725 | 1.530 |
| Bias | 0.000 | 0.003 | 0.006 | 0.301 | 0.302 | 0.306 | 1.226 | 1.225 | 1.230 |
| Rel. Bias | 0.001 | 0.005 | 0.021 | 0.430 | 0.603 | 1.018 | 1.752 | 2.451 | 4.099 |
| SD | 0.077 | 0.079 | 0.078 | 0.085 | 0.090 | 0.089 | 0.085 | 0.089 | 0.088 |
| MSE | 0.006 | 0.006 | 0.006 | 0.098 | 0.099 | 0.101 | 1.511 | 1.509 | 1.520 |
Table 3.
Simulation results for path c′, the direct effect of treatment on outcome (population value = .2).
| All confounders | Half of confounders | No confounders | |||||||
|---|---|---|---|---|---|---|---|---|---|
| b = .7 | b = .5 | b = .3 | b = .7 | b = .5 | b = .3 | b = .7 | b = .5 | b = .3 | |
|
N = 100
| |||||||||
| Mean | 0.171 | 0.190 | 0.190 | 0.134 | 0.153 | 0.138 | 0.001 | 0.020 | 0.006 |
| Bias | −0.029 | −0.010 | −0.010 | −0.066 | −0.047 | −0.062 | −0.199 | −0.180 | −0.194 |
| Rel. Bias | −0.143 | −0.048 | −0.048 | −0.332 | −0.236 | −0.309 | −0.997 | −0.899 | −0.969 |
| SD | 0.216 | 0.221 | 0.221 | 0.231 | 0.236 | 0.242 | 0.270 | 0.273 | 0.290 |
| MSE | 0.048 | 0.049 | 0.049 | 0.058 | 0.058 | 0.062 | 0.112 | 0.107 | 0.121 |
|
| |||||||||
|
N = 250
| |||||||||
| Mean | 0.197 | 0.186 | 0.186 | 0.156 | 0.145 | 0.146 | 0.009 | −0.003 | −0.002 |
| Bias | −0.003 | −0.014 | −0.014 | −0.044 | −0.055 | −0.054 | −0.191 | −0.203 | −0.202 |
| Rel. Bias | −0.015 | −0.070 | −0.070 | −0.219 | −0.275 | −0.269 | −0.956 | −1.017 | −1.008 |
| SD | 0.131 | 0.132 | 0.132 | 0.147 | 0.146 | 0.146 | 0.174 | 0.172 | 0.177 |
| MSE | 0.017 | 0.018 | 0.018 | 0.024 | 0.024 | 0.024 | 0.067 | 0.071 | 0.072 |
|
| |||||||||
|
N = 500
| |||||||||
| Mean | 0.192 | 0.188 | 0.188 | 0.146 | 0.143 | 0.150 | 0.000 | −0.004 | 0.003 |
| Bias | −0.008 | −0.012 | −0.012 | −0.054 | −0.057 | −0.050 | −0.200 | −0.204 | −0.197 |
| Rel. Bias | −0.040 | −0.058 | −0.058 | −0.270 | −0.285 | −0.249 | −1.002 | −1.022 | −0.983 |
| SD | 0.093 | 0.096 | 0.096 | 0.103 | 0.106 | 0.104 | 0.123 | 0.122 | 0.119 |
| MSE | 0.009 | 0.009 | 0.009 | 0.013 | 0.014 | 0.013 | 0.055 | 0.057 | 0.053 |
|
| |||||||||
|
N = 1000
| |||||||||
| Mean | 0.199 | 0.197 | 0.197 | 0.152 | 0.150 | 0.149 | 0.003 | 0.001 | 0.000 |
| Bias | −0.001 | −0.003 | −0.003 | −0.048 | −0.050 | −0.051 | −0.197 | −0.199 | −0.200 |
| Rel. Bias | −0.005 | −0.016 | −0.016 | −0.240 | −0.251 | −0.255 | −0.987 | −0.996 | −1.001 |
| SD | 0.067 | 0.068 | 0.068 | 0.075 | 0.075 | 0.074 | 0.091 | 0.088 | 0.089 |
| MSE | 0.005 | 0.005 | 0.005 | 0.008 | 0.008 | 0.008 | 0.047 | 0.047 | 0.048 |
Table 4.
Simulation results for path ab, the indirect effect of treatment on outcome (population values are .7, .5, and .3).
| All confounders | Half of confounders | No confounders | |||||||
|---|---|---|---|---|---|---|---|---|---|
| b = .7 | b = .5 | b = .3 | b = .7 | b = .5 | b = .3 | b = .7 | b = .5 | b = .3 | |
|
N = 100
| |||||||||
| Mean | 0.760 | 0.535 | 0.340 | 1.001 | 0.789 | 0.604 | 1.369 | 1.223 | 1.082 |
| Bias | 0.060 | 0.035 | 0.040 | 0.301 | 0.289 | 0.304 | 0.669 | 0.723 | 0.782 |
| Rel. Bias | 0.086 | 0.069 | 0.133 | 0.430 | 0.579 | 1.013 | 0.956 | 1.447 | 2.606 |
| SD | 0.510 | 0.424 | 0.378 | 0.620 | 0.534 | 0.463 | 0.844 | 0.769 | 0.675 |
| MSE | 0.264 | 0.181 | 0.145 | 0.475 | 0.369 | 0.307 | 1.159 | 1.114 | 1.066 |
|
| |||||||||
|
N = 250
| |||||||||
| Mean | 0.727 | 0.516 | 0.311 | 0.973 | 0.775 | 0.579 | 1.324 | 1.185 | 1.047 |
| Bias | 0.027 | 0.016 | 0.011 | 0.273 | 0.275 | 0.279 | 0.624 | 0.685 | 0.747 |
| Rel. Bias | 0.038 | 0.031 | 0.037 | 0.390 | 0.549 | 0.931 | 0.891 | 1.371 | 2.492 |
| SD | 0.283 | 0.235 | 0.198 | 0.362 | 0.306 | 0.258 | 0.507 | 0.453 | 0.406 |
| MSE | 0.081 | 0.056 | 0.039 | 0.205 | 0.169 | 0.144 | 0.646 | 0.675 | 0.723 |
|
| |||||||||
|
N = 500
| |||||||||
| Mean | 0.701 | 0.499 | 0.296 | 0.940 | 0.748 | 0.559 | 1.277 | 1.145 | 1.009 |
| Bias | 0.001 | −0.001 | −0.004 | 0.240 | 0.248 | 0.259 | 0.577 | 0.645 | 0.709 |
| Rel. Bias | 0.001 | −0.002 | −0.014 | 0.343 | 0.496 | 0.864 | 0.824 | 1.290 | 2.364 |
| SD | 0.196 | 0.158 | 0.140 | 0.246 | 0.203 | 0.178 | 0.353 | 0.316 | 0.284 |
| MSE | 0.038 | 0.025 | 0.020 | 0.118 | 0.103 | 0.099 | 0.458 | 0.516 | 0.584 |
|
| |||||||||
|
N = 1000
| |||||||||
| Mean | 0.702 | 0.504 | 0.307 | 0.943 | 0.755 | 0.570 | 1.284 | 1.149 | 1.019 |
| Bias | 0.002 | 0.004 | 0.007 | 0.243 | 0.255 | 0.270 | 0.584 | 0.649 | 0.719 |
| Rel. Bias | 0.003 | 0.008 | 0.023 | 0.348 | 0.511 | 0.901 | 0.834 | 1.299 | 2.396 |
| SD | 0.145 | 0.119 | 0.094 | 0.186 | 0.159 | 0.129 | 0.271 | 0.242 | 0.216 |
| MSE | 0.021 | 0.014 | 0.009 | 0.094 | 0.091 | 0.090 | 0.414 | 0.480 | 0.563 |
Table 5.
95% Confidence interval coverage proportions for path ab.
| All confounders | Half of confounders | No confounders | |||||||
|---|---|---|---|---|---|---|---|---|---|
| N | b = .7 | b = .5 | b = .3 | b = .7 | b = .5 | b = .3 | b = .7 | b = .5 | b = .3 |
| 100 | 0.937 | 0.925 | 0.929 | 0.966 | 0.969 | 0.971 | 1.000 | 1.000 | 1.000 |
| 250 | 0.947 | 0.945 | 0.946 | 0.941 | 0.939 | 0.914 | 1.000 | 1.000 | 1.000 |
| 500 | 0.940 | 0.944 | 0.924 | 0.893 | 0.872 | 0.786 | 1.000 | 1.000 | 1.000 |
| 1000 | 0.943 | 0.935 | 0.946 | 0.773 | 0.650 | 0.434 | 1.000 | 1.000 | 1.000 |
We are primarily interested in the estimates for path b and for the indirect effect, ab. Tables 2 and 4 show that when all confounders are included in the propensity model, unbiased estimates are obtained for both b and ab, regardless of the size of b. When no confounders are included (i.e. the classical approach), the estimates are biased. When some but not all of the confounders are included in the propensity model, then the estimates are biased although not as severely as when the propensity model is not included. It is also important to note that not including the propensity model resulted in substantial underestimation of path a (see Table 1) and path c′ (see Table 3). In fact, c′ was estimated to be 0 using the classical approach with no adjustment for confounding; therefore, a researcher would conclude that the effect of the treatment on the outcome is fully mediated by M. On the other hand, inclusion of some but not all of the confounders in the propensity model did not result in substantial bias for the estimates of a and c′.
Confidence interval coverage for ab was excellent (range of .92 to .95) when all confounders were included in the propensity model (see Table 5) regardless of sample size or the size of the population effect of b. However, when half of the confounders were included in the propensity model, confidence interval coverage was acceptable for smaller sample sizes and larger values of the population effect of b but coverage was unacceptable and deteriorated as sample size increased and the size of the population effect of b decreased. The acceptable coverage with smaller sample sizes was likely due to the confidence intervals becoming too wide to be useful. When a propensity model was not included at all, coverage was unacceptably high for all sample size conditions and sizes of the population effect of b.
To summarize, the results showed that if all confounders are included in the propensity model, then an unbiased estimate of the effect of the mediator on the outcome is obtained. If the propensity score model is not used (i.e. the classical approach) then the estimates of the effect of the mediator on the outcome is severely biased. If some, but not all, of the confounders are included in the propensity model, then the estimates are biased although not as severely as when the propensity model is not included. In some cases (e.g. path b), the effect is overestimated and in other cases (e.g. path a), the effect is underestimated when the confounders are not included. The size of the effect of path b does not seem to influence the results.
Discussion
If all the confounders are included in the propensity model, then all estimates in the mediation model studied here are unbiased. If some confounders are omitted from the propensity model, then the estimates for path b and ab were biased although not as severely as the classical approach. If applied researchers included a propensity model for M and incorporated the resulting estimated propensity scores into the classical approach (i.e. the C+PM approach), it would be an improvement over the current classical approach. Another option is to include the confounders in the classical approach directly, for example via a regression model, although it is often the case that there are many potential confounders and they are not particularly of substantive interest. Propensity scores are a means of summarizing a large number of confounders. It should be noted that just like the classical approach or using the classical approach with a regression adjustment for confounders, the use of propensity scores assumes that there are no unmeasured confounders, since only measured confounders may be included in the propensity model. Nevertheless, incorporating propensity scores represents a substantial improvement over methods such as the classical approach which generally include very few, if any, potential confounders. Note that the primary assumption in C+PM is that there are no unmeasured confounders of the mediator and outcome. Thus, if the researcher had measured all possible confounders in the study and included them in the analysis, this assumption would be met. Of course, practically, this would be nearly impossible to implement because the researcher is most likely not aware of all the confounders and therefore has not measured them. In addition, it is impossible to know whether one has included all possible confounders, so it is impossible to know whether the assumption has been met. However, as more confounders are included, the assumption becomes more plausible and estimates are less biased. The general recommendation is to include all variables that are thought to be confounders of the relationship between M and Y. The few variables, such as gender or race, typically included in studies using the classical approach probably do not include all the confounders that result in the selection bias present in M. Therefore, it is advisable to include as many potential confounders as is practically possible.
Even if the researcher had measured all possible confounders and could include them in the analysis, there are several disadvantages to doing this. First, there is a practical limit on the number of confounders that may be included depending on the sample size. Second, inclusion of the confounders in, for example, an SEM assumes that the confounders are linearly related to the intervention, mediator, and outcome. The researcher can partly get around this assumption by including all possible interactions among the confounders and/or including quadratic terms, but then there will be even more variables to include in the analysis. Thus, it is usually impractical to include enough potential confounders to come close to meeting this assumption.
Every method makes assumptions, some of which are not testable, and researchers should make clear the assumptions made. The classical approach used to test mediation usually does not include confounders, which is essentially the equivalent of using a t-test to test non-randomized treatment effects in the non-mediation context. No researcher would do this; rather they would include confounders as in an ANCOVA. A better approach, for the reasons give above, is to use propensity score methods to adjust for confounding. The main point of this article is to convince researchers to adjust for confounders when assessing mediation, specifically by using propensity models.
Limitations and Future Directions
In the simulation study, we added the logit propensity as a covariate in the models. As mentioned previously, there are other methods for incorporating the propensity scores such as matching, weighting, or subclassification. In addition, there are methods other than logistic regression for estimating the propensities. We plan to investigate these other methods in the mediation context in future simulation studies. The simulation presented here is small; we plan to include many more confounders and non-linear relationships between the confounders and M and Y in future studies. The present simulations also did not address whether the C+PM method proposed here outperforms the more complicated methods, such as principal stratification (Frangakis & Rubin, 2002), that have been proposed for mediation (Jo, 2008). However, we are currently addressing this issue. Nevertheless, this simulation shows that as long as all confounders are measured and included in the model and the additivity assumption holds (i.e. no interaction between T and M), then unbiased estimates can be obtained by simply including a propensity model for M to model the selection bias and proceeding as usual. It is important to note that any confounders included in the propensity model should measured prior to T and M and therefore cannot be affected by T or M. In other words, as with propensity score methods in the non-mediation context, propensity score models should not include post-treatment or time-varying confounders. Finally, we used the Sobel standard errors for the indirect effect because they are less computationally intensive than bootstrap standard errors but bootstrap standard errors may be more accurate than the Sobel standard errors (e.g. Shrout & Bolger, 2002).
In conclusion, we recommend including confounders of the mediator to outcome pathway when assessing mediation. One easy way to do this is to use a propensity model for selection into levels of the mediator as proposed above.
Acknowledgments
Preparation of this article was supported by NIDA Center Grant P50 DA100075 and NIDA R03 DA026543-01. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute on Drug Abuse (NIDA) or the National Institutes of Health (NIH).
References
- Baron RM, Kenny DA. The moderator-mediator variable distinction in social psychological research: Conceptual, strategic and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Cole DA, Maxwell SE. Testing mediation models with longitudinal data: Questions and tips in the use of structural equation modeling. Journal of Abnormal Psychology. 2003;112:558–577. doi: 10.1037/0021-843X.112.4.558. [DOI] [PubMed] [Google Scholar]
- Collins LM, Graham JW, Flaherty B. An alternative framework for defining mediation. Multivariate Behavioral Research. 1998;33:295–312. doi: 10.1207/s15327906mbr3302_5. [DOI] [PubMed] [Google Scholar]
- Frangakis CE, Rubin DB. Principal stratification in causal inference. Biometrics. 2002;58:20–29. doi: 10.1111/j.0006-341x.2002.00021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallop R, Small DS, Lin JY, Elliot MR, Joffe M, Ten Have TR. Mediation analysis with principal stratification. Statistics in Medicine. 2009;28:1108–1130. doi: 10.1002/sim.3533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirano K, Imbens GW. The propensity score with continuous treatments. In: Gelman A, Meng X-L, editors. Applied bayesian modeling and causal inference from incomplete-data perspectives. Hoboken, NJ: John Wiley & Sons; 2004. [Google Scholar]
- Holland PW. Statistics and causal inference. Journal of the American Statistical Association. 1986;81:945–970. [Google Scholar]
- Imai K, van Dyk DA. Causal inference with general treatment regimes: Generalizing the propensity score. Journal of the American Statistical Association. 2004;99:854–866. [Google Scholar]
- Jo B. Causal inference in randomized experiments with mediational processes. Psychological Methods. 2008;13:314–336. doi: 10.1037/a0014207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang J, Schafer JL. Demystifying double robustness: A comparison of alternative strategies for estimating a population mean from incomplete data. Statistical Science. 2007;22(4):523–539. doi: 10.1214/07-STS227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee BK, Lessler J, Stuart EA. Improving propensity score weighting using machine learning. Statistics in Medicine. 2010;29:337–346. doi: 10.1002/sim.3782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little RJA, Rubin DB. Causal effects in clinical and epidemiological studies via potential outcomes: Concepts and analytical approaches. Annual Review of Public Health. 2000;21:121–145. doi: 10.1146/annurev.publhealth.21.1.121. [DOI] [PubMed] [Google Scholar]
- Liu C. Robit regression: A simple robust alternative to logistic and probit regression. In: Gelman A, Meng X-L, editors. Applied bayesian modeling and causal inference from incomplete-data perspectives. Hoboken, NJ: John Wiley & Sons; 2004. [Google Scholar]
- Luellen JK, Shadish WR, Clark MH. Propensity scores: An introduction and experimental test. Evaluation Review. 2005;29:530–558. doi: 10.1177/0193841X05275596. [DOI] [PubMed] [Google Scholar]
- Lynch KG, Kerry M, Gallop R, Ten Have TR. Causal mediation analyses for randomized trials. Health Services Outcomes Research Methodology. 2008;8:57–76. doi: 10.1007/s10742-008-0028-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Fairchild AJ, Fritz MS. Mediation analysis. Annual Review of Psychology. 2007;58:593–614. doi: 10.1146/annurev.psych.58.110405.085542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test the significance of the intervening variable effect. Psychological Methods. 2002;7:83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Taborga MP, Morgan-Lopez AA. Mediation designs for tobacco prevention research. Drug and Alcohol Dependence. 2002;68:S69–S83. doi: 10.1016/s0376-8716(02)00216-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCaffrey DF, Ridgeway G, Morral AR. Propensity score estimation with boosted regression for evaluating causal effects in observational studies. Psychological Methods. 2004;9:403–425. doi: 10.1037/1082-989X.9.4.403. [DOI] [PubMed] [Google Scholar]
- Robins JM, Greenland S. Identifiability and exchangeability of direct and indirect effects. Epidemiology. 1992;3:143–155. doi: 10.1097/00001648-199203000-00013. [DOI] [PubMed] [Google Scholar]
- Robins JM, Rotnitzky A, Zhao LP. Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. Journal of the American Statistical Association. 1995;90:106–121. [Google Scholar]
- Rosenbaum PR. The consequences of adjustment for a concomitant variable that has been affected by the treatment. Journal of the Royal Statistical Society. 1984;147:656–666. [Google Scholar]
- Rosenbaum PR. Observational studies. 2. New York: Springer; 2002. [Google Scholar]
- Rosenbaum PR, Rubin DB. Assessing sensitivity to an unobserved covariate in an observational study with binary outcome. Journal of the Royal Statistical Society. 1983a;45:212–218. [Google Scholar]
- Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983b;70:41–55. [Google Scholar]
- Rosenbaum PR, Rubin DB. Reducing bias in observational studies using subclassification on the propensity score. Journal of the American Statistical Association. 1984;79:516–524. [Google Scholar]
- Rosenbaum PR, Rubin DB. Constructing a control group using multivariate matched sampling methods that incorporate the propensity score. American Statistician. 1985;39:33–38. [Google Scholar]
- Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
- Rubin DB. Direct and indirect causal effects via potential outcomes. Scandinavian Journal of Statistics. 2004;31:161–170. [Google Scholar]
- Rubin DB. Causal inference using potential outcomes: Design, modeling, decisions. Journal of the American Statistical Association. 2005;100:322–331. [Google Scholar]
- Schafer JL, Kang J. Average causal effects from non-randomized studies: A practical guide and simulated example. Psychological Methods. 2008;13(4):279–313. doi: 10.1037/a0014268. [DOI] [PubMed] [Google Scholar]
- Shrout PE, Bolger N. Mediation in experimental and nonexperimental studies: New procedures and recommendations. Psychological Methods. 2002;7:422–445. [PubMed] [Google Scholar]
- Sobel ME. Asymptotic intervals for indirect effects in structural equations models. In: Leinhart S, editor. Sociological methodology. San Francisco: Jossey-Bass; 1982. pp. 290–312. [Google Scholar]
- Sobel ME. Identification of causal parameters in randomized studies with mediating variables. Journal of Educational and Behavioral Statistics. 2008;33:230–251. [Google Scholar]
- Ten Have TR, Joffe M, Lynch K, Maisto S, Brown G, Beck A. Causal mediation analysis with rank-preserving models. Biometrics. 2007;63:926–934. doi: 10.1111/j.1541-0420.2007.00766.x. [DOI] [PubMed] [Google Scholar]
- VanderWeele T. The use of propensity score methods in psychiatric research. International Journal of Methods in Psychiatric Research. 2006;15:95–103. doi: 10.1002/mpr.183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winship C, Morgan SL. The estimation of causal effects from observational data. Annual Review of Sociology. 1999;25:659–706. [Google Scholar]